Optical Analysis of Perovskite III-V Nanowires Interpenetrated Tandem Solar Cells
Abstract
:1. Introduction
2. Materials and Methods
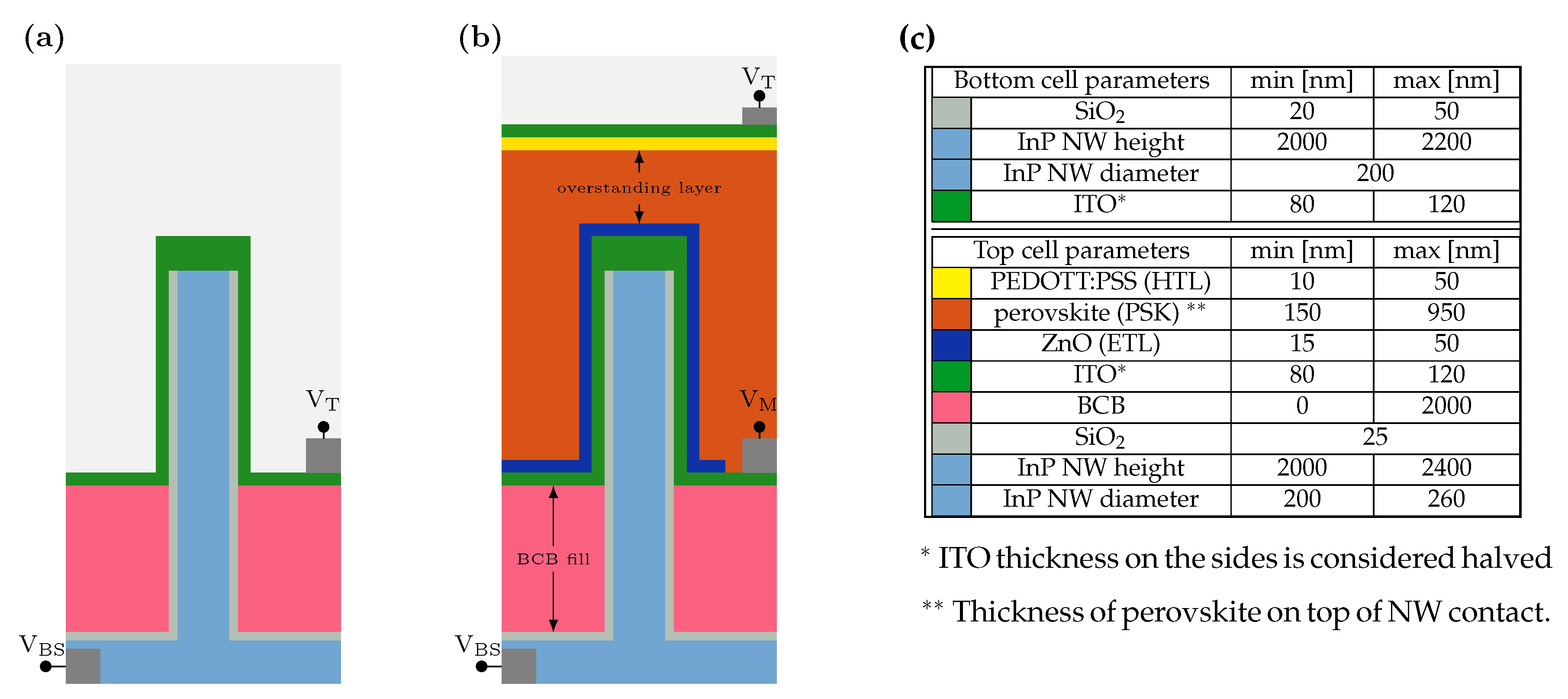
2.1. Layout and Materials
2.2. Numerical Analysis
3. Results and Discussion
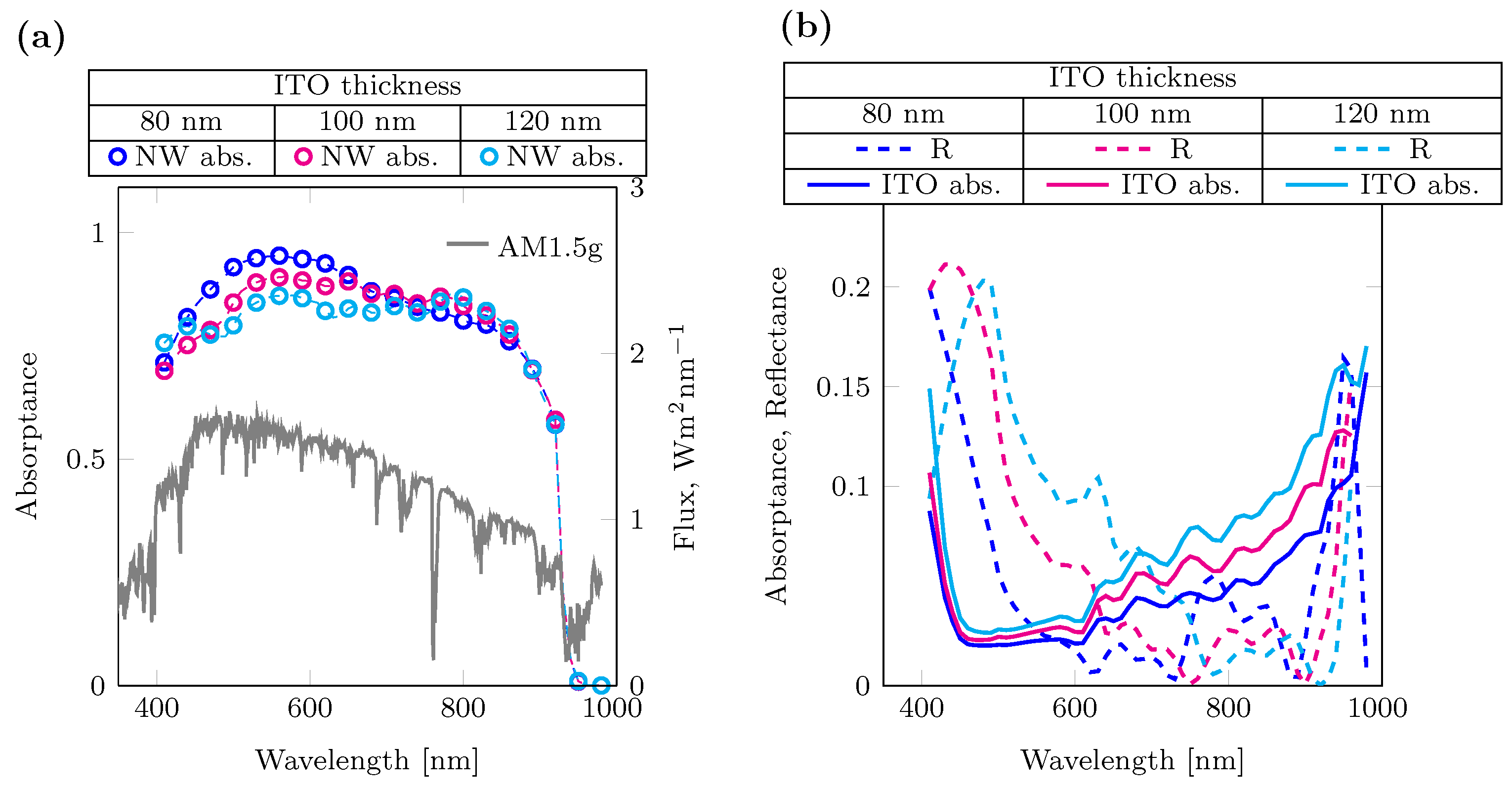
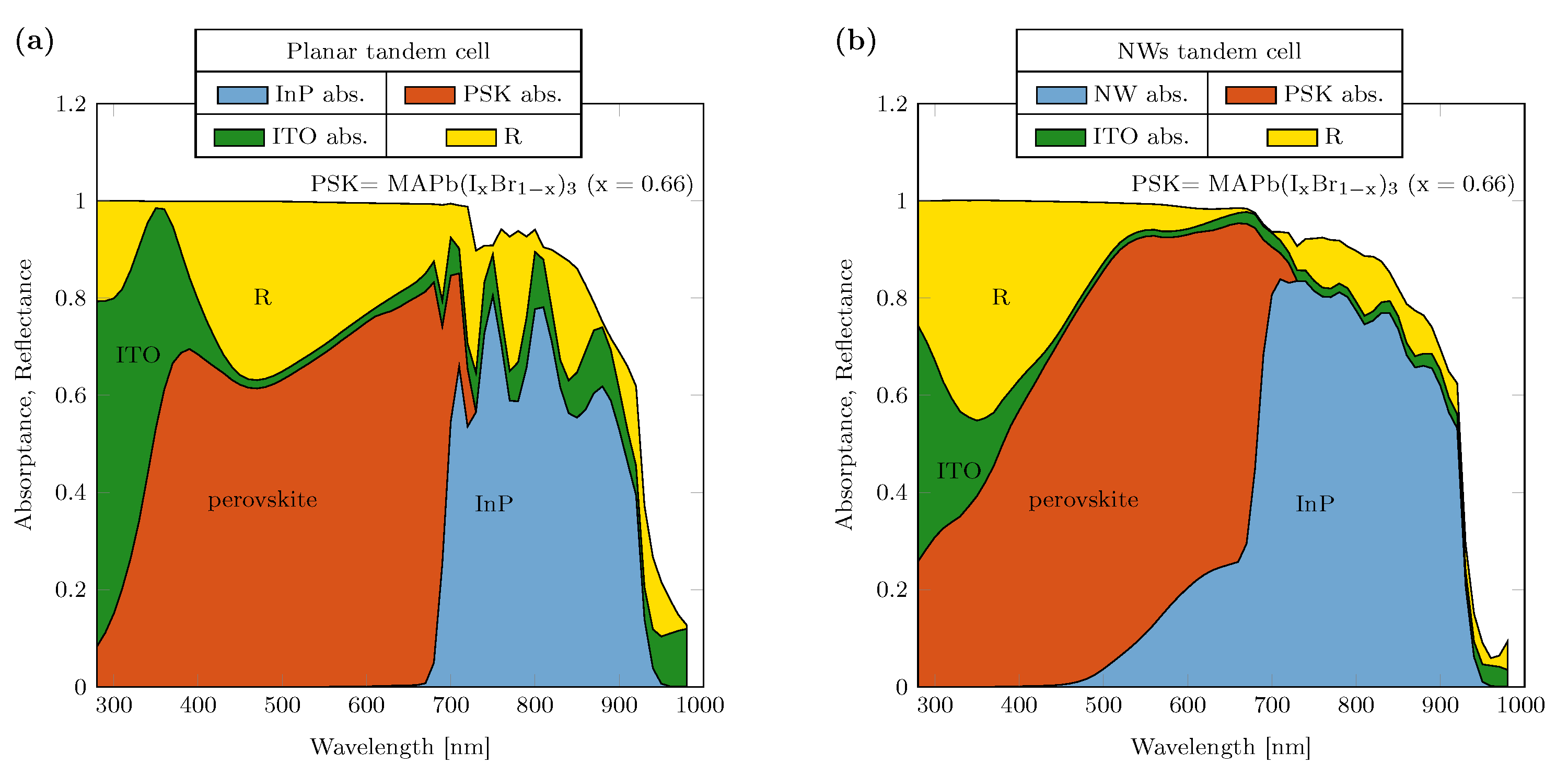
3.1. Bottom Cell
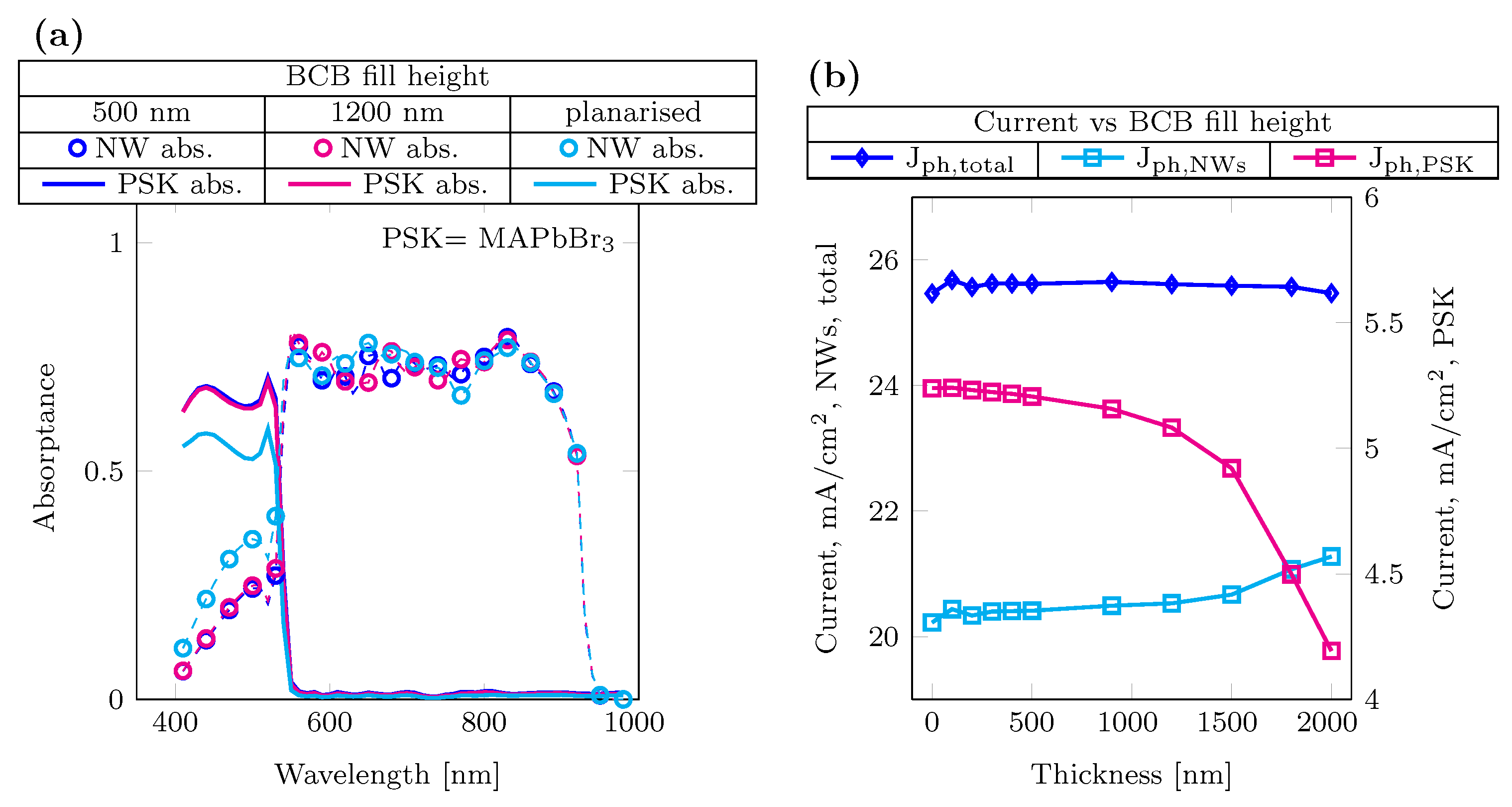
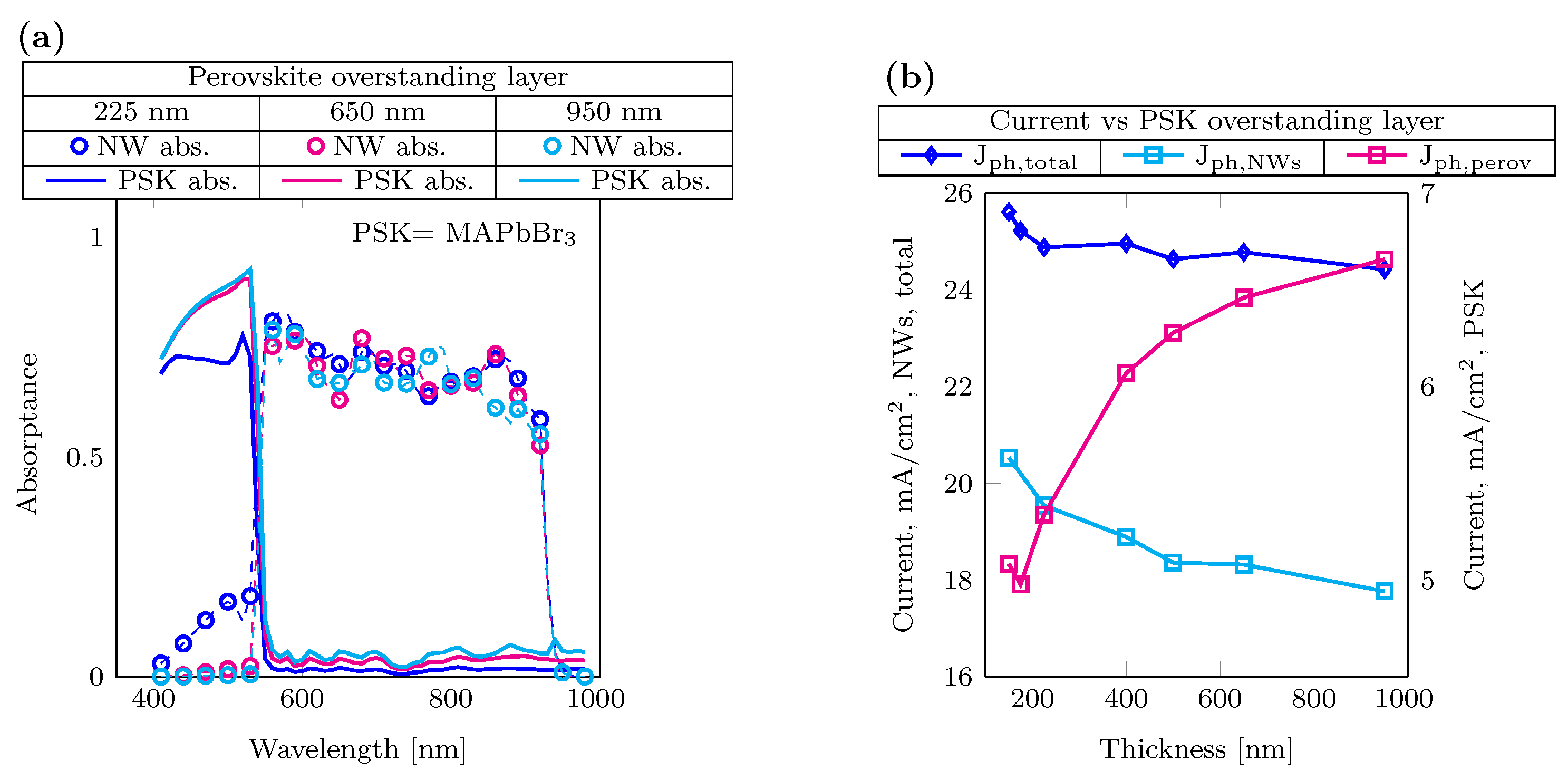
3.2. 3T Tandem Solar Cell
3.3. 2T Tandem Solar Cell
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, Z.; Fan, S.; Cui, Y. Nanostructured photon management for high performance solar cells. Mater. Sci. Eng. R Rep. 2010, 70, 330–340. [Google Scholar] [CrossRef]
- Hu, L.; Chen, G. Analysis of Optical Absorption in Silicon Nanowire Arrays for Photovoltaic Applications. Nano Lett. 2007, 7, 3249–3252. [Google Scholar] [CrossRef] [PubMed]
- Anttu, N. Absorption of light in a single vertical nanowire and a nanowire array. Nanotechnology 2019, 30, 104004. [Google Scholar] [CrossRef] [PubMed]
- Anttu, N.; Xu, H.Q. Efficient light management in vertical nanowire arrays for photovoltaics. Opt. Express 2013, 21, A558–A575. [Google Scholar] [CrossRef] [PubMed]
- Hrachowina, L.; Anttu, N.; Borgström, M.T. Wafer-Scale Synthesis and Optical Characterization of InP Nanowire Arrays for Solar Cells. Nano Lett. 2021, 21, 7347–7353. [Google Scholar] [CrossRef] [PubMed]
- van Dam, D.; van Hoof, N.J.J.; Cui, Y.; van Veldhoven, P.J.; Bakkers, E.P.A.M.; Gómez Rivas, J.; Haverkort, J.E.M. High-Efficiency Nanowire Solar Cells with Omnidirectionally Enhanced Absorption Due to Self-Aligned Indium–Tin–Oxide Mie Scatterers. ACS Nano 2016, 10, 11414–11419. [Google Scholar] [CrossRef] [PubMed]
- Wallentin, J.; Anttu, N.; Asoli, D.; Huffman, M.; Åberg, I.; Magnusson, M.H.; Siefer, G.; Fuss-Kailuweit, P.; Dimroth, F.; Witzigmann, B.; et al. InP Nanowire Array Solar Cells Achieving 13.8% Efficiency by Exceeding the Ray Optics Limit. Science 2013, 339, 1057–1060. [Google Scholar] [CrossRef] [PubMed]
- Caroff, P.; Messing, M.E.; Borg, B.M.; Dick, K.A.; Deppert, K.; Wernersson, L.E. InSb heterostructure nanowires: MOVPE growth under extreme lattice mismatch. Nanotechnology 2009, 20, 495606. [Google Scholar] [CrossRef]
- Cahen, D.; Kronik, L.; Hodes, G. Are Defects in Lead-Halide Perovskites Healed, Tolerated, or Both? Acs Energy Lett. 2021, 6, 4108–4114. [Google Scholar] [CrossRef]
- Unger, E.L.; Kegelmann, L.; Suchan, K.; Sörell, D.; Korte, L.; Albrecht, S. Roadmap and roadblocks for the band gap tunability of metal halide perovskites. J. Mater. Chem. A 2017, 5, 11401–11409. [Google Scholar] [CrossRef]
- Noh, J.H.; Im, S.H.; Heo, J.H.; Mandal, T.N.; Seok, S.I. Chemical Management for Colorful, Efficient, and Stable Inorganic–Organic Hybrid Nanostructured Solar Cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Ho-Baillie, A.; Snaith, H.J. The emergence of perovskite solar cells. Nat. Photon. 2014, 8, 506–514. [Google Scholar] [CrossRef]
- Wang, R.; Mujahid, M.; Duan, Y.; Wang, Z.K.; Xue, J.; Yang, Y. A Review of Perovskites Solar Cell Stability. Adv. Funct. Mater. 2019, 29, 1808843. [Google Scholar] [CrossRef]
- Unger, E.L.; Hoke, E.T.; Bailie, C.D.; Nguyen, W.H.; Bowring, A.R.; Heumüller, T.; Christoforo, M.G.; McGehee, M.D. Hysteresis and transient behavior in current–voltage measurements of hybrid-perovskite absorber solar cells. Energy Environ. Sci. 2014, 7, 3690–3698. [Google Scholar] [CrossRef]
- Löper, P.; Moon, S.J.; Martín de Nicolas, S.; Niesen, B.; Ledinsky, M.; Nicolay, S.; Bailat, J.; Yum, J.H.; De Wolf, S.; Ballif, C. Organic–inorganic halide perovskite/crystalline silicon four-terminal tandem solar cells. Phys. Chem. Chem. Phys. 2015, 17, 1619–1629. [Google Scholar] [CrossRef]
- Futscher, M.H.; Ehrler, B. Modeling the Performance Limitations and Prospects of Perovskite/Si Tandem Solar Cells under Realistic Operating Conditions. Acs Energy Lett. 2017, 2, 2089–2095. [Google Scholar] [CrossRef]
- Sahli, F.; Werner, J.; Kamino, B.A.; Bräuninger, M.; Monnard, R.; Paviet-Salomon, B.; Barraud, L.; Ding, L.; Diaz Leon, J.J.; Sacchetto, D.; et al. Fully textured monolithic perovskite/silicon tandem solar cells with 25.2 power conversion efficiency. Nat. Mater. 2018, 17, 820–826. [Google Scholar] [CrossRef]
- Jäger, K.; Korte, L.; Rech, B.; Albrecht, S. Numerical optical optimization of monolithic planar perovskite-silicon tandem solar cells with regular and inverted device architectures. Opt. Express 2017, 25, A473–A482. [Google Scholar] [CrossRef] [PubMed]
- Al-Ashouri, A.; Köhnen, E.; Li, B.; Magomedov, A.; Hempel, H.; Caprioglio, P.; Márquez, J.A.; Vilches, A.B.M.; Kasparavicius, E.; Smith, J.A.; et al. Monolithic perovskite/silicon tandem solar cell with >29% efficiency by enhanced hole extraction. Science 2020, 370, 1300–1309. [Google Scholar] [CrossRef] [PubMed]
- Wagner, P.; Tockhorn, P.; Hall, S.; Albrecht, S.; Korte, L. Performance of Monolithic Two- and Three-Terminal Perovskite/Silicon Tandem Solar Cells Under Varying Illumination Conditions. Solar RRL 2023, 7, 2200954. [Google Scholar] [CrossRef]
- Tayagaki, T.; Makita, K.; Tachibana, T.; Mizuno, H.; Oshima, R.; Takato, H.; Sugaya, T. Impact of loading topology and current mismatch on current–voltage curves of three-terminal tandem solar cells with interdigitated back contacts. Sol. Energy Mater. Sol. Cells 2021, 221, 110901. [Google Scholar] [CrossRef]
- Raja, W.; Schmid, M.; Toma, A.; Wang, H.; Alabastri, A.; Proietti Zaccaria, R. Perovskite Nanopillar Array Based Tandem Solar Cell. Acs Photon. 2017, 4, 2025–2035. [Google Scholar] [CrossRef]
- Jäger, K.; Albrecht, S. Perovskite-Based Tandem Solar Cells. In Hybrid Perovskite Solar Cells; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 17; pp. 463–508. [Google Scholar] [CrossRef]
- Näsström, H.; Shargaieva, O.; Becker, P.; Mathies, F.; Zizak, I.; Schröder, V.R.F.; List-Kratochvil, E.J.W.; Unold, T.; Unger, E. Combinatorial inkjet printing for compositional tuning of metal-halide perovskite thin films. J. Mater. Chem. A 2022, 10, 4906–4914. [Google Scholar] [CrossRef]
- Lee, W.; Lee, J.; Yun, H.; Kim, J.; Park, J.; Choi, C.; Kim, D.C.; Seo, H.; Lee, H.; Yu, J.W.; et al. High-Resolution Spin-on-Patterning of Perovskite Thin Films for a Multiplexed Image Sensor Array. Adv. Mater. 2017, 29, 1702902. [Google Scholar] [CrossRef] [PubMed]
- Sakai, S.; Umeno, M. Theoretical analysis of new wavelength-division solar cells. J. Appl. Phys. 1980, 51, 5018–5024. [Google Scholar] [CrossRef]
- Warren, E.; Rienaecker, M.; Schnabel, M.; Deceglie, M.; Peibst, R.; Tamboli, A.; Stradins, P. Operating principles of three-terminal solar cells. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2648–2650. [Google Scholar] [CrossRef]
- Warren, E.L.; McMahon, W.E.; Rienäcker, M.; VanSant, K.T.; Whitehead, R.C.; Peibst, R.; Tamboli, A.C. A Taxonomy for Three-Terminal Tandem Solar Cells. Acs Energy Lett. 2020, 5, 1233–1242. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Lemarchand, F.; Lequime, M. Refractive index determination of SiO2 layer in the UV/Vis/NIR range: Spectrophotometric reverse engineering on single and bi-layer designs. J. Eur. Opt. Soc. Rapid Publ. 2013, 8. [Google Scholar]
- Stelling, C.; Singh, C.R.; Karg, M.; König, T.A.F.; Thelakkat, M.; Retsch, M. Plasmonic nanomeshes: Their ambivalent role as transparent electrodes in organic solar cells. Sci. Rep. 2017, 7, 42530. [Google Scholar] [CrossRef]
- Brittman, S.; Garnett, E.C. Measuring n and k at the Microscale in Single Crystals of CH3NH3PbBr3 Perovskite. J. Phys. Chem. C 2016, 120, 616–620. [Google Scholar] [CrossRef]
- Nishigaki, Y.; Matsushita, A.; Tejada, A.; Matsui, T.; Fujiwara, H. Appendix A: Optical Constants of Hybrid Perovskite Materials. In Hybrid Perovskite Solar Cells; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 541–562. [Google Scholar] [CrossRef]
- Chen, C.W.; Hsiao, S.Y.; Chen, C.Y.; Kang, H.W.; Huang, Z.Y.; Lin, H.W. Optical properties of organometal halide perovskite thin films and general device structure design rules for perovskite single and tandem solar cells. J. Mater. Chem. A 2015, 3, 9152–9159. [Google Scholar] [CrossRef]
- Manley, P.; Abdi, F.F.; Berglund, S.; Islam, A.T.M.N.; Burger, S.; van de Krol, R.; Schmid, M. Absorption Enhancement for Ultrathin Solar Fuel Devices with Plasmonic Gratings. Acs Appl. Energy Mater. 2018, 1, 5810–5815. [Google Scholar] [CrossRef]
- Burger, S.; Zschiedrich, L.; Pomplun, J.; Schmidt, F. JCMsuite: An Adaptive FEM Solver for Precise Simulations in Nano-Optics. In Integrated Photonics and Nanophotonics Research and Applications; Optica Publishing Group: Washington, DC, USA, 2008; p. ITuE4. [Google Scholar] [CrossRef]
- Chen, Y.; Höhn, O.; Tucher, N.; Pistol, M.E.; Anttu, N. Optical analysis of a III-V-nanowire-array-on-Si dual junction solar cell. Opt. Express 2017, 25, A665–A679. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Park, M.R.; Lee, H.J.; Lee, G.H. Thickness dependence of electrical properties of ITO film deposited on a plastic substrate by RF magnetron sputtering. Appl. Surf. Sci. 2006, 253, 409–411. [Google Scholar] [CrossRef]
- Hu, Z.; Lin, Z.; Su, J.; Zhang, J.; Chang, J.; Hao, Y. A Review on Energy Band-Gap Engineering for Perovskite Photovoltaics. Solar RRL 2019, 3, 1900304. [Google Scholar] [CrossRef]
- Wallentin, J.; Persson, J.M.; Wagner, J.B.; Samuelson, L.; Deppert, K.; Borgström, M.T. High-Performance Single Nanowire Tunnel Diodes. Nano Lett. 2010, 10, 974–979. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tirrito, M.; Manley, P.; Becker, C.; Unger, E.; Borgström, M.T. Optical Analysis of Perovskite III-V Nanowires Interpenetrated Tandem Solar Cells. Nanomaterials 2024, 14, 518. https://doi.org/10.3390/nano14060518
Tirrito M, Manley P, Becker C, Unger E, Borgström MT. Optical Analysis of Perovskite III-V Nanowires Interpenetrated Tandem Solar Cells. Nanomaterials. 2024; 14(6):518. https://doi.org/10.3390/nano14060518
Chicago/Turabian StyleTirrito, Matteo, Phillip Manley, Christiane Becker, Eva Unger, and Magnus T. Borgström. 2024. "Optical Analysis of Perovskite III-V Nanowires Interpenetrated Tandem Solar Cells" Nanomaterials 14, no. 6: 518. https://doi.org/10.3390/nano14060518
APA StyleTirrito, M., Manley, P., Becker, C., Unger, E., & Borgström, M. T. (2024). Optical Analysis of Perovskite III-V Nanowires Interpenetrated Tandem Solar Cells. Nanomaterials, 14(6), 518. https://doi.org/10.3390/nano14060518





