Sensing at the Nanoscale Using Nitrogen-Vacancy Centers in Diamond: A Model for a Quantum Pressure Sensor
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussions
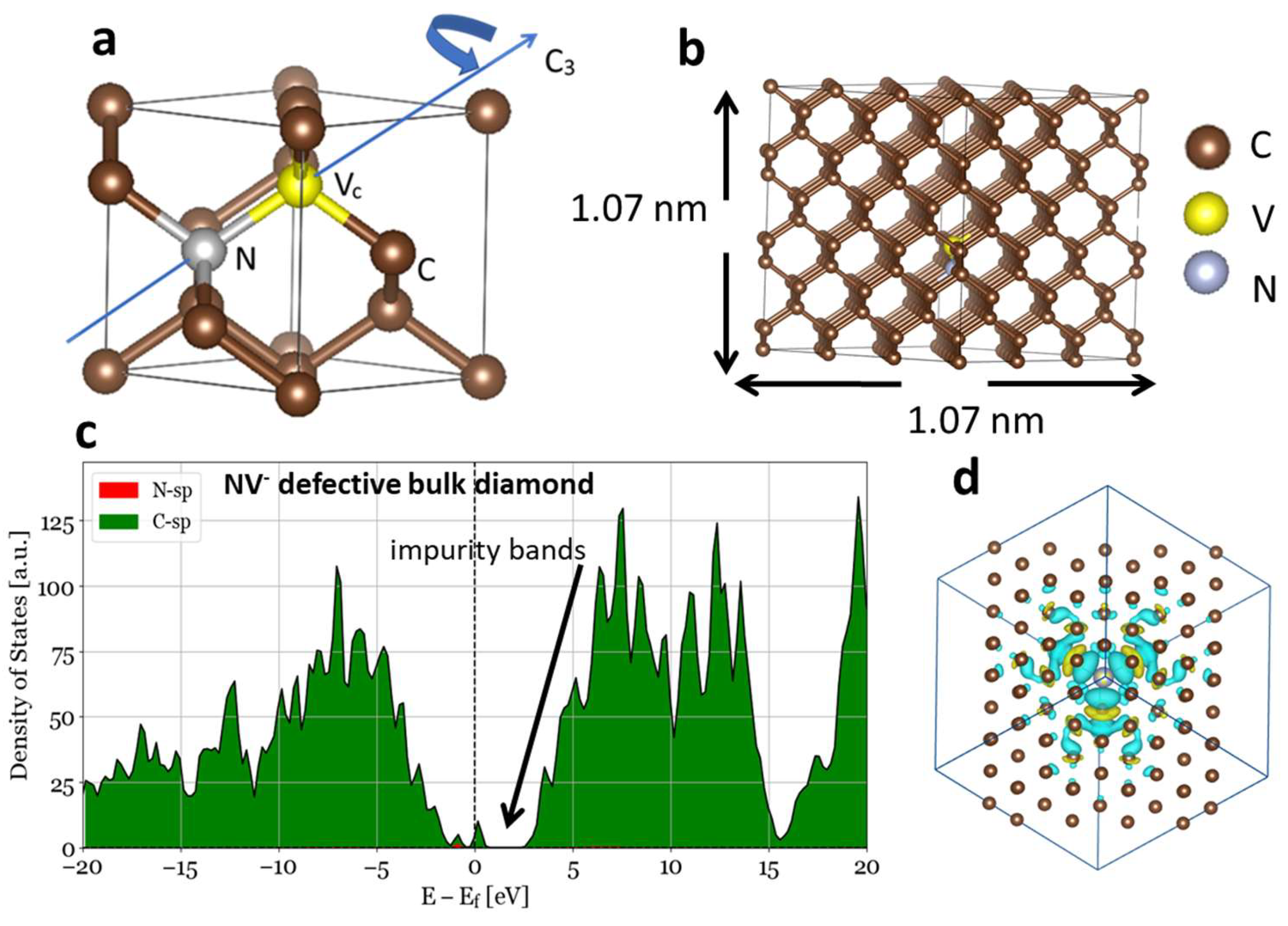
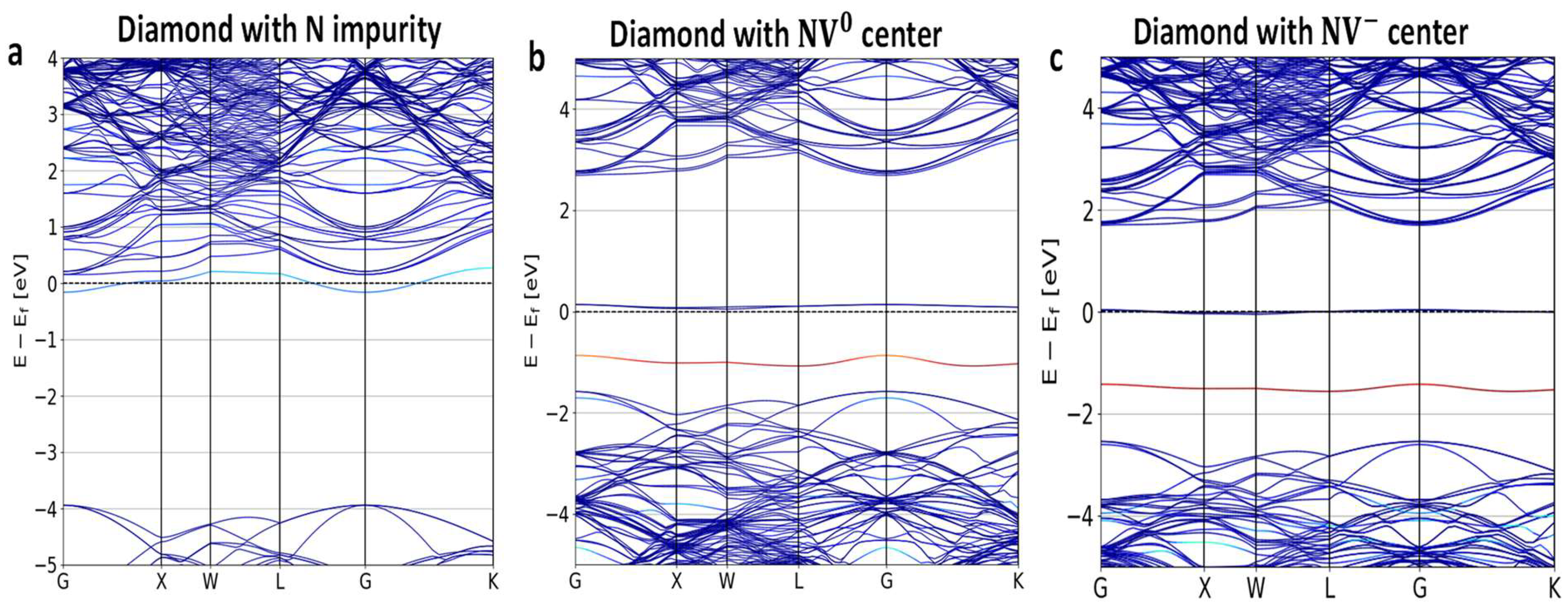
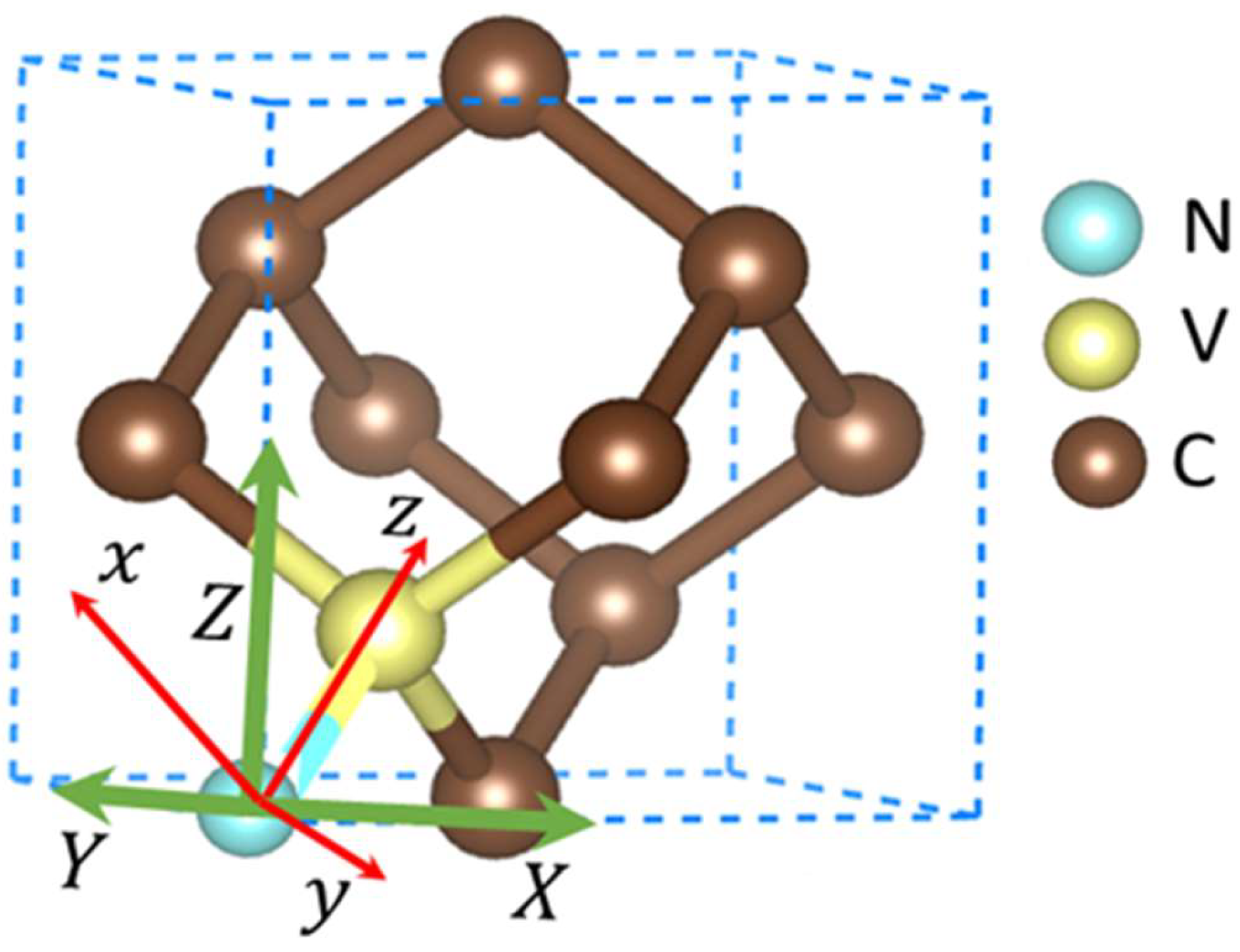
3.1. Density of States and Bandstructures of NV-Defective Diamond
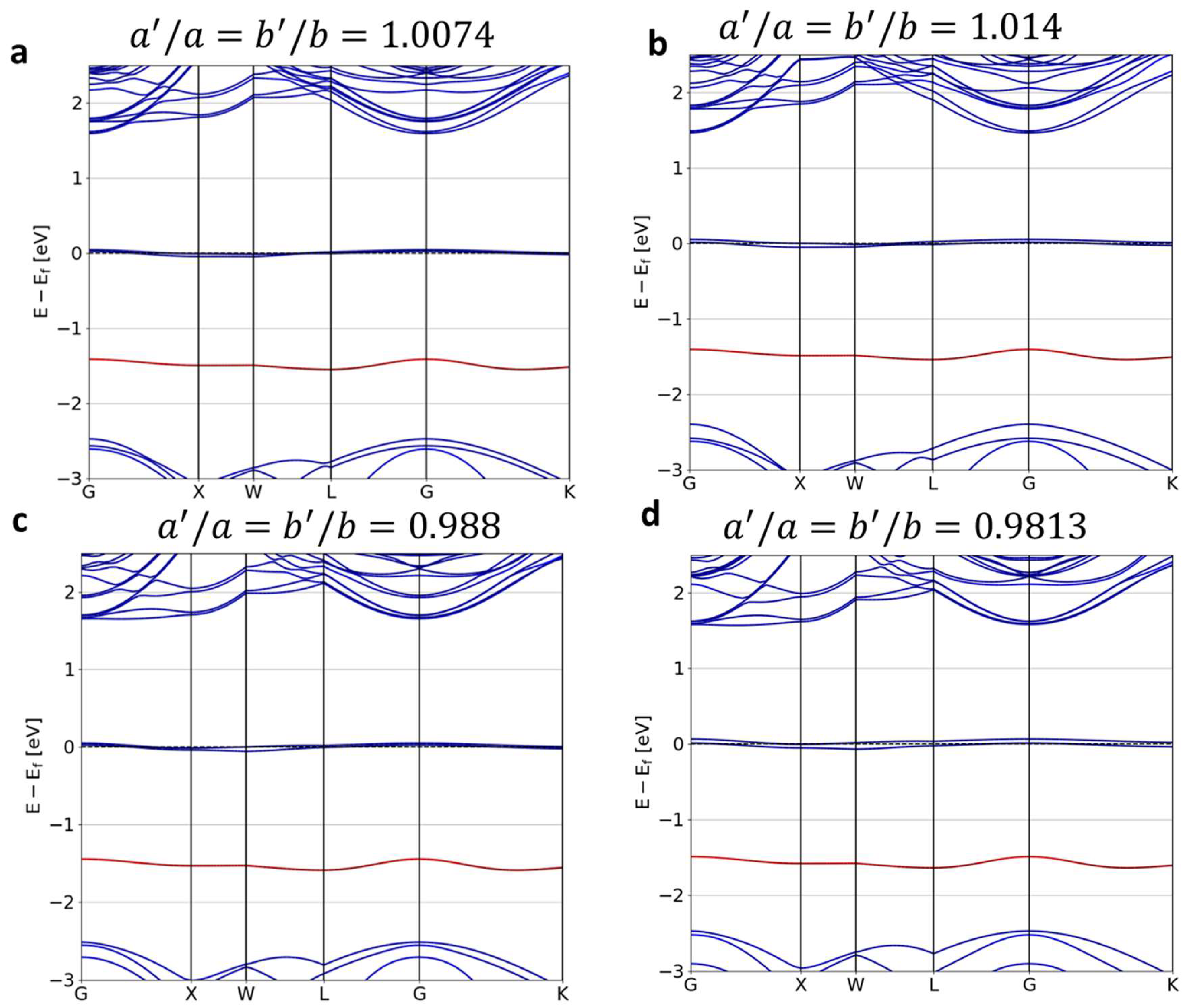
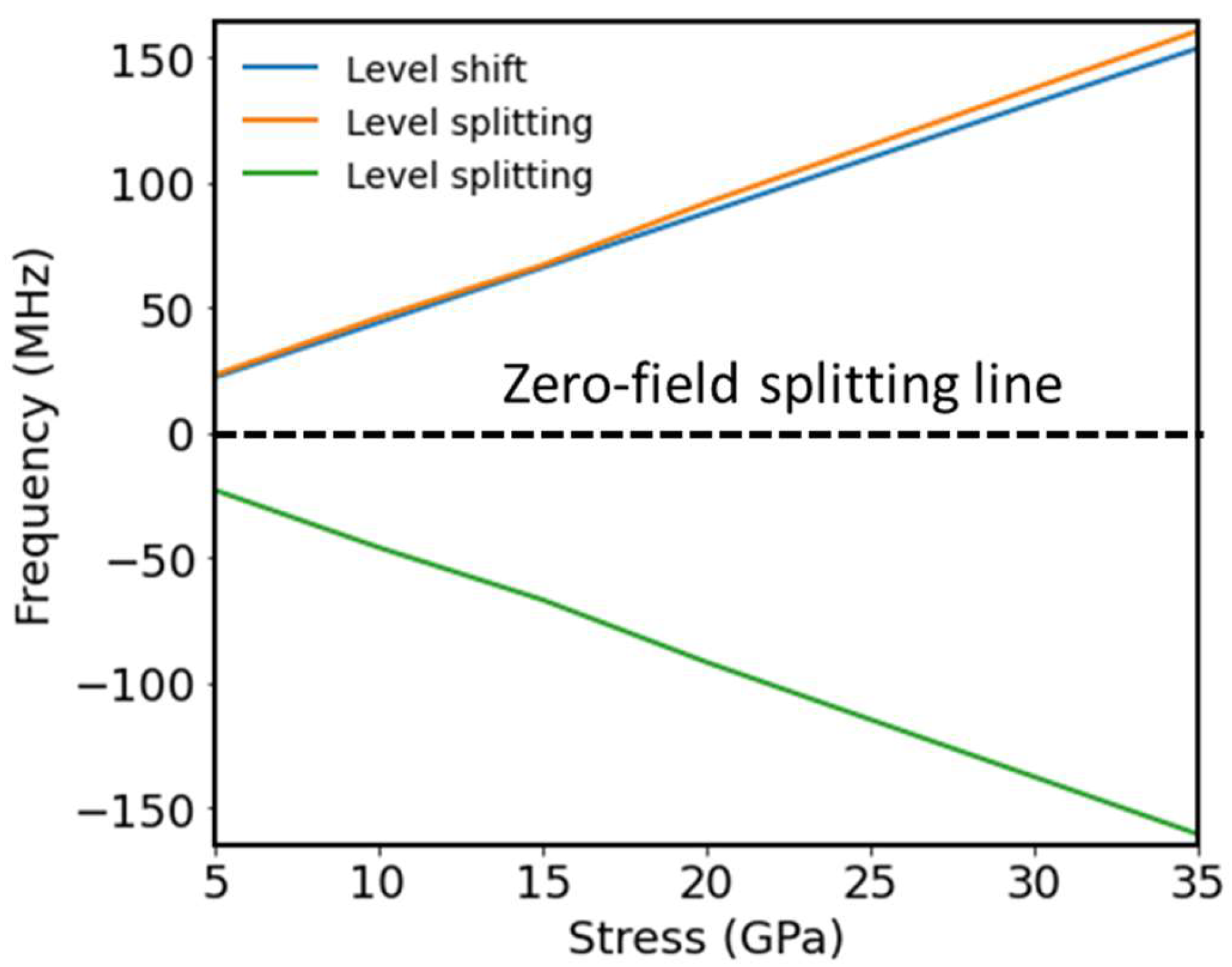
3.2. Theoretical Model of the NV Center under Stress
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ivády, V.; Simon, T.; Maze, J.R.; Abrikosov, I.A.; Gali, A. Pressure and temperature dependence of the zero-field splitting in the ground state of NV centers in diamond: A first-principles study. Phys. Rev. B 2014, 90, 235205. [Google Scholar] [CrossRef]
- Balasubramanian, G.; Chan, I.Y.; Kolesov, R.; Al-Hmoud, M.; Tisler, J.; Shin, C.; Kim, C.; Wojcik, A.; Hemmer, P.R.; Krueger, A.; et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, M.V.G.; Togan, E.; Zibrov, A.S.; et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Arlett, J.L.; Myers, E.B.; Roukes, M.L. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 2011, 6, 203–215. [Google Scholar] [CrossRef]
- Crawford, S.E.; Shugayev, R.A.; Paudel, H.P.; Lu, P.; Syamlal, M.; Ohodnicki, P.R.; Chorpening, B.; Gentry, R.; Duan, Y. Quantum Sensing for Energy Applications: Review and Perspective. Adv. Quantum Technol. 2021, 4, 2100049. [Google Scholar] [CrossRef]
- Bürgler, B.; Sjolander, T.F.; Brinza, O.; Tallaire, A.; Achard, J.; Maletinsky, P. All-optical nuclear quantum sensing using nitrogen-vacancy centers in diamond. NPJ Quantum Inf. 2023, 9, 56. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, T.; Li, Y.; Zeng, S.; Liu, Q.; Bi, M. Highly-Efficient Graphene Pressure Sensor with Hierarchical Alarm for Detecting the Transient Internal Pressure of Transformer Bushing. J. Electr. Eng. Technol. 2023, 18, 3071–3082. [Google Scholar] [CrossRef]
- Liang, M.; Fang, X.; Li, S.; Wu, G.; Ma, M.; Zhang, Y. A fiber Bragg grating tilt sensor for posture monitoring of hydraulic supports in coal mine working face. Measurement 2019, 138, 305–313. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Z.; Zhang, D.; Wei, Q. A Fiber Bragg Grating Pressure Sensor and Its Application to Pipeline Leakage Detection. Adv. Mech. Eng. 2013, 5, 590451. [Google Scholar] [CrossRef]
- Jang, S.P.; Cho, C.Y.; Nam, J.H.; Lim, S.-H.; Shin, D.; Chung, T.-Y. Numerical study on leakage detection and location in a simple gas pipeline branch using an array of pressure sensors. J. Mech. Sci. Technol. 2010, 24, 983–990. [Google Scholar] [CrossRef]
- Aparna, J.; Philip, S.; Topkar, A. Thermal energy harvester powered piezoresistive pressure sensor system with wireless operation for nuclear reactor application. Rev. Sci. Instrum. 2019, 90, 044705. [Google Scholar] [CrossRef]
- He, Q.; Pan, F.; Wang, D.; Liu, H.; Guo, F.; Wang, Z.; Ma, Y. Microstructure and properties of 316L stainless steel foils for pressure sensor of pressurized water reactor. Nucl. Eng. Technol. 2020, 53, 172–177. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Zhang, F.-X.; Zhao, Q.-C.; Che, C.-R. Real-time monitoring of pressure and temperature of oil well using a carbon-coated and bellow-packaged optical fiber sensor. Opt. Fiber Technol. 2021, 67, 102703. [Google Scholar] [CrossRef]
- Cameron, D.A.; Durlofsky, L.J.; Benson, S.M. Use of above-zone pressure data to locate and quantify leaks during carbon storage operations. Int. J. Greenh. Gas Control. 2016, 52, 32–43. [Google Scholar] [CrossRef]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Yacoby, A.; Walsworth, R.; Lukin, M.D. Erratum: High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2011, 7, 270. [Google Scholar] [CrossRef]
- Maclaurin, D.; Doherty, M.W.; Hollenberg, L.C.L.; Martin, A.M. Measurable Quantum Geometric Phase from a Rotating Single Spin. Phys. Rev. Lett. 2012, 108, 240403. [Google Scholar] [CrossRef]
- Segawa, T.F.; Igarashi, R. Nanoscale quantum sensing with Nitrogen-Vacancy centers in nanodiamonds—A magnetic resonance perspective. Prog. Nucl. Magn. Reson. Spectrosc. 2023, 134–135, 20–38. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Q.; Cheng, H.; Huang, H.; Shao, J.; Ye, Y.; Liu, G.-S.; Chen, L.; Luo, Y.; Chen, Z. Nanodiamond-Based Optical-Fiber Quantum Probe for Magnetic Field and Biological Sensing. ACS Sens. 2022, 7, 3660–3670. [Google Scholar] [CrossRef]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-Vacancy Centers in Diamond: Nanoscale Sensors for Physics and Biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef]
- Holzgrafe, J.; Gu, Q.; Beitner, J.; Kara, D.M.; Knowles, H.S.; Atatüre, M. Nanoscale NMR Spectroscopy Using Nanodiamond Quantum Sensors. Phys. Rev. Appl. 2020, 13, 044004. [Google Scholar] [CrossRef]
- Ho, K.O.; Wong, K.C.; Leung, M.Y.; Pang, Y.Y.; Leung, W.K.; Yip, K.Y.; Zhang, W.; Xie, J.; Goh, S.K.; Yang, S. Recent developments of quantum sensing under pressurized environment using the nitrogen vacancy (NV) center in diamond. J. Appl. Phys. 2021, 129, 241101. [Google Scholar] [CrossRef]
- Alléaume, R.; Treussart, F.; Messin, G.; Dumeige, Y.; Roch, J.-F.; Beveratos, A.; Brouri-Tualle, R.; Poizat, J.-P.; Grangier, P. Experimental open-air quantum key distribution with a single-photon source. New J. Phys. 2004, 6, 92. [Google Scholar] [CrossRef]
- Beveratos, A.; Brouri, R.; Gacoin, T.; Villing, A.; Poizat, J.-P.; Grangier, P. Single Photon Quantum Cryptography. Phys. Rev. Lett. 2002, 89, 187901. [Google Scholar] [CrossRef]
- Sun, L.; Yang, L.; Dou, J.-H.; Li, J.; Skorupskii, G.; Mardini, M.; Tan, K.O.; Chen, T.; Sun, C.; Oppenheim, J.J.; et al. Room-Temperature Quantitative Quantum Sensing of Lithium Ions with a Radical-Embedded Metal–Organic Framework. J. Am. Chem. Soc. 2022, 144, 19008–19016. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Waxman, A.; Bouchard, L.-S.; Budker, D. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Phys. Rev. Lett. 2010, 104, 070801. [Google Scholar] [CrossRef]
- Toyli, D.M.; Christle, D.J.; Alkauskas, A.; Buckley, B.B.; Van de Walle, C.G.; Awschalom, D.D. Measurement and Control of Single Nitrogen-Vacancy Center Spins above 600 K. Phys. Rev. X 2012, 2, 031001. [Google Scholar] [CrossRef]
- Barfuss, A.; Kasperczyk, M.; Kölbl, J.; Maletinsky, P. Spin-stress and spin-strain coupling in diamond-based hybrid spin oscillator systems. Phys. Rev. B 2019, 99, 174102. [Google Scholar] [CrossRef]
- Teissier, J.; Barfuss, A.; Appel, P.; Neu, E.; Maletinsky, P. Strain coupling of a nitrogen-vacancy center spin to a diamond mechanical oscillator. Phys. Rev. Lett. 2014, 113, 020503. [Google Scholar] [CrossRef]
- MacQuarrie, E.R.; Gosavi, T.A.; Jungwirth, N.R.; Bhave, S.A.; Fuchs, G.D. Mechanical Spin Control of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2013, 111, 227602. [Google Scholar] [CrossRef]
- Rogers, L.J.; Doherty, M.W.; Barson, M.S.J.; Onoda, S.; Ohshima, T.; Manson, N.B. Singlet levels of the NV−Centre in diamond. New J. Phys. 2015, 17, 013048. [Google Scholar] [CrossRef]
- Grazioso, F.; Patton, B.R.; Delaney, P.; Markham, M.L.; Twitchen, D.J.; Smith, J.M. Measurement of the full stress tensor in a crystal using photoluminescence from point defects: The example of nitrogen vacancy centers in diamond. Appl. Phys. Lett. 2013, 103, 101905. [Google Scholar] [CrossRef]
- Ovartchaiyapong, P.; Lee, K.W.; Myers, B.A.; Jayich, A.C.B. Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator. Nat. Commun. 2014, 5, 4429. [Google Scholar] [CrossRef]
- Barry, J.F.; Schloss, J.M.; Bauch, E.; Turner, M.J.; Hart, C.A.; Pham, L.M.; Walsworth, R.L. Sensitivity optimization for NV-diamond magnetometry. Rev. Mod. Phys. 2020, 92, 015004. [Google Scholar] [CrossRef]
- Liu, K.S.; Ma, X.; Rizzato, R.; Semrau, A.L.; Henning, A.; Sharp, I.D.; Fischer, R.A.; Bucher, D.B. Using Metal–Organic Frameworks to Confine Liquid Samples for Nanoscale NV-NMR. Nano Lett. 2022, 22, 9876–9882. [Google Scholar] [CrossRef]
- Shugayev, R.A.; Crawford, S.E.; Baltrus, J.P.; Diemler, N.A.; Ellis, J.E.; Kim, K.-J.; Cvetic, P.C. Synthesis and Quantum Metrology of Metal–Organic Framework-Coated Nanodiamonds Containing Nitrogen Vacancy Centers. Chem. Mater. 2021, 33, 6365–6373. [Google Scholar] [CrossRef]
- Zyubin, A.S.; Mebel, A.M.; Hayashi, M.; Chang, H.C.; Lin, S.H. Quantum chemical modeling of photoadsorption properties of the nitrogen-vacancy point defect in diamond. J. Comput. Chem. 2008, 30, 119–131. [Google Scholar] [CrossRef]
- Gruber, A.; Dräbenstedt, A.; Tietz, C.; Fleury, L.; Wrachtrup, J.; von Borczyskowski, C. Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers. Science 1997, 276, 2012–2014. [Google Scholar] [CrossRef]
- Mittiga, T.; Hsieh, S.; Zu, C.; Kobrin, B.; Machado, F.; Bhattacharyya, P.; Rui, N.Z.; Jarmola, A.; Choi, S.; Budker, D.; et al. Imaging the Local Charge Environment of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2018, 121, 246402. [Google Scholar] [CrossRef]
- Manson, N.B.; Harrison, J.P.; Sellars, M.J. Nitrogen-vacancy center in diamond: Model of the electronic structure and associated dynamics. Phys. Rev. B 2006, 74, 104303. [Google Scholar] [CrossRef]
- Robledo, L.; Bernien, H.; van der Sar, T.; Hanson, R. Spin dynamics in the optical cycle of single nitrogen-vacancy centres in diamond. New J. Phys. 2011, 13, 025013. [Google Scholar] [CrossRef]
- Doherty, M.W.; Struzhkin, V.V.; Simpson, D.A.; McGuinness, L.P.; Meng, Y.; Stacey, A.; Karle, T.J.; Hemley, R.J.; Manson, N.B.; Hollenberg, L.C.L.; et al. Electronic Properties and Metrology Applications of the Diamond NV Center under Pressure. Phys. Rev. Lett. 2014, 112, 047601. [Google Scholar] [CrossRef] [PubMed]
- Loubser, J.H.N.; van Wyk, J.A. Electron spin resonance in the study of diamond. Rep. Prog. Phys. 1978, 41, 1201–1248. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Ajoy, A.; Cappellaro, P. Stable three-axis nuclear-spin gyroscope in diamond. Phys. Rev. A 2012, 86, 062104. [Google Scholar] [CrossRef]
- Doherty, M.W.; Acosta, V.M.; Jarmola, A.; Barson, M.S.J.; Manson, N.B.; Budker, D.; Hollenberg, L.C.L. Temperature shifts of the resonances of the NV center in diamond. Phys. Rev. B 2014, 90, 041201. [Google Scholar] [CrossRef]
- Udvarhelyi, P.; Shkolnikov, V.O.; Gali, A.; Burkard, G.; Pályi, A. Spin-strain interaction in nitrogen-vacancy centers in diamond. Phys. Rev. B 2018, 98, 075201. [Google Scholar] [CrossRef]
- Gali, Á. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics 2019, 8, 1907–1943. [Google Scholar] [CrossRef]
- Chou, J.-P.; Retzker, A.; Gali, A. Nitrogen-Terminated Diamond (111) Surface for Room-Temperature Quantum Sensing and Simulation. Nano Lett. 2017, 17, 2294–2298. [Google Scholar] [CrossRef] [PubMed]
- Barson, M.S.J.; Peddibhotla, P.; Ovartchaiyapong, P.; Ganesan, K.; Taylor, R.L.; Gebert, M.; Mielens, Z.; Koslowski, B.; Simpson, D.A.; McGuinness, L.P.; et al. Nanomechanical Sensing Using Spins in Diamond. Nano Lett. 2017, 17, 1496–1503. [Google Scholar] [CrossRef]
- Mzyk, A.; Sigaeva, A.; Schirhagl, R. Relaxometry with Nitrogen Vacancy (NV) Centers in Diamond. Acc. Chem. Res. 2022, 55, 3572–3580. [Google Scholar] [CrossRef]
- Sadzak, N.; Héritier, M.; Benson, O. Coupling a Single Nitrogen-Vacancy Center in Nanodiamond to Superparamagnetic Nanoparticles. Sci. Rep. 2018, 8, 8430. [Google Scholar] [CrossRef]
- Löfgren, R.; Öberg, S.; Larsson, J.A. The diamond NV-center transition energies in the vicinity of an intrinsic stacking fault. AIP Adv. 2022, 12, 035009. [Google Scholar] [CrossRef]
- Löfgren, R.; Pawar, R.; Öberg, S.; Larsson, J.A. The bulk conversion depth of the NV-center in diamond: Computing a charged defect in a neutral slab. New J. Phys. 2019, 21, 053037. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press (OUP): Oxford, UK, 1995. [Google Scholar]
- Zhu, P.; Yang, G.; Sun, J.; Fan, R.; Zhang, P.; Yoneyama, Y.; Tsubaki, N. A hollow Mo/HZSM-5 zeolite capsule catalyst: Preparation and enhanced catalytic properties in methane dehydroaromatization. J. Mater. Chem. A 2017, 5, 8599–8607. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Straumanis, M.E.; Aka, E.Z. Precision Determination of Lattice Parameter, Coefficient of Thermal Expansion and Atomic Weight of Carbon in Diamond1. J. Am. Chem. Soc. 1951, 73, 5643–5646. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Abinitio Molecular-Dynamics for Liquid-Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Yao, M.-M.; Zhu, T.-Y.; Shu, D.-J. Effects of external stress field on the charge stability of nitrogen vacancy centers in diamond. Appl. Phys. Lett. 2017, 111, 042108. [Google Scholar] [CrossRef]
- Jahn, H.A.; Teller, E.; Donnan, F.G. Stability of polyatomic molecules in degenerate electronic states—I—Orbital degeneracy. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 220–235. [Google Scholar]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef]
- Hughes, A.E.; Runciman, W.A. Uniaxial stress splitting of doubly degenerate states of tetragonal and trigonal centres in cubic crystals. Proc. Phys. Soc. 1967, 90, 827–838. [Google Scholar] [CrossRef]
- Kehayias, P.; Turner, M.J.; Trubko, R.; Schloss, J.M.; Hart, C.A.; Wesson, M.; Glenn, D.R.; Walsworth, R.L. Imaging crystal stress in diamond using ensembles of nitrogen-vacancy centers. Phys. Rev. B 2019, 100, 174103. [Google Scholar] [CrossRef]
- Bodrog, Z.; Gali, A. The spin–spin zero-field splitting tensor in the projector-augmented-wave method. J. Phys. Condens. Matter 2013, 26, 015305. [Google Scholar] [CrossRef]
- Childress, L.; Gurudev Dutt, M.V.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef]
- Chang, D.E.; Sørensen, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum Optics with Surface Plasmons. Phys. Rev. Lett. 2006, 97, 053002. [Google Scholar] [CrossRef]
- Shugayev, R.; Devkota, J.; Crawford, S.; Lu, P.; Buric, M. Giant Microwave Spontaneous Emission Enhancements in Planar Aperture Waveguide Structures. Adv. Quantum Technol. 2021, 4, 2000151. [Google Scholar] [CrossRef]
- Husen, S.; Bachmann, C.; Giardini, D. Locally triggered seismicity in the central Swiss Alps following the large rainfall event of August 2005. Geophys. J. Int. 2007, 171, 1126–1134. [Google Scholar] [CrossRef]
- Miller, S.A.; Collettini, C.; Chiaraluce, L.; Cocco, M.; Barchi, M.; Kaus, B.J.P. Aftershocks driven by a high-pressure CO2 source at depth. Nature 2004, 427, 724–727. [Google Scholar] [CrossRef]
- Doetsch, J.; Gischig, V.S.; Villiger, L.; Krietsch, H.; Nejati, M.; Amann, F.; Jalali, M.; Madonna, C.; Maurer, H.; Wiemer, S.; et al. Subsurface Fluid Pressure and Rock Deformation Monitoring Using Seismic Velocity Observations. Geophys. Res. Lett. 2018, 45, 10389–10397. [Google Scholar] [CrossRef]
- Monacelli, L.; Casula, M.; Nakano, K.; Sorella, S.; Mauri, F. Quantum phase diagram of high-pressure hydrogen. Nat. Phys. 2023, 19, 845–850. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
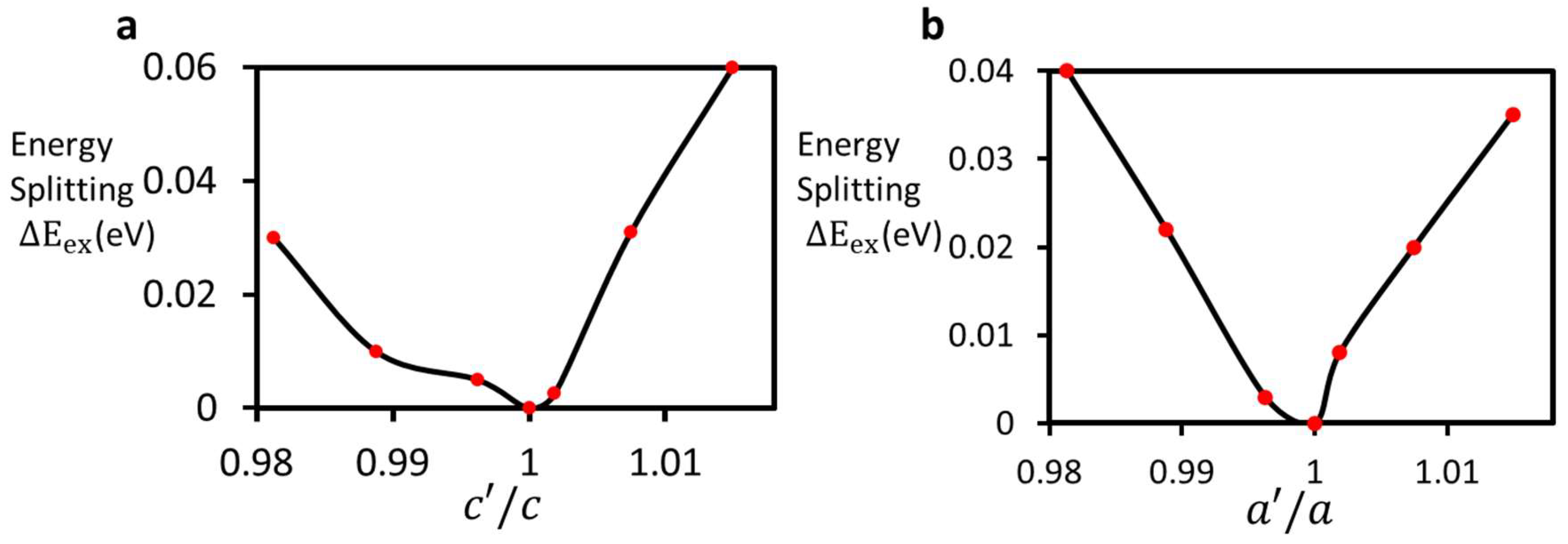
| Change in Lattice (Å) | Splitting of Excited State (meV) | Band Gap Changes (meV) | Change in Lattice (Å) | Splitting of Excited State (meV) | Band Gap Changes (meV) |
|---|---|---|---|---|---|
| 10.87 | 30 | 50 | 10.87 | 35 | 55 |
| 10.79 | 10 | 30 | 10.79 | 20 | 40 |
| 10.71 | 0 | 0.0 | 10.71 | 0 | 0.0 |
| 10.67 | 10 | 30 | 10.67 | 3 | 15 |
| 10.59 | 31 | 25 | 10.59 | 22 | 25 |
| 10.51 | 60 | 30 | 10.51 | 40 | 35 |
| Applied-Stress Direction | NV Sub-Ensemble Direction | Shift/Splitting per Unit Pressure |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paudel, H.P.; Lander, G.R.; Crawford, S.E.; Duan, Y. Sensing at the Nanoscale Using Nitrogen-Vacancy Centers in Diamond: A Model for a Quantum Pressure Sensor. Nanomaterials 2024, 14, 675. https://doi.org/10.3390/nano14080675
Paudel HP, Lander GR, Crawford SE, Duan Y. Sensing at the Nanoscale Using Nitrogen-Vacancy Centers in Diamond: A Model for a Quantum Pressure Sensor. Nanomaterials. 2024; 14(8):675. https://doi.org/10.3390/nano14080675
Chicago/Turabian StylePaudel, Hari P., Gary R. Lander, Scott E. Crawford, and Yuhua Duan. 2024. "Sensing at the Nanoscale Using Nitrogen-Vacancy Centers in Diamond: A Model for a Quantum Pressure Sensor" Nanomaterials 14, no. 8: 675. https://doi.org/10.3390/nano14080675
APA StylePaudel, H. P., Lander, G. R., Crawford, S. E., & Duan, Y. (2024). Sensing at the Nanoscale Using Nitrogen-Vacancy Centers in Diamond: A Model for a Quantum Pressure Sensor. Nanomaterials, 14(8), 675. https://doi.org/10.3390/nano14080675






