The Impact of Carbon on Electronic Structure of N-Doped ZnO Films: Scanning Photoelectron Microscopy Study and DFT Calculations
Abstract
:1. Introduction
2. Methods
2.1. Deposition of ZnO:N Thin Films
2.2. Scanning Photoelectron Microscopy Measurements
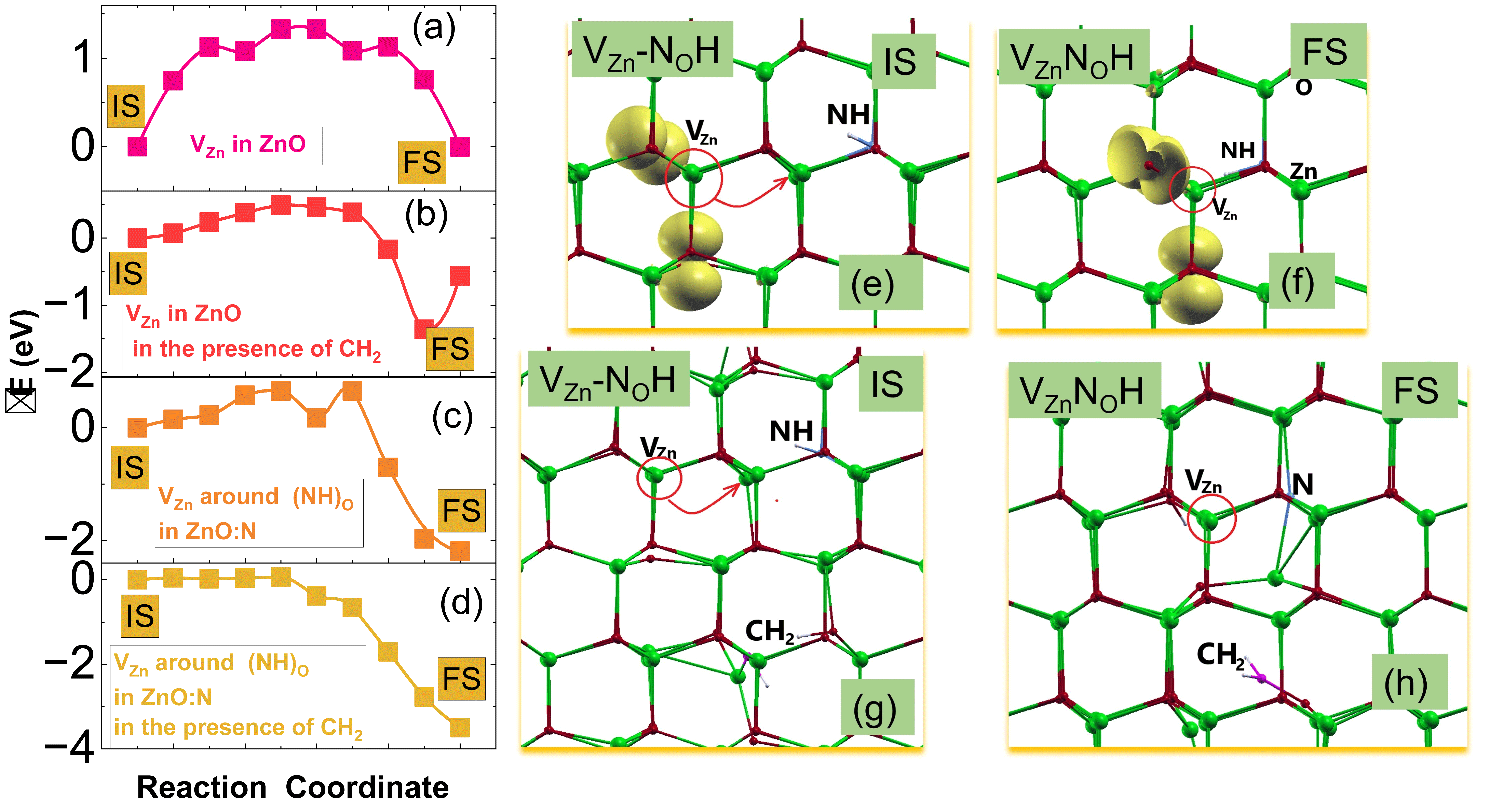
2.3. Computational Methods
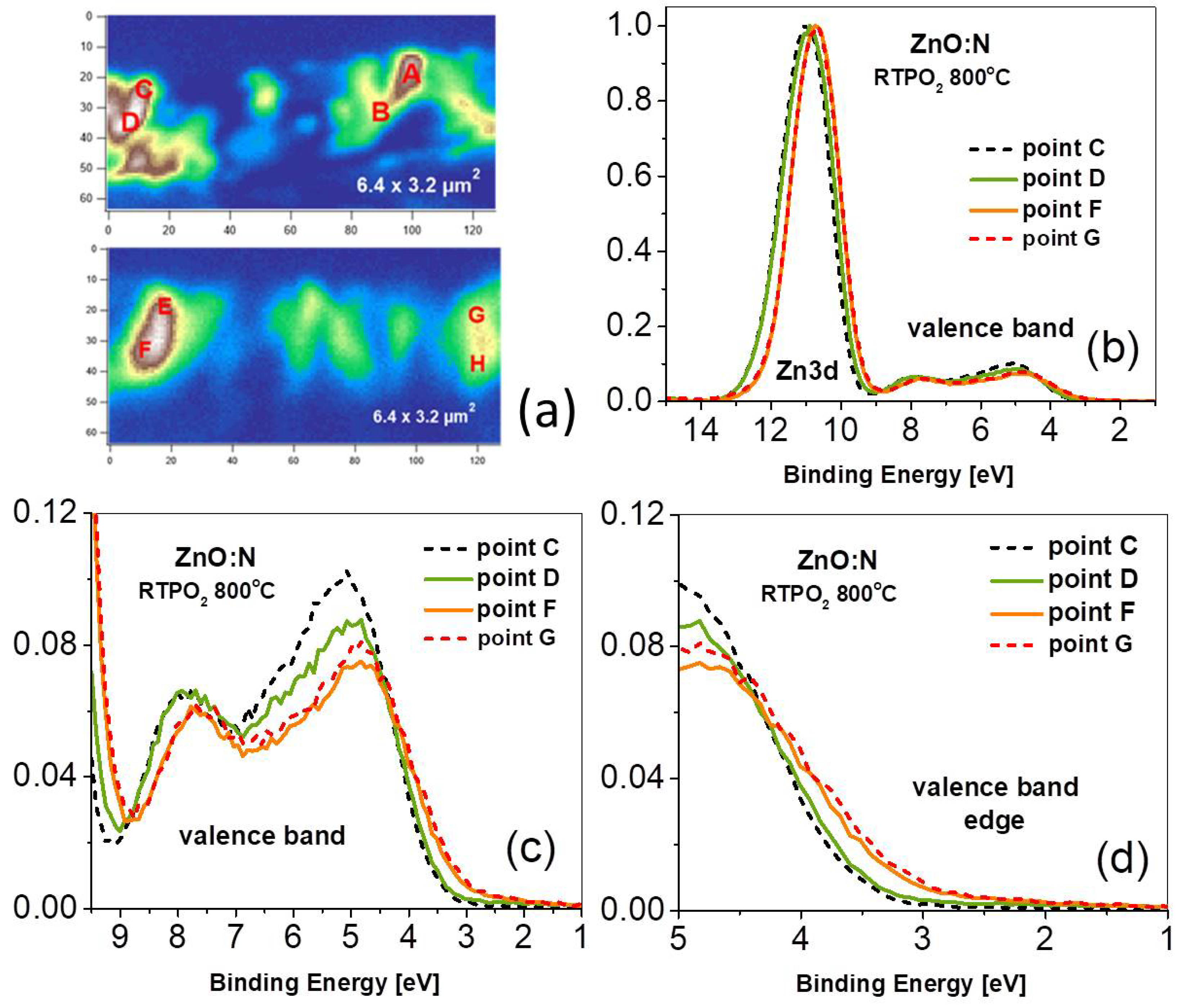
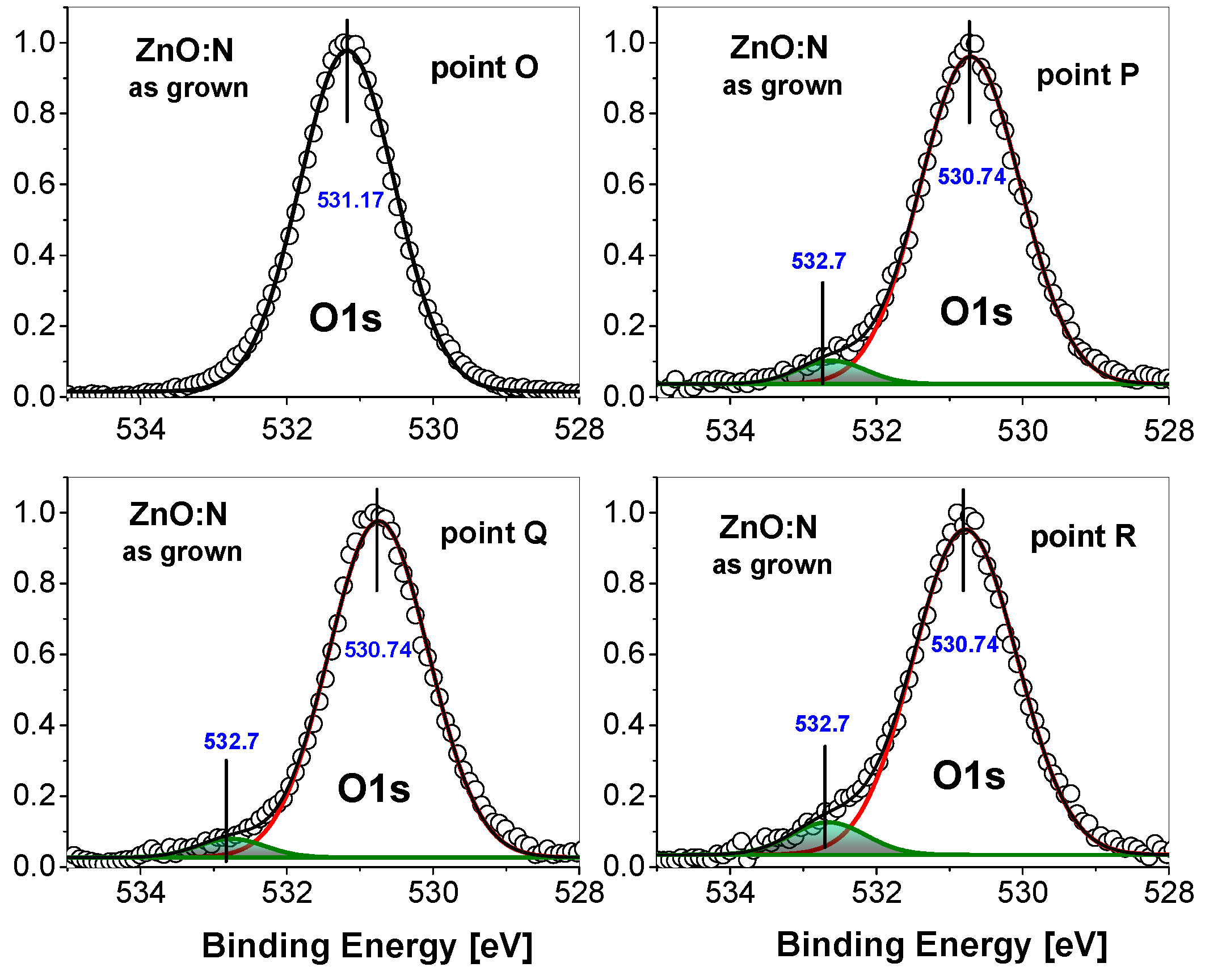
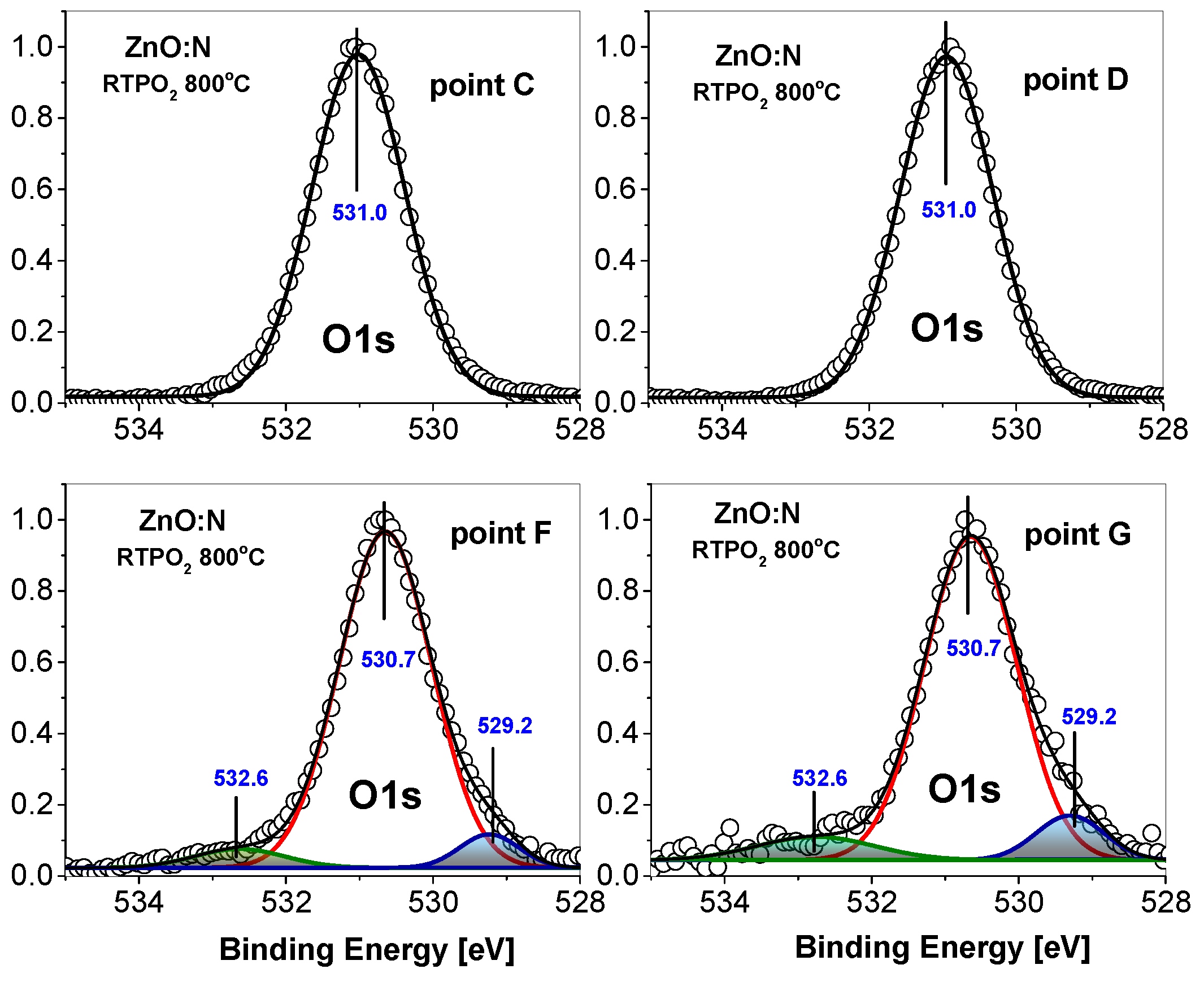
3. Experimental Results
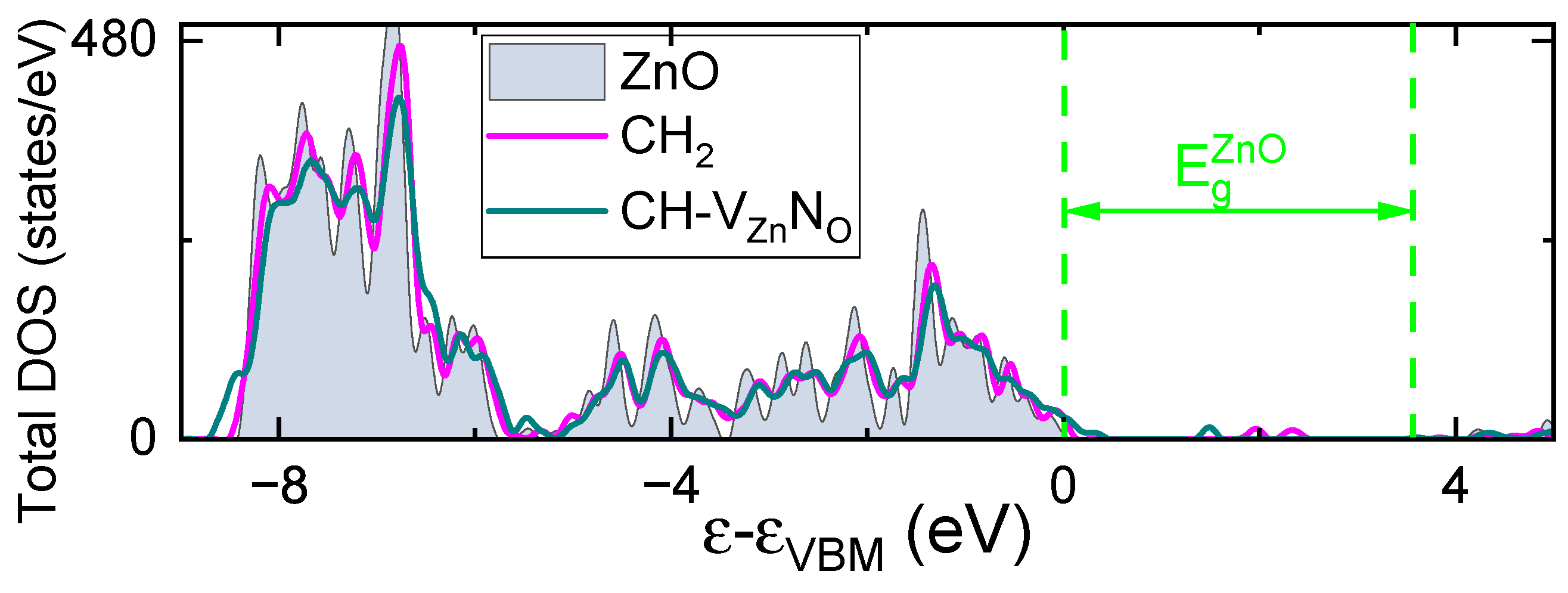
4. Discussion
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amini, M.; Saniz, R.; Lamoen, D.; Partoens, B. The Role of the VZn-NO-H Complex in the p-Type Conductivity in ZnO. Phys. Chem. Chem. Phys. 2015, 17, 5485–5489. [Google Scholar] [CrossRef] [PubMed]
- Senthilkumar, K.; Yoshida, T.; Fujita, Y. Formation of D-V(Zn) defects and possible p-type conductivity of ZnO nanoparticle via hydrogen adsorption. J. Mater. Sci. 2018, 53, 11977. [Google Scholar] [CrossRef]
- Gluba, M.A.; Nickel, N.H.; Karpensky, N. Interstitial zinc clusters in zinc oxide. Phys. Rev. B 2015, 88, 245201. [Google Scholar] [CrossRef]
- Pal, S.; Gogurla, N.; Das, A.; Singha, S.; Kumar, P.; Kanjilal, D.; Singha, A.; Chattopadhyay, S.; Jana, D.; Sarkar, A. Clustered vacancies in ZnO: Chemical aspects andconsequences on physical properties. J. Phys. D Appl. Phys. 2018, 51, 105107. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Liang, G.; Li, Y.; Lai, R.; Ding, T.; Wu, K. Observation of a phonon bottleneck in copper-doped colloidal quantum dots. Nat. Commun. 2019, 10, 4532. [Google Scholar] [CrossRef]
- Makkonen, V.P.I.; Korhonen, E.; Tuomisto, F. Identification of vacancy defect complexes in transparent semiconducting oxides ZnO, In2O3 and SnO2. J. Phys. Condens. Matter 2016, 28, 224002. [Google Scholar] [CrossRef]
- Schifano, R.; Jakiela, R.; Galeckas, A.; Kopalko, K.; Johansen, K.; Vines, L. Role of intrinsic and extrinsic defects in H implanted hydrothermally grown ZnO. J. Appl. Phys. 2019, 126, 125707. [Google Scholar] [CrossRef]
- Guziewicz, E.; Godlewski, M.; Wachnicki, L.; Krajewski, T.; Luka, G.; Gieraltowska, S.; Jakiela, R.; Stonert, A.; Lisowski, W.; Krawczyk, M.; et al. ALD grown Zinc Oxide with controllable electrical properties. Semicond. Sci. Technol. 2012, 27, 074011. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, D.; Shen, L.; Zhang, H.; Zhang, X.; Yang, B. Alkylthiol-Enabled Se Powder Dissolution in Oleylamine at Room Temperature for the Phosphine-Free Synthesis of Copper-Based Quaternary Selenide Nanocrystals. J. Am. Chem. Soc. 2012, 134, 7207. [Google Scholar] [CrossRef]
- Mishra, S.; Witkowski, B.S.; Jakiela, R.; Khosravizadeh, Z.; Paszkowicz, W.; Sulich, A.; Volnianska, O.; Wozniak, W.; Guziewicz, E. Cathodoluminescent Imaging of ZnO:N Films: Study ofAnnealing Processes Leading to Enhanced AcceptorLuminescence. Phys. Status Solidi A 2023, 220, 2200466. [Google Scholar] [CrossRef]
- Guziewicz, E.; Przezdziecka, E.; Snigurenko, D.; Jarosz, D.; Witkowski, B.; Dluzewski, P.; Paszkowicz, W. Abundant Acceptor Emission from Nitrogen-Doped ZnO Films Prepared by Atomic Layer Deposition under Oxygen-Rich Conditions. ACS Appl. Mater. Int. 2017, 9, 26143–26150. [Google Scholar] [CrossRef] [PubMed]
- Guziewicz, E.; Volnianska, O.; Demchenko, I.; Zeller, P.; Amati, M.; Gregoratti, L. Valence-Band Electronic Structure of ZnO and ZnO:N: Experimental and Theoretical Evidence of Defect Complexes. Phys. Rev. Appl. 2022, 18, 044021. [Google Scholar] [CrossRef]
- Krtschil, A.; Look, D.; Fang, Z.Q.; Dadgar, A.; Diez, A.; Krost, A. Local p-type conductivity in n-GaN and n-ZnO layers due to inhomogeneous dopant incorporation. Phys. B 2006, 703, 376–377. [Google Scholar] [CrossRef]
- Krtschil, A.; Dadgar, A.; Oleynik, N.; Blasing, J.; Diez, A.; Krost, A. Local p-type conductivity in zinc oxide dual-doped with nitrogen and arsenic. Appl. Phys. Lett. 2005, 87, 262105. [Google Scholar] [CrossRef]
- Volnianska, O.; Ivanov, V.; Wachnicki, L.; Guziewicz, E. Effect of Strain and Surface Proximity on the Acceptor Grouping in ZnO. ACS Omega 2023, 8, 43099–43108. [Google Scholar] [CrossRef]
- Herng, T.; Lau, S.; Wang, L.; Zhao, B.; Yu, S.F.; Tanemura, M.; Akaike, A.; Teng, K. Magnetotransport properties of p-type carbon-doped ZnO thin films. Appl. Phys. Lett. 2009, 95, 012505. [Google Scholar] [CrossRef]
- Tan, S.; Sun, X.W.; Yu, Z.; Wu, P.; Lo, G.Q.; Kwong, D.L. p-type conduction in unintentional carbon-doped ZnO thin films. Appl. Phys. Lett. 2007, 91, 072101. [Google Scholar] [CrossRef]
- Pan, H.; Yi, J.B.; Shen, L.; Wu, R.Q.; Yang, J.H.; Lin, J.Y.; Feng, Y.P.; Ding, J.; Van, L.; Yin, J.H. Room-temperature Ferromagnetism in Carbon-Doped ZnO. Phys. Rev. Lett. 2007, 99, 127201. [Google Scholar] [CrossRef]
- Akbar, S.; Hasanain, S.; Abbas, M.; Ozcan, S.; Ali, B.; Shah, S. Defect induced Ferromagnetism in carbon-doped ZnO thin films. Solid State Commun. 2011, 151, 17–20. [Google Scholar] [CrossRef]
- Park, J.W.; Kim, D.H.; Choi, S.H.; Lee, M.; Lim, D. The role of carbon doping in ZnO. J. Korean Phys. Soc. 2010, 57, 1482–1485. [Google Scholar]
- Sakong, S.; Kratzer, P. Density functional study of carbon doping in ZnO. Semicond. Sci. Technol. 2011, 26, 014038. [Google Scholar] [CrossRef]
- Lyons, J.L.; Steiauf, D.; Janotti, A.; de Walle, C.G.V. Carbon as a Shallow Donor in Transparent Conducting Oxides. Phys. Rev. Appl. 2014, 2, 064005. [Google Scholar] [CrossRef]
- Ye, L.; Yu, J.; Zhang, H.; Li, H.; Pang, D.; Tang, Y.; Kong, C.; Fang, L.; Ruan, H.; Li, W. Carbon-doped ZnO thin films: A transparent conductive oxide for application in solar-blind photodetectors. Appl. Phys. Lett. 2024, 125, 012104. [Google Scholar] [CrossRef]
- Hui, X.; You-Wen, Z.; Tong, L.; Zhi-Yuan, D.; Jun, Y.; Jing-Ming, L. C-H complex defects and their influence in ZnO single crystal. Chin. Phys. B 2015, 24, 107704. [Google Scholar] [CrossRef]
- Sun, L.; Hu, L.; Ye, Z. Evidence for the carbon-nitrogen complex in ZnO nanostructures with ver high nitrogen doping. Phys. Chem. Chem. Phys. 2013, 15, 1369–1373. [Google Scholar] [CrossRef]
- Shikuku, R.; Abdulla-Al-Mamun, M. A new visible-light-responsive carbon-nitrogen-co-doped zinc oxide photocatalysts: Applications on dye remediation. MRS Adv. 2024, 9, 1015–1022. [Google Scholar] [CrossRef]
- Liu, S.; Li, C.; Yu, J.; Xiang, Q. Improved visible-light photocatalytic activity of porous carbon self-doped ZnO nanosheet-assembled flowers. CrystEngComm 2011, 13, 2533–2541. [Google Scholar] [CrossRef]
- Zeller, P.; Amati, M.; Sezen, H.; Scardameglia, M.; Struzzi, C.; Bittencourt, C.; Lantz, G.; Hajlaoui, M.; Papalazarou, E.; Marino, M.; et al. Scanning Photoelectron Spectro-Microscopy: A Modern Tool for the Study of Materials at the Nanoscale. Phys. Stat. Sol. A 2018, 215, 1800308. [Google Scholar] [CrossRef]
- Amati, M.; Barinov, A.; Feyer, V.; Gregoratti, L.; Al-Hada, M.; Locatelli, A.; Mentes, T.; Sezen, H.; Schneider, C.; Kiskinova, M. Photoelectron microscopy at Elettra: Recent advances and perspectives. J. Electron Spectr. Rel. Phenom. 2018, 224, 59–67. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892(R). [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 2005, 13, 5188. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Accurate prediction of defect properties in density functional supercell calculations. Model. Simulat. Mater. Sci. Eng. 2009, 17, 084002. [Google Scholar] [CrossRef]
- Sarwar, M.; Witkowski, B.S.; Sulich, A.; Guziewicz, E. Low-temperature cathodoluminescence of nitrogen-doped ZnO films deposited at low-temperature by atomic layer deposition. Acta Phys. Pol. A 2022, 141, 135–139. [Google Scholar] [CrossRef]
- Moulder, J.F.; Stickle, W.; Sobol, P.; Bomben, K. X-Ray Photoelectron Spectroscopy. A Reference Book of Standard Spectra for Identification and Interpretation of XPS Data; Perkin-Elmer Corp. Physical Electronics Division: Eden Prairie, MN, USA, 1992; pp. 40–46. [Google Scholar]
- Brzhezinskaya, M.; Mishakov, I.V.; Bauman, Y.I.; Shubin, Y.V.; Maksimova, T.A.; Stoyanovskii, V.O.; Gerasimov, E.Y.; Vedyagin, A.A. One-pot functionalization of catalytically derived carbon nanostructures with heteroatoms for toxic-free environment. Appl. Surf. Sci. 2022, 590, 153055. [Google Scholar] [CrossRef]
- Rabchinskii, M.; Sysoev, V.; Brzhezinskaya, M.; Solomatin, M.; Gabrelian, V.; Kirilenko, D.; Stolyarova, D.; Saveliev, S.; Shvidchenko, A.; Cherviakova, P.D.; et al. Rationalizing Graphene–ZnO Composites for Gas Sensing via Functionalization with Amines. Nanomaterials 2024, 14, 735. [Google Scholar] [CrossRef]
- Guziewicz, E.; Wozniak, W.; Mishra, S.; Jakiela, R.; Guziewicz, M.; Ivanov, V.Y.; Lusakowska, E.; Schifano, R. Hydrogen in As-Grown and Annealed ZnO Films Grown by Atomic Layer Deposition. Phys. Stat. Solidi A 2021, 218, 2000318. [Google Scholar] [CrossRef]
- Rezaie, S.; Bafghi, Z.G.; Manavizadeh, N. Carbon-doped ZnO nanotube-based highly effective hydrogen gas sensor: A first-principles study. Int. J. Hydrogen Energy 2020, 45, 14174. [Google Scholar] [CrossRef]
- Li, P.; Luo, W. Properties of carbon impurities in ZnO: A hybrid functional study. Phys. Rev. B 2016, 94, 075202. [Google Scholar] [CrossRef]
- Wang, Y.F.; Shao, Y.C.; Hsieh, S.H.; Chang, Y.K.; Yeh, P.H.; Hsueh, H.C.; Chiou, J.W.; Wang, H.T.; Ray, S.C.; Tsai, H.M.; et al. Origin of magnetic properties in carbon implanted ZnO nanowires. Sci. Rep. 2018, 8, 7758. [Google Scholar] [CrossRef] [PubMed]
- Erhart, P.; Albe, K. Diffusion of zinc vacancies and interstitials in zinc oxide. Appl. Phys. Lett. 2006, 88, 201918. [Google Scholar] [CrossRef]
- Gebauer, R. Oxygen Vacancies in Zirconia and Their Migration: The Role of Hubbard-U Parameters in Density Functional Theory. Crystals 2023, 13, 574. [Google Scholar] [CrossRef]
- Putungan, D.B.; Llemitand, C.L.T.; Santos-Putungan, A.B.; Sarmago, R.V.; Gebauer, R. Biaxial compressive strain enhances calcium binding and mobility on two-dimensional Sc2C: A density functional theory investigation. Phys. Chem. Chem. Phys. 2024, 26, 4298–4305. [Google Scholar] [CrossRef]
- Sfuncia, G.; Nicotra, G.; Giannazzo, F.; Pécz, B.; Gueorguiev, G.K.; Kakanakova-Georgieva, A. 2D graphitic-like gallium nitride and other structural selectivity in confinement at the graphene/SiC interface. CrystEngComm 2023, 25, 5810–5817. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Farmer, W.; Hsiao, C.L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Ankit, K.; Gueorguiev, G.K. Density functional theory-fed phase field model for semiconductor nanostructures: The case of self-induced core-shell InAlN nanorods. CrystEngComm 2024, 24, 4717–4727. [Google Scholar] [CrossRef]
- Petralanda, U.; Trizio, L.D.; Gariano, G.; Cingolani, R.; Manna, L.; Artyukhin, S. Triggering Cation Exchange Reactions by Doping. J. Phys. Chem. Lett. 2018, 9, 4895–4900. [Google Scholar] [CrossRef]
- Mishra, S.; Przezdziecka, E.; Wozniak, W.; Adhikari, A.; Jakieala, R.; Paszkowicz, W.; Sulich, A.; Kopalko, K.; Guziewicz, E. Structural Properties of Thin ZnO Films Deposited by ALD under O-rich and Zn-rich Growth Conditions and Their Relationship with Electrical Parameters. Materials 2021, 14, 4048. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guziewicz, E.; Mishra, S.; Amati, M.; Gregoratti, L.; Volnianska, O. The Impact of Carbon on Electronic Structure of N-Doped ZnO Films: Scanning Photoelectron Microscopy Study and DFT Calculations. Nanomaterials 2025, 15, 30. https://doi.org/10.3390/nano15010030
Guziewicz E, Mishra S, Amati M, Gregoratti L, Volnianska O. The Impact of Carbon on Electronic Structure of N-Doped ZnO Films: Scanning Photoelectron Microscopy Study and DFT Calculations. Nanomaterials. 2025; 15(1):30. https://doi.org/10.3390/nano15010030
Chicago/Turabian StyleGuziewicz, Elzbieta, Sushma Mishra, Matteo Amati, Luca Gregoratti, and Oksana Volnianska. 2025. "The Impact of Carbon on Electronic Structure of N-Doped ZnO Films: Scanning Photoelectron Microscopy Study and DFT Calculations" Nanomaterials 15, no. 1: 30. https://doi.org/10.3390/nano15010030
APA StyleGuziewicz, E., Mishra, S., Amati, M., Gregoratti, L., & Volnianska, O. (2025). The Impact of Carbon on Electronic Structure of N-Doped ZnO Films: Scanning Photoelectron Microscopy Study and DFT Calculations. Nanomaterials, 15(1), 30. https://doi.org/10.3390/nano15010030





