Two-Dimensional Materials for Raman Thermometry on Power Electronic Devices
Abstract
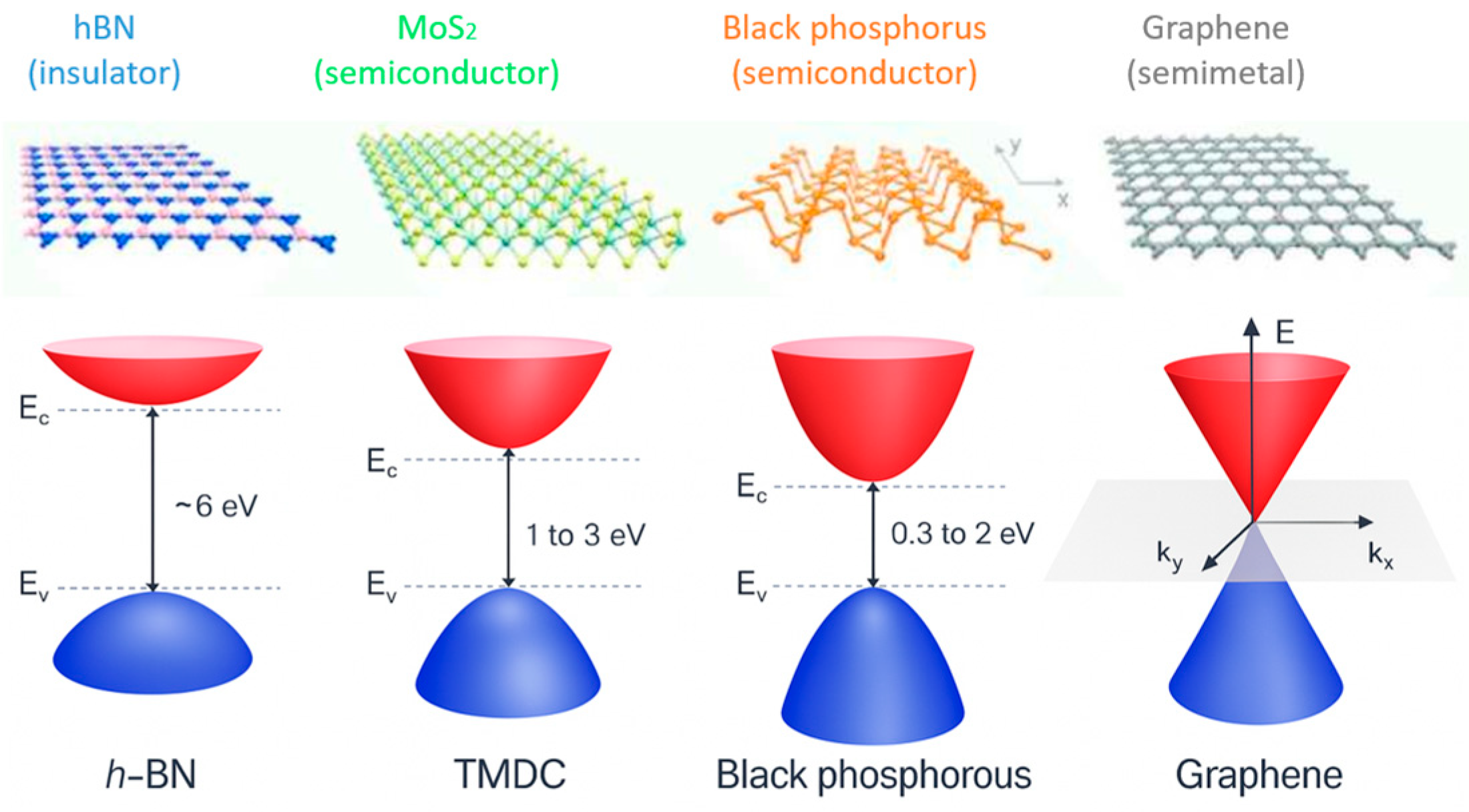
1. Introduction
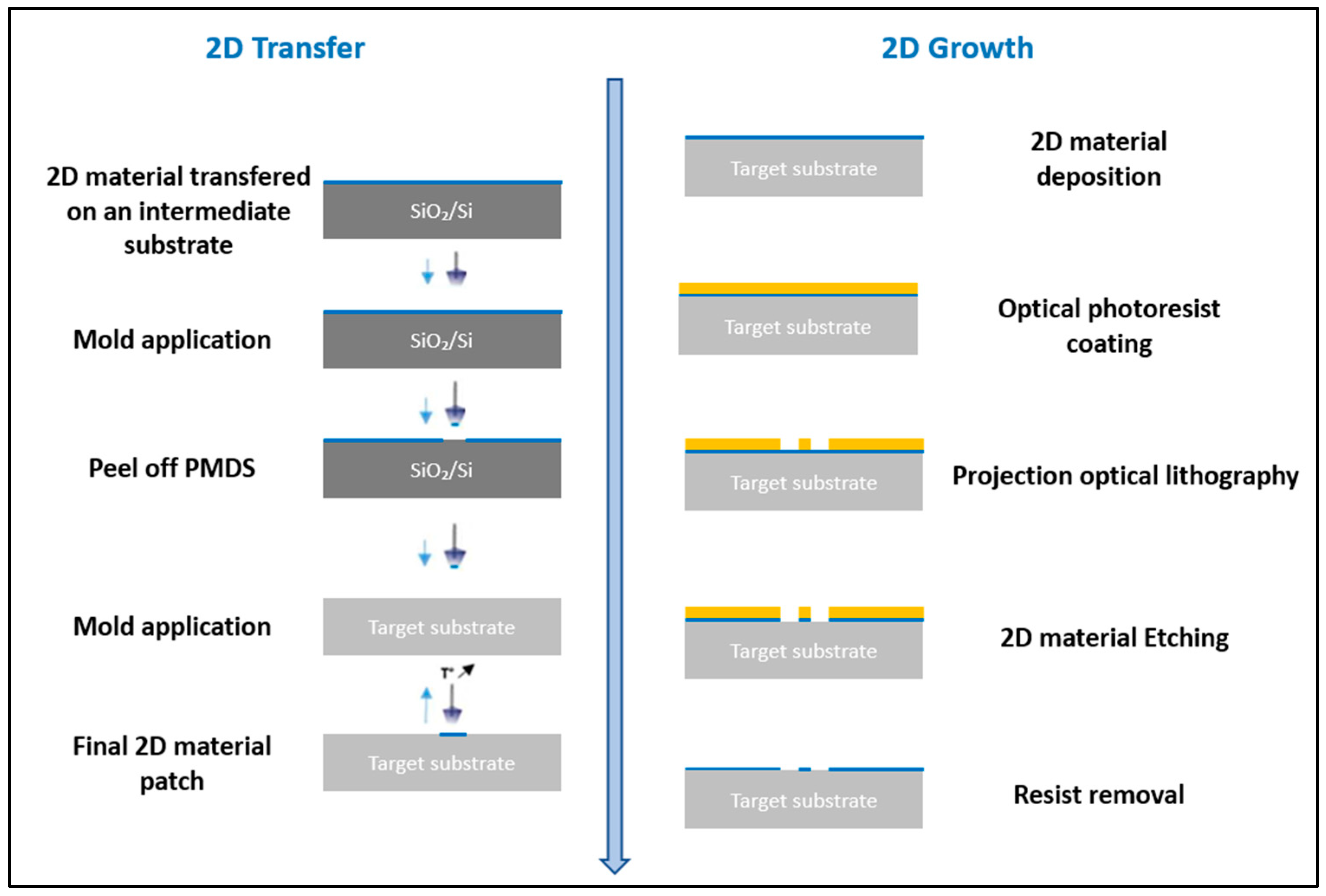
2. Two-Dimensional Patches Manufacturing
2.1. Two-Dimensional Materials Growth by MBE
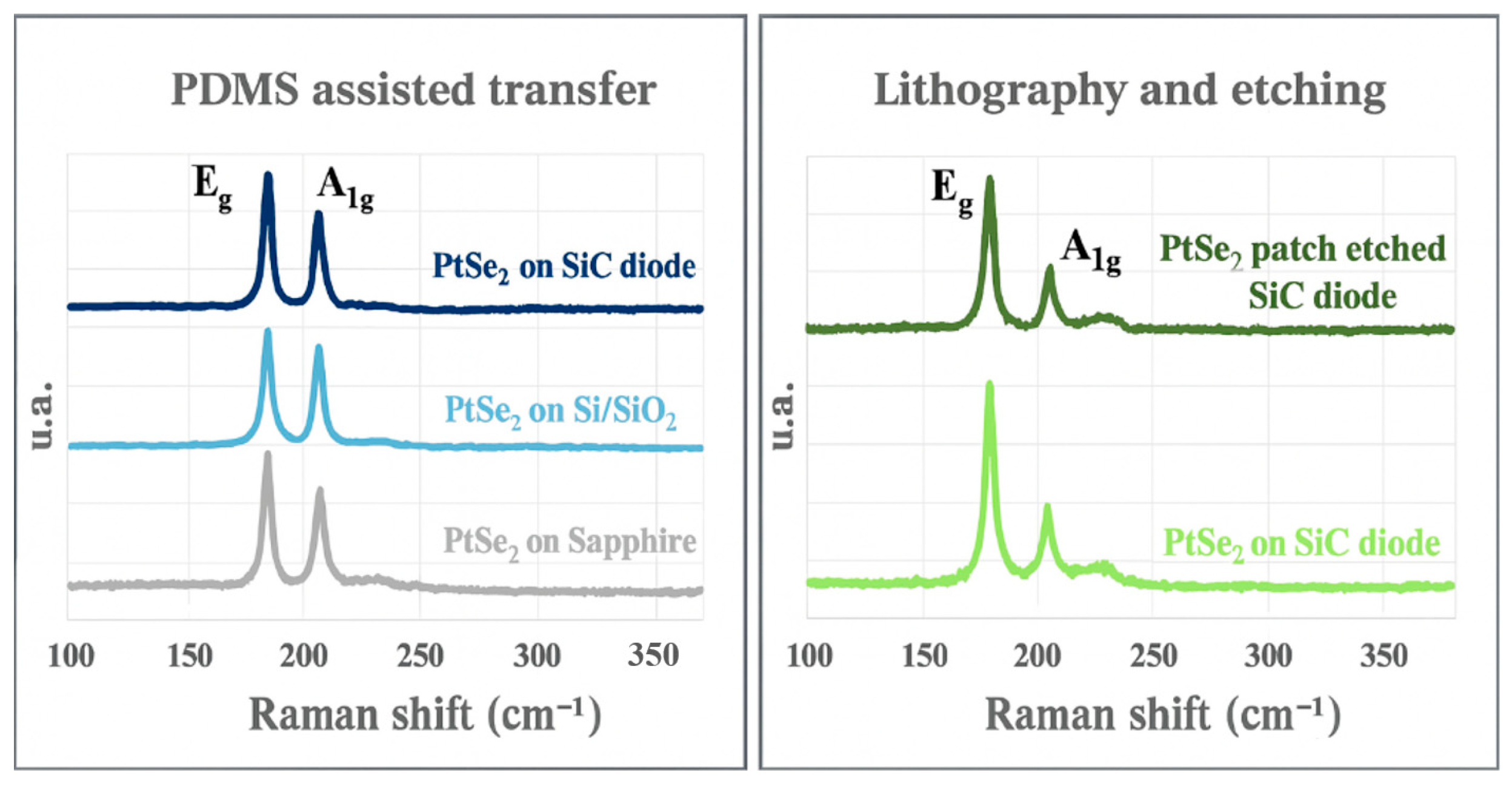
2.2. Two-Dimensional Transfer Technique from Initial Substrate to Power Devices
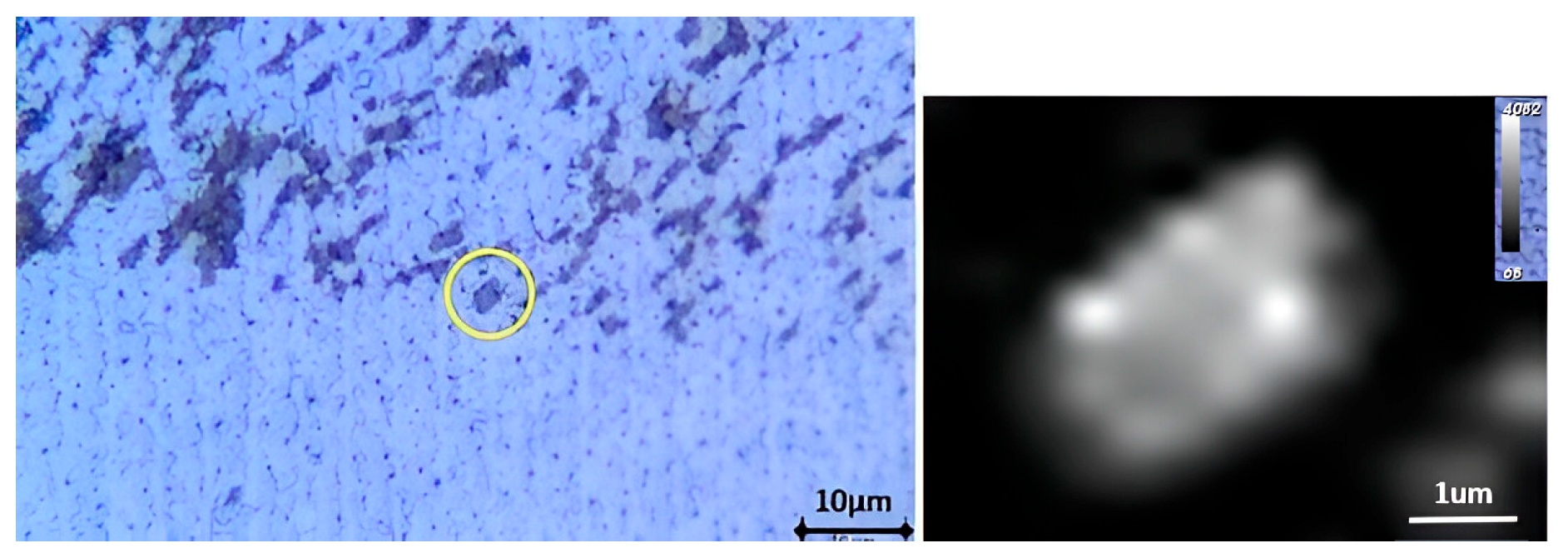
2.3. Direct 2D Growth and Patches Manufacturing on Power Devices
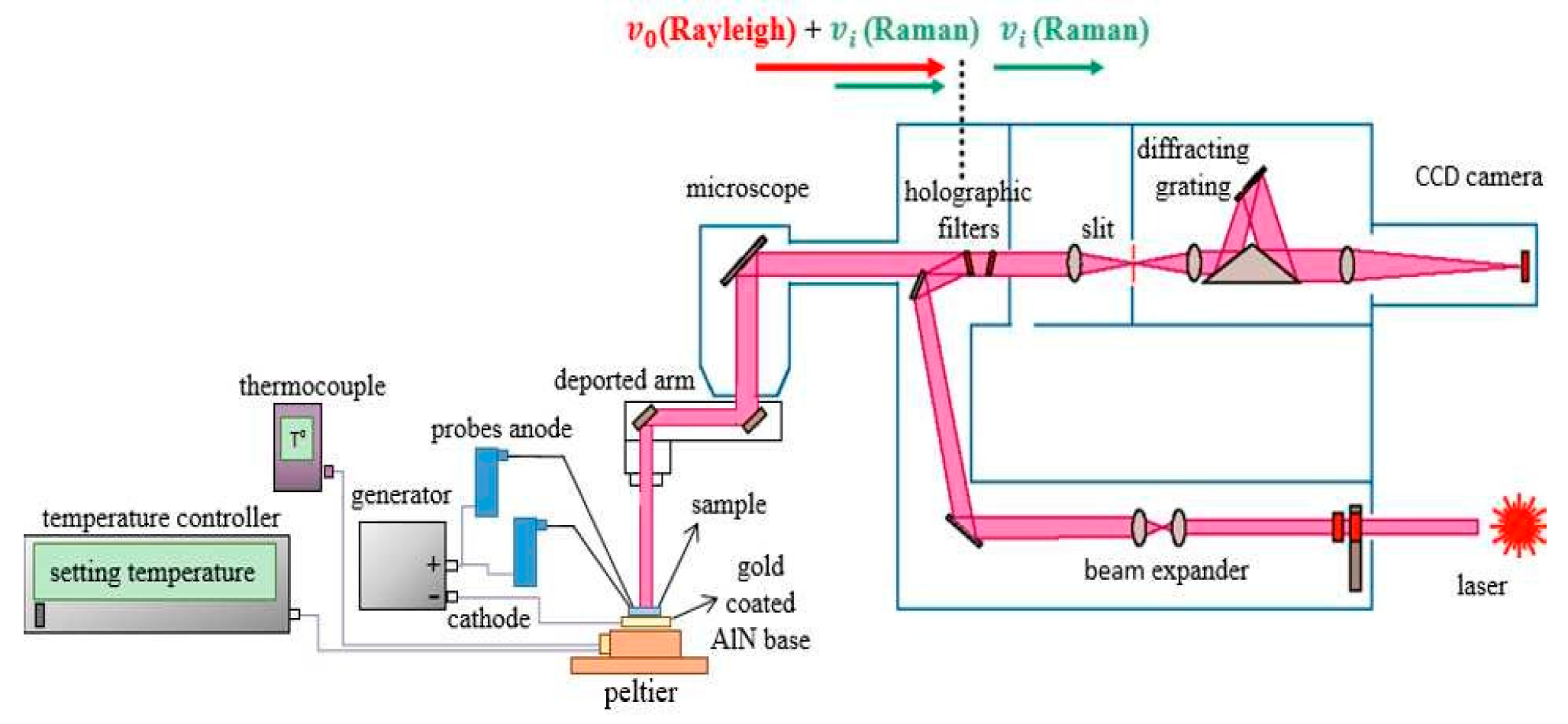
3. Experimental Setup for Thermal Measurements
3.1. Raman Spectroscopy Principle
- (i)
- Elastic scattering with no change of light frequency (Rayleigh);
- (ii)
- Inelastic scattering (Raman effect) involving atomic vibration modes (phonons) and change of frequency: ωs = ω0 − ωp for Stokes line (creation of a phonon) and ωs = ω0 + ωp for the anti-Stokes line (annihilation of a phonon). The Raman peaks (quasi-Lorentzian functions) are characteristic of the material investigated and depend on both temperature and stress. The Full Width Half Maximum (FWHM) of the peaks is very small allowing accurate monitoring of the peak shift and the intensity of the anti-Stokes and Stokes peaks. Moreover, due to its high spatial resolution (<1 μm), micro-Raman spectroscopy is a powerful tool for local measurements of temperature in micro-devices.
- (i)
- The temperature T relates to the intensity ratio IAS/IS of anti-Stokes and Stokes lines (AS/S), following the formula [18]:
- (ii)
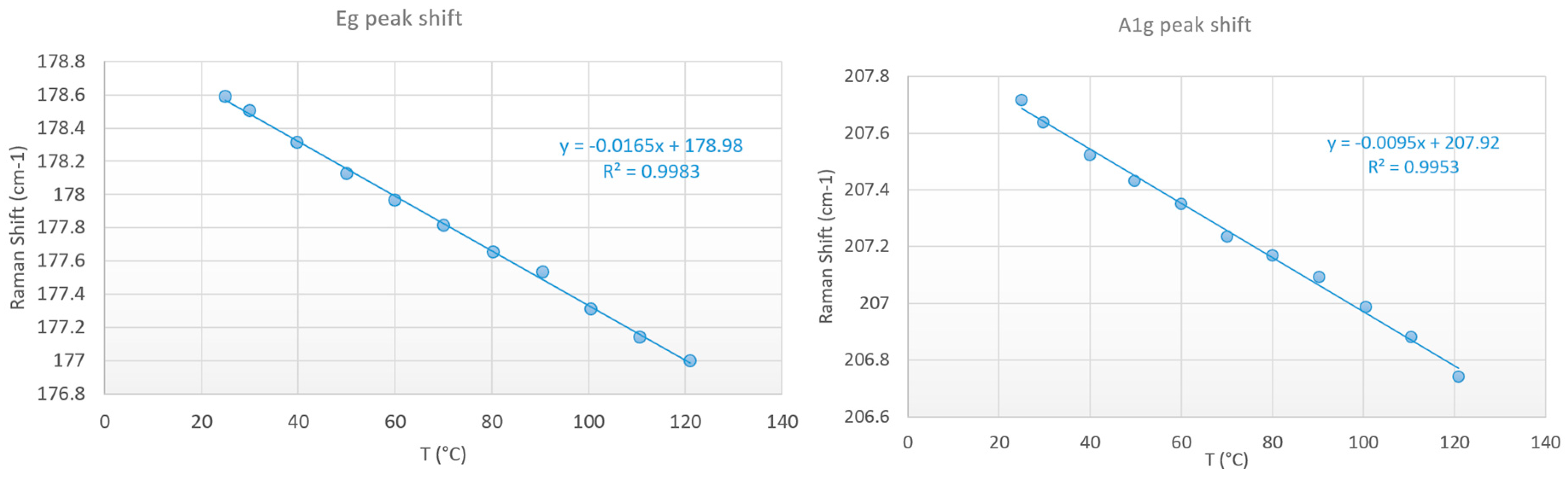
- Temperature can also be measured from the Raman peak position. The temperature dependence of the Raman frequency ωp is approximately linear:
3.2. Instrumentation and Thermal Setup
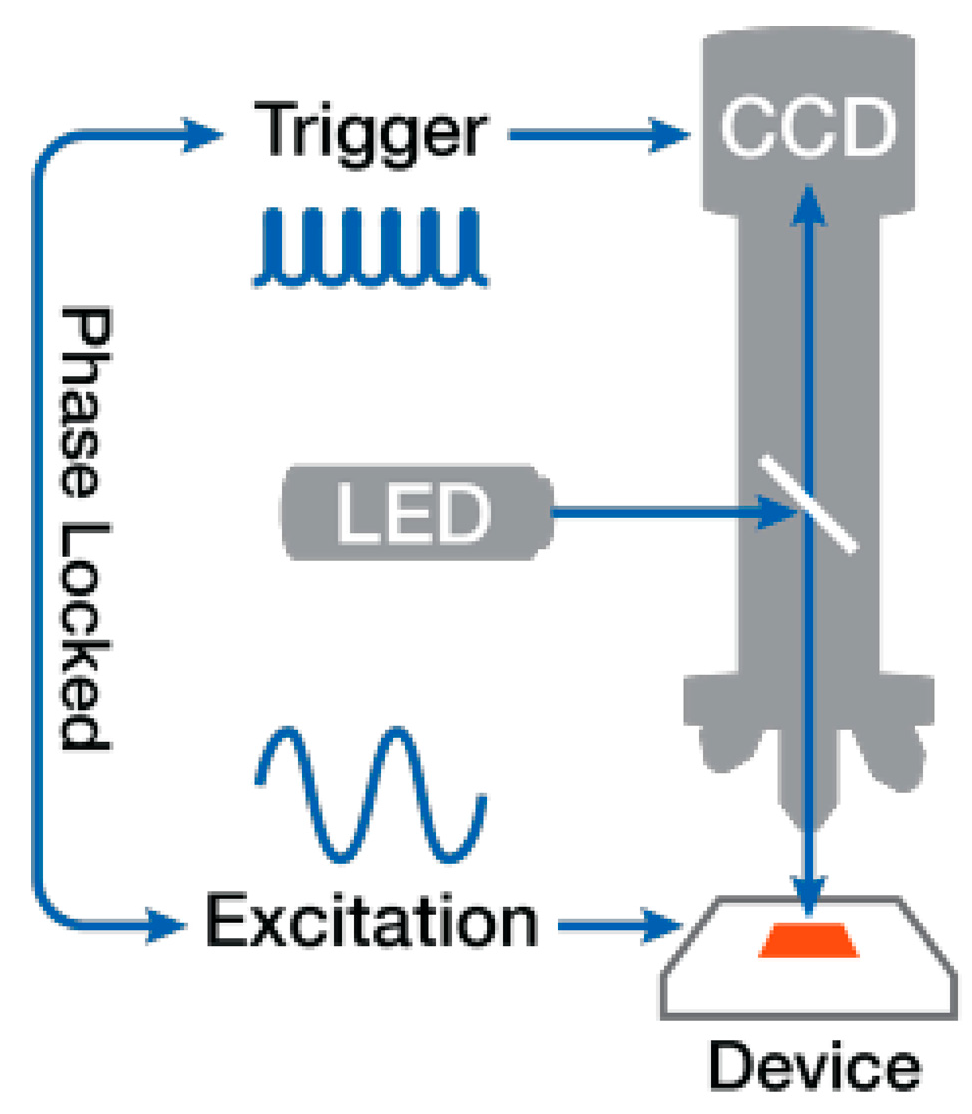
3.3. Thermoreflectance Principle
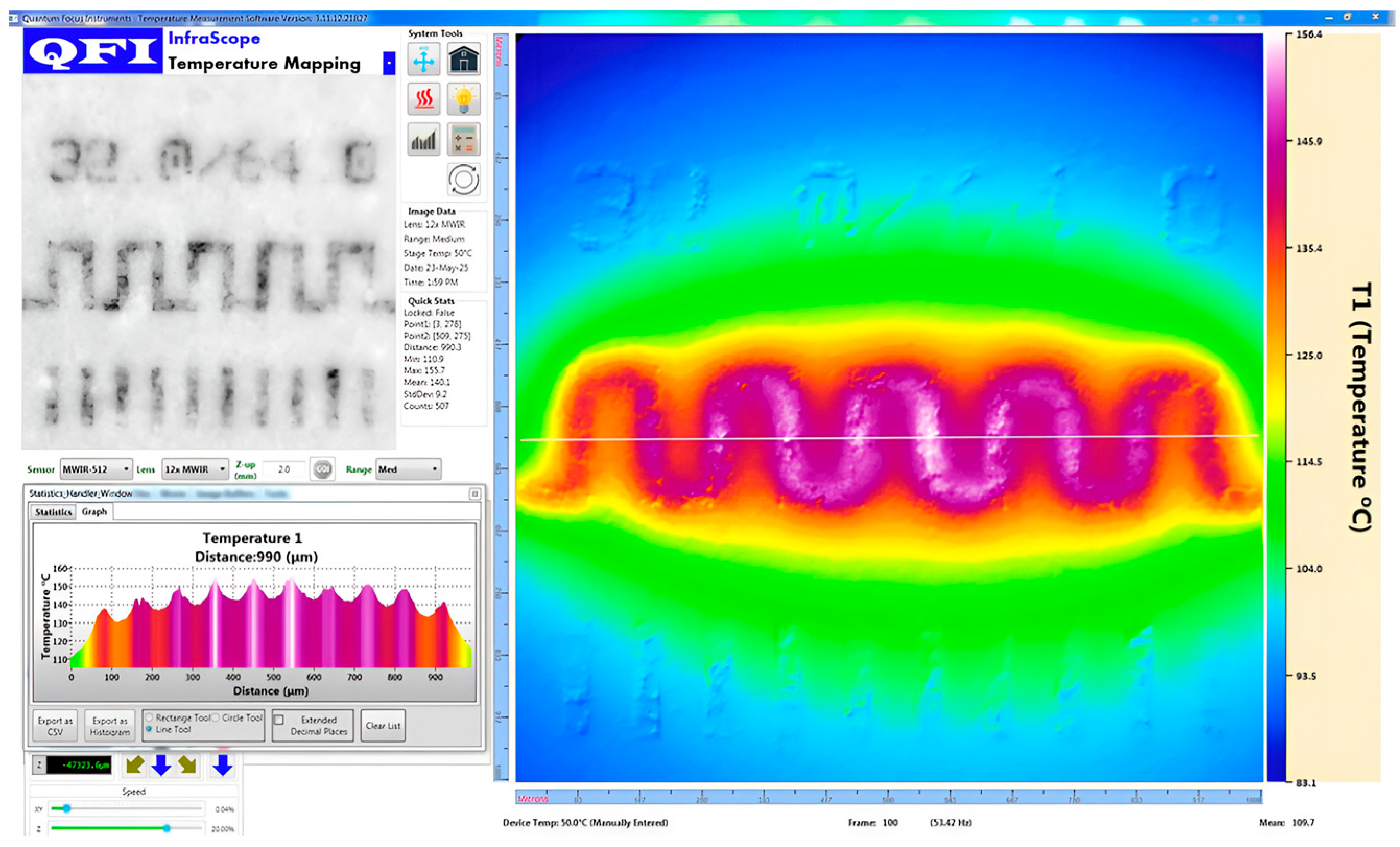
3.4. Thermoreflectance Thermal Setup
4. Experiments and Results
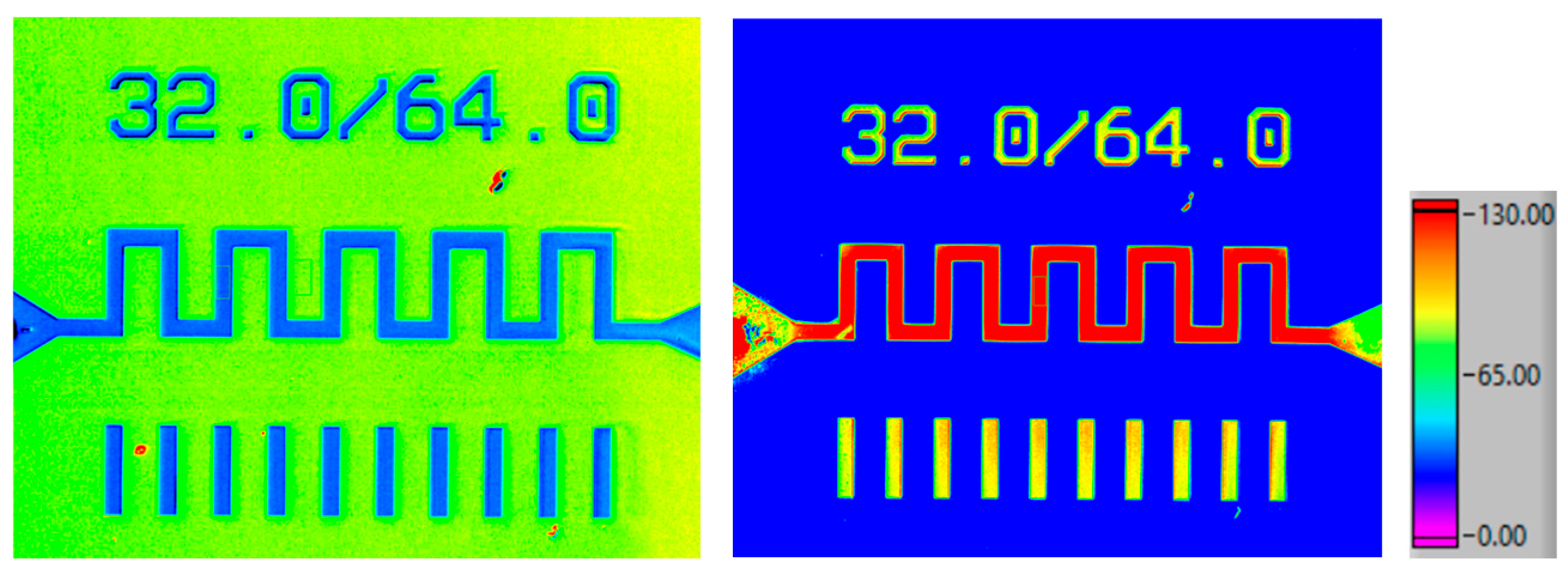
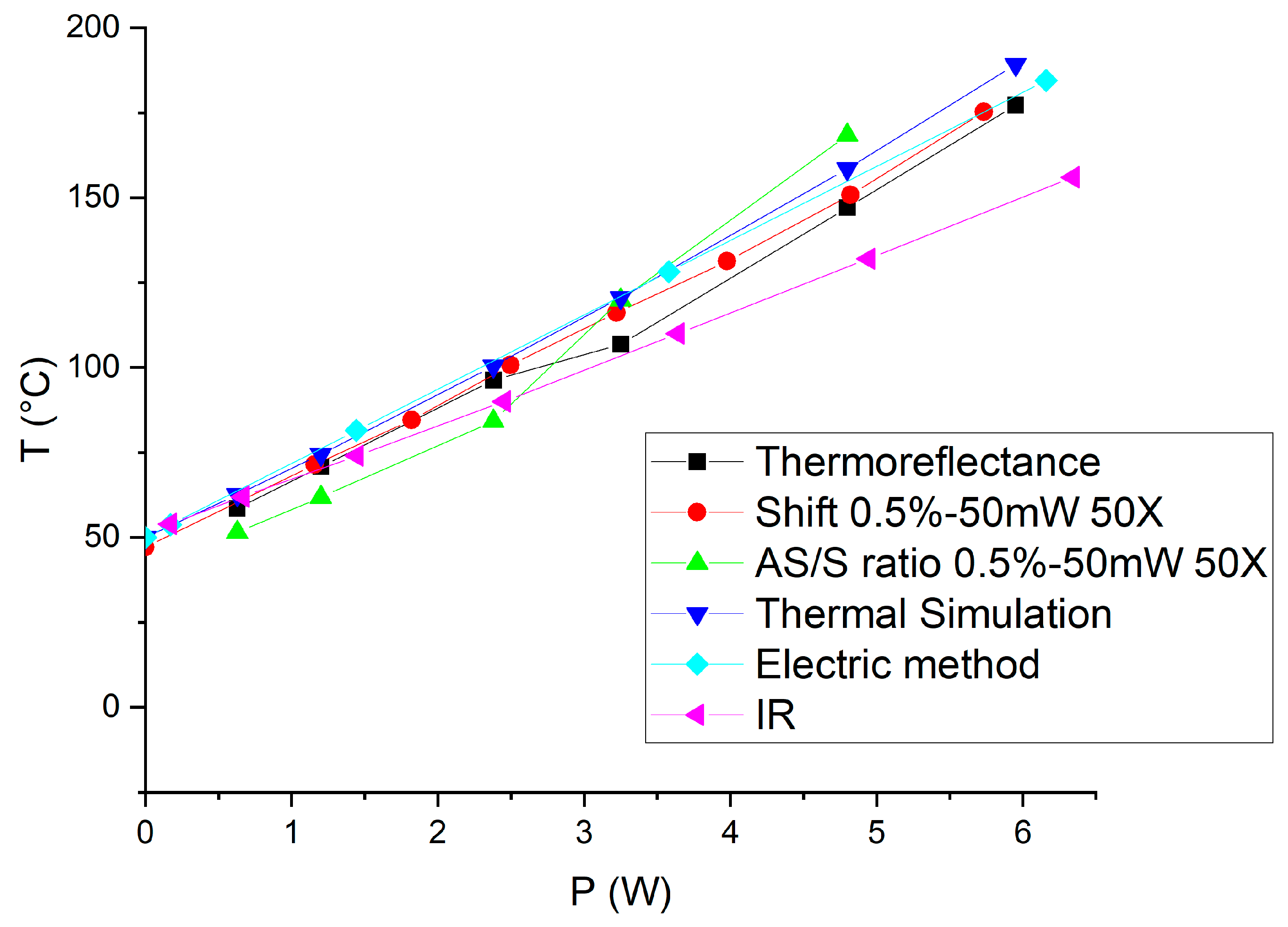
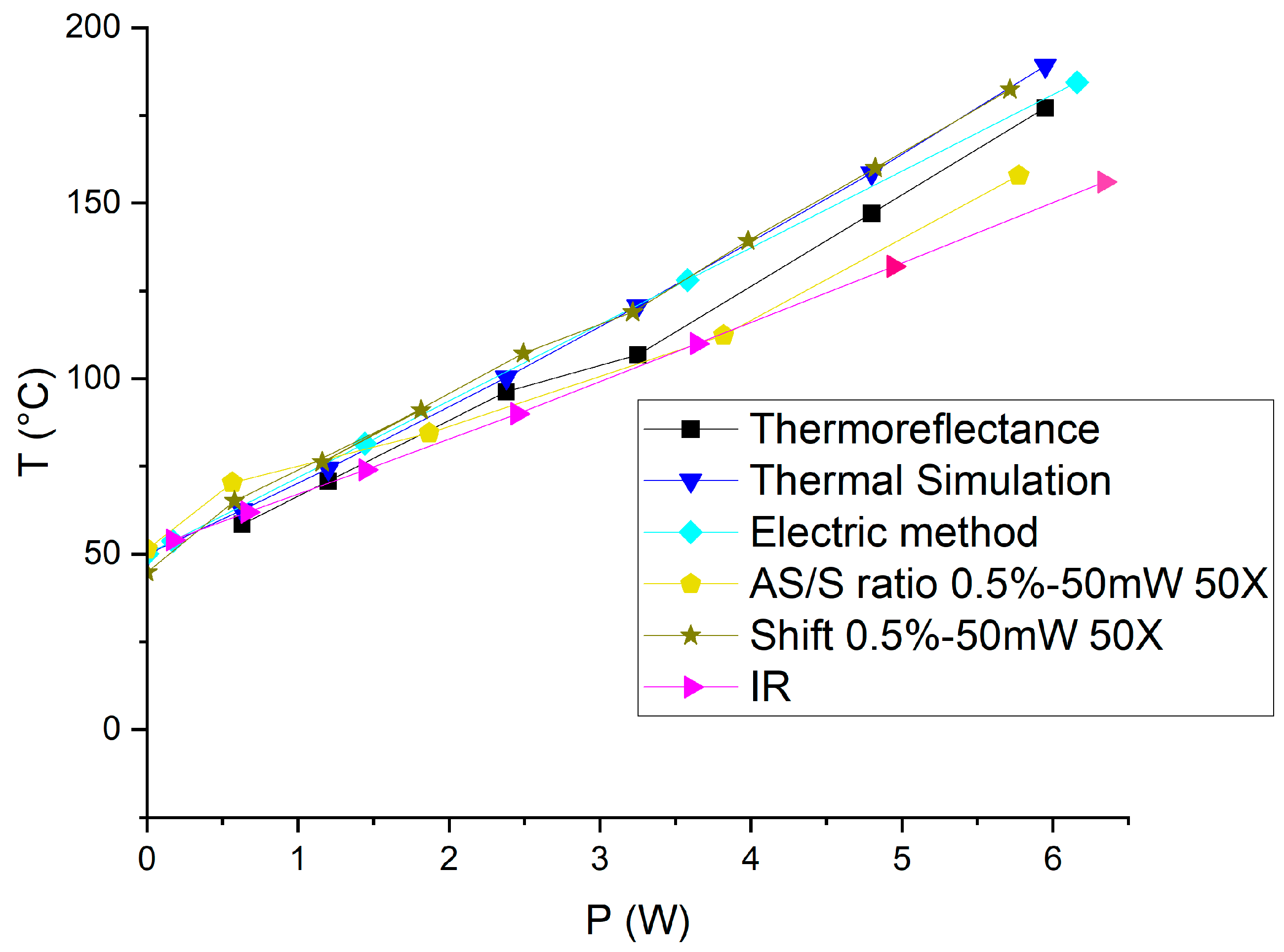
4.1. Serpentine Gold Resistors on Silicon Substrate
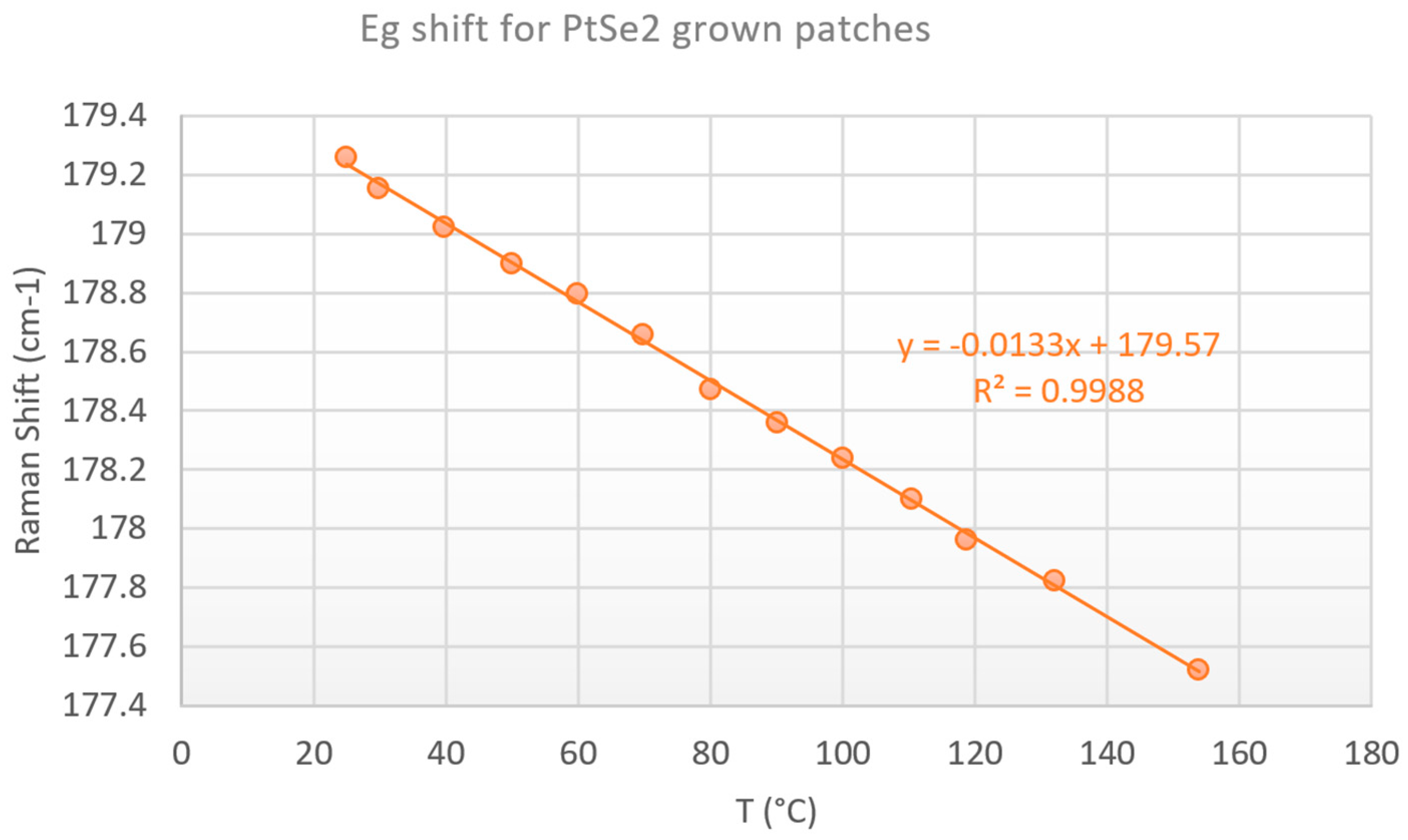
4.1.1. Raman Spectroscopy Results for the Gold Resistor
4.1.2. Thermoreflectance Results for the Gold Resistor
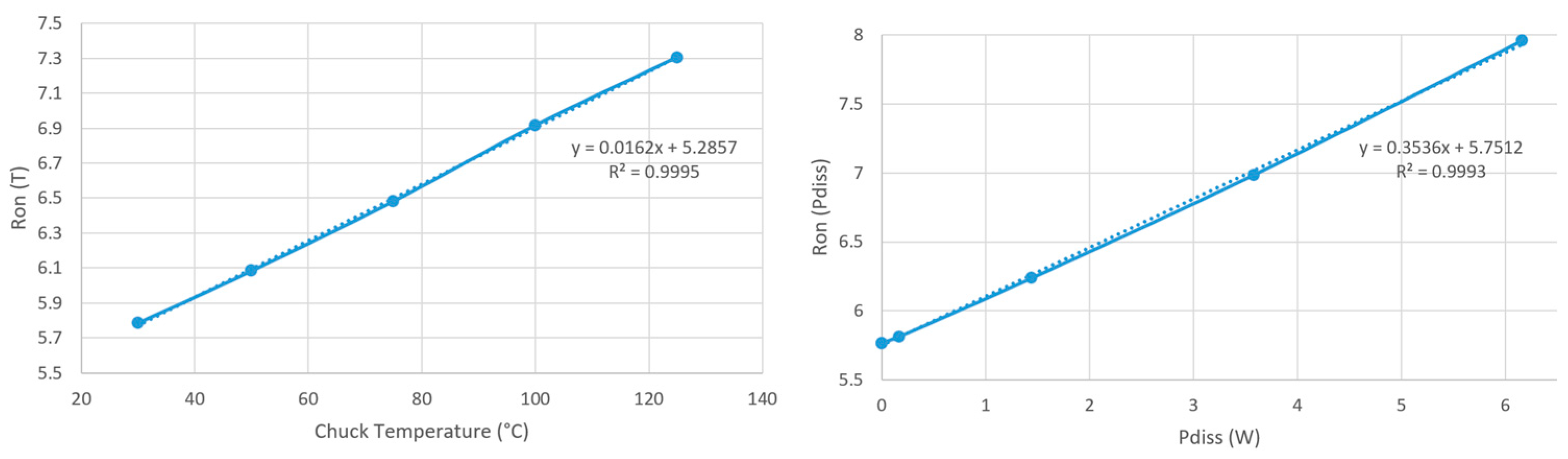
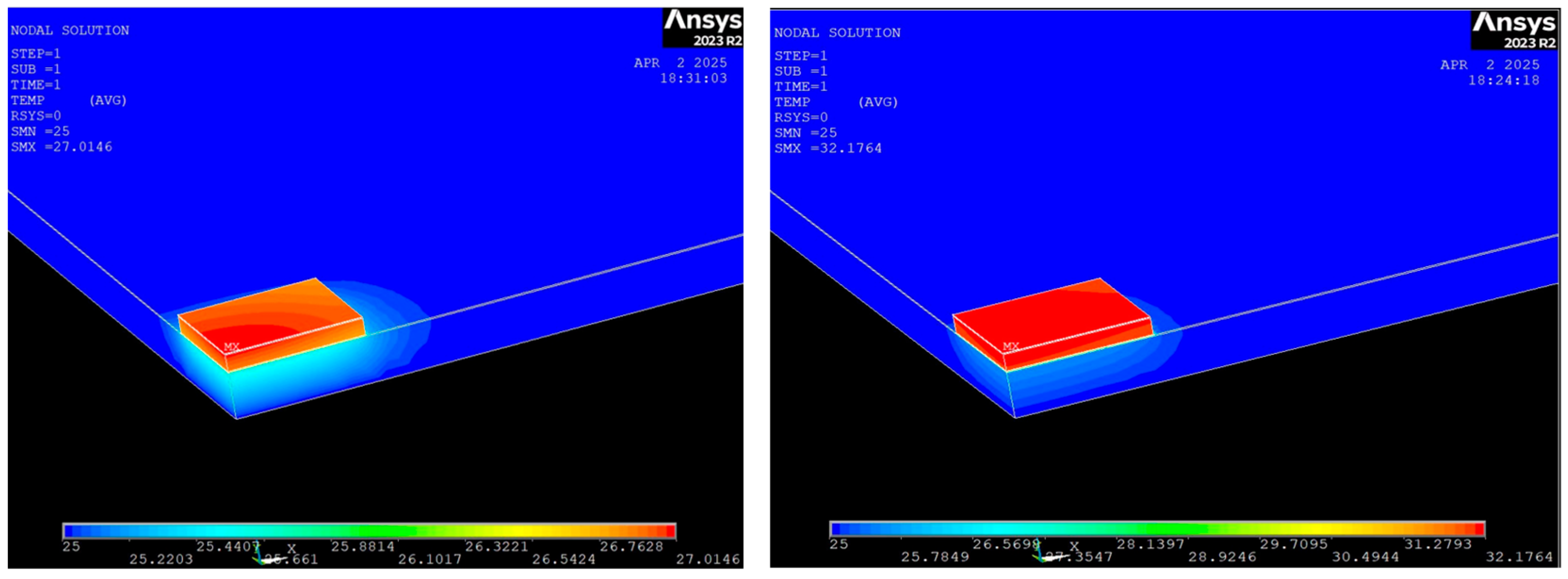
4.1.3. Three-Dimensional Finite Element Simulation Results
4.1.4. Electrical Method Results
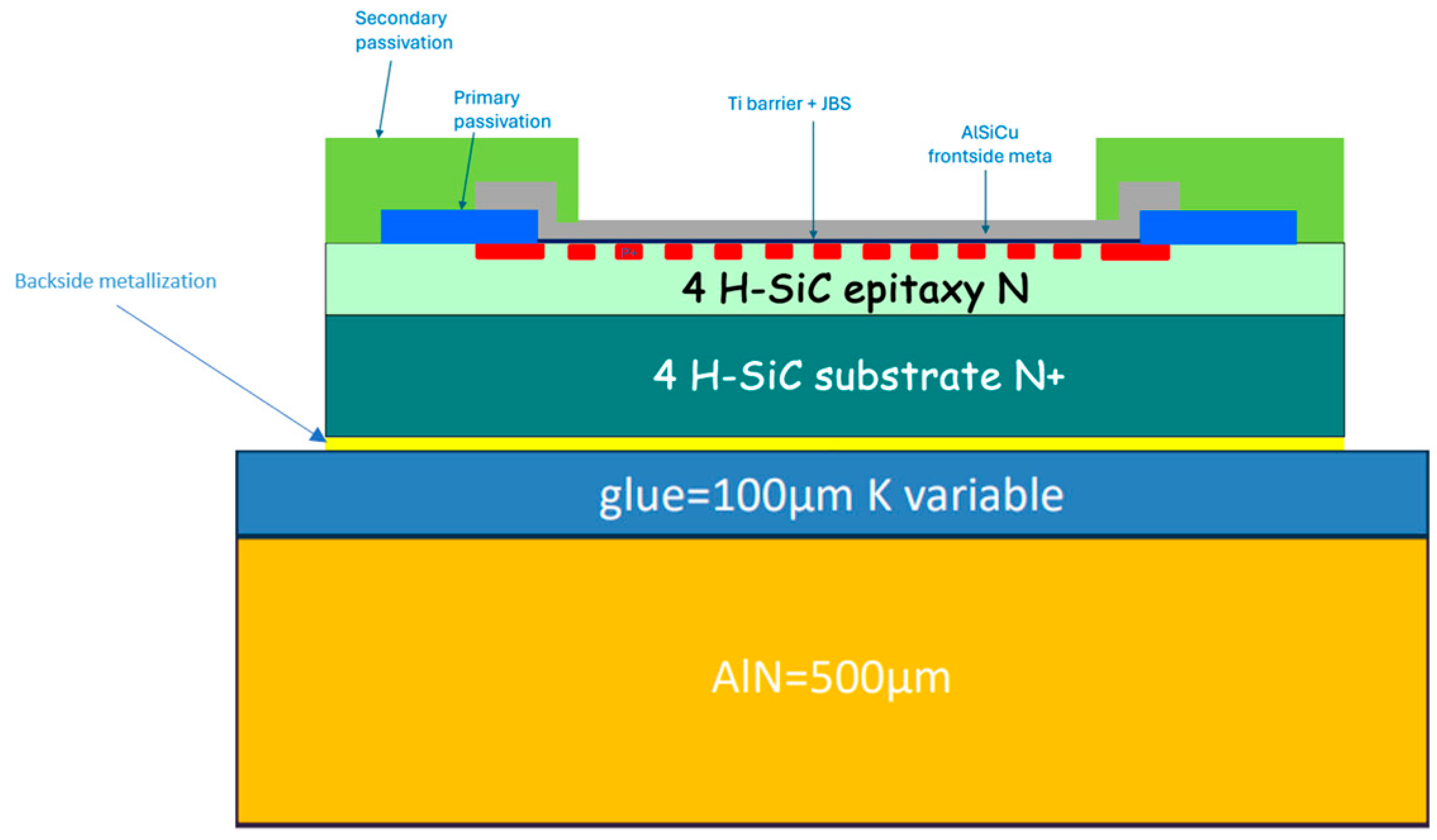
4.2. SiC JBS Diode
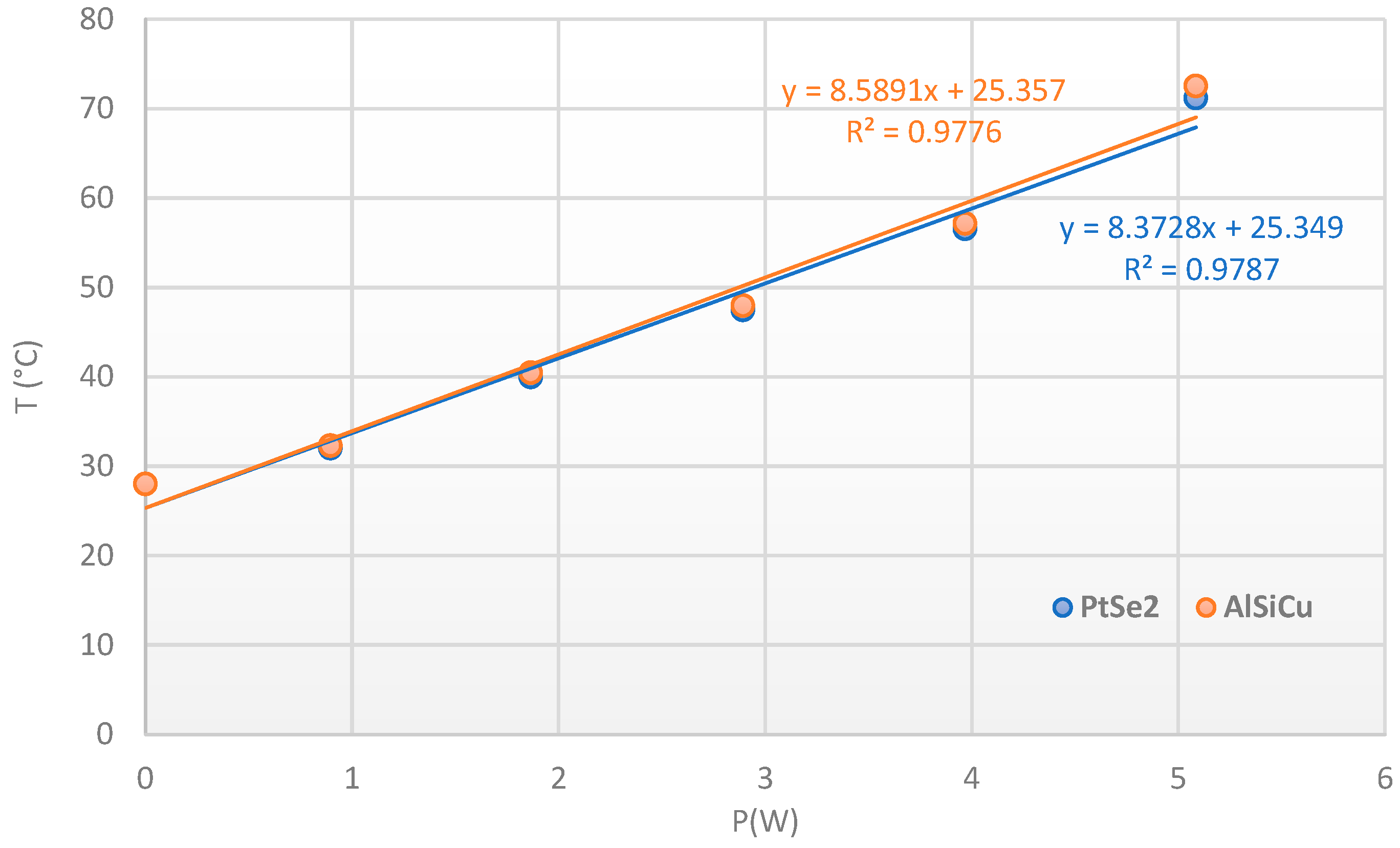
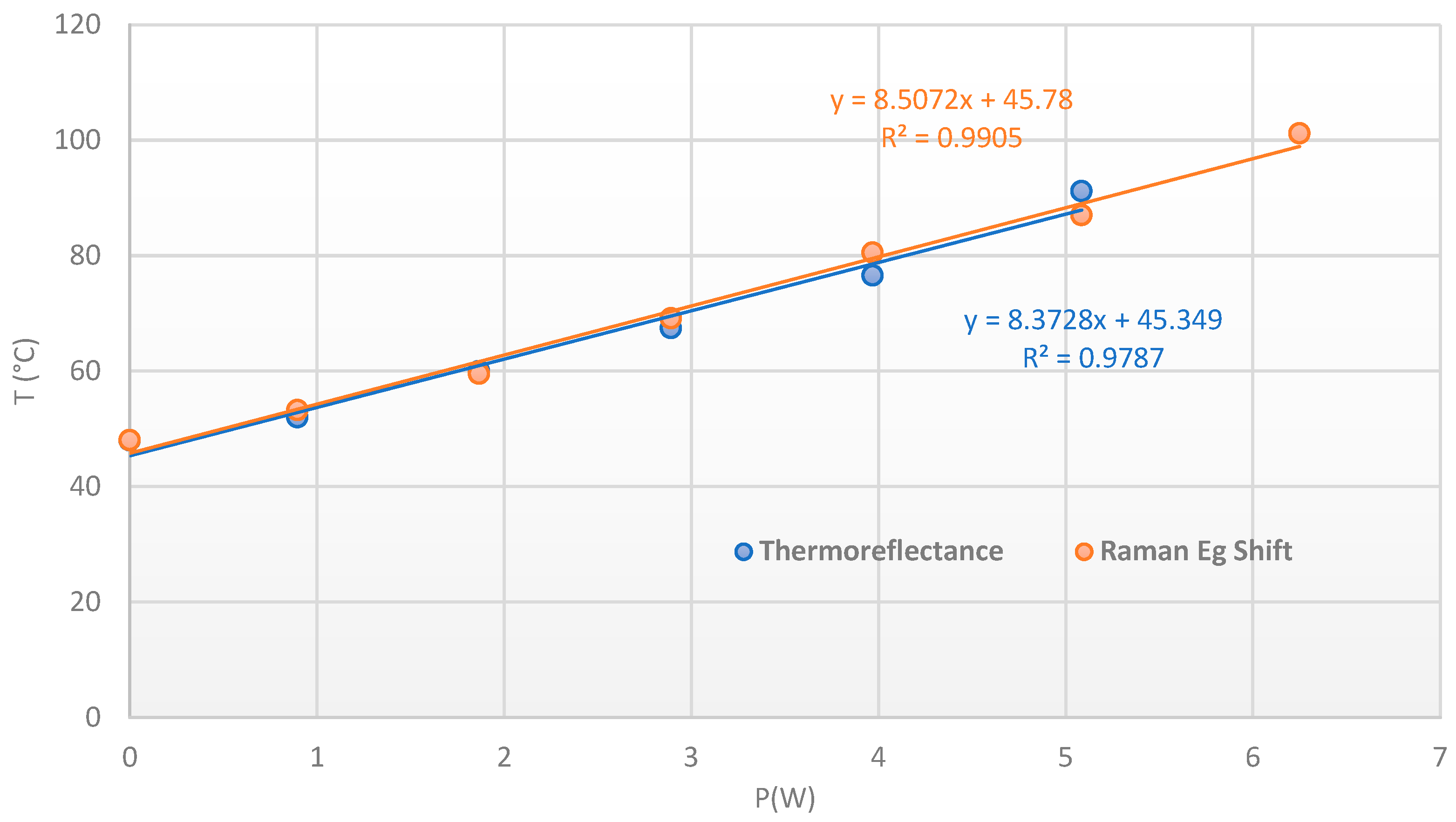
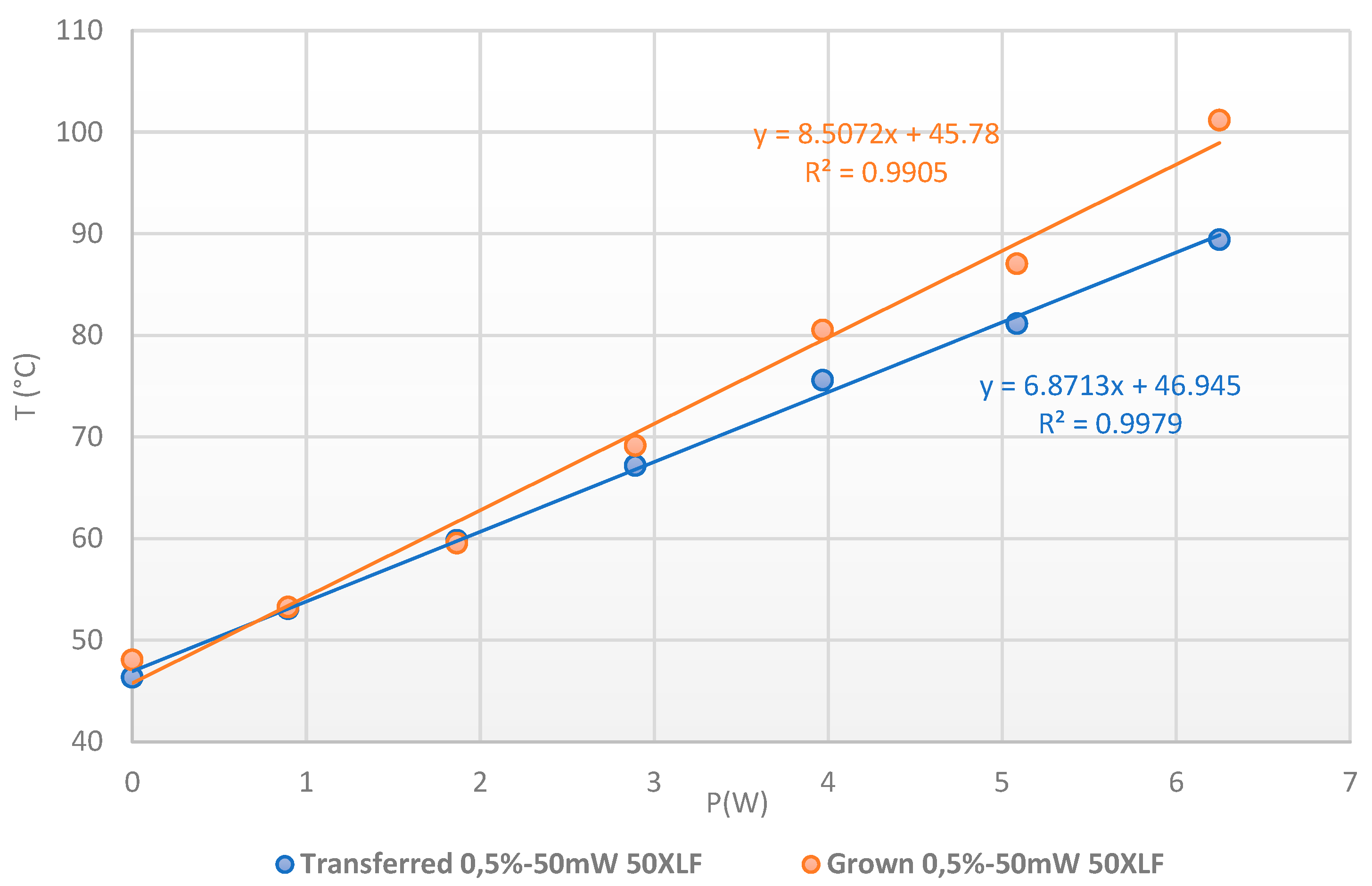
4.2.1. Thermoreflectance Results for the SiC JBS Diode
4.2.2. Raman Spectroscopy Results for the SiC JBS Diode
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- STMicroelectronics. STMicroelectronics Company Presentation; STMicroelectronics: Geneva, Switzerland, 2024. [Google Scholar]
- Baczkowski, L.; Jacquet, J.-C.; Jardel, O.; Gaquiere, C.; Moreau, M.; Carisetti, D.; Brunel, L.; Vouzelaud, F.; Mancuso, Y. Thermal Characterization Using Optical Methods of AlGaN/GaN HEMTs on SiC Substrate in RF Operating Conditions. IEEE Trans. Electron Devices 2015, 62, 3992–3998. [Google Scholar] [CrossRef]
- Available online: https://microsanj.com/products/thermoreflectance-imaging/sanjscope-nt220 (accessed on 18 August 2025).
- Jakani, A.; Sommet, R.; Gaillard, F.; Nallatamby, J.-C. Comparison of GaN HEMTs Thermal Results through different measurements methodologies: Validation with 3D simulation. In Proceedings of the 27th International Workshop on Thermal Investigations of ICs and Systems, Berlin, Germany, 23 September 2021. [Google Scholar] [CrossRef]
- Kuball, M.; Hayes, J.; Uren, M.; Martin, I.; Birbeck, J.; Balmer, R.; Hughes, B. Measurement of temperature in active high-power AlGaN/GaN HFETs using Raman spectroscopy. IEEE Electron Device Lett. 2002, 23, 7–9. [Google Scholar] [CrossRef]
- Sarua, A.; Bullen, A.; Haynes, M.; Kuball, M. High-Resolution Raman Temperature Measurements in GaAs p-HEMT Multifinger Devices. IEEE Trans. Electron Devices 2007, 54, 1838–1842. [Google Scholar] [CrossRef]
- Lundh, J.S.; Zhang, T.; Zhang, Y.; Xia, Z.; Wetherington, M.; Lei, Y.; Kahn, E.; Rajan, S.; Terrones, M.; Choi, S. 2D Materials for Universal Thermal Imaging of Micro- and Nanodevices: An Application to Gallium Oxide Electronics. ACS Appl. Electron. Mater. 2020, 2, 2945–2953. [Google Scholar] [CrossRef]
- Carisetti, D.; Cholet, J.; Frogé, L.; Seneor, P.; Dlubak, B.; Carré, E.; Desgué, E.; Garabedian, P.; Legagneux, P.; Renaudin, V.; et al. 2D Materials for Raman Thermal Measurements on Power Electronics Devices. In Proceedings of the 2024 30th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Toulouse, France, 25–27 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Lim, S.; Suk, J.W. Flexible temperature sensors based on two-dimensional materials for wearable devices. Nanotechnology 2023, 34, 042001. [Google Scholar] [CrossRef]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Lee, J.Y.; Shin, J.-H.; Lee, G.-H.; Lee, C.-H. Two-Dimensional Semiconductor Optoelectronics Based on van der Waals Heterostructures. Nanomaterials 2016, 6, 193. [Google Scholar] [CrossRef]
- Brocero, G.; Guhel, Y.; Eudeline, P.; Sipma, J.P.; Gaquiere, C.; Boudart, B. Measurement of Self-Heating Temperature in AlGaN/GaN HEMTs by Using Cerium Oxide Micro-Raman Thermometers. IEEE Trans. Electron Devices 2019, 66, 4156–4163. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, J.; Yu, Z.; Yu, P.; Xu, K.; Lau, S.P.; Zhou, W.; Liu, Z.; Wang, X.; Ji, W.; et al. High-Electron-Mobility and Air-Stable 2D Layered PtSe2 FETs. Adv. Mater. 2017, 29, 1604230. [Google Scholar] [CrossRef]
- Desgué, E.; Verschueren, I.; Tharrault, M.; Dosenovic, D.; Largeau, L.; Grimaldi, E.; Pommier, D.; Jussey, D.; Moreau, B.; Carisetti, D.; et al. Growth of Highly Conductive PtSe2 Films Controlled by Raman Metrics for High-Frequency Photodetectors and Optoelectronic Mixers at 1.55 µm. arXiv 2025, arXiv:2503.20659. [Google Scholar]
- Ji, J.; Zhou, Y.; Zhou, B.; Desgué, E.; Legagneux, P.; Jepsen, P.U.; Bøggild, P. Probing Carrier Dynamics in Large-Scale MBE-Grown PtSe2 Films by Terahertz Spectroscopy. ACS Appl. Mater. Interfaces 2023, 15, 51319–51329. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Q.; Xu, D.; Zhu, Y.; Kim, S.; Cui, Y.; Zhong, L.; Liu, M. Capillary-Force-Assited Clen-Stamp Transfer of Two-Dimensional Materials. Nano Lett. 2017, 17, 6961–6967. [Google Scholar] [CrossRef]
- Tharrault, M.; Desgué, E.; Carisetti, D.; Plaçais, B.; Voisin, C.; Legagneux, P.; Baudin, E. Raman Spectroscopy of Monolayer to Bulk PtSe2 Exfoliated Crystals. 2D Mater. 2025, 11, 025011. [Google Scholar] [CrossRef]
- Tuschel, D. Raman Thermometry. Spectroscopy 2016, 31, 8–13. [Google Scholar]
- Karrame, K.; Jakani, A.; Kakou, N.L.A.; Chang, C.; Colas, M.; Nallatamby, J.C.; Sommet, R. Thermal Simulation and Characterization of GaN HEMT Using Gate Resistance Thermometry and Thermoreflectance Imaging. In Proceedings of the 2022 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Limoges, France, 6–8 July 2022. [Google Scholar]
- Karrame, K.; Chang, C.; Nallatamby, J.-C.; Colas, M.; Sommet, R. Joint Use of Thermal Characterization and Simulation of AlGaN/GaN High-Electron Mobility Transistors in Transient and Steady State Regimes to Estimate the Hotspot Temperature. Electronics 2025, 14, 935. [Google Scholar] [CrossRef]
- Favaloro, T.; Bahk, J.H.; Shakouri, A. Export Citation Characterization of the Temperature Dependence of the Thermoreflectance Coefficient for Conductive Thin Films. AIP Publ. 2015, 86, 24903. [Google Scholar]
- Burzo, M.G.; Komarov, P.L.; Raad, P.E. Optimized thermo-reflectance system for measuring the thermal properties of thin-films and their interfaces. In Proceedings of the Twenty-Second Annual IEEE Semiconductor Thermal Measurement And Management Symposium, Dallas, TX, USA, 14–16 March 2006; pp. 87–94. [Google Scholar] [CrossRef]
- Paasschens, J.C.J.; Harmsma, S.; van der Toorn, R. Dependence of thermal resistance on ambient and actual temperature. In Proceedings of the IEEE Bipolar/BiCMOS Circuits and Technology Meeting (BCTM), Montreal, QC, Canada, 12–14 September 2024; pp. 96–99. [Google Scholar]
- Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=66a15d609a3f4c829cb6ad08f0dafc01&ckck=1 (accessed on 18 August 2025).
- Beaudhuin, M. Thermal Conductivity Measurement of Thin Layers by the 3ω Method; Technical Note TN-2006/00375; Koninklijke Philips Electronics N.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Available online: https://www.st.com/resource/en/datasheet/stpsc20g12-y.pdf (accessed on 18 August 2025).
- Qian, X.; Jiang, P.; Yang, R. Anisotropic thermal conductivity of 4H and 6H silicon carbide measured using time-domain thermoreflectance. Mater. Today Phys. 2017, 3, 70–75. [Google Scholar] [CrossRef]
- Available online: https://www.epotek.com/docs/en/Datasheet/H20E.pdf (accessed on 18 August 2025).









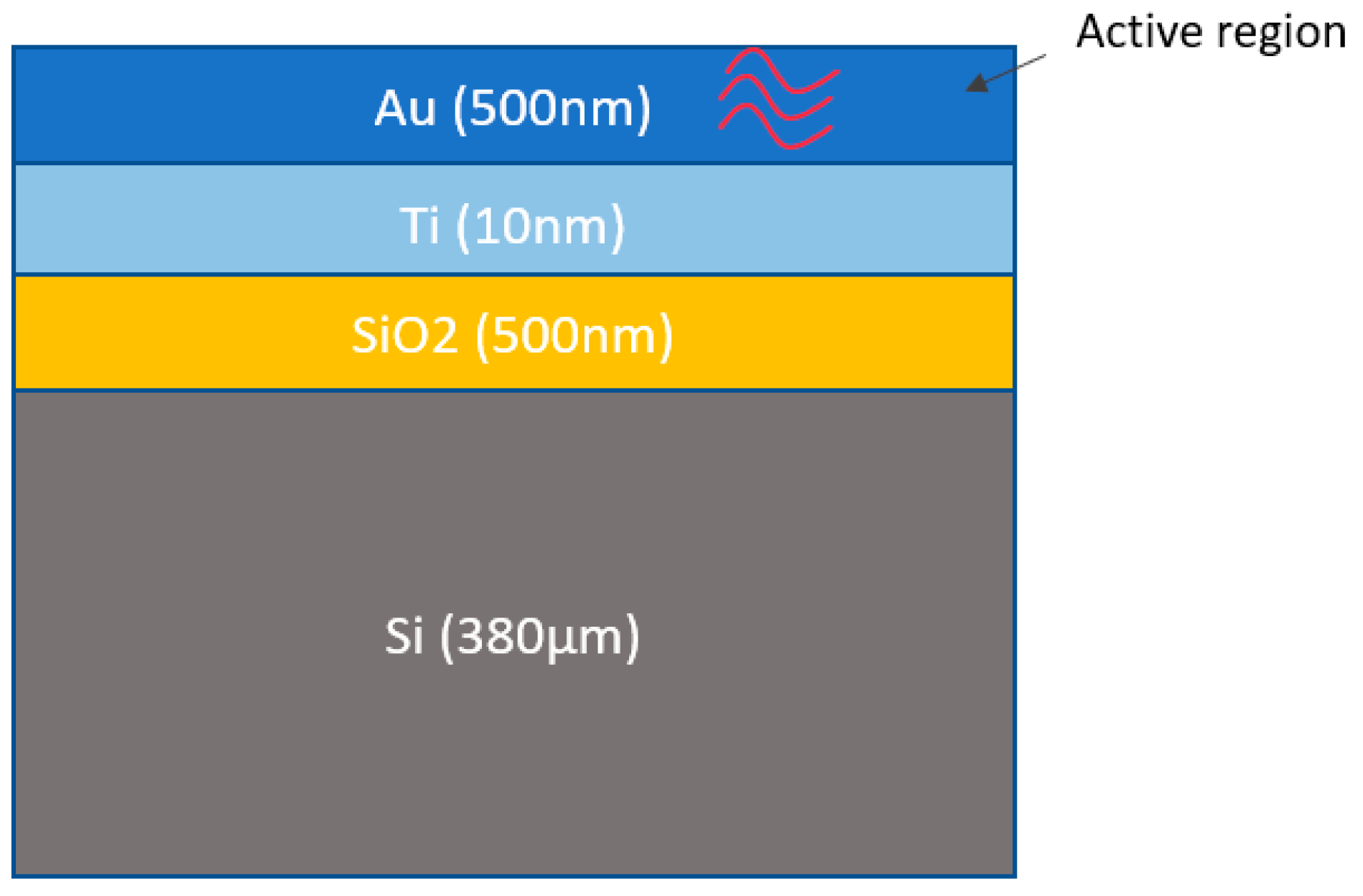








| Materials | k (W/m/°C) | n | |
|---|---|---|---|
| Gold (Au) | 315 | - | |
| Titanium (Ti) | 17 | - | [24] |
| Silicon Dioxide (SiO2) | 1.28 | - | [25] |
| Silicon (Si) | 145 | 1.3 |
| Method | Symbol | Slope (Rth) | Intercept (T0) | R-Square |
|---|---|---|---|---|
| Thermoreflectance |  | 21.898 | 42.996 | 0.9925 |
| Raman Eg shift |  | 22.099 | 45.501 | 0.9972 |
| Raman Eg AS/S ratio |  | 19.884 | 49.256 | 0.9937 |
| Raman A1g shift |  | 23.204 | 48.139 | 0.9972 |
| Raman A1g AS/S ratio |  | 17.209 | 53.915 | 0.9814 |
| Electric method |  | 21.827 | 50 | 1 |
| Thermal simulation |  | 23.343 | 47.251 | 0.9981 |
| Infrared method |  | 16.509 | 50.488 | 0.9996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boussekri, M.; Frogé, L.; Sommet, R.; Cholet, J.; Carisetti, D.; Dlubak, B.; Desgué, E.; Garabedian, P.; Legagneux, P.; Sarazin, N.; et al. Two-Dimensional Materials for Raman Thermometry on Power Electronic Devices. Nanomaterials 2025, 15, 1344. https://doi.org/10.3390/nano15171344
Boussekri M, Frogé L, Sommet R, Cholet J, Carisetti D, Dlubak B, Desgué E, Garabedian P, Legagneux P, Sarazin N, et al. Two-Dimensional Materials for Raman Thermometry on Power Electronic Devices. Nanomaterials. 2025; 15(17):1344. https://doi.org/10.3390/nano15171344
Chicago/Turabian StyleBoussekri, Mohammed, Lucie Frogé, Raphael Sommet, Julie Cholet, Dominique Carisetti, Bruno Dlubak, Eva Desgué, Patrick Garabedian, Pierre Legagneux, Nicolas Sarazin, and et al. 2025. "Two-Dimensional Materials for Raman Thermometry on Power Electronic Devices" Nanomaterials 15, no. 17: 1344. https://doi.org/10.3390/nano15171344
APA StyleBoussekri, M., Frogé, L., Sommet, R., Cholet, J., Carisetti, D., Dlubak, B., Desgué, E., Garabedian, P., Legagneux, P., Sarazin, N., Moreau, M., Brunel, D., Seneor, P., Carré, E., Martin, M.-B., Renaudin, V., & Moinet, T. (2025). Two-Dimensional Materials for Raman Thermometry on Power Electronic Devices. Nanomaterials, 15(17), 1344. https://doi.org/10.3390/nano15171344








