Multi-Scale Modeling of Transport Properties in Cementitious Materials with GO Admixture
Abstract
1. Introduction
2. Research Significance
3. Materials and Methods
3.1. Materials
3.2. Testing
4. Results
4.1. Hydration Study of Cementitious Materials with GO
4.1.1. Reaction of OPC with GO Admixture
4.1.2. Hydration Kinetics of OPC-GO System
4.2. Modeling of Multi-Scale Microstructure of Cementitious Materials with GO
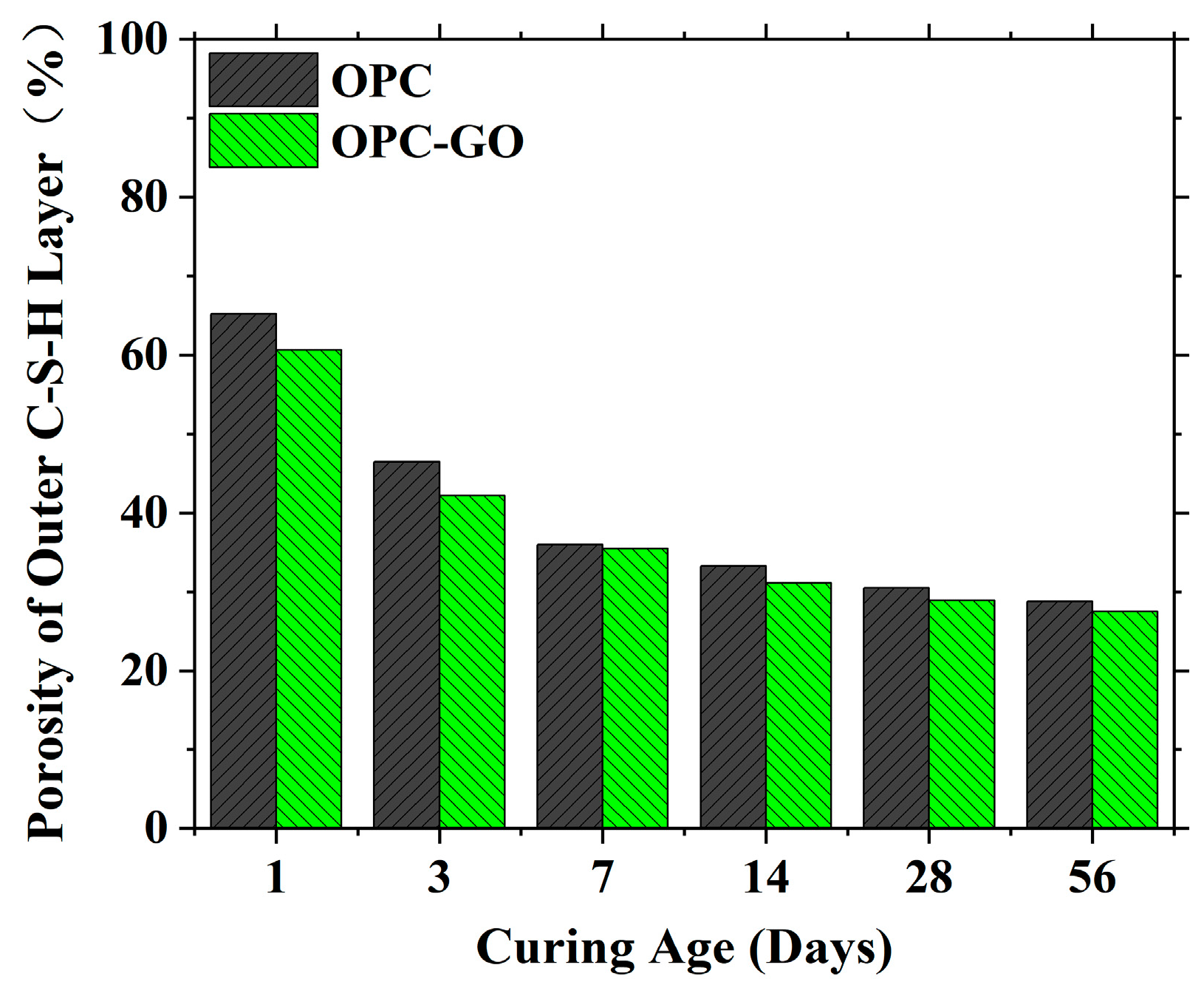
4.2.1. The Microstructure Modeling of the Outer C-S-H Layer at the Sub-Microscale
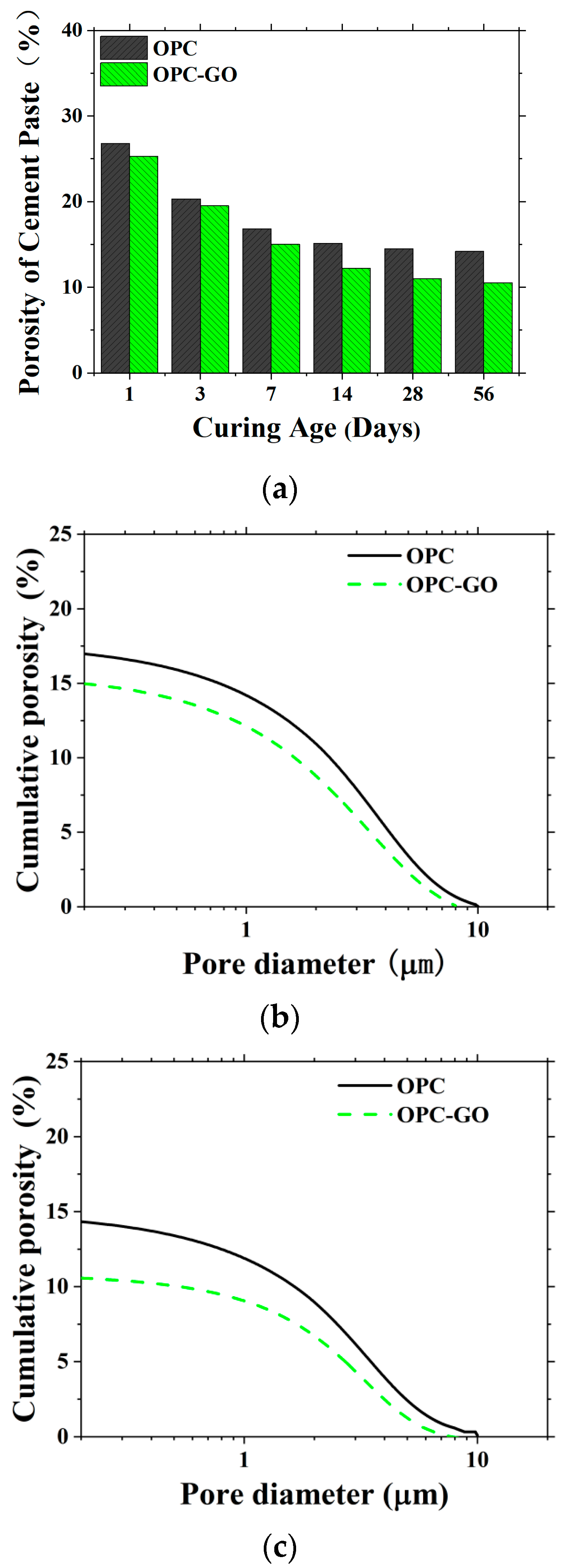
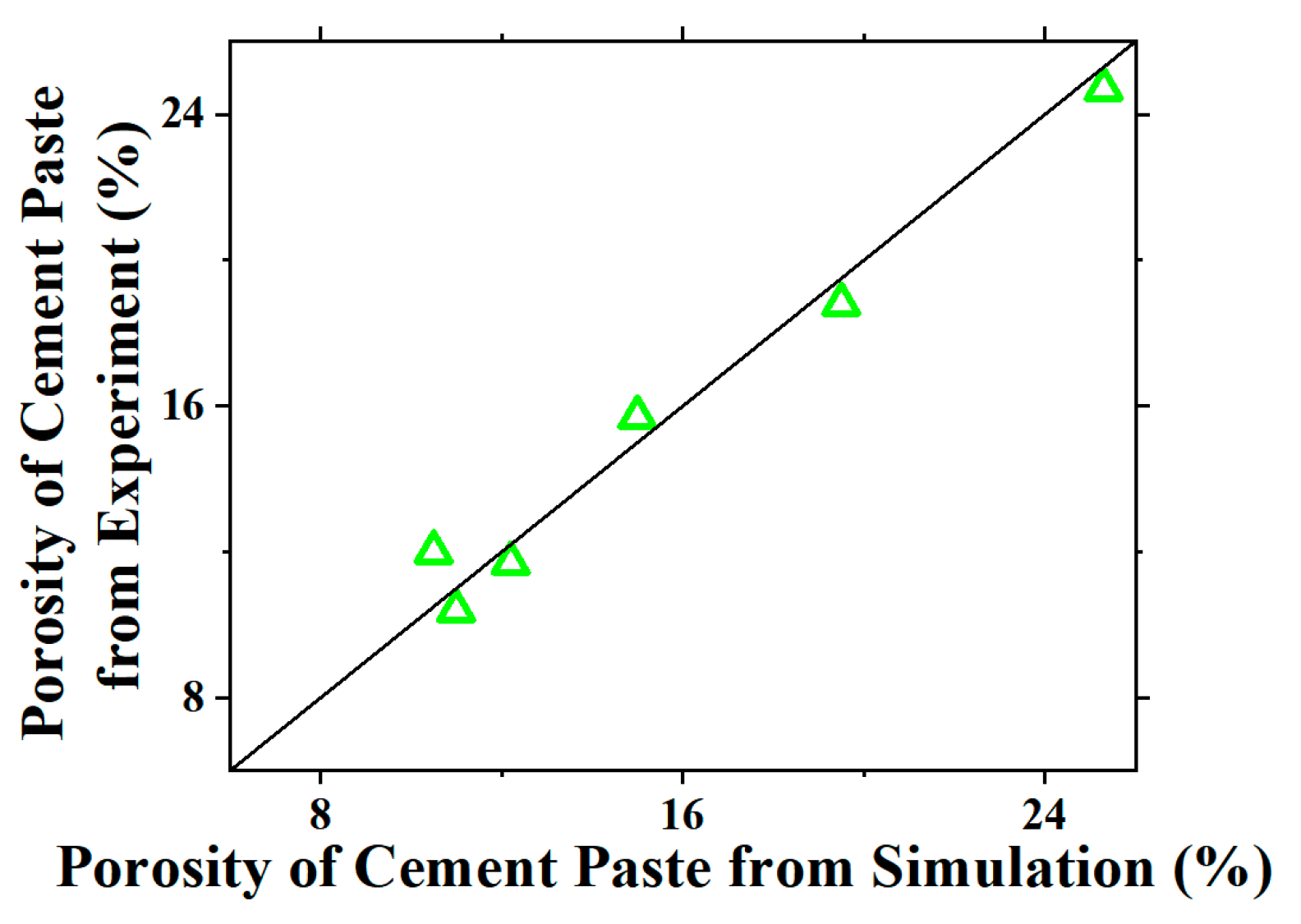
4.2.2. Microstructure Modeling of Bulk Cement Paste in Mortar at Microscale
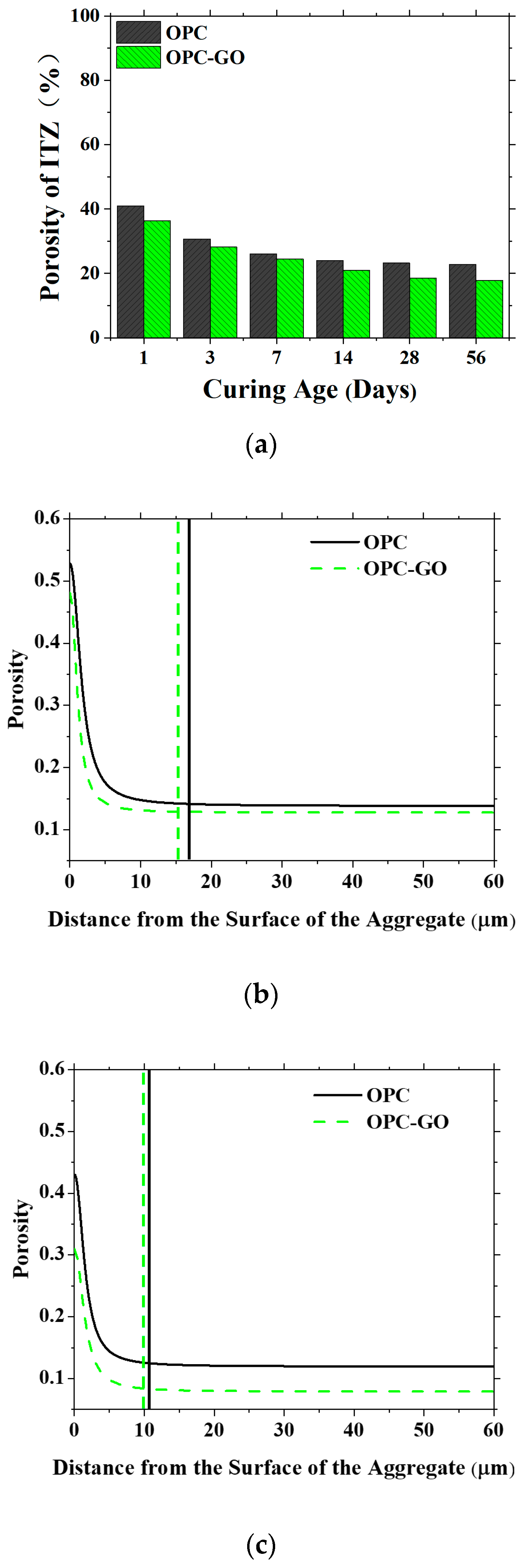
4.2.3. The Microstructure Modeling of the ITZ in Mortar at the Microscale
4.2.4. The Microstructure Modeling of Cement Mortar at the Mesoscale
4.3. The Modeling of the Transport Properties of Cementitious Materials with GO
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Hou, D.S.; Ma, H.Y. Multi-scale study water and ions transport in the cement-based materials: From molecular dynamics to random walk. Microporous Mesoporous Mater. 2021, 325, 111330. [Google Scholar] [CrossRef]
- Mohammed, A.; Sanjayan, J.G.; Duan, W.H.; Nazari, A. Incorporating graphene oxide in cement composites: A study of transport properties. Constr. Build. Mater. 2015, 84, 341–347. [Google Scholar] [CrossRef]
- Tong, L.Y.; Xiong, Q.X.; Zhang, M.Z.; Meng, Z.Z.; Meftah, F.; Liu, Q.F. Multi-scale modelling and statistical analysis of heterogeneous characteristics effect on chloride transport properties in concrete. Constr. Build. Mater. 2023, 367, 130096. [Google Scholar] [CrossRef]
- Du, H.J.; Pang, S.D. Effect of colloidal nano-silica on the mechanical and durability performances of mortar. Key Eng. Mater. 2015, 629, 443–448. [Google Scholar] [CrossRef]
- Gaitero, J.J.; Campillo, I.; Guerrero, A. Reduction of the calcium leaching rate of cement paste by addition of silica nanoparticles. Cem. Concr. Res. 2008, 38, 1112–1118. [Google Scholar] [CrossRef]
- Krishnan, P.; Zhang, M.H.; Yu, L.Y.; Feng, H.J. Photocatalytic degradation of particulate pollutants and self-cleaning performance of TiO2-containing silicate coating and mortar. Constr. Build. Mater. 2013, 44, 309–316. [Google Scholar] [CrossRef]
- Li, H.; Xiao, H.G.; Guan, X.C.; Wang, Z.T.; Yu, L. Chloride diffusion in concrete containing nano-TiO2 under coupled effect of scouring. Compos. Part B-Eng. 2014, 56, 698–704. [Google Scholar] [CrossRef]
- Senff, L.; Tobaldi, D.M.; Lucas, S.; Hotza, D.; Ferreira, V.M.; Labrincha, J.A. Formulation of mortars with nano-SiO2 and nano-TiO2 for degradation of pollutants in buildings. Compos. Part B-Eng. 2013, 44, 40–47. [Google Scholar] [CrossRef]
- Kawashima, S.; Seo, J.-W.T.; Corr, D.; Hersam, M.C.; Shah, S.P. Dispersion of CaCO3 nanoparticles by sonication and surfactant treatment for application in fly ash–cement systems. Mater. Struct. 2014, 47, 1011–1023. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Zu, T.; Shi, C.; Duan, W.H.; Shah, S.P. Influence of nanolimestone on the hydration, mechanical strength, and autogenous shrinkage of ultrahigh-performance concrete. J. Mater. Civ. Eng. 2016, 28, 04015068. [Google Scholar] [CrossRef]
- Azhari, F.; Banthia, N. Cement-based sensors with carbon fibers and carbon nanotubes for piezoresistive sensing. Cem. Concr. Compos. 2012, 34, 866–873. [Google Scholar] [CrossRef]
- Collins, F.; Lambert, J.; Duan, W.H. The influences of admixtures on the dispersion, workability, and strength of carbon nanotube-OPC paste mixtures. Cem. Concr. Compos. 2012, 34, 201–207. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Aza, C.A. Self sensing carbon nanotube (CNT) and nanofiber (CNF) cementitious composites for real time damage assessment in smart structures. Cem. Concr. Compos. 2014, 53, 162–169. [Google Scholar] [CrossRef]
- Tyson, B.M.; Abu Al-Rub, R.K.; Yazdanbakhsh, A.; Grasley, Z. Carbon Nanotubes and Carbon Nanofibers for Enhancing the Mechanical Properties of Nanocomposite Cementitious Materials. J. Mater. Civ. Eng. 2011, 23, 1028–1035. [Google Scholar] [CrossRef]
- Sun, H.F.; Zou, H.; Ren, J.; Xu, G.; Xing, F. Synthesis of a novel graphene oxide/belite cement composite and its effects on flexural strength and interfacial transition zone of ordinary portland cement mortars. Constr. Build. Mater. 2023, 402, 133009. [Google Scholar] [CrossRef]
- Zhang, W.C.; Zhao, M.X.; Yang, Z.Y.; Guo, R.X.; Wang, X.Y.; Lin, R.S. Properties of red sandstone-limestone-cement ternary composites: Hydration mechanism, microstructure, and high-temperature damage. Dev. Built Environ. 2024, 17, 100346. [Google Scholar] [CrossRef]
- Meng, S.Q.; Ouyang, X.W.; Fu, J.Y.; Niu, Y.F.; Ma, Y.W. The role of graphene/graphene oxide in cement hydration. Nanotechnol. Rev. 2021, 10, 768–778. [Google Scholar] [CrossRef]
- Gong, K.; Pan, Z.; Korayem, A.H.; Qiu, L.; Li, D.; Collins, F.; Wang, C.M.; Duan, W.H. Reinforcing Effects of Graphene Oxide on Portland Cement Paste. J. Mater. Civ. Eng. 2015, 27, A4014010. [Google Scholar] [CrossRef]
- Indukuri, C.S.R.; Nerella, R. Enhanced transport properties of graphene oxide based cement composite material. J. Build. Eng. 2021, 37, 102174. [Google Scholar] [CrossRef]
- Hou, D.S.; Lu, Z.Y.; Li, X.Y.; Ma, H.Y.; Li, Z.J. Reactive molecular dynamics and experimental study of graphene-cement composites: Structure, dynamics and reinforcement mechanisms. Carbon 2017, 115, 188–208. [Google Scholar] [CrossRef]
- Alkhateb, H.; Al-Ostaz, A.; Cheng, A.H.-D.; Li, X. Materials genome for graphene-cement nanocomposites. J. Nanomechanics Micromechanics 2013, 3, 67–77. [Google Scholar] [CrossRef]
- Fan, D.; Lue, L.; Yang, S.T. Molecular dynamics study of interfacial stress transfer in graphene-oxide cementitious composites. Comput. Mater. Sci. 2017, 139, 56–64. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, Y. Quantitative Analysis on Reaction Degree of Slag-Cement Composite System Based on Back-Scattered-Electron Image. J. Chin. Ceram. Soc. 2015, 43, 563–569. [Google Scholar] [CrossRef]
- Sun, H.; Liu, S.; Cao, K.; Yu, D.; Memon, S.A.; Liu, W.; Zhang, X.; Xing, F.; Zhao, D. Degradation mechanism of cement mortar exposed to combined sulfate–chloride attack under cyclic wetting–drying condition. Mater. Struct. 2021, 54, 138. [Google Scholar] [CrossRef]
- Sun, H.F.; Xu, G.; Lian, W.X.; Kastiukas, G.; Zhang, J.L.; Zhang, X.G.; Liu, W.; Xing, F.; Ren, J. Electrochemical synthesis and property characterisation of graphene oxide using water as electrolyte. Chem. Phys. Lett. 2022, 786, 139206. [Google Scholar] [CrossRef]
- Chu, D.C.; Kleib, J.; Amar, M.; Benzerzour, M.; Abriak, N.-E. Determination of the degree of hydration of Portland cement using three different approaches: Scanning electron microscopy (SEM-BSE) and Thermogravimetric analysis (TGA). Case Stud. Constr. Mater. 2021, 15, e00754. [Google Scholar] [CrossRef]
- Ashraf, W.; Olek, J.; Tian, N. Multiscale characterization of carbonated wollastonite paste and application of homogenization schemes to predict its effective elastic modulus. Cem. Concr. Compos. 2016, 72, 284–298. [Google Scholar] [CrossRef]
- Wang, Q.; Yin, M.; Chen, K. Backscattered Electron Image Analysis of the Modification Mechanism of Vitrified Microspheres on Aerated Concrete. J. Yancheng Inst. Technol. (Nat. Sci. Ed.) 2018, 31, 1–5. [Google Scholar] [CrossRef]
- Ye, T.; Yang, H.; Ye, X. Quantitative analysis of content of cement components by backscatter scanning technique. Cement 2011, 4, 14–15. [Google Scholar] [CrossRef]
- Wang, P.; Feng, S.; Liu, X. Application of Backscattered Electron Imaging and Image Analysis in Microstructure Research on Cement-Based Materials. J. Chin. Ceram. Soc. 2011, 39, 1659–1665. [Google Scholar] [CrossRef]
- Long, W.J.; Gu, Y.C.; Xiao, B.X.; Zhang, Q.M.; Xing, F. Micro-mechanical properties and multi-scaled pore structure of graphene oxide cement paste: Synergistic application of nanoindentation, X-ray computed tomography, and SEM-EDS analysis. Constr. Build. Mater. 2018, 179, 661–674. [Google Scholar] [CrossRef]
- Tong, T.; Fan, Z.; Liu, Q.; Wang, S.; Tan, S.S.; Yu, Q. Investigation of the effects of graphene and graphene oxide nanoplatelets on the micro- and macro-properties of cementitious materials. Constr. Build. Mater. 2016, 106, 102–114. [Google Scholar] [CrossRef]
- Ma, H. Multi-Scale Modeling of the Microstructure and Transport Properties of Contemporary Concrete. Ph.D. Thesis, The Hong Kong University of Science and Technology, Hong Kong, China, 2013. [Google Scholar]
- Bentz, D.P. Three-dimensional computer simulation of portland cement hydration and microstructure development. J. Am. Ceram. Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- CEMHYD3D, B.D. A Three-Dimensional Cement Hydration and Microstructure Development Modeling Package, Version 3.0; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2000. [Google Scholar]
- Liao, W.; Sun, X.; Kumar, A.; Sun, H.; Ma, H. Hydration of binary portland cement blends containing silica fume: A decoupling method to estimate degrees of hydration and pozzolanic reaction. Front. Mater. 2019, 6, 78. [Google Scholar] [CrossRef]
- Riding, K.A.; Poole, J.L.; Folliard, K.J.; Juenger, M.C.G.; Schindler, A.K. Modeling Hydration of Cementitious Systems. Aci Mater. J. 2012, 109, 225–234. [Google Scholar]
- Zeng, T. Transient Resistivity-Based Concrete Performance Characterization and Pore Structure Analysis. Master’s Thesis, Chongqing University: Chong Qing, China, 2021. [Google Scholar]
- Li, X.Y.; Lu, Z.Y.; Chuah, S.; Li, W.G.; Liu, Y.M.; Duan, W.H.; Li, Z.J. Effects of graphene oxide aggregates on hydration degree, sorptivity, and tensile splitting strength of cement paste. Compos. Part A-Appl. Sci. Manuf. 2017, 100, 1–8. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Effect of nano-silica on the hydration and microstructure development of Ultra-High Performance Concrete (UHPC) with a low binder amount. Constr. Build. Mater. 2014, 65, 140–150. [Google Scholar] [CrossRef]
- Zhao, L.; Guo, X.L.; Ge, C.; Li, Q.; Guo, L.P.; Shu, X.; Liu, J.P. Investigation of the effectiveness of PC@GO on the reinforcement for cement composites. Constr. Build. Mater. 2016, 113, 470–478. [Google Scholar] [CrossRef]
- Chen, X.; Han, Y.; Ding, X.; Hou, D. Multiscale Calculation of Elastic Modulus of Cement Paste Based on Grid Nanoindentation Technology. J. Shanghai Jiaotong Univ. 2022, 56, 1199–1207. [Google Scholar] [CrossRef]
- Tian, Z.S. Research on the Transport Performance of Cement-Based Matereals Based on a Multi-Scale Model. Master’s Thesis, Zhejiang University, Hangzhou, China, 2019. [Google Scholar]
- Cwang, C.; Sun, W.; Jiang, J.; Sun, G.; Qiao, Y. Development on Cement-Based Composite Materials in Multi-Scale. J. Chin. Ceram. Soc. 2011, 39, 726–738. [Google Scholar] [CrossRef]
- Zhou, C.H. Investigations on the Relationships Between Compressive Strength of Cement Pastes and Mortars and Their Pore Structure of Multiscale Characteristics. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Scrivener, K.L.; Crumbie, A.K.; Laugesen, P. The interfacial transition zone (ITZ) between cement paste and aggregate in concrete. Interface Sci. 2004, 12, 411–421. [Google Scholar] [CrossRef]
- Ma, H.Y.; Li, Z.J. Multi-Aggregate Approach for Modeling Interfacial Transition Zone in Concrete. Aci Mater. J. 2014, 111, 189–199. [Google Scholar] [CrossRef]
- Sun, H.F.; Ren, Z.L.; Ling, L.; Memon, S.A.; Ren, J.; Liu, B.; Xing, F. Influence of Graphene Oxide on Interfacial Transition Zone of Mortar. J. Nanomater. 2020, 2020, 8919681. [Google Scholar] [CrossRef]




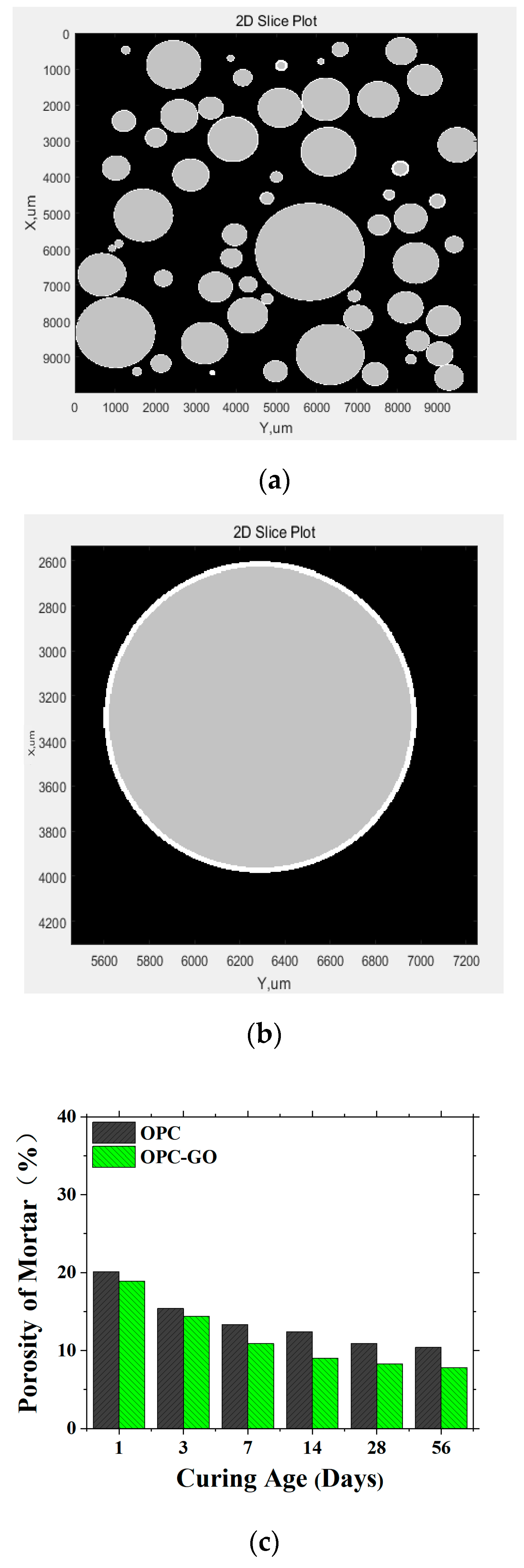
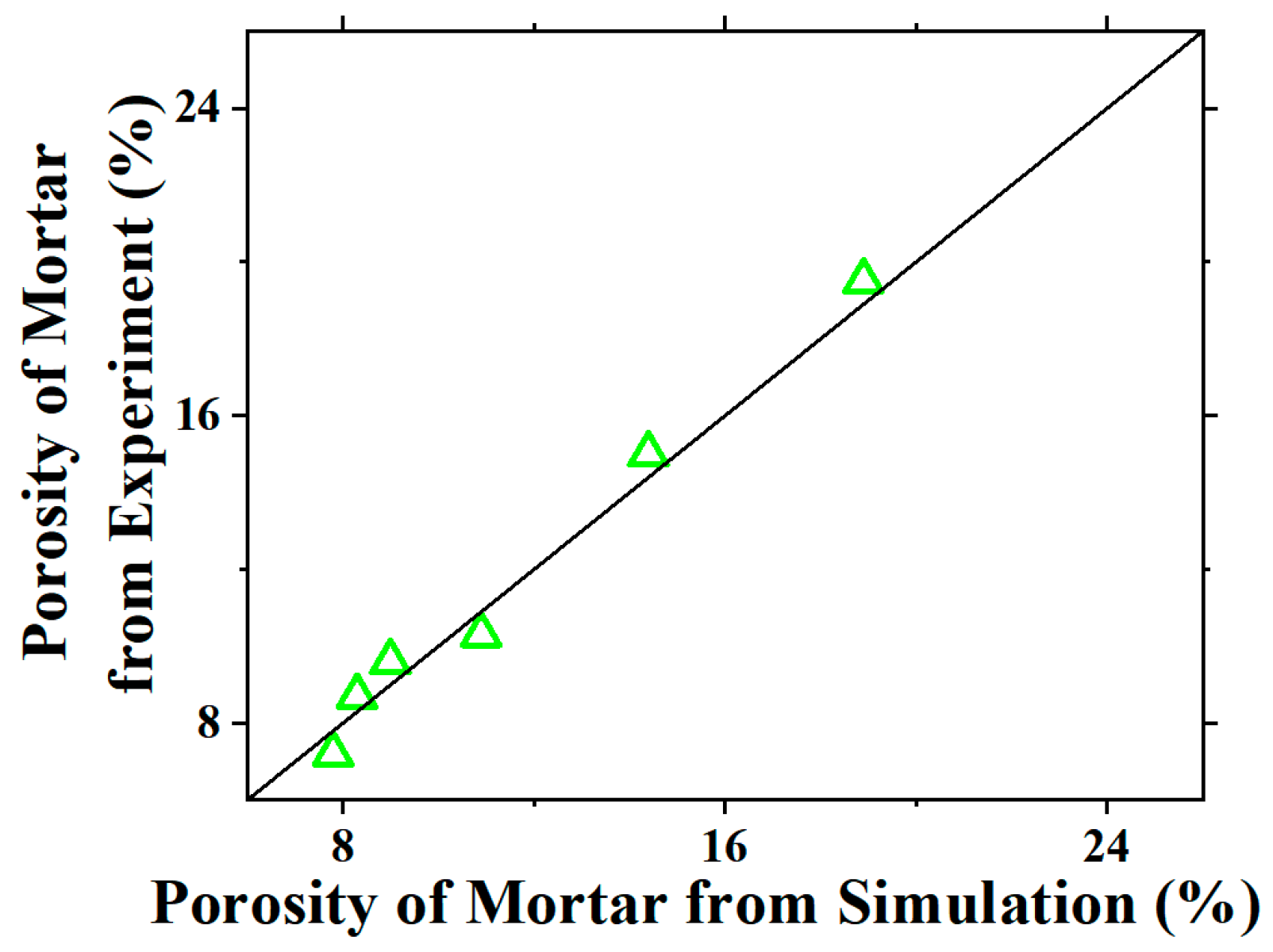



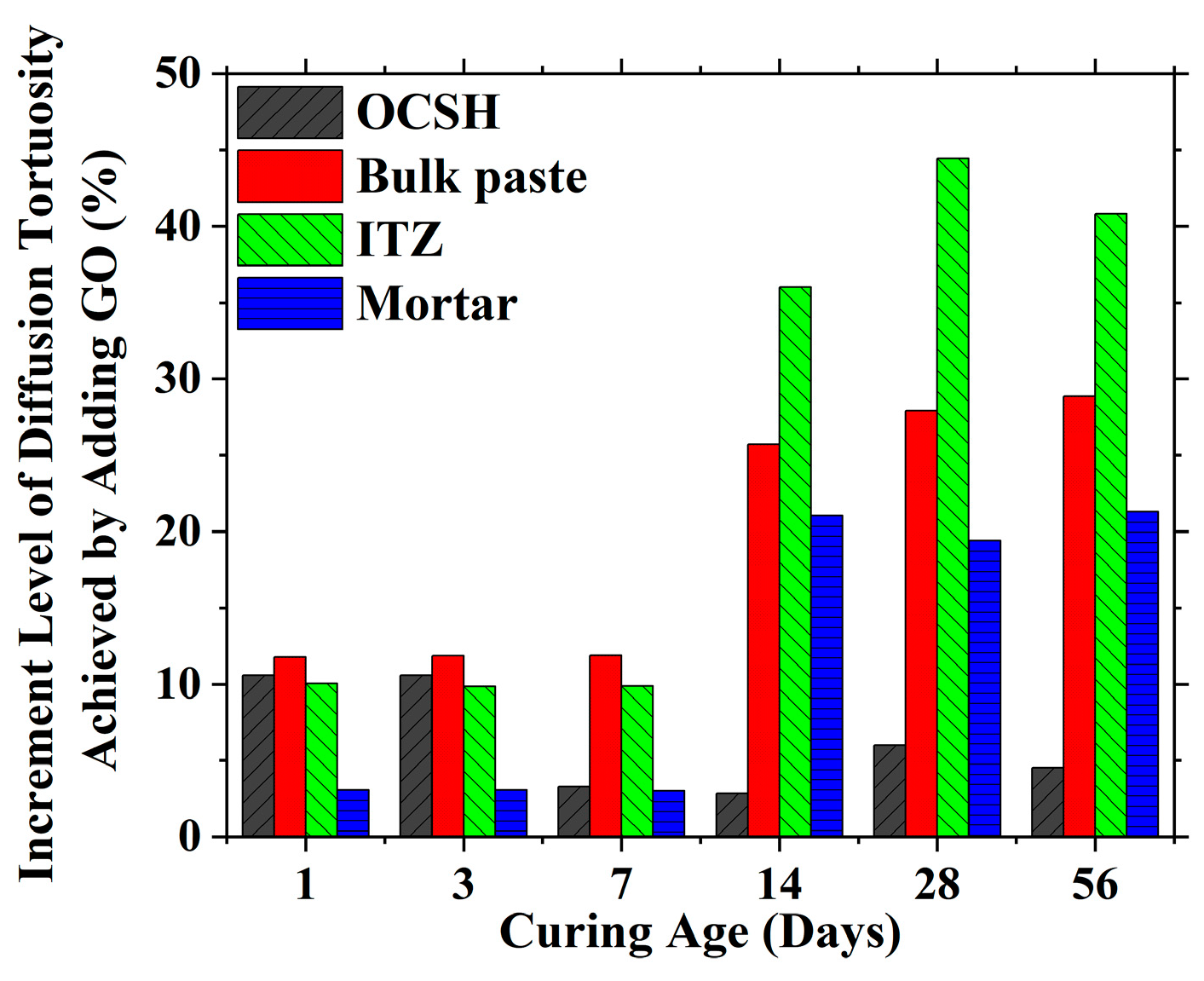
| Mineral Composition | Mass Fraction (%) |
|---|---|
| 58.38 | |
| 15.22 | |
| 7.57 | |
| 12.13 | |
| 4.62 | |
| Specific density | 3.12 |
| Specimen Identification | ||||
|---|---|---|---|---|
| OPC | 0.766 | 18.04 | 0.77 | 0.9954 |
| OPC-GO | 0.78 | 16.99 | 0.88 | 0.9844 |
| Specimen Identification | 1 Day | 3 Days | 7 Days | 14 Days | 28 Days | 56 Days |
|---|---|---|---|---|---|---|
| OPC | 17 | 12.1 | 9.7 | 9 | 8.3 | 8 |
| OPC-GO | 15.4 | 11.2 | 9.3 | 8.7 | 8 | 7.7 |
| Phase Identification | 1 Day | 3 Days | 7 Days | 14 Days | 28 Days | 56 Days |
|---|---|---|---|---|---|---|
| OCSH | 6.90 | 9.25 | 1.39 | 6.61 | 5.25 | 4.51 |
| Bulk paste | 5.60 | 3.94 | 10.71 | 19.21 | 24.14 | 26.06 |
| ITZ | 11.29 | 8.11 | 6.30 | 12.50 | 20.43 | 21.93 |
| Mortar | 5.97 | 6.49 | 18.05 | 27.42 | 23.85 | 25.00 |
| Phase Identification | 1 Day | 3 Days | 7 Days | 14 Days | 28 Days | 56 Days |
|---|---|---|---|---|---|---|
| OCSH | 10.59 | 10.57 | 3.28 | 2.85 | 6.00 | 4.52 |
| Bulk paste | 11.77 | 11.84 | 11.88 | 25.71 | 27.91 | 28.85 |
| ITZ | 10.05 | 9.84 | 9.88 | 36.00 | 44.44 | 40.81 |
| Mortar | 3.07 | 3.05 | 2.99 | 21.04 | 19.39 | 21.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Kang, W.; Lian, W.; Xing, F.; Sun, H.; Ma, H. Multi-Scale Modeling of Transport Properties in Cementitious Materials with GO Admixture. Nanomaterials 2025, 15, 222. https://doi.org/10.3390/nano15030222
Liu B, Kang W, Lian W, Xing F, Sun H, Ma H. Multi-Scale Modeling of Transport Properties in Cementitious Materials with GO Admixture. Nanomaterials. 2025; 15(3):222. https://doi.org/10.3390/nano15030222
Chicago/Turabian StyleLiu, Bing, Weichen Kang, Weixing Lian, Feng Xing, Hongfang Sun, and Hongyan Ma. 2025. "Multi-Scale Modeling of Transport Properties in Cementitious Materials with GO Admixture" Nanomaterials 15, no. 3: 222. https://doi.org/10.3390/nano15030222
APA StyleLiu, B., Kang, W., Lian, W., Xing, F., Sun, H., & Ma, H. (2025). Multi-Scale Modeling of Transport Properties in Cementitious Materials with GO Admixture. Nanomaterials, 15(3), 222. https://doi.org/10.3390/nano15030222







