Switchable Negative Group Delay Based on Sandwich Topological Protection Structure in Terahertz Band
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterizations
2.3. Calculations
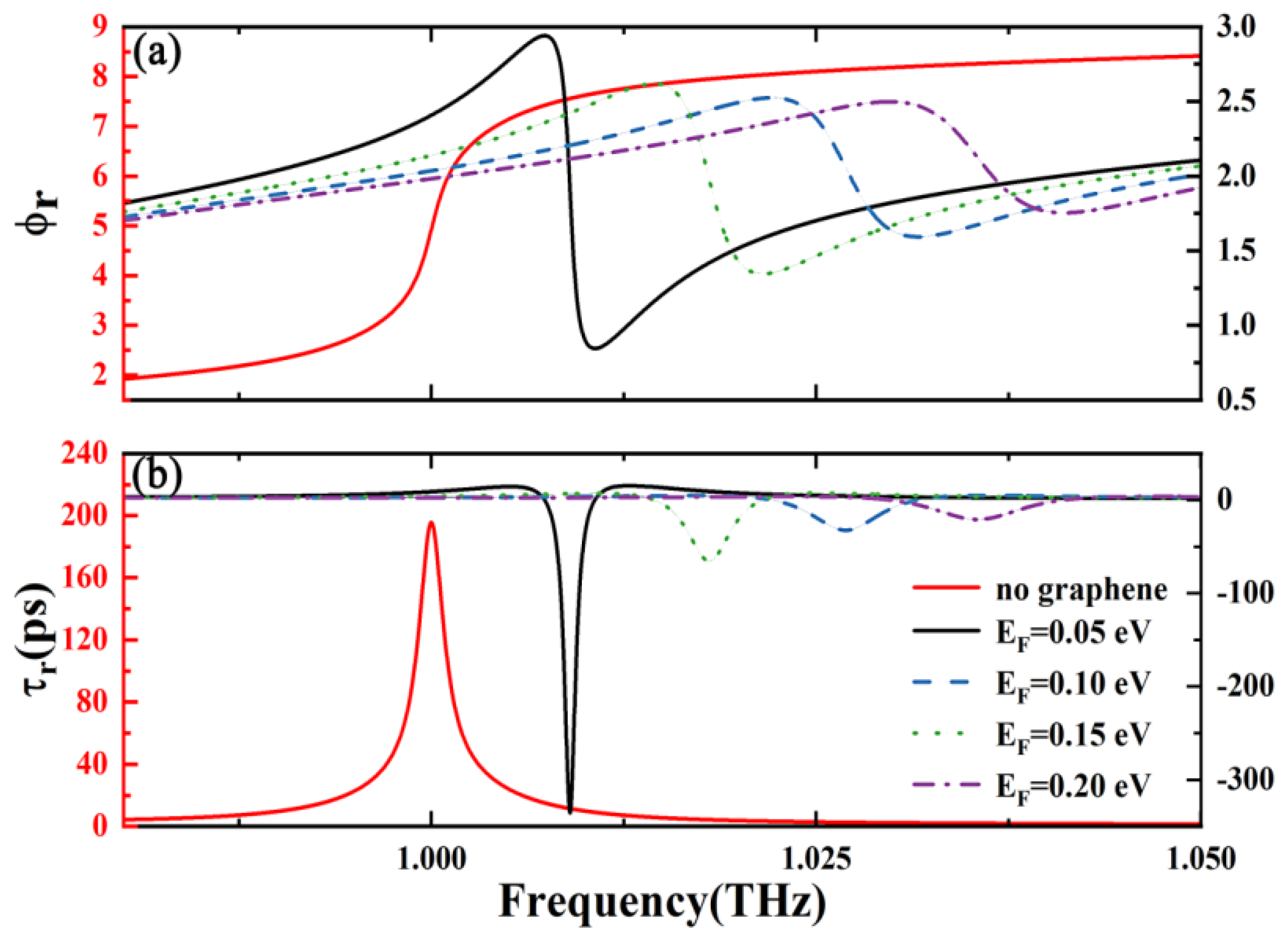
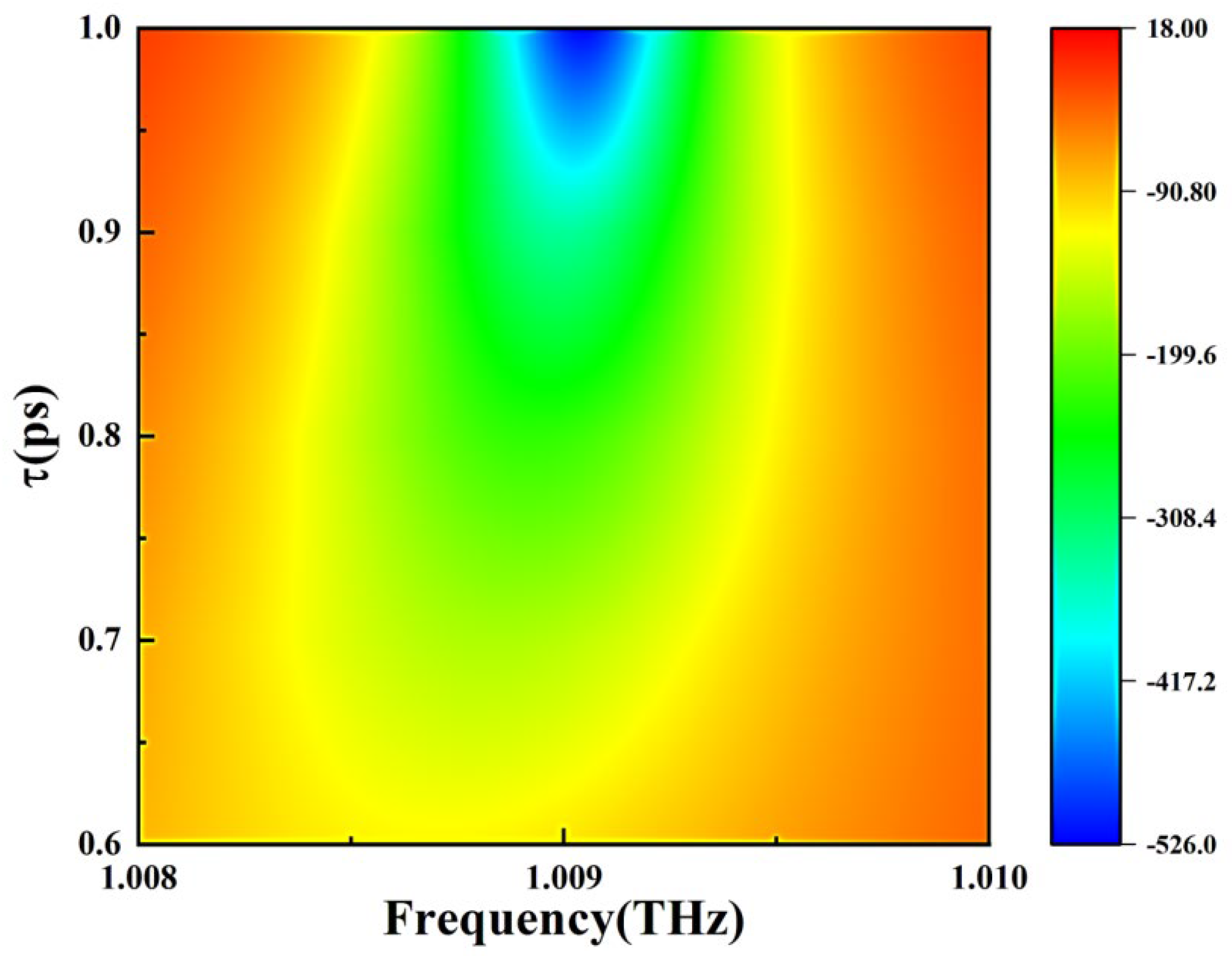
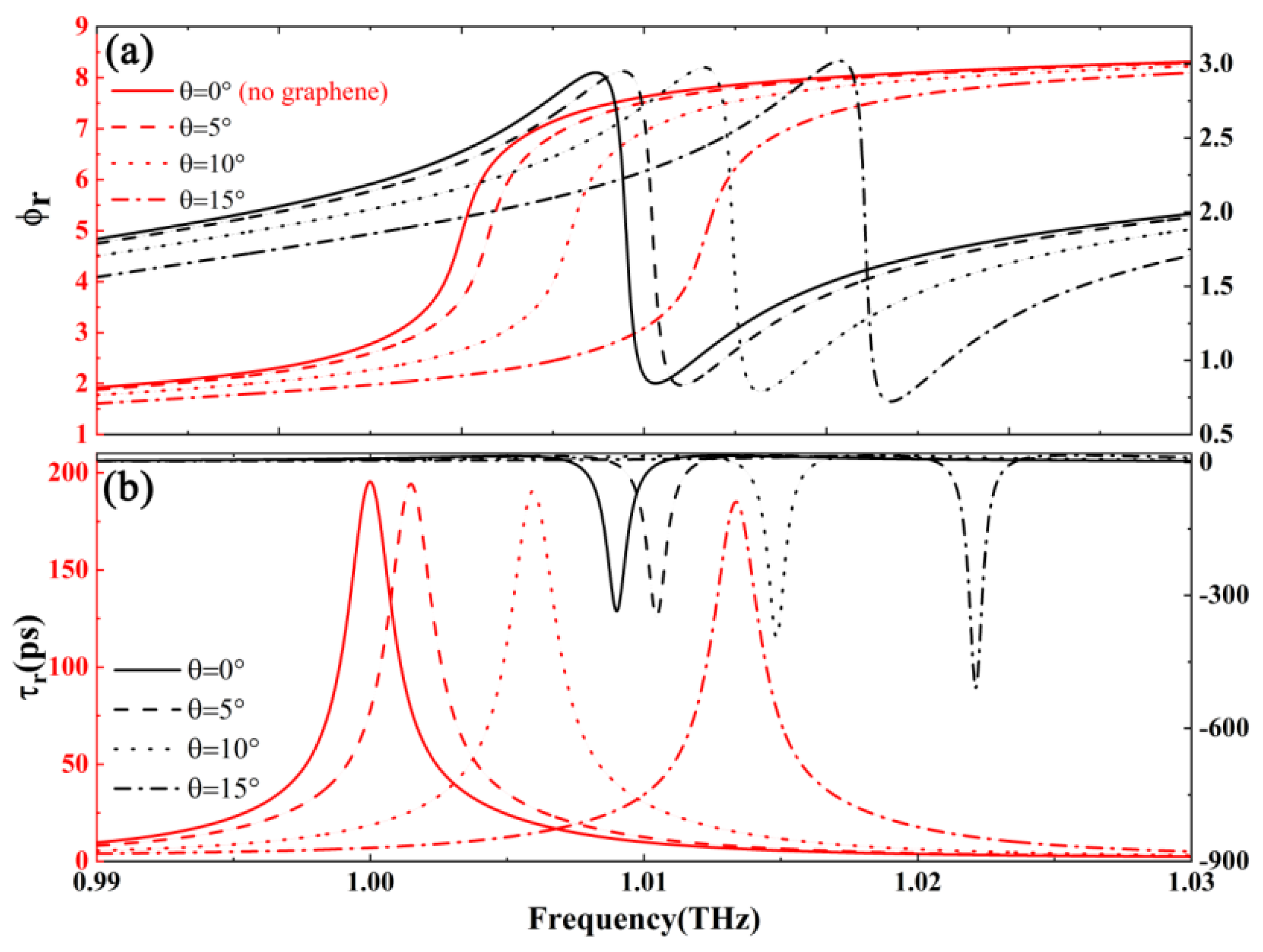
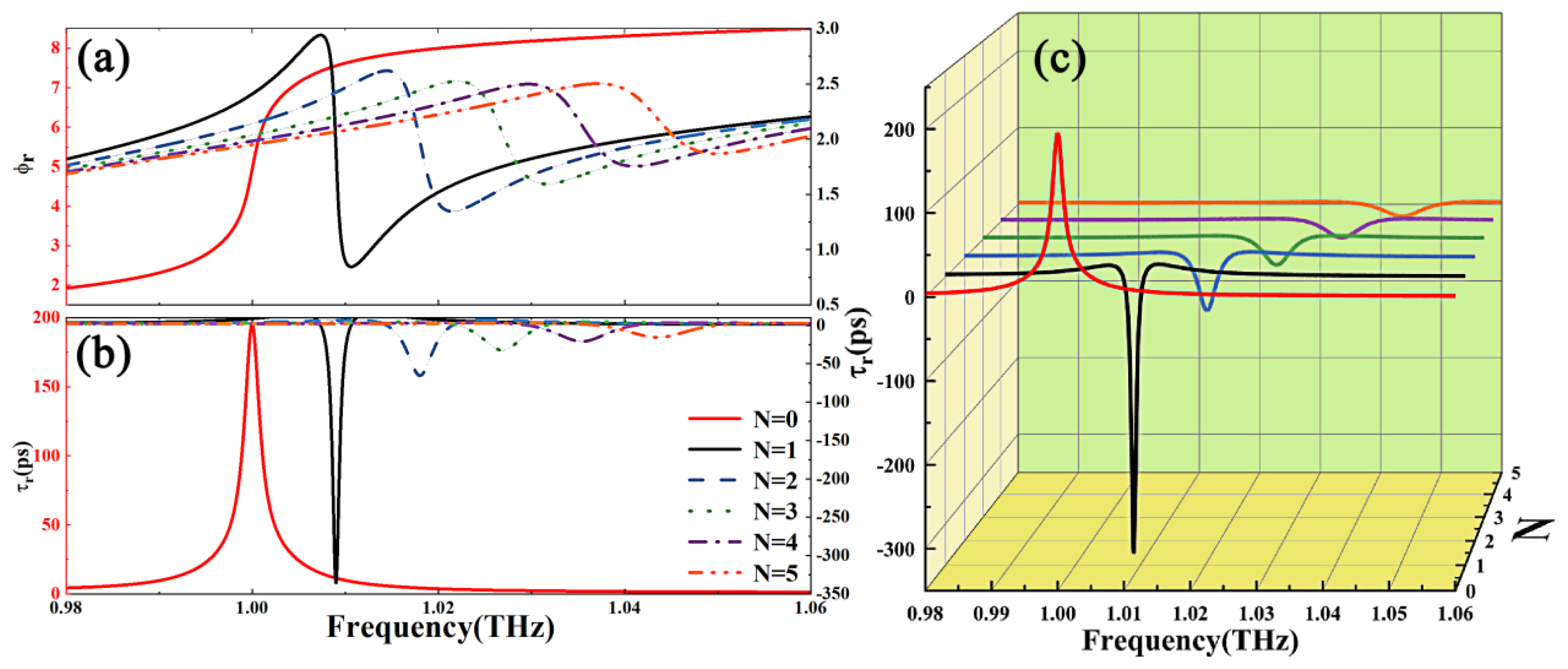
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; Lou, F.L.; et al. Terahertz communications and sensing for 6G and beyond: A comprehensive review. IEEE Commun. Tutor. 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Cai, X.; Cheng, X.; Tufvesson, F. Toward 6G with terahertz communications: Understanding the propagation channels. IEEE Commun. Mag. 2024, 62, 32–38. [Google Scholar] [CrossRef]
- Richardson, D.J. Filling the light pipe. Science 2010, 330, 327–328. [Google Scholar] [CrossRef] [PubMed]
- Tucker, R.S.; Ku, P.C.; Chang-Hasnain, C.J. Slow-light optical buffers: Capabilities and fundamental limitations. J. Light. Technol. 2005, 23, 4046–4066. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, Q.; Wang, S.; Chen, Z.; Sillanpää, M.A.; Li, T. Optomechanical anti-lasing with infinite group delay at a phase singularity. Phys. Rev. Lett. 2021, 127, 273603. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wang, D.; Deng, C.; Lu, M.; Huang, L.; Hu, G.; Yun, B.; Zhang, R.; Li, M.; Dong, J. Large group delay in silicon-on-insulator chirped spiral Bragg grating waveguide. IEEE Photonics J. 2021, 13, 5500205. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Wang, D.; Huang, Q.; Zhang, C.; Zhang, X. Large group delay and low loss optical delay line based on chirped waveguide Bragg gratings. Opt. Express 2023, 31, 4630–4638. [Google Scholar] [CrossRef]
- Das, R.; Schneider, T. Integrated group delay units for real-time reconfigurable spectrum sensing of mm-wave signals. Opt. Lett. 2020, 45, 4778–4781. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Tan, Q.; Gan, Y.; Zhang, W.; Xiong, J. Polarization-insensitive classical electromagnetically induced transparency metamaterial with large group delay by Dirac semimetal. Results Phys. 2020, 19, 103377. [Google Scholar] [CrossRef]
- Li, C.; Qi, D.; Hao, F. Metal-insulator-metal plasmonic waveguide for low-distortion slow light at telecom frequencies. J. Mod. Opt. 2014, 61, 627–630. [Google Scholar] [CrossRef]
- Tang, G.J.; He, X.T.; Shi, F.L.; Liu, J.W.; Chen, X.D.; Dong, J.W. Topological photonic crystals: Physics, designs, and applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Hu, Z.; Bongiovanni, D.; Jukić, D.; Tang, L.; Song, D.; Morandotti, R.; Chen, Z.; Buljan, H. Sub-symmetry-protected topological states. Nat. Phys. 2023, 19, 992–998. [Google Scholar] [CrossRef]
- Arora, S.; Bauer, T.; Barczyk, R.; Verhagen, E.; Kuipers, L. Direct quantification of topological protection in symmetry-protected photonic edge states at telecom wavelengths. Light. Sci. Appl. 2021, 10, 9. [Google Scholar] [CrossRef]
- He, L.; Liu, D.; Zhang, H.; Zhang, F.; Zhang, W.; Feng, X.; Huang, Y.; Cui, K.; Liu, F.; Zhang, W.; et al. Topologically Protected Quantum Logic Gates with Valley-Hall Photonic Crystals. Adv. Mater. 2024, 36, 2311611. [Google Scholar] [CrossRef]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Walasik, W.; Litchinitser, N.M. Optically tunable topological photonic crystal. Optica 2019, 6, 839–844. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Jiang, L.; Dai, X.; Xiang, Y.; Wen, S. Tunable Group Delay of the Optical Pulse Reflection from Fabry-Perot Cavity with the Insertion of Graphene Sheets. IEEE Photonics J. 2014, 6, 3200109. [Google Scholar] [CrossRef]
- Chen, H.J.; Sun, B.B.; Wu, H.W.; Fang, X.W. Manipulation of slow and superluminal light based on a graphene nanoribbon resonator. Eur. Phys. J. D 2017, 71, 67. [Google Scholar] [CrossRef]
- Capmany, J.; Domenech, D.; Munoz, P. Graphene Integrated Microwave Photonics. J. Light. Technol. 2014, 32, 3785–3796. [Google Scholar] [CrossRef]
- Lu, H.; Zeng, C.; Zhang, Q.; Liu, X.; Hossain, M.M.; Reineck, P.; Gu, M. Graphene-based active slow surface plasmon polaritons. Sci. Rep. 2015, 5, 8443. [Google Scholar] [CrossRef]
- MinovKoppensich, F.H.L.; Chang, D.E.; Javier, G. Graphene plasmonics: A platform for strong light-matter interaction. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef]
- Tang, T.T.; Zhang, Y.; Park, C.H.; Geng, B.; Girit, C.; Hao, Z.; Wang, F. A tunable phonon–exciton Fano system in bilayer graphene. Nat. Nanotechnol. 2010, 5, 32–36. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Xu, J.; Li, W.; Li, J.; Peng, Y.; He, M. Optical bistability modulation based on graphene sandwich structure with topological interface modes. Opt. Express 2023, 31, 40490–40497. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Feng, J.; Han, S.; Xu, Z.; Mao, W.; Zhang, T.; Bae, S.H. Photonic van der Waals integration from 2D materials to 3D nanomembranes. Nat. Rev. Mater. 2023, 8, 498–517. [Google Scholar] [CrossRef]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, S.; Yu, P.; Li, J.X.; Xie, B.Y.; Li, Z.C.; Tian, J.G. Dynamically tunable broadband mid-infrared cross polarization converter based on graphene metamaterial. Appl. Phys. Lett. 2013, 103, 223102. [Google Scholar] [CrossRef]
- Zhan, T.; Shi, X.; Dai, Y.; Liu, X.; Zi, J. Transfer matrix method for optics in graphene layers. J. Phys. Conf. Ser. 2013, 25, 215301. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Liu, Q.; Liu, Y.; Wei, Y.; Weng, R.; Zhou, Y.; Jiang, L. Enhanced Group Delay of the Pulse Reflection with Graphene Surface Plasmon via Modified Otto Configuration. Adv. Condens. Matter Phys. 2017, 2017, 1569621. [Google Scholar] [CrossRef]
- Guan, Z.; Chen, X.D.; Mo, H.C.; Liu, J.W.; Shu, Q.Y.; Cao, Y.; Dong, J.W. Tunable topological boundary modes enabled by synthetic translation dimension. APL Photonics 2024, 9, 076116. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Pan, X.; Tang, J.; Peng, X.; Peng, Y. Switchable Negative Group Delay Based on Sandwich Topological Protection Structure in Terahertz Band. Nanomaterials 2025, 15, 251. https://doi.org/10.3390/nano15040251
Xu J, Pan X, Tang J, Peng X, Peng Y. Switchable Negative Group Delay Based on Sandwich Topological Protection Structure in Terahertz Band. Nanomaterials. 2025; 15(4):251. https://doi.org/10.3390/nano15040251
Chicago/Turabian StyleXu, Jiao, Xianmin Pan, Jiao Tang, Xianghua Peng, and Yuxiang Peng. 2025. "Switchable Negative Group Delay Based on Sandwich Topological Protection Structure in Terahertz Band" Nanomaterials 15, no. 4: 251. https://doi.org/10.3390/nano15040251
APA StyleXu, J., Pan, X., Tang, J., Peng, X., & Peng, Y. (2025). Switchable Negative Group Delay Based on Sandwich Topological Protection Structure in Terahertz Band. Nanomaterials, 15(4), 251. https://doi.org/10.3390/nano15040251




