On the Frequency Response of Nanostructured Thermoacoustic Loudspeakers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermoacoustic Loudspeaker Fabrication
2.2. Electric Characterization
2.3. Thermal Characterization
2.3.1. Setup
2.3.2. Method
2.4. Acoustic Characterization
2.4.1. Setup
2.4.2. Method
3. Results
4. Discussion
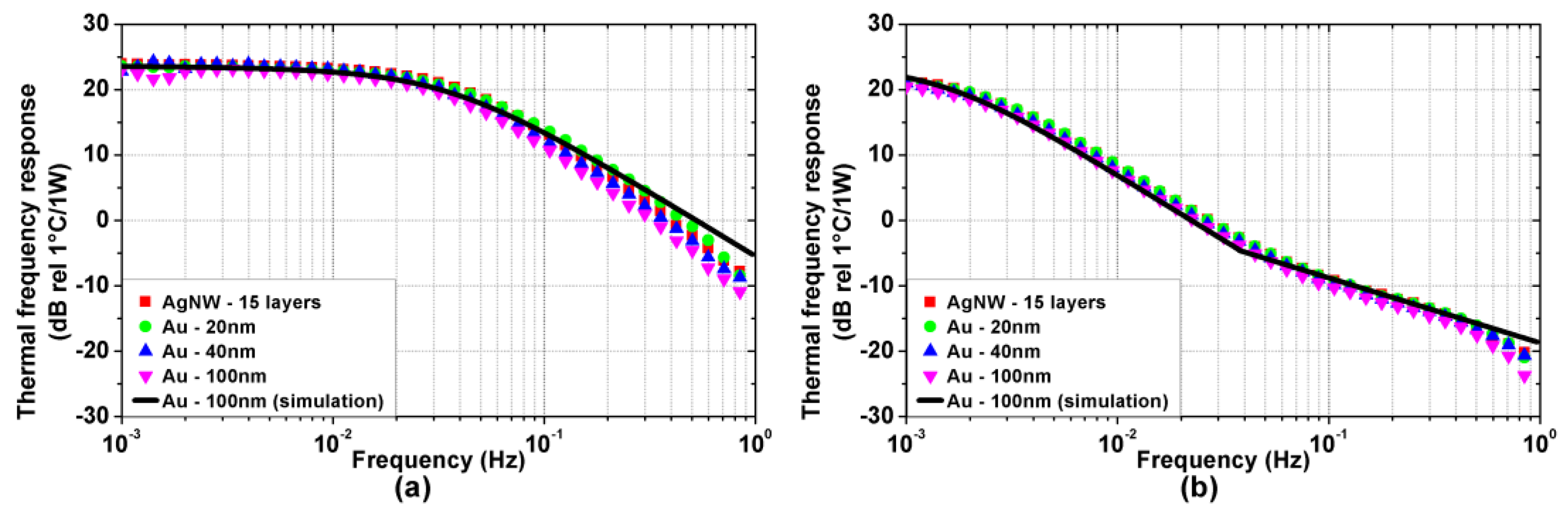
4.1. Thermal Behavior
4.2. Acoustic Behavior
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnold, H.D.; Crandall, I.B. The thermophone as a precision source of sound. Phys. Rev. 1898, 10, 22–38. [Google Scholar] [CrossRef]
- Aliev, A.E.; Mayo, N.K.; Jung De Andrade, M.; Robles, R.O.; Fang, S.; Baughman, R.H.; Zhang, M.; Chen, Y.; Lee, J.A.; Kim, S.J. Alternative nanostructures for thermophones. ACS Nano 2015, 9, 4743–4756. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Lin, X.; Jiang, K.; Liu, P.; Li, Q.; Fan, S. Thermoacoustic chips with carbon nanotube thin yarn arrays. Nano Lett. 2013, 13, 4795–4801. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Xie, D.; Yang, Y.; Ren, T.L.; Lin, Y.X.; Chen, Y.; Wang, Y.F.; Zhou, C.J.; Peng, P.G.; Wang, L.G.; et al. Flexible, ultrathin, and transparent sound-emitting devices using silver nanowires film. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Tian, H.; Xie, D.; Yang, Y.; Ren, T.L.; Feng, T.T.; Wang, Y.F.; Zhou, C.J.; Peng, P.G.; Wang, L.G.; Liu, L.T. Poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate)-based organic, ultrathin, and transparent sound-emitting device. Appl. Phys. Lett. 2011, 99, 233503. [Google Scholar] [CrossRef]
- Tian, H.; Xie, D.; Yang, Y.; Ren, T.-L.; Wang, Y.-F.; Zhou, C.-J.; Peng, P.-G.; Wang, L.-G.; Liu, L.-T. Transparent, flexible, ultrathin sound source devices using Indium Tin oxide films. Appl. Phys. Lett. 2011, 99, 43503. [Google Scholar] [CrossRef]
- Dutta, R.; Albee, B.; Van Der Veer, W.E.; Harville, T.; Donovan, K.C.; Papamoschou, D.; Penner, R.M. Gold nanowire thermophones. J. Phys. Chem. C 2014, 118, 29101–29107. [Google Scholar] [CrossRef]
- Fei, W.; Zhou, J.; Guo, W. Low-voltage driven graphene foam thermoacoustic speaker. Small 2015, 11, 2252–2256. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.S.; Hong, S.K.; Lee, J.M.; Kang, D.S.; Cho, B.J.; Choi, J.W. Free-standing graphene thermophone on a polymer-mesh substrate. Small 2016, 12, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Bobinger, M.R.; La Torraca, P.; Mock, J.; Becherer, M.; Cattani, L.; Angeli, D.; Larcher, L.; Lugli, P. Solution-processing of copper nanowires for transparent heaters and thermo-acoustic loudspeakers. IEEE Trans. Nanotechnol. 2018. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, Z.; Feng, C.; Liu, L.; Bai, Z.Q.; Wang, Y.; Qian, L.; Zhang, Y.; Li, Q.; Jiang, K.; et al. Flexible, stretchable, transparent carbon nanotube thin film loudspeakers. Nano Lett. 2008, 8, 4539–4545. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhu, T.; Xu, J. Model for thermoacoustic emission from solids. Appl. Phys. Lett. 2010, 96. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Y.; Wang, Z. Wideband flat frequency response of thermo-acoustic emission. J. Phys. D Appl. Phys. 2012, 45, 345401. [Google Scholar] [CrossRef]
- Daschewski, M.; Boehm, R.; Prager, J.; Kreutzbruck, M.; Harrer, A. Physics of thermo-acoustic sound generation. J. Appl. Phys. 2013, 114. [Google Scholar] [CrossRef]
- Hu, H.; Wang, D.; Wang, Z. Solution for acoustic field of thermo-acoustic emission from arbitrary source. AIP Adv. 2014, 4. [Google Scholar] [CrossRef]
- Daschewski, M.; Kreutzbruck, M.; Prager, J. Influence of thermodynamic properties of a thermo-acoustic emitter on the efficiency of thermal airborne ultrasound generation. Ultrasonics 2015, 63, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Asadzadeh, S.S.; Moosavi, A.; Huynh, C.; Saleki, O. Thermo acoustic study of carbon nanotubes in near and far field: Theory, simulation, and experiment. J. Appl. Phys. 2015, 117. [Google Scholar] [CrossRef]
- La Torraca, P.; Larcher, L.; Bobinger, M.; Pavan, P.; Seeber, B.; Lugli, P. Physical modeling and characterization of thermo-acoustic loudspeakers made of silver nano-wire films. J. Appl. Phys. 2017, 121. [Google Scholar] [CrossRef]
- Bobinger, M.; Angeli, D.; Colasanti, S.; La Torraca, P.; Larcher, L.; Lugli, P. Infrared, transient thermal, and electrical properties of silver nanowire thin films for transparent heaters and energy-efficient coatings. Phys. Status Solid 2017, 214, 1600466. [Google Scholar] [CrossRef]
- Farina, A. Simultaneous measurement of impulse response and distortion with a swept-sine technique. Present at the 108th AES Convention, Paris, France, 19–22 February 2000. [Google Scholar] [CrossRef]
- Farina, A. Advancements in impulse response measurements by sine sweeps. Present at the 122nd AES Convention, Vienna, Austria, 5–8 May 2007. [Google Scholar]
- Berzborn, M.; Bomhardt, R.; Klein, J.; Richter, J.G.; Vorländer, M. The ITA-Toolbox: An open source MATLAB toolbox for acoustic measurements and signal processing. In Proceedings of the 43th Annual German Congress on Acoustics, Kiel, Germany, 6–9 March 2017; pp. 222–225. [Google Scholar]
- AES2-2012: AES Standard for Acoustics—Methods of Measuring and Specifying the Performance of Loudspeakers for Professional Applications—Drive Units; Audio Engineering Society: New York, NY, USA, 2012.
- Beranek, L.L.; Mellow, T. Acoustics: Sound Fields and Transducers; Academic Press: Cambridge, MA, USA, 2012; ISBN 9780123914217. [Google Scholar]
- Aliev, A.E.; Lima, M.D.; Fang, S.; Baughman, R.H. Underwater sound generation using carbon nanotube projectors. Nano Lett. 2010, 10, 2374–2380. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Liu, P.; Liu, L.; Li, Q.; Feng, Z.; Fan, S.; Jiang, K. High frequency response of carbon nanotube thin film speaker in gases. J. Appl. Phys. 2011, 110, 1–6. [Google Scholar] [CrossRef]





| Substrate | Active Film | Electrical Resistance Re (Ω) | Heat Capacity Per Unit Area |
|---|---|---|---|
| Kapton—75 μm | AgNW—15 layers | 3.82 | 39.3 × 10−3 [19] |
| Kapton—75 μm | Gold—20 nm | 2.51 | 50.2 × 10−3 |
| Kapton—75 μm | Gold—40 nm | 1.23 | 100.5 × 10−3 |
| Kapton—75 μm | Gold—100 nm | 0.39 | 251.2 × 10−3 |
| Glass—1.5 mm | AgNW—15 layers | 2.92 | 39.3 × 10−3 [19] |
| Glass—1.5 mm | Gold—20 nm | 2.54 | 50.2 × 10−3 |
| Glass—1.5 mm | Gold—40 nm | 0.94 | 100.5 × 10−3 |
| Glass—1.5 mm | Gold—100 nm | 0.36 | 251.2 × 10−3 |
| Property | Symbol (Unit) | Air | Kapton | Glass |
|---|---|---|---|---|
| Thermal conductivity | 0.0263 | 0.12 | 1 | |
| Density | 1.16 | 1420 | 2500 | |
| Specific heat | 1007 | 1090 | 750 | |
| Thermal diffusivity | 22.6 × 10−6 | 77.5 × 10−9 | 533.3 × 10−9 | |
| Thermal effusivity | 5.5 | 431 | 1369.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torraca, P.L.; Bobinger, M.; Servadio, M.; Pavan, P.; Becherer, M.; Lugli, P.; Larcher, L. On the Frequency Response of Nanostructured Thermoacoustic Loudspeakers. Nanomaterials 2018, 8, 833. https://doi.org/10.3390/nano8100833
Torraca PL, Bobinger M, Servadio M, Pavan P, Becherer M, Lugli P, Larcher L. On the Frequency Response of Nanostructured Thermoacoustic Loudspeakers. Nanomaterials. 2018; 8(10):833. https://doi.org/10.3390/nano8100833
Chicago/Turabian StyleTorraca, Paolo La, Marco Bobinger, Maurizio Servadio, Paolo Pavan, Markus Becherer, Paolo Lugli, and Luca Larcher. 2018. "On the Frequency Response of Nanostructured Thermoacoustic Loudspeakers" Nanomaterials 8, no. 10: 833. https://doi.org/10.3390/nano8100833
APA StyleTorraca, P. L., Bobinger, M., Servadio, M., Pavan, P., Becherer, M., Lugli, P., & Larcher, L. (2018). On the Frequency Response of Nanostructured Thermoacoustic Loudspeakers. Nanomaterials, 8(10), 833. https://doi.org/10.3390/nano8100833





