Dielectric Metasurface-Based High-Efficiency Mid-Infrared Optical Filter
Abstract
:1. Introduction
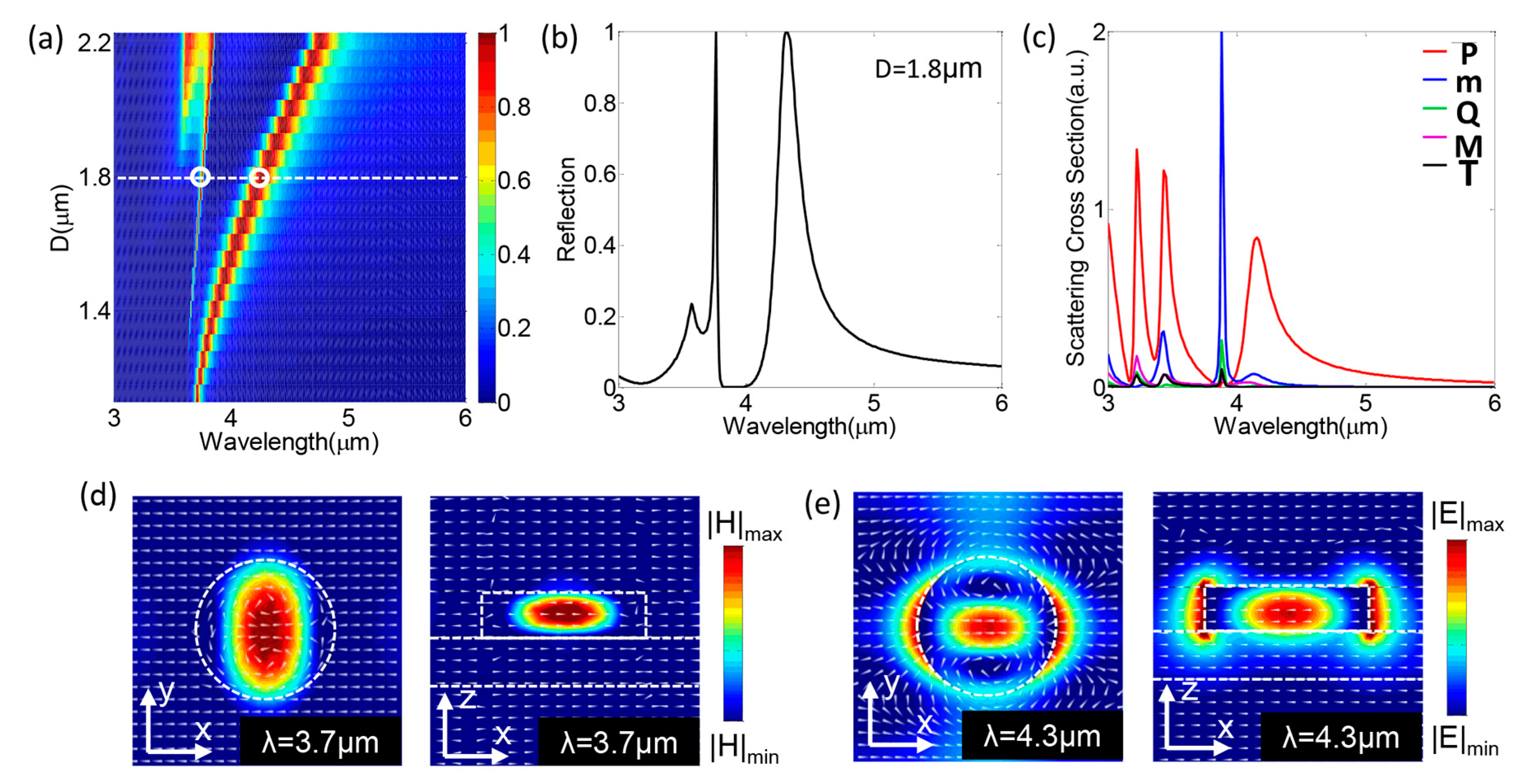
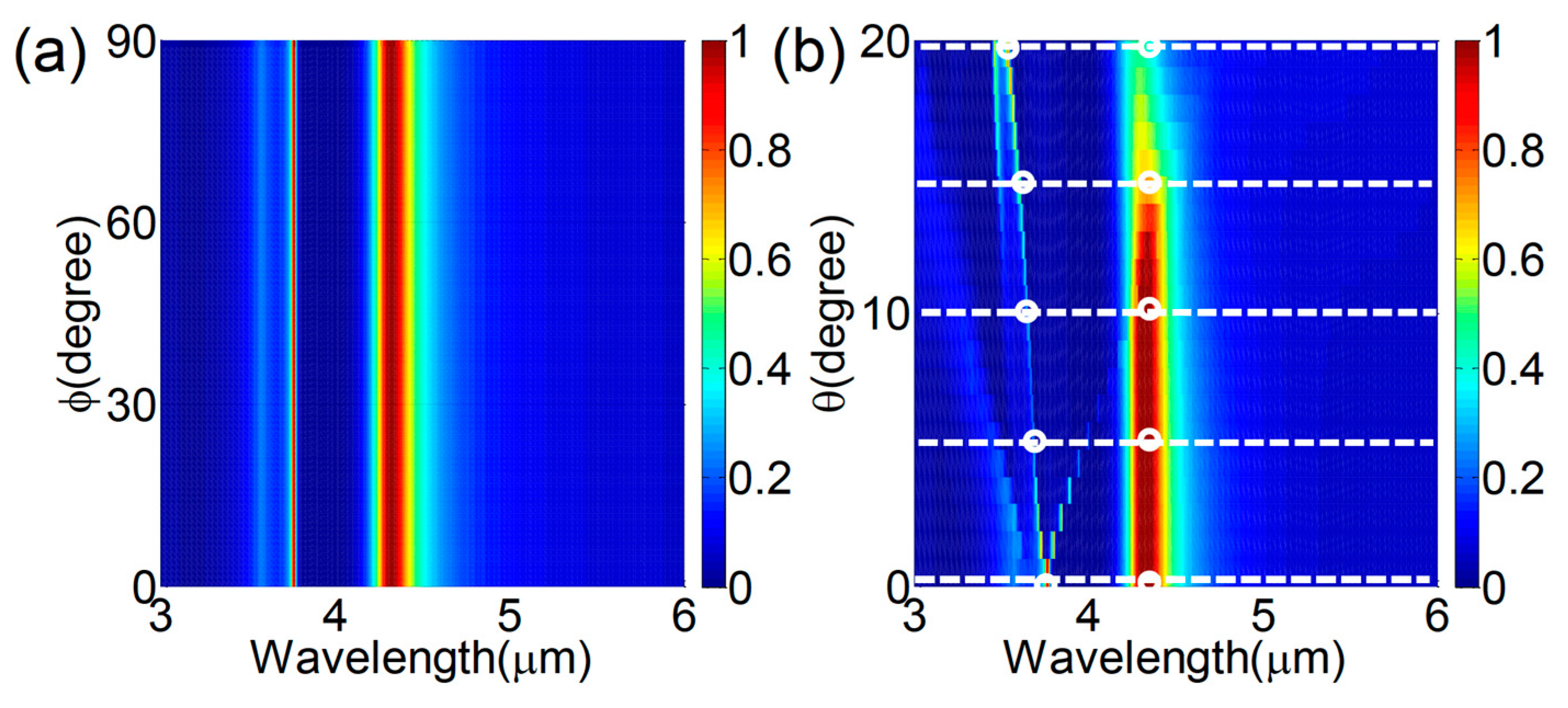
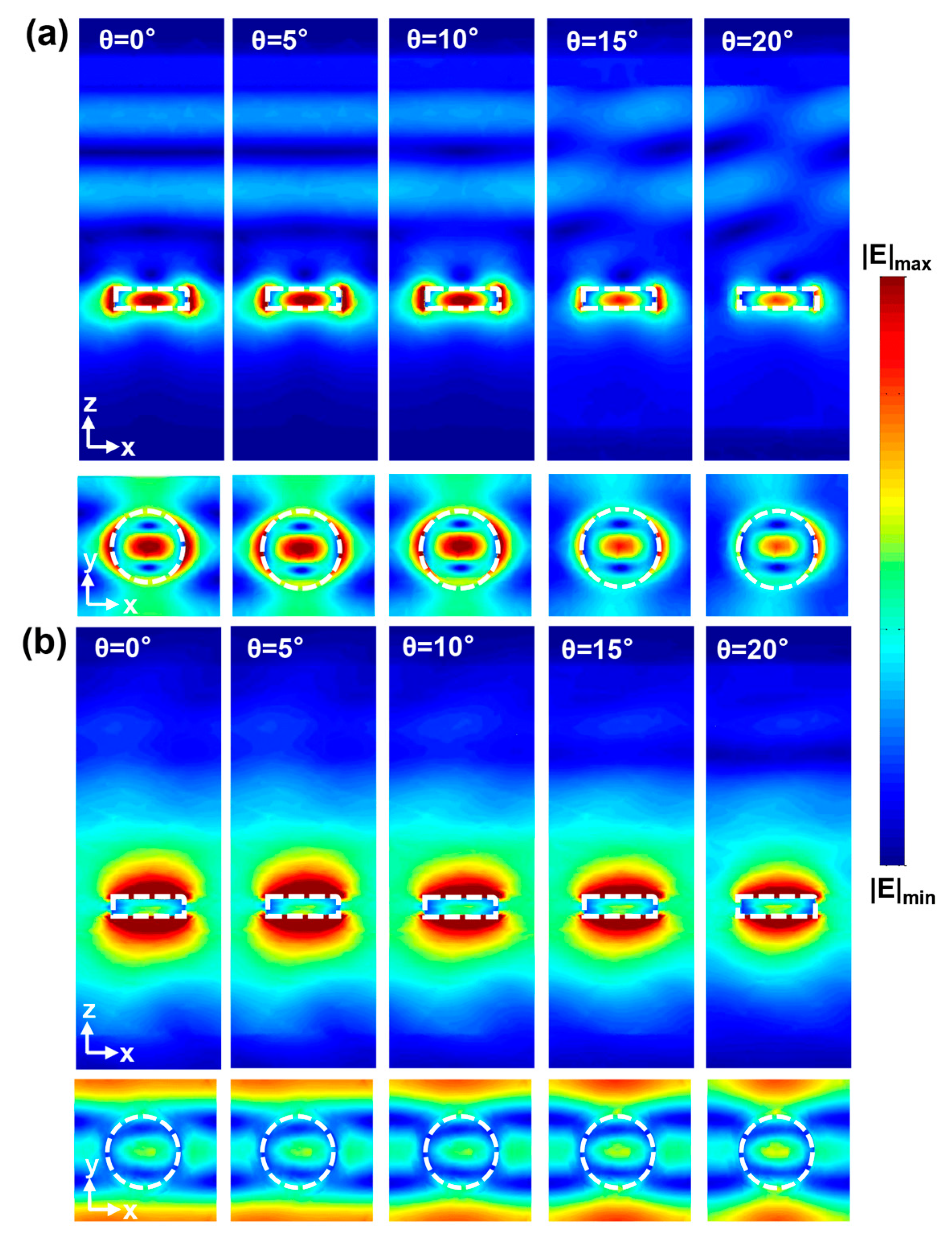
2. Design, Results, and Discussions
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rephaeli, E.; Raman, A.; Fan, S. Broadband photonic structures to achieve high-performance daytime radiative cooling. Nano Lett. 2013, 13, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.; Gu, M. Radiative cooling: Principles, progress, and potentials. Adv. Sci. 2016, 3, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Korobkin, D.; Urzhumov, Y.; Shvets, G. Enhanced near-field resolution in midinfrared using metamaters. J. Opt. Soc. Am. B 2006, 23, 468–478. [Google Scholar] [CrossRef]
- Kyoung, J.; Hwang, S. Configurable plasmonic band-pass filters operating under the addition rule. ACS Photonics 2016, 3, 819–827. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Yang, H.; Li, J.; Yu, P.; Cheng, H.; Tian, J. Simultaneous control of light polarization and phase distributions using plasmonic metasurfaces. Adv. Funct. Mater. 2015, 25, 704–710. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.; Lai, Y.; Chu, C.H.; Chen, J.; Lu, S.; Chen, J.; Xu, B.; Kuan, C.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wan, X.; Shen, X.; Luo, Y.; Cui, T.J. Planar bifunctional Luneburg-fisheye lens made of an anisotropic metasurface. Laser Photonics Rev. 2014, 8, 757–765. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Guo, Z.; Li, R.; Zhang, J.; Zhang, A.; Li, Y.; Liu, Y.; Wang, X.; Qu, S. L-shaped metasurface for both the linear and circular polarization conversions. J. Opt. 2015, 17, 065103. [Google Scholar] [CrossRef]
- Li, R.; Guo, Z.; Wang, W.; Zhang, J.; Zhang, A.; Liu, J.; Qu, S.; Gao, J. High-efficiency cross polarization converters by plasmonic metasurface. Plasmonics 2015, 10, 1167–1172. [Google Scholar] [CrossRef]
- Monticone, F.; Alù, A. Metamaterials and plasmonics: From nanoparticles to nanoantenna arrays, metasurfaces, and metamaterials. Chin. Phys. B 2014, 23, 047809. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liu, Z.; Cheng, H.; Liu, W.; Tang, C.; Gu, C.; Li, J.; Chen, H.; Chen, S.; Tian, J. Single-layer plasmonic metasurface half-wave plates with wavelength-independent polarization conversion angle. ACS Photonics 2017, 4, 2061–2069. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Z.; Zhou, K.; Sun, Y.; Shen, F.; Li, Y.; Qu, S.; Liu, S. Polarization-independent longitudinal multi-focusing metalens. Opt. Express 2015, 23, 29855–29866. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kim, I.; Zhang, L.; Mehmood, M.Q.; Anwar, M.S.; Saleem, M.; Qiu, C.W. Dielectric meta-holograms enabled with dual magnetic resonances in visible light. ACS Nano 2017, 11, 9382–9389. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Hanham, S.M.; Albella, P.; Ng, B.; Lu, H.T.; Gong, Y.; Hong, M. Terahertz all-dielectric magnetic mirror metasurfaces. ACS Photonics 2016, 3, 1010–1018. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.; Wang, W.; Chen, J.; Chen, Z. High Q-factor with the excitation of anapole modes in dielectric split nanodisk arrays. Opt. Express 2017, 25, 22375–22387. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Li, J.; Su, R.; Yao, B.; Fang, H.; Li, K.; Wang, X. Efficient silicon metasurfaces for visible light. ACS Photonics 2017, 4, 544–551. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, W. All-dielectric heterogeneous metasurface as an efficient ultra-broadband reflector. Adv. Opt. Mater. 2017, 5, 1–9. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, L.; Guo, K.; Shen, F.; Yin, Z. High-Order dielectric metasurfaces for high-efficiency polarization beam splitters and optical vortex generators. Nanoscale Res. Lett. 2017, 12, 512. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Zhu, A.; Paniagua-Domínguez, R.; Fu, Y.; Luk’yanchuk, B.; Kuznetsov, A.I. High-transmission dielectric metasurface with 2 π phase control at visible wavelengths. Laser Photonics Rev. 2015, 9, 412–418. [Google Scholar] [CrossRef]
- Yin, Z.; Chen, F.; Zhu, L.; Guo, K.; Shen, F.; Zhou, Q.; Guo, Z. High-efficiency dielectric metasurfaces for simultaneously engineering polarization and wavefront. J. Mater. Chem. C 2018, 6, 6354. [Google Scholar] [CrossRef]
- Shen, F.; An, N.; Tao, Y.; Zhou, H.; Jiang, Z.; Guo, Z. Unidirectional scattering Anomalous forward scattering of gain-assisted dielectric shell-coated metallic core spherical particles. Nanophotonics 2017, 6, 1063–1072. [Google Scholar] [CrossRef]
- Li, Z.; Yao, K.; Xia, F.; Shen, S.; Tian, J.; Liu, Y. Graphene plasmonic metasurfaces to steer infrared light. Sci. Rep. 2014, 5, 12423. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Guo, Z. Molecular detection by active Fano-sensor. Ann. Phys. 2017, 529, 1600259. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, X.; Shen, F.; Zhou, Q.; Gao, J.; Guo, K. Active-tuning and polarization-independent absorber and sensor in the infrared region based on the phase change material of Ge2Sb2Te5 (GST). Sci. Rep. 2018, 8, 12433. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, C.; Amirtharaj, P.M. High-accuracy midinfrared (450cm−1 ≤ ω ≤ 4000cm−1) refractive index values of silicon. J. Appl. Phys. 2005, 97, 123526. [Google Scholar] [CrossRef]
- Retherford, R.S.; Sabia, R.; Sokira, V.P. Effect of surface quality on transmission performance for (111) CaF2. Appl. Surf. Sci. 2001, 183, 264–269. [Google Scholar] [CrossRef]
- Lee, W.; Kaltenecker, K.; Nirantar, S.; Withayachumnankul, W.; Walther, M.; Bhaskaran, M.; Fischer, B.M.; Sriram, S.; Fumeaux, C. Terahertz near-field imaging of dielectric resonators. Opt. Express 2017, 25, 3756–3764. [Google Scholar] [CrossRef] [PubMed]
- Herzberger, M.; Salzberg, C. Refractive indices of infrared optical materials and color correction of infrared lenses. J. Opt. Soc. Am. 1962, 52, 420–427. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y. Enhancement of optical magnetic modes by controlling the handedness of symmetry breaking in Fano metamolecules. IEEE J. Quantum Elect. 2015, 51, 7300108. [Google Scholar] [CrossRef]
- Tian, J.; Yang, Y.; Qiu, M.; Laurell, F.; Pasiskevicius, V.; Jang, H. All-dielectric KTiOPO4 metasurfaces based on multipolar resonances in the terahertz region. Opt. Express 2017, 25, 24068–24080. [Google Scholar] [CrossRef] [PubMed]
- Terekhov, P.D.; Baryshnikova, K.V.; Shalin, A.S.; Karabchevsky, A.; Evlyukhin, A.B. Resonant forward scattering of light by high-refractive-index dielectric nanoparticles with toroidal dipole contribution. Opt. Lett. 2017, 42, 835–838. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; James, A.R.; Hartmann, N.F.; Baldwin, J.K.; Dominguez, J.; Sinclair, M.B.; Luk, T.S.; Wolf, O.; Liu, S.; Doorn, S.K.; et al. Solitary oxygen dopant emission from carbon nanotubes modified by dielectric metasurfaces. ACS Nano 2017, 11, 6431–6439. [Google Scholar] [CrossRef] [PubMed]
- Staude, I.; Miroshnichenko, A.E.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I.; et al. Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef] [PubMed]


| p | Electric dipole moment | m | Magnetic dipole moment |
|---|---|---|---|
| Electric quadrupole tensors | Magnetic quadrupole tensors | ||
| E | The electric field | T | Toroidal dipole moment |
| Cartesian components in the coordinate system | Relative permittivity of vacuum | ||
| Relative permittivity of Si | c | The speed of light in vacuum |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, F.; Kang, Q.; Wang, J.; Guo, K.; Zhou, Q.; Guo, Z. Dielectric Metasurface-Based High-Efficiency Mid-Infrared Optical Filter. Nanomaterials 2018, 8, 938. https://doi.org/10.3390/nano8110938
Shen F, Kang Q, Wang J, Guo K, Zhou Q, Guo Z. Dielectric Metasurface-Based High-Efficiency Mid-Infrared Optical Filter. Nanomaterials. 2018; 8(11):938. https://doi.org/10.3390/nano8110938
Chicago/Turabian StyleShen, Fei, Qianlong Kang, Jingjing Wang, Kai Guo, Qingfeng Zhou, and Zhongyi Guo. 2018. "Dielectric Metasurface-Based High-Efficiency Mid-Infrared Optical Filter" Nanomaterials 8, no. 11: 938. https://doi.org/10.3390/nano8110938
APA StyleShen, F., Kang, Q., Wang, J., Guo, K., Zhou, Q., & Guo, Z. (2018). Dielectric Metasurface-Based High-Efficiency Mid-Infrared Optical Filter. Nanomaterials, 8(11), 938. https://doi.org/10.3390/nano8110938






