A Simple and Efficient Method for Designing Broadband Terahertz Absorber Based on Singular Graphene Metasurface
Abstract
1. Introduction
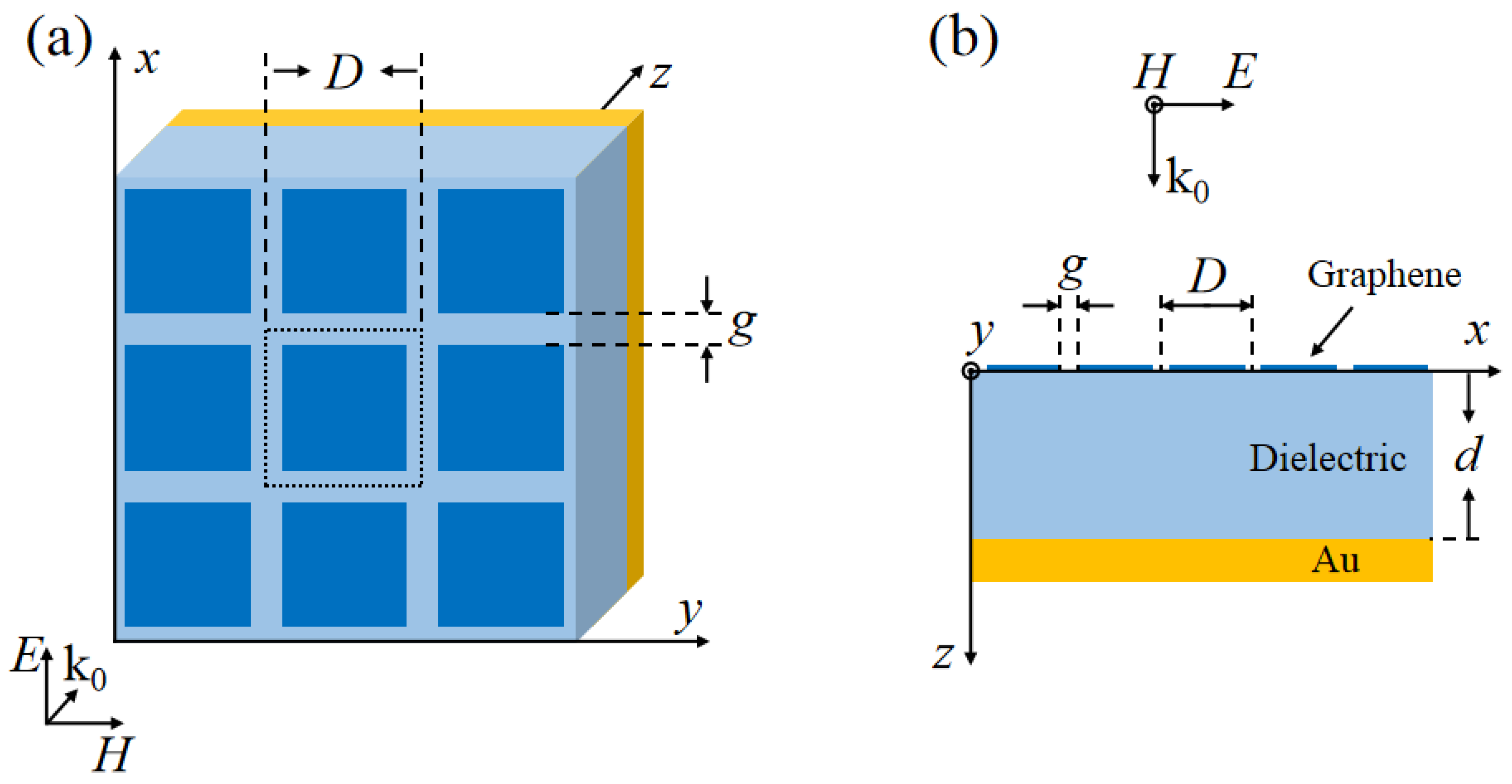
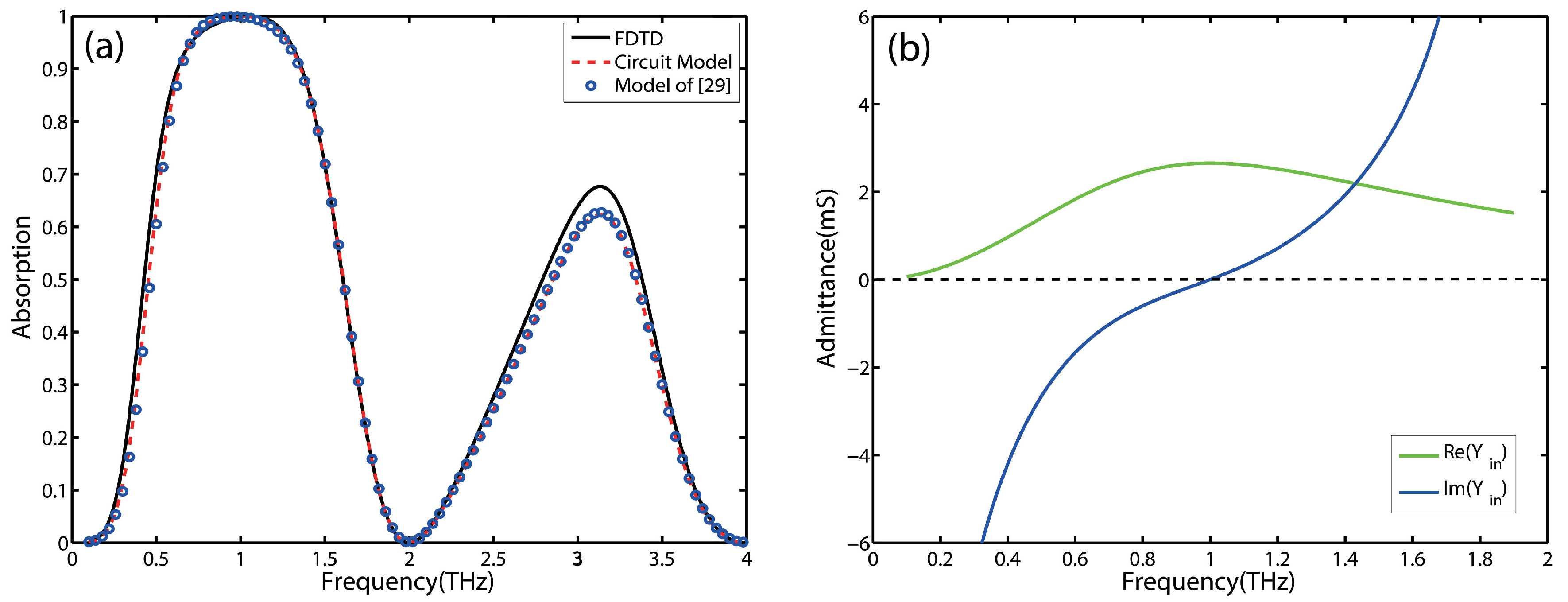
2. Equivalent Circuit Model Approach
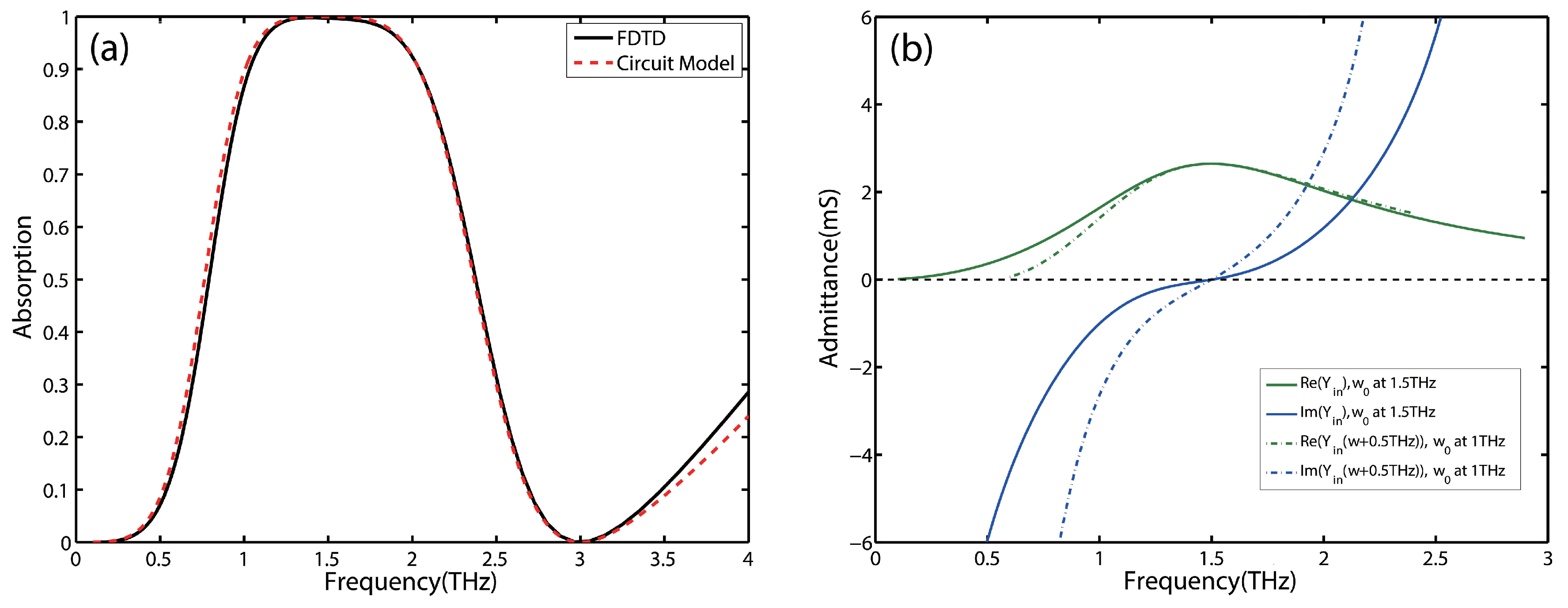
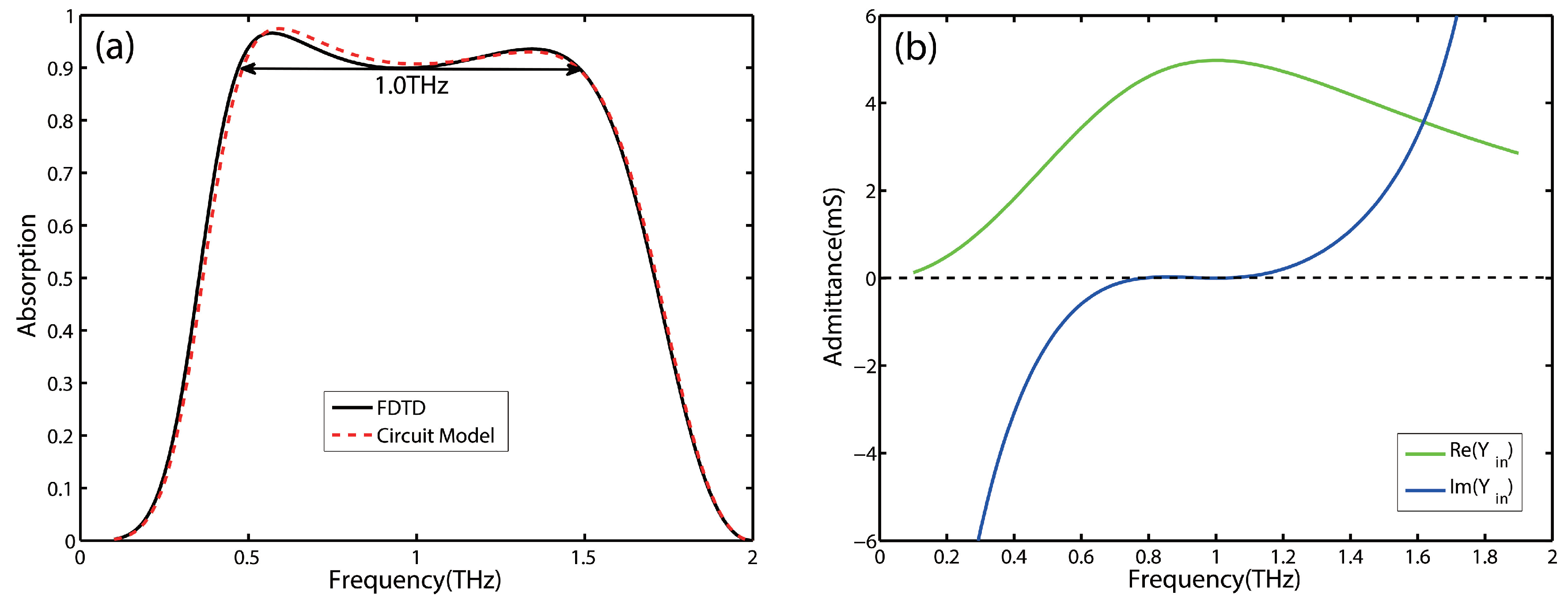
3. Broadband Absorber Design
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alves, F.; Grbovic, D.; Kearney, B.; Lavrik, N.V.; Karunasiri, G. Bi-material terahertz sensors using metamaterial structures. Opt. Express 2013, 21, 13256–13270. [Google Scholar] [CrossRef] [PubMed]
- Carranza, I.E.; Grant, J.P.; Gough, J.; Cumming, D. Terahertz metamaterial absorbers implemented in CMOS technology for imaging applications: Scaling to large format focal plane arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 4700508. [Google Scholar]
- Mittendorff, M.; Winnerl, S.; Kamann, J.; Eroms, J.; Weiss, D.; Schneider, H.; Helm, M. Ultrafast graphene-based broadband THz detector. Appl. Phys. Lett. 2013, 103, 021113. [Google Scholar] [CrossRef]
- Le, L.N.; Thang, N.M.; Thuy, L.M.; Tung, N.T. Hybrid semiconductor–dielectric metamaterial modulation for switchable bi-directional THz absorbers. Opt. Commun. 2017, 383, 244–249. [Google Scholar] [CrossRef]
- Wang, B.X.; Wang, L.L.; Wang, G.Z.; Huang, W.Q.; Li, X.F.; Zhai, X. Frequency Continuous Tunable Terahertz Metamaterial Absorber. J. Lightwave Technol. 2014, 32, 1183–1189. [Google Scholar] [CrossRef]
- Williams, G.P. Filling the THz gap-high power sources and applications. Rep. Prog. Phys. 2006, 69, 301–326. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Cong, L.; Tan, S.; Yahiaoui, R.; Yan, F.P.; Zhang, W.; Singh, R. Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: A comparison with the metasurfaces. Appl. Phys. Lett. 2015, 106, 001107. [Google Scholar] [CrossRef]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep. 2016, 634, 1–72. [Google Scholar] [CrossRef]
- Liu, X.; Fan, K.; Shadrivov, I.V.; Padilla, W.J. Experimental realization of a terahertz all-dielectric metasurface absorber. Opt. Express 2017, 25, 191–201. [Google Scholar] [CrossRef]
- Yi, Z.; Chen, J.; Cen, C.; Chen, X.; Zhou, Z.; Tang, Y.; Ye, X.; Xiao, S.; Luo, W.; Wu, P. Tunable Graphene-based Plasmonic Perfect Metamaterial Absorber in the THz Region. Micromachines 2019, 10, 194. [Google Scholar] [CrossRef] [PubMed]
- Rahmanzadeh, M.; Rajabalipanah, H.; Abdolali, A. Multilayer graphene-based metasurfaces: Robust design method for extremely broadband, wide-angle, and polarization-insensitive terahertz absorbers. Appl. Opt. 2018, 57, 959–968. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Besteiro, L.V.; Huang, Y.; Wu, J.; Fu, L.; Tan, H.H.; Jagadish, C.; Wiederrecht, G.P.; Govorov, A.O.; Wang, Z. Broadband Metamaterial Absorbers. Adv. Opt. Mater. 2019, 7, 1800995. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Kim, H.; Lee, Y.; Xu, X.; Park, J.-S.; Zheng, Y.; Balakrishnan, J.; Lei, T.; Kim, H.R.; Song, Y.I.; et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574–578. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Gu, M.; Qin, K.; Xiao, S. Absorption enhancement in graphene with an efficient resonator. Opt. Quantum Electron. 2017, 49, 1013–1018. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Guo, C.C.; Liu, K.; Zhang, J.F.; Ye, W.M.; Yuan, X.D.; Qin, S.Q. Electrically tunable polarizer based on anisotropic absorption of graphene ribbons. Appl. Phys. A 2014, 114, 1017–1021. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S. Realization of wide-angle and wideband absorber using metallic and graphene-based metasurface for mid-infrared and low THz frequency. Opt. Quant. Electron. 2018, 50, 378. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Y.-B.; Dong, J.; Tang, M.-C.; Jiang, Y.-N.; Zeng, X.-P. Ultra-thin and broadband tunable metamaterial graphene absorber. Opt. Express 2018, 26, 1681–1688. [Google Scholar] [CrossRef]
- Mou, N.; Sun, S.; Dong, H.; Dong, S.; He, Q.; Zhou, L.; Zhang, L. Hybridization-induced broadband terahertz wave absorption with graphene metasurfaces. Opt. Express 2018, 26, 11728–11736. [Google Scholar] [CrossRef]
- Huang, M.L.; Cheng, Y.Z.; Cheng, Z.Z.; Chen, H.R.; Mao, X.S.; Gong, R.Z. Design of a Broadband Tunable Terahertz Metamaterial Absorber Based on Complementary Structural Graphene. Materials 2018, 11, 540. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Chen, Y.; Cai, G.; Liu, N.; Zhu, J.; Song, Z.; Liu, Q.H. Broadband absorber with periodically sinusoidally patterned graphene layer in terahertz range. Opt. Express 2018, 25, 11223–11232. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; He, W.; Yang, F.; Ran, J.; Gao, B.; Zhang, W.-L. Polarization-independent and angle-insensitive broadband absorber with a target-patterned graphene layer in the terahertz regime. Opt. Express 2018, 26, 25558–25566. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.W.; Lv, J.; Zhang, L.; Que, L.; Zhou, Y.; Jiang, Y. An ultra-broadband and polarization-independent metamaterial absorber with bandwidth of 3.7 THz. Opt. Commun. 2019, 431, 255–260. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Liu, P.-K. Excitation of surface plasmon polaritons by electron beam with graphene ribbon arrays. J. Appl. Phys. 2017, 121, 1113104. [Google Scholar] [CrossRef]
- He, X.; Yao, Y.; Zhu, Z.; Chen, M.; Zhu, L.; Yang, W.; Yang, Y.; Wu, F.; Jiang, J. Active graphene metamaterial absorber for terahertz absorption bandwidth intensity and frequency control. Opt. Mater. Express 2018, 8, 1031–1042. [Google Scholar] [CrossRef]
- Andryieuski, A.; Lavrinenko, A.V. Graphene metamaterials based tunable terahertz absorber: Effective surface conductivity approach. Opt. Express 2013, 21, 9144–9155. [Google Scholar] [CrossRef] [PubMed]
- Barzegar-Parizi, S.; Tavakol, M.R.; Khavasi, A. Deriving Surface Impedance for 2-D Arrays of Graphene Patches Using a Variational Method. IEEE J. Quantum Electron. 2017, 53, 7000106. [Google Scholar] [CrossRef]
- Padooru, Y.R.; Yakovlev, A.B.; Kaipa, C.S.R.; Hanson, G.W.; Medina, F.; Mesa, F. Dual capacitive-inductive nature of periodic graphene patches: Transmission characteristics at low-terahertz frequencies. Phys. Rev. B 2013, 87, 115401. [Google Scholar] [CrossRef]
- Luukkonen, O.; Simovski, C.; Granet, G.; Goussetis, G.; Lioubtchenko, D.; Räisänen, A.V.; Tretyakov, S.A. Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Trans. Antennas Propag. 2008, 56, 1624–1632. [Google Scholar] [CrossRef]
- Khavasi, A. Design of ultra-broadband graphene absorber using circuit theory. J. Opt. Soc. Am. B 2015, 32, 1941–1946. [Google Scholar] [CrossRef]
- Tretyakov, S. Summation of Wire Fields. In Analytical Modeling in Applied Electromagnetics; Artech House Publishers: Boston, MA, USA; London, UK, 2003; pp. 76–79. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Guo, L.; Zhang, Q. A Simple and Efficient Method for Designing Broadband Terahertz Absorber Based on Singular Graphene Metasurface. Nanomaterials 2019, 9, 1351. https://doi.org/10.3390/nano9101351
Liu Z, Guo L, Zhang Q. A Simple and Efficient Method for Designing Broadband Terahertz Absorber Based on Singular Graphene Metasurface. Nanomaterials. 2019; 9(10):1351. https://doi.org/10.3390/nano9101351
Chicago/Turabian StyleLiu, Zhongmin, Liang Guo, and Qingmao Zhang. 2019. "A Simple and Efficient Method for Designing Broadband Terahertz Absorber Based on Singular Graphene Metasurface" Nanomaterials 9, no. 10: 1351. https://doi.org/10.3390/nano9101351
APA StyleLiu, Z., Guo, L., & Zhang, Q. (2019). A Simple and Efficient Method for Designing Broadband Terahertz Absorber Based on Singular Graphene Metasurface. Nanomaterials, 9(10), 1351. https://doi.org/10.3390/nano9101351



