Experiment and Simulation of a Selective Subwavelength Filter with a Low Index Contrast
Abstract
:1. Introduction
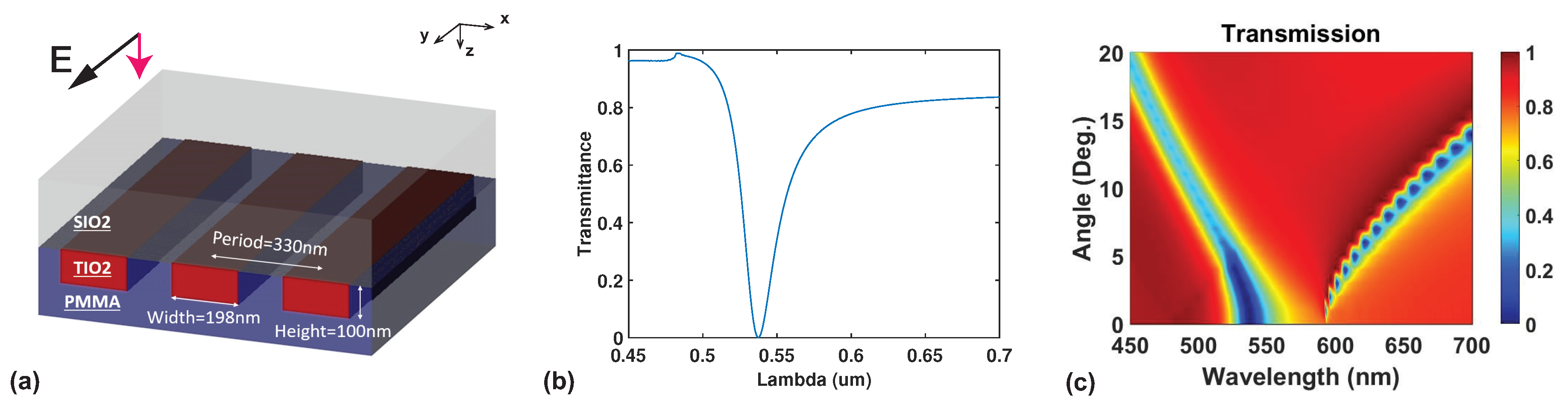
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, Y.; Ye, D.; Celanovic, I.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Optical broadband angular selectivity. Science 2014, 343, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Kosten, E.D.; Atwater, J.H.; Parsons, J.; Polman, A.; Atwater, H.A. Highly efficient GaAs solar cells by limiting light emission angle. Light Sci. Appl. 2013, 2, e45. [Google Scholar] [CrossRef]
- Sakr, E.; Bermel, P. Angle-Selective Reflective Filters for Exclusion of Background Thermal Emission. Phys. Rev. Appl. 2017, 7, 044020. [Google Scholar] [CrossRef]
- Mbise, G.W.; Bellac, D.L.; Niklasson, G.A.; Granqvist, C.G. Angular selective window coatings: Theory and experiments. J. Phys. D: Appl. Phys. 1997, 30, 2103. [Google Scholar] [CrossRef]
- Halir, R.; Bock, P.J.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Schmid, J.H.; Lapointe, J.; Xu, D.X.; Wangüemert-Pérez, J.G.; Molina-Fernández, Í.; et al. Waveguide sub-wavelength structures: A review of principles and applications. Laser Photonics Rev. 2015, 9, 25–49. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef]
- Silberstein, E.; Lalanne, P.; Hugonin, J.P.; Cao, Q. Use of grating theories in integrated optics. J. Opt. Soc. Am. A 2001, 18, 2865–2875. [Google Scholar] [CrossRef]
- Mateus, C.F.R.; Huang, M.C.Y.; Deng, Y.; Neureuther, A.R.; Chang-Hasnain, C.J. Ultrabroadband mirror using low-index cladded subwavelength grating. IEEE Photonics Technol. Lett. 2004, 16, 518–520. [Google Scholar] [CrossRef]
- Zhou, Y.; Moewe, M.; Kern, J.; Huang, M.C.Y.; Chang-Hasnain, C.J. Surface-normal emission of a high-Q resonator using a subwavelength high-contrast grating. Opt. Express 2008, 16, 17282–17287. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Wu, Y.K.; Luo, X.; Guo, L.J. Plasmonic nanoresonators for high-resolution colour filtering and spectral imaging. Nat. Commun. 2010, 1, 59. [Google Scholar] [CrossRef]
- Pu, M.; Ma, X.; Guo, Y.; Li, X.; Luo, X. Theory of microscopic meta-surface waves based on catenary optical fields and dispersion. Opt. Express 2018, 26, 19555–19562. [Google Scholar] [CrossRef] [PubMed]
- Shao, T.; Tang, F.; Sun, L.; Ye, X.; He, J.; Yang, L.; Zheng, W. Fabrication of Antireflective Nanostructures on a Transmission Grating Surface Using a One-Step Self-Masking Method. Nanomaterials 2019, 9, 180. [Google Scholar] [CrossRef] [PubMed]
- Kroker, S.; Brückner, F.; Kley, E.B.; Tünnermann, A. Enhanced angular tolerance of resonant waveguide grating reflectors. Opt. Lett. 2011, 36, 537–539. [Google Scholar] [CrossRef] [PubMed]
- Ito, K.; Iizuka, H. Directional thermal emission control by coupling between guided mode resonances and tunable plasmons in multilayered graphene. J. Appl. Phys. 2016, 120, 163105. [Google Scholar] [CrossRef]
- Dong, B.; Hu, T.; Luo, X.; Chang, Y.; Guo, X.; Wang, H.; Kwong, D.L.; Lo, G.Q.; Lee, C. Wavelength-Flattened Directional Coupler Based Mid-Infrared Chemical Sensor Using Bragg Wavelength in Subwavelength Grating Structure. Nanomaterials 2018, 8, 893. [Google Scholar] [CrossRef]
- Bomzon, Z.; Kleiner, V.; Hasman, E. Pancharatnam–Berry phase in space-variant polarization-state manipulations with subwavelength gratings. Opt. Lett. 2001, 26, 1424–1426. [Google Scholar] [CrossRef]
- Lerman, G.M.; Levy, U. Generation of a radially polarized light beam using space-variant subwavelength gratings at 1064 nm. Opt. Lett. 2008, 33, 2782–2784. [Google Scholar] [CrossRef]
- Shiraishi, K.; Oyama, S.; Tsai, C.S. A Polarizer Using Thin Metallic-Film Subwavelength Grating for Infrared to Terahertz Region. J. Light. Technol. 2011, 29, 670–676. [Google Scholar] [CrossRef]
- Gou, Y.; Xuan, Y. The application of the microstructured metallic grating to light emission extraction. Chin. Sci. Bull. 2013, 58, 696–700. [Google Scholar] [CrossRef] [Green Version]
- Stafeev, S.S.; Kotlyar, V.V.; Nalimov, A.G.; Kotlyar, M.V.; O’Faolain, L. Subwavelength gratings for polarization conversion and focusing of laser light. Photonics Nanostruct. Fundam. Appl. 2017, 27, 32–41. [Google Scholar] [CrossRef]
- Huang, M.C.Y.; Zhou, Y.; Chang-Hasnain, C.J. A surface-emitting laser incorporating a high-index-contrast subwavelength grating. Nat. Photon. 2007, 1, 119–122. [Google Scholar] [CrossRef]
- Chang-Hasnain, C.J.; Yang, W. High-contrast gratings for integrated optoelectronics. Adv. Opt. Photon. 2012, 4, 379–440. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh, A.; Park, G.C.; Mørk, J.; Chung, I.S. Hybrid grating reflector with high reflectivity and broad bandwidth. Opt. Express 2014, 22, 21175–21184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, X.; Wu, T.; Xu, Y.; Li, X.; Bai, D.; Zhu, G.; Zhu, H.; Wang, Y. Angular-dependent polarization-insensitive filter fashioned with zero-contrast grating. Opt. Express 2015, 23, 15235–15241. [Google Scholar] [CrossRef] [PubMed]
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Nanoimprint lithography. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1996, 14, 4129–4133. [Google Scholar] [CrossRef]
- Battaglia, C.; Söderström, K.; Escarré, J.; Haug, F.J.; Dominé, D.; Cuony, P.; Boccard, M.; Bugnon, G.; Denizot, C.; Despeisse, M.; et al. Efficient light management scheme for thin film silicon solar cells via transparent random nanostructures fabricated by nanoimprinting. Appl. Phys. Lett. 2010, 96, 213504. [Google Scholar] [CrossRef] [Green Version]
- Ooms, M.D.; Dinh, C.T.; Sargent, E.H.; Sinton, D. Photon management for augmented photosynthesis. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef]
- Kuo, H.C.; Hung, C.W.; Chen, H.C.; Chen, K.J.; Wang, C.H.; Sher, C.W.; Yeh, C.C.; Lin, C.C.; Chen, C.H.; Cheng, Y.J. Patterned structure of REMOTE PHOSPHOR for phosphor-converted white LEDs. Opt. Express 2011, 19, A930–A936. [Google Scholar] [CrossRef]
- DeVore, J.R. Refractive Indices of Rutile and Sphalerite. J. Opt. Soc. Am. 1951, 41, 416–419. [Google Scholar] [CrossRef]
- Sultanova, N.; Kasarova, S.; Nikolov, I. Dispersion Properties of Optical Polymers. Acta Phys. Pol. A 2009, 116, 585–587. [Google Scholar] [CrossRef]
- Karagodsky, V.; Chang-Hasnain, C.J. Physics of near-wavelength high contrast gratings. Opt. Express 2012, 20, 10888–10895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kikuta, H.; Yoshida, H.; Iwata, K. Ability and Limitation of Effective Medium Theory for Subwavelength Gratings. OPT REV 1995, 2, 92–99. [Google Scholar] [CrossRef]
- Lalanne, P.; Hugonin, J.P. High-order effective-medium theory of subwavelength gratings in classical mounting: Application to volume holograms. J. Opt. Soc. Am. A 1998, 15, 1843–1851. [Google Scholar] [CrossRef]
- Huang, C.Y.; Wang, D.Y.; Wang, C.H.; Chen, Y.T.; Wang, Y.T.; Jiang, Y.T.; Yang, Y.J.; Chen, C.C.; Chen, Y.F. Efficient Light Harvesting by Photon Downconversion and Light Trapping in Hybrid ZnS Nanoparticles/Si Nanotips Solar Cells. ACS Nano 2010, 4, 5849–5854. [Google Scholar] [CrossRef] [PubMed]
- FDTD Solutions. Lumerical’s Nanophotonic FDTD Simulation Software; Lumerical Inc.: Vancouver, BC, Canada, 2017. [Google Scholar]
- Robinson, J.; Rahmat-Samii, Y. Particle Swarm Optimization in Electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Karagodsky, V.; Sedgwick, F.G.; Chang-Hasnain, C.J. Theoretical analysis of subwavelength high contrast grating reflectors. Opt. Express 2010, 18, 16973–16988. [Google Scholar] [CrossRef]
- Lalanne, P.; Hugonin, J.P.; Chavel, P. Optical properties of deep lamellar Gratings: A coupled Bloch-mode insight. J. Light. Technol. 2006, 24, 2442–2449. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Asbahii, M.; Lim, J.-Y.; Xie, H.; Koh, C.-W.; Goh, M.-H.; Ong, K.-S.; Zhang, H.; Ding, D. Experiment and Simulation of a Selective Subwavelength Filter with a Low Index Contrast. Nanomaterials 2019, 9, 1497. https://doi.org/10.3390/nano9101497
Li T, Asbahii M, Lim J-Y, Xie H, Koh C-W, Goh M-H, Ong K-S, Zhang H, Ding D. Experiment and Simulation of a Selective Subwavelength Filter with a Low Index Contrast. Nanomaterials. 2019; 9(10):1497. https://doi.org/10.3390/nano9101497
Chicago/Turabian StyleLi, Tao, Mohamed Asbahii, Jian-Yee Lim, Hong Xie, Chan-Wai Koh, Min-Hao Goh, Kian-Soo Ong, Hang Zhang, and Ding Ding. 2019. "Experiment and Simulation of a Selective Subwavelength Filter with a Low Index Contrast" Nanomaterials 9, no. 10: 1497. https://doi.org/10.3390/nano9101497
APA StyleLi, T., Asbahii, M., Lim, J.-Y., Xie, H., Koh, C.-W., Goh, M.-H., Ong, K.-S., Zhang, H., & Ding, D. (2019). Experiment and Simulation of a Selective Subwavelength Filter with a Low Index Contrast. Nanomaterials, 9(10), 1497. https://doi.org/10.3390/nano9101497




