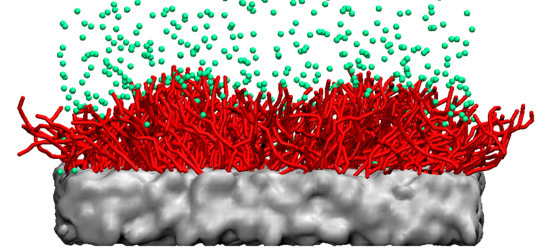
Tuning the Properties of Nanogel Surfaces by Grafting Charged Alkylamine Brushes
Abstract
:1. Introduction
2. Coarse-Grained Modelling
2.1. Dissipative Particle Dynamics
2.2. Coarse-Grained Models
2.3. Simulation Details and Observables
3. Results and Discussion
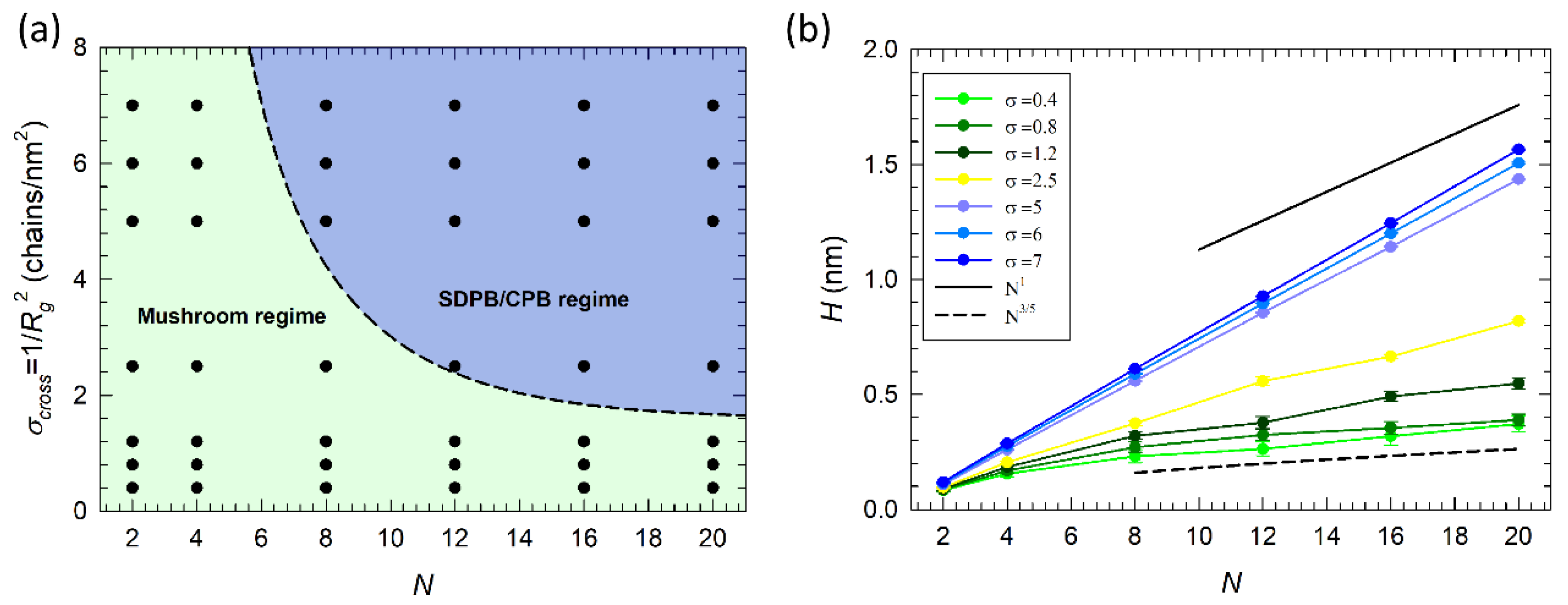
3.1. Scaling Behavior of Alkylamine Brushes
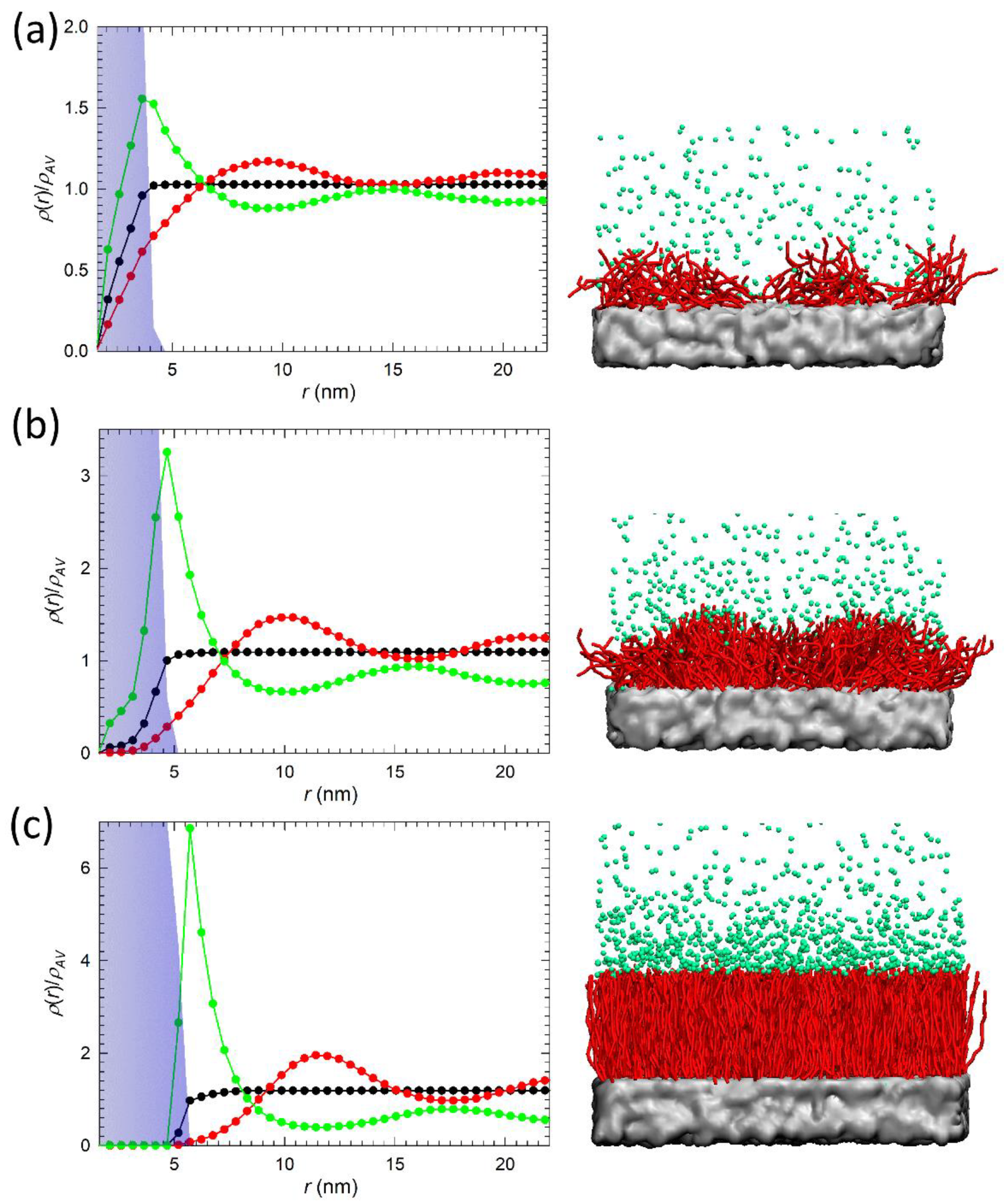
3.2. Distribution of Polymer, Water, and Ions
3.3. Osmotic Compressibility of the Coating
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, L.; Yan, C.; Zheng, Z. Functional polymer surfaces for controlling cell behaviors. Mater. Today 2018, 21, 38–59. [Google Scholar] [CrossRef]
- Hui, Y.; Yi, X.; Hou, F.; Wibowo, D.; Zhang, F.; Zhao, D.; Gao, H.; Zhao, C.-X. Role of nanoparticle mechanical properties in cancer drug delivery. ACS Nano 2019, 13, 7410–7424. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Badoux, M.; Billing, M.; Klok, H.-A. Polymer brush interfaces for protein biosensing prepared by surface-initiated controlled radical polymerization. Polym. Chem. 2019, 10, 2925–2951. [Google Scholar] [CrossRef]
- Mullner, M.; Dodds, S.J.; Nguyen, T.-H.; Senyschyn, D.; Porter, C.J.H.; Boyd, B.J.; Caruso, F. Size and rigidity of cylindrical polymer brushes dictate long circulating properties in vivo. ACS Nano 2015, 9, 1294–1304. [Google Scholar] [CrossRef]
- Faivre, J.; Shrestha, B.R.; Burdynska, J.; Xie, G.; Moldovan, F.; Delair, T.; Benayoun, S.; David, L.; Matyjaszewski, K.; Banquy, X. Wear protection without surface modification using a synergistic mixture of molecular brushes and linear polymers. ACS Nano 2017, 11, 1762–1769. [Google Scholar] [CrossRef]
- Yu, Q.; Ista, L.K.; Gu, R.; Zauscher, S.; Lopez, G.P. Nanopatterned polymer brushes: Conformation, fabrication and applications. Nanoscale 2016, 8, 680–700. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.; Zhang, D.; Chen, F.; Fan, P.; Zhong, M.; Xiao, S.; Chang, Y.; Gong, X.; Yang, J.; et al. Design of salt-responsive and regenerative antibacterial polymer brushes with integrated bacterial resistance, killing, and release properties. J. Mater. Chem. B 2019, 7, 5762–5774. [Google Scholar] [CrossRef]
- Uz, M.; Bulmus, V.; Alsoy Altinkaya, S. Effect of PEG grafting density and hydrodynamic volume on gold nanoparticle–cell interactions: An investigation on cell cycle, apoptosis, and DNA damage. Langmuir 2016, 32, 5997–6009. [Google Scholar] [CrossRef]
- Zhao, C.; Li, L.; Wang, Q.; Yu, Q.; Zheng, J. Effect of film thickness on the antifouling performance of poly(hydroxy-functional methacrylates) grafted surfaces. Langmuir 2011, 27, 4906–4913. [Google Scholar] [CrossRef]
- Emilsson, G.; Schoch, R.L.; Feuz, L.; Hook, F.; Lim, R.Y.H.; Dahlin, A.B. Strongly stretched protein resistant poly(ethylene glycol) brushes prepared by grafting-to. ACS Appl. Mater. Interfaces 2015, 7, 7505–7515. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Bhushan, B. Smart polymer brushes and their emerging applications. RSC Adv. 2012, 2, 8557–8578. [Google Scholar] [CrossRef]
- Xu, X.; Billing, M.; Ruths, M.; Klok, H.-A.; Yu, J. Structure and functionality of polyelectrolyte brushes: A surface force perspective. Chem. Asian J. 2018, 13, 3411–3436. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Banik, M.; Chen, G.; Sinha, S.; Mukherjee, R. Polyelectrolyte brushes: Theory, modelling, synthesis and applications. Soft Matter 2015, 11, 8550–8583. [Google Scholar] [CrossRef] [PubMed]
- Arima, Y.; Iwata, H. Effects of surface functional groups on protein adsorption and subsequent cell adhesion using self-assembled monolayers. J. Mater. Chem. 2007, 17, 4079–4087. [Google Scholar] [CrossRef]
- Tomita, S.; Soejima, T.; Shiraki, K.; Yoshimoto, K. Enzymatic fingerprinting of structurally similar homologous proteins using polyion complex library constructed by tuning pegylated polyamine functionalities. Analyst 2014, 139, 6100–6103. [Google Scholar] [CrossRef]
- Zou, Y.; Li, D.; Shen, M.; Shi, X. Polyethylenimine-based nanogels for biomedical applications. Macromol. Biosci. 2019, e1900272. [Google Scholar] [CrossRef]
- Lou, B.; Beztsinna, N.; Mountrichas, G.; Van den Dikkenberg, J.B.; Pispas, S.; Hennink, W.E. Small nanosized poly(vinyl benzyl trimethylammonium chloride) based polyplexes for siRNA delivery. Int. J. Pharm. 2017, 525, 388–396. [Google Scholar] [CrossRef]
- Tamura, A.; Oishi, M.; Nagasaki, Y. Efficient siRNA delivery based on pegylated and partially quaternized polyamine nanogels: Enhanced gene silencing activity by the cooperative effect of tertiary and quaternary amino groups in the core. J. Control. Release 2010, 146, 378–387. [Google Scholar] [CrossRef]
- Cavallaro, G.; Lazzara, G.; Milioto, S.; Parisi, F.; Evtugyn, V.; Rozhina, E.; Fakhrullin, R. Nanohydrogel formation within the halloysite lumen for triggered and sustained release. ACS Appl. Mater. Interfaces 2018, 10, 8265–8273. [Google Scholar] [CrossRef]
- Myerson, J.W.; McPherson, O.; DeFrates, K.G.; Towslee, J.H.; Marcos-Contreras, O.A.; Shuvaev, V.V.; Braender, B.; Composto, R.J.; Muzykantov, V.R.; Eckmann, D.M. Cross-linker-modulated nanogel flexibility correlates with tunable targeting to a sterically impeded endothelial marker. ACS Nano 2019. [Google Scholar] [CrossRef] [PubMed]
- Cuggino, J.C.; Blanco, E.R.O.; Gugliotta, L.M.; Alvarez Igarzabal, C.I.; Calderon, M. Crossing biological barriers with nanogels to improve drug delivery performance. J. Control. Release 2019, 307, 221–246. [Google Scholar] [CrossRef] [PubMed]
- Karg, M.; Pich, A.; Hellweg, T.; Hoare, T.; Lyon, L.A.; Crassous, J.J.; Suzuki, D.; Gumerov, R.A.; Schneider, S.; Potemkin, I.I.; et al. Nanogels and microgels: From model colloids to applications, recent developments, and future trends. Langmuir 2019, 35, 6231–6255. [Google Scholar] [CrossRef] [PubMed]
- Mauri, E.; Moroni, I.; Magagnin, L.; Masi, M.; Sacchetti, A.; Rossi, F. Comparison between two different click strategies to synthesize fluorescent nanogels for therapeutic applications. React. Funct. Polym. 2016, 105, 35–44. [Google Scholar] [CrossRef]
- Esmaeilzadeh, P.; Groth, T. Switchable and obedient interfacial properties that grant new biomedical applications. ACS Appl. Mater. Interfaces 2019, 11, 25637–25653. [Google Scholar] [CrossRef]
- Hajebi, S.; Rabiee, N.; Bagherzadeh, M.; Ahmadi, S.; Rabiee, M.; Roghani-Mamaqani, H.; Tahriri, M.; Tayebi, L.; Hamblin, M.R. Stimulus-responsive polymeric nanogels as smart drug delivery systems. Acta Biomater. 2019, 92, 1–18. [Google Scholar] [CrossRef]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodriguez-Ropero, F.; Van der Vegt, N.F.A. Systematic coarse-graining methods for soft matter simulations—A review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Posocco, P.; Posel, Z.; Fermeglia, M.; Lisal, M.; Pricl, S. A molecular simulation approach to the prediction of the morphology of self-assembled nanoparticles in diblock copolymers. J. Mater. Chem. 2010, 20, 10511–10520. [Google Scholar] [CrossRef]
- Posel, Z.; Posocco, P.; Lisal, M.; Fermeglia, M.; Pricl, S. Highly grafted polystyrene/polyvinylpyridine polymer gold nanoparticles in a good solvent: Effects of chain length and composition. Soft Matter 2016, 12, 3600–3611. [Google Scholar] [CrossRef]
- Posel, Z.; Posocco, P.; Fermeglia, M.; Lisal, M.; Pricl, S. Modeling hierarchically structured nanoparticle/diblock copolymer systems. Soft Matter 2013, 9, 2936–2946. [Google Scholar] [CrossRef]
- Posocco, P.; Hassan, Y.M.; Barandiaran, I.; Kortaberria, G.; Pricl, S.; Fermeglia, M. Combined mesoscale/experimental study of selective placement of magnetic nanoparticles in diblock copolymer films via solvent vapor annealing. J. Phys. Chem. C 2016, 120, 7403–7411. [Google Scholar] [CrossRef]
- Sologan, M.; Marson, D.; Polizzi, S.; Pengo, P.; Boccardo, S.; Pricl, S.; Posocco, P.; Pasquato, L. Patchy and janus nanoparticles by self-organization of mixtures of fluorinated and hydrogenated alkanethiolates on the surface of a gold core. ACS Nano 2016, 10, 9316–9325. [Google Scholar] [CrossRef] [PubMed]
- Posocco, P.; Gentilini, C.; Bidoggia, S.; Pace, A.; Franchi, P.; Lucarini, M.; Fermeglia, M.; Pricl, S.; Pasquato, L. Self-organization of mixtures of fluorocarbon and hydrocarbon amphiphilic thiolates on the surface of gold nanoparticles. ACS Nano 2012, 6, 7243–7253. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Anderson, R.L.; Bray, D.J.; Ferrante, A.S.; Noro, M.G.; Stott, I.P.; Warren, P.B. Dissipative particle dynamics: Systematic parametrization using water-octanol partition coefficients. J. Chem. Phys. 2017, 147, 094503. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Zou, W.; Koenig, P.H.; McConaughy, S.D.; Weaver, M.R.; Eike, D.M.; Schmidt, M.J.; Larson, R.G. Multiscale modeling of the effects of salt and perfume raw materials on the rheological properties of commercial threadlike micellar solutions. J. Phys. Chem. B 2017, 121, 2468–2485. [Google Scholar] [CrossRef]
- Pivkin, I.V.; Karniadakis, G.E. A new method to impose no-slip boundary conditions in dissipative particle dynamics. J. Comput. Phys. 2005, 207, 114–128. [Google Scholar] [CrossRef]
- Warren, P.B.; Vlasov, A.; Anton, L.; Masters, A.J. Screening properties of gaussian electrolyte models, with application to dissipative particle dynamics. J. Chem. Phys. 2013, 138, 204907. [Google Scholar] [CrossRef]
- Gonzalez-Melchor, M.; Mayoral, E.; Velazquez, M.E.; Alejandre, J. Electrostatic interactions in dissipative particle dynamics using the Ewald sums. J. Chem. Phys. 2006, 125, 224107. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Dimitrov, D.; Milchev, A.; Binder, K. Polymer brushes on flat and curved substrates: Scaling concepts and computer simulations. Macromol. Symp. 2007, 252, 47–57. [Google Scholar] [CrossRef]
- Rodriguez-Ropero, F.; Van der Vegt, N.F.A. Ionic specific effects on the structure, mechanics and interfacial softness of a polyelectrolyte brush. Faraday Discuss. 2013, 160, 297–309. [Google Scholar] [CrossRef] [PubMed]
- Weir, M.P.; Parnell, A.J. Water soluble responsive polymer brushes. Polymers 2011, 3, 2107–2132. [Google Scholar] [CrossRef]
- Wu, T.; Gong, P.; Szleifer, I.; Vlcek, P.; Subr, V.; Genzer, J. Behavior of surface-anchored poly(acrylic acid) brushes with grafting density gradients on solid substrates: 1. Experiment. Macromolecules 2007, 40, 8756–8764. [Google Scholar] [CrossRef]





| Bead Type | W | C | N+ | Na+ | Cl− | S |
|---|---|---|---|---|---|---|
| W | 25.00 (1.000) | 45.00 (1.0370) | 14.50 (1.0120) | 25.0 (1.000) | 25.00 (1.000) | 24.64 (1.0450) |
| C | - | 22.00 (1.0740) | 22.50 (1.0490) | 45.0 (1.0370) | 45.00 (1.0370) | 26.34 (1.0820) |
| N+ | - | - | 21.50 (1.0240) | 14.50 (1.0120) | 14.50 (1.0120) | 20.92 (1.0570) |
| Na+ | - | - | - | 25.00 (1.000) | 25.00 (1.000) | 24.64 (1.0450) |
| Cl− | - | - | - | - | 25.00 (1.000) | 24.64 (1.0450) |
| S | - | - | - | - | - | 25.00 (1.000) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posel, Z.; Posocco, P. Tuning the Properties of Nanogel Surfaces by Grafting Charged Alkylamine Brushes. Nanomaterials 2019, 9, 1514. https://doi.org/10.3390/nano9111514
Posel Z, Posocco P. Tuning the Properties of Nanogel Surfaces by Grafting Charged Alkylamine Brushes. Nanomaterials. 2019; 9(11):1514. https://doi.org/10.3390/nano9111514
Chicago/Turabian StylePosel, Zbyšek, and Paola Posocco. 2019. "Tuning the Properties of Nanogel Surfaces by Grafting Charged Alkylamine Brushes" Nanomaterials 9, no. 11: 1514. https://doi.org/10.3390/nano9111514
APA StylePosel, Z., & Posocco, P. (2019). Tuning the Properties of Nanogel Surfaces by Grafting Charged Alkylamine Brushes. Nanomaterials, 9(11), 1514. https://doi.org/10.3390/nano9111514