Super Ductility of Nanoglass Aluminium Nitride
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
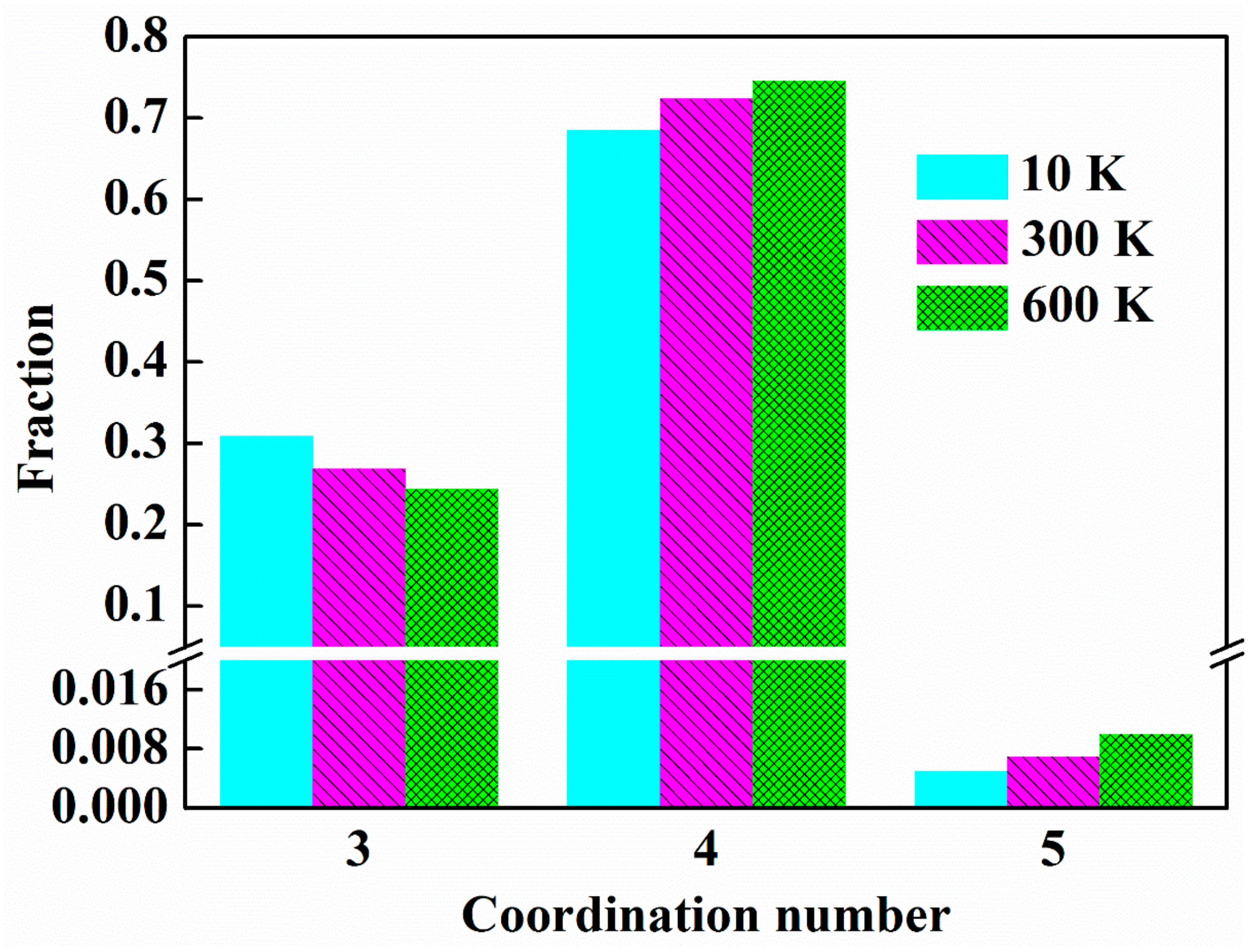
3.1. Structural of ng-AlN
3.2. Comparison between Mechanical Properties of ng-AlN and a-AlN
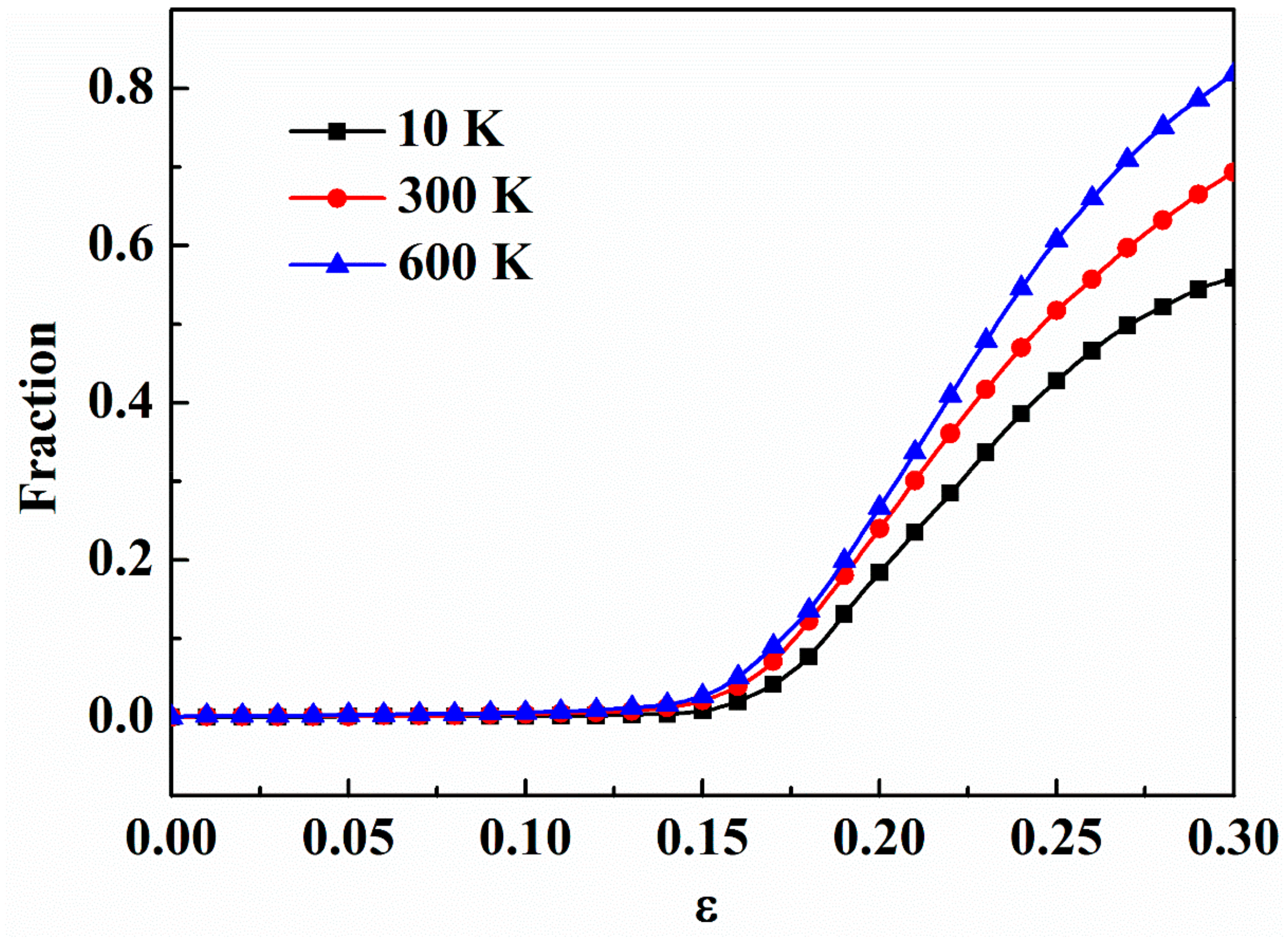
3.3. Effect of Temperature
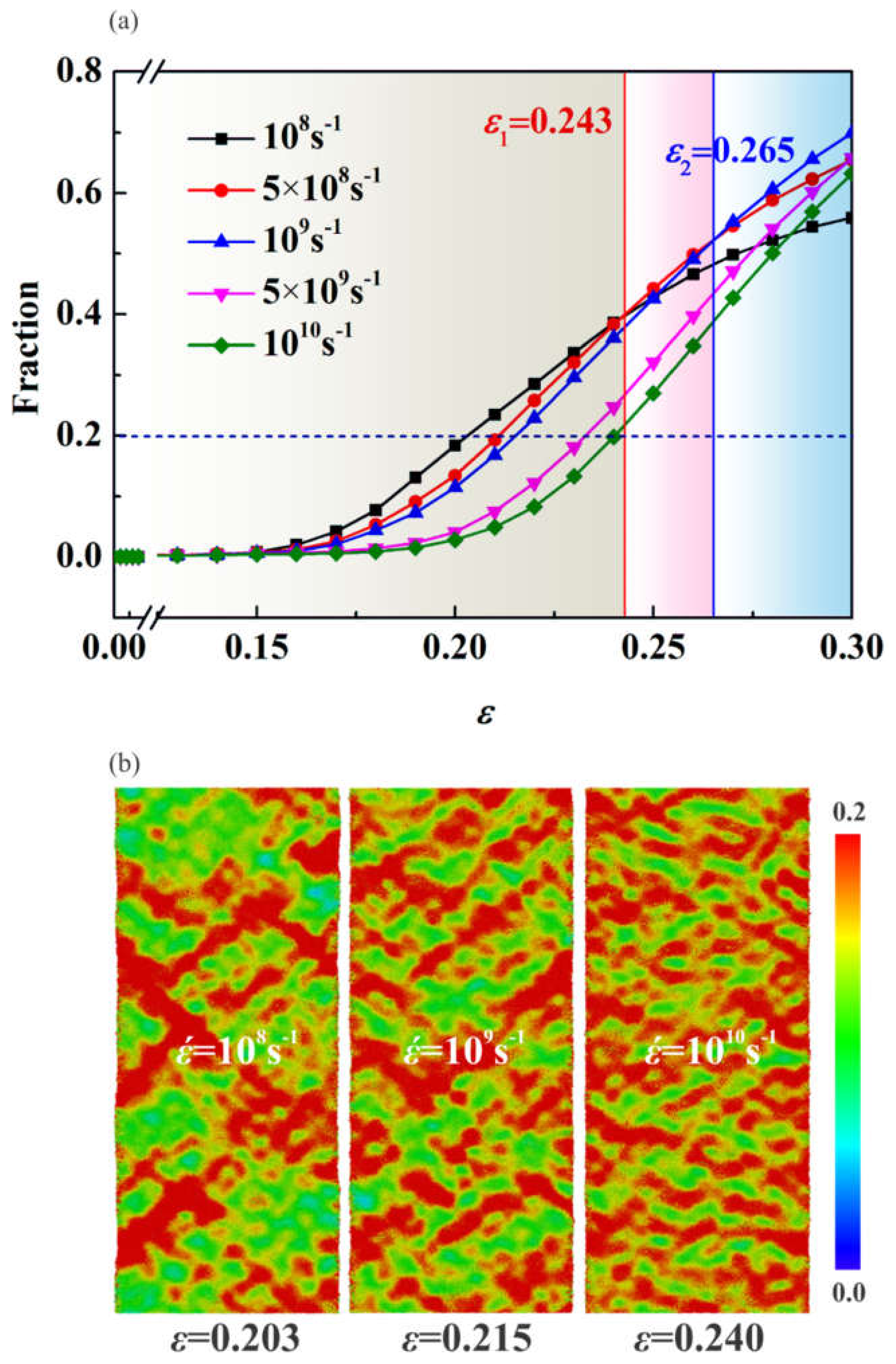
3.4. Effect of Strain Rate
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials: GaN, AlN, InN, BN, SiC, SiGe; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Slack, G.A. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321–335. [Google Scholar] [CrossRef]
- Slack, G.A.; Tanzilli, R.A.; Pohl, R.O.; Vandersande, J.W. The intrinsic thremal conductivity of AlN. J. Phys. Chem. Solids 1987, 48, 641–647. [Google Scholar] [CrossRef]
- Slack, G.A.; Bartram, S.F. Thermal expansion of some diamondlike crystals. J. Appl. Phys. 1975, 46, 89–98. [Google Scholar] [CrossRef]
- Yim, W.M.; Paff, R.J. Thermal expansion of AlN, sapphire, and silicon. J. Appl. Phys. 1974, 45, 1456–1457. [Google Scholar] [CrossRef]
- Chin, V.W.L.; Tansley, T.L.; Osotchan, T. Electron mobilities in gallium, indium, and aluminum nitrides. J. Appl. Phys. 1994, 75, 7365–7372. [Google Scholar] [CrossRef]
- Davidge, R.W. Mechanical properties of ceramic materials. Contemp. Phys. 1969, 10, 105–124. [Google Scholar] [CrossRef]
- Heard, H.C.; Cline, F.C. Mechanical behaviour of polycrystalline BeO, Al2O3 and AlN at high pressure. J. Mater. Sci. 1980, 15, 1889–1897. [Google Scholar] [CrossRef]
- Guo, J.J.; Reddy, K.M.; Hirata, A.; Fujita, T.; Gazonas, G.A.; McCauley, J.W.; Chen, M.W. Sample size induced brittle-to-ductile transition of single-crystal aluminum nitride. Acta Mater. 2015, 88, 252–259. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Guo, A.; Geng, H.; Ren, S.; Tao, X.; Liu, J. Enhanced plasticity by nanocrystallite in bulk amorphous Al2O3–ZrO2–Y2O3. Int. J. Plast. 2016, 79, 314–327. [Google Scholar] [CrossRef]
- Gandhi, A.S.; Jayaram, V. Plastically deforming amorphous ZrO2-Al2O3. Acta Mater. 2003, 51, 1641–1649. [Google Scholar] [CrossRef]
- Paul, A.; Jayaram, V. Deformation and structural densification in Al2O3–Y2O3 glass. Acta Mater. 2011, 59, 82–92. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Fu, T.; Huang, C.; Xiang, H.; Hu, N.; Yan, C. Investigation of mechanical behaviour of amorphous aluminium nitride. Materialia 2018, 2, 148–156. [Google Scholar] [CrossRef]
- Gleiter, H. Nanoglasses: A new kind of noncrystalline material and the way to an age of new technologies? Small 2016, 12, 2225–2233. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Kramer, A.; Birringer, R.; Gleiter, H.; Gonser, U. Modified Atomic Structure in A Pd-Fe-Si Nanoglass A Mossbauer study. J. Non Cryst. Solids 1989, 113, 167–170. [Google Scholar] [CrossRef]
- Gleiter, H.; Schimmel, T.; Hahn, H. Nanostructured solids—From nanoglasses to quantum transistors. Nano Today 2014, 9, 17–68. [Google Scholar] [CrossRef]
- Fang, J.X.; Vainio, U.; Puff, W.; Wurschum, R.; Wang, X.L.; Wang, D.; Ghafari, M.; Jiang, F.; Sun, J.; Hahn, H.; et al. Atomic structure and structural stability of Sc75Fe25 nanoglasses. Nano Lett. 2012, 12, 458–463. [Google Scholar] [CrossRef]
- Şopu, D.; Ritter, Y.; Gleiter, H.; Albe, K. Deformation behavior of bulk and nanostructured metallic glasses studied via molecular dynamics simulations. Phys. Rev. B 2011, 83, 100202. [Google Scholar] [CrossRef]
- Adibi, S.; Sha, Z.-D.; Branicio, P.S.; Joshi, S.P.; Liu, Z.-S.; Zhang, Y.-W. A transition from localized shear banding to homogeneous superplastic flow in nanoglass. Appl. Phys. Lett. 2013, 103, 211905. [Google Scholar] [CrossRef]
- Sha, Z.D.; Branicio, P.S.; Pei, Q.X.; Liu, Z.S.; Lee, H.P.; Tay, T.E.; Wang, T.J. Strong and superplastic nanoglass. Nanoscale 2015, 7, 17404–17409. [Google Scholar] [CrossRef]
- Chen, N.; Louzguine-Luzgin, D.V.; Xie, G.Q.; Sharma, P.; Perepezko, J.H.; Esashi, M.; Yavari, A.R.; Inoue, A. Structural investigation and mechanical properties of a representative of a new class of materials: Nanograined metallic glasses. Nanotechnology 2013, 24, 045610. [Google Scholar] [CrossRef]
- Wang, J.Q.; Chen, N.; Liu, P.; Wang, Z.; Louzguine-Luzgin, D.V.; Chen, M.W.; Perepezko, J.H. The ultrastable kinetic behavior of an Au-based nanoglass. Acta Mater. 2014, 79, 30–36. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Kübel, C.; Nandam, S.H.; Wang, C.; Mu, X.; Adjaoud, O.; Albe, K.; Hahn, H. Structure and Properties of Nanoglasses. Adv. Eng. Mater. 2018, 20, 1800404. [Google Scholar] [CrossRef]
- Kushima, A.; Liu, X.H.; Zhu, G.; Wang, Z.L.; Huang, J.Y.; Li, J. Leapfrog cracking and nanoamorphization of ZnO nanowires during in situ electrochemical lithiation. Nano Lett. 2011, 11, 4535–4541. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Peng, X.; Fu, T.; Huang, C.; Feng, C.; Yin, D.; Wang, Z. Molecular dynamics simulation of nano-indentation of (111) cubic boron nitride with optimized Tersoff potential. Appl. Surf. Sci. 2016, 382, 309–315. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Fu, T.; Zhu, X.; Hu, N.; Yan, C. Strengthening mechanisms of graphene coated copper under nanoindentation. Comput. Mater. Sci. 2018, 144, 42–49. [Google Scholar] [CrossRef]
- Fu, T.; Peng, X.; Huang, C.; Zhao, Y.; Weng, S.; Chen, X.; Hu, N. Effects of twin boundaries in vanadium nitride films subjected to tensile/compressive deformations. Appl. Surf. Sci. 2017, 426, 262–270. [Google Scholar] [CrossRef]
- Huang, C.; Peng, X.; Yang, B.; Zhao, Y.; Xiang, H.; Chen, X.; Li, Q.; Fu, T. Molecular dynamics simulations for responses of nanotwinned diamond films under nanoindentation. Ceram. Int. 2017, 43, 16888–16894. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Huang, C.; Fu, T.; Yang, B.; Hu, N.; Xi, Y.; Yan, C. Notch effects on deformation of crystalline and amorphous AlN—A nanoscale study. Ceram. Int. 2019, 45, 907–917. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P. Interaction potential for aluminum nitride: A molecular dynamics study of mechanical and thermal properties of crystalline and amorphous aluminum nitride. J. Appl. Phys. 2011, 109, 033514. [Google Scholar] [CrossRef]
- Xiang, H.; Li, H.; Fu, T.; Huang, C.; Peng, X. Formation of prismatic loops in AlN and GaN under nanoindentation. Acta Mater. 2017, 138, 131–139. [Google Scholar] [CrossRef]
- Branicio, P.S.; Nakano, A.; Kalia, R.K.; Vashishta, P. Shock loading on AlN ceramics: A large scale molecular dynamics study. Int. J. Plast. 2013, 51, 122–131. [Google Scholar] [CrossRef]
- Brostow, W.; Dussault, J.; Fox, B. Construction of voronoi polyhedral. J. Comput. Phys. 1978, 29, 81–92. [Google Scholar] [CrossRef]
- Adelman, S.A.; Doll, J.D. Generalized Langevin equation approach for atom/solid-surface scattering: General formulation for classical scattering off harmonic solids. J. Chem. Phys. 1976, 64, 2375–2388. [Google Scholar] [CrossRef]
- Tsai, D.H. The virial theorem and stress calculation in molecular dynamics. J. Chem. Phys. 1979, 70, 1375–1382. [Google Scholar] [CrossRef]
- Shimizu, S.O.F.; Li, J. Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Durandurdu, M. Uncovering Nanoclusters in Amorphous AlN: An Ab Initio Study. J. Am. Ceram. Soc. 2015, 98, 1095–1098. [Google Scholar] [CrossRef]
- Sheng, H.W.; Luo, W.K.; Alamgir, F.M.; Bai, J.M.; Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 2006, 439, 419–425. [Google Scholar] [CrossRef]
- Schuh, C.; Hufnagel, T.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Johnson, W.L.; Samwer, K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys. Rev. Lett. 2005, 95, 195501. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Jin, Z.-H. Stagnation accommodated global plasticity in nanoglass composites. Scr. Mater. 2015, 106, 46–51. [Google Scholar] [CrossRef]
- Cowper, G.R.; Symonds, P.S. Strain hardening and strain rate effect in the impact loading of cantilever beams. Small Bus. Econ. 1957, 31, 235–263. [Google Scholar]
- Li, M.C.; Jiang, M.Q.; Li, G.; He, L.; Sun, J.; Jiang, F. Ductile to brittle transition of fracture of a Zr-based bulk metallic glass: Strain rate effect. Intermetallics 2016, 77, 34–40. [Google Scholar] [CrossRef]
- Li, M.C.; Jiang, M.Q.; Yang, S.; Jiang, F.; He, L.; Sun, J. Effect of strain rate on yielding strength of a Zr-based bulk metallic glass. Mater. Sci. Eng. A 2017, 680, 21–26. [Google Scholar] [CrossRef] [Green Version]










| Ec (eV) | B (GPa) | C11 (GPa) | C12 (GPa) | Y (GPa) | |
|---|---|---|---|---|---|
| a-AlN | −5.480 | 98.8 | 155.6 | 70.4 | 111.7 |
| ng-AlNd = 8 nm | −5.474 | 96.6 | 153.0 | 68.4 | 110.7 |
| ng-AlNd = 4 nm | −5.469 | 95.1 | 151.0 | 67.2 | 109.6 |
| ng-AlNd = 1 nm | −5.454 | 90.9 | 145.6 | 63.6 | 106.9 |
| B (GPa) | C11 (GPa) | C12 (GPa) | Y (GPa) | |
|---|---|---|---|---|
| 10 K | 90.9 | 145.6 | 63.6 | 106.9 |
| 150 K | 92.7 | 147.7 | 65.2 | 107.7 |
| 300 K | 92.6 | 147.7 | 65.0 | 107.9 |
| 450 K | 91.5 | 146.0 | 64.2 | 106.8 |
| 600 K | 89.2 | 142.7 | 62.4 | 104.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Peng, X.; Huang, C.; Yang, B.; Hu, N.; Wang, M. Super Ductility of Nanoglass Aluminium Nitride. Nanomaterials 2019, 9, 1535. https://doi.org/10.3390/nano9111535
Zhao Y, Peng X, Huang C, Yang B, Hu N, Wang M. Super Ductility of Nanoglass Aluminium Nitride. Nanomaterials. 2019; 9(11):1535. https://doi.org/10.3390/nano9111535
Chicago/Turabian StyleZhao, Yinbo, Xianghe Peng, Cheng Huang, Bo Yang, Ning Hu, and Mingchao Wang. 2019. "Super Ductility of Nanoglass Aluminium Nitride" Nanomaterials 9, no. 11: 1535. https://doi.org/10.3390/nano9111535
APA StyleZhao, Y., Peng, X., Huang, C., Yang, B., Hu, N., & Wang, M. (2019). Super Ductility of Nanoglass Aluminium Nitride. Nanomaterials, 9(11), 1535. https://doi.org/10.3390/nano9111535





