Numerical Analysis of the Correlation between Arc Plasma Fluctuation and Nanoparticle Growth–Transport under Atmospheric Pressure
Abstract
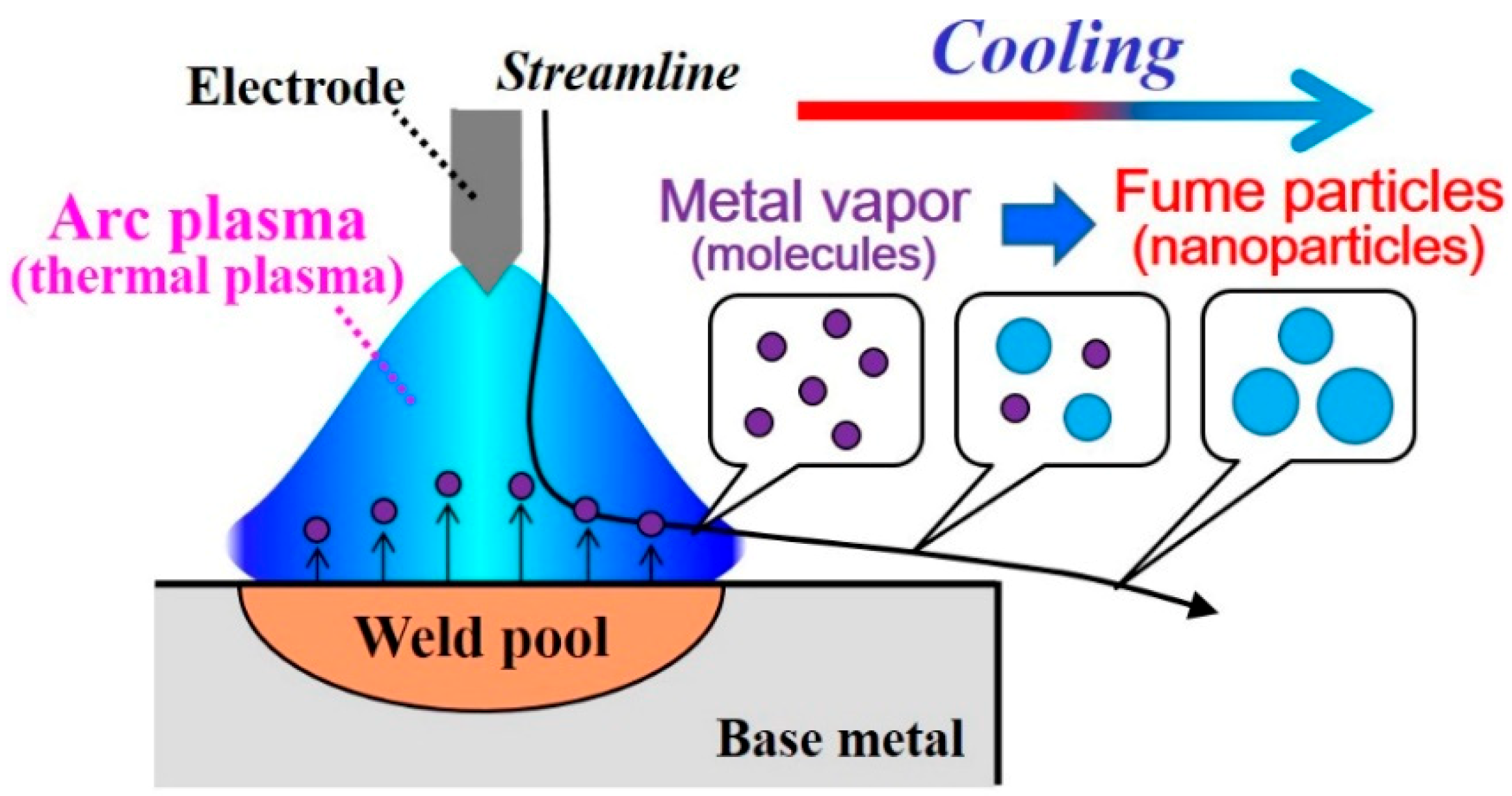
:1. Introduction
2. Model Description
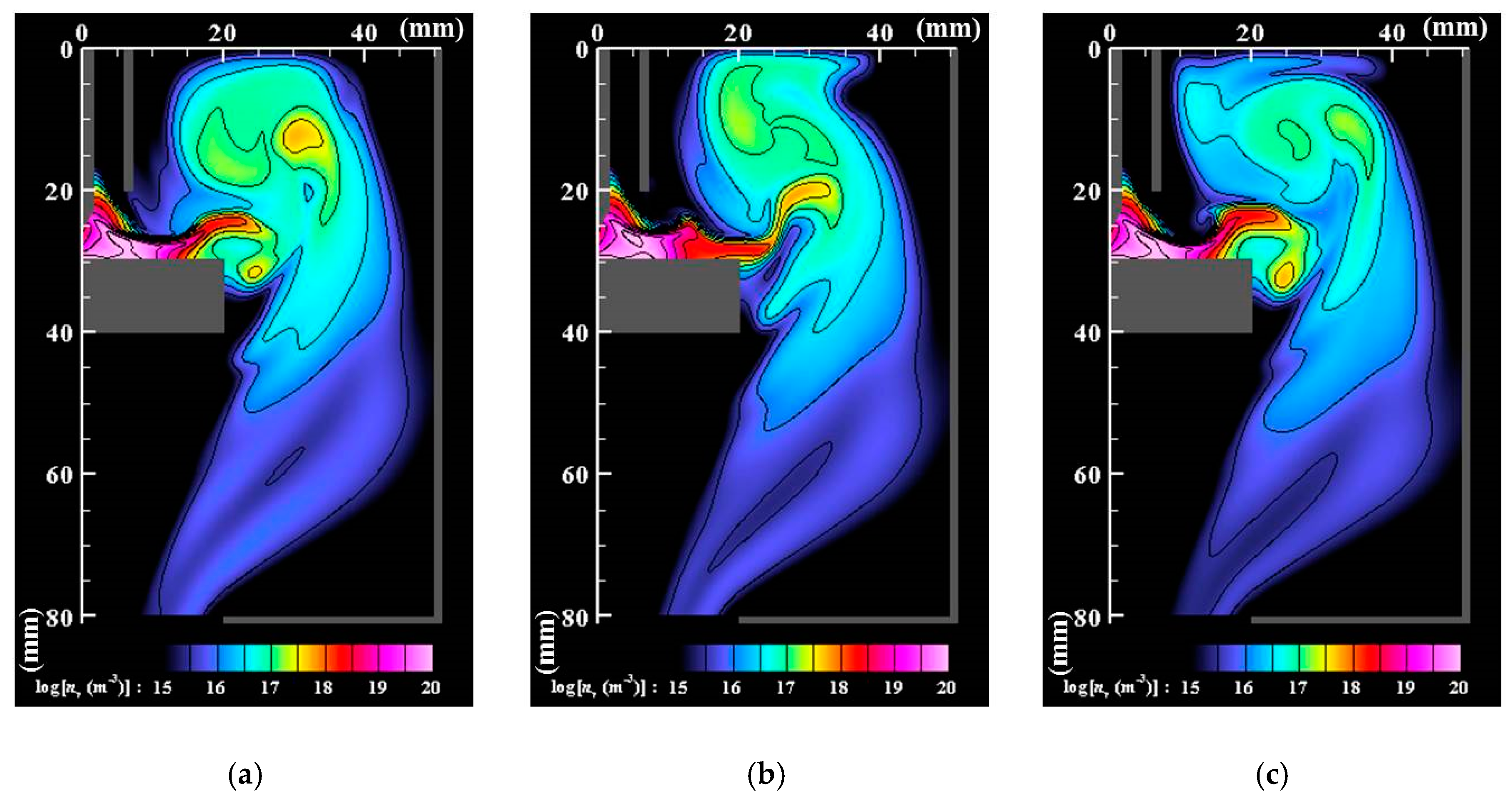
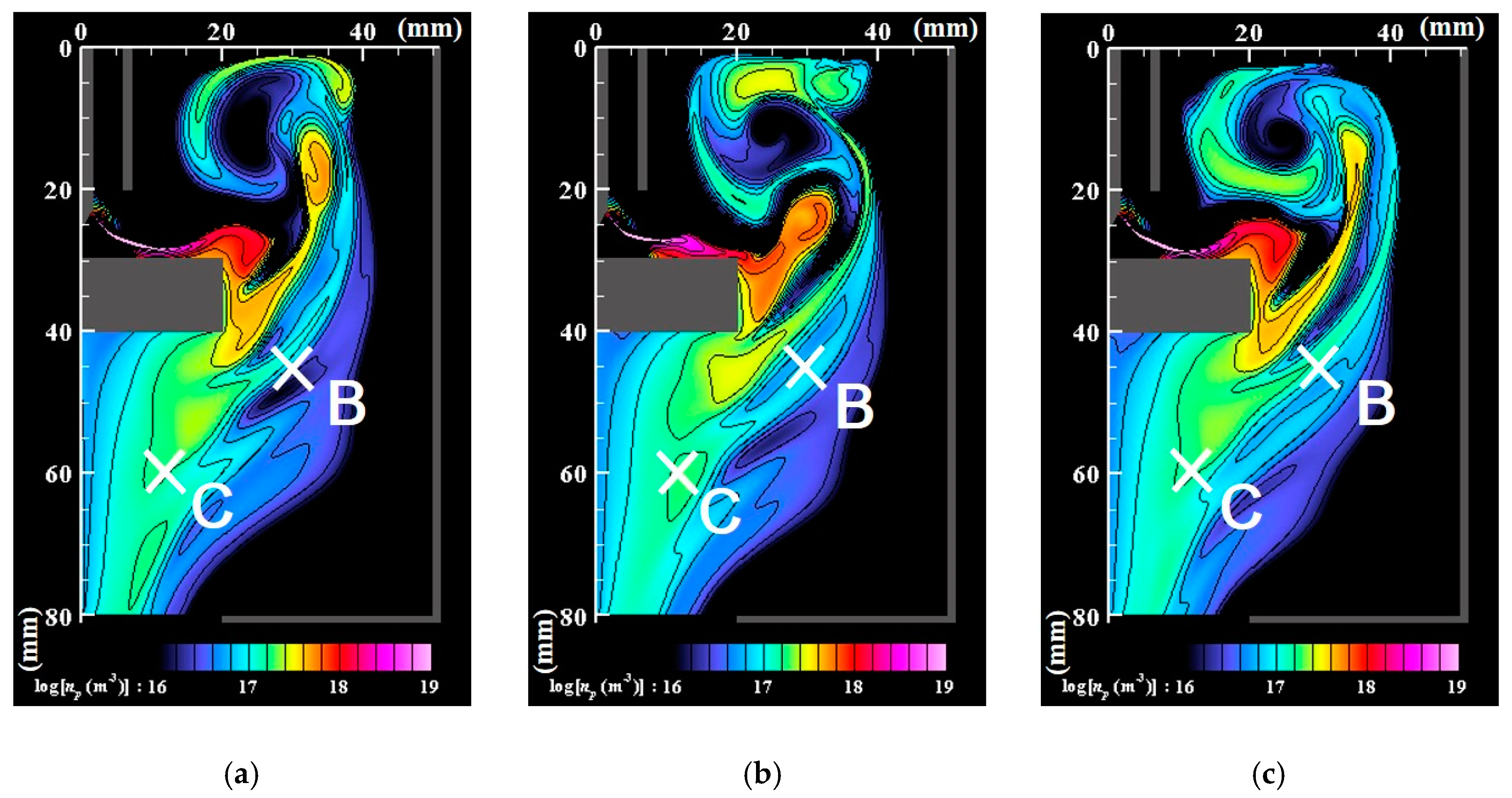
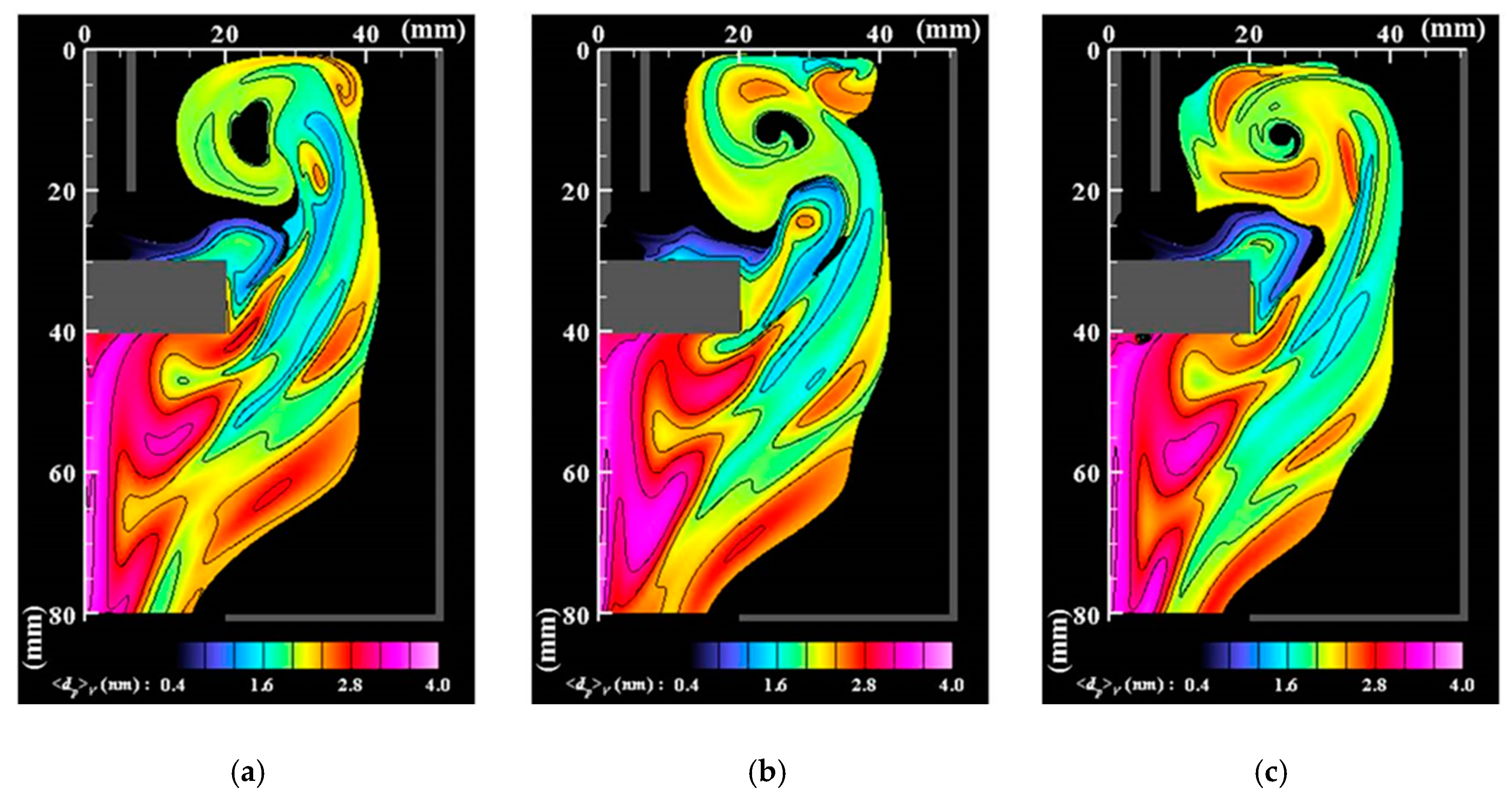
3. Results and Discussion
4. Conclusions
- ➢
- The core region of the arc plasma is almost stationary, whereas the fringe fluctuates because of fluid dynamic instability between the arc plasma and the shielding gas.
- ➢
- Numerous small particles are generated around the arc plasma’s fringe because of supersaturation. In the downstream region, the vapor molecules decrease by condensation. The nanoparticles decrease by coagulation. These processes are important contributions to particle growth.
- ➢
- The correlation analysis results suggest that the distribution of growing nanoparticles distant from the arc plasma can be controlled via control of the temperature fluctuation at the arc plasma’s fringe.
Author Contributions
Funding
Conflicts of Interest
References
- Berlinger, B.; Benker, N.; Weinbruch, S.; L’Vov, B.V.; Ebert, M.; Koch, W.; Ellingsen, D.G.; Thomassen, Y. Physicochemical characterisation of different welding aerosols. Anal. Bioanal. Chem. 2011, 399, 1773–1780. [Google Scholar] [CrossRef] [PubMed]
- Shigeta, M.; Tanaka, M. Visualization of electromagnetic-thermal-fluid phenomena in arc welding. Jpn. J. Appl. Phys. 2019, 59, SA0805. [Google Scholar] [CrossRef] [Green Version]
- Yoshii, C.; Morimoto, Y.; Kido, M. Welder’s Pneumoconiosi—Pulmonary Disease Caused by Inhalation of Welding Fumes. J. Aerosol Res. 2005, 20, 238–242. (In Japanese) [Google Scholar] [CrossRef]
- Shigeta, M.; Murphy, A.B. Thermal plasmas for nanofabrication. J. Phys. D Appl. Phys. 2011, 44, 174025. [Google Scholar] [CrossRef]
- Julien, C.M.; Mauger, A. Nanostructured MnO2 as Electrode Materials for Energy Storage. Nanomaterials 2017, 7, 396. [Google Scholar] [CrossRef] [Green Version]
- Akhtar, T.S.; Cooke, K.O.; Khan, T.I.; Shar, M.A. Nanoparticle Enhanced Eutectic Reaction during Diffusion Brazing of Aluminium to Magnesium. Nanomaterials 2019, 9, 370. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Aharonovich, I.; Levchenko, I.; Ostrikov, K.K.; Spizzirri, P.G.; Rubanov, S.; Prawer, S. Plasma-enabled growth of single-crystalline SiC/AlSiC core-shell nanowires on porous alumina templates. Cryst. Growth Des. 2012, 12, 2917–2922. [Google Scholar] [CrossRef]
- Zhang, R.; Engholm, M. Recent Progress on the Fabrication and Properties of Silver Nanowire-Based Transparent Electrodes. Nanomaterials 2018, 8, 628. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, M.; Watanabe, T. Vaporization mechanism from Sn–Ag mixture by Ar–H2 Arc for nanoparticle preparation. Thin Solid Films 2008, 516, 6645–6649. [Google Scholar] [CrossRef]
- Jenkins, N.T.; Eagar, T.W. Chemical analysis of welding nanoparticles—Airborne particle size is the most important factor in determining the accuracy of a method for chemical analysis. Weld. J. N. Y. 2005, 84, 87–93. [Google Scholar]
- Carpenter, K.R.; Monaghan, B.J.; Norrish, J. Influence of Shielding Gas on Fume Size Morphology and Particle Composition for Gas Metal Arc Welding. ISIJ Int. 2008, 28, 1570–1576. [Google Scholar] [CrossRef] [Green Version]
- Shigeta, M.; Watanabe, T. Growth mechanism of silicon-based functional nanoparticles fabricated by inductively coupled thermal plasmas. J. Phys. D Appl. Phys. 2007, 40, 2407–2419. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Numerical investigation of cooling effect on platinum nanoparticle formation in inductively coupled thermal plasmas. J. Appl. Phys. 2008, 103, 074903. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Two-dimensional analysis of nanoparticle formation in induction thermal plasmas with counterflow cooling. Thin Solid Films 2008, 516, 4415–4422. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Two-Directional Nodal Model for Co-Condensation Growth of Multi-Component Nanoparticles in Thermal Plasma Processing. J. Therm. Spray Technol. 2009, 18, 1022–1037. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Growth model of binary alloy nanopowders for thermal plasma synthesis. J. Appl. Phys. 2010, 108, 043306. [Google Scholar] [CrossRef]
- Colombo, V.; Ghedini, E.; Gherardi, M.; Sanibondi, P.; Shigeta, M. A Two-Dimensional nodal model with turbulent effects for the synthesis of Si nano-particles by inductively coupled thermal plasmas. Plasma Sources Sci. Technol. 2012, 21, 025001. [Google Scholar] [CrossRef]
- Shigeta, M. Simple nonequilibrium model of collective growth and transport of metal nanomist in a thermal plasma process. Theor. Appl. Mech. Jpn. 2015, 63, 147–154. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Effect of precursor fraction on silicide nanopowder growth under thermal plasma conditions: A computational study. Powder Technol. 2016, 288, 191–201. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T. Effect of Saturation Pressure Difference on Metal-Silicide Nanopowder Formation in Thermal Plasma Fabrication. Nanomaterials 2016, 6, 43. [Google Scholar] [CrossRef] [Green Version]
- Shigeta, M. Numerical Study of Axial Magnetic Effects on a Turbulent Thermal Plasma Jet for Nanopowder Production Using 3D Time-Dependent Simulation. J. Flow Control Meas. Vis. 2018, 6, 107–123. [Google Scholar] [CrossRef] [Green Version]
- Tashiro, S.; Zeniya, T.; Yamamoto, K.; Tanaka, M.; Nakata, K.; Murphy, A.B.; Yamamoto, E.; Yamazaki, K.; Suzuki, K. Numerical analysis of fume formation mechanism in arc welding. J. Phys. D Appl. Phys. 2010, 43, 434012. [Google Scholar] [CrossRef] [Green Version]
- Sanibondi, P. Numerical investigation of the effects of iron oxidation reactions on the fume formation mechanism in arc welding. J. Phys. D Appl. Phys. 2015, 48, 345202. [Google Scholar] [CrossRef]
- Shigeta, M.; Miyake, M.; Tanaka, M. Numerical analysis of collective growth of primary nanoparticles in arc welding. Q. J. Jpn. Weld. Soc. 2015, 33, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Shigeta, M.; Minami, S.; Tanaka, M. Modeling for collective growth of fume primary particles with charge effect in arc welding. Weld. World 2018, 62, 203–213. [Google Scholar] [CrossRef]
- Boselli, M.; Colombo, V.; Ghedini, E.; Gherardi, M.; Sanibondi, P. Two-dimensional time-dependent modelling of fume formation in a pulsed gas metal arc welding process. J. Phys. D Appl. Phys. 2013, 46, 224006. [Google Scholar] [CrossRef]
- Phanse, G.M.; Pratsinis, S.E. Theory for Aerosol Generation in Laminar Flow Condensers. Aerosol Sci. Technol. 1989, 11, 100–119. [Google Scholar] [CrossRef]
- Shigeta, M. Modeling and Simulation of a Turbulent-like Thermal Plasma Jet for Nanopowder Production. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 16–28. [Google Scholar] [CrossRef] [Green Version]
- Shigeta, M. Turbulence modelling of thermal plasma flows. J. Phys. D Appl. Phys. 2016, 49, 493001. [Google Scholar] [CrossRef]
- Terasaki, H.; Tanaka, M.; Ushio, M. Effect of Metal Vapor on Electron Temperature in Helium Gas Tungsten Arcs. Metall. Mater. Trans. A 2002, 33, 1183–1188. [Google Scholar] [CrossRef]
- Guisbiers, G.; Kazan, M.; Overschelde, O.V.; Wautelet, M.; Pereira, S. Mechanical and thermal properties of metallic and semiconductive nanostructures. J. Phys. Chem. 2008, 112, 4097–4103. [Google Scholar] [CrossRef]
- Tanaka, M.; Terasaki, H.; Ushio, M.; Lowke, J.J. Numerical Study of a Free-burning Argon Arc with Anode Melting. Plasma Chem. Plasma Process. 2003, 23, 585–606. [Google Scholar] [CrossRef]
- Nemchinsky, V.A.; Shigeta, M. Simple equations to describe aerosol growth. Model. Simul. Mater. Sci. Eng. 2012, 20, 045017. [Google Scholar] [CrossRef]
- Pratsinis, S.E. Simultaneous nucleation, condensation, and coagulation in aerosol reactors. J. Colloid Interface Sci. 1988, 124, 416–427. [Google Scholar] [CrossRef]
- Murphy, A.B. A comparison of treatments of diffusion in thermal plasmas. J. Phys. D Appl. Phys. 1996, 29, 1922–1932. [Google Scholar] [CrossRef]
- Girshick, S.L.; Chiu, P.C.; McMurry, P.H. Time-dependent aerosol models and homogeneous nucleation rates. Aerosol Sci. Technol. 1990, 13, 465–477. [Google Scholar] [CrossRef]
- Friedlander, S.K. Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: New York, NY, USA, 2000; p. 283. [Google Scholar]
- Matsushita, Y. Outflow Boundary Condition in the Finite Volume Method for Unsteady–State Fluid Flow Computation with Variable Density. Comput. Therm. Sciences 2011, 3, 531–537. [Google Scholar] [CrossRef]
- Boulos, M.I.; Fauchais, P.; Pfender, E. Thermal plasmas Fundamentals and Applications; Plenum Press: New York, NY, USA, 1994; Volume 1, pp. 385–392. [Google Scholar]
- Menart, J.; Lin, L. Numerical study of high-intensity free-burning arc. J. Thermophys. Heat Transf. 1998, 12, 500–506. [Google Scholar] [CrossRef]
- The Japan Institute of Metals and Materials. Metals Data Book; Maruzen: Tokyo, Japan, 1993; pp. 8–98. (In Japanese) [Google Scholar]
- Konishi, K.; Shigeta, M.; Tanaka, M.; Murata, A.; Murata, T.; Murphy, A.B. Reliability evaluation of Fowler-Milne method in a temperature measurement of Gas Tungsten Arc. Q. J. Jpn. Weld. Soc. 2015, 33, 42–48. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Yoshida, T.; Akashi, K. Preparation of Ultrafine Iron Particles using an RF Plasma. Trans. Jpn. Inst. Met. 1981, 22, 371–378. [Google Scholar] [CrossRef] [Green Version]
- Leparoux, M.; Schreuders, C.; Shin, J.W.; Siegman, S. Induction plasma synthesis of carbide nano-powders. Adv. Eng. Mater. 2005, 7, 349–353. [Google Scholar] [CrossRef]
- Rao, N.; Girshick, S.L.; Heberlein, J.; McMurry, P.; Jones, S.; Hansen, D.; Micheel, B. Nanoparticle Formation Using a Plasma Expansion Process. Plasma Chem. Plasma Process. 1995, 15, 581–606. [Google Scholar] [CrossRef]
- Leparoux, M.; Kihn, Y.; Paris, S.; Schreuders, C. Microstructure analysis of RF plasma synthesized TiCN nanopowders. Int. J. Refract. Met. Hard Mater. 2008, 26, 277–285. [Google Scholar] [CrossRef]
- Leparoux, M.; Schreuders, C.; Fauchais, P. Improved Plasma Synthesis of Si-nanopowders by Quenching. Adv. Eng. Mater. 2008, 10, 1147–1150. [Google Scholar] [CrossRef]
- Shigeta, M.; Watanabe, T.; Nishiyama, H. Numerical investigation for nano-particle synthesis in an RF inductively coupled plasma. Thin Solid Films 2004, 457, 192–200. [Google Scholar] [CrossRef]






| Property | Parameter |
|---|---|
| Cathode material | Tungsten with 5.0 wt % of La2O3 |
| Cathode diameter | 3.2 mm |
| Cathode length | 25.0 mm |
| Cathode tip angle | 60.0 degrees |
| Anode material | Iron |
| Anode diameter | 40.0 mm |
| Anode thickness | 10.0 mm |
| Distance between cathode and anode | 5.0 mm |
| Shielding gas nozzle material | Iron |
| Shielding gas nozzle inner diameter | 12.2 mm |
| Shielding gas nozzle length | 20.0 mm |
| Shielding gas nozzle thickness | 1.0 mm |
| Shielding gas | Argon |
| Shielding gas flow rate | 15.0 L/min |
| Current | 150.0 A |
| Voltage | 10.5 V |
| Outer case material | Iron |
| Outer case inner diameter | 100.0 mm |
| Outer case length | 80.0 mm |
| Outer case outlet diameter | 40.0 mm |
| Outer case temperature | 300.0 K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shigeta, M.; Tanaka, M.; Ghedini, E. Numerical Analysis of the Correlation between Arc Plasma Fluctuation and Nanoparticle Growth–Transport under Atmospheric Pressure. Nanomaterials 2019, 9, 1736. https://doi.org/10.3390/nano9121736
Shigeta M, Tanaka M, Ghedini E. Numerical Analysis of the Correlation between Arc Plasma Fluctuation and Nanoparticle Growth–Transport under Atmospheric Pressure. Nanomaterials. 2019; 9(12):1736. https://doi.org/10.3390/nano9121736
Chicago/Turabian StyleShigeta, Masaya, Manabu Tanaka, and Emanuele Ghedini. 2019. "Numerical Analysis of the Correlation between Arc Plasma Fluctuation and Nanoparticle Growth–Transport under Atmospheric Pressure" Nanomaterials 9, no. 12: 1736. https://doi.org/10.3390/nano9121736
APA StyleShigeta, M., Tanaka, M., & Ghedini, E. (2019). Numerical Analysis of the Correlation between Arc Plasma Fluctuation and Nanoparticle Growth–Transport under Atmospheric Pressure. Nanomaterials, 9(12), 1736. https://doi.org/10.3390/nano9121736






