Guidelines for Selecting Interlayer Spacers in Synthetic 2D-Based Antiferromagnets from First-Principles Simulations
Abstract
:1. Introduction
2. Methodology
3. Ir(111)/Co/nGr/Fe
3.1. Structural Optimisations
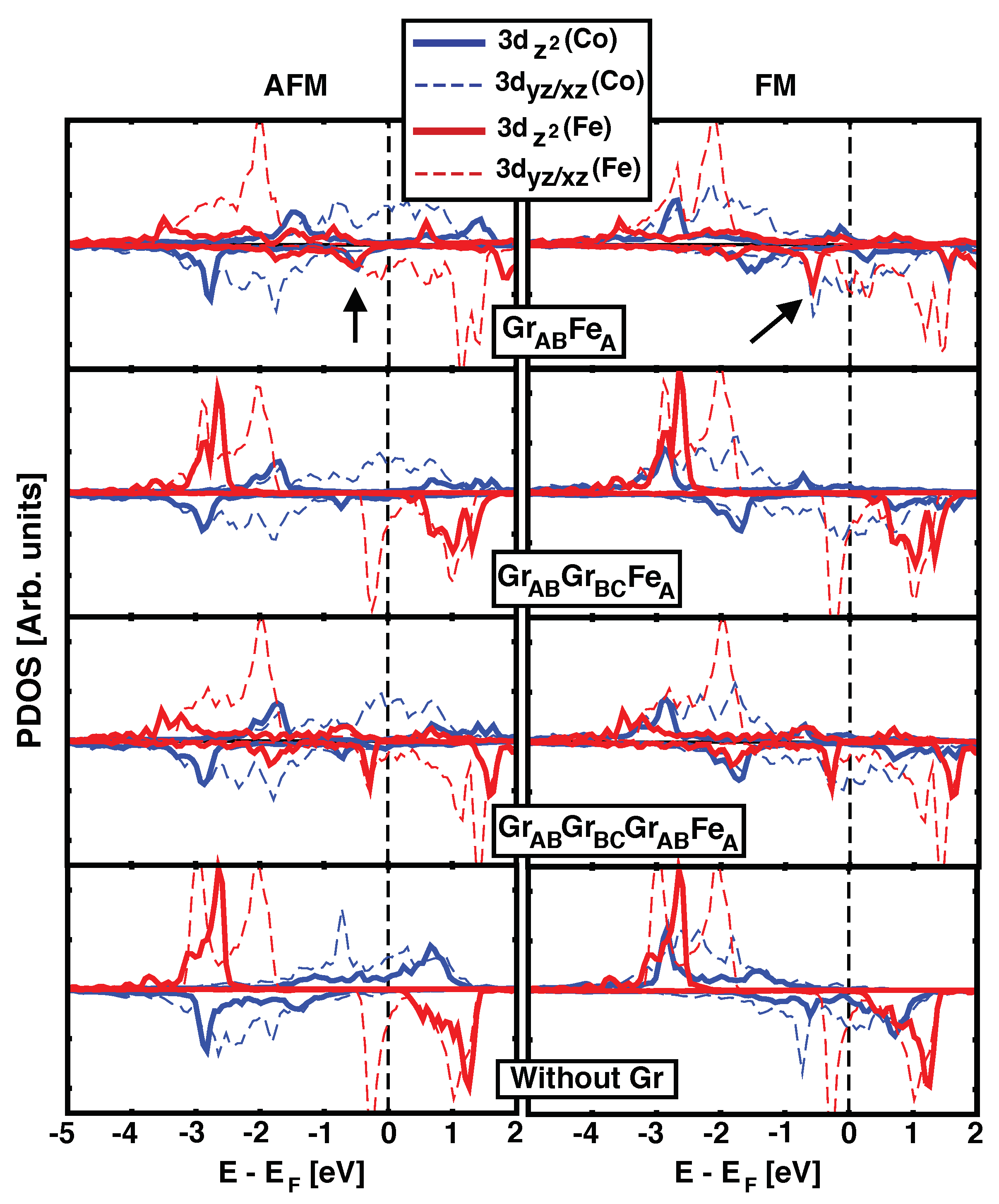
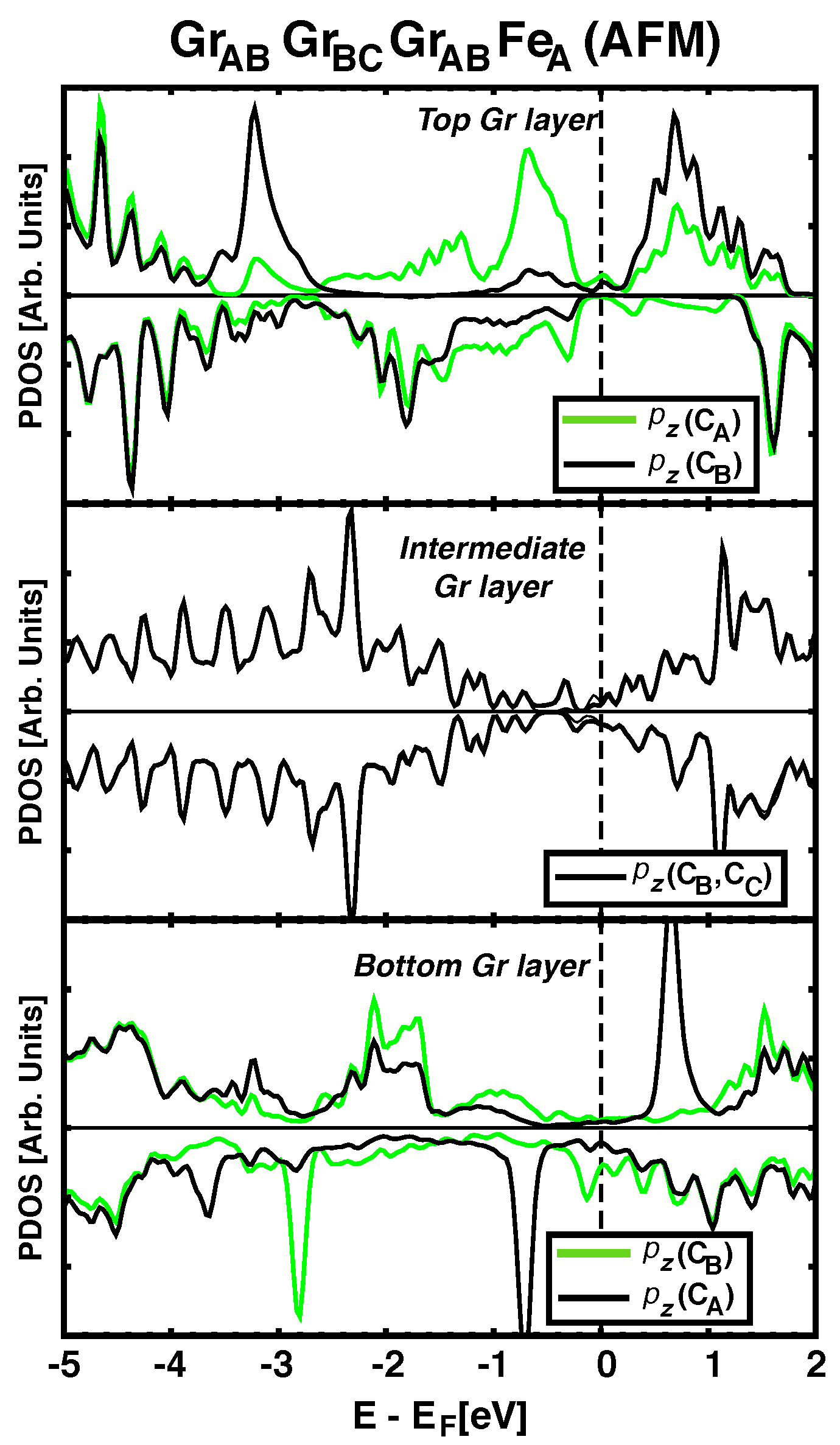
3.2. Electronic Structure and Projected DOS
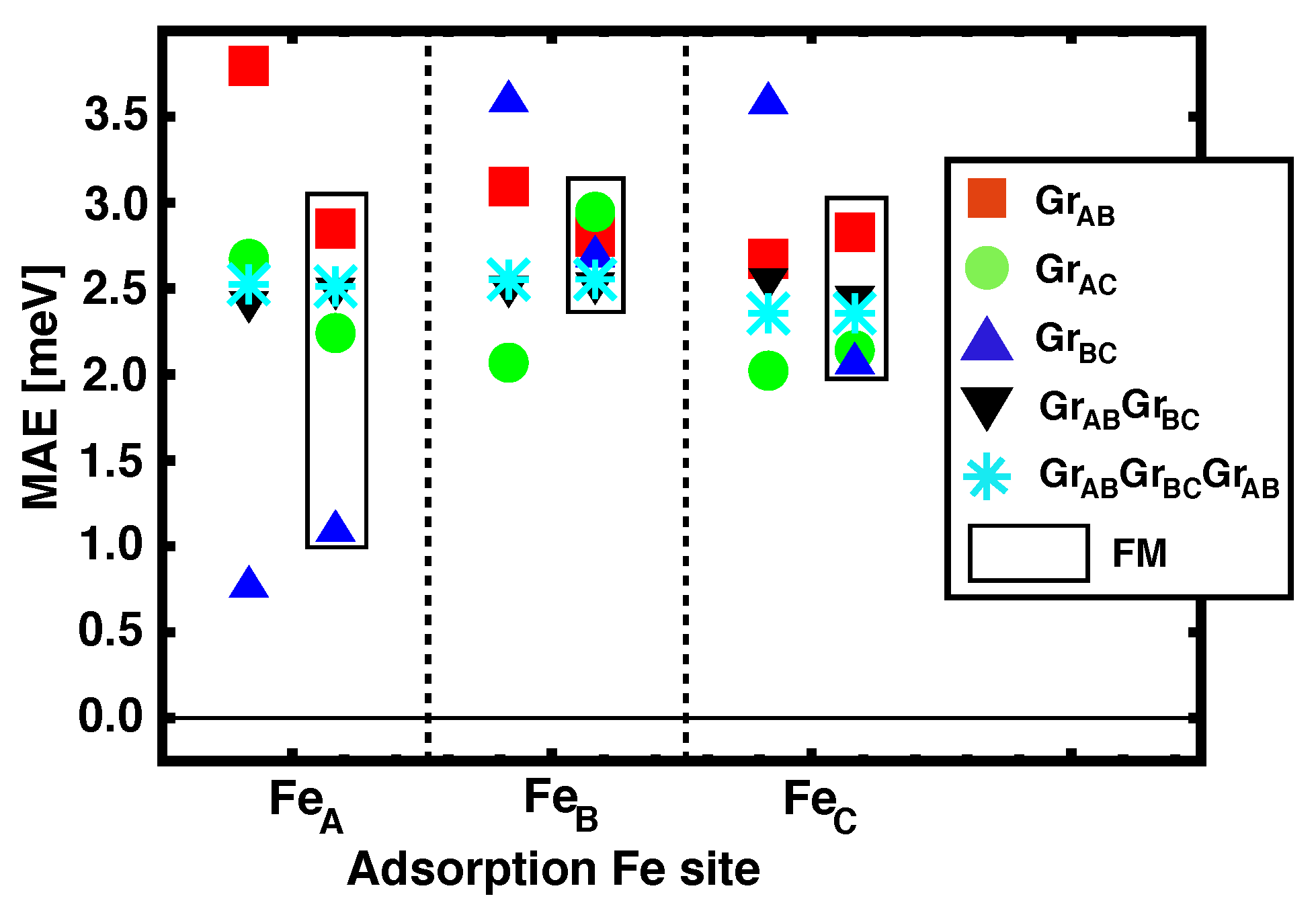
3.3. Magnetic Anisotropy Energies
4. Ir(111)/Co/h-BN/Fe
4.1. Structural Optimisations
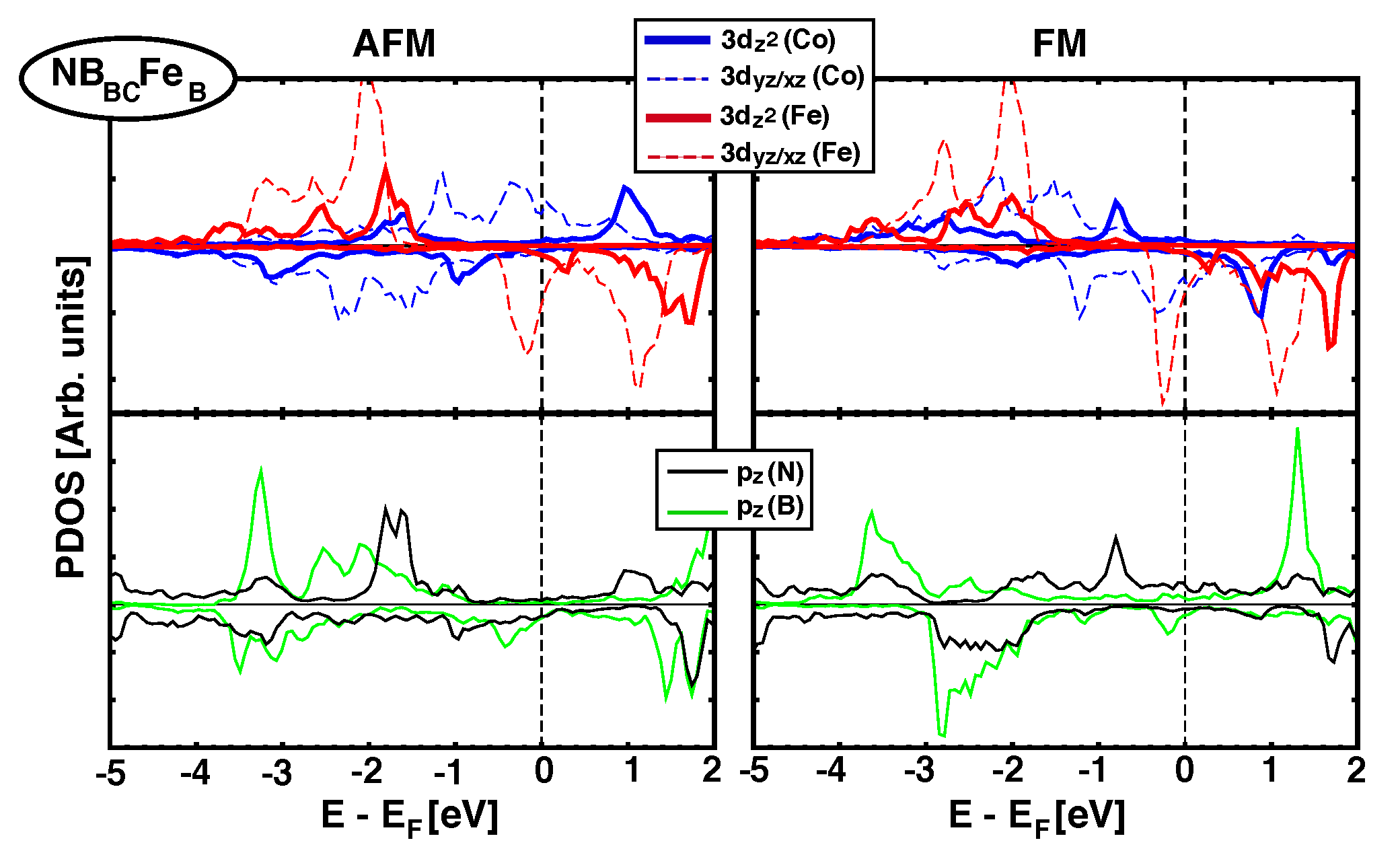
4.2. Electronic Structure and Projected DOS
4.3. Magnetic Anisotropy Energies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef] [Green Version]
- Jungwirth, T.; Sinova, J.; Manchon, A.; Marti, X.; Wunderlich, J.; Felser, C. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 2018, 14, 200. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Martin, M.B.; Godel, F.; Anane, A.; Petroff, F.; Dlubak, B.; Seneor, P. 2D-MTJs: introducing 2D materials in magnetic tunnel junctions. J. Phys. D Appl. Phys. 2017, 50, 203002. [Google Scholar] [CrossRef]
- Bruno, P. Theory of interlayer magnetic coupling. Phys. Rev. B 1995, 52, 411–439. [Google Scholar] [CrossRef] [Green Version]
- De Vries, J.J.; Kohlhepp, J.; den Broeder, F.J.A.; Coehoorn, R.; Jungblut, R.; Reinders, A.; de Jonge, W.J.M. Exponential Dependence of the Interlayer Exchange Coupling on the Spacer Thickness in MBE-grown Fe/SiFe/Fe Sandwiches. Phys. Rev. Lett. 1997, 78, 3023–3026. [Google Scholar] [CrossRef]
- Pruneda, J.M.; Robles, R.; Bouarab, S.; Vega, A. Antiferromagnetic interlayer coupling in Fe/c-SiFe/Fe sandwiches and multilayers. Phys. Rev. B 2001, 65, 024440. [Google Scholar] [CrossRef] [Green Version]
- Gargiani, P.; Cuadrado, R.; Vasili, H.B.; Pruneda, M.; Valvidares, M. Graphene-based synthetic antiferromagnets and ferrimagnets. Nat. Commun. 2017, 8, 699. [Google Scholar]
- Yang, H.; Vu, A.D.; Hallal, A.; Rougemaille, N.; Coraux, J.; Chen, G.; Schmid, A.K.; Chshiev, M. Anatomy and Giant Enhancement of the Perpendicular Magnetic Anisotropy of Cobalt-Graphene Heterostructures. Nano Lett. 2016, 16, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Karpan, V.M.; Giovannetti, G.; Khomyakov, P.A.; Talanana, M.; Starikov, A.A.; Zwierzycki, M.; van den Brink, J.; Brocks, G.; Kelly, P.J. Graphite and Graphene as Perfect Spin Filters. Phys. Rev. Lett. 2007, 99, 176602. [Google Scholar] [CrossRef] [Green Version]
- Karpan, V.M.; Khomyakov, P.A.; Starikov, A.A.; Giovannetti, G.; Zwierzycki, M.; Talanana, M.; Brocks, G.; van den Brink, J.; Kelly, P.J. Theoretical prediction of perfect spin filtering at interfaces between close-packed surfaces of Ni or Co and graphite or graphene. Phys. Rev. B 2008, 78, 195419. [Google Scholar] [CrossRef] [Green Version]
- Yazyev, O.V.; Pasquarello, A. Magnetoresistive junctions based on epitaxial graphene and hexagonal boron nitride. Phys. Rev. B 2009, 80, 035408. [Google Scholar] [CrossRef] [Green Version]
- Martin, M.B.; Dlubak, B.; Weatherup, R.S.; Yang, H.; Deranlot, C.; Bouzehouane, K.; Petroff, F.; Anane, A.; Hofmann, S.; Robertson, J.; et al. Sub-nanometer Atomic Layer Deposition for Spintronics in Magnetic Tunnel Junctions Based on Graphene Spin-Filtering Membranes. ACS Nano 2014, 8, 7890–7895. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.B.; Dlubak, B.; Weatherup, R.S.; Piquemal-Banci, M.; Yang, H.; Blume, R.; Schloegl, R.; Collin, S.; Petroff, F.; Hofmann, S.; et al. Protecting nickel with graphene spin-filtering membranes: A single layer is enough. Appl. Phys. Lett. 2015, 107, 012408. [Google Scholar] [CrossRef] [Green Version]
- Lazić, P.; Sipahi, G.M.; Kawakami, R.K.; Žutić, I. Graphene spintronics: Spin injection and proximity effects from first principles. Phys. Rev. B 2014, 90, 085429. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Caneva, S.; Martin, M.B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; Petroff, F.; et al. Magnetic tunnel junctions with monolayer hexagonal boron nitride tunnel barriers. Appl. Phys. Lett. 2016, 108, 102404. [Google Scholar] [CrossRef] [Green Version]
- Piquemal-Banci, M.; Galceran, R.; Godel, F.; Caneva, S.; Martin, M.B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; et al. Insulator-to-Metallic Spin-Filtering in 2D-Magnetic Tunnel Junctions Based on Hexagonal Boron Nitride. ACS Nano 2018, 12, 4712–4718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coraux, J.; N’Diaye, A.T.; Busse, C.; Michely, T. Structural Coherency of Graphene on Ir(111). Nano Lett. 2008, 8, 565–570. [Google Scholar] [CrossRef]
- Laskowski, R.; Blaha, P.; Gallauner, T.; Schwarz, K. Single-Layer Model of the Hexagonal Boron Nitride Nanomesh on the Rh(111) Surface. Phys. Rev. Lett. 2007, 98, 106802. [Google Scholar] [CrossRef]
- Decker, R.; Brede, J.; Atodiresei, N.; Caciuc, V.; Blügel, S.; Wiesendanger, R. Atomic-scale magnetism of cobalt-intercalated graphene. Phys. Rev. B 2013, 87, 041403(R). [Google Scholar] [CrossRef] [Green Version]
- Avvisati, G.; Lisi, S.; Gargiani, P.; Pia, A.D.; Luca, O.D.; Pacile, D.; Cardoso, C.; Varsano, D.; Prezzi, D.; Ferretti, A.; et al. FePc Adsorption on the Moire Superstructure of Graphene Intercalated with a Cobalt Layer. J. Phys. Chem. 2017, 121, 1639. [Google Scholar] [CrossRef] [Green Version]
- Soler, J.; Artacho, E.; Gale, J.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulations. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kleinman, L.; Bylander, D.M. Efficacious Form for Model Pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef] [PubMed]
- Louie, S.; Froyen, S.; Cohen, M. Nonlinear ionic pseudopotentials in spin-density-functional calculations. Phys. Rev. B 1982, 26, 1738. [Google Scholar] [CrossRef]
- Cuadrado, R.; Cerdá, J.I. Fully relativistic pseudopotential formalism under an atomic orbital basis: Spin–orbit splittings and magnetic anisotropies. J. Phys. Condens. Matter 2012, 24, 086005. [Google Scholar] [CrossRef]
- Cuadrado, R.; Klemmer, T.J.; Chantrell, R.W. Magnetic anisotropy of Fe1-y X y Pt-L10 [X = Cr, Mn, Co, Ni, Cu] bulk alloys. Appl. Phys. Lett. 2014, 105, 152406. [Google Scholar] [CrossRef] [Green Version]
- Cuadrado, R.; Liu, K.; Klemmer, T.J.; Chantrell, R.W. In-plane/out-of-plane disorder influence on the magnetic anisotropy of Fe1-yMnyPt-L10 bulk alloy. Appl. Phys. Lett. 2016, 108, 123102. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef]




| nGr | C Sites | Fe Sites | Eads (AFM/FM) | JCo−Fe | δC−C | zC−Fe | zCo−C | |
|---|---|---|---|---|---|---|---|---|
| 1 | GrAB | A | 1.66 (1.41) | 254.13 | 0.27 | 2.02 | 2.11 | |
| B | 1.61 (1.51) | 97.74 | 0.28 | 2.21 | 2.09 | |||
| C | 0.34 (0.32) | 14.13 | 0.15 | 2.98 | 2.06 | |||
| GrAC | A | 1.13 (1.11) | 15.74 | 0.01 | 2.03 | 3.10 | ||
| B | 0.26 (0.27) | −8.47 | 0.00 | 2.97 | 3.14 | |||
| C | 1.13 (1.12) | 15.69 | 0.01 | 2.04 | 3.10 | |||
| GrBC | A | 0.32 (0.31) | 10.33 | 0.01 | 3.02 | 2.03 | ||
| B | 1.41 (1.30) | 105.47 | 0.26 | 2.21 | 2.08 | |||
| C | 1.53 (1.30) | 226.63 | 0.26 | 2.04 | 2.10 | |||
| 2 | GrABGrBC | A | 0.20 | −0.10 | 0.01 | 3.17 | 2.06 | |
| B | 0.97 | −3.60 | 0.01 | 2.03 | 2.06 | |||
| C | 0.99 | −1.65 | 0.01 | 2.03 | 2.06 | |||
| 3 | GrABGrBCGrAB | A | 0.98 | 0.01 | 0.01 | 2.03 | 2.06 | |
| B | 0.96 | −0.07 | 0.01 | 2.03 | 2.06 | |||
| C | 0.20 | 0.04 | 0.01 | 3.18 | 2.06 |
| B/N Sites | Fe Sites | Eads (AFM/FM) | JCo−Fe | δB−N | zFe−BN | zBN−Co | |
|---|---|---|---|---|---|---|---|
| BNAB | A | 0.38(0.38) | 3.0 | −0.15 | 3.05 | 2.08 | |
| B | 0.92 (0.81) | 108.3 | −0.22 | 2.31 | 2.11 | ||
| C | 0.44 (0.43) | 13.1 | −0.14 | 3.01 | 2.09 | ||
| BNAC | A | 0.75 (0.75) | −1.8 | 0.12 | 2.19 | 2.89 | |
| B | 0.40 (0.40) | −4.1 | 0.00 | 3.10 | 3.23 | ||
| *C | 1.48 (1.46) | 20.2 | 0.13 | 2.20 | 3.00 | ||
| BNBC | A | 0.48 (0.52) | −35.1 | −0.08 | 2.91 | 2.26 | |
| B | 0.68(0.76) | −75.4 | −0.10 | 2.94 | 2.25 | ||
| *C | 1.65(1.62) | 36.8 | 0.16 | 2.18 | 2.87 | ||
| NBAB | *A | 1.58(1.55) | 27.0 | 0.14 | 2.19 | 2.97 | |
| B | 0.47 (0.59) | −126.5 | −0.12 | 2.87 | 2.28 | ||
| C | 0.48 (0.51) | −34.9 | −0.09 | 2.90 | 2.31 | ||
| NBAC | *A | 1.45 (1.44) | 12.7 | 0.13 | 2.20 | 3.02 | |
| B | 0.41 (0.42) | −6.5 | 0.00 | 3.04 | 3.12 | ||
| C | 0.76 (0.77) | −7.1 | 0.12 | 2.19 | 2.87 | ||
| NBBC | A | 0.44(0.43) | 11.2 | −0.14 | 3.05 | 2.08 | |
| B | 0.92(0.81) | 101.2 | −0.22 | 2.33 | 2.11 | ||
| C | 0.85(0.77) | 83.8 | 0.23 | 2.17 | 2.11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadrado, R.; Pruneda, M. Guidelines for Selecting Interlayer Spacers in Synthetic 2D-Based Antiferromagnets from First-Principles Simulations. Nanomaterials 2019, 9, 1764. https://doi.org/10.3390/nano9121764
Cuadrado R, Pruneda M. Guidelines for Selecting Interlayer Spacers in Synthetic 2D-Based Antiferromagnets from First-Principles Simulations. Nanomaterials. 2019; 9(12):1764. https://doi.org/10.3390/nano9121764
Chicago/Turabian StyleCuadrado, Ramón, and Miguel Pruneda. 2019. "Guidelines for Selecting Interlayer Spacers in Synthetic 2D-Based Antiferromagnets from First-Principles Simulations" Nanomaterials 9, no. 12: 1764. https://doi.org/10.3390/nano9121764
APA StyleCuadrado, R., & Pruneda, M. (2019). Guidelines for Selecting Interlayer Spacers in Synthetic 2D-Based Antiferromagnets from First-Principles Simulations. Nanomaterials, 9(12), 1764. https://doi.org/10.3390/nano9121764





