Size-Dependent Critical Temperature and Anomalous Optical Dispersion in Ferromagnetic CrI3 Nanotubes
Abstract
:1. Introduction
2. Numerical Method
3. Results and Discussion
3.1. Structural Characterization
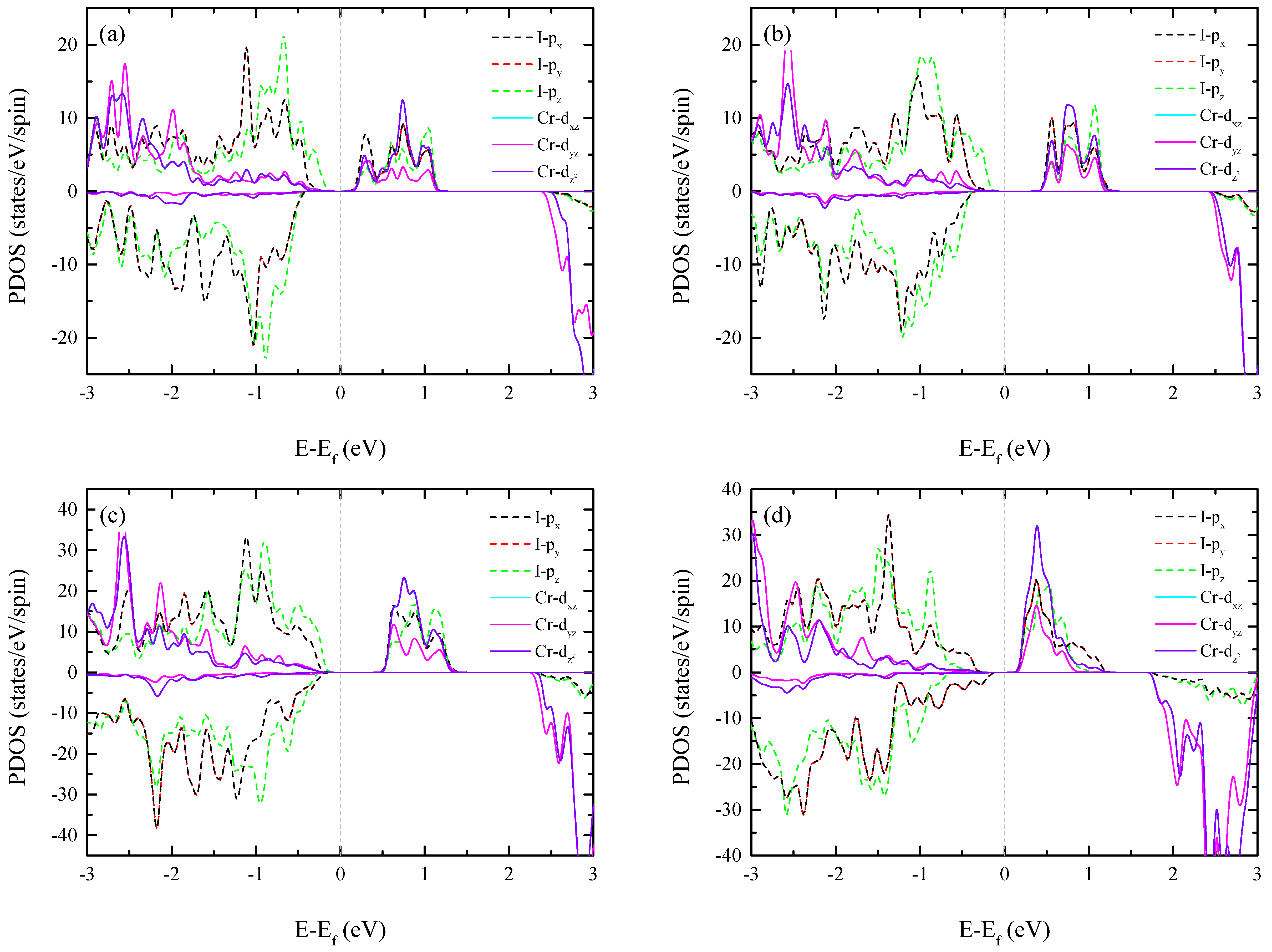
3.2. Electronic Band Structures
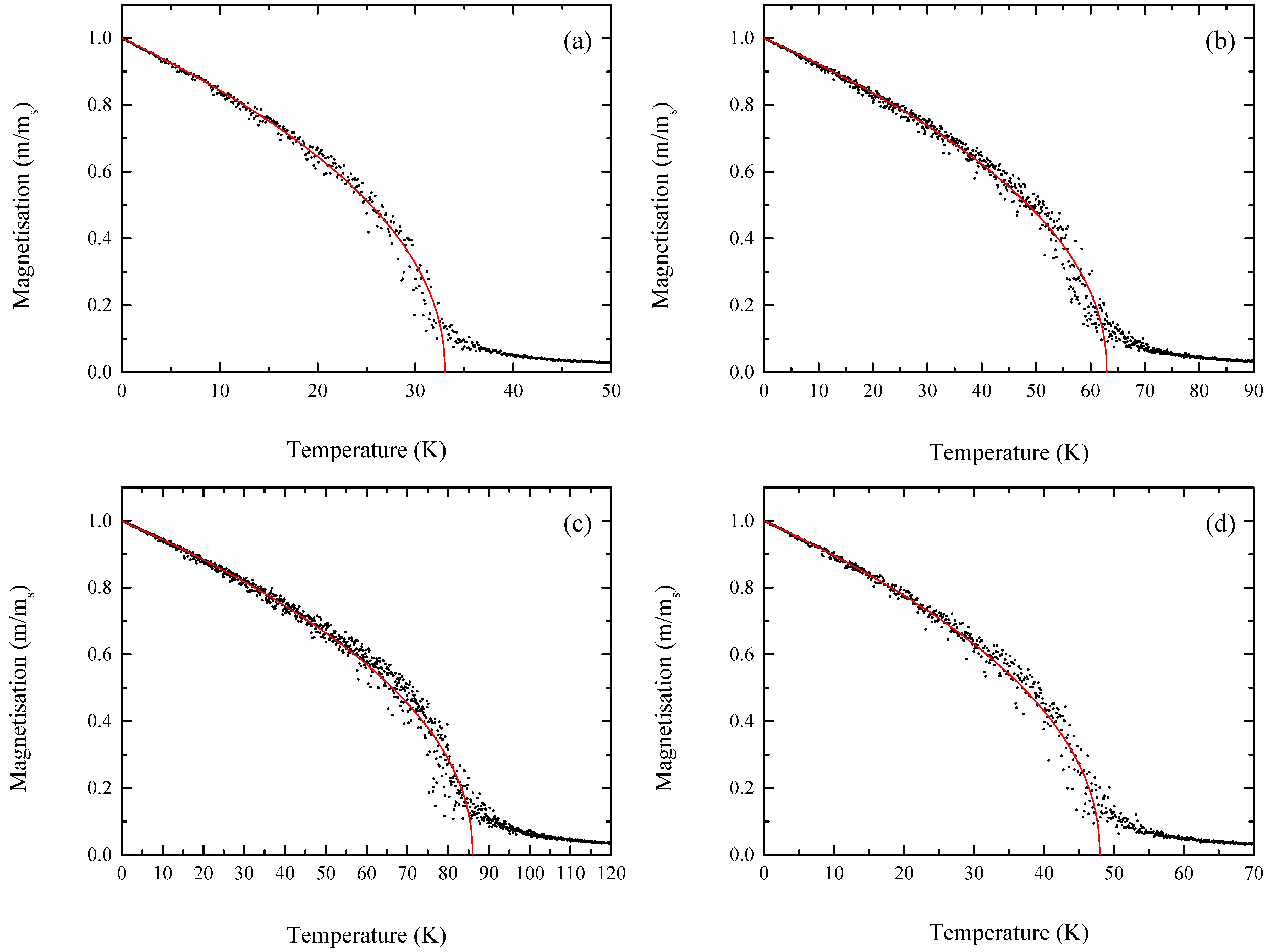
3.3. Curie Temperature
3.4. Optical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem. Mater. 2015, 27, 612–620. [Google Scholar] [CrossRef]
- Lado, J.L.; Fernández-Rossier, J. On the origin of magnetic anisotropy in two dimensional CrI 3. 2D Mater. 2017, 4, 035002. [Google Scholar] [CrossRef] [Green Version]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Laird, E.A.; Kuemmeth, F.; Steele, G.A.; Grove-Rasmussen, K.; Nygård, J.; Flensberg, K.; Kouwenhoven, L.P. Quantum transport in carbon nanotubes. Rev. Mod. Phys. 2015, 87, 703–764. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Chen, Z. curved pi-conjugation, aromaticity, and the related chemistry of small fullerenes. Chem. Rev. 2005, 105, 3643–3696. [Google Scholar]
- Dresselhaus, M.S.; Dresselhaus, G.; Saito, R. Physics of carbon nanotubes. Carbon 1995, 33, 883–891. [Google Scholar] [CrossRef] [Green Version]
- Eklund, P.C.; Holden, J.M.; Jishi, R.A. Vibrational modes of carbon nanotubes; Spectroscopy and theory. Carbon 1995, 33, 959–972. [Google Scholar] [CrossRef]
- Sinnott, S.B.; Andrews, R. Carbon nanotubes: Synthesis, properties, and applications. Crit. Rev. Solid State Mater. Sci. 2001, 26, 145–249. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Q.; Kawazoe, Y.; Jena, P. Exfoliating biocompatible ferromagnetic Cr-trihalide monolayers. Phys. Chem. Chem. Phys. 2016, 18, 8777–8784. [Google Scholar] [CrossRef] [PubMed]
- Kronig, R.D.L. On the theory of dispersion of X-Rays. JOSA 1926, 12, 547–557. [Google Scholar] [CrossRef]
- Kramers, H.A. La diffusion de la lumière par les atomes. Atti del Congresso Internationale dei Fisici. Como 1927, 2, 545–557. [Google Scholar]
- Dobardžić, E.; Milošević, I.; Nikolić, B.; Vuković, T.; Damnjanović, M. Single-wall carbon nanotubes phonon spectra: Symmetry-based calculations. Phys. Rev. B 2003, 68, 045408. [Google Scholar] [CrossRef]
- Lee, R.K.F.; Cox, B.J.; Hill, J.M. The geometric structure of single-walled nanotubes. Nanoscale 2010, 2, 859–872. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C. Science of fullerenes and carbon nanotubes. Adv. Mater. 1997, 9, 1193. [Google Scholar]
- Moaied, M.; Alvarez, J.V.; Palacios, J.J. Hydrogenation-induced ferromagnetism on graphite surfaces. Phys. Rev. B 2014, 90, 115441. [Google Scholar] [CrossRef]
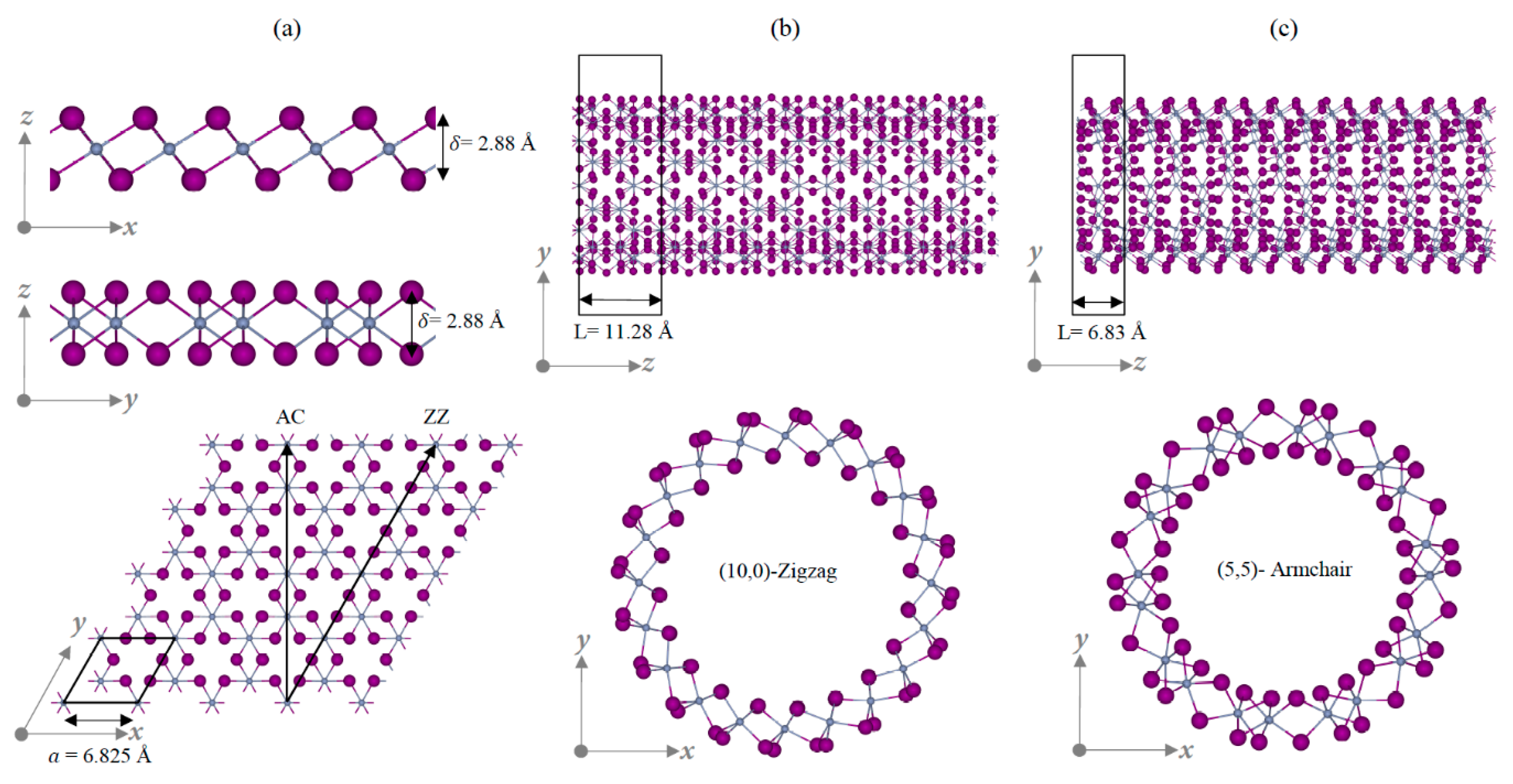



| Compound | L (Å) | d (Å) | dcalculated (Å) | dCr–I (Å) | δ (Å) | Eg (eV) |
|---|---|---|---|---|---|---|
| (5,0)-ZZ | 11.821 | 12.01 | 10.87 | 2.71 | 2.83 | 0.435 |
| (5,5)-AC | 6.825 | 19.30 | 18.82 | 2.68 | 2.93 | 0.695 |
| (10,0)-ZZ | 11.821 | 21.81 | 21.73 | 2.68 | 2.95 | 0.809 |
| (10,10)-AC | 6.825 | 35.93 | 37.65 | 2.69 | 2.96 | 0.427 |
| Compound | MCr (µB) | MI (µB) | Mcell (µB) | Eex (×10−3 eV) | J (×10−3 eV) | Tc (K) |
|---|---|---|---|---|---|---|
| (5,0)-ZZ | 3.55 | −0.18 | 60.36 | 351.81 | 1.95 | 33 |
| (5,5)-AC | 3.47 | −0.16 | 60.09 | 675.81 | 3.75 | 63 |
| (10,0)-ZZ | 3.42 | −0.14 | 119.66 | 1859.97 | 5.17 | 86 |
| (10,10)-AC | 3.39 | 0.14 | 119.30 | 1044.06 | 2.90 | 48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moaied, M.; Hong, J. Size-Dependent Critical Temperature and Anomalous Optical Dispersion in Ferromagnetic CrI3 Nanotubes. Nanomaterials 2019, 9, 153. https://doi.org/10.3390/nano9020153
Moaied M, Hong J. Size-Dependent Critical Temperature and Anomalous Optical Dispersion in Ferromagnetic CrI3 Nanotubes. Nanomaterials. 2019; 9(2):153. https://doi.org/10.3390/nano9020153
Chicago/Turabian StyleMoaied, Mohammed, and Jisang Hong. 2019. "Size-Dependent Critical Temperature and Anomalous Optical Dispersion in Ferromagnetic CrI3 Nanotubes" Nanomaterials 9, no. 2: 153. https://doi.org/10.3390/nano9020153
APA StyleMoaied, M., & Hong, J. (2019). Size-Dependent Critical Temperature and Anomalous Optical Dispersion in Ferromagnetic CrI3 Nanotubes. Nanomaterials, 9(2), 153. https://doi.org/10.3390/nano9020153





