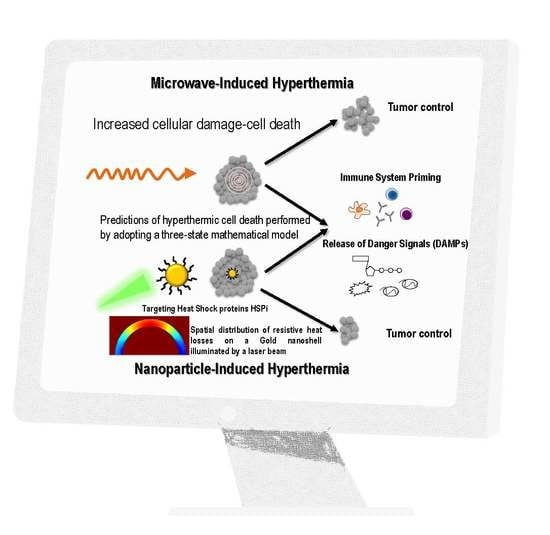
Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach
Abstract
:1. Introduction
2. Materials and Methods
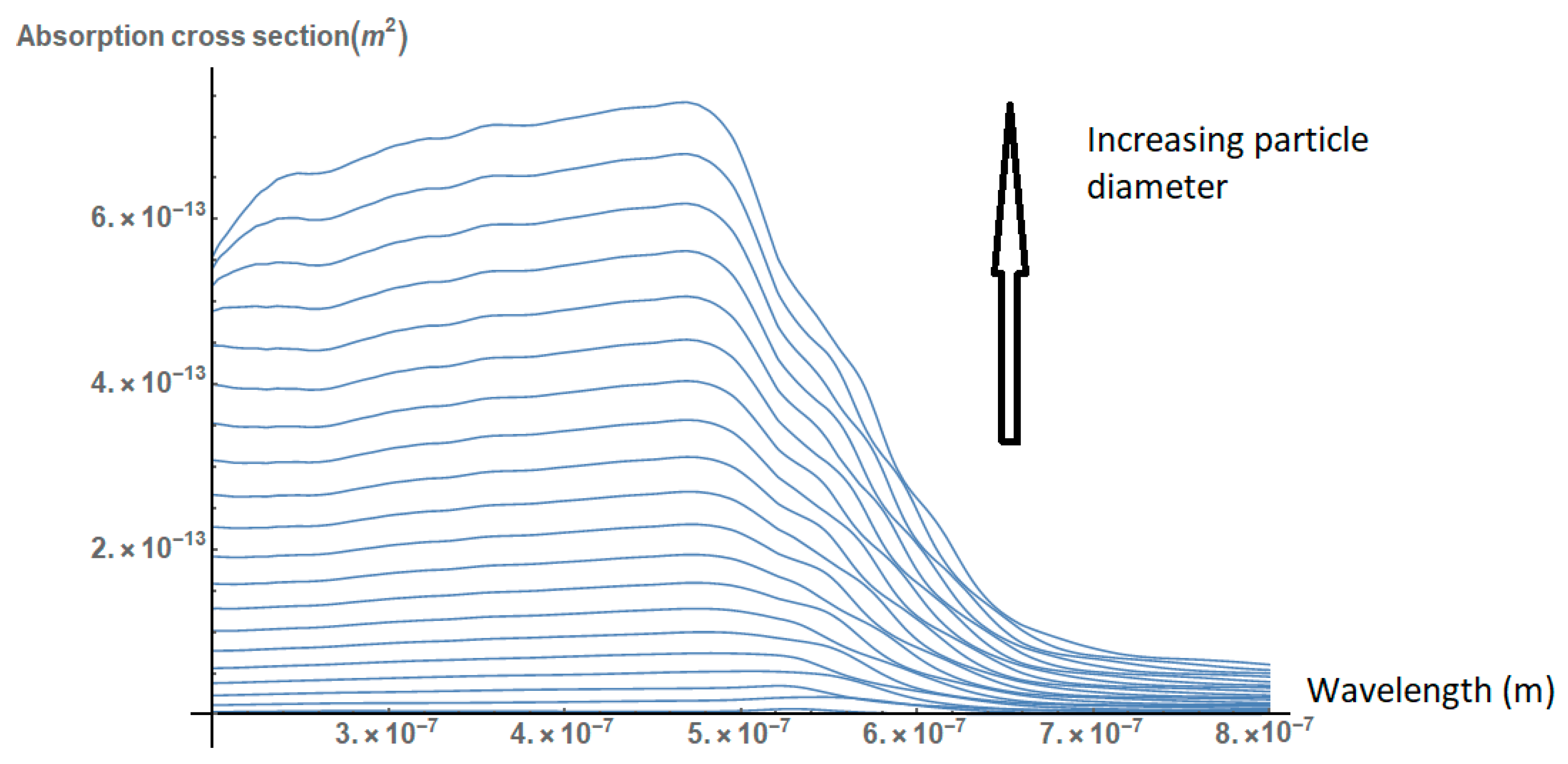
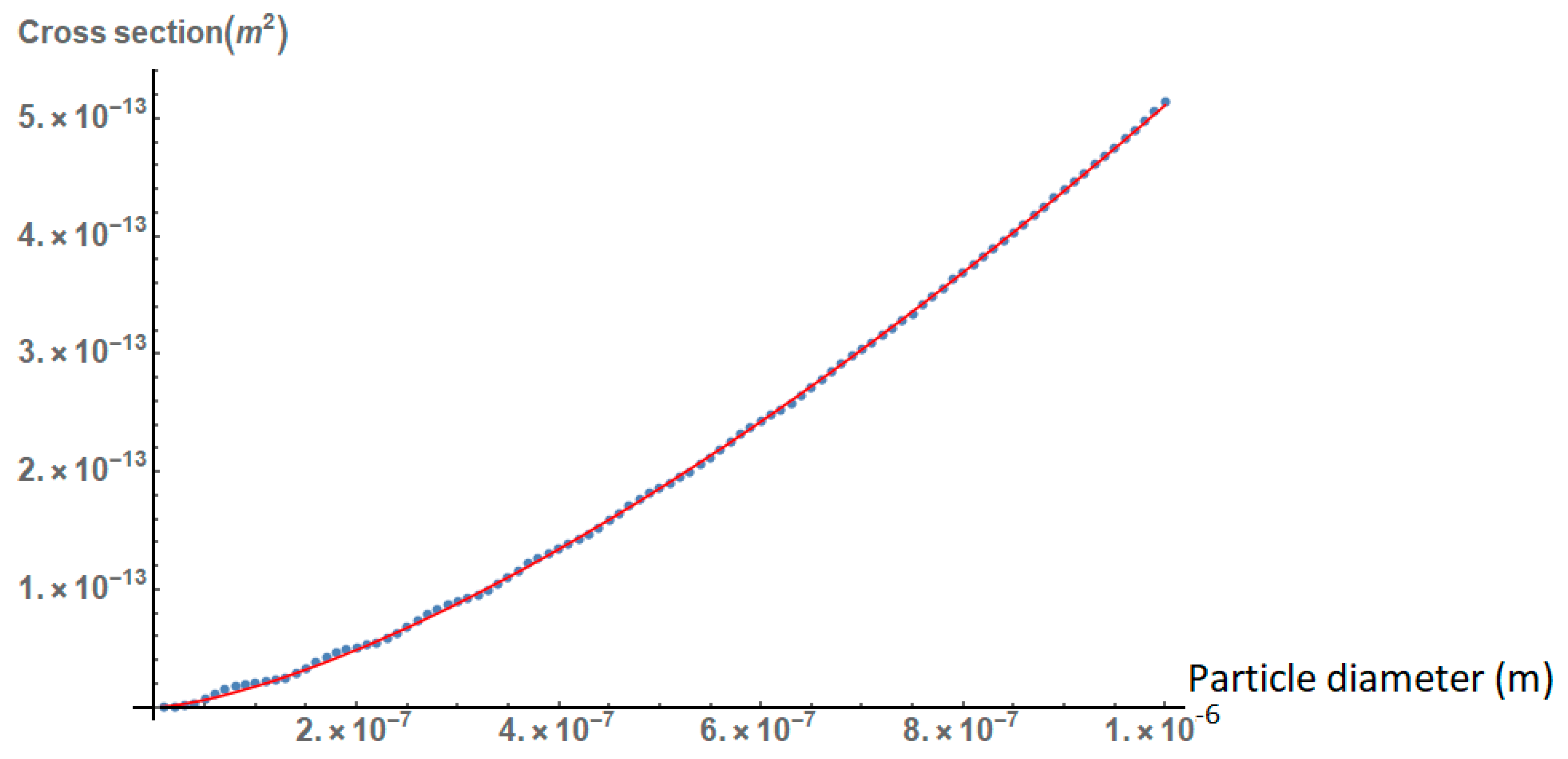
2.1. Effect of the Size, Shape, and Structure of the Nanoparticles on Their Absorption Efficiency
2.2. Simulations for Nanoparticle and Microwave-Induced Hyperthermia and Hyperthermic Cell Death
2.3. Nanoparticle- and Microwave-Induced Hyperthermia
2.4. Estimation of Hyperthermic Cell Death
2.5. Tumor Growth Model
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pavlopoulou, A.; Bagos, P.G.; Koutsandrea, V.; Georgakilas, A.G. Molecular determinants of radiosensitivity in normal and tumor tissue: A bioinformatic approach. Cancer Lett. 2017, 403, 37–47. [Google Scholar] [CrossRef]
- Prasad, V. Tisagenlecleucel—The first approved CAR-T-cell therapy: Implications for payers and policy makers. Nat. Rev. Clin. Oncol. 2017, 15, 11–12. [Google Scholar] [CrossRef]
- Dewhirst, M.W.; Vujaskovic, Z.; Jones, E.; Thrall, D. Re-setting the biologic rationale for thermal therapy. Int. J. Hyperth. 2005, 21, 779–790. [Google Scholar] [CrossRef]
- Dimitriou, N.M.; Tsekenis, G.; Balanikas, E.C. Gold nanoparticles, radiations and the immune system: Current insights into the physical mechanisms and the biological interactions of this new alliance towards cancer therapy. Pharmacol. Ther. 2017, 178, 1–17. [Google Scholar] [CrossRef]
- Cherukuri, P.; Glazer, E.S.; Curley, S.A. Targeted hyperthermia using metal nanoparticles. Adv. Drug Deliv. Rev. 2010, 62, 339–345. [Google Scholar] [CrossRef] [Green Version]
- Keisari, Y. Tumor abolition and antitumor immunostimulation by physico-chemical tumor ablation. Front. Biosci. 2017, 22, 310–347. [Google Scholar] [CrossRef]
- Van de Broek, B.; Devoogdt, N.; D’Hollander, A.; Gijs, H.L.; Jans, K.; Lagae, L.; Muyldermans, S.; Maes, G.; Borghs, G. Specific cell targeting with nanobody conjugated branched gold nanoparticles for photothermal therapy. ACS Nano 2011, 5, 4319–4328. [Google Scholar] [CrossRef]
- Liu, H.; Liu, T.; Wu, X.; Li, L.; Tan, L.; Chen, D.; Tang, F. Targeting gold nanoshells on silica nanorattles: A drug cocktail to fight breast tumors via a single irradiation with near-infrared laser light. Adv. Mater. 2012, 24, 755–761. [Google Scholar] [CrossRef]
- von Maltzahn, G.; Park, J.H.; Agrawal, A.; Bandaru, N.K.; Das, S.K.; Sailor, M.J.; Bhatia, S.N. Computationally guided photothermal tumor therapy using long-circulating gold nanorod antennas. Cancer Res. 2009, 69, 3892–3900. [Google Scholar] [CrossRef]
- Pattani, V.P.; Tunnell, J.W. Nanoparticle-mediated photothermal therapy: A comparative study of heating for different particle types. Lasers Surg. Med. 2012, 44, 675–684. [Google Scholar] [CrossRef]
- He, C.; Hu, Y.; Yin, L.; Tang, C.; Yin, C. Effects of particle size and surface charge on cellular uptake and biodistribution of polymeric nanoparticles. Biomaterials 2010, 31, 3657–3666. [Google Scholar] [CrossRef]
- Vinluan, R.D., 3rd; Zheng, J. Serum protein adsorption and excretion pathways of metal nanoparticles. Nanomedicine 2015, 10, 2781–2794. [Google Scholar] [CrossRef]
- Armanetti, P.; Pocoví-Martínez, S.; Flori, A.; Avigo, C.; Cassano, D.; Menichetti, L.; Voliani, V. Dual photoacoustic/ultrasound multi-parametric imaging from passion fruit-like nano-architectures. Nanomed. Nanotechnol. Boil. Med. 2018, 14, 1787–1795. [Google Scholar] [CrossRef]
- Cassano, D.; Summa, M.; Pocoví-Martínez, S.; Mapanao, A.-K.; Catelani, T.; Bertorelli, R.; Voliani, V. Biodegradable Ultrasmall-in-Nano Gold Architectures: Mid-Period In Vivo Distribution and Excretion Assessment. Part. Part. Syst. Charact. 2018, 1800464. [Google Scholar] [CrossRef]
- Levy, R.; Shaheen, U.; Cesbron, Y.; See, V. Gold nanoparticles delivery in mammalian live cells: A critical review. Nano Rev. 2010, 1, 4889. [Google Scholar] [CrossRef]
- Jondal, D.E.; Thompson, S.M.; Butters, K.A.; Knudsen, B.E.; Anderson, J.L.; Carter, R.E.; Roberts, L.R.; Callstrom, M.R.; Woodrum, D.A. Heat Stress and Hepatic Laser Thermal Ablation Induce Hepatocellular Carcinoma Growth: Role of PI3K/mTOR/AKT Signaling. Radiology 2018, 172944. [Google Scholar] [CrossRef]
- Soni, S.; Tyagi, H.; Taylor, R.A.; Kumar, A. Investigation on nanoparticle distribution for thermal ablation of a tumour subjected to nanoparticle assisted thermal therapy. J. Therm. Boil. 2014, 43, 70–80. [Google Scholar] [CrossRef]
- Vriend, L.E.M.; van den Tempel, N.; Oei, A.L.; L’Acosta, M.; Pieterson, F.J.; Franken, N.A.P.; Kanaar, R.; Krawczyk, P.M. Boosting the effects of hyperthermia-based anticancer treatments by HSP90 inhibition. Oncotarget 2017, 8, 97490–97503. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen (Contributions to the optics of turbid media, especially colloidal metal suspensions). Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Ellis, R.J.; Hartl, F.U. Principles of protein folding in the cellular environment. Curr. Opin. Struct. Boil. 1999, 9, 102–110. [Google Scholar] [CrossRef]
- Calderwood, S.K.; Murshid, A. Molecular Chaperone Accumulation in Cancer and Decrease in Alzheimer’s Disease: The Potential Roles of HSF1. Front. Neurosci. 2017, 11, 192. [Google Scholar] [CrossRef]
- Kroemer, G.; Galluzzi, L.; Kepp, O.; Zitvogel, L. Immunogenic cell death in cancer therapy. Annu. Rev. Immunol. 2013, 31, 51–72. [Google Scholar] [CrossRef]
- O’Neill, D.P.; Peng, T.; Stiegler, P.; Mayrhauser, U.; Koestenbauer, S.; Tscheliessnigg, K.; Payne, S.J. A Three-State Mathematical Model of Hyperthermic Cell Death. Ann. Biomed. Eng. 2011, 39, 570–579. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. PLoS Comput. Boil. 2014, 10, e1003800. [Google Scholar] [CrossRef]
- Tuersun, P.; Han, X.E. Optical absorption analysis and optimization of gold nanoshells. Appl. Opt. 2013, 52, 1325–1329. [Google Scholar] [CrossRef]
- Keribig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer: New York, NY, USA, 2015. [Google Scholar]
- Averitt, R.D.; Westcott, S.L.; Halas, N.J. Linear optical properties of gold nanoshells. J. Opt. Soc. Am. B 1999, 16, 1824–1832. [Google Scholar] [CrossRef]
- Available online: https://refractiveindex.info/ (accessed on 28 October 2018).
- Gans, R. Über die Form ultramikroskopischer Silberteilchen. Ann. Phys. 1915, 352, 270–284. [Google Scholar] [CrossRef]
- Papavassiliou, G.C. Optical properties of small inorganic and organic metal particles. Prog. Solid State Chem. 1979, 12, 185–271. [Google Scholar] [CrossRef]
- Link, S.; Mohamed, M.B.; El-Sayed, M.A. Simulation of the Optical Absorption Spectra of Gold Nanorods as a Function of Their Aspect Ratio and the Effect of the Medium Dielectric Constant. J. Phys. Chem. B 1999, 103, 3073–3077. [Google Scholar] [CrossRef] [Green Version]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]
- Qian, L.P.; Zhou, L.H.; Too, H.-P.; Chow, G.-M. Gold decorated NaYF4:Yb,Er/NaYF4/silica (core/shell/shell) upconversion nanoparticles for photothermal destruction of BE(2)-C neuroblastoma cells. J. Nanopart. Res. 2011, 13, 499–510. [Google Scholar] [CrossRef]
- Ali, M.Y.; Grimm, C.F.; Ritter, M.; Mohr, L.; Allgaier, H.-P.; Weth, R.; Bocher, W.O.; Endrulat, K.; Blum, H.E.; Geissler, M. Activation of dendritic cells by local ablation of hepatocellular carcinoma. J. Hepatol. 2005, 43, 817–822. [Google Scholar] [CrossRef]
- Rai, N.K.; Rai, K.S. Effect of metabolic heat generation and blood perfusion on the heat transfer in the tissues with a blood vessel. Heat Mass Transf. 1999, 35, 75–79. [Google Scholar] [CrossRef]
- Gowrishankar, T.R.; Stewart, D.A.; Martin, G.T.; Weaver, J.C. Transport lattice models of heat transport in skin with spatially heterogeneous, temperature-dependent perfusion. Biomed. Eng. Online 2004, 3, 42. [Google Scholar] [CrossRef]
- Jiao, J.; Guo, Z. Thermal interaction of short-pulsed laser focused beams with skin tissues. Phys. Med. Boil. 2009, 54, 4225–4241. [Google Scholar] [CrossRef]
- Cornelissen, L.H.; Bronneberg, D.; Oomens, C.W.J.; Baaijens, F.P.T. Diffusion measurements in epidermal tissues with fluorescent recovery after photobleaching. Skin Res. Technol. 2008, 14, 462–467. [Google Scholar] [CrossRef]
- Blanco-Andujar, C.; Ortega, D.; Southern, P.; Nesbitt, S.A.; Thanh, N.T.K.; Pankhurst, Q.A. Real-time tracking of delayed-onset cellular apoptosis induced by intracellular magnetic hyperthermia. Nanomedicine 2015, 11, 121–136. [Google Scholar] [CrossRef]
- Feng, Y.; Oden, J.T.; Rylander, M.N. A Two-State Cell Damage Model Under Hyperthermic Conditions: Theory and In Vitro Experiments. J. Biomech. Eng. 2008, 130, 041016. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.-C.; Rege, K.; Heys, J.J. Spatiotemporal Temperature Distribution and Cancer Cell Death in Response to Extracellular Hyperthermia Induced by Gold Nanorods. ACS Nano 2010, 4, 2892–2900. [Google Scholar] [CrossRef] [Green Version]
- Proia, D.A.; Kaufmann, G.F. Targeting Heat-Shock Protein 90 (HSP90) as a Complementary Strategy to Immune Checkpoint Blockade for Cancer Therapy. Cancer Immunol. Res. 2015, 3, 583–589. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Al-Azayzih, A.; Somanath, P.R. Discrete functions of GSK3α and GSK3β isoforms in prostate tumor growth and micrometastasis. Oncotarget 2015, 6, 5947–5962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuber, A.; Purdey, M.; Schartner, E.; Forbes, C.; van der Hoek, B.; Giles, D.; Abell, A.; Monro, T.; Ebendorff-Heidepriem, H. Detection of gold nanoparticles with different sizes using absorption and fluorescence based method. Sens. Actuators B Chem. 2016, 227, 117–127. [Google Scholar] [CrossRef] [Green Version]
- Sambou, A.; Ngom, B.D.; Gomis, L.; Beye, A.C. Turnability of the Plasmonic Response of the Gold Nanoparticles in Infrared Region. Am. J. Nanomater. 2016, 4, 63–69. [Google Scholar] [CrossRef]
- Brace, C.L. Microwave tissue ablation: Biophysics, technology, and applications. Crit. Rev. Biomed. Eng. 2010, 38, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Saldanha, D.F.; Khiatani, V.L.; Carrillo, T.C.; Yap, F.Y.; Bui, J.T.; Knuttinen, M.G.; Owens, C.A.; Gaba, R.C. Current tumor ablation technologies: Basic science and device review. Semin. Interv. Radiol. 2010, 27, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Zhang, A.; Liu, P.; Xu, L.X. Study of tumor growth under hyperthermia condition. Comput. Math. Methods Med. 2012, 2012, 198145. [Google Scholar] [CrossRef] [PubMed]
- Tait, S.W.; Ichim, G.; Green, D.R. Die another way--non-apoptotic mechanisms of cell death. J. Cell Sci. 2014, 127, 2135–2144. [Google Scholar] [CrossRef]
- Nikolaou, M.; Pavlopoulou, A.; Georgakilas, A.G.; Kyrodimos, E. The challenge of drug resistance in cancer treatment: A current overview. Clin. Exp. Metastasis 2018, 35, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Pavlopoulou, A.; Oktay, Y.; Vougas, K.; Louka, M.; Vorgias, C.E.; Georgakilas, A.G. Determinants of resistance to chemotherapy and ionizing radiation in breast cancer stem cells. Cancer Lett. 2016, 380, 485–493. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Morris, J.H.; Cook, H.; Kuhn, M.; Wyder, S.; Simonovic, M.; Santos, A.; Doncheva, N.T.; Roth, A.; Bork, P.; et al. The STRING database in 2017: Quality-controlled protein-protein association networks, made broadly accessible. Nucleic Acids Res. 2017, 45, D362–D368. [Google Scholar] [CrossRef]
- Tang, X.; Tan, L.; Shi, K.; Peng, J.; Xiao, Y.; Li, W.; Chen, L.; Yang, Q.; Qian, Z. Gold nanorods together with HSP inhibitor-VER-155008 micelles for colon cancer mild-temperature photothermal therapy. Acta Pharm. Sin. B 2018. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.Y.; Hodge, S.; Tai, K.; Hou, H.; Khan, N.; Hoopes, P.J.; Samkoe, K.S. Oxygen microenvironment affects the uptake of nanoparticles in head and neck tumor cells. Proc. SPIE Int. Soc. Opt. Eng. 2013, 8584, 85840F. [Google Scholar] [CrossRef] [PubMed]












| Specific Heat Capacity Cp (J/kg/°C) | Density ρ (kg/m³) | Thermal Conductivity k (W/m∙°C) | Blood Perfusion Rate w (m³/m³∙s) | Metabolic Heat Source qm (W/kg) | Diffusivity m2/s | |
|---|---|---|---|---|---|---|
| Blood | 3617 [34] | 1050 [34] | 0.52 [34] | - | 1090 [35] | - |
| Dermis | 3300 [36] | 1200 [36] | 0.45 [36] | 1.25 × 10−3 [36] | 1200 [37] | - |
| Epidermis | 3590 [36] | 1200 [36] | 0.23 [36] | 0 [36] | 1200 [37] | 6.2 × 10−11 [38] |
| Fat | 2348 [34] | 911 [34] | 0.21 [34] | 1.25 × 10−3 [36] | 464 [37] | - |
| Tumor/Muscle | 3421 [34] | 1090 [34] | 0.49 [34] | 1.65 × 10−3 [34] | 991 [34] |
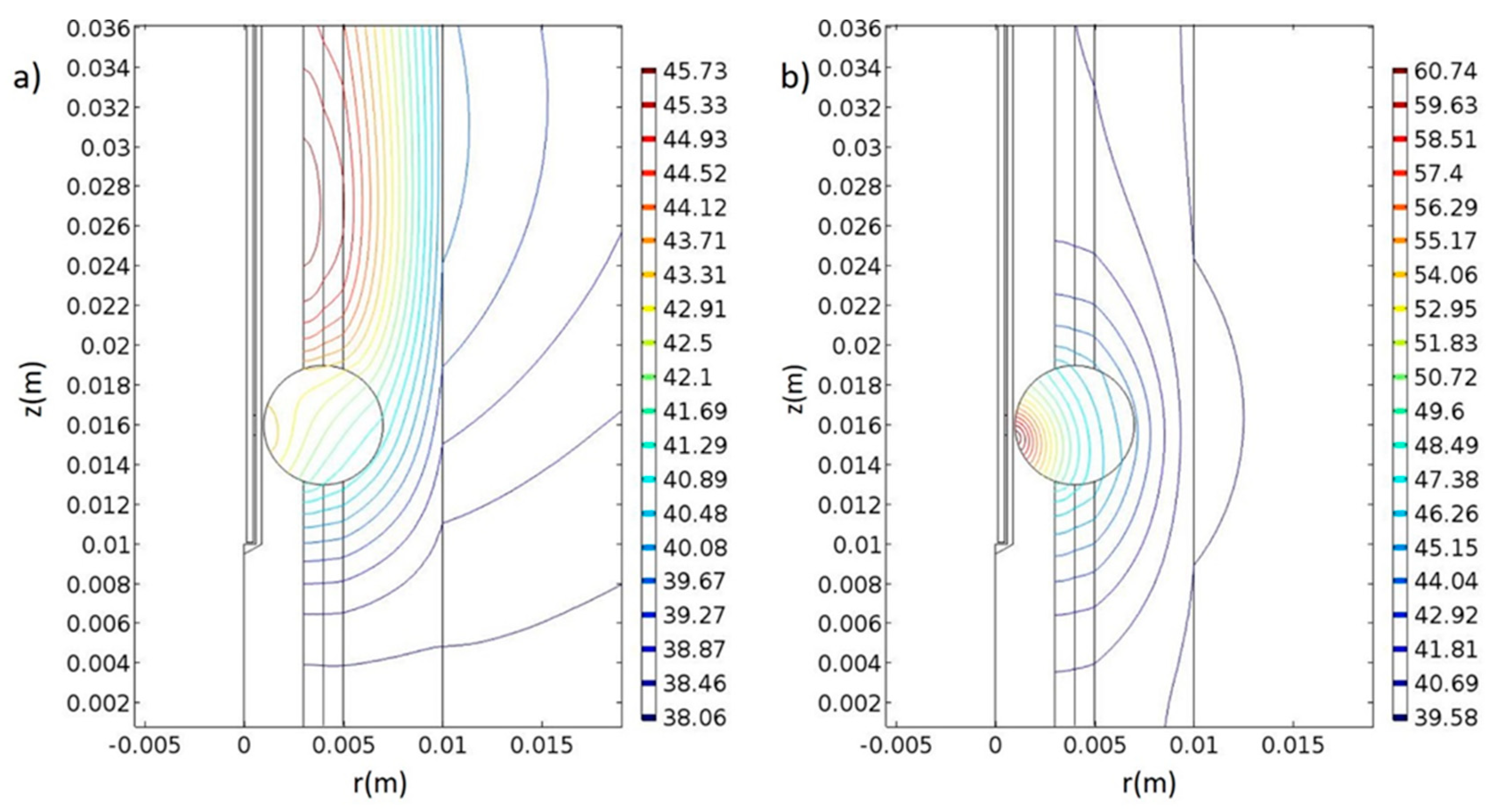
| AuNP 20 nm (Surrounded by 225 nm of Water) (Figure 7a,c) | AuSiO2NP 30 nm (Surrounded by 225 nm of Water) (Figure 7b,d) | |
|---|---|---|
| Max element size | 39.2 nm | 38.4 nm |
| Min element size | 4.9 nm | 4.8 nm |
| Max element growth rate | 1.45 | 1.45 |
| Curvature factor | 0.5 | 0.5 |
| Resolution of narrow regions | 0.6 | 0.6 |
| Melanoma (Figure 9) | Prostate (Figure 10) | |
|---|---|---|
| Max element size | 5.36 mm | 5.36 mm |
| Min element size | 24 μm | 24.5 μm |
| Max element growth rate | 1.3 | 1.3 |
| Curvature factor | 0.3 | 0.3 |
| Resolution of narrow regions | 1 | 1 |
| Melanoma | Prostate Cancer | |
|---|---|---|
| Temperature (degrees Celsius) | 48 | 50 |
| (min−1) | 0.25481 | 0.18946 |
| (min−1) | 0.66477 | 0.23063 |
| (degrees Celsius) | 40.1513 | 39.678 |
| (hours−1) | 0.59547 | (no data) |
| 0.208 (no data) |
| Melanoma | Melanoma (HSP90 Inhibited) | Prostate Cancer | |
|---|---|---|---|
| α0 (s−1) | 0.328 ± 0.003 | 0.237 ± 0.005 | 0.243 ± 0.016 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitriou, N.M.; Pavlopoulou, A.; Tremi, I.; Kouloulias, V.; Tsigaridas, G.; Georgakilas, A.G. Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach. Nanomaterials 2019, 9, 167. https://doi.org/10.3390/nano9020167
Dimitriou NM, Pavlopoulou A, Tremi I, Kouloulias V, Tsigaridas G, Georgakilas AG. Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach. Nanomaterials. 2019; 9(2):167. https://doi.org/10.3390/nano9020167
Chicago/Turabian StyleDimitriou, Nikolaos M., Athanasia Pavlopoulou, Ioanna Tremi, Vassilis Kouloulias, Georgios Tsigaridas, and Alexandros G. Georgakilas. 2019. "Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach" Nanomaterials 9, no. 2: 167. https://doi.org/10.3390/nano9020167
APA StyleDimitriou, N. M., Pavlopoulou, A., Tremi, I., Kouloulias, V., Tsigaridas, G., & Georgakilas, A. G. (2019). Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach. Nanomaterials, 9(2), 167. https://doi.org/10.3390/nano9020167