Experimental Convection Heat Transfer Analysis of a Nano-Enhanced Industrial Coolant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
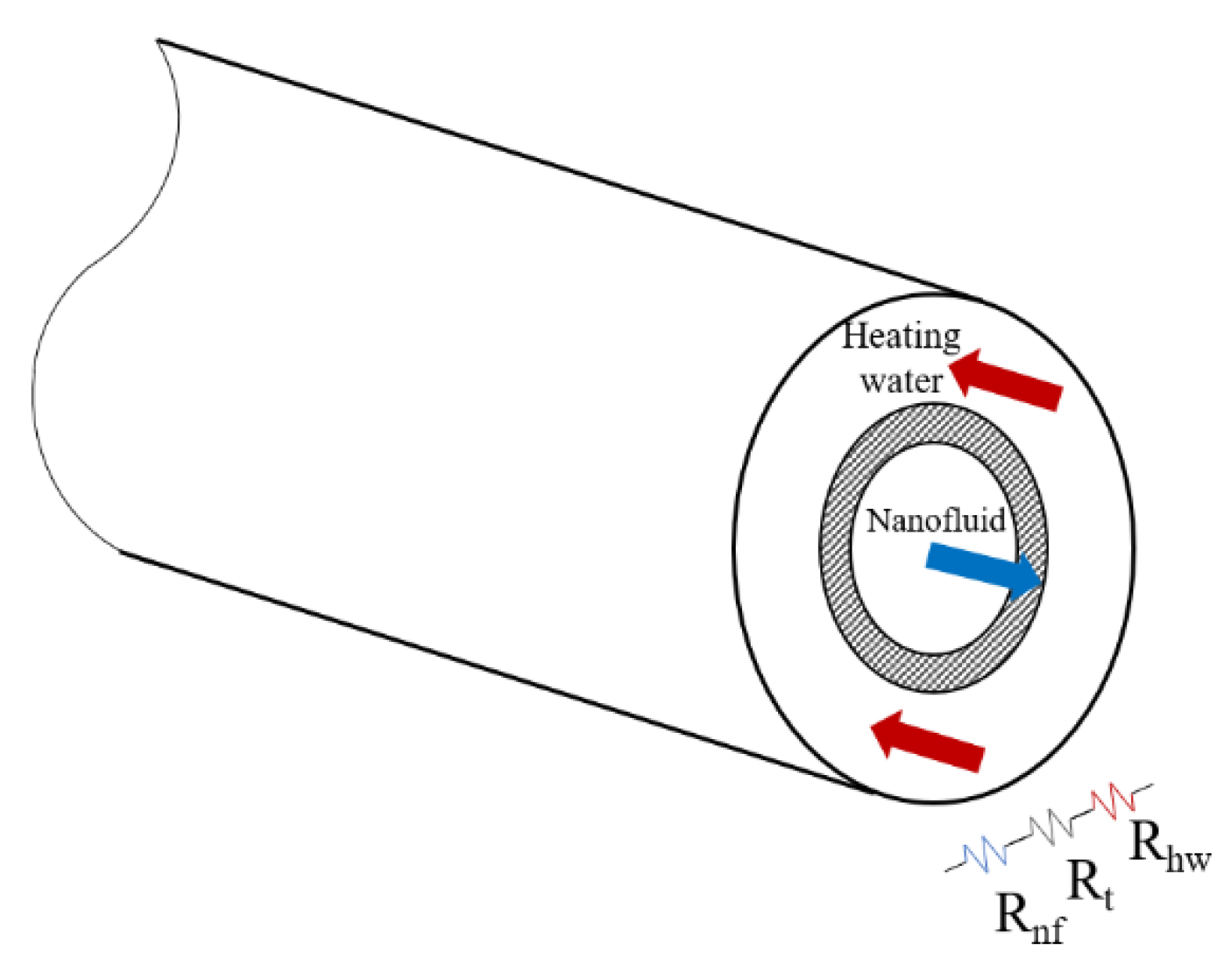
2.2. Experimental Setup
2.3. Methods
2.4. Data Analysis
2.4.1. Convection Coefficients
2.4.2. Dimensionless Analysis
3. Results and Discussion
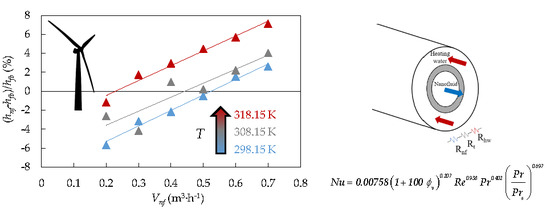
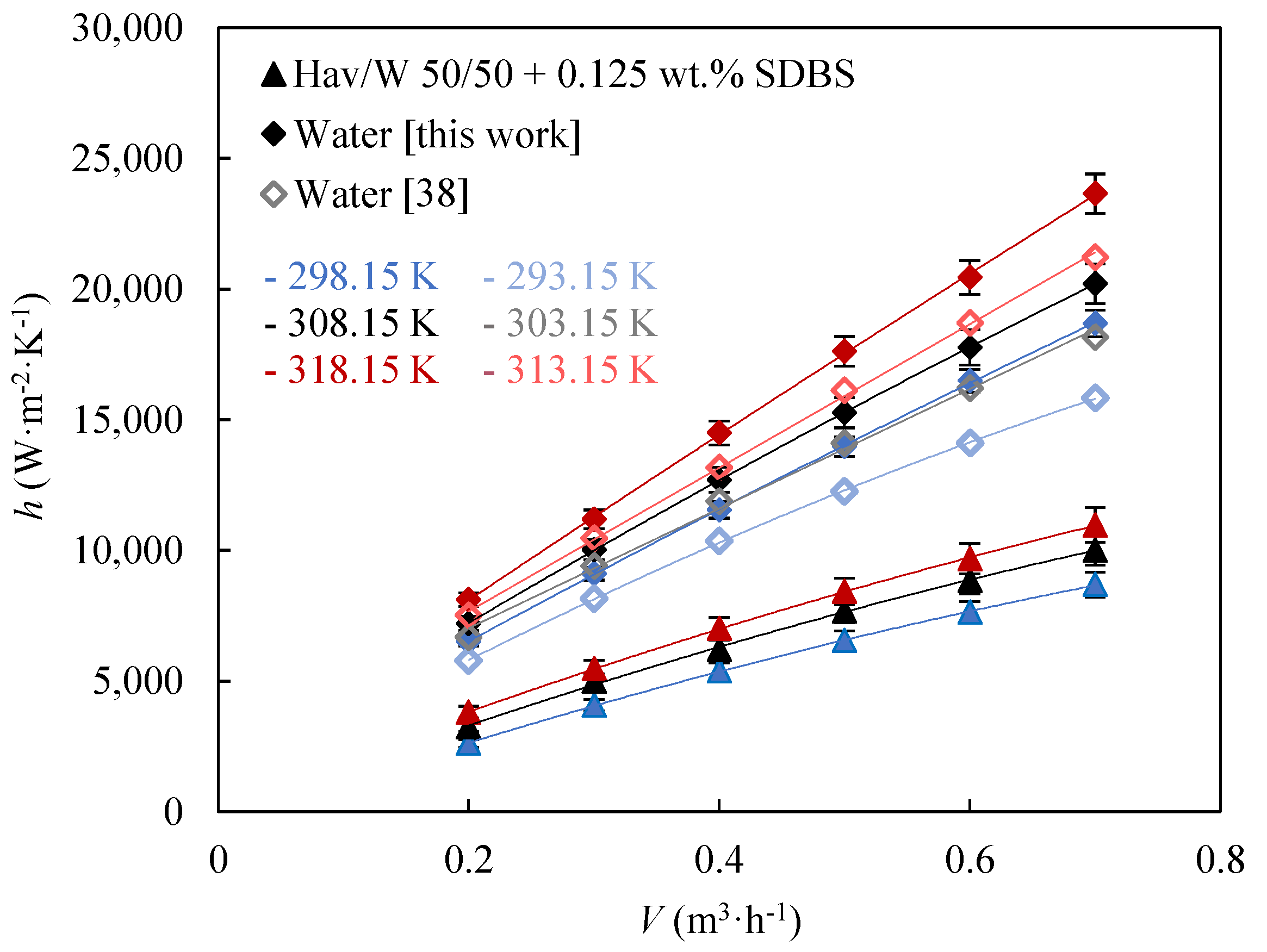
3.1. Validation
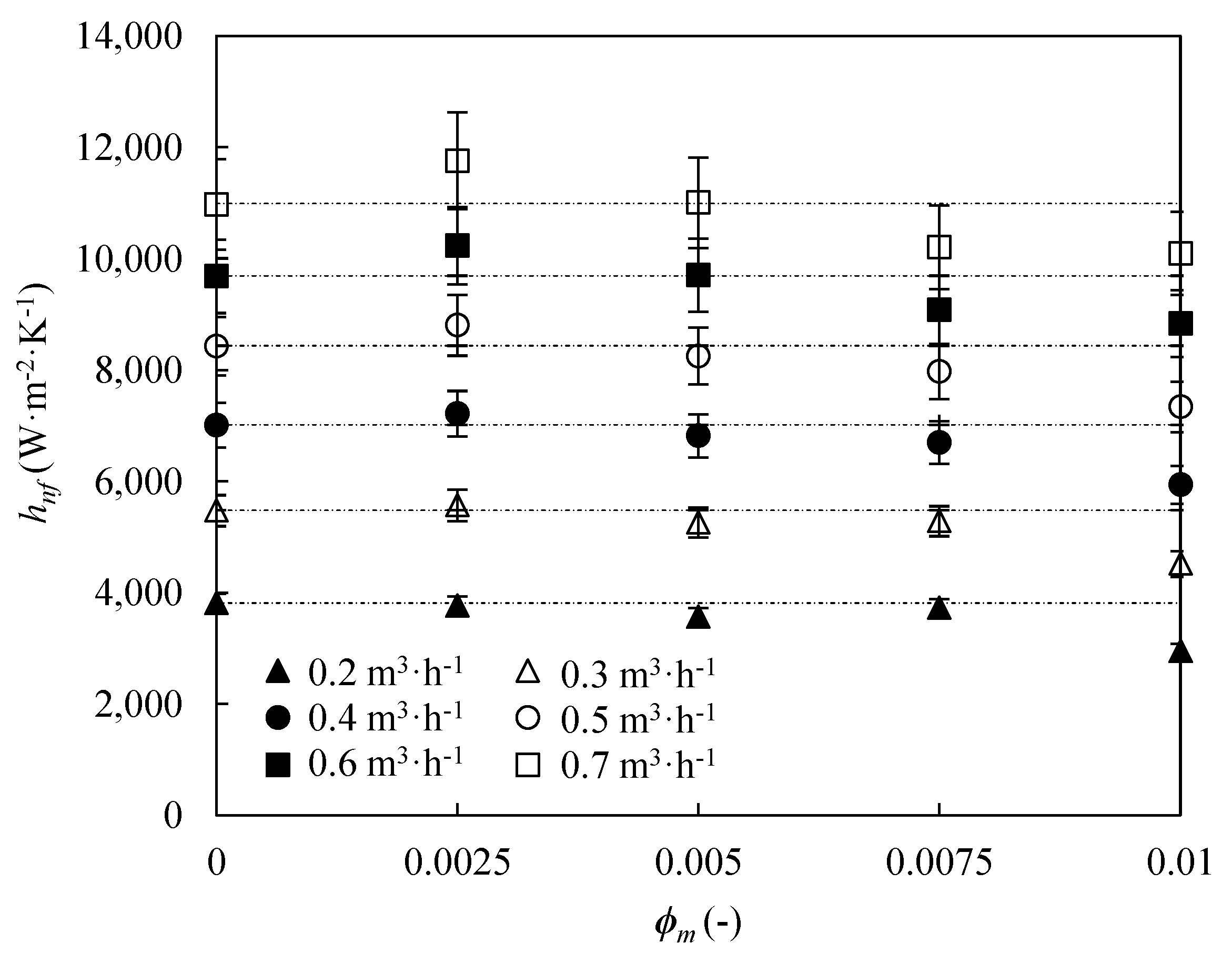
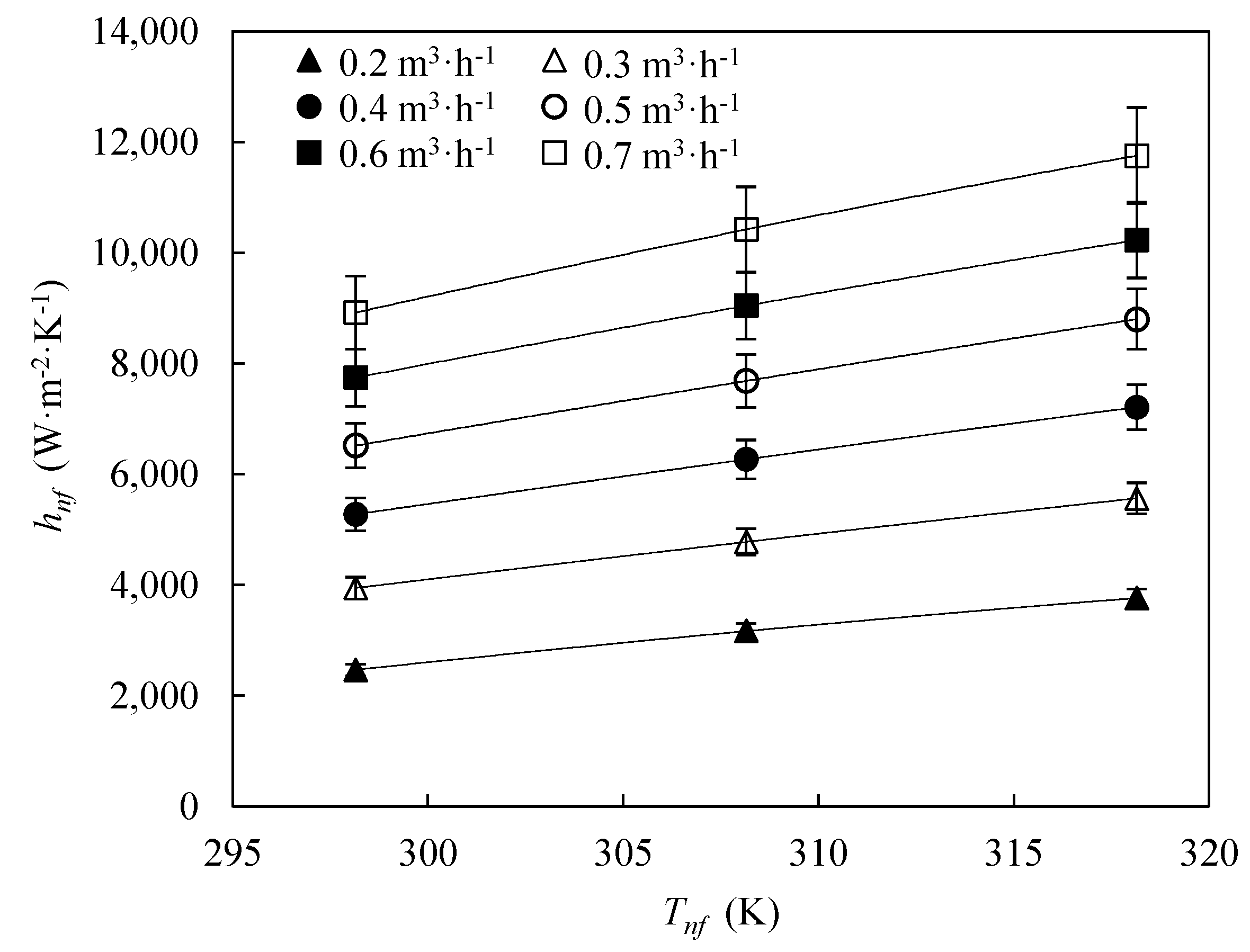
3.2. Heat Transfer Coefficients
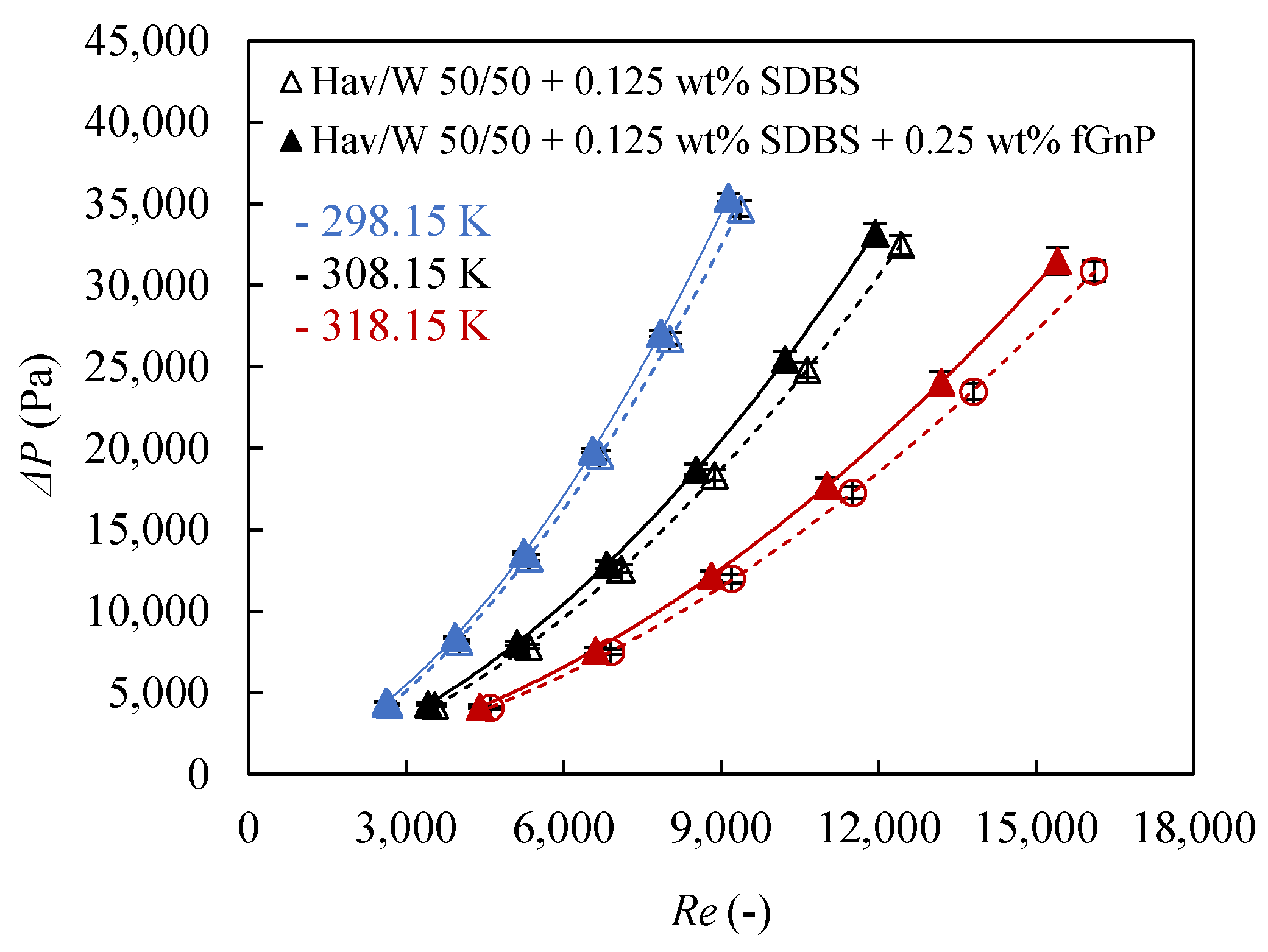
3.3. Pressure Drops
3.4. Dimensionless Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| c1–c8 | Correlation fitting constants |
| cp | Isobaric specific heat capacity, J·kg−1·K |
| d1 | Inner diameter of the inner tube of the tube-in-tube heat exchanger, m |
| d2 | Outer diameter of the inner tube of the tube-in-tube heat exchanger, m |
| d3 | Inner diameter of the outer tube of the tube-in-tube heat exchanger, m |
| f | Darcy friction factor |
| fGnP | Functionalized graphene nanoplatelets |
| h | Convection heat transfer coefficient, W·m−2·K−1 |
| Hav/W 50/50 | Havoline® XLC Pre-mixed 50/50 |
| k | Thermal conductivity, W·m−1·K−1 |
| lh | Effective length for heat exchange, m |
| lΔp | Effective length for pressure drop, m |
| Nu | Nusselt number, dimensionless |
| Pr | Prandtl number, dimensionless |
| Heat flow rate, W | |
| R | Thermal resistance, K·W−1 |
| Re | Reynolds number, dimensionless |
| SDBS | Sodium dodecyl benzene sulphonate |
| T | Temperature, K |
| V | Volumetric flow rate, m3·s−1 |
| Vol % | Nanoadditive volume concentration, % |
| wt % | Nanoadditive mass concentration, % |
| ΔP | Pressure drop along the tube-in-tube heat exchanger, Pa |
| Δθlm | Logarithmic mean temperature difference, K |
| ρ | Density, kg·m−3 |
| η | Dynamic viscosity, Pa·s |
| ϕm | Nanoadditive mass fraction, dimensionless |
| Subscripts | |
| cw | Cooling water |
| hw | Heating water |
| in | Inlet |
| m | Mean |
| nf | Nanofluid |
| out | Outlet |
| t | Inner tube of the tube-in-tube heat exchanger |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publ.-Fed 1995, 231, 99–106. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Garg, J.; Poudel, B.; Chiesa, M.; Gordon, J.B.; Ma, J.J.; Wang, J.B.; Ren, Z.F.; Kang, Y.T.; Ohtani, H.; Nanda, J.; et al. Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys. 2008, 103, 074301. [Google Scholar] [CrossRef]
- Namburu, P.K.; Kulkarni, D.P.; Misra, D.; Das, D.K. Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture. Exp. Therm. Fluid Sci. 2007, 32, 397–402. [Google Scholar] [CrossRef]
- Moreno, G.; Olderburg, S.J.; You, S.M.; Kim, J.H. Pool boling heat transfer of alumina-water, zinc oxide-water and alumina-water+ethylene glycol nanofluids. In Proceedings of the ASME 2005 Summer Heat Transfer Conference collocated with the ASME 2005 Pacific Rim Technical Conference and Exhibition on Integration and Packaging of MEMS, NEMS, and Electronic Systems, San Francisco, CA, USA, 17–22 July 2005; Volume 2, pp. 625–632. [Google Scholar]
- Peyghambarzadeh, S.M.; Hashemabadi, S.H.; Hoseini, S.M.; Sei, M. Experimental study of heat transfer enhancement using water/ethylene glycol based nanofluids as a new coolant for car radiators. Int. Commun. Heat Mass Transf. 2011, 38, 1283–1290. [Google Scholar] [CrossRef]
- Esfahani, M.A.; Toghraie, D. Experimental investigation for developing a new model for the thermal conductivity of Silica/Water-Ethylene glycol (40%–60%) nanofluid at different temperatures and solid volume fractions. J. Mol. Liq. 2017, 232, 105–112. [Google Scholar] [CrossRef]
- Fal, J.; Żyła, G. Experimental studies on viscosity, thermal and electrical conductivity of aluminum nitride–ethylene glycol (AlN–EG) nanofluids. Thermochim. Acta 2016, 637, 11–16. [Google Scholar]
- Yu, W.; Xie, H. A Review on Nanofluids: Preparation, Stability Mechanisms and Applications. J. Nanomater. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Wang, B.; Hao, J.; Li, H. Remarkable improvements in the stability and thermal conductivity of graphite/ethylene glycol nanofluids caused by a graphene oxide percolation structure. Dalt. Trans. 2013, 42, 5866–5873. [Google Scholar] [CrossRef]
- Ghozatloo, A.; Rashidi, A.; Shariaty-niassar, M. Convective heat transfer enhancement of graphene nanofluids in shell and tube heat exchanger. Exp. Therm. Fluid Sci. 2014, 53, 136–141. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Mehrali, M.; Tahan Latibari, S.; Mehrali, M.; Kazi, S.N.; Oon, C.S.; Metselaar, H.S.C. Experimental Investigation of Convective Heat Transfer Using Graphene Nanoplatelet Based Nanofluids under Turbulent Flow Conditions. Ind. Eng. Chem. Res. 2014, 53, 12455–12465. [Google Scholar] [CrossRef]
- Ijam, A.; Saidur, R.; Ganesan, P.; Golsheikh, A.M. International Journal of Heat and Mass Transfer Stability, thermo-physical properties and electrical conductivity of graphene oxide-deionized water/ethylene glycol based nanofluid. Int. J. Heat Mass Transf. 2015, 87, 92–103. [Google Scholar] [CrossRef]
- Żyła, G.; Vallejo, J.P.; Fal, J.; Lugo, L. Nanodiamonds—Ethylene Glycol nanofluids: Experimental investigation of fundamental physical properties. Int. J. Heat Mass Transf. 2018, 121, 1201–1213. [Google Scholar] [CrossRef]
- Iacobazzi, F.; Milanese, M.; Colangelo, G.; Lomascolo, M.; de Risi, A. An explanation of the Al2O3 nanofluid thermal conductivity based on the phonon theory of liquid. Energy 2016, 116, 786–794. [Google Scholar] [CrossRef]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated maxwell model. J. Nanopart. Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Milanese, M.; Iacobazzi, F.; Colangelo, G.; de Risi, A. An investigation of layering phenomenon at the liquid–solid interface in Cu and CuO based nanofluids. Int. J. Heat Mass Transf. 2016, 103, 564–571. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U.S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316–4318. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.R.; Choi, S.U.S.; Eastman, J.A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Evans, W.; Prasher, R.; Fish, J.; Meakin, P.; Phelan, P.; Keblinski, P. Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transf. 2008, 51, 1431–1438. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; de Risi, A.; Laforgia, D. Cooling of electronic devices: Nanofluids contribution. Appl. Therm. Eng. 2017, 127, 421–435. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- De Risi, A.; Milanese, M.; Colangelo, G.; Laforgia, D. High efficiency nanofluid cooling system for wind turbines. Therm. Sci. 2014, 18, 543–554. [Google Scholar]
- EL Sebaay, A.; Ramadan, M.; Adma, M.A.A. Studying the effect of non-linear loads harmonics on electric generator power rating selection. Eur. Sci. J. 2017, 13, 155–160. [Google Scholar] [CrossRef]
- AMSC SeaTitan 10 MW Wind Turbine. Available online: https://www.amsc.com/wp-content/uploads/wt10000_DS_A4_0212.pdf (accessed on 6 January 2019).
- Chamsa-ard, W.; Brundavanam, S.; Fung, C.C.; Fawcett, D.; Poinerm, G. Nanofluid types, their synthesis, properties and incorporation in direct solar thermal collectors: A review. Nanomaterials 2017, 7, 131. [Google Scholar] [CrossRef] [PubMed]
- Sani, E.; Vallejo, J.P.; Cabaleiro, D.; Lugo, L. Functionalized graphene nanoplatelet-nanofluids for solar thermal collectors. Sol. Energy Mater. Sol. Cells 2018, 185, 205–209. [Google Scholar] [CrossRef]
- Kole, M.; Dey, T.K. Thermal conductivity and viscosity of Al2O3 nanofluid based on car engine coolant. J. Phys. D Appl. Phys. 2010, 43, 315501. [Google Scholar] [CrossRef]
- Kole, M.; Dey, T.K. Viscosity of alumina nanoparticles dispersed in car engine coolant. Exp. Therm. Fluid Sci. 2010, 34, 677–683. [Google Scholar] [CrossRef]
- Elias, M.M.; Mahbubul, I.M.; Saidur, R.; Sohel, M.R.; Shahrul, I.M.; Khaleduzzaman, S.S.; Sadeghipour, S. Experimental investigation on the thermo-physical properties of Al2O3 nanoparticles suspended in car radiator coolant. Int. Commun. Heat Mass Transf. 2014, 54, 48–53. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Álvarez-Regueiro, E.; Cabaleiro, D.; Fernández-Seara, J.; Fernández, J.; Lugo, L. Thermophysical properties of funtionalized graphene nanoplatelet dispersions for improving efficiency in a wind turbine cooling system. Appl. Therm. Eng. 2019. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Solangi, K.H.; Amiri, A.; Luhur, M.R.; Ghavimi, S.A.A.; Zubir, M.N.M.; Kazi, S.N.; Badarudin, A. Experimental investigation of the propylene glycol-treated graphene nanoplatelets for the enhancement of closed conduit turbulent convective heat transfer. Int. Commun. Heat Mass Transf. 2016, 73, 43–53. [Google Scholar] [CrossRef]
- Amiri, A.; Shanbedi, M.; Chew, B.T.; Kazi, S.N.; Solangi, K.H. Toward improved engine performance with crumpled nitrogen-doped graphene based water–ethylene glycol coolant. Chem. Eng. J. 2016, 289, 583–595. [Google Scholar] [CrossRef]
- Arzani, H.K.; Amiri, A.; Kazi, S.N.; Badarudin, A.; Chew, B.T. Heat transfer performance of water-based tetrahydrofurfuryl polyethylene glycol-treated graphene nanoplatelet nanofluids. RSC Adv. 2016, 6, 65654–65669. [Google Scholar] [CrossRef]
- Agromayor, R.; Cabaleiro, D.; Pardinas, A.A.; Vallejo, J.P.; Fernandez-Seara, J.; Lugo, L. Heat transfer performance of functionalized graphene nanoplatelet aqueous nanofluids. Materials 2016, 9, 455. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Tavernier, J.; Vallejo, J.P.; Cabaleiro, D.; Fernández-Seara, J.; Lugo, L. Heat transfer performance of a nano-enhanced propylene glycol: Water mixture. Int. J. Therm. Sci. 2019. accepted. [Google Scholar]
- Babita; Sharma, S.K.; Gupta, S.M. Preparation and evaluation of stable nanofluids for heat transfer application: A review. Exp. Therm. Fluid Sci. 2016, 79, 202–212. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Reference Fluid Thermodynamic and Transport Properties (REFPROP). NIST Standard Reference Database. 2002. Available online: https://www.nist.gov/srd (accessed on 6 January 2019).
- Gnielinski, V. G2 Heat Transfer in Concentric Annular and Parallel Plate Ducts. In VDI Heat Atlas; VDI-Gesellschaft Verfahrenstechnik-und-Chemieingenieurwesen, V.D.I., Ed.; Springer: Berlin, Germany, 2010; pp. 701–708. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurements; JCGM 100: Sèvres, France, 2008. [Google Scholar]
- Gnielinski, V. G1 Heat Transfer in Pipe Flow. In VDI Heat Atlas; VDI-Gesellschaft Verfahrenstechnik-und-Chemieingenieurwesen, V.D.I., Ed.; Springer: Berlin, Germany, 2010; pp. 691–700. [Google Scholar]
- Gnielinski, V. Heat transfer coefficients for turbulent flow in concentric annular ducts. Heat Transf. Eng. 2009, 30, 431–436. [Google Scholar] [CrossRef]
- He, Y.; Jin, Y.; Chen, H.; Ding, Y.; Cang, D.; Lu, H. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 2007, 50, 2272–2281. [Google Scholar] [CrossRef]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water based Al2O3 and Al2O3-Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar] [CrossRef]
- Pang, C.; Lee, J.W.; Kang, Y.T. Review on combined heat and mass transfer characteristics in nanofluids. Int. J. Therm. Sci. 2015, 87, 49–67. [Google Scholar] [CrossRef]
- Tohidi, A.; Hosseinalipour, S.M.; Ghasemi Monfared, Z.; Mujumdar, A.S. Laminar Heat Transfer Enhancement Utilizing Nanofluids in a Chaotic Flow. J. Heat Transf. 2014, 136, 091704. [Google Scholar] [CrossRef]
- Bowers, J.; Cao, H.; Qiao, G.; Li, Q.; Zhang, G.; Mura, E.; Ding, Y. Flow and heat transfer behaviour of nanofluids in microchannels. Prog. Nat. Sci. Mater. Int. 2018, 28, 225–234. [Google Scholar] [CrossRef]
- Heris, S.Z.; Etemad, S.G.; Esfahany, M.N. Experimental investigation of oxide nanofluids laminar flow convective heat transfer. Int. Commun. Heat Mass Transf. 2006, 33, 529–535. [Google Scholar] [CrossRef]
- Farajollahi, B.; Etemad, S.G.; Hojjat, M. Heat transfer of nanofluids in a shell and tube heat exchanger. Int. J. Heat Mass Transf. 2010, 53, 12–17. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. An experimental study on the heat transfer performance and pressure drop of TiO2-water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transf. 2010, 53, 334–344. [Google Scholar] [CrossRef]
- Azmi, W.H.; Sharma, K.V.; Sarma, P.K.; Mamat, R.; Anuar, S.; Dharma Rao, V. Experimental determination of turbulent forced convection heat transfer and friction factor with SiO2 nanofluid. Exp. Therm. Fluid Sci. 2013, 51, 103–111. [Google Scholar] [CrossRef]
- Nikulin, A.; Moita, A.S.; Moreira, A.L.N.; Murshed, S.M.S.; Huminic, A.; Grosu, Y.; Faik, A.; Nieto-Maestre, J.; Khliyeva, O. Effect of Al2O3 nanoparticles on laminar, transient and turbulent flow of isopropyl alcohol. Int. J. Heat Mass Transf. 2019, 130, 1032–1044. [Google Scholar] [CrossRef]


| Thermophysical Property | Hav/W 50/50 + 0.125 wt % SDBS | 0.25 wt % Nanofluid | 0.50 wt % Nanofluid | 0.75 wt % Nanofluid | 1.0 wt % Nanofluid |
|---|---|---|---|---|---|
| ρ (kg·m−3) | 1068.1 | 1068.9 | 1070.1 | 1071.1 | 1072.1 |
| cp (J·kg−1·K−1) | 3302 | 3296 | 3290 | 3284 | 3278 |
| k (W·m−1·K−1) | 0.390 | 0.397 | 0.405 | 0.412 | 0.418 |
| η (mPa·s) | 3.53 | 3.62 | 3.67 | 3.75 | 3.88 |
| Parameter | Nomenclature | Value (103 m) |
|---|---|---|
| Inner diameter of the inner tube | d1 | 8 |
| Outer diameter of the inner tube | d2 | 10 |
| Inner diameter of the outer tube | d3 | 15 |
| Effective length for heat exchange | lh | 930 |
| Effective length for pressure drop | lΔP | 1180 |
| Tm nf (K) | Vnf (m3·h−1) | Vhw (m3·h−1) |
|---|---|---|
| 298.15 | 0.2–0.7 | 0.8 |
| 308.15 | 0.2–0.7 | 0.8 |
| 318.15 | 0.2–0.7 | 0.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez-Regueiro, E.; Vallejo, J.P.; Fernández-Seara, J.; Fernández, J.; Lugo, L. Experimental Convection Heat Transfer Analysis of a Nano-Enhanced Industrial Coolant. Nanomaterials 2019, 9, 267. https://doi.org/10.3390/nano9020267
Álvarez-Regueiro E, Vallejo JP, Fernández-Seara J, Fernández J, Lugo L. Experimental Convection Heat Transfer Analysis of a Nano-Enhanced Industrial Coolant. Nanomaterials. 2019; 9(2):267. https://doi.org/10.3390/nano9020267
Chicago/Turabian StyleÁlvarez-Regueiro, Eva, Javier P. Vallejo, José Fernández-Seara, Josefa Fernández, and Luis Lugo. 2019. "Experimental Convection Heat Transfer Analysis of a Nano-Enhanced Industrial Coolant" Nanomaterials 9, no. 2: 267. https://doi.org/10.3390/nano9020267
APA StyleÁlvarez-Regueiro, E., Vallejo, J. P., Fernández-Seara, J., Fernández, J., & Lugo, L. (2019). Experimental Convection Heat Transfer Analysis of a Nano-Enhanced Industrial Coolant. Nanomaterials, 9(2), 267. https://doi.org/10.3390/nano9020267