Opto-thermally Excited Fabry-Perot Resonance Frequency Behaviors of Clamped Circular Graphene Membrane
Abstract
:1. Introduction
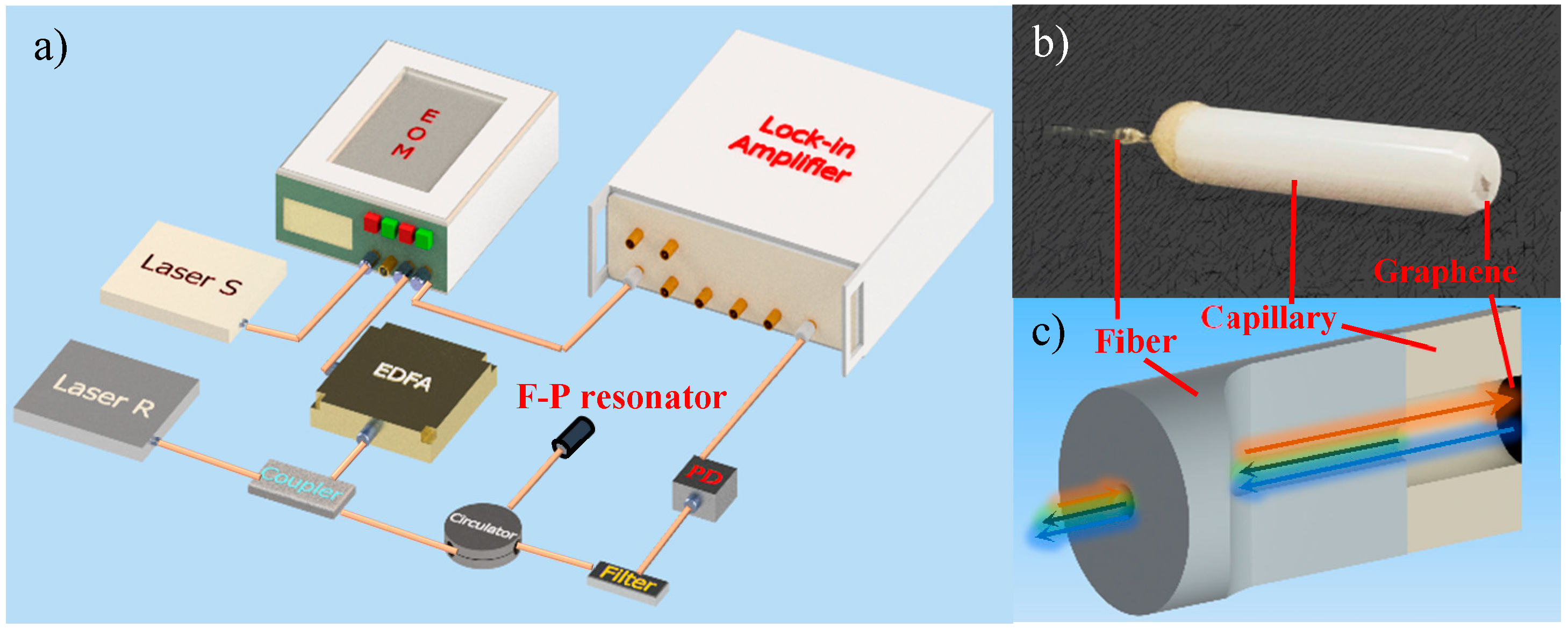
2. The Model Adapted to Opto-Thermal F-P Resonance Measurement
3. Simulation on the Effects of Opto-Mechanical Parameters
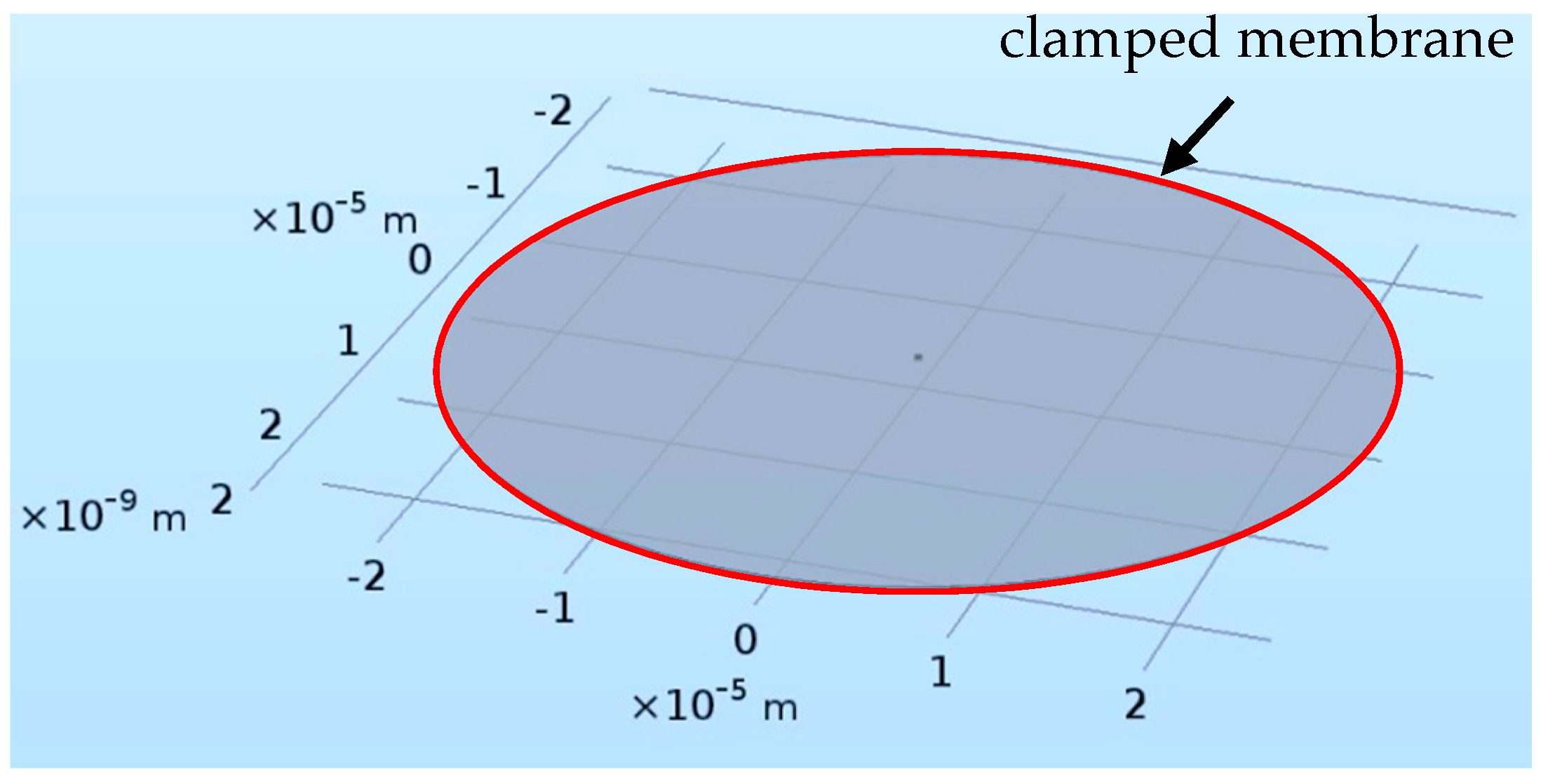
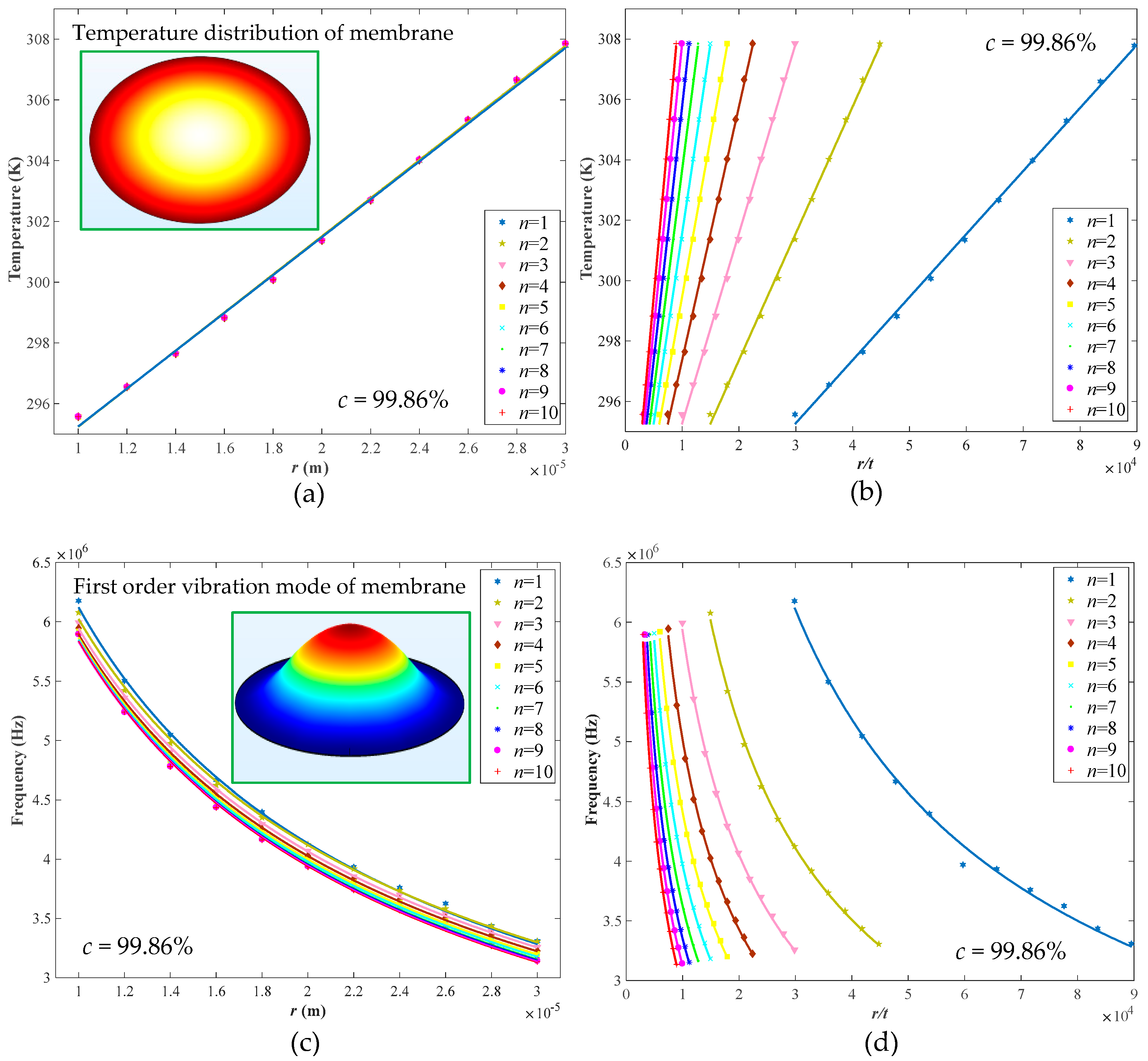
3.1. Structure Properties of Graphene Membrane
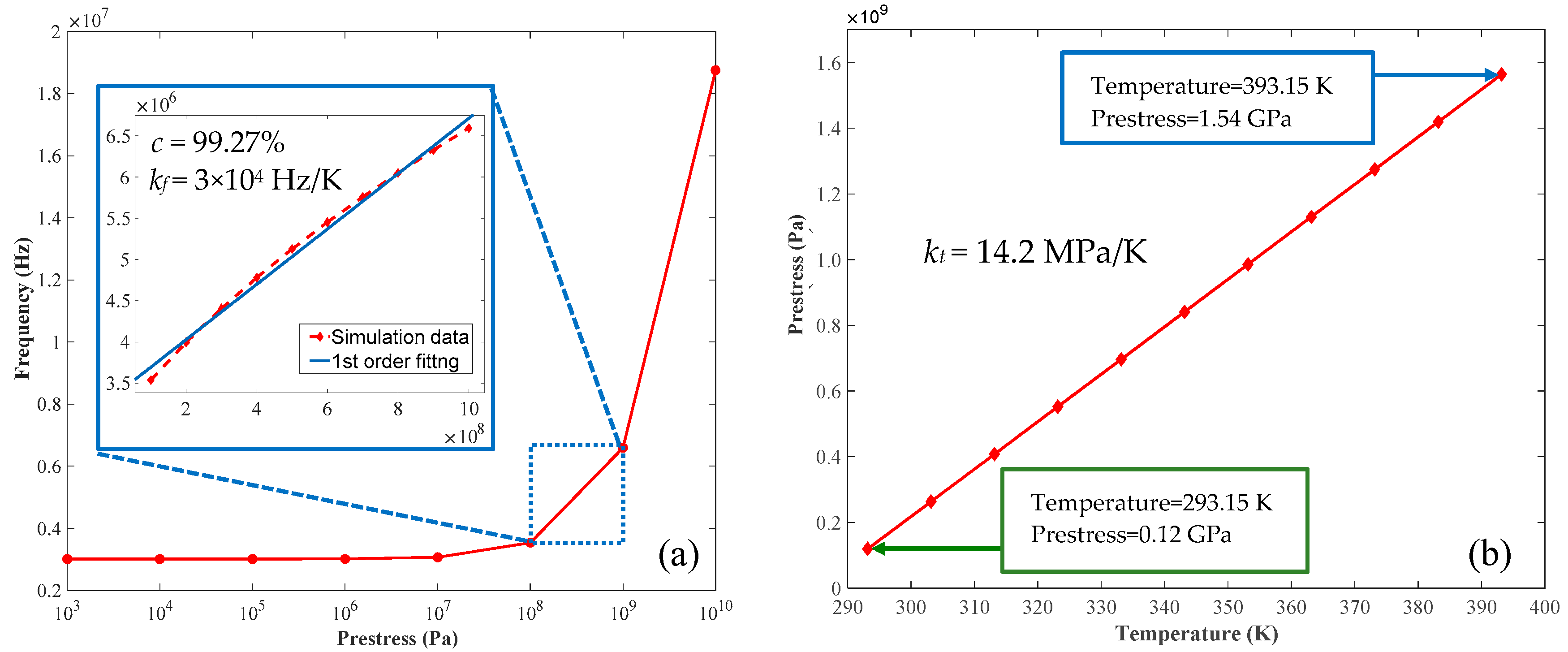
3.2. Film Prestress
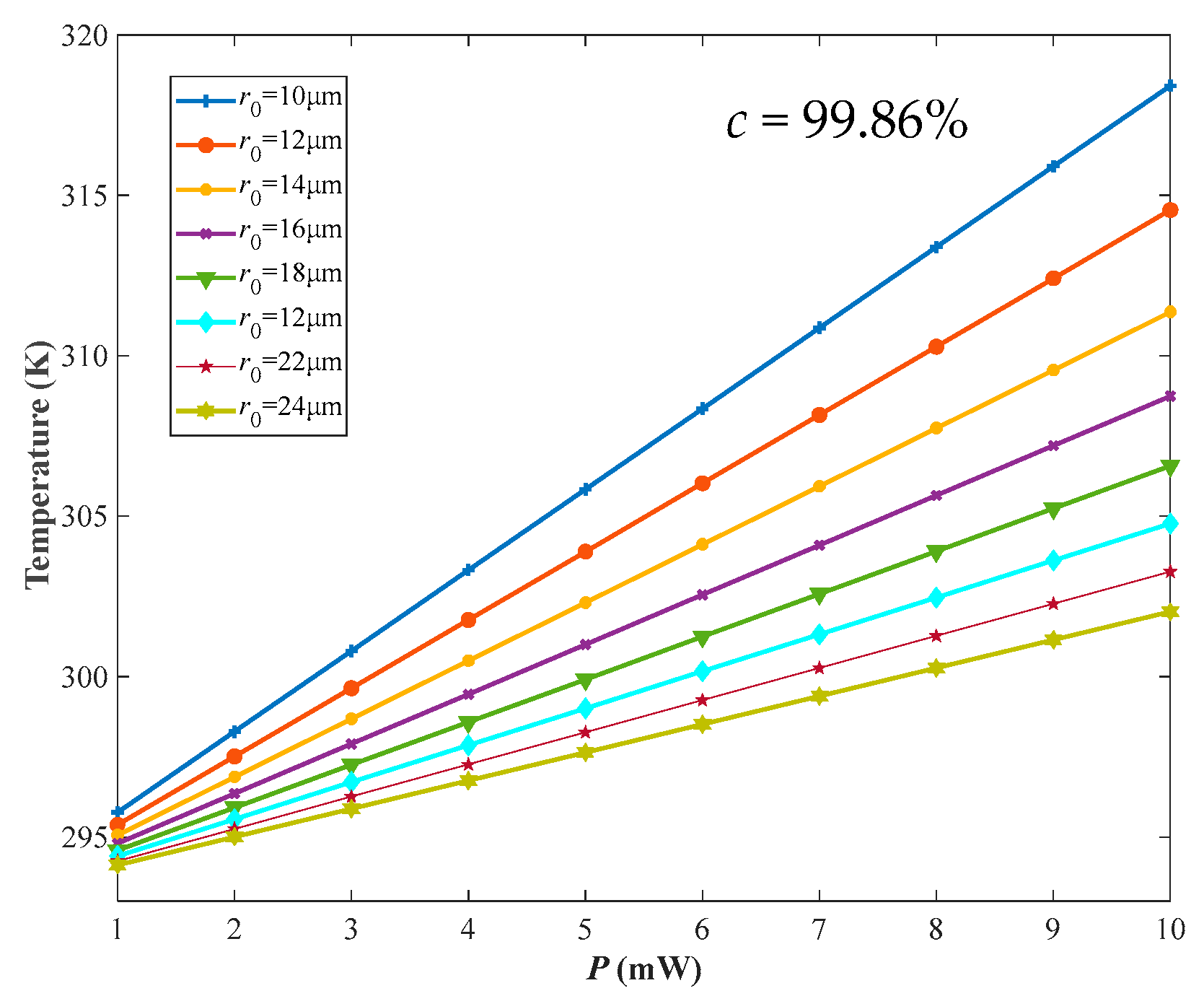
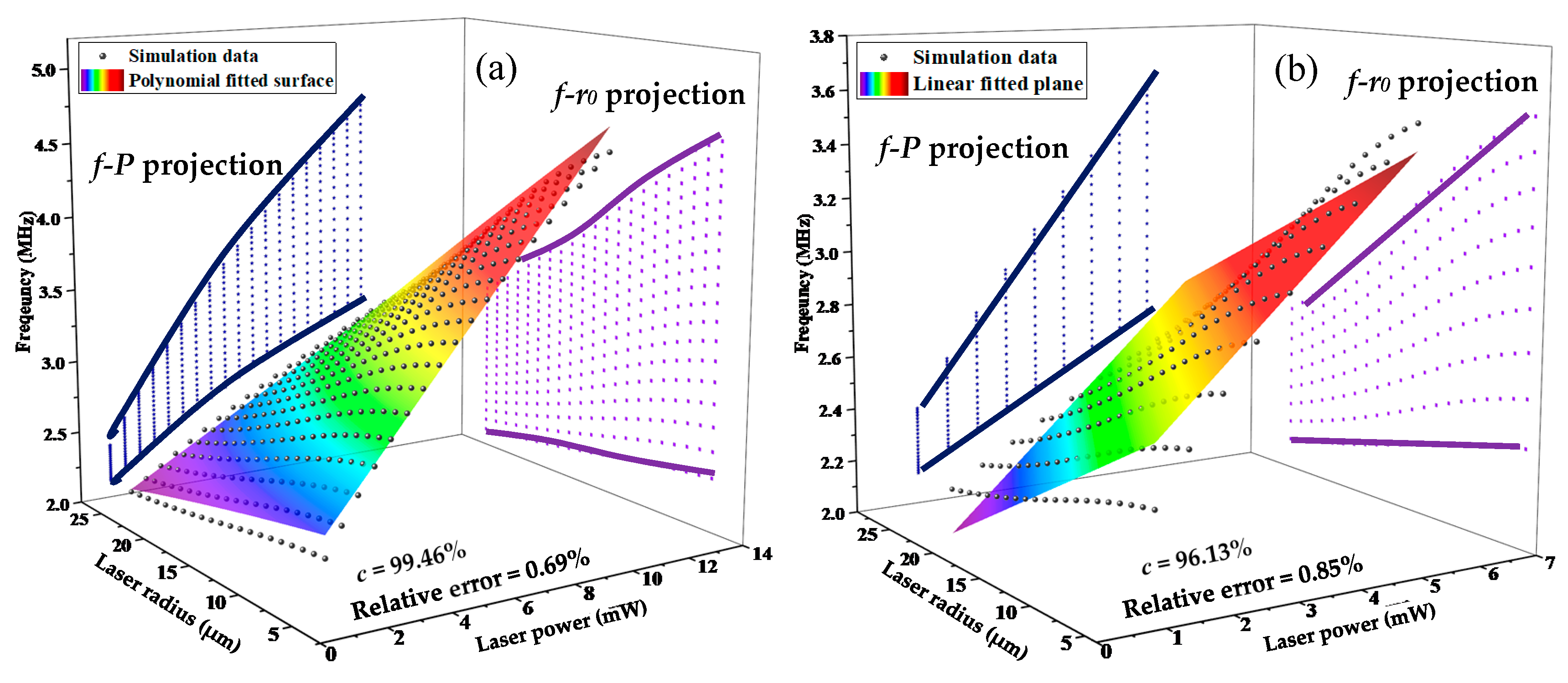
3.3. Laser Actuation Parameters
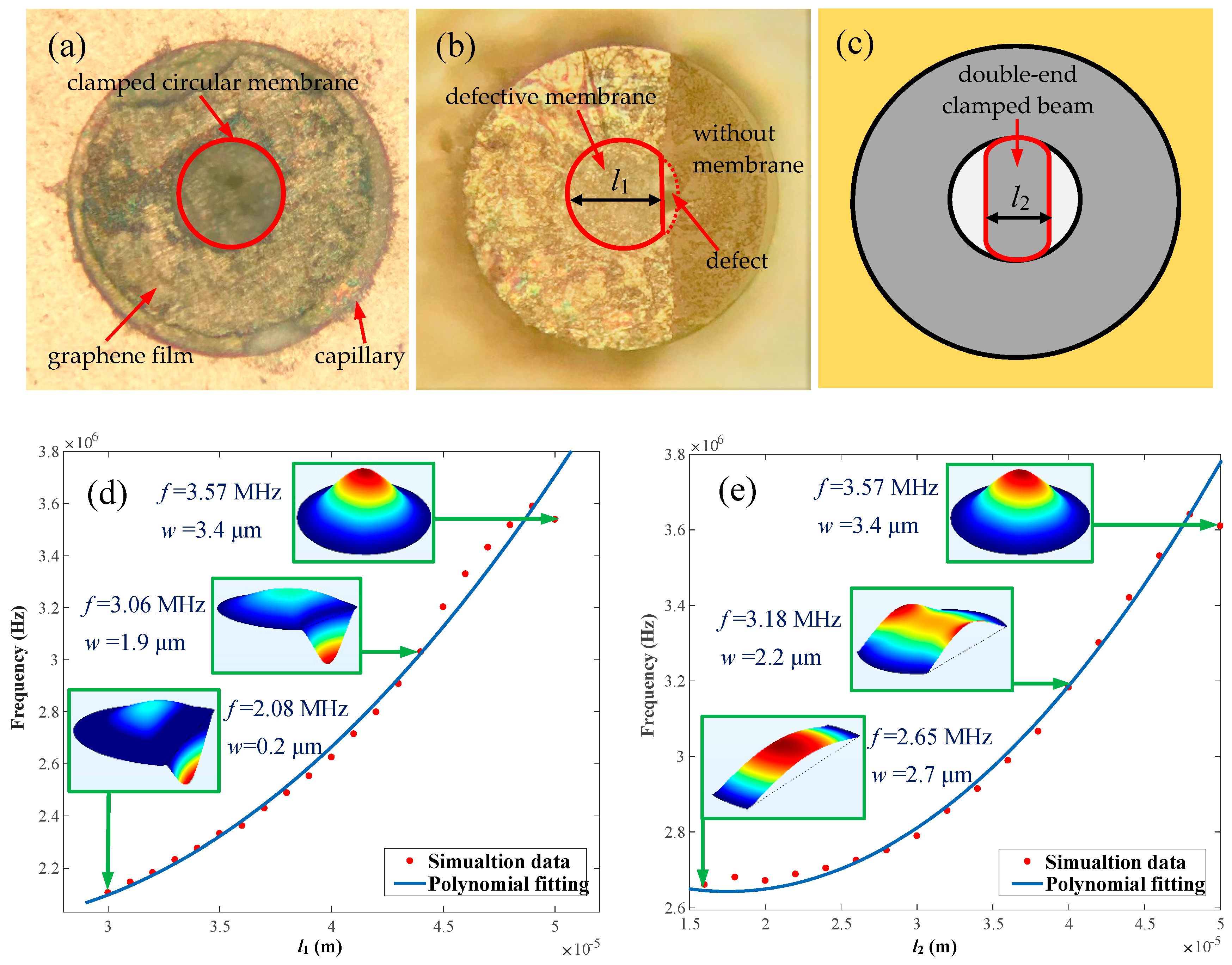
3.4. Clamped Boundary Conditions
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, H.; Mendoza, D.; Benítez, J.L. Thermal diffusivity of few-layers graphene measured by an all-optical method. J. Phys. D-Appl. Phys. 2015, 48, 465501. [Google Scholar] [CrossRef]
- Chang, H.; Wu, H. Graphene-based nanomaterials: Synthesis, properties, and optical and optoelectronic applications. Adv. Funct. Mater. 2013, 23, 1984–1997. [Google Scholar] [CrossRef]
- Wang, D.; Fan, S.; Jin, W. Graphene diaphragm analysis for pressure or acoustic sensor applications. Microsyst. Technol. 2013, 21, 117–122. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Liu, Z.; Welsher, K.; Robinson, J.T.; Goodwin, A.; Zaric, S.; Dai, H. Nano-graphene oxide for cellular imaging and drug delivery. Nano Res. 2008, 1, 203. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Yang, H.; Zhu, C.; Chen, X.; Chen, G. A graphene platform for sensing biomolecules. Angew. Chem. Int. Ed. 2009, 48, 4785. [Google Scholar] [CrossRef]
- Shan, C.; Yang, H.; Song, J.; Han, D.; Ivaska, A.; Niu, L. Direct electrochemistry of glucose oxidase and bio sensing for glucose based on graphene. Anal. Chem. 2009, 81, 2378–2382. [Google Scholar] [CrossRef]
- Chang, H.; Tang, L.; Wang, Y.; Jiang, J.; Li, J. Graphene fluorescence resonance energy transfer aptasensor for the thrombin detection. Anal. Chem. 2010, 82, 2341–2346. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van, A.M.; Verbridge, S.S. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Rosenblatt, S.; Bolotin, K.I. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Oshidari, Y.; Hatakeyama, T.; Kometani, R. High quality factor graphene resonator fabrication using resist shrinkage-induced strain. Appl. Phys. Express 2012, 5, 7201. [Google Scholar] [CrossRef]
- Kwon, O.K.; Lee, G.Y.; Hwang, H.J. Molecular dynamics modeling and simulations to understand gate-tunable graphene-nanoribbon-resonator. Phys. E 2012, 45, 194–200. [Google Scholar] [CrossRef]
- Kwon, O.K.; Lee, J.H.; Park, J. Molecular dynamics simulation study on graphene nanoribbon resonators tuned by adjusting axial strain. Curr. Appl. Phys. 2013, 13, 360–365. [Google Scholar] [CrossRef]
- Mei, T.; Lee, J.; Xu, Y. Frequency tuning of graphene nanoelectromechanical resonators via electrostatic gating. Micromachines 2018, 9, 312. [Google Scholar] [CrossRef]
- Larsen, T.; Schmid, S.; Villanueva, L.G.; Boisen, A. Photothermal analysis of individual nanoparticulate samples using micromechanical resonators. ACS Nano 2013, 7, 6188–6193. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Malvar, O.; Davis, Z.J.; Tamayo, J.; Calleja, M. Nanomechanical plasmon spectroscopy of single gold nanoparticles. Nano Lett. 2018, 18, 7165–7170. [Google Scholar] [CrossRef]
- Pini, V.; Ramos, D.; Dominguez, C.M. Optimization of the readout of microdrum optomechanical resonators. Microelectron. Eng. 2017, 183, 37–41. [Google Scholar] [CrossRef]
- Serra, E. Microfabrication of large-area circular high-stress silicon nitride membranes for optomechanical applications. AIP Adv. 2016, 6, 065004. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.F.; Park, C.H. Controlling inelastic light scattering quantum pathways in graphene. Nature 2011, 471, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.Y.; Lee, K.M.; Shrestha, R. Thermal conductivity measurement of few layer graphene film by a micropipette sensor with laser point heating source. Mater. Res. Express 2016, 3, 055004. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonic 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Cai, W.; Moore, A.L.; Zhu, Y. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 1148. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Xu, X.; Pereira, L.F.; Wang, Y. Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun. 2014, 5, 3689. [Google Scholar] [CrossRef]
- Lee, J.; Wang, Z.; He, K. High frequency MoS2 nanomechanical resonators. ACS Nano 2013, 7, 6086–6091. [Google Scholar] [CrossRef]
- She, Y.; Li, C.; Lan, T. The effect of viscous air damping on an optically actuated multilayer MoS2 nanomechanical resonator using Fabry-Perot interference. Nanomaterials 2016, 6, 162. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lan, T.; Yu, X. Room-temperature pressure-induced optically-actuated Fabry-Perot nanomechanical resonator with multilayer graphene diaphragm in air. Nanomaterials 2017, 7, 366. [Google Scholar] [CrossRef] [PubMed]
- Dolleman, R.J.; Houri, S.; Chandrashekar, A. Opto-thermally excited multimode parametric resonance in graphene membranes. Sci. Rep. 2018, 8, 9366. [Google Scholar] [CrossRef] [PubMed]
- Pop, E.; Varshney, V.; Roy, A.K. Thermal properties of graphene: Fundamentals and applications. MRS Bull. 2012, 37, 1273–1281. [Google Scholar] [CrossRef]
- Smith, A.D.; Vazirs, S.; Delin, A. Strain engineering in suspended graphene devices for pressure sensor application. In Proceedings of the 13th IEEE International Conference on Ultimate Integration on Silicon, Grenoble, France, 6–7 March 2012; pp. 21–24. [Google Scholar]
- Xing, R.; Jian, S.S. Numerical analysis on the multilayer nanoring waveguide pair. IEEE Photonics Technol. Lett. 2016, 28, 2779–2782. [Google Scholar] [CrossRef]
- Wang, H.; Kurata, K.; Fukunaga, T. In-situ measurement of the heat transport in defect- engineered free-standing single-layer graphene. Sci. Rep. 2016, 6, 21823. [Google Scholar] [CrossRef] [PubMed]
- Mustapha, H.M.; Mohamed, M.A.; Hamzah, A.A. Design analysis of graphene membrane mechanics and vibration response. In Proceedings of the IEEE International Conference on Semiconductor Electronics, Kuala Lumpur, Malaysia, 17–19 August 2016; pp. 121–124. [Google Scholar]
- Yan, R.; Simpson, J.R.; Bertolazzi, S. Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent Raman spectroscopy. ACS Nano 2014, 8, 986–993. [Google Scholar] [CrossRef]
- He, Y.; Yu, W.; Ouyang, G. Interface adhesion properties of graphene membranes: Thickness and temperature effect. J. Phys. Chem. C 2015, 119, 5420–5425. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Fan, S. Measurement of the adhesion energy of pressurized graphene diaphragm using optical fiber Fabry-Perot interference. IEEE Sens. J. 2016, 16, 3664–3669. [Google Scholar] [CrossRef]
- Gupta, A.; Chen, G.; Joshi, P.; Tadigadapa, S. Raman scattering from high-frequency phonons in supported n-graphene layer films. Nano Lett. 2006, 6, 2667–2673. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Kitipornchai, S.; He, X.Q.; Liew, K.M. Continuum model for the vibration of multilayered graphene sheets. Phys. Rev. B 2005, 72, 75443. [Google Scholar] [CrossRef]
- Pereira, V.M.; Neto, A.H.C. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801. [Google Scholar] [CrossRef] [PubMed]
- Dolleman, R.J.; Lloyd, D.; Bunch, J.S. Transient thermal characterization of suspended monolayer MoS2. Phys. Rev. Mater. 2018, 2, 114008. [Google Scholar] [CrossRef]
- Kang, J.W.; Lee, J.H.; Hwang, H.J. Developing accelerometer based on graphene nanoribbon resonators. Phys. Lett. A 2012, 376, 3248–3255. [Google Scholar] [CrossRef]
- Lee, S.; Chen, C.; Deshpande, V.V. Electrically integrated SU-8 clamped graphene drum resonators for strain engineering. Appl. Phys. Lett. 2013, 102, 153101. [Google Scholar] [CrossRef]
- Shi, F.T.; Fan, S.C.; Li, C.; Peng, X.B. Modeling and analysis of a novel ultrasensitive differential resonant graphene micro-accelerometer with wide measurement range. Sensors 2018, 18, 2266. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.-T.; Fan, S.-C.; Li, C.; Li, Z.-A. Opto-thermally Excited Fabry-Perot Resonance Frequency Behaviors of Clamped Circular Graphene Membrane. Nanomaterials 2019, 9, 563. https://doi.org/10.3390/nano9040563
Shi F-T, Fan S-C, Li C, Li Z-A. Opto-thermally Excited Fabry-Perot Resonance Frequency Behaviors of Clamped Circular Graphene Membrane. Nanomaterials. 2019; 9(4):563. https://doi.org/10.3390/nano9040563
Chicago/Turabian StyleShi, Fu-Tao, Shang-Chun Fan, Cheng Li, and Zi-Ang Li. 2019. "Opto-thermally Excited Fabry-Perot Resonance Frequency Behaviors of Clamped Circular Graphene Membrane" Nanomaterials 9, no. 4: 563. https://doi.org/10.3390/nano9040563
APA StyleShi, F. -T., Fan, S. -C., Li, C., & Li, Z. -A. (2019). Opto-thermally Excited Fabry-Perot Resonance Frequency Behaviors of Clamped Circular Graphene Membrane. Nanomaterials, 9(4), 563. https://doi.org/10.3390/nano9040563






