Densely Distributed Multiple Resonance Modes in a Fan-Shaped Plasmonic Nanostructure Demonstrated by FEM Simulations
Abstract
1. Introduction
2. Structure Design
3. Results and Discussions
3.1. The Coupling Mechanism of the Multiple Resonance Modes
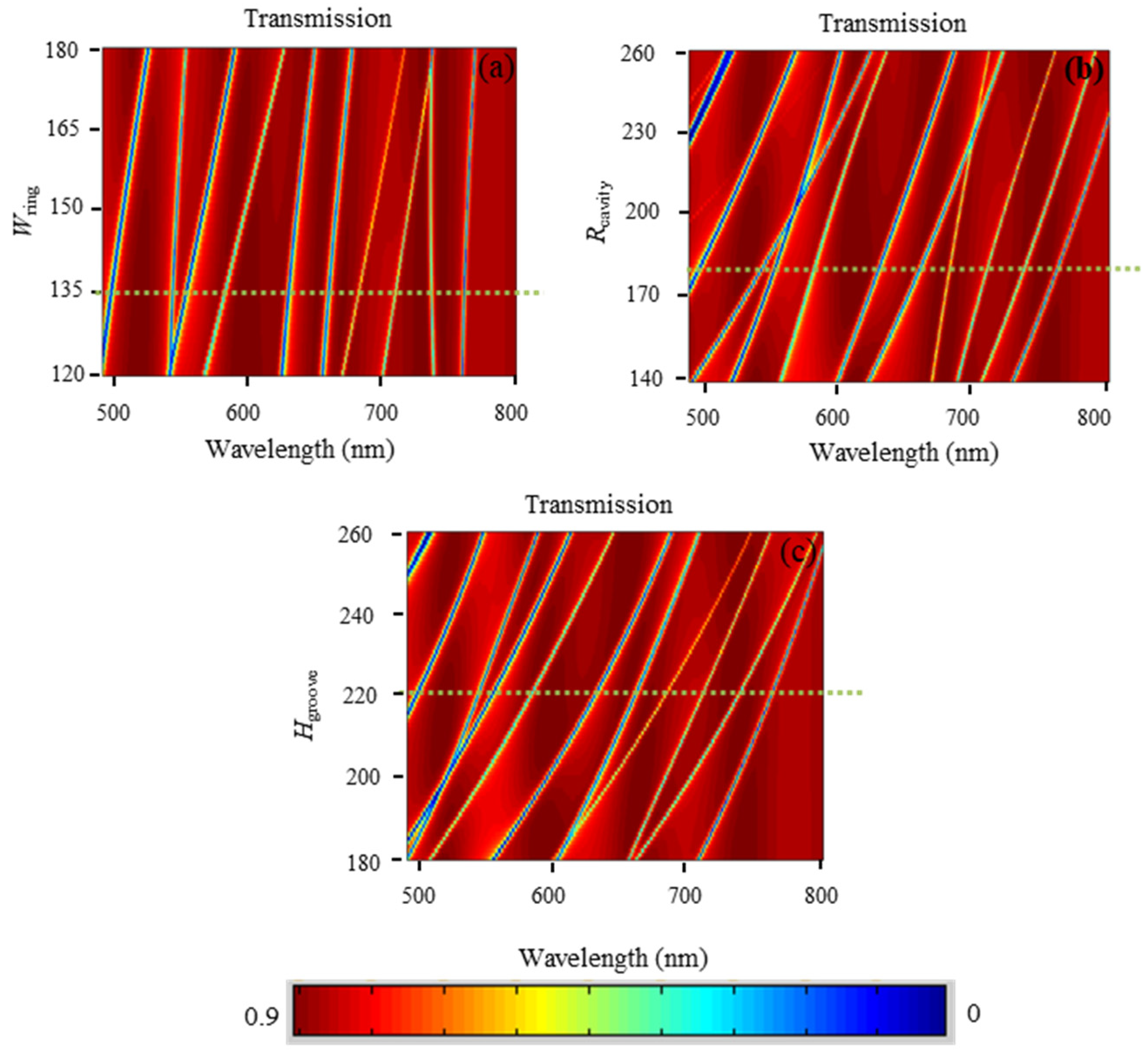
3.2. The Dependence of the Resonance Modes on Structure Parameters
3.3. The Tunability of Resonance Modes by Adjusting the Geometrical Asymmetry
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ambati, M.; Nam, S.H.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Observation of stimulated emission of surface plasmon polaritons. Nano Lett. 2008, 8, 3998–4001. [Google Scholar] [CrossRef] [PubMed]
- Biggins, J.S.; Yazdi, S.; Ringe, E. Magnesium nanoparticle plasmonics. Nano Lett. 2018, 18, 3752–3758. [Google Scholar] [CrossRef] [PubMed]
- Stelling, C.; Fossati, S.; Dostalek, J.; Retsch, M. Surface plasmon modes of nanomesh-on-mirror nanocavities prepared by nanosphere lithography. Nanoscale 2018, 10, 17983–17989. [Google Scholar] [CrossRef] [PubMed]
- Holmgaard, T.; Gosciniak, J.; Bozhevolnyi, S.I. Long-range dielectric-loaded surface plasmon-polariton waveguides. Opt. Express 2010, 18, 23009–23015. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhang, Y.J.; Zhang, Y.J.; Chen, L.; Liu, Y.; Yang, J.H. Ag nanotwin-assisted grain growth-induced by stress in SiO2/Ag/SiO2 nanocap arrays. Nanomaterials 2018, 8, 436. [Google Scholar] [CrossRef] [PubMed]
- Ignatyeva, D.O.; Kalish, A.N.; Achanta, V.G.; Song, Y.J.; Belotelov, V.I.; Zvezdin, A.K. Control of surface plasmon-polaritons in magnetoelectric heterostructures. J. Lightw. Technol. 2018, 36, 2660–2666. [Google Scholar] [CrossRef]
- Yang, S.Y.; Tang, C.C.; Liu, Z.; Wang, B.; Wang, C.; Li, J.J.; Wang, L.; Gu, C.Z. Simultaneous excitation of extremely high-Q factor trapped and octupolar modes in terahertz metamaterials. Opt. Express 2017, 25, 15938–15946. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.D.; Xiang, J.; Jiang, S.; Dai, Q.F.; Tie, S.L.; Lan, S. Radiation of the high-order plasmonic modes of large gold nanospheres excited by surface plasmon polaritons. Nanoscale 2018, 10, 9153–9163. [Google Scholar] [CrossRef]
- Ee, H.S.; No, Y.S.; Kim, J.Y.; Park, H.G.; Seo, M.K. Long-range surface plasmon polariton detection with a graphene photodetector. Opt. Lett. 2018, 43, 2889–2892. [Google Scholar] [CrossRef]
- Chen, K.; Razinskas, G.; Vieker, H.; Gross, H.; Wu, X.F.; Beyer, A.; Gölzhäuser, A.; Hecht, B. High-Q, low-mode-volume and multiresonant plasmonic nanoslit cavities fabricated by helium ion milling. Nanoscale 2018, 10, 17148–17155. [Google Scholar] [CrossRef]
- Lv, J.W.; Mu, H.W.; Lu, X.L.; Liu, Q.; Liu, C.; Sun, T.; Chu, P.K. Localized surface plasmon resonance properties of symmetry-broken Au-ITO-Ag multilayered nanoshells. Appl. Phys. A 2018, 124, 437. [Google Scholar] [CrossRef]
- Zhong, R.B.; Yu, C.P.; Hu, M.; Liu, S.G. Surface plasmon polaritons light radiation source with asymmetrical structure. AIP Adv. 2018, 8, 015327. [Google Scholar] [CrossRef]
- Darweesh, A.A.; Bauman, S.J.; Debu, D.T.; Herzog, J.B. The role of rayleigh-wood anomalies and surface plasmons in optical enhancement for nano-gratings. Nanomaterials 2018, 8, 809. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.X.; Xie, Y.Y.; Ye, Y.C.; Fu, L.X.; Li, L.L.; Su, Y.; Xiao, Y.; Liu, Y. A novel manipulation for implementing logic operations based on plasmonic resonators. IEEE Photonics J. 2019, 11, 2700110. [Google Scholar] [CrossRef]
- Muhammad, N.; Khan, A.D.; Deng, Z.L.; Khan, K.; Yadav, A.; Liu, Q.; Ouyang, Z.B. Plasmonic Spectral Splitting in Ring/Rod Metasurface. Nanomaterials 2017, 7, 397. [Google Scholar] [CrossRef] [PubMed]
- Berini, P.; Leon, I.D. Surface plasmon-polariton amplifiers and lasers. Nat. Photonics 2012, 6, 16–24. [Google Scholar] [CrossRef]
- Zand, I.; Mahigir, A.; Pakizeh, T.; Abrishamian, M.S. Selective-mode optical nanofilters based on plasmonic complementary split-ring resonators. Opt. Express 2012, 20, 7516–7525. [Google Scholar] [CrossRef]
- Wang, J.M.; Wei, W.; Yan, X.; Zhang, J.N.; Zhang, X.; Ren, X.M. Near-infrared hybrid plasmonic multiple quantum well nanowire lasers. Opt. Express 2017, 25, 9358–9366. [Google Scholar] [CrossRef]
- Qin, L.L.; Wu, S.L.; Deng, J.H.; Li, L.J.; Li, X.F. Tunable light absorbance by exciting the plasmonic gap mode for refractive index sensing. Opt. Lett. 2018, 43, 1427–1430. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Lin, J.Y.; Wong, S.W.; Deng, F.; Zhu, L.; Yang, Y.; He, Y.J.; Tu, Z.H. Spoof surface plasmon polaritons power divider with large isolation. Sci. Rep. 2018, 8, 5947. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Liu, L.; Lu, H.Y.; Zhan, P.; Du, W.; Wan, M.J.; Wang, Z.L. Ultra-broadband tunable resonant light trapping in a two-dimensional randomly microstructured plasmonic-photonic absorber. Sci. Rep. 2017, 7, 43803. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Li, G.Y.; Li, K.; Wang, Z.H.; Xu, A.S. A compact wavelength demultiplexing structure based on arrayed MIM plasmonic nano-disk cavities. Opt. Commun. 2012, 285, 5519–5523. [Google Scholar] [CrossRef]
- Khan, A.D. Refractive index sensing with fano resonant L-shaped metasurface. Opt. Mater. 2018, 82, 168–174. [Google Scholar] [CrossRef]
- Chen, J.J.; Wang, C.; Zhang, R.; Xiao, J.H. Multiple plasmon-induced transparencies in coupled-resonator systems. Opt. Lett. 2012, 37, 5133–5135. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, X.M.; Gong, Y.K.; Mao, D.; Wang, G.X. Analysis of nanoplasmonic wavelength demultiplexing based on metal-insulator-metal waveguides. J. Opt. Soc. Am. B 2011, 28, 1616–1621. [Google Scholar] [CrossRef]
- Hu, F.F.; Zhou, Z.P. Wavelength filtering and demultiplexing structure based on aperture-coupled plasmonic slot cavities. J. Opt. Soc. Am. B 2011, 28, 2518–2523. [Google Scholar] [CrossRef]
- Liu, D.D.; Sun, Y.; Fan, Q.B.; Mei, M.F.; Wang, J.C.; Pan, Y.W.; Lu, J. Tunable plasmonically induced transparency with asymmetric multi-rectangle resonators. Plasmonics 2016, 11, 1621–1628. [Google Scholar] [CrossRef]
- Hu, F.F.; Yi, H.X.; Zhou, Z.P. Wavelength demultiplexing structure based on arrayed plasmonic slot cavities. Opt. Lett. 2011, 36, 1500–1502. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Wang, R.B.; Zhang, Z.Y.; Tang, J.; Zhang, W.D.; Xue, C.Y.; Yan, S.B. Electromagnetically induced transparency and refractive index sensing for a plasmonic waveguide with a stub coupled ring resonator. Plasmonics 2017, 12, 1007–1013. [Google Scholar] [CrossRef]
- Chen, Z.; Song, X.K.; Duan, G.Y.; Wang, L.L.; Yu, L. Multiple Fano resonances control in MIM side-coupled cavities systems. IEEE Photonics J. 2015, 7, 2701009. [Google Scholar] [CrossRef]
- Zhang, B.H.; Wang, L.L.; Li, H.J.; Zhai, X.; Xia, S.X. Two kinds of double Fano resonances induced by an asymmetric MIM waveguide structure. J. Opt. 2016, 18, 065001. [Google Scholar] [CrossRef]
- Yang, H.U.; Archangel, J.D.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B 2015, 91, 235137. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B 2012, 86, 235147. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.G.; Lin, X.S.; Tao, J.; Jin, X.P. A subwavelength coupler-type MIM optical filter. Opt. Express 2009, 17, 7549–7554. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Ouyang, Z.; Liu, Q.; Lin, M. Densely Distributed Multiple Resonance Modes in a Fan-Shaped Plasmonic Nanostructure Demonstrated by FEM Simulations. Nanomaterials 2019, 9, 975. https://doi.org/10.3390/nano9070975
Wang Q, Ouyang Z, Liu Q, Lin M. Densely Distributed Multiple Resonance Modes in a Fan-Shaped Plasmonic Nanostructure Demonstrated by FEM Simulations. Nanomaterials. 2019; 9(7):975. https://doi.org/10.3390/nano9070975
Chicago/Turabian StyleWang, Qiong, Zhengbiao Ouyang, Qiang Liu, and Mi Lin. 2019. "Densely Distributed Multiple Resonance Modes in a Fan-Shaped Plasmonic Nanostructure Demonstrated by FEM Simulations" Nanomaterials 9, no. 7: 975. https://doi.org/10.3390/nano9070975
APA StyleWang, Q., Ouyang, Z., Liu, Q., & Lin, M. (2019). Densely Distributed Multiple Resonance Modes in a Fan-Shaped Plasmonic Nanostructure Demonstrated by FEM Simulations. Nanomaterials, 9(7), 975. https://doi.org/10.3390/nano9070975





