1. Introduction
In recent decades, in the field of telecommunications, there has been an increased interest in the use of vortex beams—electromagnetic waves with orbital angular momentum (OAM)—a special type of wavefront with helicoidal dislocation, characterized by “donut” shape of intensity pattern and phase singularity in the center of the field distribution. This interest is due to the fact that various quantized states of the projection of the orbital angular momentum on the direction of propagation can be used both for coding signals and for multiplexing of communication channels. Thus, vortex beams open up additional opportunities both for increasing the information transfer rate (capacity) and for increasing the noise immunity and security of communication channels since the OAM order of wave can be decoded only by coaxial receiving (line of sight). Among the main directions in the development of infocommunication technologies are radiophotonics–hybrid systems that combine the processes of signals processing, transfer, and conversion in both radio and optical ranges. At present, in radiophotonics, the microwave range is being investigated, including the terahertz frequency range of 0.1−50 THz as the most promising from the point of view of low congestion of the electromagnetic spectrum. Moreover, such a range promises higher data transfer rates as well.
A promising direction of radiophotonics in the field of telecommunications is the development of Radio-over-fiber (RoF) systems [
1], which use the transmission of microwave radio signals over optical fiber without need of GHz local oscillator (LO) at the remote antenna unit (RAU), which makes it possible to directly convert modulated optical signal into radio domain (after amplification and filtering) and transmit it in air channel. In the context of the development of RoF systems, the problem arises of converting signals that carry orbital angular momentum in the optical domain into signals that carry OAM in the radio range. In this paper, we consider the process of converting vortex beams of the optical range in the wavelength range λ ≈ 1.5 μm (C-band) into vortex beams of the radio band in the range of frequencies exceeding 100 GHz.
Nonlinear media with nonzero polarizability (dielectric susceptibility) of the second-order are widely used for converting electromagnetic waves from the optical domain into radio band in the terahertz range based on the difference frequency generation (DFG), second harmonic generation (SHG), etc. In this case, the nonlinear medium, which is the source of generation, is modified by additional inclusions (is doped) or structurally changed in order to increase the conversion efficiency. Thus, in [
2], a lattice of photonic crystals is used do achieve effective DFG. In article [
3], lasing occurs in a strip metal waveguide with the inclusion of GaAs impurities. In [
4], a rectangular metal waveguide is used, filled with periodically alternating layers of LiTaO
3 with the opposite orientation of the optical axes. Authors of [
5] demonstrated the difference frequency generation in a 2D plasmon waveguide consisting of a LiNbO
3 layer and located between two flat nonmetallic layers. In [
6], the generation of a difference frequency by Gaussian beams is described, and the results of experimental generation of a difference frequency in a LiNbO
3 crystal containing planar waveguides are presented.
With regards to research on the transformation of vortex beams in nonlinear media with second-order polarizability, the following papers can be noted. It was shown in [
7] that when the second harmonic is generated, the topological charge of the vortex beam
l doubles, where
l is an integer quantum number and determines the projection of the orbital angular momentum on the direction of propagation, due to the dependence of the electromagnetic field of the vortex beam on the azimuthal angle φ in the form of e
ilφ.
In [
8], a hypothesis is expressed and an indirect theoretical substantiation and numerical simulation results are presented, confirming the fact that the topological charge of the output vortex beam is equal to the sum of the charges of the input vortex beams when generating the sum harmonic (frequency). In [
9], the laws of conservation of the topological charge during the generation of the second harmonic, including the state with a fractional topological charge
l, are studied theoretically and experimentally. The works [
10,
11] experimentally confirm the law of conservation of the topological charge during the generation of the second harmonic [
10] of the sum harmonic [
11], where the theoretical substantiation of the results obtained is also given. In [
12], it was experimentally established that in a multilayer nonlinear medium with periodically alternating layers of LiTaO
3 with oppositely directed optical axes to ensure spatial phase matching during the generation of the sum harmonic, topological charges are summed. In [
13] a two-dimensional periodically poled LiTaO
3 nonlinear photonic crystal is used to generate conical third harmonic; phase matching is achieved by crystal poling. Moreover, it was shown [
14] that the filamentation of femtosecond pulses (used to ensure phase matching condition) allows the formation of a vortex mode due to the third-harmonic generation (THG) process in Ti: sapphire chirped pulse amplifier. Note that in this work, the law of conservation of the topological charge of vortex beams was justified theoretically; it was experimentally confirmed in [
15] in the framework of the THG process in PPLT in the optical range: the processes of frequency doubling and generation of the sum harmonic are considered. It is also shown in the article that the conversion efficiency decreases with an increase of the OAM order. The authors of [
16] experimentally demonstrate the formation of multiple copies of the SH beams carrying the doubled OAMs using a two-dimensional PPLT crystal: the doubling of the topological charge during the second harmonic generation (SHG) in the vicinity of a wavelength of 920 nm is proved. Article [
17] experimentally shows the possibility of generating the second harmonic by plasmons, and the topological charge doubles as the frequency is doubled. PPLN crystals are also used to generate infrared radiation with a wavelength of the order of several microns [
18]. In addition to PPLN/PPLT crystals, KTP crystals can also be used for SHG of Laguerre–Gauss modes [
19]. In [
20], a hybrid lithium niobate/silicon waveguide scheme with a high generation efficiency of the order of 3.5 × 10
−4 W
−1 at 3 THz is used to achieve a terahertz signal by generating a difference frequency. In addition to classical PPLNs, aperiodic PPLNs (APPLNs) are also investigated: in [
21], a similar crystal is used for cascade DFG (CDFG), which results in terahertz radiation; the conversion efficiency of this approach is almost 3 times higher, but it is achieved at a low temperature—about 10 K. In [
22], the optical pump wave and the incident wave propagate in a lithium niobate crystal not co-directionally, but towards each other, which, according to the authors, allows optical feedback without resonance cavity and helps to generate narrow-band THz radiation. A terahertz signal can also be generated using a 2D InxGa1-xSe crystal [
23] using DFG with a conversion efficiency of the order of 10
−5.
Authors of [
24] use computational experiments and theoretical description and models to show the influence of the length of a nonlinear medium on the process of parametric amplification of light in the process of Laguerre–Gaussian modes coupling, the law of conservation of topological charge is established, and the influence of the radial indices of Laguerre–Gaussian modes on the process of parametric amplification is also investigated. In [
25], a theoretical model for nonlinear transformations of LG modes is developed: an exact solution for the single-pass no-cavity regime was obtained and simulation modeling was carried out. The authors of [
26] obtained an analytical solution for terahertz waves in planar waveguides based on the coupled mode theory based on the DFG process.
Non-linear media can also be used in quantum applications. For example, to generate pairs of entangled photons carrying OAM. Thus, in [
27], such photons are formed due to the spontaneous parametric down-conversion process in nonlinear 3-mm-long β-barium borate (BBO) crystal. It is shown that entangled photons conserve the orbital angular momentum in similar schemes used to test Bell’s theorem. The authors of [
28] use spontaneous four-wave mixing (SFWM) to create correlated photon pairs carrying OAM. These pairs can significantly increase the information capacity of quantum systems due to the additional physical degree of freedom; within the framework of [
2], similar photonic systems were used to develop quantum memory based on cold Rb ensembles.
There are a lot of papers regarding the generation of terahertz vortices. For example, the authors of [
29,
30] form an OAM signal in the THz range based on DFG (pump wavelengths λ
1 = 1.56 μm and λ
2 = 1.50~1.64 μm) using a 4′-dimethylamino- N-methyl-4-stilbazolium tosylate (DAST) crystal with fairly high efficiency (according to the authors, more than 90%); however, only continuous wave systems are considered. In [
31], terahertz vortex pulses of the order of 2 and −2 are also formed by DFG in ZnTe crystal with a pump wavelength of about 800 nm. The conversion efficiency for THz signal generation using DFG can be increased by using nanophotonic lithium niobate chips or nanophotonic waveguides, as shown in [
32,
33], respectively. In addition to crystals, there are some interesting methods for generating THz vortexes using undulators [
34]. It should be noted that the propagation of terahertz vortexes in the air [
35] and optical fibers [
36] is also currently being studied.
Finally, we can mention some alternative solutions for the THz generation. The terahertz signal in [
37] is formed by fast tuning of the DFB laser optical frequency using a fiber optical interferometer. In [
38], a terahertz signal with a power of the milliwatt order is nonlinearly generated using an optimized mid-infrared quantum cascade laser. The authors of [
39] used intra-cavity mixing of two lasers—DFB and Fabry–Perot—operating in the infrared range to generate a frequency comb in the terahertz band with an input power of the order of several microwatts. In conclusion, we note that the conversion of OAM signals can also be implemented in a linear regime. For example, in [
40], a theoretical model of the linear transformation of infrared vortexes into the visible region was developed, and experimental confirmation of this process was carried out.
Analysis of works in the field of converting optical radiation into the radio range based on the use of nonlinear media with a second-order susceptibility shows that the theoretical substantiation and modeling of the ongoing generation processes is based on a system of three equations describing the processes within the slowly varying envelope approximation [
41], regardless of the structural organization of a nonlinear environment.
Despite the “genetic” relationship of various three-wave mixing processes—generation of the second harmonic, sum frequency, parametric amplification, generation of a difference frequency—each of these processes has its own characteristics, in particular, a distinctive feature of the process of generating a difference frequency in the radio range is a very low energy conversion efficiency caused by two factors: (1) the smallness of the ratio of the nonlinear part of the polarization to the linear one, which is typical for all three-wave processes, excluding the region of extremely high values of the electric field strength of the initial harmonics; (2) due to the dipole mechanism of wave emission in the crystal, the power of the dipole radiation is proportional to the square of the frequency, therefore, in the investigated frequency range, the ratio of the radiation powers in both radio and optical ranges is a small quantity proportional to the square of the ratio of the corresponding frequencies and in the context of this work amounts to ~10−5−10−6 since the frequency of optical signal is about 200 THz and the radio signal is only 0.1 THz.
Note that topological charge of optical vortices (or laser beams with singular phase and/or polarization) is a more interesting and less studied characteristic than the OAM. On propagation, the charge of a vortex can only be integer (it can be fractional only in the source plane), while the OAM can be both integer and fractional. Therefore, under distortions, including random ones, the topological charge changes discretely, when the distortions reach a certain magnitude, whereas the OAM changes continuously with an arbitrarily small distortion or a simple shift of the center of the optical vortex [
42]. The purpose of this work was to study the process of converting radiation from the optical range to the radio domain under the conditions specified previous paragraph.
2. Transformation of Vortex Compositions in Linear Media
In homogeneous linear media, electromagnetic waves are described by a system of inhomogeneous wave equations that are in fact a direct consequence of Maxwell’s equations:
where
c is the speed of light,
n is the refractive index,
is the vector potential, φ is the scalar potential,
is the current density, ρ is the density of free charges, and
is the Laplace operator (in CGS system of units).
The emission of monochromatic waves with frequency ω is determined by the Helmholtz equations following from the system of Equation (1).
where
is the wave number and
are the Fourier transforms of the corresponding fields.
From a mathematical point of view, the system of Equation (2) is structurally equivalent to the inhomogeneous equation
where
is a certain radiated field (or one of the components in the case of a vector field), and
is a volumetric source of radiation.
In the most general approach, the problem of wave propagation in a linear medium can be formulated as a problem in which radiation is generated not only by a volumetric source
, but also by some surface source ψ. Thus, the task is to find a solution of Equation (3) in a half-space
of three-dimensional space (
x,
y,
z) if a certain initial field distribution
is given on the boundary plane
.
It is known that electromagnetic fields carrying angular momentum (vortex beams, vortexes) [
43] are spatial structures with a coordinate dependence in the Cartesian system given by
or in a cylindrical coordinate system
where
m is the topological charge of the vortex, the physical meaning of which is that
m is proportional to the projection of the angular momentum on the direction of wave propagation (in this case–
z axis), and functions (5) or (6) are eigenfunctions of the
z-component of the angular momentum operator and
i is imaginary one.
Let us show that a necessary condition for radiation carrying angular momentum in the case of continuous sources is the vortex structure of both volumetric and surface sources, which is preserved during propagation in space.
Now, we consider Equation (3) in the paraxial approximation. In this case, instead of Equation (3), we will have the inhomogeneous parabolic equation
where
is the transverse component of the Laplace operator. The solution to the radiation Equations (4) and (7) is represented by the integral relation:
where the Green’s function
G(
x,
y,
z) has the Cartesian form
Now, let us go over to a cylindrical coordinate system
and assume that both volumetric and surface sources have a vortex structure. In this case, the corresponding functions—sources of vortexes—are defined by the following expressions:
The radiated field, in accordance with expression (8), has the form
where the cylindrical Green’s function
G is defined as
In representation (12), it is easy to perform integration over angle
if we use the integral representation of the Bessel function
which is relevant for an arbitrary angle
. As a result, the radiation field defined by expression (11) can be represented in the following form
where the functions
and
are given by the relations:
Expressions (14)−(16) give a solution to the problem of propagation of radiation carrying an angular momentum upon excitation of a wave by surface and volumetric sources. Solution (14), due to the linearity of the original equations, is generalized to the case when the radiation sources are represented by vortex superpositions:
In this case, instead of (14), we obtain
where
are determined in accordance with expressions (15) and (16). Note that in expressions (17) and (18) ξ and
k are just indexes of summation.
Thus, topological charges in the case of vortex emission by surface and volumetric sources are conserved during propagation in the linear regime.
3. Three-Wave Mixing in a Nonlinear Medium
The propagation of electromagnetic waves in nonlinear media is determined by the polarization vector
, which in symbolic scalar form can be represented as an expansion in powers of the electric field strength.
where
is the linear polarizability,
is the quadratic polarizability, and
is the cubic Kerr polarizability.
Let us consider the process of three-wave mixing, in which the quadratic term plays a decisive role. In this case, describing an isotropic medium, the nonlinear part of the polarization vector can be represented as
Hence, propagation of electromagnetic waves in a nonlinear medium will be described by the following equation:
where
is the vector of the electric field strength,
c is the speed of light in vacuum, ε is the dielectric constant of the medium,
is the vector of nonlinear polarization.
For narrowband signals with a carrier frequency ω used in telecommunication systems (i.e., when Δω << ω, where Δω is the spectrum width), the commonly used approach to solve Equation (21) is to use the method of SVEA, according to which the electric field is represented in the form
where
,
is the
z-coordinate function slowly varying on the wavelength scale, satisfying the condition:
In the case when two waves with frequencies ω
1 and ω
2 propagate in a nonlinear medium with quadratic polarization, so that
In this case, the quadratic polarization is represented as
Polarization (25), due to the dipole radiation mechanism, leads to the following processes in the medium that occur at different frequencies:
—optical rectification;
or
—frequency doubling;
—generation of the sum frequency;
—generation of the difference frequency. From the point of view of radio photonics, the process of the difference frequency generation leads to the generation of radio waves as a result of mixing the initial waves of the optical range. Generation of the difference frequency when searching for a solution to Equation (21) in the form (22) leads to a system of equations:
where
are the envelopes corresponding to signals with frequencies
and wave numbers
,
is the transverse component of the Laplace operator.
Let us estimate the influence of nonlinear effects on changes in electromagnetic fields during propagation along a nonlinear medium of length
in the case when the process is initiated by laser radiation of power
with beams of radius
.
where
,
is the wave impedance of vacuum,
is the universal magnetic constant,
is the universal electric constant.
Now, we introduce the following dimensionless quantities:
For an approximate physical estimate of the change in electric fields from system (26), we obtain
In Equation (29), γ is a dimensionless parameter characterizing nonlinearity:
Expression (29) is justified for small values
, which in this context are on the order of several centimeters. Taking into account that
, the system of Equation (29) yields estimates for the relative change in optical fields
ξ = 1, 2:
In the conditions typical for telecommunication applications, the initial physical quantities have the following values: ~1 Watt, ~1 mm, ~1−10 cm, ~1.5 μm.
The nonlinearity parameter is a very small value:
, and the changes in optical fields in the entire terahertz range of 0.1−10 THz are, in accordance with estimation (32), the following values (in order of magnitude):
In this case, the change in the optical fields can be neglected, and the system of nonlinear Equation (26), which describes the process of generation of the difference frequency, is reduced to a linear equation of the type (7):
with the volumetric radiation source
if we reckon that the phase matching condition
is satisfied. In expression (34), the fields
and
correspond to fields propagating in a linear medium.
The solution of Equation (34) can be found according to expression (8) in which there is no surface source:
and where the Green’s function is determined by expression (9) in which it should be assumed
.
When the three-wave mixing process is initiated by laser radiation, the optical fields are represented by a set of Laguerre–Gauss (LG) beams:
The complex amplitude of laser beams can have different shapes [
44,
45,
46,
47], in particular, the set of Laguerre–Gauss beams can be described by the following distribution:
where
is the radius of curvature of the parabolic front of the beam,
is the radius of the beam, σ
0 is the radius of the beam waist,
is the Rayleigh confocal parameter, and
is the associated Laguerre polynomial.
Since the influence of the radial order of the set of Gauss–Laguerre beams n is not considered in this work, the class of LG field distributions can be narrowed down by setting n = 0.
Passing in the integral representation (35) to the limit
z0 and taking into account that the relation holds
where
and
are the Dirac delta functions, we obtain an approximate solution
where
and
are the power of optical radiation at frequencies
and
.
To derive the expression (39), the first nonzero term was taken into account in the expansion of field (34) in powers of the coordinate z in a Taylor series.
In the case of generating a vortex with a topological charge when for the power of the radio signal, from (38) one can obtain the ratio:
4. Modeling of Nonlinear Processes by a Modified Method of Slowly Varying Envelope Approximation
In [
48], a modified method of slowly varying envelope approximation was developed based on the factorization of a slowly varying amplitude into two factors, one of which is forced to obey the parabolic equation, and the second one depends only on the coordinate in the propagation direction and obeys a differential equation, which makes it possible to improve accuracy when describing the three-wave mixing process. In this method, in contrast to the search for a solution to Equation (21) in the form (22), the envelope
is represented in a more detailed multiplicative form, so that
where
is a solution to the parabolic equation:
If the electric field represents a certain superposition of waves with frequencies
, wavenumbers
, and directions of polarization
, then the electric field strength and polarization can be represented in the form
Then, from Equation (21), it follows that:
As a result of the scalar representation, the electric field in the medium can be written as a sum of three waves describing the propagation of vortex beams with projections of angular momentum
m1,
m2, and
m3 at frequencies ω
1, ω
2, and ω
3:
where
ε
1, ε
2, and ε
3 are the values of dielectric constants at frequencies ω
1, ω
2, and ω
3, respectively; Φ
ξ are the distributions of the set (36) corresponding to the azimuthal indices
mξ.
Now, we can write scalar nonlinear polarization in the form:
which corresponds to Equation (44) in the scalar representation for vortex fields. For a nonlinear medium, represented in the form (20), we get:
In expression (48), when squaring, we consider only the terms corresponding to the process of generating the difference frequency. Thus, in expression (48), one should consider:
Comparing expressions (47) and (48), we find:
Using Equation (45) for each of the propagating waves, we can get the system of equations:
where
Analyzing the system of Equation (51), we see that the left-hand sides of each equation do not depend on the angle φ, thus, solutions to system (51) exist when the condition is satisfied. Consequently, in a quadratic nonlinear medium, from the initial vortex beams carrying angular moments with azimuthal indices m1 and m2 at frequencies ω1 and ω2, a vortex beam of difference frequency is generated, which transfers angular momentum with a projection on the direction of propagation equal to the difference of projections
Following the method outlined in [
5], we multiply each of the
v-th equation of system (50) by a complex conjugate factor
and integrate the equations over the cross section of the corresponding beams. Finally, to determine the amplitudes
Av, we obtain the system:
where the following notation is introduced:
In expressions (53), the functions
and
are determined by the relations:
The analysis of the influence of nonlinear effects given in
Section 2 allows us to assert that under conditions typical for telecommunication applications, the system of nonlinear Equation (52) is reduced to the third equation, in which
.
As a result, the solution is determined by the integral
5. Simulation of the Propagation of Optical Vortexes
Simulation of the propagation processes of vortexes in the optical range and their transformation into vortexes in the terahertz radio range was carried out using the numerical solution of the system of Equation (52) and on the basis of the integral representation (56) [
49]. The Runge–Kutta method in the Matlab package of mathematical modeling is used to solve system (52). It should be noted that the simulation results based on the system of Equation (52) and integral representation (55) under the conditions defined in
Section 2 are practically identical, the order of differences is
.
The difference frequency generation process was investigated in the radio frequency range 100 GHz−700 GHz. The optical radiation corresponded to the C-band wavelengths. The pump laser power was P1 = P2 = 1 W. The effective nonlinear susceptibility of the nonlinear medium in which the conversion process takes place is , the refractive indices at optical frequencies are n1 = n2 = 2.2, at radio frequencies n3 = 2.5.
To generate radio vortex beams with a topological charge
m3 = 1, Gauss–Laguerre laser modes with radial indices
n1 =
n2 = 0 and azimuthal indices
m1 = 1,
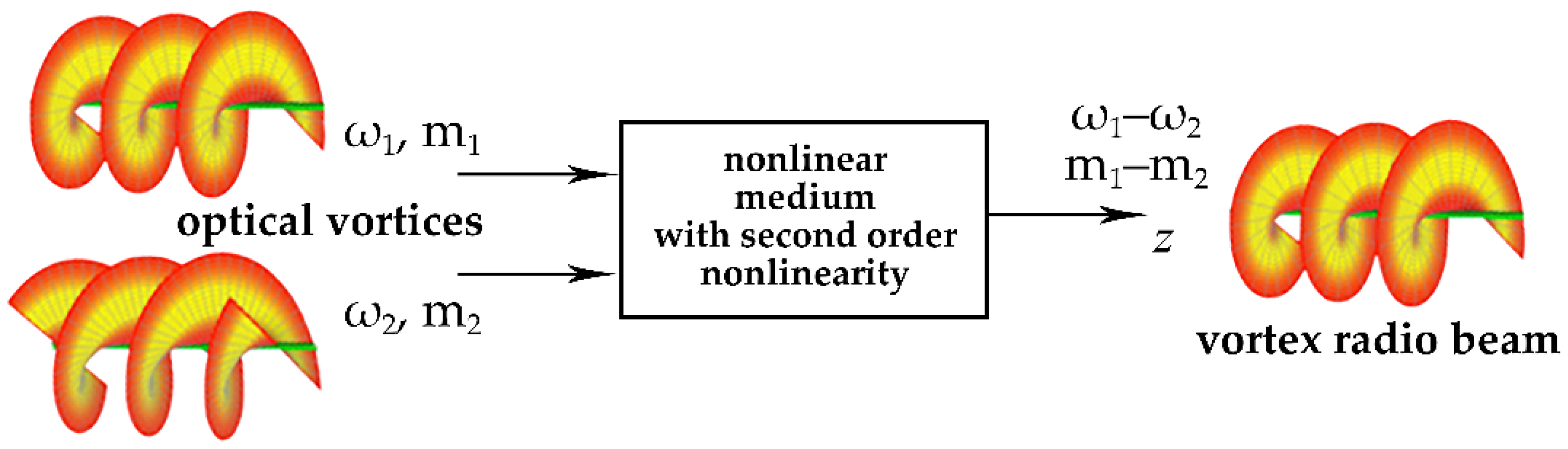
m2 = 0 were used. The simulated system is shown in
Figure 1 [
49].
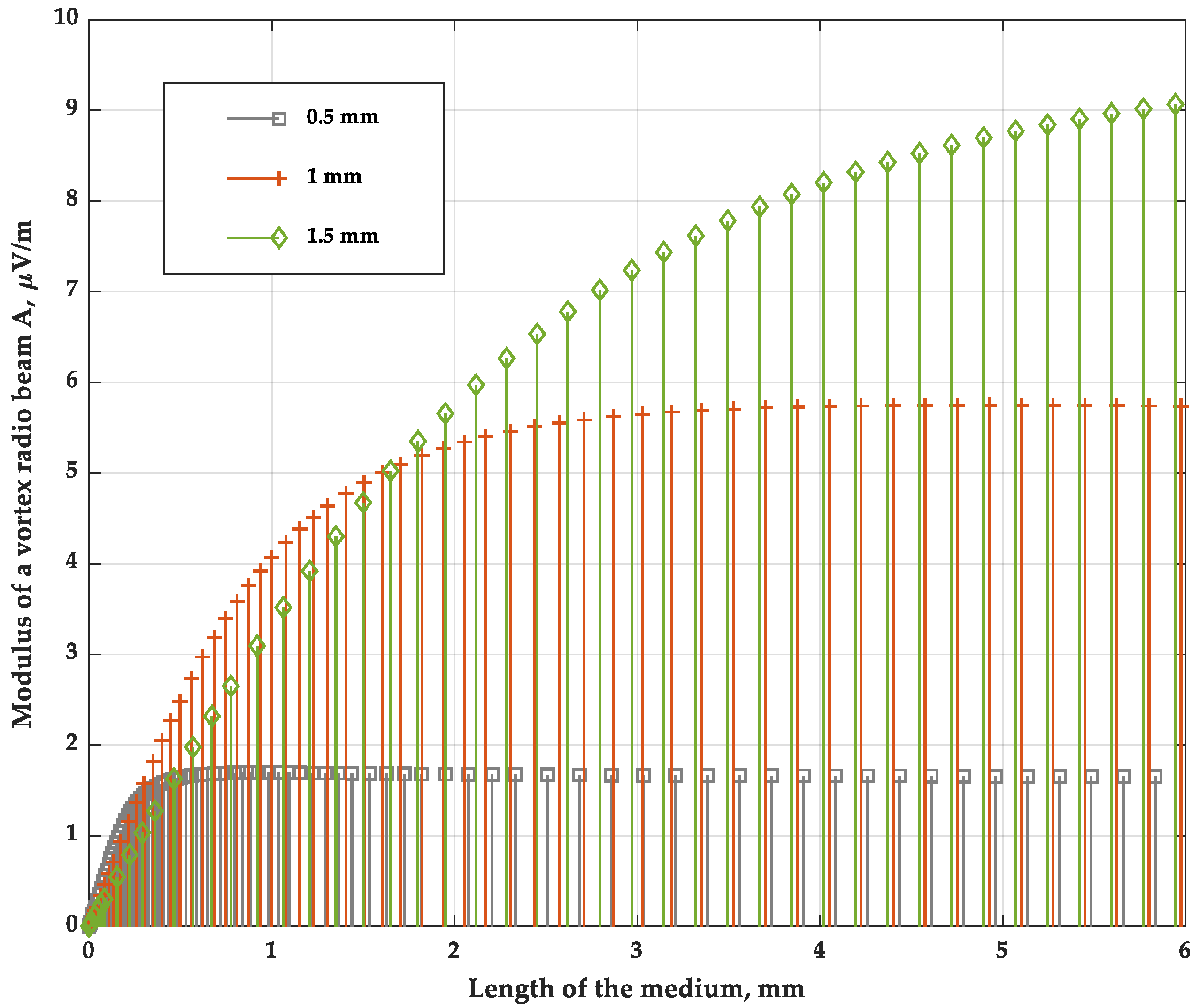
From the point of view of technical applications of the results, it should be interesting to study the nature of the change in the modulus of the amplitude of the obtained radio-vortex beam, obeying relation (21), with a change in the length of the nonlinear crystal, which is shown in
Figure 2. Calculations were carried out for a radio vortex beam with a topological charge
m3 = 1 depending on the length of the nonlinear medium for different values of the waist radii of the pump laser beams. It follows from the data obtained that at small lengths of the nonlinear medium, a linear dependence of the amplitude on the length is observed, which is consistent with expression (32). With an increase in the length of the nonlinear crystal, the amplitudes of the vortex radio beams reach the corresponding asymptotic values [
49,
50].
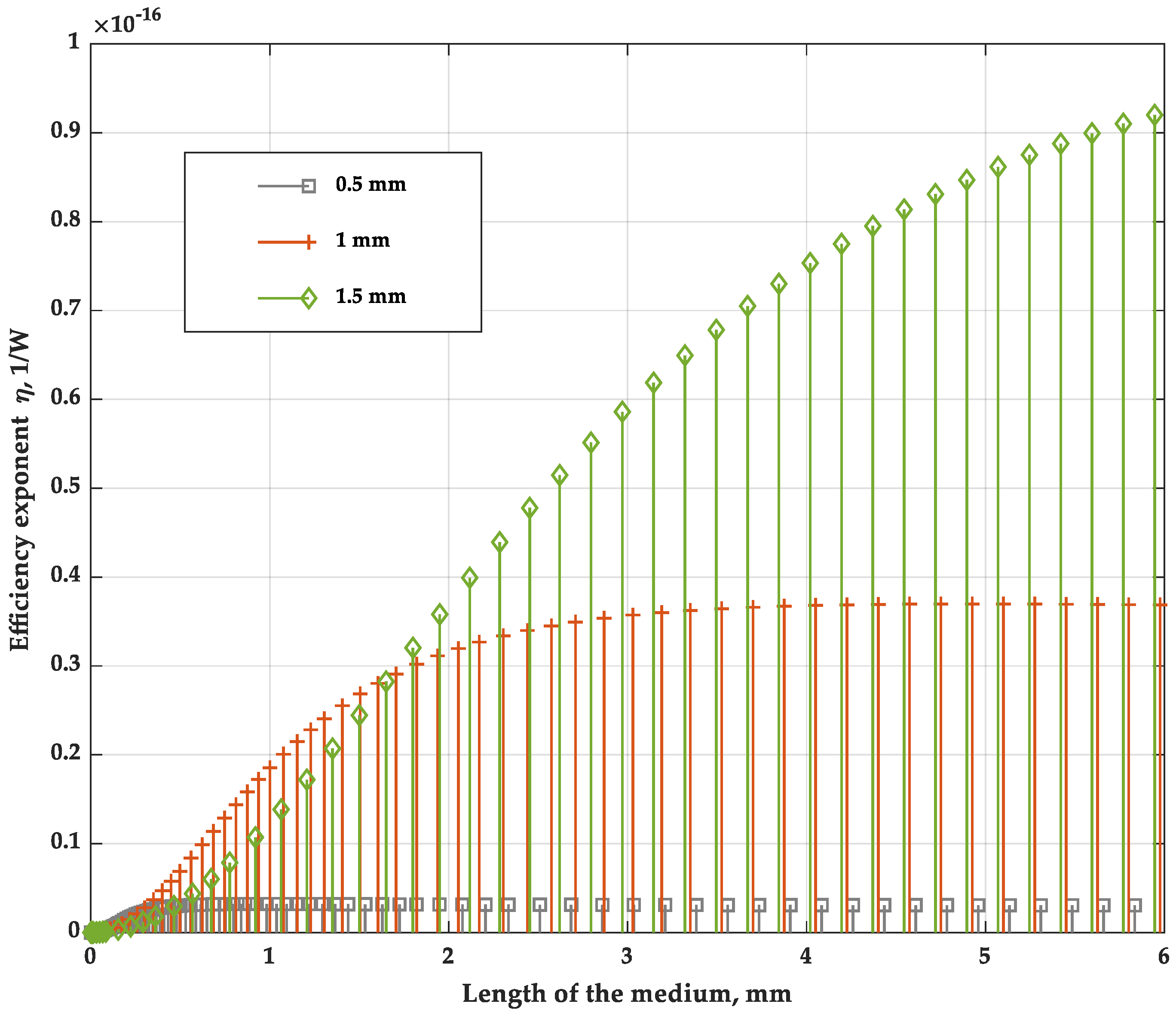
Figure 3 shows the dependence of the efficiency index η of the vortex radio beam generation on the length of the crystal [
49]. The efficiency index, in accordance with the work [
6], is determined by the ratio having the unit of 1/W:
where
P1 and
P2 are the powers of the optical pumping lasers, and
P3 is the power of the vortex radio beam. The choice of this ratio to efficiency estimation is due to the fact that these values are independent of the power of the original optical beams. Expression (40) confirms this fact, as well as the quadratic dependence on the length of the nonlinear medium in the region of small values.
Calculations show that the dependences of the amplitude A3 of the difference frequency and the efficiency index η on the crystal length for different values of the waist radius have a similar asymptotic character.
Figure 4 shows the dependence of the efficiency index of generation of a radio vortex beam on the frequency difference between the pump lasers. With an increase in the frequency difference, the value of η noticeably increases, which is due to the dipole radiation mechanism, as noted above [
49].
Figure 5 shows the dependence of the efficiency index on the waist radius of the laser beams. This dependence has an extreme nature, i.e., for a given pump power, there is a value of the beam waist radius at which the maximum radiation conversion efficiency is observed. This dependence is caused by the extreme dependence of the intensity of Gaussian beams on the waist radius, which at a given radiation power
P can be represented as:
Thus, it is shown that with an increase in the length of the nonlinear medium, an asymptotic behavior of the efficiency index of the considered conversion is observed, which makes it possible to determine the geometric dimensions of the converting device. With an increase in the frequency difference, the generation efficiency increases. The performed calculations allow one to select the technical parameters of the converter depending on the system under consideration. The observed dependences are in qualitative agreement with the work [
6].
The results obtained in this research can be used to construct promising high-speed hybrid RoF transmission systems [
19], mainly in the submillimeter and microwave ranges, using the orbital angular momentum as an additional parameter for encoding and multiplexing multimedia data. The DFG process described in this paper will make it possible to avoid complex systems for converting vortex optical beams into radio beams while maintaining the vortex wavefront of an electromagnetic wave.