Wavelength Sensing Based on Whispering Gallery Mode Mapping
Abstract
:1. Introduction
2. Materials and Methods
2.1. PMMA Microspheres
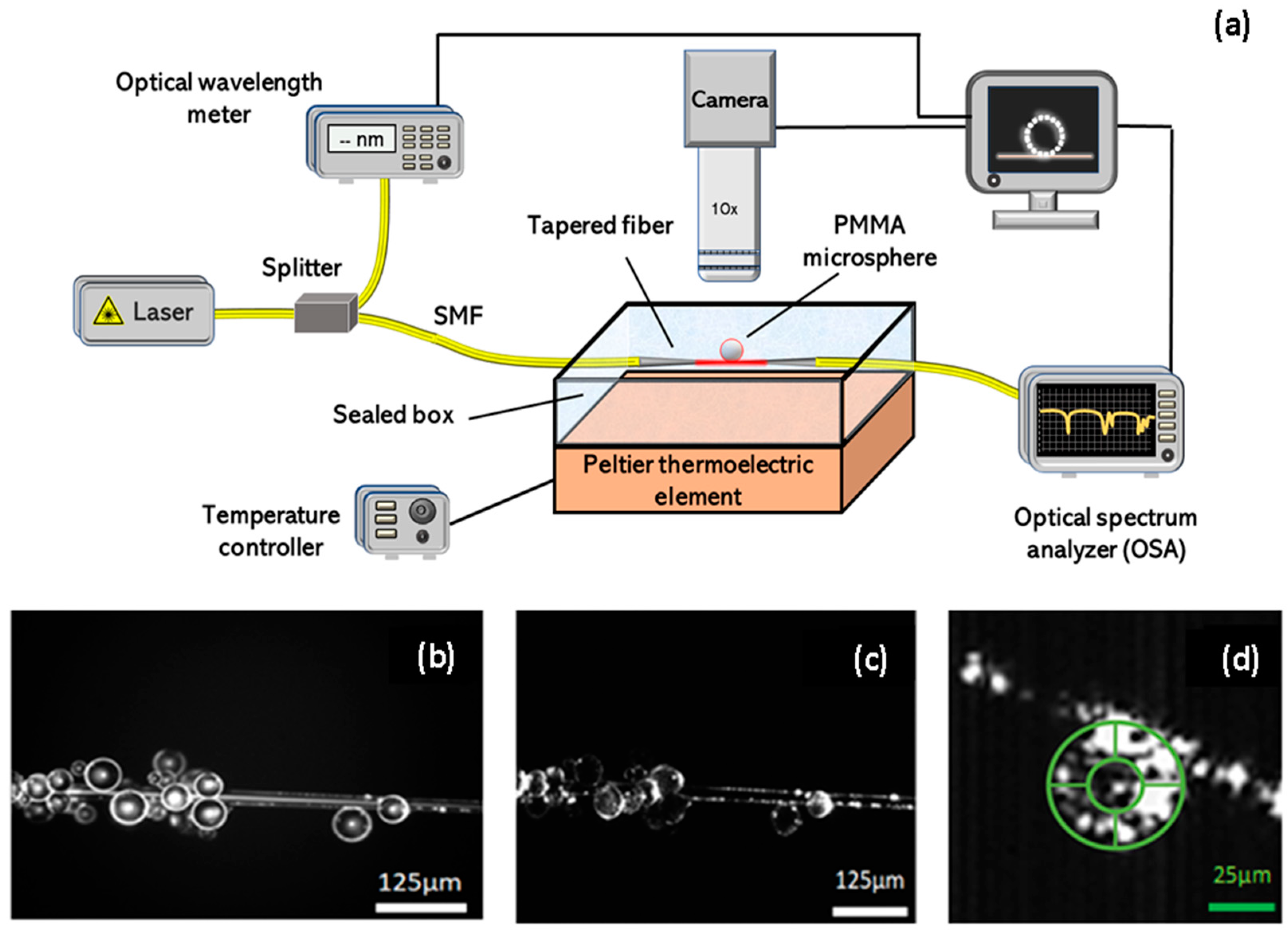
2.2. Experimental Setup
2.3. Image and Data Processing
2.4. COMSOL Simulation Methodology
3. Results and Discussion
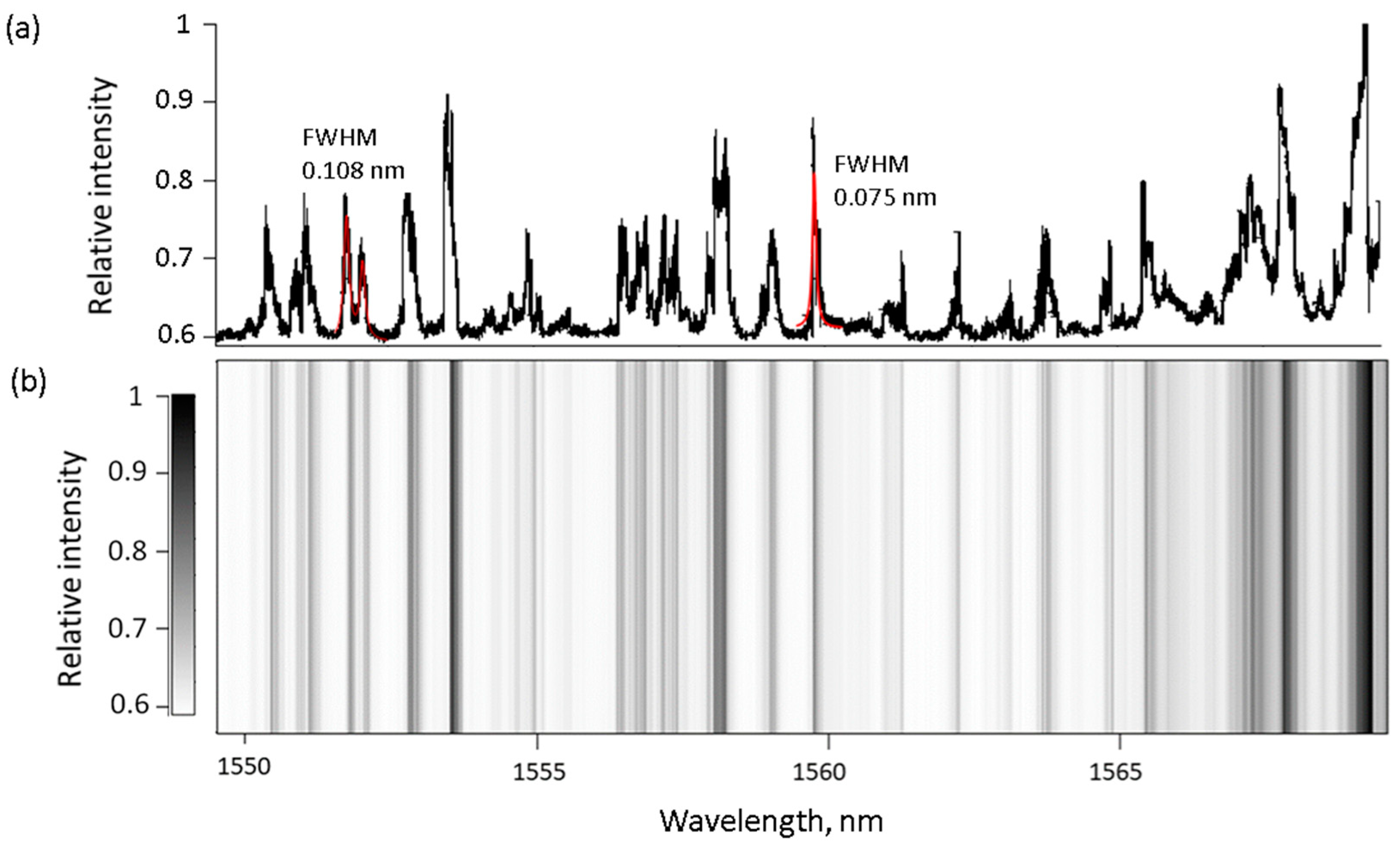
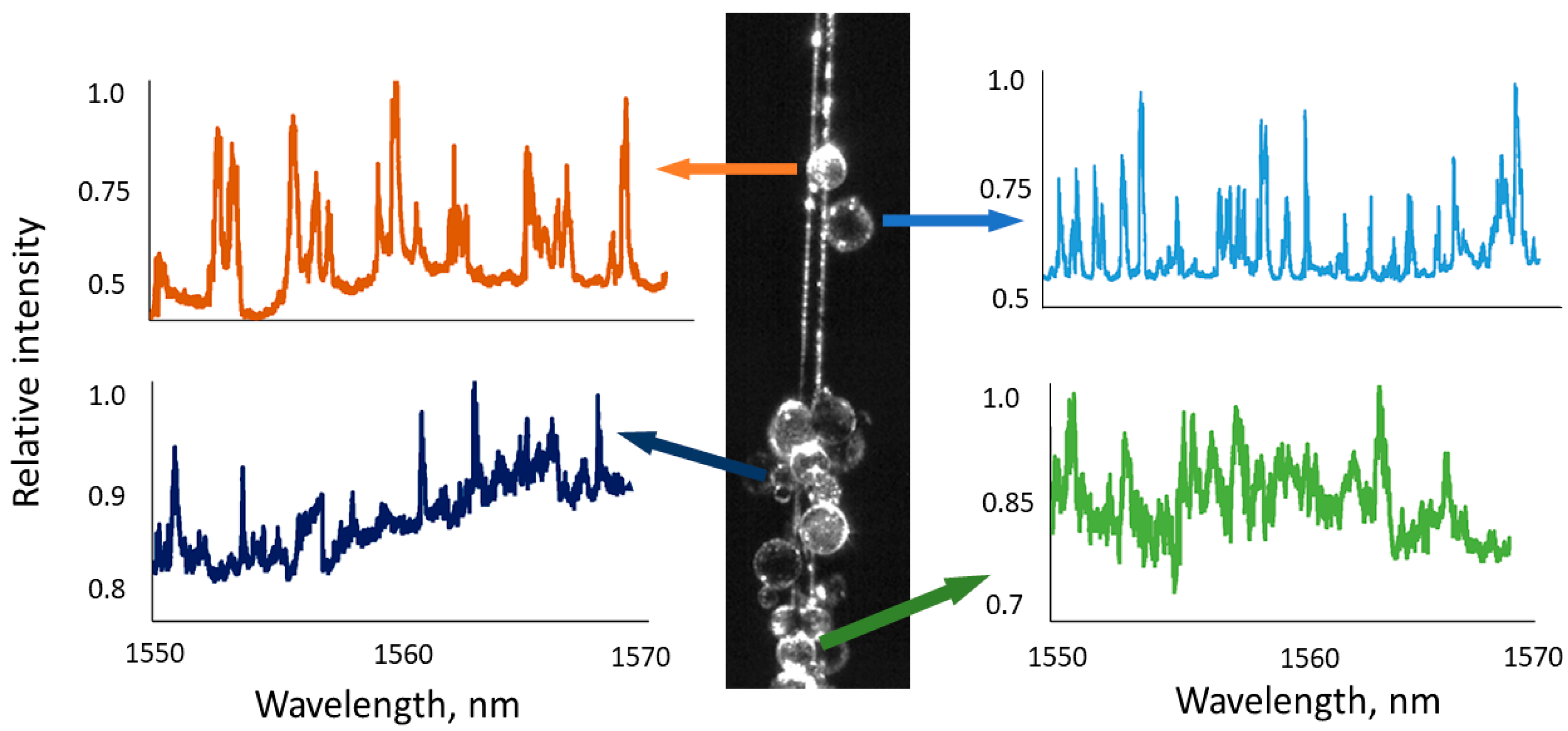
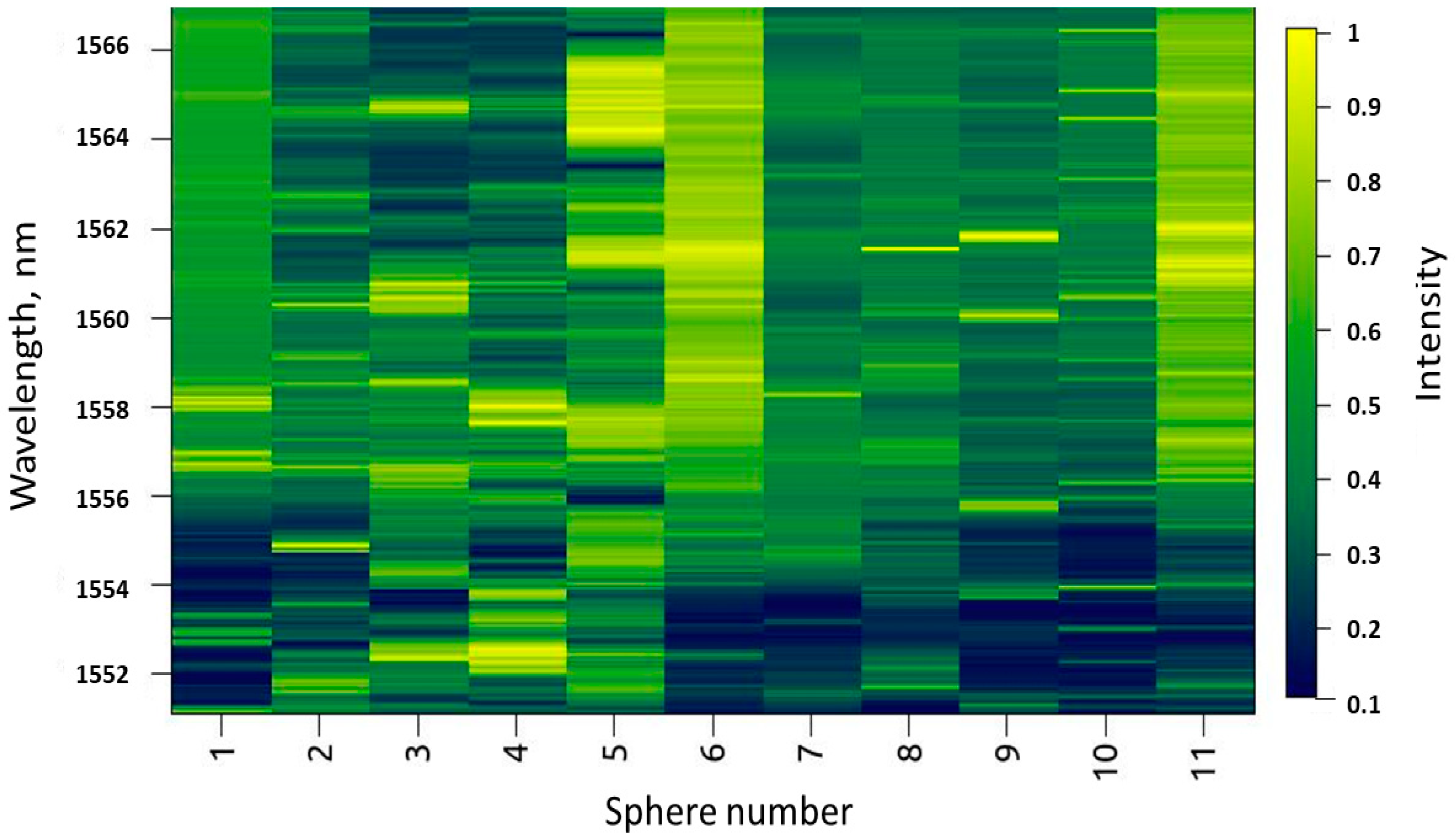
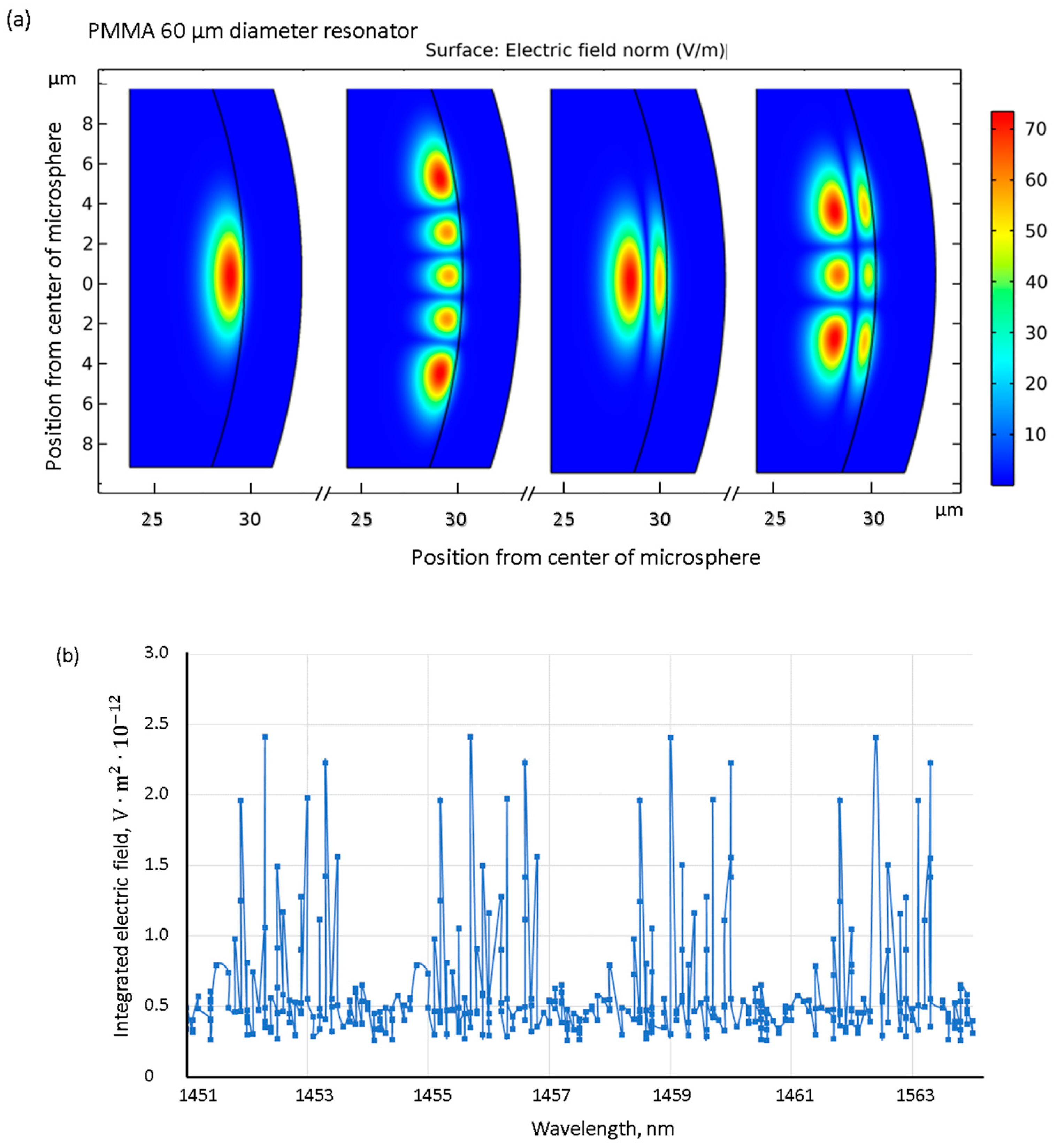
3.1. Mode Map Generated from Microspheres
3.2. Mode Map Generated from a Single Microsphere
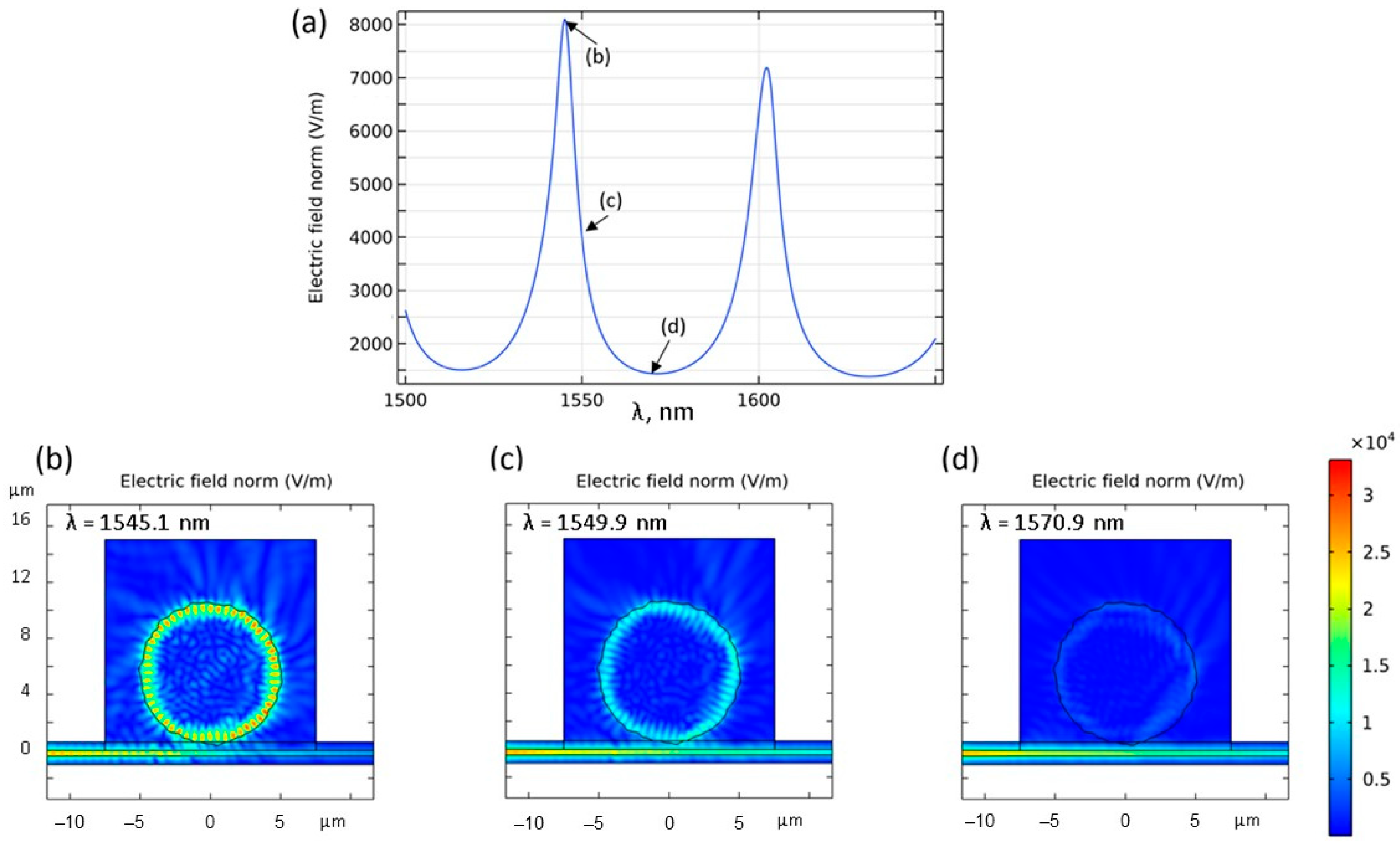
3.3. COMSOL Simulations
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagatsuma, T.; Horiguchi, S.; Minamikata, Y.; Yoshimizu, Y.; Hisatake, S.; Kuwano, S.; Yoshimoto, N.; Terada, J.; Takahashi, H. Terahertz Wireless Communications Based on Photonics Technologies. Opt. Express 2013, 21, 23736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Mahony, M. Future Optical Networks. Opt. Fiber Telecommun. V1B 2008, 24, 611–640. [Google Scholar] [CrossRef]
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; et al. Micro-Combs: A Novel Generation of Optical Sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Barth, I.; Conteduca, D.; Reardon, C.; Johnson, S.; Krauss, T.F. Common-Path Interferometric Label-Free Protein Sensing with Resonant Dielectric Nanostructures. Light Sci. Appl. 2020, 9, 96. [Google Scholar] [CrossRef] [PubMed]
- Toropov, N.; Cabello, G.; Serrano, M.P.; Gutha, R.R.; Rafti, M.; Vollmer, F. Review of Biosensing with Whispering-Gallery Mode Lasers. Light Sci. Appl. 2021, 10, 42. [Google Scholar] [CrossRef]
- Dobosz, M.; Kożuchowski, M. Overview of the Laser-Wavelength Measurement Methods. Opt. Lasers Eng. 2017, 98, 107–117. [Google Scholar] [CrossRef]
- Petermann, A.B.; Varkentin, A.; Roth, B.; Morgner, U.; Meinhardt-Wollweber, M. All-Polymer Whispering Gallery Mode Sensor System. Opt. Express 2016, 24, 6052. [Google Scholar] [CrossRef]
- Righini, G.C.; Dumeige, Y.; Féron, P.; Ferrari, M.; Conti, G.N.; Ristic, D.; Soria, S. Whispering Gallery Mode Microresonators: Fundamentals and Applications. Riv. Nuovo Cim. 2011, 34, 435–488. [Google Scholar] [CrossRef]
- Zhu, J.; Ozdemir, S.K.; Xiao, Y.F.; Li, L.; He, L.; Chen, D.R.; Yang, L. On-Chip Single Nanoparticle Detection and Sizing by Mode Splitting in an Ultrahigh-Q Microresonator. Nat. Photonics 2010, 4, 46–49. [Google Scholar] [CrossRef]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-High-Q Toroid Microcavity on a Chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef]
- Qiulin, M.; Huang, L.; Guo, Z.; Rossmann, T. Spectral Shift Response of Optical Whispering-Gallery Modes Due to Water Vapor Adsorption and Desorption. Meas. Sci. Technol. 2010, 21, 115206. [Google Scholar] [CrossRef] [Green Version]
- Ascorbe, J.; Corres, J.M.; Arregui, F.J.; Matias, I.R. Recent Developments in Fiber Optics Humidity Sensors. Sensors 2017, 17, 893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reinis, P.K.; Milgrave, L.; Draguns, K.; Brice, I.; Alnis, J.; Atvars, A. High-Sensitivity Whispering Gallery Mode Humidity Sensor Based on Glycerol Microdroplet Volumetric Expansion. Sensors 2021, 21, 1746. [Google Scholar] [CrossRef]
- Boyd, R.W.; Heebner, J.E. Sensitive Disk Resonator Photonic Biosensor. Appl. Opt. 2001, 40, 5742–5747. [Google Scholar] [CrossRef] [PubMed]
- Schliesser, A.; Anetsberger, G.; Rivière, R.; Arcizet, O.; Kippenberg, T.J. High-Sensitivity Monitoring of Micromechanical Vibration Using Optical Whispering Gallery Mode Resonators. New J. Phys. 2008, 10, 095015. [Google Scholar] [CrossRef]
- Li, B.B.; Wang, Q.Y.; Xiao, Y.F.; Jiang, X.F.; Li, Y.; Xiao, L.; Gong, Q. On Chip, High-Sensitivity Thermal Sensor Based on High- Q Polydimethylsiloxane-Coated Microresonator. Appl. Phys. Lett. 2010, 96, 2008–2011. [Google Scholar] [CrossRef] [Green Version]
- Berkis, R.; Alnis, J.; Brice, I.; Atvars, A.; Draguns, K.; Grundšteins, K.; Reinis, P.K. Mode Family Analysis for PMMA WGM Micro Resonators Using Spot Intensity Changes. In Proceedings of the SPIE, Laser Resonators, Microresonators, and Beam Control XXIII, Online, 6–11 March 2021; Volume 11672, p. 1167217. [Google Scholar]
- Brice, I.; Grundsteins, K.; Draguns, K.; Atvars, A.; Alnis, J. Whispering Gallery Mode Resonator Temperature Compensation and Refractive Index Sensing in Glucose. Sensors 2021, 21, 7184. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Sun, H.D. Advances and Prospects for Whispering Gallery Mode Microcavities. Adv. Opt. Mater. 2015, 3, 1136–1162. [Google Scholar] [CrossRef]
- Brice, I.; Grundsteins, K.; Atvars, A.; Alnis, J.; Viter, R.; Ramanavicius, A. Whispering Gallery Mode Resonator and Glucose Oxidase Based Glucose Biosensor. Sens. Actuators B Chem. 2020, 318, 128004. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Z.; Ping Shum, P.; Xu, Z.; Keiser, G.; Humbert, G.; Zhang, H.; Zeng, S.; Dinh, X.Q. Sensing and Lasing Applications of Whispering Gallery Mode Microresonators. Opto-Electron. Adv. 2018, 1, 18001501–18001510. [Google Scholar] [CrossRef]
- Matsko, A.B.; Ilchenko, V.S. Optical Resonators With Whispering-Gallery Modes—Part I: Basics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 3–14. [Google Scholar] [CrossRef]
- Bogaerts, W.; de Heyn, P.; van Vaerenbergh, T.; de Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; van Thourhout, D.; Baets, R. Silicon Microring Resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Atvars, A. Analytical Description of Resonances in Fabry–Perot and Whispering Gallery Mode Resonators. J. Opt. Soc. Am. B 2021, 38, 3116–3129. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of Optical Microsphere Resonators. Opt. Lett. 1996, 2799, 453–455. [Google Scholar] [CrossRef]
- Vernooy, D.W.; Ilchenko, V.S.; Mabuchi, H.; Streed, E.W.; Kimble, H.J. High-Q Measurements of Fused-Silica Microspheres in the near Infrared. Opt. Lett. 1998, 23, 247–249. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Liu, J.; Shang, C.; Xie, C.; Guo, H.; Qian, K.; Xue, C.; Liu, J. Fabrication and Spectral Characterizations of High Q Asymmetric Resonant Cavities. Opt. Commun. 2015, 355, 269–273. [Google Scholar] [CrossRef]
- Petermann, A.B.; Hildebrandt, T.; Morgner, U.; Roth, B.W.; Meinhardt-Wollweber, M. Polymer Based Whispering Gallery Mode Humidity Sensor. Sensors 2018, 18, 2383. [Google Scholar] [CrossRef] [Green Version]
- Petermann, A.B.; Rezem, M.; Roth, B.; Morgner, U.; Meinhardt-Wollweber, M. Surface-Immobilized Whispering Gallery Mode Resonator Spheres for Optical Sensing. Sens. Actuators A Phys. 2016, 252, 82–88. [Google Scholar] [CrossRef]
- Schweiger, G.; Nett, R.; Weigel, T. Microresonator Array for High-Resolution Spectroscopy. Opt. Lett. 2007, 32, 2644–2646. [Google Scholar] [CrossRef]
- Labrador-Páez, L.; Soler-Carracedo, K.; Hernández-Rodríguez, M.; Martín, I.R.; Carmon, T.; Martin, L.L. Liquid Whispering-Gallery-Mode Resonator as a Humidity Sensor. Opt. Express 2017, 25, 1165–1172. [Google Scholar] [CrossRef]
- Metzger, N.K.; Spesyvtsev, R.; Bruce, G.D.; Miller, B.; Maker, G.T.; Malcolm, G.; Mazilu, M.; Dholakia, K. Harnessing Speckle for a Sub-Femtometre Resolved Broadband Wavemeter and Laser Stabilization. Nat. Commun. 2017, 8, 15610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salgals, T.; Alnis, J.; Murnieks, R.; Brice, I.; Porins, J.; Andrianov, A.V.; Anashkina, E.A.; Spolitis, S.; Bobrovs, V. Demonstration of a Fiber Optical Communication System Employing a Silica Microsphere-Based OFC Source. Opt. Express 2021, 29, 10903–10913. [Google Scholar] [CrossRef] [PubMed]
- Popov, R.; Shankara, G.K.; von Bojnicic-Kninski, C.; Barua, P.; Mattes, D.; Breitling, F.; Nesterov-Mueller, A. Stochastic Deposition of Amino Acids into Microcavities via Microparticles. Sci. Rep. 2019, 9, 16468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petermann, A.B.; Roth, B.; Morgner, U.; Meinhardt-Wollweber, M. All-Polymer Whispering Gallery Mode Sensor for Application in Optofluidics. Opt. Data Process. Storage 2017, 3, 8–12. [Google Scholar] [CrossRef]
- Draguns, K.; Brice, I.; Atvars, A.; Alnis, J. Computer Modelling of WGM Microresonators with a Zinc Oxide Nanolayer Using COMSOL Multiphysics Software. In Proceedings of the SPIE, Laser Resonators, Microresonators, and Beam Control XXIII, Online, 6–11 March 2021; Volume 11672, p. 1167216. [Google Scholar]
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive Index Measurements of Poly(Methyl Methacrylate) (PMMA) from 0.4–1.6 µm. Appl. Opt. 2015, 54, 139–143. [Google Scholar] [CrossRef]
- Liao, J.; Yang, L. Optical whispering-gallery mode barcodes for high-precision and wide-range temperature measurements. Light Sci. Appl. 2021, 10, 32. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, K.; Jin, X. Package of a Dual-Tapered-Fiber Coupled Microsphere Resonator with High Q Factor. Opt. Commun. 2015, 350, 230–234. [Google Scholar] [CrossRef]
- Berkis, R.; Alnis, J.; Atvars, A.; Brice, I.; Draguns, K.; Grundsteins, K. Quality Factor Measurements for PMMA WGM Microsphere Resonators Using Fixed Wavelength Laser and Temperature Changes. In Proceedings of the 2019 IEEE 9th International Conference on Nanomaterials: Applications and Properties, NAP, Odessa, Ukraine, 15–20 September 2019; pp. 9–12. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berkis, R.; Reinis, P.K.; Milgrave, L.; Draguns, K.; Salgals, T.; Brice, I.; Alnis, J.; Atvars, A. Wavelength Sensing Based on Whispering Gallery Mode Mapping. Fibers 2022, 10, 90. https://doi.org/10.3390/fib10100090
Berkis R, Reinis PK, Milgrave L, Draguns K, Salgals T, Brice I, Alnis J, Atvars A. Wavelength Sensing Based on Whispering Gallery Mode Mapping. Fibers. 2022; 10(10):90. https://doi.org/10.3390/fib10100090
Chicago/Turabian StyleBerkis, Roberts, Pauls Kristaps Reinis, Lase Milgrave, Kristians Draguns, Toms Salgals, Inga Brice, Janis Alnis, and Aigars Atvars. 2022. "Wavelength Sensing Based on Whispering Gallery Mode Mapping" Fibers 10, no. 10: 90. https://doi.org/10.3390/fib10100090
APA StyleBerkis, R., Reinis, P. K., Milgrave, L., Draguns, K., Salgals, T., Brice, I., Alnis, J., & Atvars, A. (2022). Wavelength Sensing Based on Whispering Gallery Mode Mapping. Fibers, 10(10), 90. https://doi.org/10.3390/fib10100090






