Accelerated Zero-Stress Hydrothermal Aging of Dry E-Glass Fibers and Service Life Prediction Using Arrhenius Model
Abstract
:1. Introduction
2. Materials and Methods
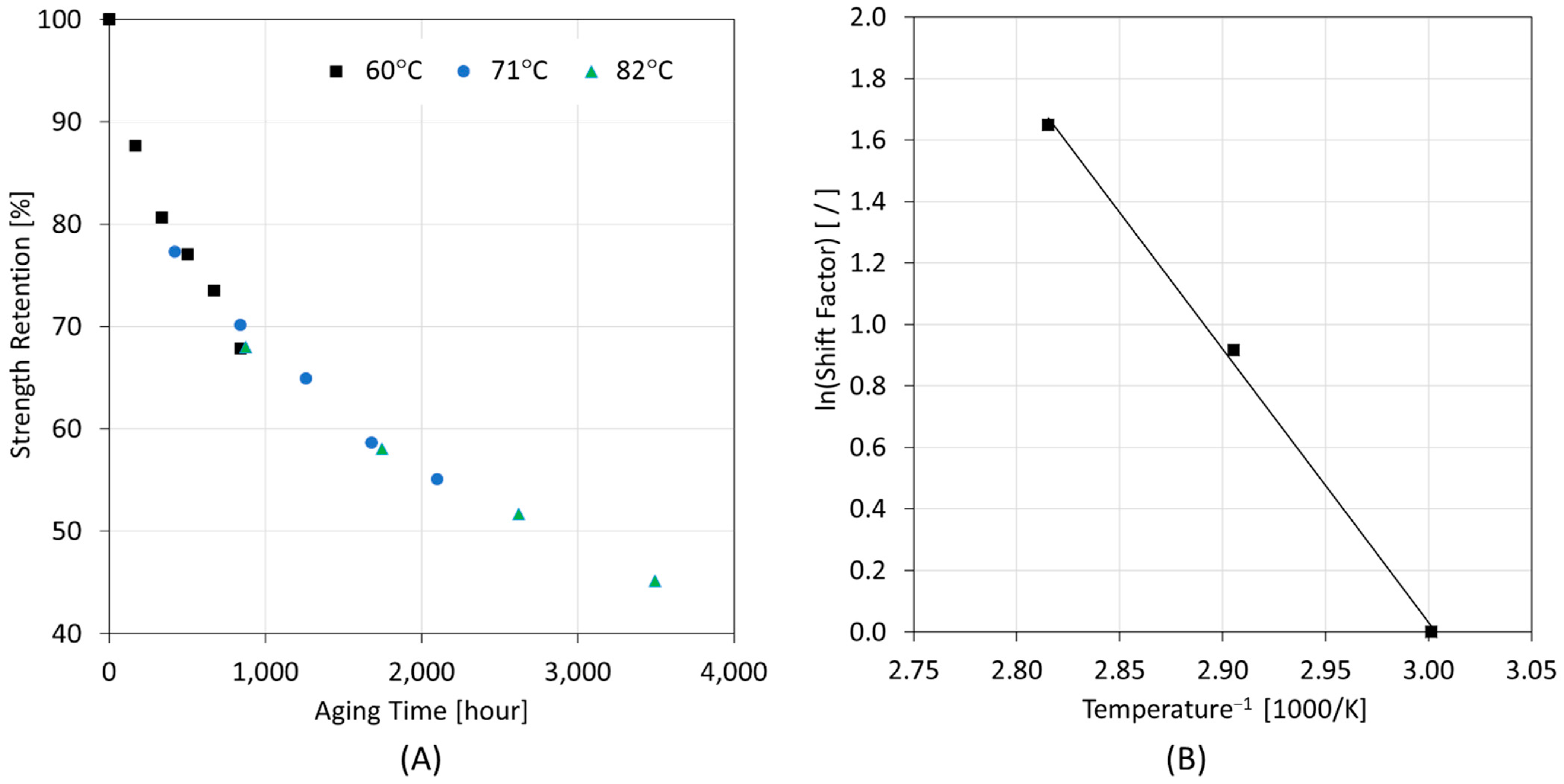
2.1. Arrhenius Model and Time-Temperature Superposition Approach
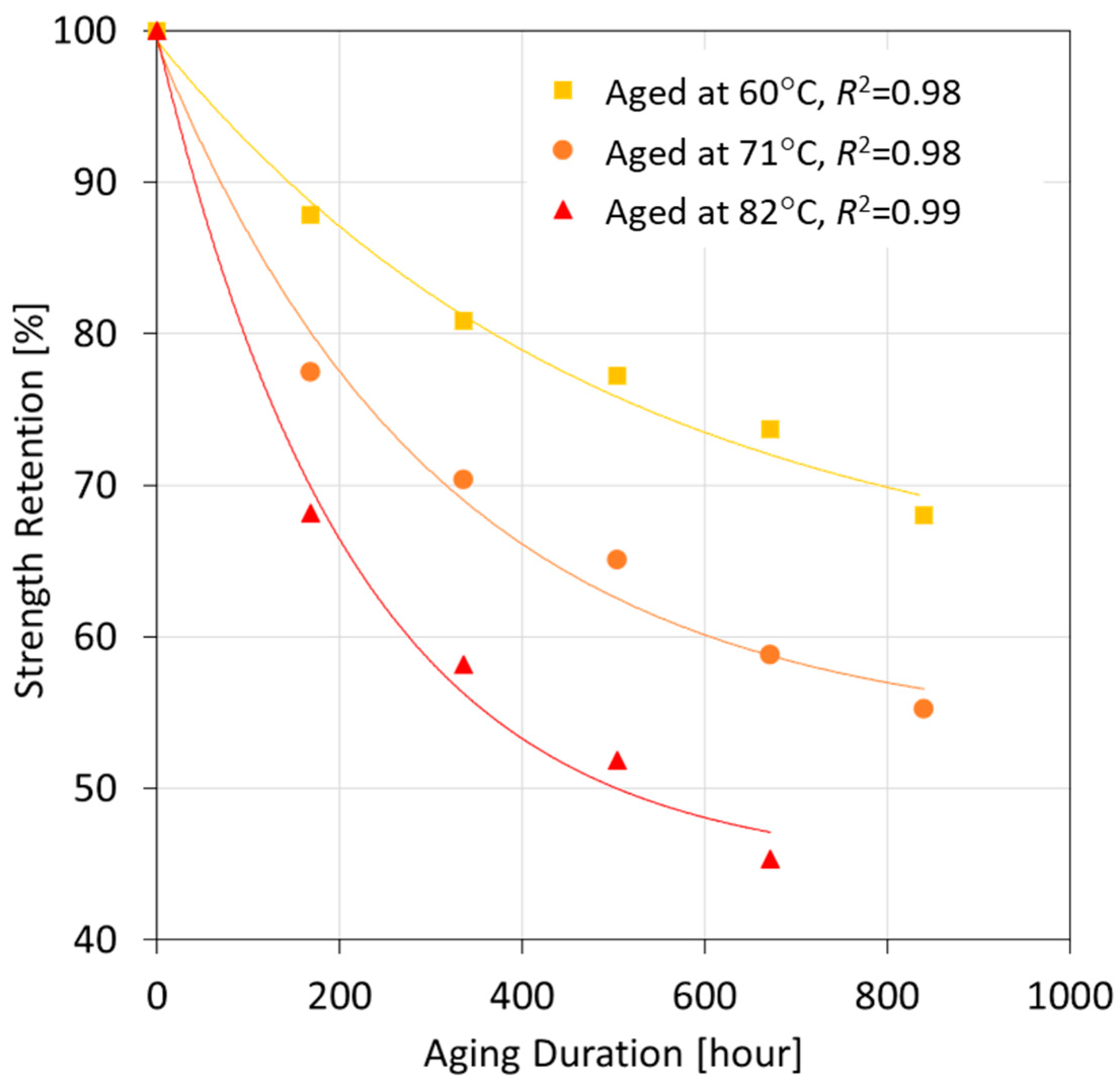
- Step 1: Plotting the property values at a specific temperature against time and fitting a curve through the points that reflect the degradation pattern.
- Step 2: Determining the retention levels, also known as lifetime points, represent the time required for a material to reach a given degree of property degradation. These are directly obtained from the fitted curve.
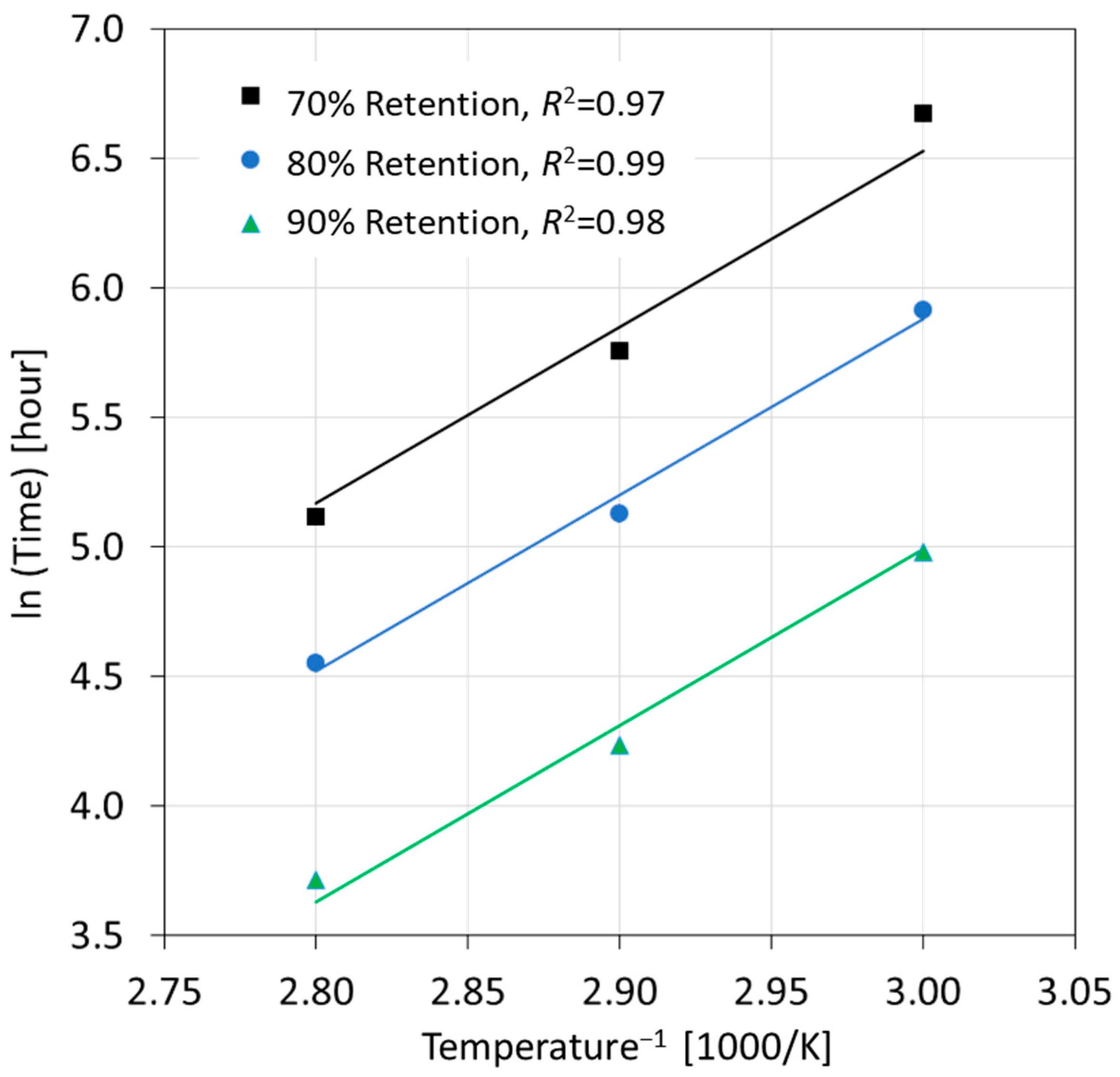
- Step 3: Plotting the logarithm retention time (hours) versus the inverse of temperature (1/T). The model is established via a linear fit with a regression coefficient (R2) value of at least 0.8.
2.2. Material and Specimen Preparation
2.3. Experimental Methods
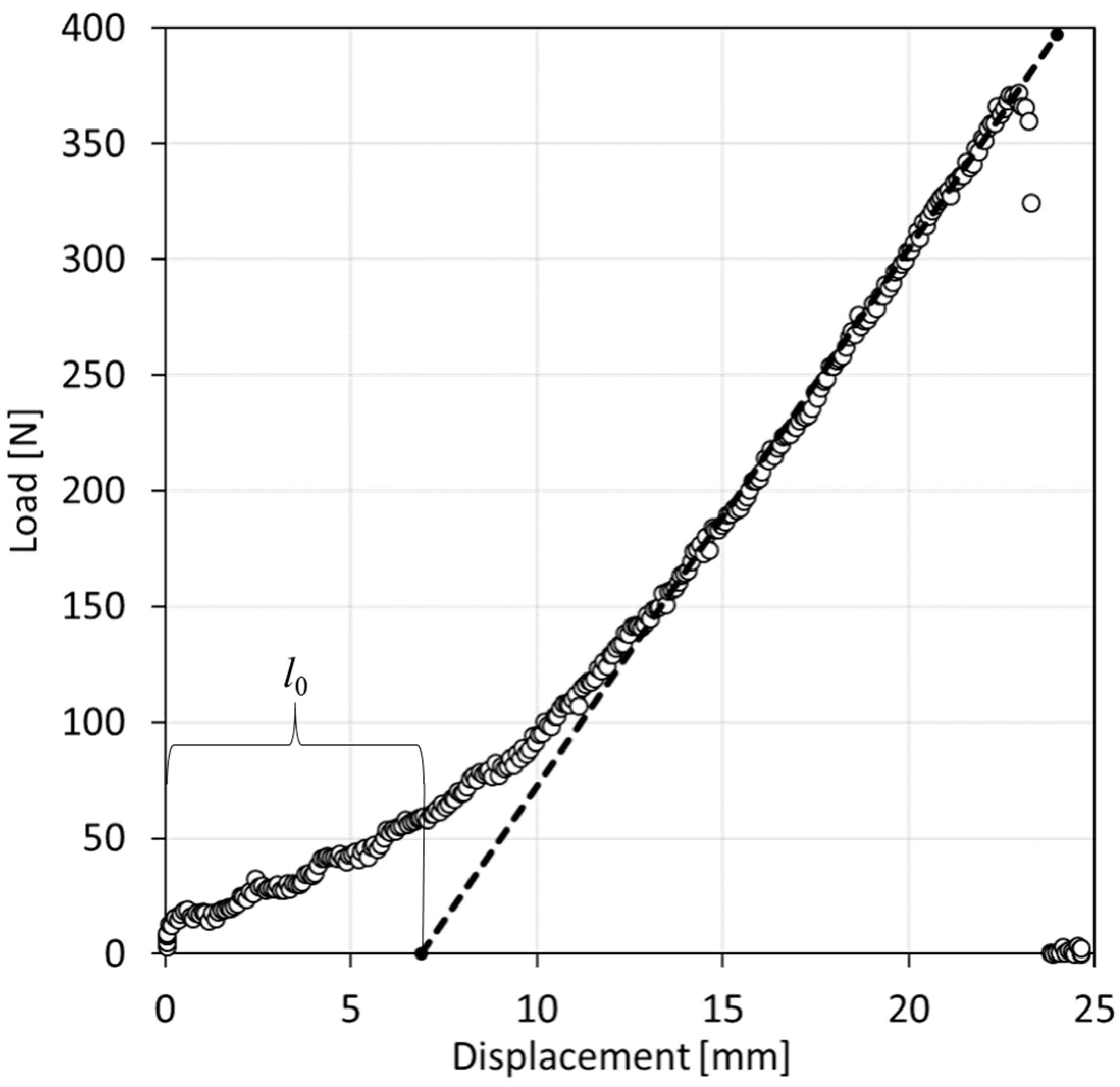
2.3.1. Test Setup for Fiber Breaking Force Measurement
2.3.2. Mass Dissolution Experiments
2.3.3. Fourier Transform Infrared Spectroscopy
2.3.4. Scanning Electron Microscopy
3. Results and Discussion
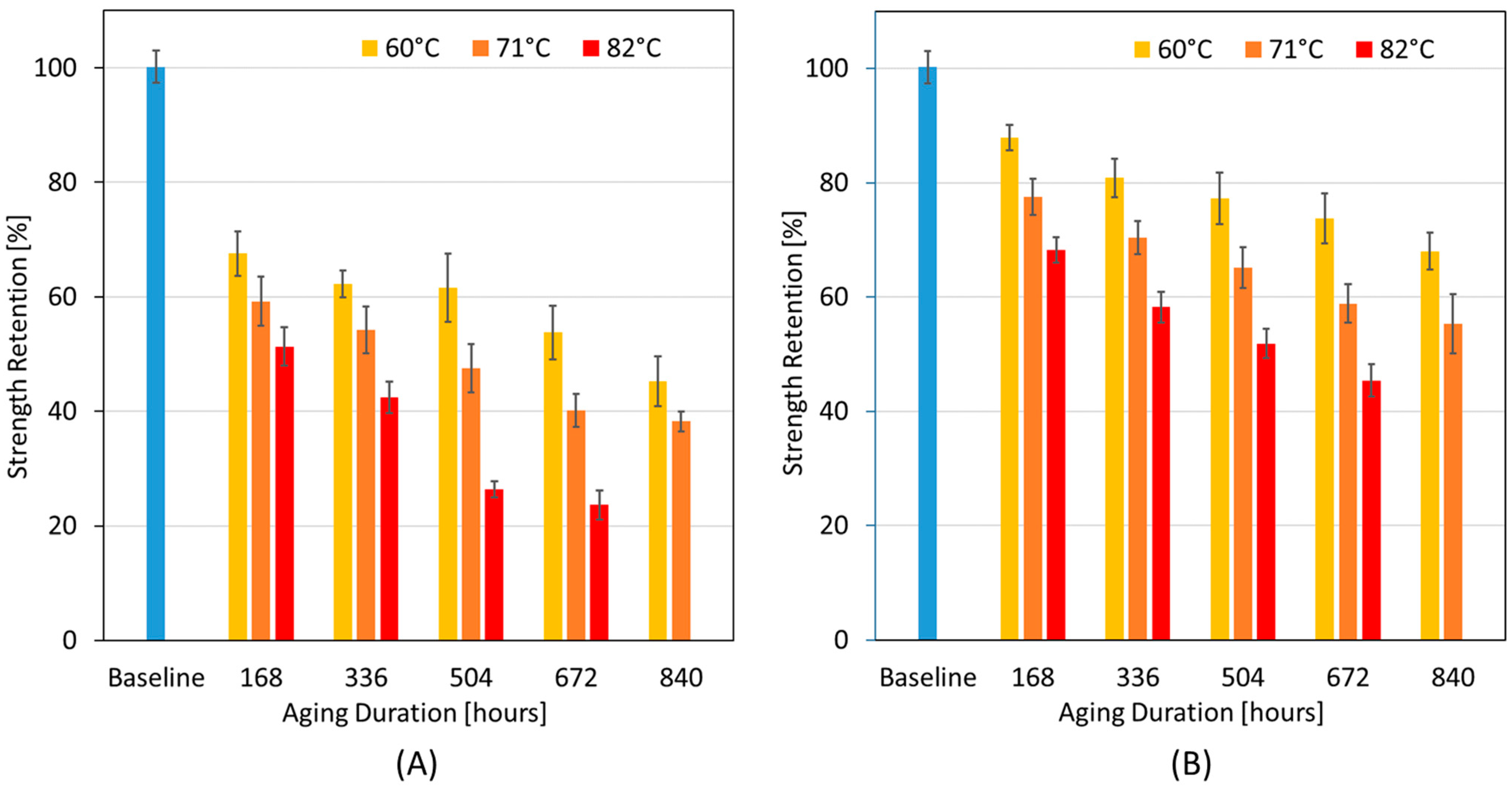
3.1. Variation in Fiber Strength
3.2. Prediction of Long-Term Behavior and Service Life of Glass Fibers
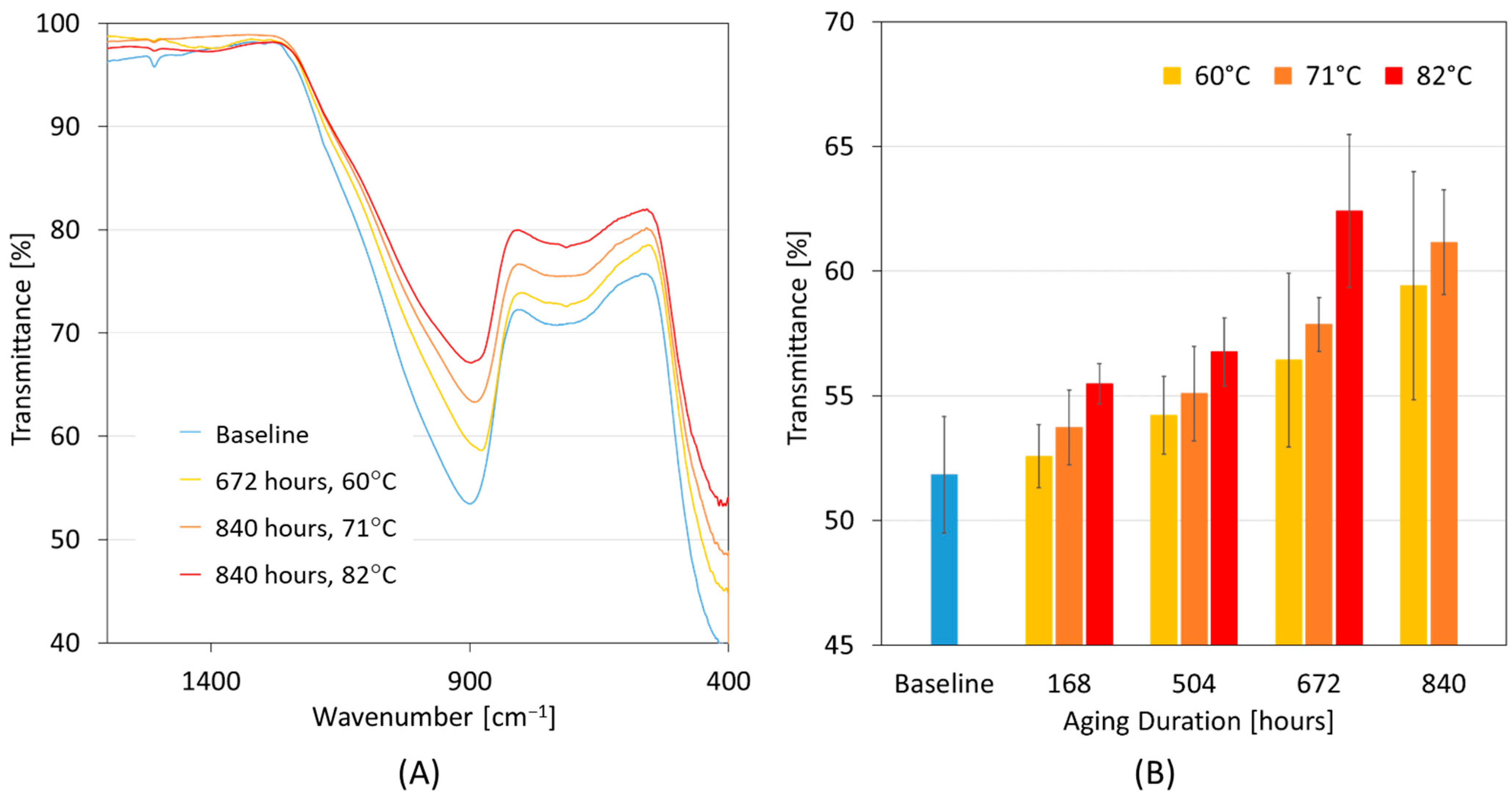
3.3. Elements Released during Degradation and Corresponding Chemical Reactions
3.4. Results from FTIR Analysis
3.5. Morphological Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T.J.C. Long-term hydrolytic degradation of the sizing-rich composite interphase. Coatings 2019, 9, 263. [Google Scholar] [CrossRef] [Green Version]
- Thomason, J.L. Glass fibre sizing: A review. Compos. Part A Appl. Sci. 2019, 127, 105619. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Vegere, K.; Kalnina, I.; Klavins, M.; Echtermeyer, A.T. Dissolution kinetics of R-glass fibres: Influence of water acidity, temperature, and stress corrosion. Fibers 2019, 7, 22. [Google Scholar] [CrossRef] [Green Version]
- Mahltig, B.; Kyosev, Y. Inorganic and Composite Fibers: Production, Properties, and Applications; Woodhead Publishing: Duxford, UK, 2018; ISBN 978-0-08-102229-0. [Google Scholar]
- Feih, S.; Wei, J.; Kingshott, P.; Sørensen, B.F. The influence of fibre sizing on the strength and fracture toughness of glass fibre composites. Compos. Part A Appl. Sci. 2005, 36, 245–255. [Google Scholar] [CrossRef]
- Ishak, Z.M.; Arifin, A.; Senawi, R. Effects of hygrothermal aging and a silane coupling agent on the tensile properties of injection molded short glass fiber reinforced poly (butylene terephthalate) composites. Eur. Polym. J. 2001, 37, 1635–1647. [Google Scholar] [CrossRef]
- Davalos, J.F.; Chen, Y.; Ray, I. Long-term durability prediction models for GFRP bars in concrete environment. J. Compos. Mater. 2012, 46, 1899–1914. [Google Scholar] [CrossRef]
- Silva, M.A.; da Fonseca, B.S.; Biscaia, H. On estimates of durability of FRP based on accelerated tests. Compos. Struct. 2014, 116, 377–387. [Google Scholar] [CrossRef]
- Idrisi, A.H.; Mourad, A.-H.I.; Abdel-Magid, B.M.; Shivamurty, B. Investigation on the durability of E-Glass/Epoxy composite exposed to seawater at elevated temperature. Polymers 2021, 13, 2182. [Google Scholar] [CrossRef] [PubMed]
- Guermazi, N.; Tarjem, A.B.; Ksouri, I.; Ayedi, H.F. On the durability of FRP composites for aircraft structures in hygrothermal conditioning. Compos. Part B Eng. 2016, 85, 294–304. [Google Scholar] [CrossRef]
- Bobbaa, S.; Lemana, Z.; Zainudina, E.; Sapuana, S. The influence of hydrothermal aging on E-glass and S-glass fiber/epoxyreinforced composite pipes. J. Mater. Environ. Sci. 2019, 10, 790–804. [Google Scholar]
- Echtermeyer, A.T.; Krauklis, A.E.; Gagani, A.I.; Sæter, E. Zero stress aging of glass and carbon fibers in water and oil—Strength reduction explained by dissolution kinetics. Fibers 2019, 7, 107. [Google Scholar] [CrossRef] [Green Version]
- Borges, C.S.; Akhavan-Safar, A.; Marques, E.A.; Carbas, R.J.; Ueffing, C.; Weißgraeber, P.; da Silva, L.F. Effect of water ingress on the mechanical and chemical properties of polybutylene terephthalate reinforced with glass fibers. Materials 2021, 14, 1261. [Google Scholar] [CrossRef]
- Shao, Y.; Kouadio, S. Durability of Fiberglass Composite Sheet Piles in Water. J. Compos. Constr. 2022, 6, 280–287. [Google Scholar] [CrossRef] [Green Version]
- Grammatikos, S.A.; Evernden, M.; Mitchels, J.; Zafari, B.; Mottram, J.T.; Papanicolaou, G.C. On the response to hygrothermal aging of pultruded FRPs used in the civil engineering sector. Mater. Des. 2016, 96, 283–295. [Google Scholar] [CrossRef] [Green Version]
- Ghabezi, P.; Harrison, N.M. Hygrothermal deterioration in carbon/epoxy and glass/epoxy composite laminates aged in marine-based environment (degradation mechanism, mechanical and physicochemical properties). J. Mater. Sci. 2022, 57, 4239–4254. [Google Scholar] [CrossRef]
- Guo, R.; Xian, G.; Li, F.; Li, C.; Hong, B. Hygrothermal resistance of pultruded carbon, glass and carbon/glass hybrid fiber reinforced epoxy composites. Constr. Build. Mater. 2022, 315, 125710. [Google Scholar] [CrossRef]
- Messana, A.; Airale, A.G.; Ferraris, A.; Sisca, L.; Carello, M. Correlation between thermo-mechanical properties and chemical composition of aged thermoplastic and thermosetting fiber reinforced plastic materials. Materwiss. Werksttech. 2017, 48, 447–455. [Google Scholar] [CrossRef]
- Fang, M.; Zhang, N.; Huang, M.; Lu, B.; Lamnawar, K.; Liu, C.; Shen, C. Effects of hydrothermal aging of carbon fiber reinforced polycarbonate composites on mechanical performance and sand erosion resistance. Polymers 2020, 12, 2453. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, P.; Guo, R.; Li, C.; Xian, G. Durability study of glass fiber reinforced polypropylene sheet under simulated seawater sea sand concrete environment. J. Mater. Res. Technol. 2022, 20, 1079–1092. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Echtermeyer, A.T. Long-term dissolution of glass fibers in water described by dissolving cylinder zero-order kinetic model: Mass loss and radius reduction. Open Chem. 2018, 16, 1189–1199. [Google Scholar] [CrossRef]
- Bashir, S.; Yang, L.; Liggat, J.; Thomason, J. Kinetics of dissolution of glass fibre in hot alkaline solution. J. Mater. Sci. 2018, 53, 1710–1722. [Google Scholar] [CrossRef] [Green Version]
- Mišíková, L.; Liška, M.; Galuskova, D. Corrosion of E-glass fibers in distilled water. Ceram. Silik. 2007, 51, 131–135. [Google Scholar]
- Jones, R.; Stewart, J. The kinetics of corrosion of e-glass fibres in sulphuric acid. J. Non-Cryst. Solids 2010, 356, 2433–2436. [Google Scholar] [CrossRef]
- Wei, B.; Cao, H.; Song, S. Tensile behavior contrast of basalt and glass fibers after chemical treatment. Mater. Des. 2010, 31, 4244–4250. [Google Scholar] [CrossRef]
- Feih, S.; Manatpon, K.; Mathys, Z.; Gibson, A.; Mouritz, A. Strength degradation of glass fibers at high temperatures. J. Mater. Sci. 2009, 44, 392–400. [Google Scholar] [CrossRef]
- Shawcor Composite Linepipe. Available online: https://www.shawcor.com/composite-systems/composite-linepipe (accessed on 22 January 2022).
- Starkova, O.; Gagani, A.I.; Karl, C.W.; Rocha, I.B.; Burlakovs, J.; Krauklis, A.E. Modelling of environmental ageing of polymers and polymer composites—Durability prediction methods. Polymers 2022, 14, 907. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Chen, S. Durability and service life prediction of GFRP bars embedded in concrete under acid environment. Nucl. Eng. Des. 2011, 241, 4095–4102. [Google Scholar] [CrossRef]
- ISO 11346; Rubber, Vulcanized or Thermoplastic—Estimation of Lifetime and Maximum Temperature of Use. International Organization for Standardization: Geneva, Switzerland, 2014.
- Bank, L.C.; Gentry, T.R.; Thompson, B.P.; Russell, J.S. Model specification for composites for civil engineering structures. Transp. Res. Rec. 2002, 1814, 227–236. [Google Scholar] [CrossRef]
- Zhu, J.; Deng, Y.; Chen, P.; Wang, G.; Min, H.; Fang, W. Prediction of long-term tensile properties of glass fiber reinforced composites under acid-base and salt environments. Polymers 2022, 14, 3031. [Google Scholar] [CrossRef]
- Hoque, M.S.; Saha, A.; Chung, H.J.; Dolez, P.I. Hydrothermal aging of fire-protective fabrics. J. Appl. Polym. Sci. 2022, 139, e52666. [Google Scholar] [CrossRef]
- Jushi Fiberglass Products for Pipes. Available online: https://www.jushi.com/en/product/product-introduction-151.html (accessed on 22 January 2022).
- ASTM D2256M-10; Standard Test Method for Tensile Properties of Yarns by the Single-Strand Method. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM D2343-17; Standard Test Method for Tensile Properties of Glass Fiber Strands, Yarns, and Rovings Used in Reinforced Plastics. ASTM International: West Conshohocken, PA, USA, 2009.
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Lara-Curzio, E. Oxidation induced stress-rupture of fiber bundles. J. Eng. Mater. Technol. 1998, 120, 105–109. [Google Scholar] [CrossRef] [Green Version]
- Grambow, B.; Müller, R. First-order dissolution rate law and the role of surface layers in glass performance assessment. J. Nucl. Mater. 2001, 298, 112–124. [Google Scholar] [CrossRef]
- Rani, M.; Choudhary, P.; Krishnan, V.; Zafar, S. Development of sustainable microwave-based approach to recover glass fibers for wind turbine blades composite waste. Resour. Conserv. Recycl. 2022, 179, 106107. [Google Scholar] [CrossRef]
- Ahmadi, A.; Ramezanzadeh, B.; Mahdavian, M. Hybrid silane coating reinforced with silanized graphene oxide nanosheets with improved corrosion protective performance. RSC Adv. 2016, 6, 54102–54112. [Google Scholar] [CrossRef]
- Abidi, N. Introduction to FTIR Microspectroscopy. In FTIR Microspectroscopy; Springer: Cham, Switzerland, 2021; pp. 1–8. ISBN 978-3-030-84424-0. [Google Scholar]



| Aging Temperature [°C] | A1 [N] | τ [Hour] | Y0 [N] | |
|---|---|---|---|---|
| 60 | 36.81 | 493.80 | 62.61 | 6802.0 |
| 71 | 45.65 | 311.52 | 53.48 | 6802.0 |
| 82 | 54.93 | 216.10 | 44.66 | 6802.0 |
| Element | Si | Ca | Al | Na | Mg | K | S | Fe |
|---|---|---|---|---|---|---|---|---|
| Concentration at 60 °C [mg/L] | 9.43 | 6.507 | 1.938 | 0.284 | 0.219 | 0.14 | 0.056 | 0.002 |
| Concentration at 82 °C [mg/L] | 16.551 | 9.056 | 3.128 | 0.42 | 0.341 | 0.133 | 0.078 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunny, J.; Nazaripoor, H.; Palacios Moreno, J.; Mertiny, P. Accelerated Zero-Stress Hydrothermal Aging of Dry E-Glass Fibers and Service Life Prediction Using Arrhenius Model. Fibers 2023, 11, 70. https://doi.org/10.3390/fib11080070
Sunny J, Nazaripoor H, Palacios Moreno J, Mertiny P. Accelerated Zero-Stress Hydrothermal Aging of Dry E-Glass Fibers and Service Life Prediction Using Arrhenius Model. Fibers. 2023; 11(8):70. https://doi.org/10.3390/fib11080070
Chicago/Turabian StyleSunny, John, Hadi Nazaripoor, Jorge Palacios Moreno, and Pierre Mertiny. 2023. "Accelerated Zero-Stress Hydrothermal Aging of Dry E-Glass Fibers and Service Life Prediction Using Arrhenius Model" Fibers 11, no. 8: 70. https://doi.org/10.3390/fib11080070
APA StyleSunny, J., Nazaripoor, H., Palacios Moreno, J., & Mertiny, P. (2023). Accelerated Zero-Stress Hydrothermal Aging of Dry E-Glass Fibers and Service Life Prediction Using Arrhenius Model. Fibers, 11(8), 70. https://doi.org/10.3390/fib11080070






