Effect of the Fiber Type and Axial Stiffness of FRCM on the Flexural Strengthening of RC Beams
Abstract
:1. Introduction
2. Previous Research
- ✓
- The FRCM strengthening of RC beams showed a significant increase in the ultimate capacity of up to 92%.
- ✓
- The increase in the ultimate capacity proportion directly with the increase of the axial stiffness of the FRCM fiber net and the number of FRCM layers. The PBO FRCM materials performed better than C-FRCM materials, which is consistent with the axial stiffness of each material.
- ✓
- The increase in ultimate strength of strengthened beams having low-strength concrete is higher than that of high-strength concrete. For example, for strengthened beam having low-strength concrete, flexural capacity increased by 32% (one layer) and 92% (four layers). For high-strength concrete, flexural capacity increased by 13% (one layer) and 73% (four layers) [11].
- ✓
- It was found that RC concrete beams reinforced with two layers of PBO FRCM, which yields an axial stiffness of approximately 83% of one layer of carbon FRP sheets, provided about a 30% increase in the ultimate load, which was almost the same increase as the CFRP strengthening. Meanwhile, two layers of carbon FRCM with an axial stiffness of about 75% that of CFRP, enhanced the ultimate load by only 15% [4].
- Two types of fibers, PBO and carbon FRCM, were investigated for the flexural strengthening.
- A very low steel reinforcement ratio (less than 0.195 ρb) was used in all of the strengthened RC beams in all of the previous research.
- In terms of the number of FRCM layers, previous researchers focused more on investigating the effect of extreme number of layers, i.e., one layer vs. four layers.
- No comparison was carried out between the three FRCM systems: glass, carbon and PBO.
3. Experimental Program
3.1. Test Specimens
3.2. Material Properties
- Ultimate tensile strain, .
- Ultimate tensile stress, .
- Modulus of elasticity of the cracked specimen, Ef.
3.3. Fabrication of Test Specimens
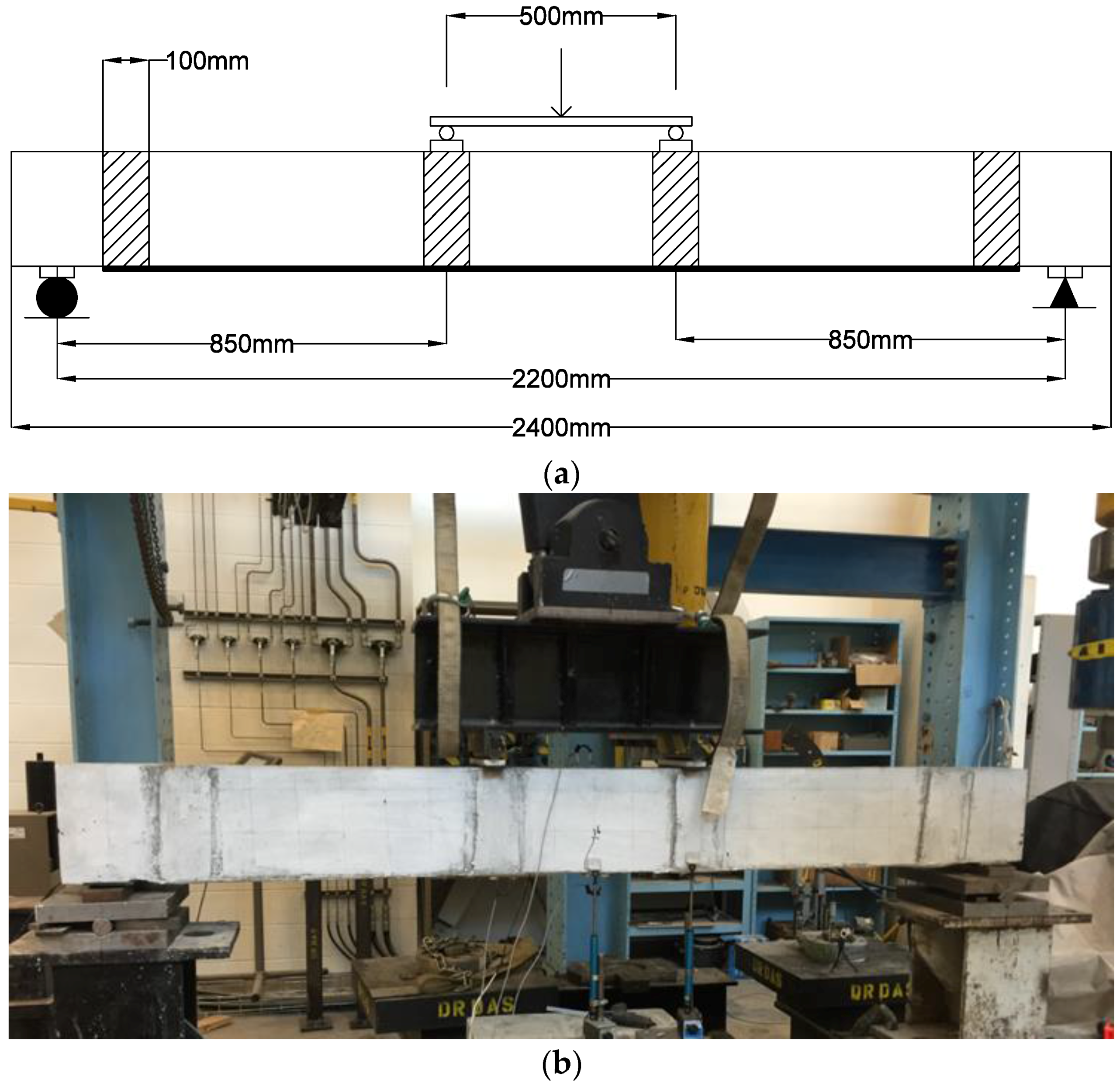
3.4. Test Set-Up and Procedures
3.5. Instrumentation
4. Test Results and Discussion
4.1. Effect of FRCM Net Fiber Type
4.2. Effect of the Axial Stiffness Ratio of Strengthening Material to the Steel Reinforcement
4.3. Load-Strain Relationship
4.4. Critical Crack Width
5. Conclusions
- PBO FRCM had a significant impact on the ultimate capacity of the strengthened beams. The increases of 33% and 25% were obtained in comparison with the control (un-strengthened beam) for beams reinforced with low and moderate reinforcement ratios, respectively.
- Both carbon and glass FRCM did not provide a noticeable enhancement in the ultimate load capacity of the strengthened beams, as they both resulted in an increase in ultimate load less than 5%. This is mainly due to the premature bond failure of the FRCM.
- The PBO and carbon FRCM increased the strengthened beams post-cracking and post-yielding stiffnesses.
- It was noticed that as the increase in the ultimate strength decreases, the axial stiffness ratio (EAFRCM/EASteel) decreases.
- The theoretical analysis carried out according to the ACI 549.4R-13 guidelines shows that the predicted results are within an acceptable accuracy compared to the experimental results.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Theoretical Analysis According to ACI 549.4R-13
- Plane sections remain plane after loading.
- The bond between the FRCM system and the concrete substrate remains effective.
- The maximum compressive strain in concrete is 0.003.
- FRCM has a bilinear behavior to failure where only the second linear part of the curve is used in analysis and design.

References
- Types and Causes of Concrete Deterioration. Available online: http://www.cement.org/docs/default-source/fc_concrete_technology/durability/is536-types-and-causes-of-concrete-deterioration.pdf?sfvrsn=4 (accessed on 4 August 2016).
- Bisby, L.A.; Briglio, M.B. ISIS Canada Educational Module No. 5: An Introduction to Structural Health Monitoring; Prepared by ISIS Canada; ISIS Canada: Winnipeg, Manitoba, Canada, 2004. [Google Scholar]
- Corrosion Central, NACE. Available online: https://www.nace.org/Corrosion-Central/Industries/Highways-and-Bridges/ (accessed on 4 August 2016).
- D’Ambrisi, A.; Focacci, F. Flexural strengthening of RC beams with cement based composites. J. Compos. Constr. 2011, 15, 707–720. [Google Scholar] [CrossRef]
- Tumialan, G.; De Luca, A. FRCM Systems. In STRUCTURE Magazine; National Council of Structural Engineers Association: Chicago, IL, USA, 2014. [Google Scholar]
- Bisby, L.A.; Stratford, T.J.; Smith, J.; Halpin, S. FRP versus Fiber Reinforced Cementitious Mortar Strengthening Systems at Elevated Temperature. In Proceedings of the 10th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures, ACI SP-279, Tampa, FL, USA, 2–4 April 2011; American Concrete Institute: Farmington Hills, MI, USA, 2011; pp. 49.1–49.20. [Google Scholar]
- Turk, A.M. Seismic Response Analysis of Masonry Minaret and Possible Strengthening by Fiber Reinforced Cementitious Matrix (FRCM) Materials. Adv. Mater. Sci. Eng. 2013, 2013, 952497. [Google Scholar] [CrossRef]
- ACI (American Concrete Institute). Design and Construction Guide of Externally Bonded FRCM Systems for Concrete and Masonry Repair and Strengthening; ACI 549.4R-13; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Arboleda, D.; Carozzi, F.; Nanni, A.; Poggi, C. Testing Procedures for the Uniaxial Tensile Characterization of Fabric-Reinforced Cementitious Matrix Composites. J. Compos. Constr. 2016, 20, 04015063. [Google Scholar] [CrossRef]
- Mobasher, B.; Peled, A.; Pahilajani, J. Distributed cracking and stiffness degradation in fabric-cement composites. Mater. Struct. 2012, 39, 317–331. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; Loreto, G.; Nanni, A. Flexural Strengthening of RC Beams with an Externally Bonded Fabric-Reinforced Cementitious Matrix. J. Compos. Constr. 2014, 18, 04014009. [Google Scholar] [CrossRef]
- Loreto, G.; Leardini, L.; Arboleda, D.; Nanni, A. Performance of RC slab-type elements strengthened with fabric-reinforced cementitious- matrix (FRCM) composites. J. Compos. Constr. 2013, 18, A4013003. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Feo, L.; Focacci, F. Experimental analysis on bond between PBO-FRCM strengthening materials and concrete. Compos. Part B 2013, 44, 524–532. [Google Scholar] [CrossRef]
- D’Antino, T.; Carloni, C.; Sneed, L.H.; Pellegrino, C. Matrix-fiber bond behavior in PBO FRCM composites: A Fracture Mechanics Approach. Eng. Fract. Mech. 2014, 117, 94–111. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Feo, L.; Focacci, F. Bond-slip relations for PBO-FRCM materials externally bonded to concrete. Compos. Part B 2012, 43, 2938–2949. [Google Scholar] [CrossRef]
- SikaWrap®-350G Grid. grc.sika.com. Available online: http://grc.sika.com/dms/getdocument.get/1d5e3ced-4748-3bf2-9f66-3b5cb8e403d5/010206020040000001_SikaWrap_350_G_gr.pdf (accessed on 7 August 2016).
- Sika® Monotop®-623. Available online: https://can.sika.com/dms/getdocument.get/91bef53e-75e5-3a27-b78c-2e8e67b244b8/SikaMonoTop623_pds.pdf (accessed on 2 November 2016).
- Ruredil S.p.A. Ruredil X Mesh Gold. Available online: http://english.ruredil.it/SchedeProdottoENG/RuredilXMeshGOLD_ing_1.pdf (accessed on 2 November 2016).
- ICC-Evaluation Service ESR-3265. Ruredil X Mesh C10 and Ruredil X Mesh Gold Fabric-Reinforced Cementitious Matrix (FRCM) Composite Systems. Available online: http://www.icc-es.org/Reports/pdf_files/load_file.cfm?file_type=pdf&file_name=ESR-3265.pdf (accessed on 7 August 2016).
- Ruredil S.p.A. Ruredil X Mesh C10. Available online: http://www.bob-fr.com/DOCPDF/ruredilxmeshc10_datasheet_0214en.pdf (accessed on 2 November 2016).
- ICC-Evaluation Service. 2013. Acceptance Criteria for Masonry and Concrete Strengthening Using Fiber-Reinforced Cementitious Matrix (FRCM) Composite Systems. AC434, Whittier, CA. Available online: http://www.icc-es.org/Criteria_Development/1110-post/17_AC434_final.pdf (accessed on 30 July 2016).
- Jabr, A.; Elragaby, A.; Ghrib, F. Flexural Strengthening of RC Beams Using Glass-FRCM. In Proceedings of the 5th International Structural Specialty Conference (CSCE 2016), London, UK, 1–4 June 2016.
- Ombres, L. Analysis of the bond between Fabric Reinforced Cementitious Mortar (FRCM) strengthening systems and concrete. Compos. Part B 2015, 69, 418–426. [Google Scholar] [CrossRef]


















| Group | Beam | Internal Steel Reinforcement | External FRCM Strengthening | % EAFRCM/EASteel | |||
|---|---|---|---|---|---|---|---|
| Bars | Reinforcement Ratio ρ | FRCM Material | # of Layers | E a A b (kN) | |||
| I | B2-0 | 2#10M | 0.18 ρb | - | - | - | 0 |
| B2-P | PBO | 2 | 1920 | 4.8 | |||
| B2-C | Carbon | 2 | 1200 | 3.0 | |||
| B2-G-4 | Glass | 4 | 1704 | 4.26 | |||
| II | B4-0 | 4#10M | 0.36 ρb | - | - | - | 0 |
| B4-P | PBO | 2 | 1920 | 2.4 | |||
| B4-C | Carbon | 2 | 1200 | 1.5 | |||
| B4-G | Glass | 2 | 852 | 1.06 | |||
| Type of Fabric | Young’s Modulus (GPa) | Ultimate Tensile strength (MPa) | Ultimate Tensile Strain (mm/mm) | Density (g/cm3) | Fiber Area, Af (mm2/mm) | Equivalent Thickness (mm) |
|---|---|---|---|---|---|---|
| Glass | 80 | 2600 | 0.0345 | 2.6 | 0.0475 | 0.023 a |
| PBO | 270 | 5800 | 0.0215 | 1.56 | 0.05 | 0.046 a |
| Carbon | 240 | 4800 | 0.018 | 1.82 | 0.05 | 0.047 b |
| Type of FRCM | Modulus of Elasticity of the Cracked Specimen Ef, (GPa) | Ultimate Tensile Strength ffu (MPa) | Ultimate Tensile Strain εfu (mm/mm) | Fiber Area per Unit Width Af (mm2/mm) | Axial Stiffness (EA) per 150-mm Strip (kN) |
|---|---|---|---|---|---|
| Glass 1 | 59.8 | 715 | 0.009 | 0.0475 | 426 |
| PBO 2 | 128 | 1664 | 0.018 | 0.05 | 960 |
| Carbon 3 | 80 | 1031 | 0.010 | 0.05 | 600 |
| Beam 1 | Experimental Load | Experimental Deflection | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yielding Load (kN) | Increase in Yielding Load (%) | Ultimate Load (kN) | Increase in Ultimate Load (%) | Theoretical Ultimate Load (kN) | Ratio of Exp./Theoretical Load | Def.@ Yielding Load (mm) | Defl.@ Ultimate Load (mm) | Def. @ Failure (mm) | Ratio of Pseudo-Ductility Index | Ratio of Post-Cracking Flexural Stiffness | Ratio of Post-Yielding Flexural Stiffness | Failure Mode * | |
| B2-0 | 39.8 | - | 52 | - | 50 | 1.04 | 8 | 53.6 | 53.6 | 1 | 1 | 1 | C |
| B2-P | 44.2 | 11.1 | 69.3 | 33.2 | 59.2 | 1.17 | 7.5 | 40.8 | 53.8 | 1.07 | 1.22 | 2.9 | DB-C |
| B2-C | 49 | 23.1 | 52.2 | 0 | 52.1 | 1 | 7 | 10.5 | 50 | 1.06 | 1.32 | 3.5 | DB-C |
| B2-G-4L | 46.1 | 15.8 | 54.2 | 4.2 | 55.2 | 0.98 | 7.5 | 19.4 | 64.5 | 1.28 | 1.19 | 2.6 | DB-R-C |
| B4-0 | 73.4 | - | 89.3 | - | 88.1 | 1.01 | 10.6 | 28.3 | 46.1 | 1 | 1 | 1 | C |
| B4-P | 90.1 | 22.7 | 111.4 | 24.7 | 98 | 1.14 | 10.1 | 34.3 | 44.7 | 0.88 | 1.25 | 1.07 | DB-C |
| B4-C | 86.2 | 17.4 | 91.4 | 2.3 | 94.2 | 0.97 | 10 | 15.4 | 37.8 | 0.76 | 1.23 | 1.06 | DB-C |
| B4-G | 70.5 | −3.9 | 88.6 | 0.9 | 93.1 | 0.95 | 10.6 | 25 | 44.9 | 1.02 | 1.01 | 1.01 | DB-R-C |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabr, A.; El-Ragaby, A.; Ghrib, F. Effect of the Fiber Type and Axial Stiffness of FRCM on the Flexural Strengthening of RC Beams. Fibers 2017, 5, 2. https://doi.org/10.3390/fib5010002
Jabr A, El-Ragaby A, Ghrib F. Effect of the Fiber Type and Axial Stiffness of FRCM on the Flexural Strengthening of RC Beams. Fibers. 2017; 5(1):2. https://doi.org/10.3390/fib5010002
Chicago/Turabian StyleJabr, Abdulla, Amr El-Ragaby, and Faouzi Ghrib. 2017. "Effect of the Fiber Type and Axial Stiffness of FRCM on the Flexural Strengthening of RC Beams" Fibers 5, no. 1: 2. https://doi.org/10.3390/fib5010002
APA StyleJabr, A., El-Ragaby, A., & Ghrib, F. (2017). Effect of the Fiber Type and Axial Stiffness of FRCM on the Flexural Strengthening of RC Beams. Fibers, 5(1), 2. https://doi.org/10.3390/fib5010002





