Properties of Scalable Chirped-Pulse Optical Comb in Erbium-Doped Ultrafast All-Fiber Ring Laser

Abstract

We report on a scalable chirped-pulse Er-doped all-fiber laser, passively mode-locked by single-wall carbon nitride nanotubes. The average output power is ~15 mW, which corresponds to a peak power of ~77 W, and pulse energy of ~1.9 nJ and was achieved using a single amplification stage. We observed chirped-pulse generation with a duration of ~24.6 ps at a relatively low repetition rate of ~7.9 MHz, with a signal-to-noise ratio of ~69 dB. To characterize the short-term stability of the obtained regime, we have measured the relative intensity noise of the laser, which is <−107 dBc/Hz in the range of 3 Hz–1000 kHz. It should be noted that the standard deviation of root mean square of average power does not exceed a magnitude of 0.9% for 3 h of measurement.

1. Introduction

Over the last decade, there has been an increase in the demand for high-energy and high-power laser systems of ultrashort pulses (USP) in areas such as various scientific applications [1], medical surgery [2,3], and industrial micromechanical processing [4,5]. However, the creation of such high-energy systems is a nontrivial task, which is caused by the complex nonlinear dynamics of ultrashort pulses. Recent studies show [6] that the chirped-pulse regime, also called dissipative solitons, can be a potential solution to this problem. Dissipative solitons are localized formations of the electromagnetic field, which are balanced by the exchange of energy with the environment in the presence of nonlinearity, dispersion, and/or diffraction [7]; the speed limits imposed by an electron sampler [8]. The method of amplifying chirped pulses is currently widely used for high-power optical amplification [9]. One of the advantages of dissipative solitons is an operation in the region of normal dispersion of group velocities, which will increase the pulse energy and reduce the influence of nonlinear effects [10]. Today, many research groups are conducting research related to the generation and amplification of chirped pulses. However, most of the research is based on the use of fibers with an increased mode area. Thus, using large mode area (LMA) fibers to overcome nonlinearity, Sobon et al. demonstrated a 50 MHz Er-Yb co-doped chirped pulse amplification system, generating 835 fs compressed pulses with an average power of 8.65 W [11]. The research team, led by M. Tang, generated dissipative solitons with a pulse energy of about 4 nJ and a pulse duration of about 30 ps, using an Er-doped double concentric fiber with a core combining high normal dispersion and large mode area [12]. Thus, since the appearance of the first works on the use of LMA fiber to create high-power fiber lasers, this approach has become widespread in this area [6,10,13].

However, it should be noted that the most common approach to LMA fiber fabrication is to complicate the fiber structure to obtain the lowest possible mode coupling during radiation propagation. This approach greatly complicates the fiber manufacturing process and therefore increases its cost, which in turn increases the cost of developing a laser. In this article, we used dispersion/nonlinearity and gain/loss control to create a chirped-pulse all-fiber USP laser, similar to the approach recently demonstrated in Bismuth-doped fiber lasers with a highly nonlinear cavity design by Khegai A. et al. [14]. For the first time, as far as we know, we propose to use a combined approach, which includes the use of carbon nanotubes and the regime of generation of dissipative solitons, which are known to have the best energy properties for further scaling [7]. We have developed an all-fiber erbium laser, operating in the second-order normal dispersion region, and single-wall carbon nitride nanotubes (C: BNNTs), used in lasers as a saturable absorber (SA) to reduce laser amplitude noise and provide reliable self-starting mode-locking (ML) [15,16]. As a result of the study, the stable generation of chirped pulses with a duration of 24.6 ps and a repetition rate of ~7.9 MHz was obtained. The average output power is ~15 mW, which corresponds to a peak power of ~77 W and pulse energy of ~1.9 nJ after one amplification stage. It should be noted that we measured the relative intensity of laser noise (RIN), which is <−107 dBc/Hz in the range 3 Hz–1000 kHz and the standard deviation(STD) of the average power root mean square(RMS) over a time of 3 h does not exceeded a value of 0.9%. These studies confirm a high level of generation stability compared to other devices of the same class [6,7].We hope that the presented concept opens up new opportunities for the development of low-cost high-energy mode-locked Er-doped fiber lasers.

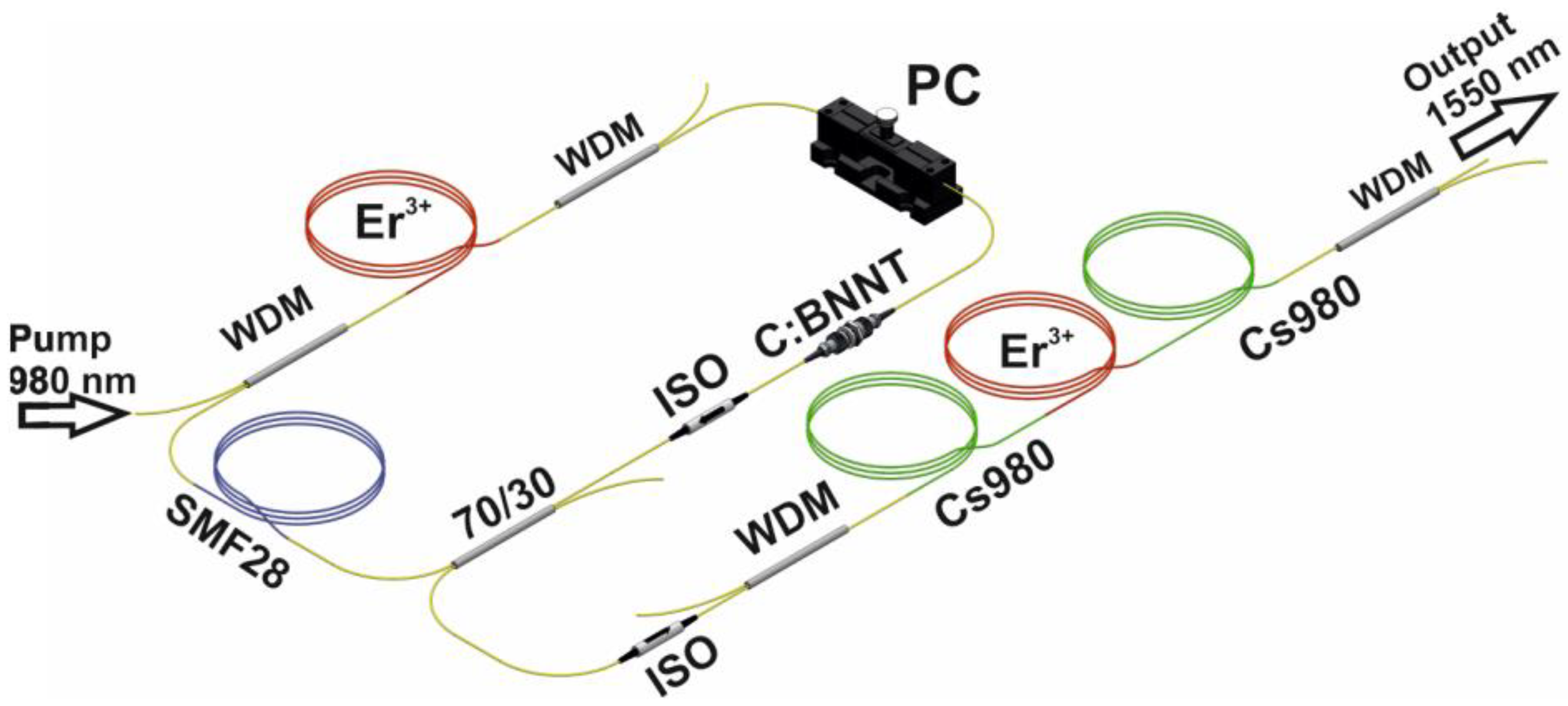
2. Materials and Methods

The experimental setup of the ML fiber laser is shown in Figure 1. The SWCNTs: BNNTs film was used as a slow passive SA inserted into a module formed by two FC/APC connectors. The SA used in the work has a response time of up to 0.5 ps and a modulation depth of about 12% (at 1550 nm), which is sufficient for the reliable start-up of USP generation [15]. Unsaturated losses of the SA used in the work were about 29.2 ± 0.5% [16]. To provide unidirectional generation, a commercially available polarization insensitive optical isolator (ISO) was used. To adjust the mode locking, a polarization controller (PC) was included into the cavity on one side of the ISO. The all-fiber ring cavity was formed by a 7.07 m active erbium-doped fiber (Lucent HE980) with a low signal core absorption of ~3 dB/m at the pump wavelength, with dispersion of D ~−54.6 ps/(nm∙km) at 1550 nm and 18.5 m SMF-28 fiber (Corning Corp.) with dispersion of D ~17.4 ps/(nm∙km) at 1550 nm. The lengths of the fibers were calculated to shift the total net-cavity GVD at 1550 nm into the slightly positive region and to ensure the chirped-pulse generation regime. The total net-cavity β₂ is estimated to be +0.12 ps² at 1550 nm.

A single-mode laser diode operating at the central wavelength of 980 nm with a maximum output power of 330 mW was used as the pump source for the erbium-doped fiber (EDF). Two wavelength demultiplexing filters (WDMs 980/1550) were used for inputting and outputting the pump radiation. The laser radiation was coupled out of the cavity through a fiber-optic coupler with a division ratio of 70/30. All-normal dispersion erbium-doped fiber amplifier (EDFA) with counter pumping was used to increase the linear chirp of the amplified pulses. EDFA also includes two wavelength demultiplexing filters for pump supply of the 10 m erbium-doped fiber with the same parameters as used inside the cavity.

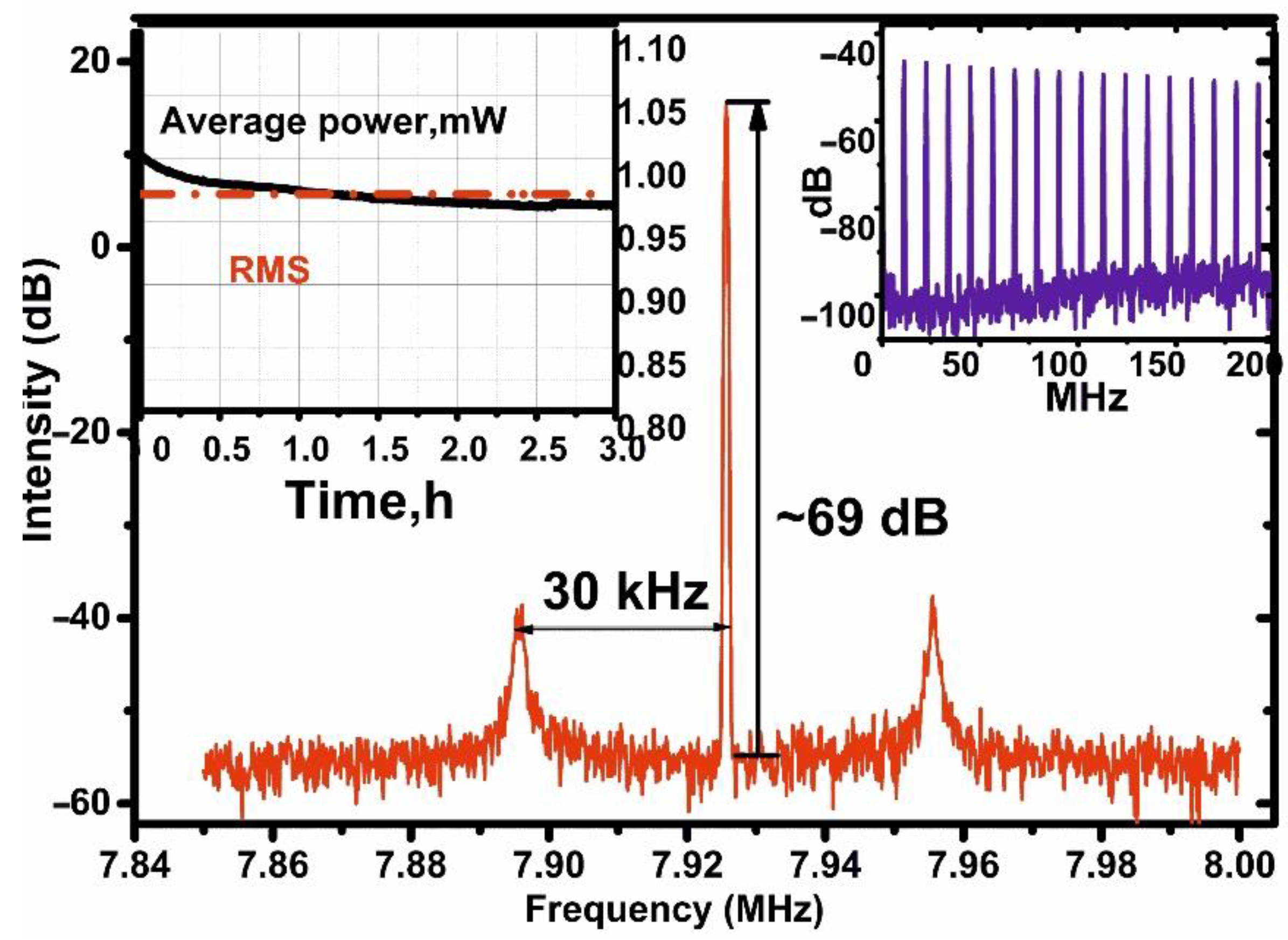
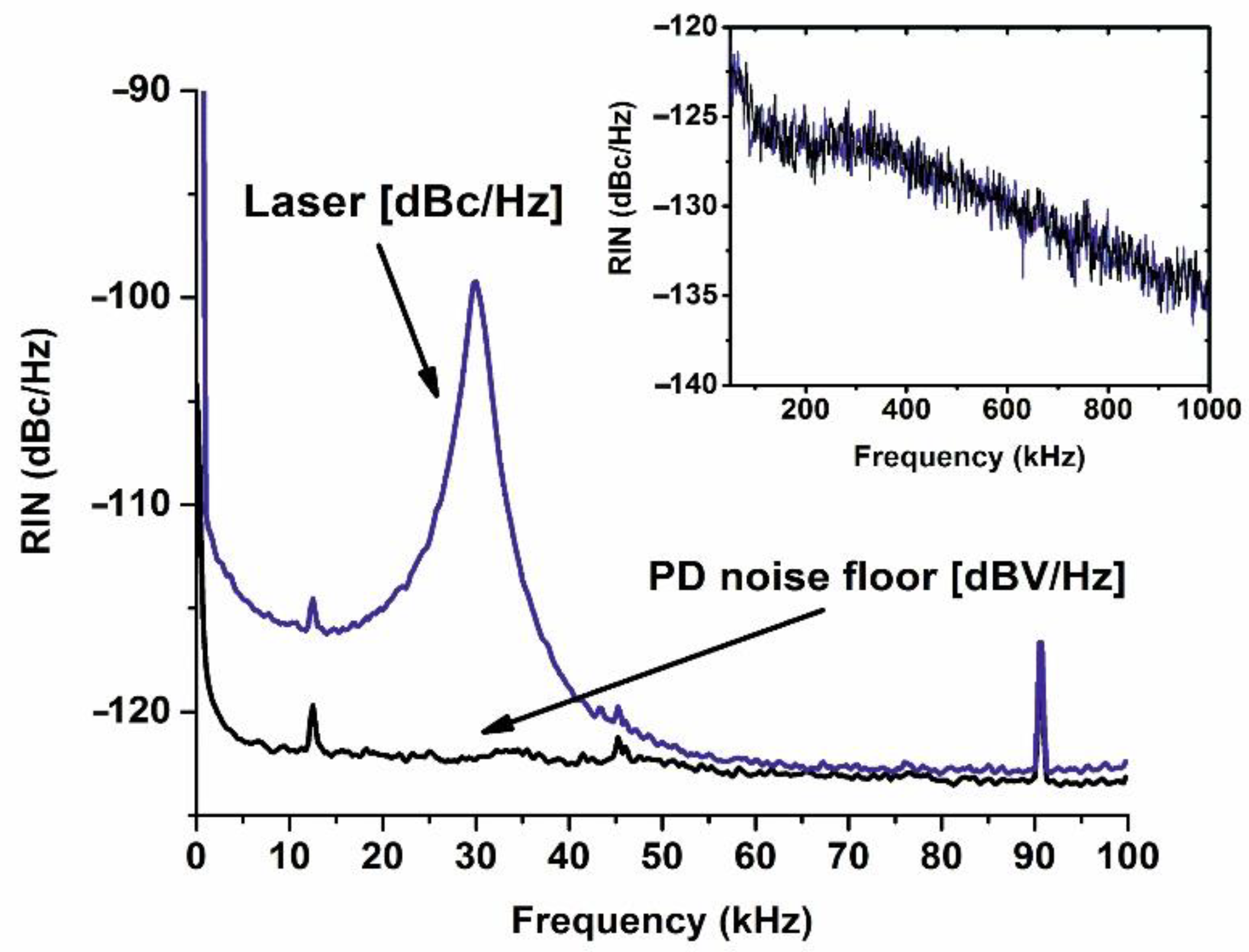
3. Experimental Results and Discussion

We have implemented a stable single-pulse self-starting generation of ultrashort pulses by adjusting the PC. The inset of Figure 2 shows the typical output pulse trace for obtained USP generation (using the oscilloscope Infinium MSO9254A; Keysight Technologies, Santa Rosa, CA, USA) at a repetition rate of 7.925 MHz corresponding to a total cavity length of ~25.57 m. The ML threshold was observed at an average pump power of ~33 mW, which is lower than usually reported in other refs connected with a chirped-pulse generation [17,18,19]. The average output power of the pulses is ~1 mW. It should be noted that such a low threshold ML compared to only ML based on NPE [20] is, on the one hand, explained by the use of C: BNNTs SA, which reliably triggers ML at low pump power, as well as complex dissipative dynamics, where the stable regime is only possible when there is a balance not only between dispersion and nonlinearity, but also in the intracavity gain and losses [7]. Figure 3 shows an experimentally observed optical spectrum before amplification at a central wavelength of 1558 nm, with a full width at half maximum (FWHM) of 15 nm (obtained using the Yokogawa AQ6370D spectrum analyzer). Remarkably, the spectrum is flat-top shaped with steep edges, which are inherent to chirped-pulse generation [7]. Unlike most of the works on dissipative solitons [21,22], no spectral filter is used for the mode-locking stabilization. The effect of spectral filtering in our laser is initiated by the effect of temporal filtering of C: BNNT itself since the generated optical spectrum is limited by the transmission spectrum of the used nanotubes (∆λ_tr ~30 nm) [16].

However, such a low ML threshold caused difficulties in recording the pulse duration. Since the peak output power of the master oscillator was too low to correctly record long pulse widths, the EDFA was used to amplify the pulses. No pulse breaking was observed after amplification of up to ~15 mW. Figure 2 shows the intensity autocorrelation (AC) trace after 10 times averaging (obtained by using the autocorrelator FR-103WS; FEMTOCHROME RESEARCH INC., Berkeley, CA, USA) and its Gaussian fitting. The red dashed line in Figure 2 shows the Gaussian fitting to the envelope of the experimental data (black dashed line). From the fitting, the autocorrelation width was estimated to be 31.8 ps which corresponds to 24.6 ps chirped-pulse width at FWHM. It results in a pulse width of assuming Gaussian pulse approximation. It should be noted that theoretically, the obtained pulses can be compressed in the case of full compensation of the chirp to a duration of about 170 fs, in accordance with the formula for pulses with the shape sech² [23]:

$${\tau }_{pulse}=0.315\frac{1}{\Delta {\nu }_{\left(FWHM\right)} }$$

(1)

where $\Delta {\nu }_{\left(FWHM\right)}$ is the width (FWHM) of the optical spectrum (about 1.86 THz in our case). The time-bandwidth product (TBP) of the pulses is equal to 35.9, indicating the presence of uncompensated chirp in the pulses. Relatively long pulses increase the intensity threshold of the nonlinear effects, such as self-phase modulation (SPM) and stimulated Raman scattering (SRS) in fiber, which could affect the laser performance in future applications. The inset of Figure 2 shows the typical output pulse train for USP generation (obtained by using the oscilloscope Infinium MSO9254A; Keysight Technologies, Santa Rosa, CA, USA).

To characterize the short-term stability of the obtained USP generation, we measured the radio frequency (RF) spectrum at the fundamental oscillation frequency of ~7.925 MHz, shown in Figure 3 (with a FEMTO 200 MHz HCA-S-200M InGaAs photodetector and using ESA FSL 3 model.03; Rohde & Schwarz GmbH & Co. KG, Munich, Germany) with a signal-to-noise ratio (SNR) ~69 dB (with ESA resolution 300 Hz). The inset in Figure 3 shows the RF spectrum in the frequency range 30 kHz–200 MHz (resolution bandwidth ~3 kHz). It should be noted that in addition to the main peak at a frequency of ~7.925 MHz, we observed two more side peaks (see Figure 3), shifted by ~30 kHz, which indicate the presence of modulation of the output signal intensity. However, the intensity modulation factor ∆I of the pulse train is estimated to be ~−39 dB, and these intensity fluctuations do not significantly affect the generation characteristics. Most likely, this feature is associated with the process of pulse formation and can be eliminated by optimizing the lengths of active and passive fibers in the cavity. There is also a slight intensity modulation in the RF spectrum (see inset to Figure 3), which is caused by current modulation on the pump diode driver.

To characterize the long-term stability of the obtained generation, we measured the output average power stability. The inset of Figure 3 shows the stability of the average optical output power with a standard deviation of ~0.9% RMS over a time of 3 h, determined mainly by temperature drift (measured with a PM200 power meter with an InGaAs S145C detector, Thorlabs Inc., Newton, NJ, USA). Additionally, we have measured the relative intensity noise (RIN) of a fiber laser with a maximum value of <−107 dBc/Hz, depicted in Figure 4, in the range 30 Hz–100 kHz (at 250 Hz resolution using ESA SR770FFT, Stanford Research Systems. CA, USA). The peaks on ~12 kHz and ~91 kHz are due to radio-frequency interference

The inset of Figure 4 shows the RIN in the high frequency range from 30 kHz to 1 MHz (300 Hz resolution using Rohde & Schwarz ESA, Munich, Germany) and corresponds to the level of PD + ESA noise floor by the black curve. It is obvious that in high-frequency range, the intensity noise level is lower than <−130 dBc/Hz and does not affect the output laser radiation. The main contribution in the total RIN level is described by 30 kHz peak that could be further suppressed as described previously.

4. Conclusions

In summary, the generation of stable chirped pulses in a ring resonator with a slightly positive second-order dispersion of +0.12 ps² was obtained. We observed chirped pulses with a duration of about 24.6 ps at a central wavelength of 1558 nm, with an average output power of 15 mW, corresponding to a maximum peak power of 77 W and maximum pulse energy of <1.9 nJ, after one amplification stage. The RIN value was <−107 dBc/Hz (3 Hz–1000 kHz) at a repetition rate of 7.925 MHz, with a signal-to-noise ratio of ~69 dB (with a resolution of ~300 Hz) in an erbium-doped ring laser with mode-locking, based on single-walled C: BNNTs SA. It should be noted that the standard deviation of the average output power did not exceed ~0.9% RMS in 3 h of measurements. Thus, the presented system is a splendid example of a high-energy laser, which can be used as a master oscillator in medical surgery and in industrial micromechanical processing, as well as a seeding laser in distributed temperature and strain fiber sensor systems.