Crustal Deformation Across and beyond Central Europe and Its Impact on Land Boundaries

Abstract

Land is a critical and limited natural resource. The Land Administration System (LAS) has been developed to resolve and adjudicate over any disputes that might arise concerning the rights and boundaries of land. Land registration and cadastre are types of land recording that need to be established. To secure the property rights, we must be sure of accuracy of the boundary points determining the size of the property. However, in addition to typical factors considered when determining the boundary point positions, such as accuracy of geodetic networks and measurement errors, the global and local crustal deformation, resulting, e.g., from the movement of tectonic plates, should be considered. In this work, the focus is on the movement of points inside the European plate due to tectonic movement, without taking into account local events caused by erosion, landslides, etc. The study area is Europe, and particular attention was paid to Poland, which is located in the centre of the European continent and does not have significant anomalous sub-areas, making it an authoritative research object. In this study, we analysed the velocity of point displacements and the boundary deformation, using GPS observations. For this reason, we used both global (IGS) and regional (ETRF) reference frames, to show differences in point velocities for the studied areas. Overall, for the needs of the real estate cadastre in Poland, information about parcel boundary points must be obtained with an accuracy better than 0.30 m. Within 25 years, the border mark may be shifted by 0.13 m due to tectonic plate movement, which is within the required accuracy. Pursuant to the current legal regulations, the measurements of the boundary points can be performed with any method, ensuring the required accuracy (0.30 m). The most commonly used are direct measurements (GNSS and tacheometry) and photogrammetric measurements. It is recommended that periodic verifications and update of the cadastre data in Poland be carried out at least once every 15 years. In the case of such relatively frequent verification and possible modernisation of data, the potential impact of tectonic plate movement on the relative boundary point displacement can be ignored, particularly in the short term. However, for a long time period it has an influence. We suggest “relatively frequent” cadastral boundary verification to be able to ignore such influence.

1. Introduction

The real estate cadastre is a public register, the purpose of which is to protect one of the most valuable rights, the property rights [1]. The extent of the property is determined by the location of the boundary points [2,3], and, therefore, these locations directly affects the area of the property, which in turn affects the value of the property [4,5]. Through it, boundary points are essential for the Land Administration System (LAS). It has to be noted that the cadastre remains a most important tool because it is capable of supporting all functions in the land management paradigm (noting that the cadastre is more correctly a number of tools within one conceptual framework). Indeed, any LAS designed to support sustainable development will make the cadastre its most important tool. The global idea of LAS is to determine the infrastructures for the implementation of land policies and land management strategies in support of sustainable development [6,7,8]. For this reason, when determining the location of the border point, it is necessary to be as accurate as possible and to take into account all possible variables influencing the obtained coordinates of the point [9]. The variables that affect the accuracy of the location of the border point are primarily errors in the geodetic control points’ positions used as a reference and the accuracy of the used method. This has to include the impact of, among others, errors in the geodetic control points’ positions used as a reference and the accuracy of the method used [10,11,12,13]. Another important aspect is to evaluate whether the accuracy of determining the location of boundary points is influenced by global and local crustal deformations due to plate tectonics.

Plate tectonics is the large-scale motion of nine large plates and many minor plates of the Earth’s lithosphere, which is the rigid crust and upper mantle (outermost shell) of the Earth. The lithosphere is cooler and more rigid and rides on the hotter fluid-like layer of the asthenosphere. The driving forces for tectonic plates motion are categorised into those related to mantle dynamics, gravity and Earth’s rotation. The friction between the mantle convection currents and gravity that exerts a downward pull on plates in subduction zones were considered as two main reasons for the plate motion due to mantle-dynamic forces. However, other theories, such as plume and surge tectonics, tried to modify earlier theories based on, e.g., 3D computer modelling [14]. Currently, gravity-related forces are considered as the main reason for plate motions and are divided into three sub-categories: the gravitational sliding away from a spreading ridge [15], slab pull [16] and the gravitational sliding away from mantle doming [17]. Other forces that have impacts on plate motions are the tidal effects due to the Sun and the Moon gravity, the polar motion, precision and nutation, the Coriolis and centrifugal forces. They are generally considered as the Earth rotation-related forces. The relative significance of these forces and their possible relationship is still under investigation. As the surveying points and boundary points are fixed on the tectonic plates, their absolute positions change over time.

The main aim of this study was to check the deformation of boundary points and answer the question of whether movement on the relative boundary point displacement is important for estimating the precise location of the cadastral parcel boundary points. This deformation was calculated based on positions and velocities of the EUREF Permanent GNSS Network (EPN) stations, in the global International GNSS Service reference frame (IGS14) and the local European Terrestrial Reference Frame (ETRF2014). These positions and velocities were derived from a multi-year combination of the EPN daily combined Station-Independent-Exchange Format (SINEX) files. The study was conducted in Europe, with special attention to Poland. Since it is located in the centre of the European continent and it does not have significant anomalous sub-areas, Poland is a reliable case study and thus this research has a universal character.

2. Background

The cadastral data are usually referenced to an ellipsoid, and the impact of vertical motions (heights) needs to be considered. Changes of heights, using a geoid as a reference surface, may be caused by: (i) locally by mining [18]; (ii) regionally by Earth crust movements [19]; and (iii) globally by the uplift of the sea level [20]. The last factor has the longest research history, for example, about 250 years for the area of the Baltic Sea [21]. The average trend of the Baltic Sea absolute uplift is about +1.3 mm/year, which is slightly below the global mean for the same period [21]. Relative to land, the value of movement in the southern part of this area is higher, whereas, in the northern part, the sea level is decreasing (down to −9 mm/year). This is due to the post-glacial rebound of the Scandinavian Peninsula. The absolute movement is calculated with the assumption of the Earth’s crust low-frequency movement, which permits treating changes of the absolute sea level as a difference between two datasets, i.e., changes of the sea level recorded by tide gauges and the vertical movement of Earth’s crust taken from GNSS permanent stations [22]. Satellite altimetry observations provide a little difference in the absolute value of the Baltic sea of +4 mm/year compared to a global uplift of +3.3 mm/year [23].

The cadastral data need to be defined in a well-defined coordinated frame, e.g., in a Terrestrial Reference Frame (TRF), which is based on a set of points with coordinates determined in a specific system [24], i.e., a Terrestrial Reference System (TRS). A Terrestrial Reference System (TRS) is a spatial reference system close to Earth’s surface and co-rotating with its diurnal motion in space. Its origin is the centre of the Earth’s mass (geocenter), the orientation is equatorial, with the pole in the Z-axis direction, and the scale is close to an SI metre [25]. Due to the geophysical effects (tidal and tectonic deformations), points on the solid surface of the Earth have small variations in time. These have been considered by using an International TRS (ITRS). The International Earth Rotation and Reference System Service (IERS) maintains, defines, promotes and realises the ITRS as defined by the International Union of Geodesy and Geophysics (IUGG) Resolution No. 2 adopted in Vienna, 1991 [26]. For details of the ITRS description and definition, the reader can refer to [27]. The International Terrestrial Reference Frame (ITRF) is a practical realisation of the ITRS. ITRF is regularly updated both by new data (e.g., reprocessing) and new strategies applied by analysis centres [28]. Twelve ITRF realisations have been published to date, starting with ITRF88 up to the latest, currently operational ITRF2014 [29]. WGS84 (World Geodetic System 1984) has been connected with ITRS since 1994 [30] and shows consistency at about 10 cm level. ITRF realisation is based on four techniques: GNSS (Global Navigation Satellite System), SLR (Satellite Laser Ranging), VLBI (Very Long Baseline Interferometry) and DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite) [31].

ITRF is currently the most accurate global reference frame, defined by the above techniques, although none of them can provide alone the defining parameters of a full reference frame. The ITRF origin is defined by SLR data, the scale is determined by SLR and VLBI and the ITRF orientation is maintained by successive ITRF releases [32]. Each ITRF combination highly depends on the availability of sites where at least two observation techniques (GNSS, VLBI, SLR and DORIS) are operated and local surveys between instrument measuring points are available. These local surveys are usually conducted either by a precise GNSS technique or by terrestrial instruments (precise total stations, levels). Connections between the positioning reference points are provided by agencies, where ITRF sites are operating, using least square adjustments of local surveys [29]. Usually, a current ITRF_yy is used, where “yy” denotes the year of the ITRF realisation. In some areas, fiducial station coordinates might be available in a local system (usually of a continent-size), e.g., ETRS (European Terrestrial Reference System) and its practical realisation ETRF_yy (European Terrestrial Reference Frame) for Europe.

In this paper, we investigate the effect of local tectonic movements on the location (defined by coordinates) of the parcel’s boundary points. To determine the above-mentioned impacts, EPN (European Permanent GNSS Network) reference stations’ velocities based on multi-year observations were used. From these velocities, practical movements were determined that may affect the change of the location of boundary points, which should be determined with the highest possible accuracy. For this reason, it is important to know whether it is necessary to take into account the movements of the tectonic plates when determining the location of boundary points.

Conversion between coordinates from different realisations, e.g., from $\left(X_1, Y_1, Z_1\right)$ to $\left(X, Y, Z\right)$, could be done using a seven-parameter similarity transformation expressed as [33,34]:

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{c}{X}_1\\ Y_1\\ Z_1\end{array}\right]+\left[\begin{array}{c}{T}_1\\ T_2\\ T_3\end{array}\right]+\left[\begin{array}{ccc}k& R_z& -R_y\\ -R_z& k& R_x\\ R_y& -R_x& k\end{array}\right]\left[\begin{array}{c}{X}_1\\ Y_1\\ Z_1\end{array}\right]$$

(1)

where $T_1, T_2, T_3$ are translation parameters, $R_x, R_y, R_z$ are rotation parameters and $k$ is a scale factor. According to the ITRF definitions and realisations, it is a kinematic (dynamic) frame, where points on the Earth’s crust exhibit position changes caused by local and global tectonic movements. As a result of that, each ITRF solution contains coordinates and velocities of its fiducial stations at a specific epoch expressed as [35]:

$${\mathit{X}}^i\left(t_c\right)={\mathit{X}}^i\left(t_0\right)+{\dot{\mathit{X}}}^i\left(t_c-t_0\right)$$

(2)

where ${\mathit{X}}^i\left(t_c\right)$ is the $[X, Y, Z]$ Cartesian coordinate vector of a fiducial station I at the epoch $t_c$, ${\mathit{X}}^i\left(t_0\right)$ is its known coordinate vector at the reference epoch $t_0$ and $\dot{\mathit{X}}$ is the corresponding velocity vector. To estimate these velocities, an absolute tectonic plate motion model was determined based on the observations in the ITRF2014 (Figure 1), using high-quality observations from 206 core sites [36,37].

3. Methods

The International Association of Geodesy (IAG) Sub-commission for the European Reference Frame (EUREF) created Resolution 1 at the 1990 meeting in Florence, states: “The IAG Subcommission for the European Reference Frame recommends that the system to be adopted by EUREF will be coincident with the ITRS at the epoch 1989.0 and fixed to the stable part of the Eurasian Plate and will be known as European Terrestrial Reference System 89 (ETRS89)” [39]. According to this definition, ETRS89 is relative to the ITRS through similarity transformation. Based on the current realisation of ITRF_yy, a corresponding reference frame in ETRS89 called ETRF_yy is established based on core sites defined in the ITRF and located in Europe. Figure 2 shows the calculation framework between current realisations of ITRF and ERTS89 at an input epoch $t_0$ to an output epoch $t_c$.

In this work, an investigation of the deformation of boundary points is carried out. This deformation is calculated based on positions and velocities of EPN stations, in the global International GNSS Service reference frame (IGS14) and the local (ETRF2014) reference frames, derived from a multi-year combination of the EPN daily combined SINEX files. This multi-year solution is used for the realisation of the regional densification of the ITRF_yy/IGS_yy between two releases and for the maintenance of the ETRS89. The multi-year combination comprises EPN-repro2 daily SINEX files from GPSweek 834 to GPSweek 1772 and routine daily EPN combined SINEX files from GPSweek 1772 to the most recent solutions. The multi-year solution is updated every 15 weeks in order to provide up-to-date coordinates and velocities [41].

There are two possibilities of transformation between station coordinates from ITRF_yy to ETRF_yy at an epoch $t_c$ [39]:

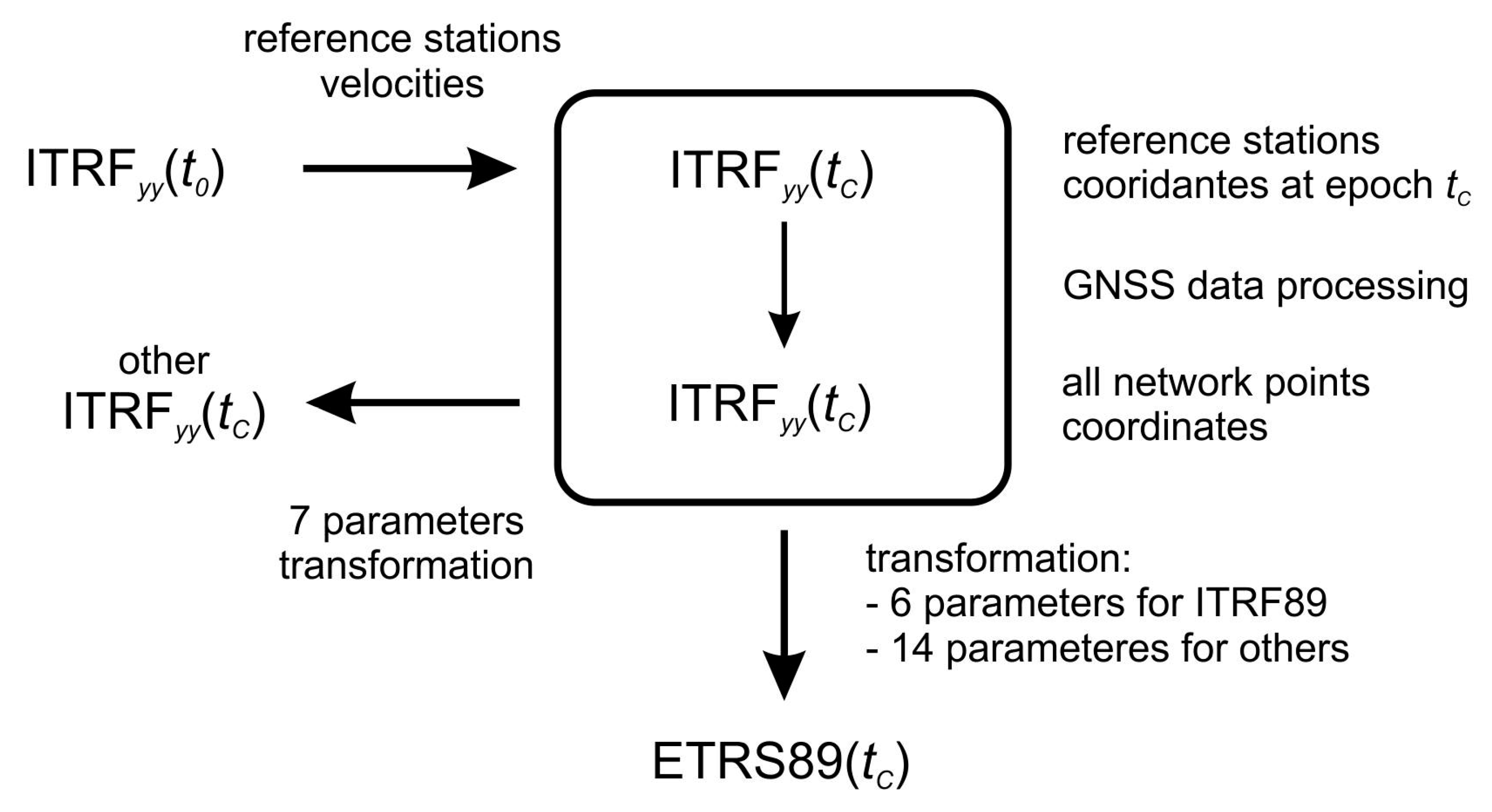
• GNSS solutions of the selected points are processed in ITRF_yy (e.g., ITRF2014) and transformed to the target ETRS89 reference frame, the ETRF_yy (e.g., ETRF2014), corresponding to the ITRF_yy. Calculations are made by a simple formula:

  $$X_{yy}^E\left(t_c\right)=X_{yy}^I\left(t_c\right)+T_{YY}+\left[\begin{array}{ccc}0& -\dot{R}{3}_{yy}& \dot{R}{2}_{yy}\\ \dot{R}{3}_{yy}& 0& -\dot{R}{1}_{yy}\\ -\dot{R}{2}_{yy}& \dot{R}{1}_{yy}& 0\end{array}\right]\times X_{yy}^I\left(t_c\right)·\left(t_c-1989.0\right)$$

  (3)

  and for the velocities:

  $${\dot{X}}_{yy}^E\left(t_c\right)=\dot{X_{yy}^I}+\left[\begin{array}{ccc}0& -\dot{R}{3}_{yy}& \dot{R}{2}_{yy}\\ \dot{R}{3}_{yy}& 0& -\dot{R}{1}_{yy}\\ -\dot{R}{2}_{yy}& \dot{R}{1}_{yy}& 0\end{array}\right]\times X_{yy}^I$$

  (4)

  where $X$ and $\dot{X}$ refer to station positions and velocities, respectively, and the indexes $I$ and $E$ represent the systems ITRS and ETRS89, respectively. The rotation rate parameters $\dot{R}{1}_{yy}, \dot{R}{1}_{yy}, \dot{R}{1}_{yy}$ are expressed in the ITRF_yy and translation vector $T_{yy}$ is the global offset between ITRF versions. The rotation and translation values are available in the literature [39].
• GNSS solutions are processed in ITRF_yy (e.g., ITRF2008) and the target ETRS89 reference frame is ETRF_xx (e.g., ETRF2000), which do not correspond to the ITRF_yy. Calculations are made in two steps: transforming coordinates at the epoch $t_0$ from ITRF_yy into ITRF_xx using Equation (1) and from epoch $t_0$ to epoch $t_c$. The second step is similar to Point 1, by using Equations (3) and (4).

Because ETRF_yy is realised and maintained by stations located on the European territory, the velocities are much smaller than those in the global ITRF_yy. Figure 3 shows the ETRF2014 horizontal velocity field (left) and vertical velocity (right) derived from the latest EPN cumulative solution. Note that the scale of horizontal displacements in Figure 1 (left) and Figure 3 (left) are different. Most of the European territory has <1 mm/year horizontal and vertical velocities. In the case of horizontal velocities, only a couple of stations, located in Turkey and the Apennine and Balkan Peninsulas, experience velocities significantly larger than 1 mm/year. As can be observed, the vector directions have a stochastic character. Therefore, in addition to global and local tectonic plate movements, the error in velocity determination must be taken into account for these stations. In the case of vertical displacement, for both ITRF2014 and ETRF2014 the velocity magnitudes are at the 1–2 mm/year level, except for the Fennoscandia region (the region including the Scandinavian Peninsula, Finland, Karelia and the Kola Peninsula) and Icelandic territory, which are uplifted against the rest of the European territory [42,43].

4. Results

Land and buildings are the basic objects of cadastral parcels. Determining the location and shape of the cadastral plot is therefore limited to determining locations of its boundary points. Since point locations are defined by their coordinates, the cadastre objects spatial accuracy will be directly related to the accuracy of determining these boundary points’ coordinates. These coordinates can be obtained by

• Direct field measurements
• Photogrammetric measurements
• Carthometric measurements

The most accurate method is positioning using direct field measurements, such as by using precise GNSS measurements and angular-linear measurements of total stations [44,45]. This kind of the measurements is used in various engineering areas (e.g., [46,47,48]). The accuracy of the photogrammetric measurements depends on the used scale and accuracy of the control points and type of land cover, and, in general, they are used for large areas. Information on the boundary point location can also be obtained from geodetic carthometric measurements (vectorisation and digitisation); however, these methods are not considered accurate enough. The low quality of their data is due to the fact that such data are obtained in a secondary process, which involves processing existing information into another form. In each of the indicated methods, the measurements are made with reference to geodetic control points with known coordinates. In the case of measurements made in small areas, it can be assumed that both the control points and boundary marks are located on the same tectonic plate and move in the same direction. In a local context, the shift of boundary characters using geodetic control points with specified coordinates that are not updated would be impossible to determine.

Based on the multi-year observations from 249 permanent reference stations covering the European continent, their positions and velocities are determined and made publicly available in both global (IGS14) and local (ETRF2000 or ETRF2014) reference frames at epoch 2010.0 [41]. Based on these products, the tectonic plate movements and velocities are computed, and contour values of the velocities are illustrated in Figure 4 and Figure 5. Since the point coordinates of parcel’s boundaries are shown in plane coordinates (X and Y), only these are analysed.

The same scale is used in Figure 4 and Figure 5 for better interpretation that shows the magnitudes of velocities in the global (IGS14) and local (ETRF2014) reference frames.

Figure 4 shows velocities in the X and Y direction in the global IGS14. Resultant of these two components is a very clear northeast direction 2D movement with a mean amplitude of 22–25 mm/year for the centre of Europe (computed as the square root of the sum of the squares of movements in X and Y directions). The Balkan and Turkey area is an exception (Peloponnese, especially). Three stations (PAT0, DYNG and TUC2) indicate no X change. Their differences are better shown in the ETRF2014 frame (Figure 5) by removing the mean shift between the two frames. Very low amplitudes of Y is shown for almost the whole European plate. The changes in X are more diverse. At least some of them have an anthropodermic origin, e.g., in the Ruhr Region (Germany)—where long term mining activity causes numerous (1000/year) earthquakes of small magnitudes [49], which is noted by the station EUSK (Figure 6). The Balkan and Turkey area is the only region where X movements have an opposite direction.

In the analysis, we focus on the territory of Poland. It is located in the centre of Europe and it does not have any significant anomalous sub-areas. The impact of mining is significantly lower than in other areas, such as the Ruhr Region. Only the EPN station (KATO) in this area has an X velocity value of 1.6 mm/year (ETRF2014), whereas the rest of the stations do not exceed 1 mm/year. Figure 7 gives the EPN stations’ location and

Table 1. EPN stations’ location and velocities located within 49–55° N and 15–24° E.

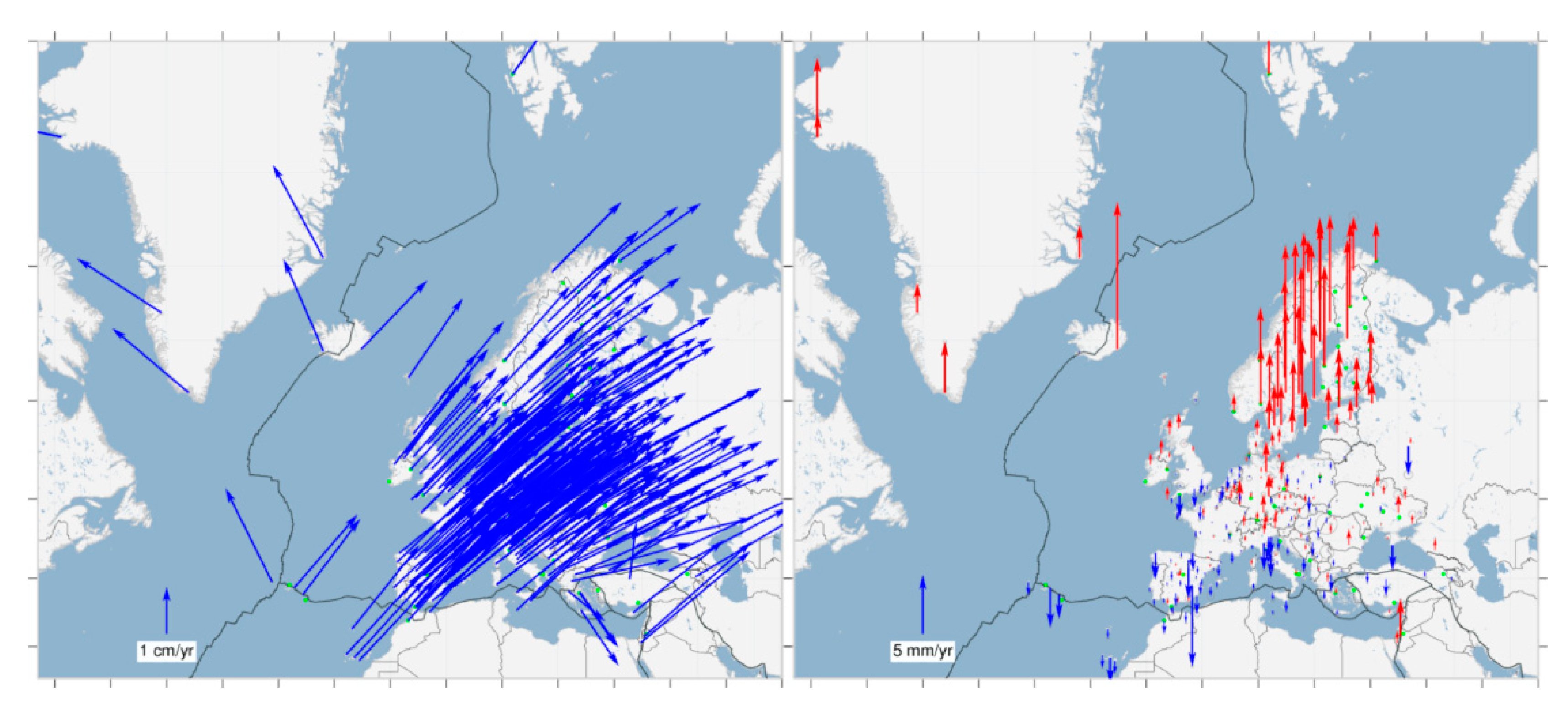
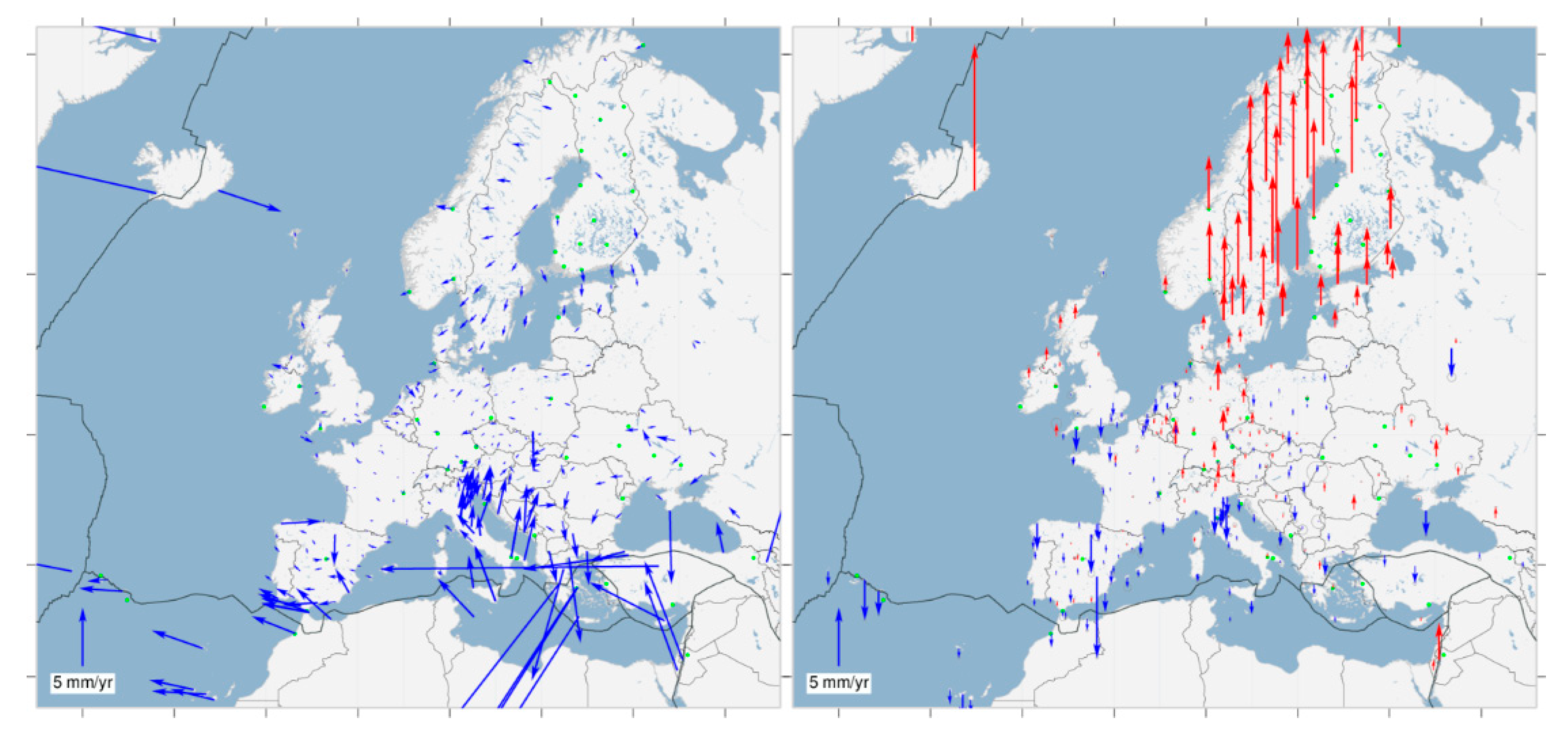
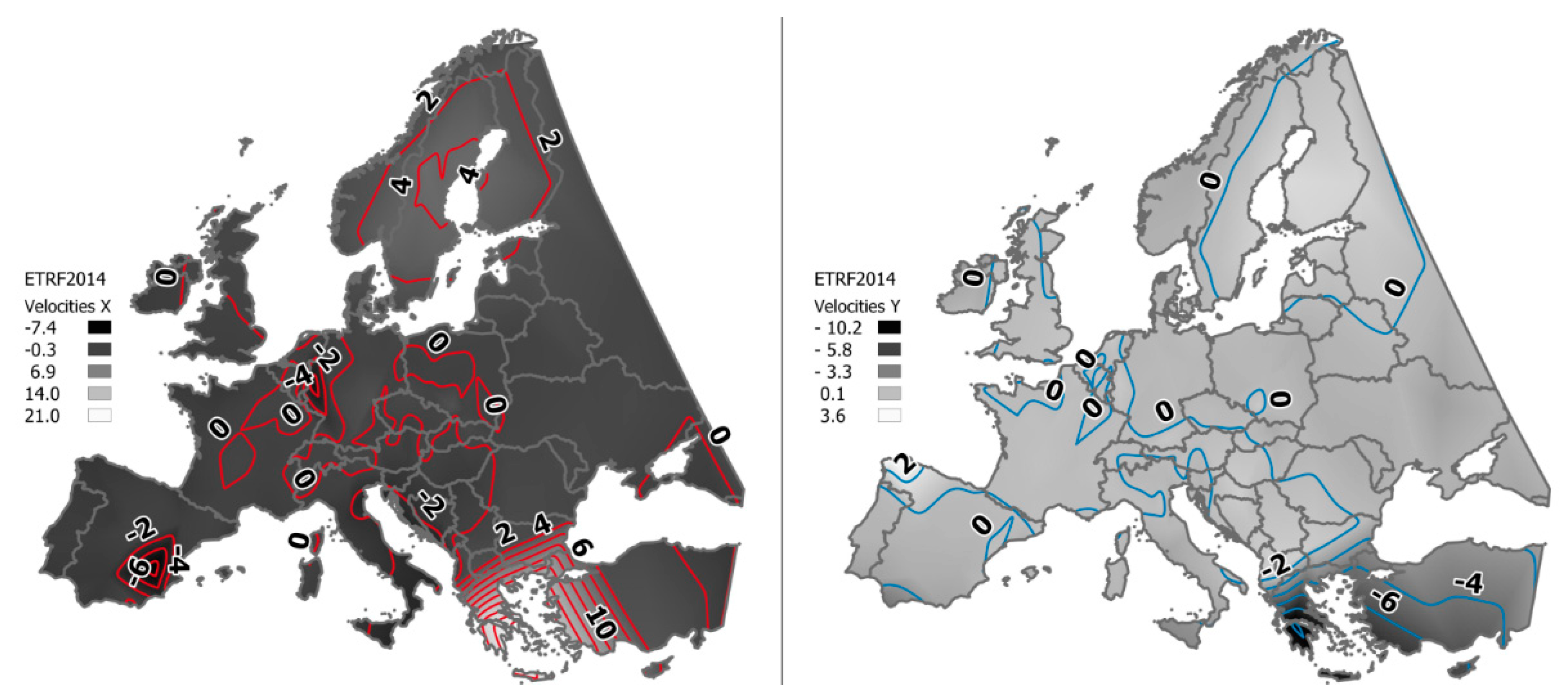
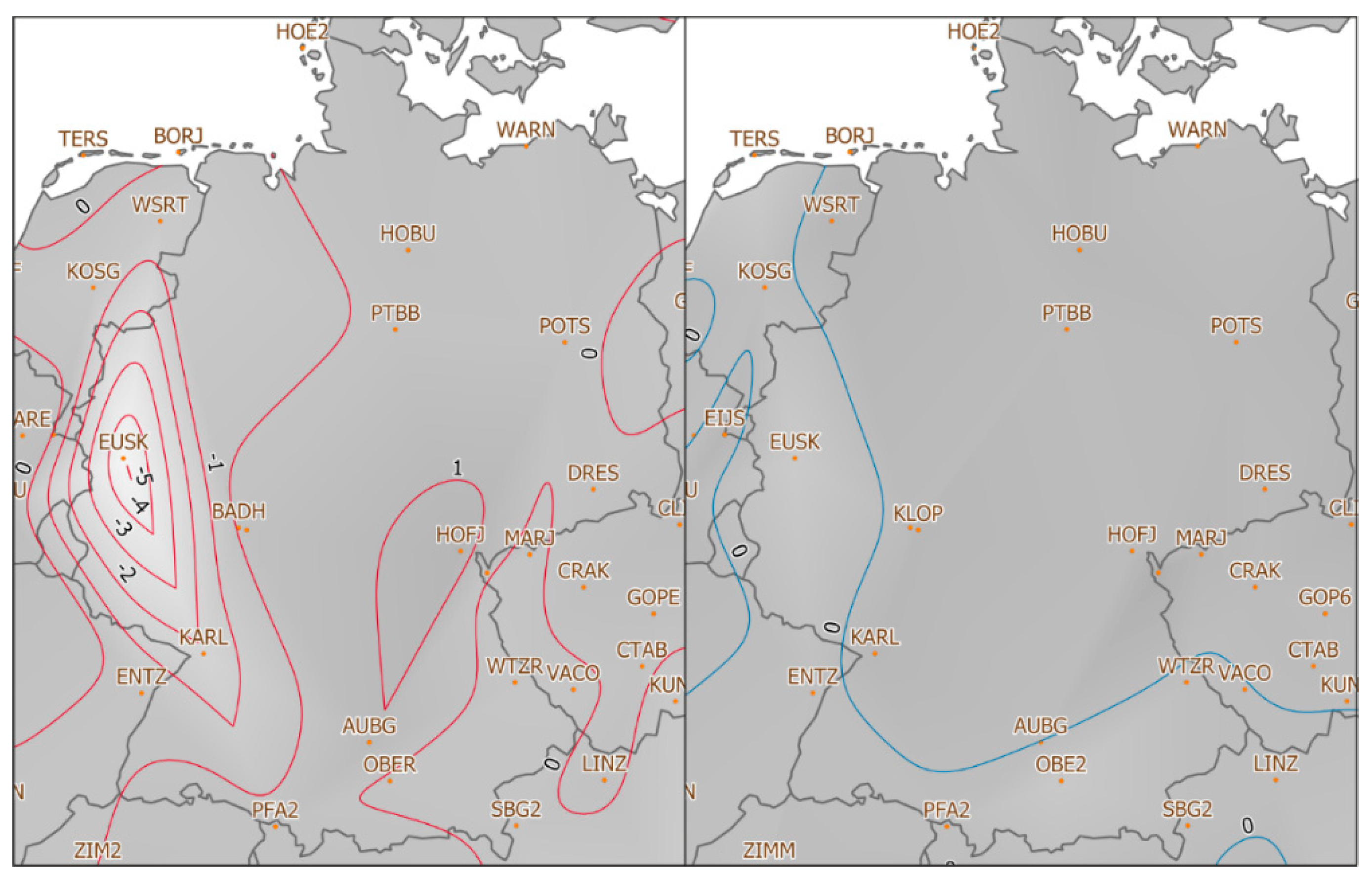
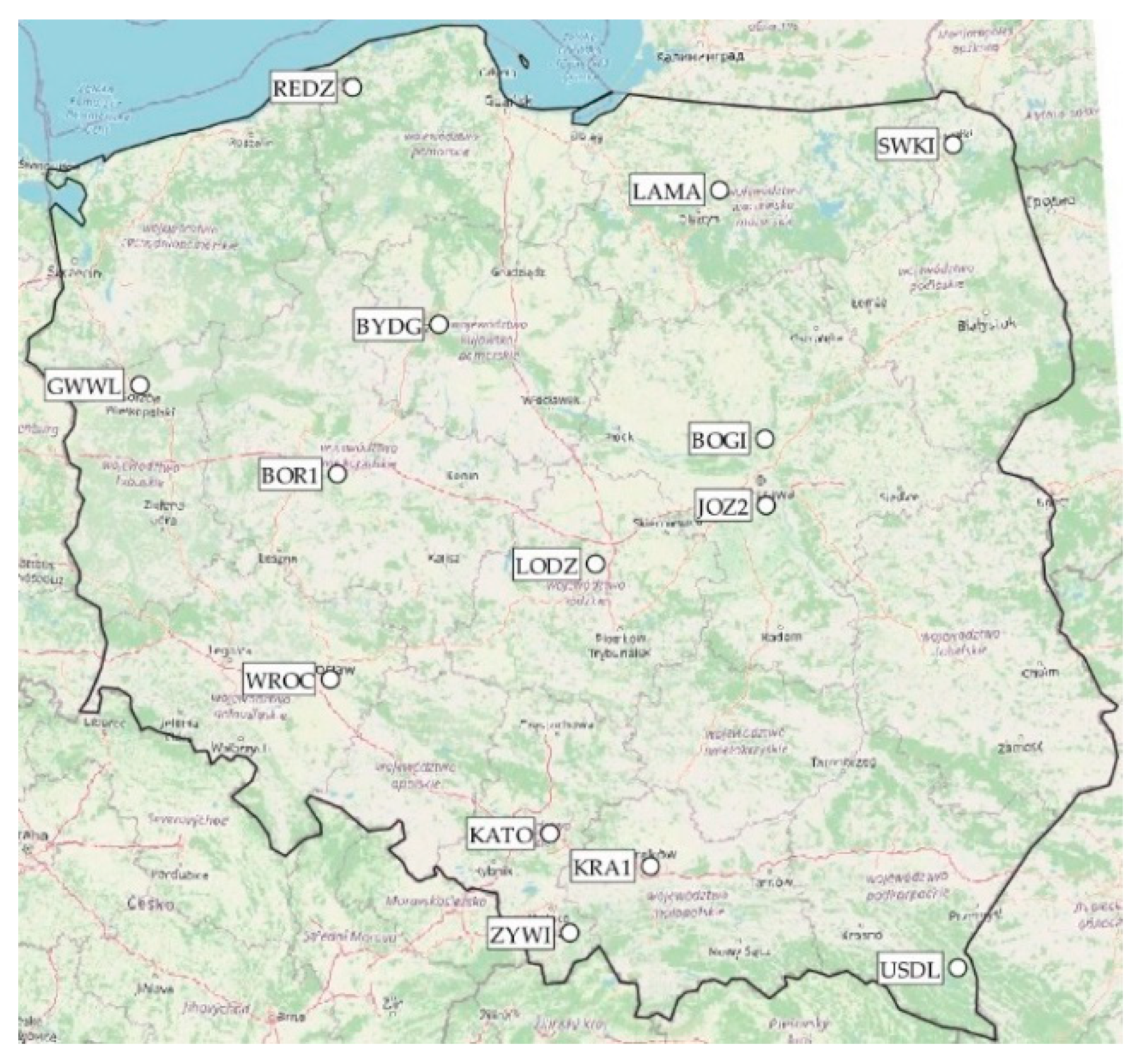
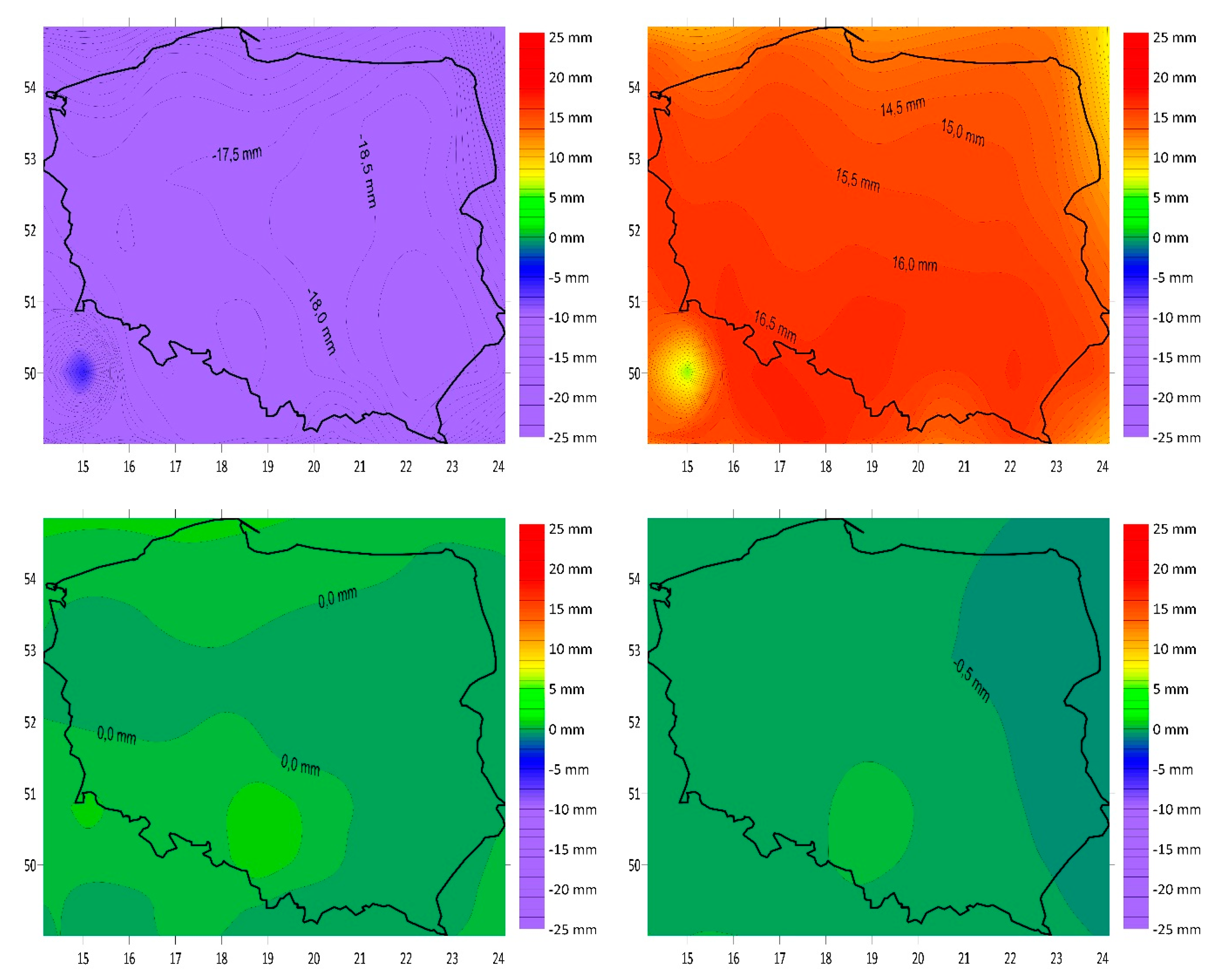
Station	Vx (mm/year)	Vy (mm/year)
BISK	0.1	−0.2
BOGI	0.1	−0.3
BOGO	−0.1	−0.6
BOR1	−0.1	−0.3
BYDG	0.0	−0.4
CFRM	0.2	−0.1
CLIB	0.7	−0.4
CPAR	0.2	−0.3
GWWL	−0.5	−0.5
JOZ2	0.0	−0.3
JOZE	0.0	−0.3
KATO	1.6	0.7
KRA1	0.2	−0.2
KUNZ	−0.7	0.0
LAMA	0.0	−0.4
LODZ	−0.4	−0.2
REDZ	0.5	−0.1
SWKI	−0.2	−0.9
TUBO	0.0	−0.1
USDL	−0.3	−0.4
WROC	0.1	−0.5
ZYWI	−0.3	−0.4

shows velocities in this area.

Poland has annually a seismic activity of about 150 low-magnitude earthquakes [51], compared to about 1000 in the Ruhr Region [49]. Thus, the impact of plate movement on cadastral data may be observed with an insignificant influence of local anomalies.

The authors determined the maximum displacements in the X and Y directions that occurred in Poland in the past 10, 25 and 50 years (

Table 2. Long-term velocities for three different periods (10, 25 and 50 years).

Reference Frame	Velocity Direction	10 Years (m)	25 Years (m)	50 Years (m)
IGS14	X	0.19	0.48	0.95
	Y	0.17	0.41	0.82
	XY	0.25	0.63	1.25
ETRF2014	X	0.05	0.13	0.25
	Y	0.05	0.13	0.25
	XY	0.07	0.18	0.35

). These values were calculated from the mean velocities for each coordinate direction of the points located within Poland’s territory, based on approximation of the velocities map, as shown in Figure 8.

These analyses show a few decimetres in the case of the global (IGS14) reference frame for a 10–25-year period, and close to 1 m for 50 years. In the case of the local European reference frame (ETRF2014), these values are 3–4 times smaller, and it was between 7 and 35 cm for the cumulative XY vector for the 10- and 50-year periods, respectively.

5. Discussion and Conclusions

Tectonic plate movements are noticeable, primarily in the global reference frames (ITRF and IGS realisations). Studies have shown a clear 2D northeast direction movement with a mean 22–25 mm/year amplitude for the centre of Europe in the global IGS14. In this context, shifts towards the northeast of 25 mm/year can be observed in Poland’s territory. The use of the ETRF frame reduces the shifts usually below 1 mm/year. For the needs of the real estate cadastre in Poland, information about parcels’ boundary points must be obtained with an accuracy of better than 0.30 m. This accuracy includes, among others, geodetic network errors and measurement errors. Within 25 years, the border mark may be shifted by 0.13 m (ETRF2014) due to the tectonic plate movement. Considering relative shift of points on the same tectonic plate, this accuracy is negligible noting the required accuracy for border points. Periodic verifications of cadastre data in Poland must be carried out at least once every 15 years (due to [52]), with the data stored in the cadastre regularly updated. In the case of such relatively frequent verification and possible modernisation of data, the potential impact of tectonic plate movement is expected to be negligible. The measurement methods used to determine the location of the boundary points utilise the control points network that move in the same way. Therefore, using traditional measuring methods, it is not possible to determine the offset resulting from the global and local crustal deformations in the absolute sense. It can be concluded that, for areas with low tectonic activity, the impact of such deformations on data disclosure in the real estate cadastre is negligible. Moreover, the movement of the plates has no effect on the surface area of the registration plots presented in the land and building database.

Concluding, this research clearly showed that the tectonic plate movement has marginal impact to the real estate cadastre in a tectonically stable regions, such as Poland. However, even this small and insignificant impact on the changes of points in some areas is still noticeable. This boils down to the conclusion that, in other, more active regions, these changes may already make a difference. The areas located in the vicinity of transformational faults (horizontal) deserve special attention, e.g., the San Andreas Fault in California, USA or the Alpine Fault on New Zealand’s South Island, where the rates of slippage average about 33–37 [53] and 40 mm/year [54], respectively). This clearly shows the need for this kind of research at different spots of the Earth. At these locations, the automation of the survey system would see the digital capture of land parcel dimensions [55], but to this end we need more research from various points of the Earth. Through connection to the geodetic network, geodetic coordinates would be assigned to parcel boundary points resulting in a coordinate cadastre. As the geodetic network moves, reflecting ground movements, adjustment for this effect could be applied to boundary points forming a dynamic coordinate cadastre. In this manner, coordinates of boundary points would encapsulate available evidence of their true ground positions [55]. Such a research can be a good benchmark. Since land administration is an important tool for delivering sustainable development [6], the cadastre has extended purposes. The cadastres provide the authoritative description of how people relate to specific land and property, and they provide basic and authoritative spatial information in digital land information systems.