The Optimal Transportation Option in an Underground Hard Coal Mine: A Multi-Criteria Cost Analysis
Abstract
:1. Introduction
- filling the gap in the economic methodology of complex transportation systems evaluation;
- embedding considerations in the trend concerning complex transportation systems of underground mines;
- focusing considerations on the pre-investment phase, making it possible to optimize costs before expenditures are incurred.
2. Materials and Methods
- KK1: costs of implementing the transportation task;
- KK2: costs of route expansion;
- KK3: rolling stock maintenance costs;
- KK4: depreciation costs;
- KK5: additional personnel costs.
- wk—total cost criterion scoring (100 points),
- nk—number of cost criteria (pcs)
- wki—scoring in the cost criterion “j” (K point).
- pkij—scoring of criterion “i” of variant “j” (K point),
- kmax—maximum cost, kmax = max (k1, …, ki, …, kn) (PLN),
- kmin—minimum cost, kmin = min (k1, …, ki, …, kn) (PLN),
- ki—cost of the variant “i” (PLN),
- wkj—scoring of the cost criterion “j” (K point).
2.1. KK1 Criterion—Costs of Implementing the Transportation Task
- Kzt—costs of implementing the transportation task (PLN),
- Kp—cost of fuel or electricity (PLN),
- Kr—labor cost (PLN),
- Ka—depreciation cost of the means of transportation (PLN),
- Ke—cost of consumables, maintenance and repair (PLN).
- Kp—fuel cost (PLN),
- Ke—electricity cost (PLN),
- Kzts(e)—cost of carrying out the transportation task using internal combustion (electric) means of transportation (PLN),
- zpP—unit fuel consumption of the tractor (g/kWh),
- Pp—engine power (kW),
- pss—motor power utilization factor (0.7–0.9),
- pse—electric motor power utilization factor (0.8–0.9),
- kon—unit cost of fuel (PLN/dm3),
- kpe—unit cost of electricity (PLN/kWh),
- δp—fuel density (kg/m3),
- rdo—value of an operator’s working day (PLN),
- rdm—value of a shunter’s working day (PLN),
- tot—duration of maintenance (min),
- tztp—duration of transport to an average distant point (min),
- zzmi—number of transport tasks possible during a shift.
- kmax = kzt max—highest cost of implementing the transportation task (PLN),
- kmin = kzt min—lowest cost of implementing the transportation task (PLN),
- ki = kzti—cost of implementing the transportation task in the variant “i” (PLN),
- wkj = wkk1—weight, the maximum number of points in criterion KK1 (K point).
2.2. Criterion KK2—Costs of Route Expansion
- Krt—cost of route expansion (PLN),
- Krcz—total cost of track elements (PLN),
- Krzt—cost of transporting track elements (PLN),
- Krr—labor cost (PLN),
- Krp—cost of pit reconstruction (PLN),
- Kmech—cost of using mechanization equipment for track construction (PLN).
- ktemi—cost of materials of the elementary track section type “i” (PLN/m),
- kpi—cost of materials of the basic track section of type “i” (PLN),
- lpi—length of the basic track section of type “i” (m).
- kcs—labor cost per day of a track carpenter (PLN),
- ncsi—occupancy of a brigade of track carpenters to build track type “i” (person),
- pti—length of track section of type “i” built in one shift by a brigade of track carpenters (m).
- kcs—labor cost per day of a track carpenter (PLN),
- ncs—occupancy of a brigade of track carpenters to build curves of the route or turnouts (person),
- nł(r)—number of curves (turnouts) built during one shift by a brigade of track carpenters (pcs).
- mine underground railroad track—bolts and nuts of various sizes, washers, spacers, lugs,
- suspension railroad track—slings, traverses, chains, brackets, stays, bolts,
- floor railways track—bolts and nuts of various sizes, anchors, and railroad loads.
- Krp—cost of transportation route expansion (PLN),
- muk—number of types of transportation systems (pcs),
- αri—the probability of expansion of transport system type “i”
- (αr1 + … + αrn = 1),
- ktei—cost of an elementary section of track type “i” (PLN/m),
- ldi—length of track section of type “i” (m),
- kri—cost of building a turnout of track type “i” (PLN/pc),
- nrri—number of turnouts in the transportation system of type “i” (pcs),
- kłi—cost of building a curve of track type “i” (PLN/pc),
- nłi—number of curves in the transportation system of type “i” (pcs).
- kmax = krpmax—highest route expansion costs (PLN),
- kmin = krpmin—lowest route expansion costs (PLN),
- ki = krpi—cost of route expansion in the variant “i” (PLN),
- wkj = wkk2—weight, the maximum number of points in criterion KK2 (K point).
2.3. Criterion KK3—Rolling Stock Maintenance Costs
- ndb—designated number of rolling stock to the baseline (pcs),
- nd—adjusted number of rolling stock (pcs),
- gt—technical readiness factor of rolling stock type “i”.
- Ku—maintenance costs (PLN),
- kot—cost of materials and consumables (PLN),
- knp—the cost of spare parts replaced during repairs (PLN),
- krot—labor cost—maintenance (PLN),
- krnp—labor cost—repairs and overhauls (PLN).
- kotm—monthly cost of maintenance (workshop) of rolling stock “i” (PLN),
- kem—annual labor cost of an employee in the position of a mechanic of tractors/locomotives of rolling stock “i” (PLN),
- nwp—workshop occupancy (person),
- nzt—occupancy of non-workshop shifts (person).
- kumi—monthly cost of materials for tractor type “i” (PLN/month),
- bui—utilization factor of rolling stock of type “i”,
- ks—monthly cost of using a standard tractor under standard conditions (PLN),
- mt—“strain” factor of a type “i” tractor:
- mtrzi—the actual number of motoring hours per month (mth),
- mts—the standard number of motoring hours per month (mth).
- nci—number of tractors of type “i” (pcs).
- kmax = kumax—highest cost of use (PLN),
- kmin = kumin—lowest cost of use (PLN),
- ki = kui—cost of use in the variant “i” (PLN),
- wkj = wkk3—weight, the maximum number of points in criterion KK3 (K point).
2.4. Criterion KK4—Depreciation Costs
- Ka—depreciation cost (PLN),
- Kcl—cost of purchasing transport sets, locomotives and carts, (PLN),
- Kcw—cost of purchasing carts, platforms, transport sets (PLN),
- Kct—cost of purchasing the tracks with infrastructure (PLN),
- Kcd—cost of purchasing traffic control and protection systems (PLN),
- Kin—cost of purchasing equipment for construction and maintenance of the tracks (PLN),
- Kw—cost of pit excavation (PLN),
- Tai—depreciation period (month).
- kmax = kamax—highest value of depreciation write-offs (PLN),
- kmin = kamin—lowest value of depreciation write-offs (PLN),
- ki = kai—value of depreciation write-offs in the variant “i” (PLN),
- wkj = wkk4—weight, the maximum number of points in criterion KK4 (K point).
2.5. Criterion KK5—Additional Personnel Costs
- Kor—annual cost of hiring additional employees (PLN),
- koi—annual cost per employee for position “i” (PLN),
- noi—number of persons employed in position “i” (person),
- mo—number of additional positions (pcs).
- Tu—useful life of the designed transportation system (months).
- kmax = komax—highest cost of additional employment of employees (PLN),
- kmin = komin—lowest cost of additional employment of employees (PLN),
- ki = ki—cost of additional employment of employees in the variant “i” (PLN),
- wkj = wkk5—weight, the maximum number of points in criterion KK5 (K point).
3. Results
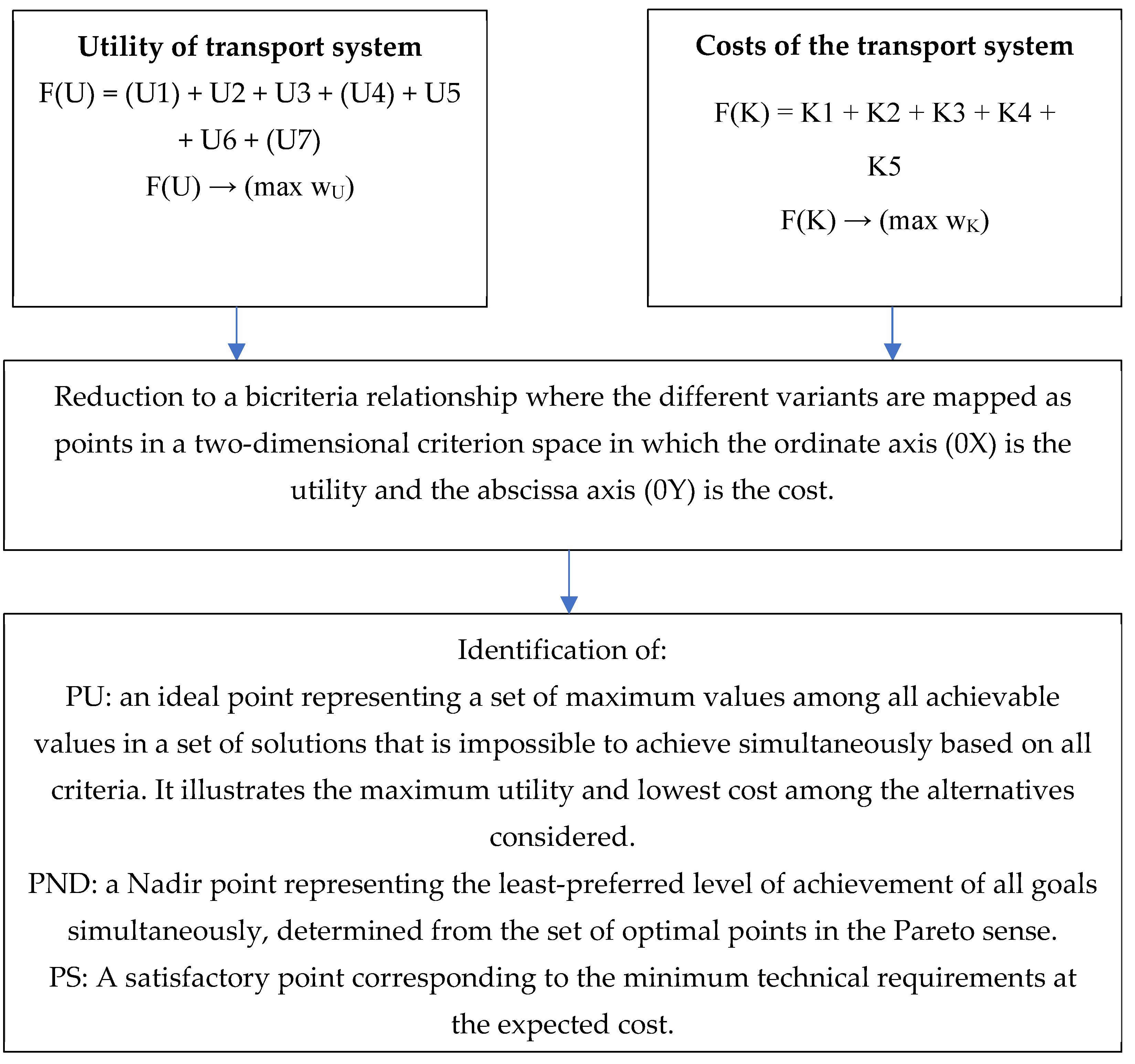
- seven utility criteria (as defined in the article Selection of the optimal design option for transportation systems. Part I—establishment and application of utility criteria [6]) (these criteria include: KU1—transportation task completion time; KU2—compatibility of transportation systems; KU3—continuous connectivity; KU4—co-use with other transportation tasks; KU5—safety; KU6—inconvenience; KU7—operation under overplanning conditions);
- five cost criteria.
- wU—total utility criterion score (U point).
F(K) → (max wK)
- wK—total cost criterion scoring (K point).
3.1. Graphic Interpretation
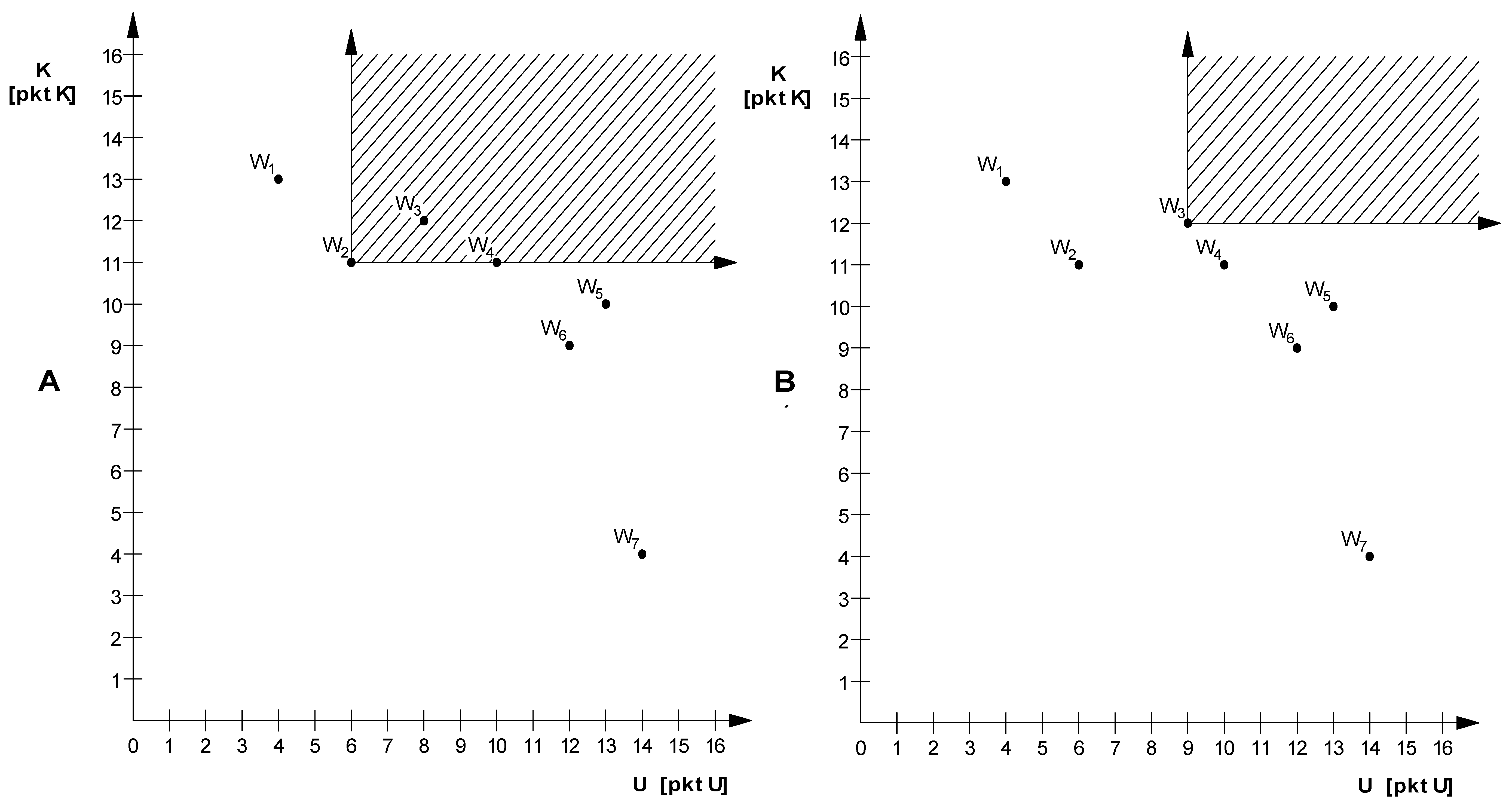
Additional Points in the Two-Dimensional Criterion Space, Necessary for Further Proceedings
- ui—the highest utility of variant “i” (U point),
- kj—the lowest cost of variant “j” (K point).
- uio—utility of variant “i”, optimal in the Pareto sense (U point),
- kio—cost of implementing variant “i”, optimal in the Pareto sense (K point).
- usi—satisfactory utility of variant “i,”
- ksj—satisfactory implementation costs of variant “j.”
- “PI,” ideal point, constant, with coordinates of 100.00 U point and 100.00 K point,
- “PDI,” defined ideal point.
- uDI—utility of the defined ideal variant (U point),
- kDI—costs of the defined ideal variant (K point).
3.2. Reduction of Dominated Variants
- ui = uj; ki > kj—weak dominance of “i” over “j” (in terms of costs),
- ui > uj; ki = kj—weak dominance of “i” over “j” (in terms of utility),
- ui > uj; ki > kj—(strong) dominance of “i” over “j” (in terms of utility and cost).
3.3. Threshold Value Method
3.4. Distance Function
- do—distance of the tested variant from the defined ideal point,
- uDI—utility coordinate of the defined ideal variant (U point),
- ui—utility of the tested variant (U point),
- kDI—cost coordinate of the defined ideal variant (K point),
- kj—cost of the tested variant (K point).
4. Conclusions
- seven utility criteria (KU1—transportation task completion time; KU2—compatibility of transportation systems; KU3—continuous connectivity; KU4—co-use with other transportation tasks; KU5—safety; KU6—inconvenience; KU7—operation under overplanning conditions);
- five cost criteria (KK1—costs of implementing the transportation task; KK2—costs of route expansion; KK3—rolling stock maintenance costs; KK4—depreciation costs; KK5—additional personnel costs).
- usability and cost assessments can be carried out for existing transport systems to optimize efficiency;
- for planned transport investments, the method is ready to be implemented;
- to improve the decision-making process, the existing IT system could be equipped with solutions supporting the use of the developed methodology, e.g., obtaining information on costs or existing transport systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Szlązak, N.; Obracaj, D.; Swolkień, J. Enhancing Safety in the Polish High-Methane Coal Mines: An Overview. Min. Metall. Explor. 2020, 37, 567–579. [Google Scholar] [CrossRef]
- Dreger, M. Variabilities in Hard Coal Production and Methane Emission in the Myslowice–Wesola Mine. J. Min. Sci. 2021, 57, 421–436. [Google Scholar] [CrossRef]
- Wysocka, M.; Chałupnik, S.; Chmielewska, I.; Janson, E.; Radziejowski, W.; Samolej, K. Natural Radioactivity in Polish Coal Mines: An Attempt to Assess the Trend of Radium Release into the Environment. Mine Water Environ. 2019, 38, 581–589. [Google Scholar] [CrossRef]
- Bogacz, P.; Cieślik, Ł.; Osowski, D.; Kochaj, P. Analysis of the Scope for Reducing the Level of Energy Consumption of Crew Transport in an Underground Mining Plant Using a Conveyor Belt System Mining Plant. Energies 2022, 15, 7691. [Google Scholar] [CrossRef]
- Dubiński, J.; Prusek, S.; Turek, M.; Wachowicz, J. Hard Coal Production Competitiveness in Poland. J. Min. Sci. 2020, 56, 322–330. [Google Scholar] [CrossRef]
- Turek, M.C.; Bednarczyk, Ł.; Jonek-Kowalska, I. Applying Utility Criteria to Select the Design Variant of the Transport System in Underground Mine Workings. Resources 2023, 12, 129. [Google Scholar] [CrossRef]
- Kaczmarek, J.; Kolegowicz, K.; Szymla, W. Restructuring of the Coal Mining Industry and the Challenges of Energy Transition in Poland (1990–2020). Energies 2022, 15, 3518. [Google Scholar] [CrossRef]
- Bąk, P.; Jonek-Kowalska, I. Planning the sale of hard coal in a mining enterprise: Problems and systemic solutions. In Proceedings of the 18th International Multidisciplinary Scientific GeoConference: SGEM 2018, Albena, Bulgaria, 2 July–8 July 2018; Conference proceedings, International Multidisciplinary Scientific GeoConference & EXPO SGEM, 2018, Sofia, STEF92 Technology, s.1015-1024. ISBN 978-619-7408-48-5. [Google Scholar] [CrossRef]
- Osička, J.; Kemmerzell, J.; Zoll, M.; Lehotský, L.; Černoch, F.; Knodt, M. What’s next for the European coal heartland? Exploring the future of coal as presented in German, Polish and Czech press. Energy Res. Soc. Sci. 2020, 61, 101316. [Google Scholar] [CrossRef]
- An, N.; Zagorščak, R.; Thomas, H.R. Transport of heat, moisture, and gaseous chemicals in hydro-mechanically altered strata surrounding the underground coal gasification reactor. Int. J. Coal Geol. 2022, 249, 103879. [Google Scholar] [CrossRef]
- Zagorščak, R.; An, N.; Palange, R.; Green, M.; Krishnan, M.; Thomas, H.R. Underground coal gasification—A numerical approach to study the formation of syngas and its reactive transport in the surrounding strata. Fuel 2019, 253, 349–360. [Google Scholar] [CrossRef]
- Soukup, K.; Hejtmánek, V.; Stańczyk, K.; Šolcová, O. Underground coal gasification: Rates of post processing gas transport. Chem. Pap. 2014, 68, 1707–1715. [Google Scholar] [CrossRef]
- Tu, J.; Wan, L.; Sun, Z. Safety Improvement of Sustainable Coal Transportation in Mines: A Contract Design Perspective. Sustainability 2023, 15, 2085. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Li, J.; Mao, Y.; Saini, V.; Kokh, S. A TGA–DSC-based study on macroscopic behaviors of coal–oxygen reactions in context of underground coal fires. J. Therm. Anal. Calorim. 2022, 147, 3185–3194. [Google Scholar] [CrossRef]
- Fabiano, B.; Currò, F.; Reverberi, A.P.; Palazzi, E. Coal dust emissions: From environmental control to risk minimization by underground transport. An applicative case-study. Process Saf. Environ. Prot. 2014, 92, 150–159. [Google Scholar] [CrossRef]
- Thakur, P. Gas Transport in Underground Coal Mines. Adv. Mine Vent. Respirable Coal Dust Combust Gas Mine Fire Control 2019, 299–312. [Google Scholar] [CrossRef]
- Wang, M.; Bao, J.; Yuan, X.; Yin, Y.; Khalid, S. Research Status and Development Trend of Unmanned Driving Technology in Coal Mine Transportation. Energies 2022, 15, 9133. [Google Scholar] [CrossRef]
- Yuan, X.; Bi, Y.; Hao, M.; Ji, Q.; Liu, Z.; Bao, J. Research on Location Estimation for Coal Tunnel Vehicle Based on Ultra-Wide Band Equipment. Energies 2022, 15, 8524. [Google Scholar] [CrossRef]
- Krauze, K.; Mucha, K.; Wydro, T.; Klempka, R.; Kutnik, A.; Hałas, W.; Ruda, P. Determining the Stability of a Mobile Manipulator for the Transport and Assembly of Arches in the Yielding Arch Support. Energies 2022, 15, 3170. [Google Scholar] [CrossRef]
- Szewerda, K.; Tokarczyk, J.; Wieczorek, A. Impact of Increased Travel Speed of a Transportation Set on the Dynamic Parameters of a Mine Suspended Monorail. Energies 2021, 14, 1528. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, R.; Sun, J. Research on the Comprehensive Evaluation Method of Driving Behavior of Mining Truck Drivers in an Open-Pit Mine. Appl. Sci. 2023, 13, 11597. [Google Scholar] [CrossRef]
- Teplická, K.; Khouri, S.; Beer, M.; Rybárová, J. Evaluation of the Performance of Mining Processes after the Strategic Innovation for Sustainable Development. Processes 2021, 9, 1374. [Google Scholar] [CrossRef]
- Fang, Y.; Peng, X. Micro-Factors-Aware Scheduling of Multiple Autonomous Trucks in Open-Pit Mining via Enhanced Metaheuristics. Electronics 2023, 12, 3793. [Google Scholar] [CrossRef]
- Ren, X.; Guo, H.; Sheng, K.; Mao, G. Real-Time Path Planning of Driverless Mining Trains with Time-Dependent Physical Constraints. Appl. Sci. 2023, 13, 3729. [Google Scholar] [CrossRef]
- Krysa, Z.; Bodziony, P.; Patyk, M. Discrete Simulations in Analyzing the Effectiveness of Raw Materials Transportation during Extraction of Low-Quality Deposits. Energies 2021, 14, 5884. [Google Scholar] [CrossRef]
- Halilović, D.; Gligorić, M.; Gligorić, Z.; Pamučar, D. An Underground Mine Ore Pass System Optimization via Fuzzy 0–1 Linear Programming with Novel Torricelli–Simpson Ranking Function. Mathematics 2023, 11, 2914. [Google Scholar] [CrossRef]
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation and Application; John Wiley: New York, NY, USA, 1986. [Google Scholar]
- Köksalan, M.M.; Wallenius, J.; Zionts, S. Multiple Criteria Decision Making: From Early History to the 21st Century; World Scientific: Singapore, 2011. [Google Scholar]
- Sahoo, S.K.; Goswami, S.S. A Comprehensive Review of Multiple Criteria Decision-Making (MCDM) Methods: Advancements, Applications, and Future Directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Li, X.; Cao, Z.; Xu, Y. Characteristics and trends of coal mine safety development. Energy Sources Part A Recovery Util. Environ. Eff. 2020. [Google Scholar] [CrossRef]
- Kong, B.; Cao, Z.; Sun, T.; Qi, C.; Zhang, Z. Safety hazards in coal mines of Guizhou China during 2011–2020. Saf. Sci. 2022, 145, 105493. [Google Scholar] [CrossRef]
- Namin, F.S.; Ghadi, A.; Saki, S. A literature review of Multi-Criteria Decision-Making (MCDM) towards mining method selection (MMS). Resour. Policy 2022, 77, 102676. [Google Scholar] [CrossRef]
- Sitorus, F.; Cilliers, J.J.; Brito-Parada, P.R. Multi-criteria decision making for the choice problem in mining and mineral processing: Applications and trends. Expert Syst. Appl. 2019, 121, 393–417. [Google Scholar] [CrossRef]
- Hao, M.; Nie, Y. Hazard identification, risk assessment and management of industrial system: Process safety in mining industry. Saf. Sci. 2022, 154, 105863. [Google Scholar] [CrossRef]
- Baloyi, V.D.; Meyer, L.D. The development of a mining method selection model through a detailed assessment of multi-criteria decision methods. Results Eng. 2020, 8, 100172. [Google Scholar] [CrossRef]
- Jiskani, I.M.; Cai, Q.; Zhou, W.; Lu, X.; Shah, S.A.A. An integrated fuzzy decision support system for analyzing challenges and pathways to promote green and climate-smart mining. Expert Syst. Appl. 2022, 188, 116062. [Google Scholar] [CrossRef]
- Jiskani, I.M.; Wei, Z.; Shahab, H.; Zhiming, W. Mining 4.0 and climate neutrality: A unified and reliable decision system for safe, intelligent, and green & climate-smart mining. J. Clean. Prod. 2023, 41015, 137313. [Google Scholar] [CrossRef]
- Chen, J.; Jiskani, I.M.; Lin, A.; Zhao, C.; Jing, P.; Liu, F.; Lu, M. A hybrid decision model and case study for comprehensive evaluation of green mine construction level. Environ. Dev. Sustain. 2023, 25, 3823–3842. [Google Scholar] [CrossRef]
- Erzurumlu, S.S.; Erzurumlu, Y.O. Sustainable mining development with community using design thinking and multi-criteria decision analysis. Resour. Policy 2015, 46, 6–14. [Google Scholar] [CrossRef]
- Matuszewicz, J. Rachunek Kosztów; Wydawnictwo Finans-Servis: Warszawa, Poland, 2011. [Google Scholar]
- Jonek-Kowalska, I. Zarządzanie Kosztami w Przedsiębiorstwach Górniczych w Polsce. Stan Aktualny i Kierunki Doskonalenia; Wydawnictwo Difin: Warszawa, Poland, 2013. [Google Scholar]
- Bąk, P. Production planning in a mining enterprise—Selected problems and solutions. Gospod. Surowcami Miner.—Miner. Resour. Manag. 2018, 24, 97–116. [Google Scholar] [CrossRef]
- Michalak, A.; Jonek-Kowalska, I. Ryzyko, Koszt Kapitału i Efektywność w Procesie Finansowania Inwestycji Rozwojowych w Górnictwie Węgla Kamiennego; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2011. [Google Scholar]
- Michalak, A.; Jonek-Kowalska, I. Finansowanie Inwestycji Rozwojowych w Górnictwie Węgla Kamiennego a Wartość Przedsiębiorstw Górniczych; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2011. [Google Scholar]
- Jonek-Kowalska, I. Long-term Analysis of the Effects of Production Management in Coal Mining in Poland. Energies 2019, 12, 3146. [Google Scholar] [CrossRef]
- Jonek-Kowalska, I. Method for Assessing the Development of Underground Hard Coal Mines on a Regional Basis: The Concept of Measurement and Research Results. Energies 2018, 11, 1370. [Google Scholar] [CrossRef]
- Jonek-Kowalska, I.; Turek, M. Dependence of Total Production Costs on Production and Infrastructure Parameters in the Polish Hard Coal Mining Industry. Energies 2017, 10, 1480. [Google Scholar] [CrossRef]
- Sadowy, J. Kryteria Oceny Ofert w Postępowaniu o Udzielnie Zamówienia Publicznego—Przykłady Zastosowania; Urząd Zamówień Publicznych: Warszawa, Poland, 2011. [Google Scholar]
- Koba, A. Pozacenowe Kryteria Oceny Ofert. Poradnik z Katalogiem Dobrych Praktyk; Urząd Zamówień Publicznych: Warszawa, Poland, 2013. [Google Scholar]
- Urbanyi-Popiołek, I. Ekonomiczne i Organizacyjne Aspekty Transportu; Wydawnictwo Uczelniane Wyższej Szkoły Gospodarki w Bydgoszczy: Bydgoszcz, Poland, 2013. [Google Scholar]
- Karwowski, T. Zasady Eksploatacji i Opłacalności Zakupu Maszyn; IBMiER: Warszawa, Poland, 1996. [Google Scholar]
- Iwin-Garzyńska, J. Kapitał Amortyzacyjny w Zarzadzaniu Finansami; Polskie Wydawnictwo Ekonomiczne: Warszawa, Poland, 2016. [Google Scholar]
- Michalak, A. Parametry efektywności w cyklu życia inwestycji. Zesz. Nauk. Politech. Śląskiej Ser. Organ. I Zarządzanie 2013, 66. Available online: https://delibra.bg.polsl.pl/dlibra/publication/85272/edition/75875/content (accessed on 30 November 2023).
- Kaliszewski, I. Wielokryterialne Podejmowanie Decyzji; Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 2008. [Google Scholar]
- Cegiełka, K. Matematyczne Wspomaganie Decyzji; Szkoła Główna Służby Pożarniczej: Warszawa, Poland, 2012. [Google Scholar]
- Montusiewicz, J. Ewolucyjna analiza wielokryterialna w zagadnieniach technicznych. Pr. Inst. Podstawowych Probl. Tech. PAN 2004, 5. Available online: https://www.infona.pl/resource/bwmeta1.element.baztech-article-BPB4-0018-0006 (accessed on 30 November 2023).
- Montusiewicz, J. Wspomaganie Procesów Projektowania i Planowania Wytwarzania w Budowie i Eksploatacji Maszyn Metodami Analizy Wielokryterialnej; Wydawnictwo Politechniki Lubelskiej: Lublin, Poland, 2012. [Google Scholar]
- Coello Coello, C.A.; Christiansen, A.D. A Multiobjective Optimization Tool for Engineering Design. Eng. Optim. 1999, 31, 337–368. [Google Scholar] [CrossRef]
- Kliber, P. Wprowadzenie Do Teorii Gier. Materiały Dydaktyczne; Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu: Poznań, Poland, 2015. [Google Scholar]
- Paszkowski, S. Podstawy Teorii Systemów i Analizy Systemowej; Wydawnictwo Wojskowej Akademii Technicznej: Warszawa, Poland, 1999. [Google Scholar]
- Konarzewska-Gubała, E. Wspomaganie decyzji wielokryterialnych: System BIPOLAR; Uniwersytet Ekonomiczny We Wrocławiu: Wrocław, Poland, 1991; Volume 76. [Google Scholar]
- Skolimowski, A.M. Decision Support Systems Based on Reference Sets. Rozprawy i Monografie, nr 40; Wydawnictwa AGH: Kraków, Poland, 1996. [Google Scholar]
- Galas, Z.; Nykowski, I.; Żółkiewski, Z. Programowanie Wielokryterialne; Państwowe Wydawnictwo Naukowe: Warszawa, Poland, 1987. [Google Scholar]
- Salukwadze, M.E. Мнoгoкритериальные задачи oптимизации в теoрии oптимальных улучшений; Miecniereba: Tibilisi, Gruzja, 1975. [Google Scholar]


| Criterion | KK1A | KK1B | KK2 | KK3 | KK4 | KK5 |
|---|---|---|---|---|---|---|
| Scoring [K point] | 20 | 10 | 14 | 10 | 16 | 30 |
| Variants | Total Cost (PLN) | Weight: wkk1 (K Point) |
|---|---|---|
| W1 | Kztsz 1 | pkk1 1 |
| … | … | … |
| Wi | Kztsz i | pkk1 i |
| … | … | … |
| Wn | Kztsz n | pkk1 n |
| Transportation System Type | Lengths of Basic Route Sections |
|---|---|
| Underground railroad | 5.0; 6.0 m |
| Floor railways | 2.0–3.0 m |
| Suspension railroad | Rail lengths: 1.6 m; 2.0 m; 2.4 m; 2.5 m; 3.0 m. Lateral stabilization—every 20–30 m |
| Variants | Expansion Cost (PLN) | Weight: wkk3 (K Point) |
|---|---|---|
| W1 | Krp 1 | pkk2 1 |
| … | … | … |
| Wi | Krp i | pkk2 i |
| …. | … | … |
| Wn | Krp n | pkk2 n |
| Variants | Cost of Use (PLN) | Weight: wkk3 (K Point) |
|---|---|---|
| W1 | Ku 1 | Pkk3 1 |
| … | … | … |
| Wi | Ku i | Pkk3 i |
| … | … | … |
| Wn | Ku n | Pkk3 n |
| Variants | Depreciation Cost (PLN) | Weight: wkk4 [K Point] |
|---|---|---|
| W1 | Ka 1 | Pkk4 1 |
| … | … | … |
| Wi | Ka i | Pkk4 i |
| … | … | … |
| Wn | Ka n | Pkk4 n |
| Variants | Cost of Additional Employment (PLN) | Weight: wkk5 (K Point) |
|---|---|---|
| W1 | Ko 1 | Pkk5 1 |
| … | … | … |
| Wi | Ko i | Pkk5 i |
| …. | … | … |
| Wn | Ko n | Pkk5 n |
| Variant | Utility (U Point) | K Costs (K Point) |
|---|---|---|
| I | 52.64 | 85.79 |
| II | 57.91 | 86.52 |
| III | 72.85 | 67.18 |
| IV | 74.12 | 79.66 |
| V | 69.80 | 37.49 |
| VI | 70.48 | 57.07 |
| VII | 82.87 | 85.14 |
| VIII | 87.57 | 86.22 |
| IX | 25.48 | 92.91 |
| X | 30.16 | 94.38 |
| Objective Function | Specification | Result | Variant |
|---|---|---|---|
| Utility | Maximum (U point) | 87.57 | VIII |
| K costs | Maximum (K point) | 94.38 | X |
| Additional Points | Marking | Type | Coordinates | |
|---|---|---|---|---|
| Utility (U Point) | K Costs (K Point) | |||
| Utopian point | PU | Designated | 87.57 | 94.38 |
| Nadir point | PND | Designated | 52.64 | 86.22 |
| Defined satisfactory point | PDS | Determined | 50.00 | 60.00 |
| Defined ideal point | PDI | Determined | 95.00 | 90.00 |
| Ideal point | PI | Constant | 100.00 | 100.00 |
| Variants | I | II | III | IV | V | VI | VII | VIII | IX | X |
|---|---|---|---|---|---|---|---|---|---|---|
| I | - | - | - | - | - | - | - | - | - | - |
| II | D | - | - | - | - | - | - | - | - | - |
| III | - | - | - | - | - | - | - | - | - | - |
| IV | - | - | D | - | - | - | - | - | - | - |
| V | - | - | - | - | - | - | - | - | - | - |
| VI | - | - | - | - | D | - | - | - | - | - |
| VII | - | - | D | D | D | D | - | - | - | - |
| VIII | D | - | - | D | D | D | D | - | - | - |
| IX | - | - | - | - | - | - | - | - | - | - |
| X | - | - | - | - | - | - | - | - | D | - |
| Bicriteria Space | Variants Belonging to the PS–PU Set |
|---|---|
| U utility–K costs | II, III (zd), IV (zd), VII, VIII |
| Variant | Geometric Distance from the Point | |
|---|---|---|
| PDI | PI | |
| U × K Bicriteria Space | ||
| I | 42.57 | 49.45 |
| II | 37.25 | 44.19 |
| III | 31.80 | 42.59 |
| IV | 23.30 | 32.92 |
| V | 58.25 | 69.43 |
| VI | 41.06 | 52.10 |
| VII | 13.07 | 22.68 |
| VIII | 8.33 | 18.56 |
| IX | 69.58 | 74.86 |
| X | 64.99 | 70.06 |
| Variants | |
|---|---|
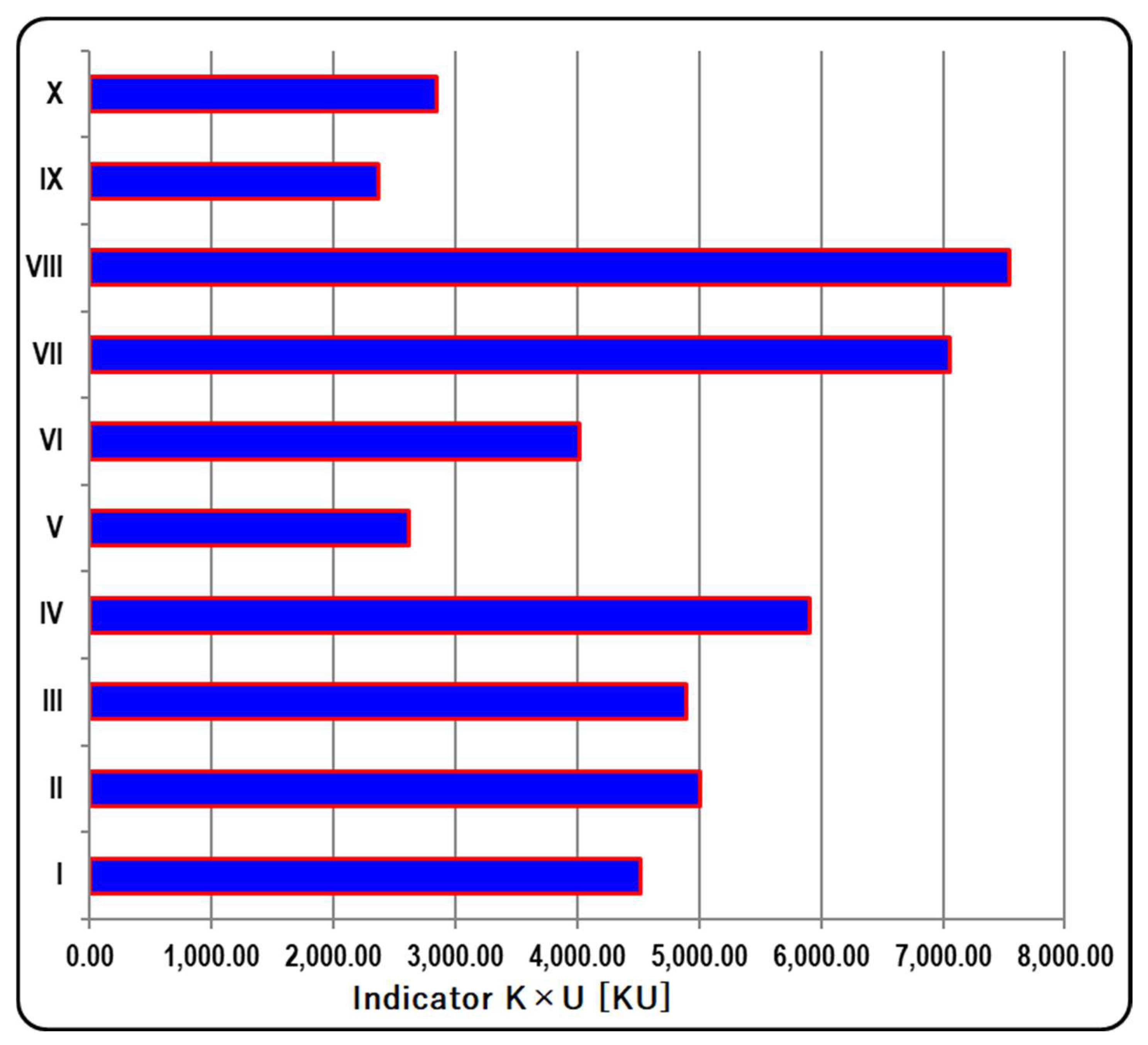
| With the largest values of the product of utility and cost ratios | VIII, VII |
| Optimal in graphic interpretation | VIII |
| Non-dominated | VII, VIII |
| Belonging to the PS–PU set (and also non-dominated) | II, VII, VIII |
| Achieving minimum distance functions | VIII |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bąk, P.; Turek, M.C.; Bednarczyk, Ł.; Jonek-Kowalska, I. The Optimal Transportation Option in an Underground Hard Coal Mine: A Multi-Criteria Cost Analysis. Resources 2024, 13, 14. https://doi.org/10.3390/resources13010014
Bąk P, Turek MC, Bednarczyk Ł, Jonek-Kowalska I. The Optimal Transportation Option in an Underground Hard Coal Mine: A Multi-Criteria Cost Analysis. Resources. 2024; 13(1):14. https://doi.org/10.3390/resources13010014
Chicago/Turabian StyleBąk, Patrycja, Marian Czesław Turek, Łukasz Bednarczyk, and Izabela Jonek-Kowalska. 2024. "The Optimal Transportation Option in an Underground Hard Coal Mine: A Multi-Criteria Cost Analysis" Resources 13, no. 1: 14. https://doi.org/10.3390/resources13010014
APA StyleBąk, P., Turek, M. C., Bednarczyk, Ł., & Jonek-Kowalska, I. (2024). The Optimal Transportation Option in an Underground Hard Coal Mine: A Multi-Criteria Cost Analysis. Resources, 13(1), 14. https://doi.org/10.3390/resources13010014








