Strategic Approaches to Define the Production Rate in Conceptual Projects of Critical Raw Materials
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
- Cst represents the productive capacity per day, in short tons;
- Tst represents the ore mass, in short tons;
- Dwy represents yearly working days;
- L represents the life of the mine;
- C represents the productive capacity per day, in tonnes;
- T represents the ore mass, in tonnes.
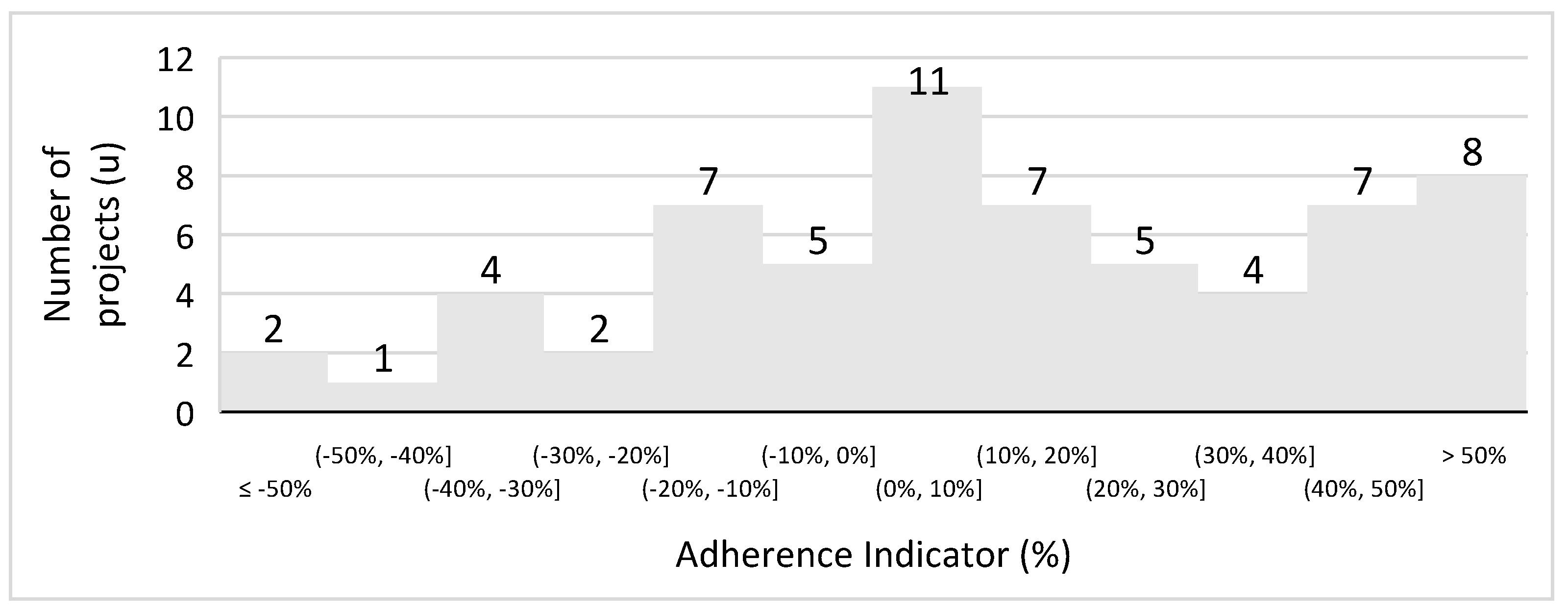
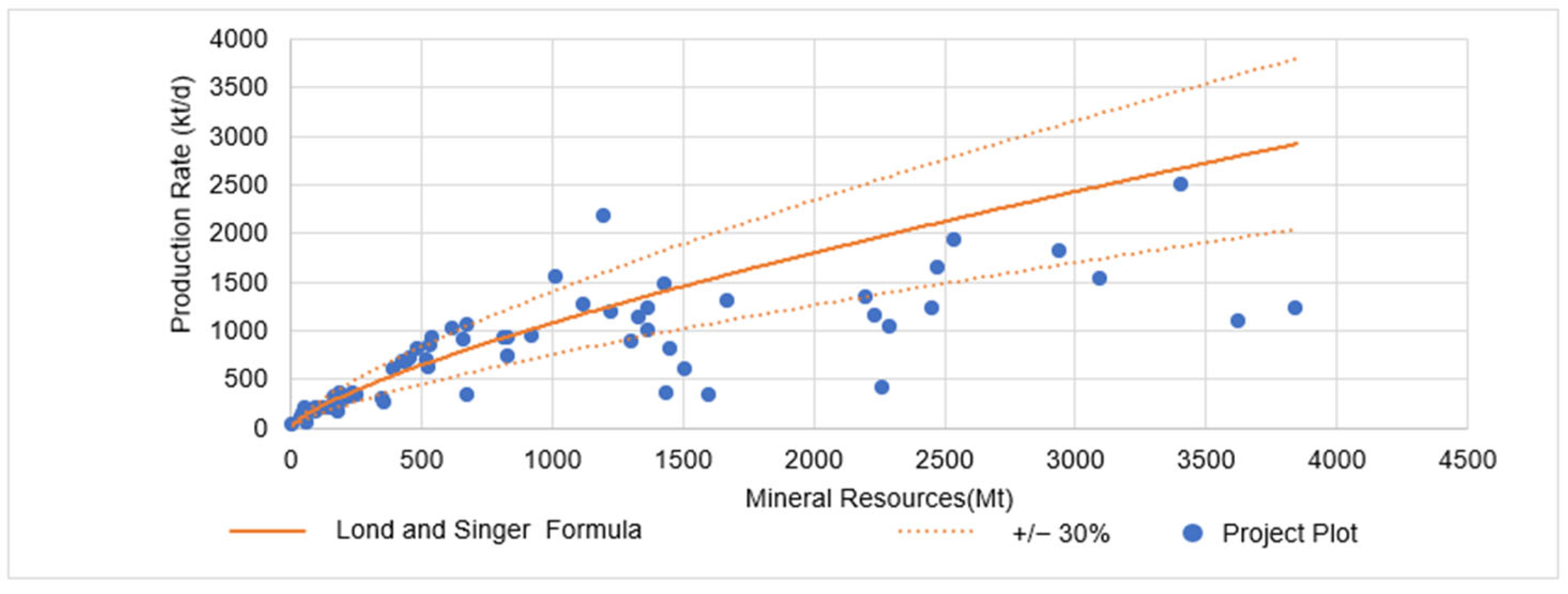
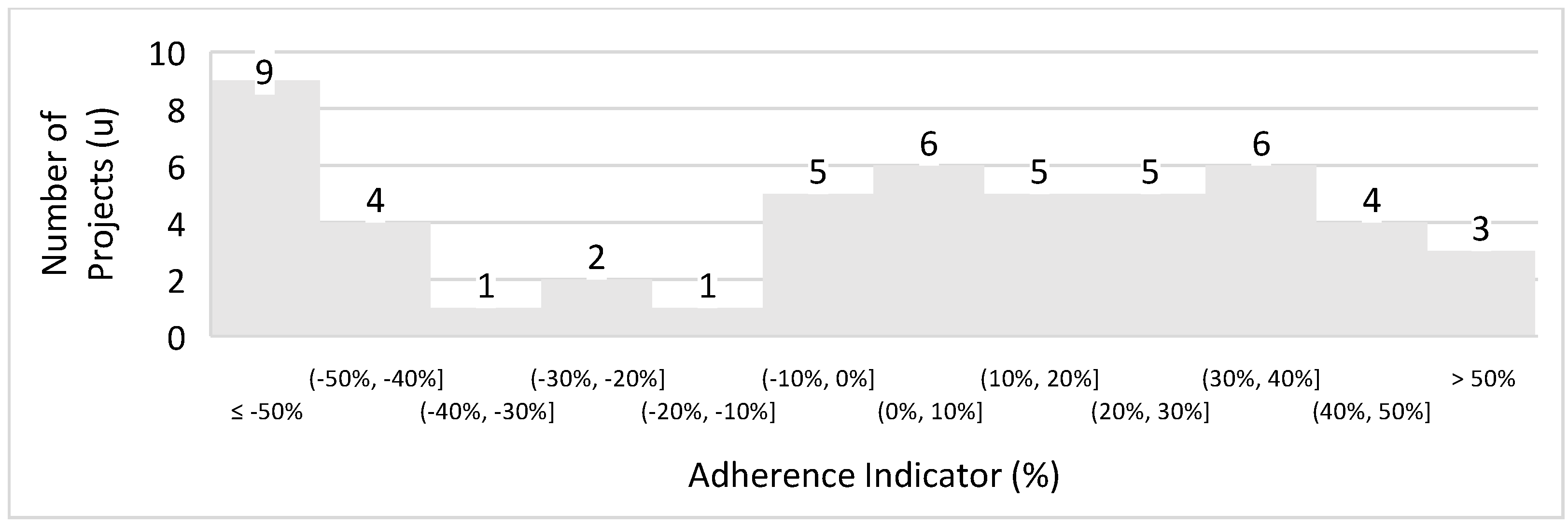
3.1. Long and Singer (2001) [4] Formula Adherence
- Cst represents the productive capacity, in short tons per day;
- Tst represents the ore mass, in short tons.
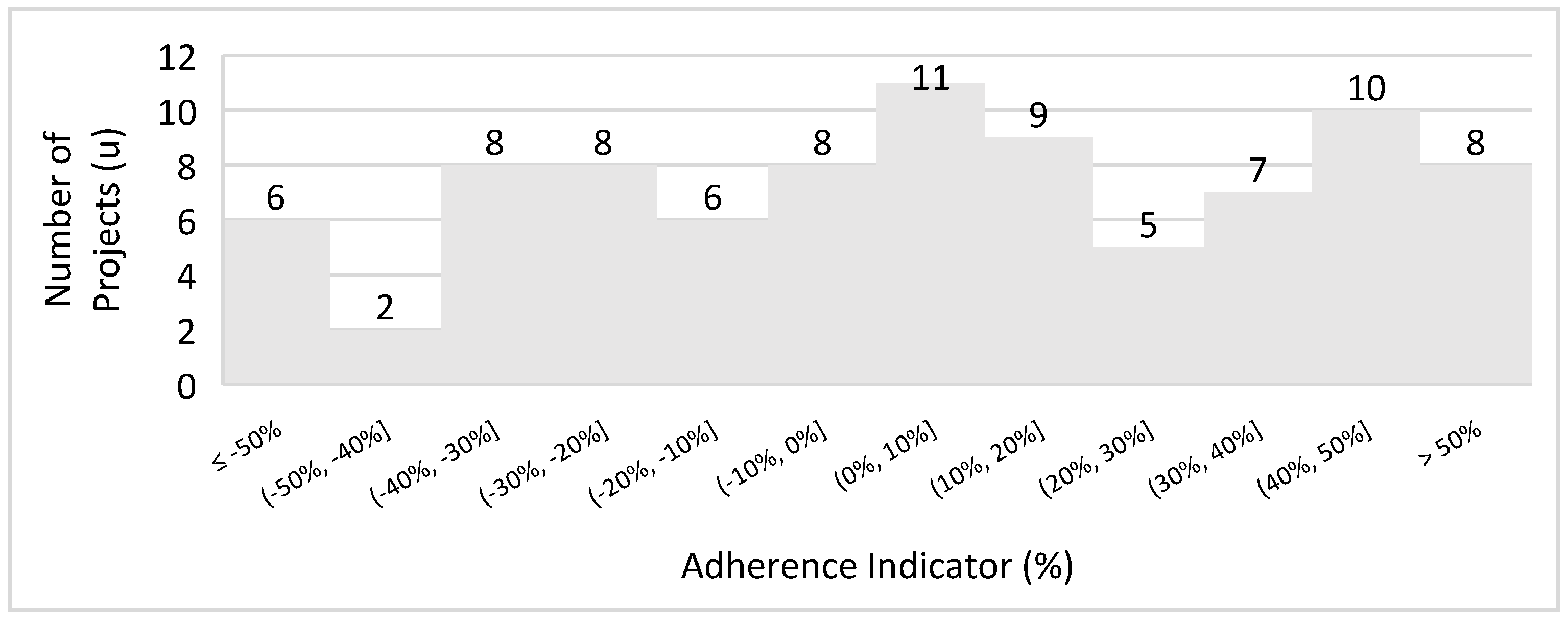
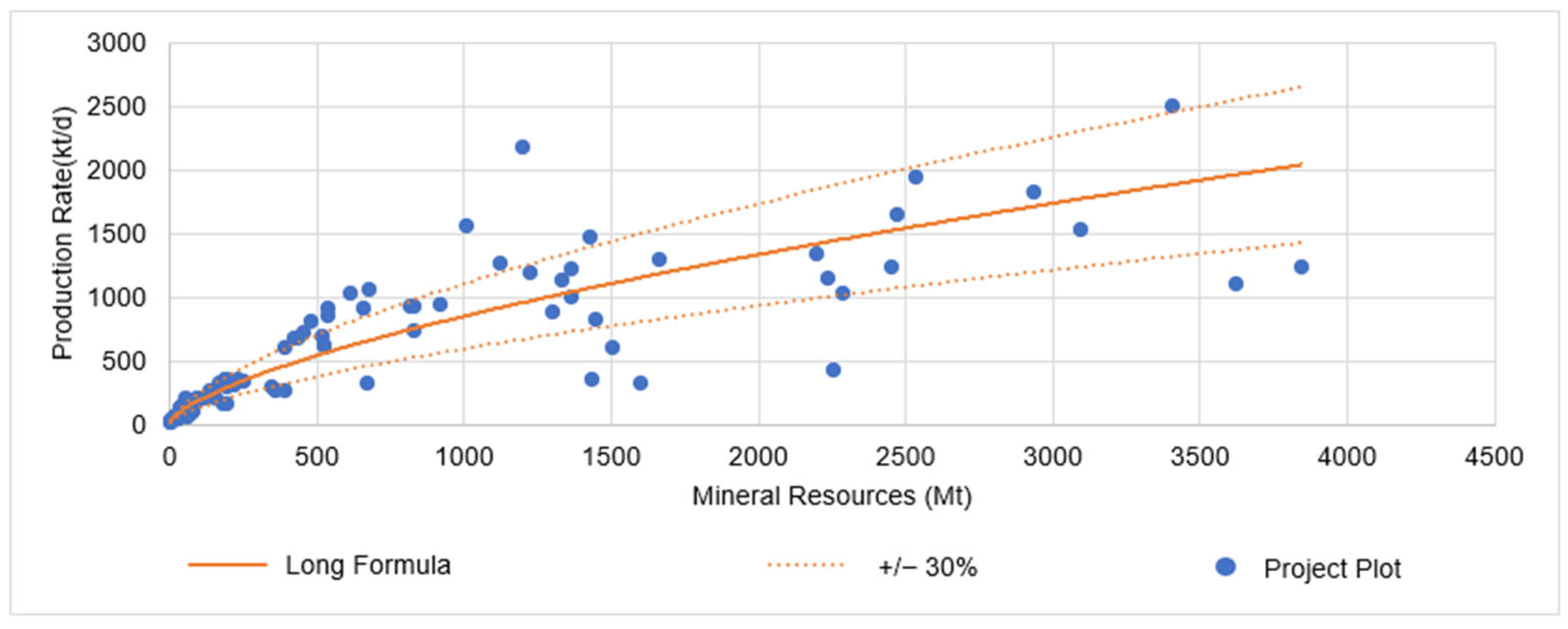
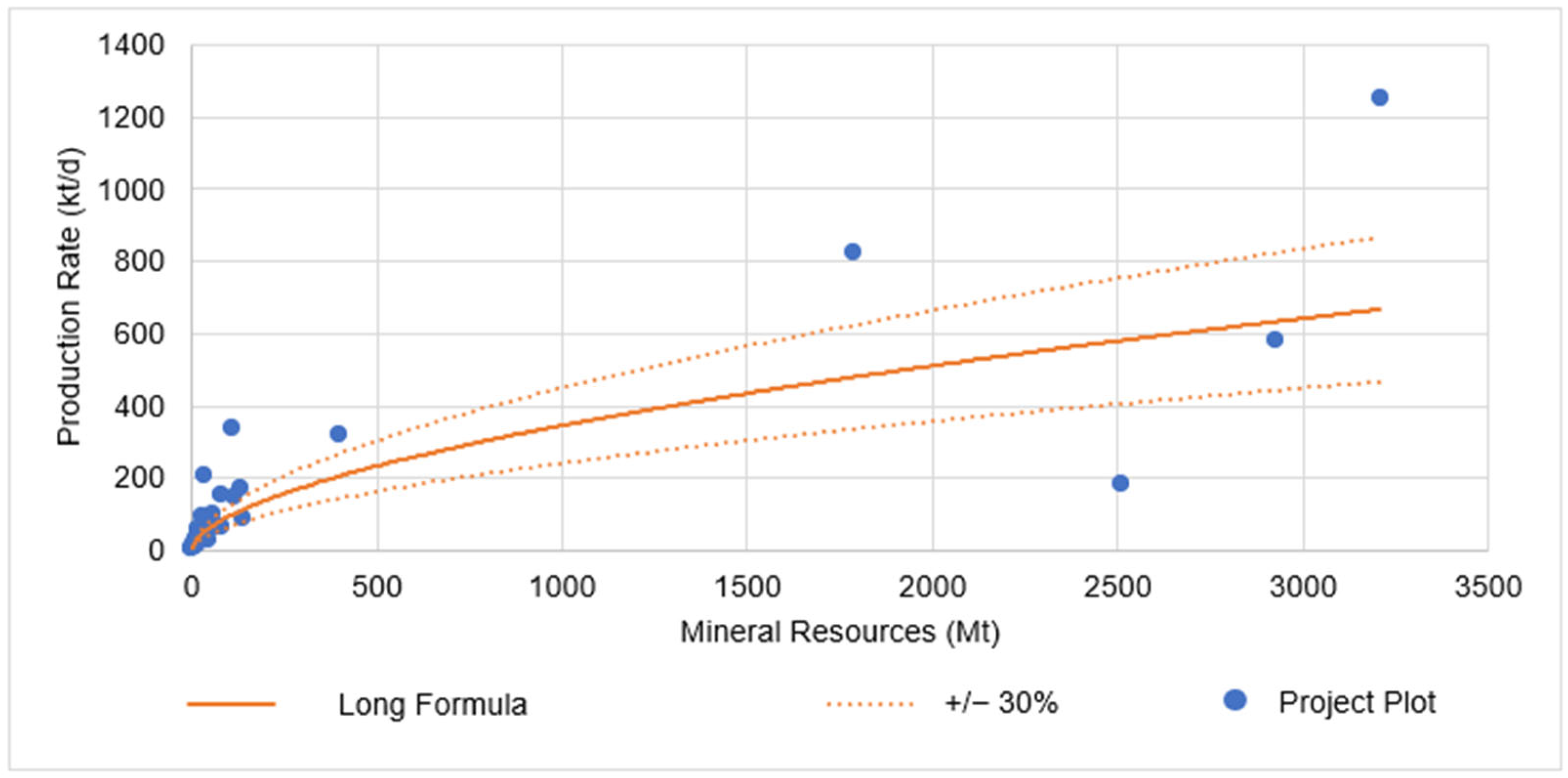
3.2. Long (2009) [22] Formula Adherence—Open-Pit and Block Caving
- C represents the productive capacity per day;
- T represents the ore mass.
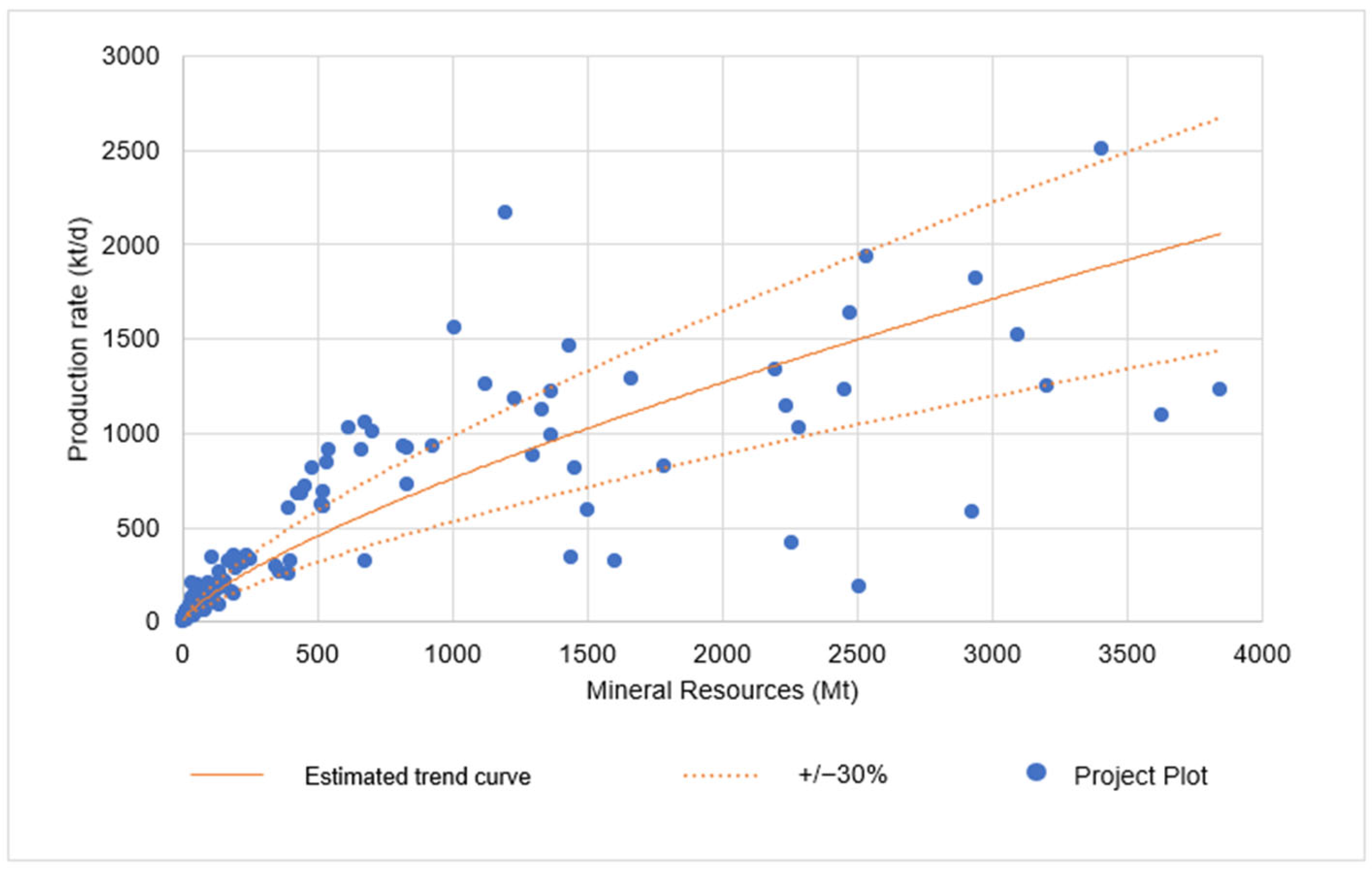
3.3. Long (2009) Formula Adherence—Underground Mining
- C represents the productive capacity per day;
- T represents the ore mass.
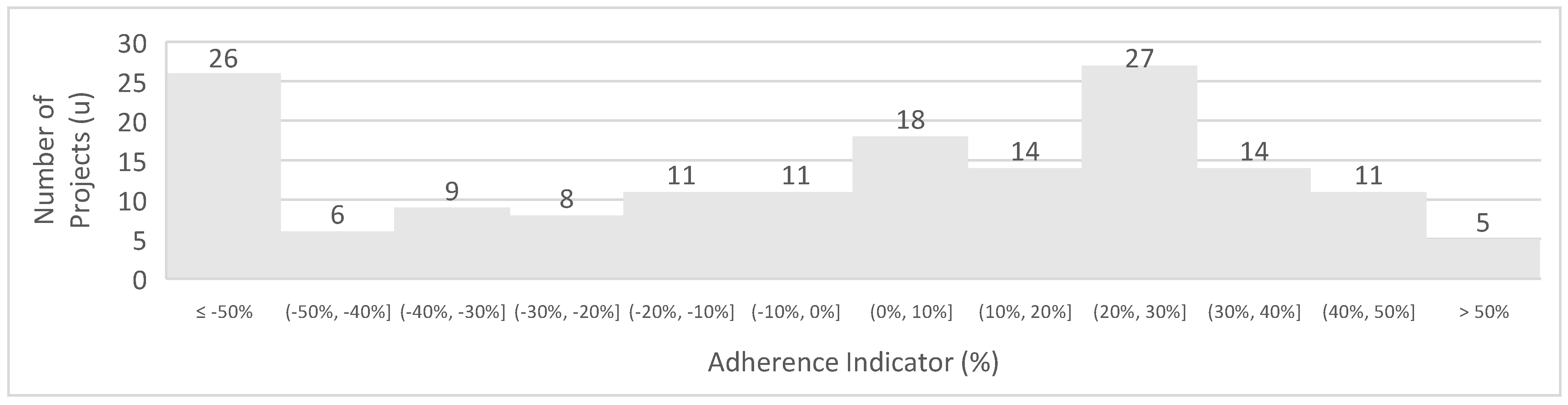
3.4. Estimation of Production Rates for Copper, Zinc, and Lead Projects
- C represents the productive capacity per day;
- T represents the ore mass.
3.5. Estimation of Production Rates for Open-Pit Copper Projects
- C represents the productive capacity per day;
- T represents the ore mass.
- C represents the productive capacity per day;
- T represents the ore mass.
3.6. Estimation of Production Rates for Underground Copper Projects
- C represents the productive capacity per day;
- T represents the ore mass.
- C represents the productive capacity per day;
- T represents the ore mass.
3.7. Estimation of Production Rates for Open-Pit Zinc and Lead Projects
- C represents the productive capacity per day;
- T represents the ore mass.
- C represents the productive capacity per day;
- T represents the ore mass.
3.8. Estimation of Production Rates for Underground Zinc and Lead Projects
- C represents the productive capacity per day;
- T represents the ore mass.
- C represents the productive capacity per day;
- T represents the ore mass.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Project | Commodities | Mining Method | Mineral Resources (t) | Project Production Rate (t/d) |
| Project 1 Africa | Zinc | OP/UG | 56,584,000 | 3739 |
| Project 2 Africa | Zinc | UG | 10,820,000 | 773 |
| Project 3 Africa | Zinc | UG | 25,900,000 | 1200 |
| Project 4 Africa | Zinc | OP | 51,292,451 | 3500 |
| Project 5 Africa | Copper | UG | 33,910,000 | 7200 |
| Project 6 Africa | Copper | OP | 49,600,000 | 5326 |
| Project 7 Africa | Copper | OP | 675,100,000 | 11,331 |
| Project 8 Africa | Copper | UG | 21,900,000 | 1643 |
| Project 1 North America | Zinc | OP | 13,660,000 | 975 |
| Project 2 North America | Zinc | OP | 43,443,000 | 3618 |
| Project 3 North America | Zinc | UG | 48,700,000 | 3227 |
| Project 4 North America | Zinc | UG | 80,900,000 | 5393 |
| Project 5 North America | Zinc | OP/UG | 15,700,000 | 1756 |
| Project 6 North America | Zinc | OP/UG | 17,340,000 | 1279 |
| Project 7 North America | Zinc | UG | 25,700,000 | 1512 |
| Project 8 North America | Zinc | OP/UG | 8,074,162 | 621 |
| Project 9 North America | Zinc | UG | 30,200,000 | 1075 |
| Project 10 North America | Zinc | OP/UG | 19,465,000 | 1315 |
| Project 11 North America | Zinc | OP | 524,510,000 | 21,369 |
| Project 12 North America | Zinc | UG | 5,757,000 | 647 |
| Project 13 North America | Zinc | OP/UG | 5,040,000 | 525 |
| Project 14 North America | Zinc | UG | 5,359,000 | 330 |
| Project 15 North America | Zinc | UG | 1,520,000 | 196 |
| Project 16 North America | Zinc | OP | 32,200,000 | 1440 |
| Project 17 North America | Zinc | UG | 21,400,000 | 1227 |
| Project 18 North America | Zinc | OP/UG | 87,100,000 | 3588 |
| Project 19 North America | Zinc | UG | 138,000,000 | 3085 |
| Project 20 North America | Zinc | OP/UG | 14,000,000 | 617 |
| Project 21 North America | Zinc | OP/UG | 14,600,000 | 1270 |
| Project 22 North America | Zinc | OP | 23,450,000 | 1908 |
| Project 23 North America | Zinc | OP | 13,080,000 | 1100 |
| Project 24 North America | Zinc | OP | 17,170,000 | 1717 |
| Project 25 North America | Zinc | OP/UG | 50,680,000 | 1825 |
| Project 26 North America | Zinc | OP | 37,061,406 | 4553 |
| Project 27 North America | Zinc | UG | 10,900,000 | 1035 |
| Project 28 North America | Zinc | UG | 2,065,649 | 254 |
| Project 29 North America | Zinc | OP/UG | 50,700,000 | 3914 |
| Project 30 North America | Zinc | OP | 194,098,000 | 5314 |
| Project 31 North America | Zinc | UG | 8,071,463 | 823 |
| Project 32 North America | Zinc | OP | 196,000,000 | 12,027 |
| Project 33 North America | Zinc | OP | 72,600,000 | 3047 |
| Project 34 North America | Zinc | UG | 17,555,676 | 550 |
| Project 35 North America | Zinc | UG | 4,435,000 | 370 |
| Project 36 North America | Zinc | UG | 66,000,000 | 2266 |
| Project 37 North America | Zinc | OP | 3,000,000 | 429 |
| Project 38 North America | Zinc | UG | 3,538,972 | 508 |
| Project 39 North America | Cooper | OP/UG | 518,077,750 | 21,634 |
| Project 40 North America | Copper | UG | 8,802,000 | 1100 |
| Project 41 North America | Copper | OP | 2,456,000,000 | 43,238 |
| Project 42 North America | Copper | OP | 1,123,000,000 | 44,114 |
| Project 43 North America | Copper | OP | 1,301,800,000 | 31,015 |
| Project 44 North America | Copper | OP/UG | 14,000,000 | 569 |
| Project 45 North America | Copper | UG | 107,381,000 | 11,929 |
| Project 46 North America | Copper | OP | 2,198,000,000 | 46,727 |
| Project 47 North America | Copper | OP | 224,251,000 | 10,859 |
| Project 49 North America | Copper | OP | 831,000,000 | 25,570 |
| Project 50 North America | Copper | UG | 1,787,000,000 | 28,800 |
| Project 51 North America | Copper | OP | 537,083,216 | 29,515 |
| Project 52 North America | Copper | UG | 4,435,000 | 370 |
| Project 53 North America | Copper | UG | 2,509,086,000 | 6494 |
| Project 54 North America | Copper | OP | 817,000,000 | 32,578 |
| Project 55 North America | Copper | OP | 426,000,000 | 23,725 |
| Project 1 Latin America | Zinc | OP | 138,583,000 | 9239 |
| Project 2 Latin America | Zinc | OP/UG | 10,537,000 | 1282 |
| Project 3 Latin America | Zinc | UG | 16,000,000 | 996 |
| Project 4 Latin America | Zinc | UG | 38,210,000 | 1804 |
| Project 5 Latin America | Zinc | UG | 17,300,000 | 861 |
| Project 6 Latin America | Zinc | UG | 59,000,000 | 3480 |
| Project 7 Latin America | Zinc | UG | 9,000,000 | 1050 |
| Project 8 Latin America | Zinc | OP/UG | 2,386,000 | 340 |
| Project 9 Latin America | Zinc | OP | 79,933,800 | 3500 |
| Project 10 Latin America | Coper | OP | 43,052,000 | 3588 |
| Project 11 Latin America | Copper | OP | 96,000,000 | 7197 |
| Project 12 Latin America | Copper | OP | 236,100,000 | 12,182 |
| Project 13 Latin America | Copper | OP | 94,268,000 | 5834 |
| Project 14 Latin America | Copper | OP | 1,433,100,000 | 51,330 |
| Project 15 Latin America | Copper | OP | 1,667,300,000 | 45,268 |
| Project 16 Latin America | Copper | OP | 51,625,000 | 3995 |
| Project 17 Latin America | Copper | OP | 1,367,000,000 | 34,675 |
| Project 18 Latin America | Copper | OP | 189,370,000 | 12,272 |
| Project 19 Latin America | Copper | OP | 392,300,000 | 21,152 |
| Project 20 Latin America | Copper | UG | 115,500,000 | 5226 |
| Project 21 Latin America | Copper | OP | 524,510,000 | 21,369 |
| Project 22 Latin America | Copper | OP | 2,475,000,000 | 57,441 |
| Project 23 Latin America | Copper | OP | 1,504,900,000 | 20,855 |
| Project 24 Latin America | Copper | UG | 3,207,000,000 | 43,838 |
| Project 25 Latin America | Copper | OP | 1,601,700,000 | 11,353 |
| Project 26 Latin America | Copper | OP | 156,700,000 | 7300 |
| Project 27 Latin America | Copper | OP | 1,200,000,000 | 76,072 |
| Project 28 Latin America | Copper | UG | 43,874,206 | 1053 |
| Project 29 Latin America | Copper | OP | 483,100,000 | 28,454 |
| Project 30 Latin America | Copper | OP | 3,408,000,000 | 87,600 |
| Project 31 Latin America | Copper | OP | 1,229,540,000 | 41,400 |
| Project 32 Latin America | Copper | OP | 3,097,000,000 | 53,377 |
| Project 33 Latin America | Copper | OP | 660,985,000 | 31,907 |
| Project 34 Latin America | Copper | OP/UG | 701,633,000 | 35,196 |
| Project 35 Latin America | Copper | OP | 1,012,000,000 | 54,520 |
| Project 36 Latin America | Copper | OP | 834,000,000 | 32,114 |
| Project 37 Latin America | Copper | OP | 3,846,000,000 | 43,200 |
| Project 38 Latin America | Copper | OP | 3,628,000,000 | 38,400 |
| Project 39 Latin America | Copper | UG | 134,300,000 | 6045 |
| Project 40 Latin America | Copper | OP | 1,452,000,000 | 28,546 |
| Project 41 Latin America | Copper | UG | 2,926,000,000 | 20,367 |
| Project 42 Latin America | Copper | OP | 1,334,800,000 | 39,286 |
| Project 43 Latin America | Copper | OP | 2,288,000,000 | 36,000 |
| Project 44 Latin America | Copper | OP | 2,236,000,000 | 40,199 |
| Project 45 Latin America | Copper | OP | 678,133,000 | 37,028 |
| Project 46 Latin America | Copper | OP | 349,100,000 | 10,260 |
| Project 47 Latin America | Copper | OP | 617,000,000 | 35,850 |
| Project 48 Latin America | Copper | OP | 105,200,000 | 6886 |
| Project 49 Latin America | Copper | OP | 57,834,000 | 6935 |
| Project 50 Latin America | Copper | OP | 440,700,000 | 23,761 |
| Project 51 Latin America | Copper | OP | 457,600,000 | 25,045 |
| Project 52 Latin America | Copper | OP | 924,440,117 | 32,656 |
| Project 1 Asia | Zinc | UG | 11,050,000 | 904 |
| Project 2 Asia | Zinc | OP | 26,080,000 | 1992 |
| Project 3 Asia | Zinc | OP | 394,000,000 | 8950 |
| Project 4 Asia | Zinc | OP/UG | 6,178,000 | 552 |
| Project 5 Asia | Zinc | OP | 18,400,000 | 1900 |
| Project 6 Asia | Zinc | UG | 9,118,000 | 912 |
| Project 7 Asia | Zinc | OP | 8,700,000 | 800 |
| Project 8 Asia | Copper | UG | 81,444,208 | 2216 |
| Project 9 Asia | Copper | OP | 8,500,000 | 708 |
| Project 10 Asia | Copper | OP | 522,752,000 | 23,996 |
| Project 11 Asia | Copper | OP | 2,940,000,000 | 63,643 |
| Project 12 Asia | Copper | OP | 60,500,000 | 2008 |
| Project 13 Asia | Copper | OP | 361,400,000 | 9126 |
| Project 1 Europe | Zinc | UG | 7,300,000 | 663 |
| Project 2 Europe | Zinc | UG | 36,800,000 | 2397 |
| Project 3 Europe | Zinc | OP | 29,168,000 | 2500 |
| Project 4 Europe | Zinc | UG | 7,790,000 | 390 |
| Project 5 Europe | Zinc | UG | 11,180,000 | 523 |
| Project 6 Europe | Zinc | UG | 17,580,000 | 2013 |
| Project 7 Europe | Zinc | UG | 16,922,000 | 952 |
| Project 8 Europe | Copper | UG | 27,590,000 | 3250 |
| Project 9 Europe | Copper | OP | 1,439,500,000 | 12,000 |
References
- Taylor, H.K. Mine Evaluation and Feasibility Studies. In Mineral Industry Costs; Hoskins, J.R., Green, W.R., Eds.; Northwest Mining Association: Reno, Nevada, 1977; pp. 1–17. [Google Scholar]
- Singer, D.A.; Menzie, W.D.; Long, K.R. A Simplified Economic Filter for Underground Mining of Massive Sulfide Deposits; USGS: Pt. Reyes, CA, USA, 2000. [Google Scholar]
- Singer, D.A.; Menzie, W.D.; Long, K.R. A Simplified Economic Filter for Open-Pit Gold-Silver Mining in the United States; USGS: Pt. Reyes, CA, USA, 1998. [Google Scholar]
- Long, K.R.; Singer, D.A. A Simplified Economic Filter for Open-Pit Mining and Heap-Leach Recovery of Copper in the United States; USGS: Pt. Reyes, CA, USA, 2001. [Google Scholar]
- Mariz, J.L.V.; de Lemos Peroni, R. Estimativa de Taxa de Produção Em Fases Prematuras de Projeto Através de Dados Segmentados Por Substância Mineral, Método de Lavra e Porte Dos Empreendimentos. In Proceedings of the 19° Simpósio de Mineração,parte integrante da ABM Week, São Paulo, Brasil, 2–4 October 2018; pp. 423–434. [Google Scholar]
- Mariz, J.L.V.; de Lemos Peroni, R. Adaptação Da Regra de Taylor à Realidade Brasileira Para Determinação Inicial Da Taxa de Produção Em Projetos Mineiros. Tecnol. Metal. Mater. Mineração 2019, 16, 1–6. [Google Scholar] [CrossRef]
- Wells, H.M. Optimization of Mining Engineering Design in Mineral Valuation. Min. Eng. 1978, 30, 1676–1684. [Google Scholar]
- Cavender, B. Determination of the Optimum Lifetime of a Mining Project Using Discounted Cash Flow and Option Pricing Techniques. Min. Eng. 1992, 44, 1262–1268. [Google Scholar]
- Lizotte, Y.; Elbrond, J. Choice of Mine-Mill Capacities and Production Schedules Using Open Ended Dynamic Programming. CIM Bull. 1982, 75, 154–163. [Google Scholar]
- Smith, L.D. A Critical Examination of the Methods and Factors Affecting the Selection of an Optimum Production Rate. CIM Mag. Bull. 1997, 90, 48–54. [Google Scholar]
- Baruti, K.R. Developed Regression Models of Mining Rate Fit on Resource and Reserve Variations in Gold Mining. Int. J. Eng. Innov. Res. 2018, 7, 159–165. [Google Scholar]
- Sabour, S.A.A. Mine Size Optimization Using Marginal Analysis. Resour. Policy 2002, 28, 145–151. [Google Scholar] [CrossRef]
- Souza, F.R.; Câmara, T.R.; Torres, V.F.N.; Nader, B.; Galery, R. Optimum Mine Production Rate Based on Price Uncertainty. REM—Int. Eng. J. 2019, 72, 625–634. [Google Scholar] [CrossRef]
- Northey, S.; Mohr, S.; Mudd, G.M.; Weng, Z.; Giurco, D. Modelling Future Copper Ore Grade Decline Based on a Detailed Assessment of Copper Resources and Mining. Resour. Conserv. Recycl. 2014, 83, 190–201. [Google Scholar] [CrossRef]
- Michaux, S.P. Estimation of the Quantity of Metals to Phase out Fossil Fuels in a Full System Replacement, Compared to Mineral Resources. Bulletin 2024, 416, 1–293. [Google Scholar] [CrossRef]
- Tabelin, C.B.; Park, I.; Phengsaart, T.; Jeon, S.; Villacorte-Tabelin, M.; Alonzo, D.; Yoo, K.; Ito, M.; Hiroyoshi, N. Copper and Critical Metals Production from Porphyry Ores and E-Wastes: A Review of Resource Availability, Processing/Recycling Challenges, Socio-Environmental Aspects, and Sustainability Issues. Resour. Conserv. Recycl. 2021, 170, 105610. [Google Scholar] [CrossRef]
- Natural Resources Canada. The Canadian Critical Minerals Strategy from Exploration to Recycling: Powering the Green and Digital Economy for Canada and the World; Natural Resources Canada: Ottawa, ON, Canada, 2022; ISBN 9780660463391.
- de Castro, F.F.; Peiter, C.C.; Góes, G.S. TD 2768—Minerais Estratégicos e Críticos: Uma Visão Internacional e Da Política Mineral Brasileira. Texto para Discussão 2022, 2768, 1–40. [Google Scholar] [CrossRef]
- Hickson, R.J.; Owen, T.L. Project Management for Mining: Handbook for Delivering Project Success, 2nd ed.; Society for Mining Metallurgy and Exploration (SME): Englewood, CO, USA, 2022; ISBN 9780873354943. [Google Scholar]
- Hickson, R.J.; Owen, T.L. Project Management for Mining: Handbook for Delivering Project Success; Society for Mining Metallurgy and Exploration (SME): Englewood, CO, USA, 2015; ISBN 9780873354035. [Google Scholar]
- Mariz, J.L.V. Análise Da Aderência Dos Métodos de Previsão Da Taxa de Produção Em Fases Prematuras de Projetos Mi-Neiros à Realidade Brasileira; Universidade Federal do Rio Grande do Sul: Rio Grande, Brazil, 2018. [Google Scholar]
- Long, K.R. A Test and Re-Estimation of Taylor’s Empirical Capacity-Reserve Relationship. Nat. Resour. Res. 2009, 18, 57–63. [Google Scholar] [CrossRef]
- Camm, T.W. Simplified Cost Models for Prefeasibility Mineral Evaluations; USGS: Pt. Reyes, CA, USA, 1991. [Google Scholar]
- Mudd, G.M.; Jowitt, S.M.; Werner, T.T. The World’s Lead-Zinc Mineral Resources: Scarcity, Data, Issues and Opportunities. Ore Geol. Rev. 2017, 80, 1160–1190. [Google Scholar] [CrossRef]


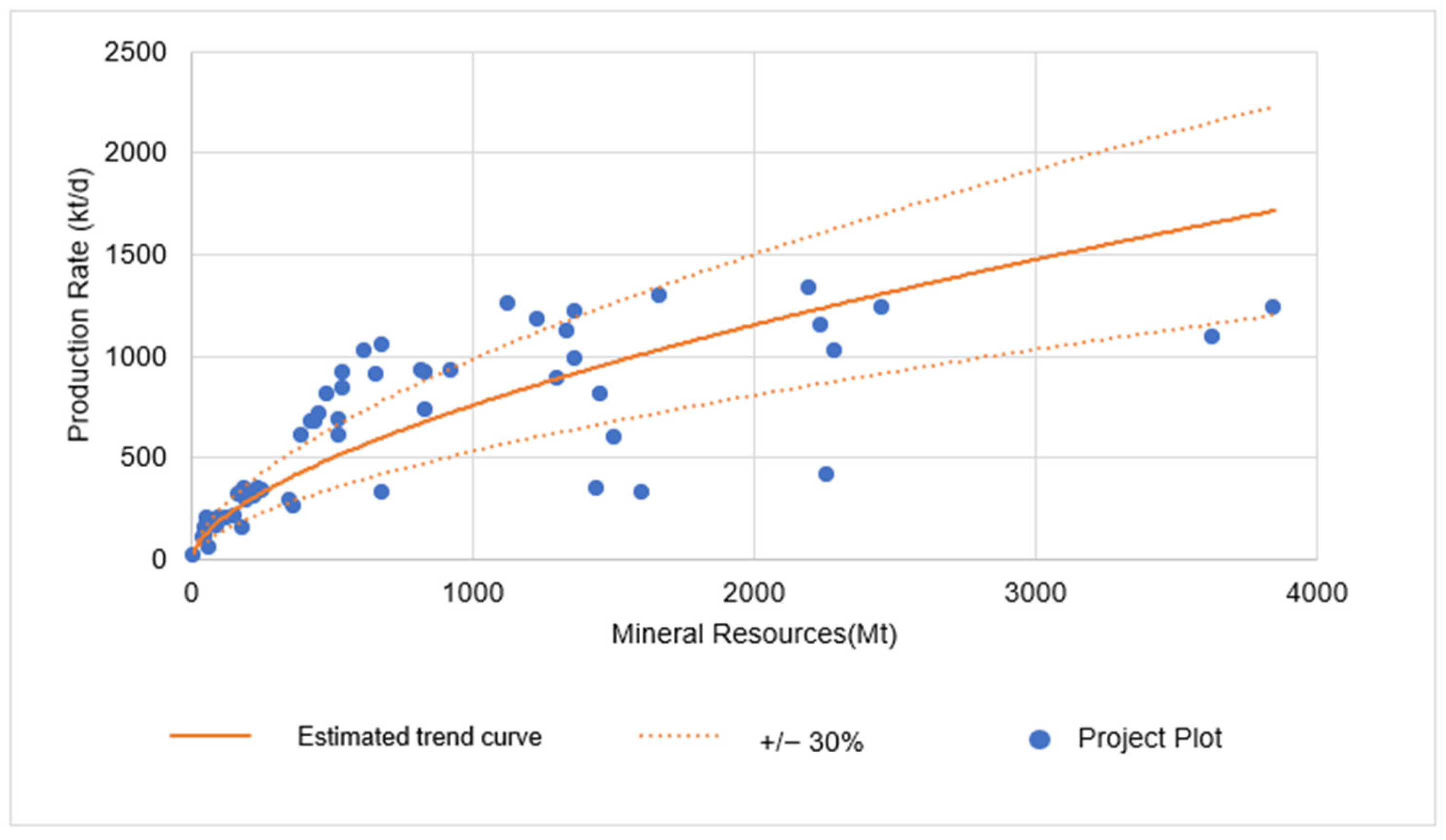


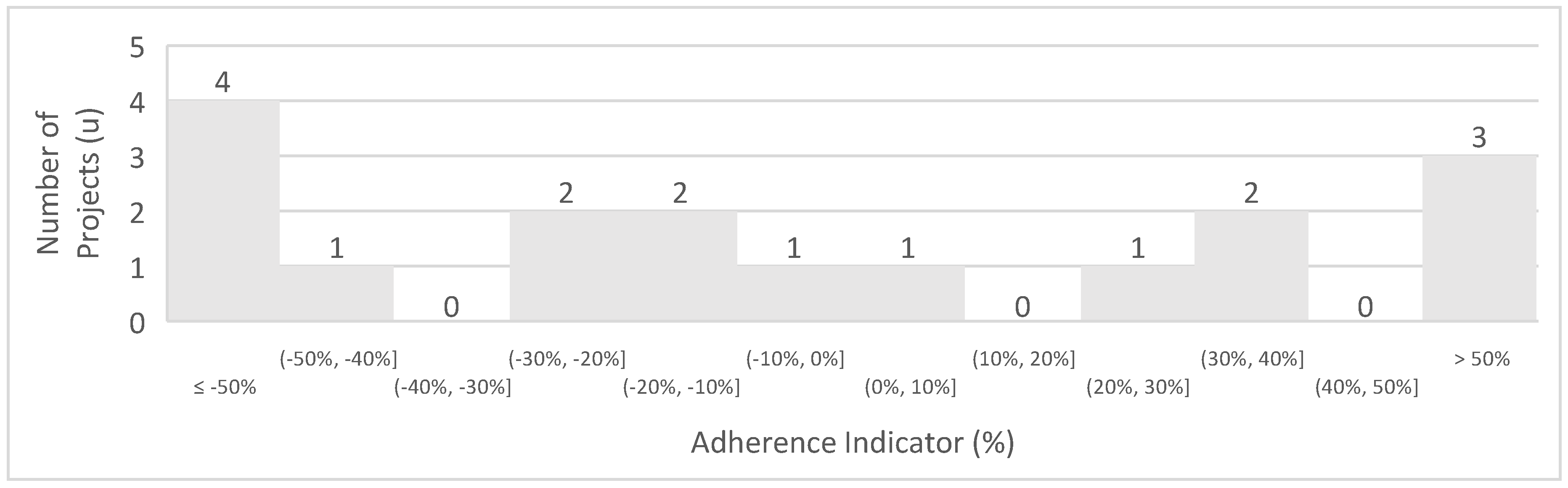
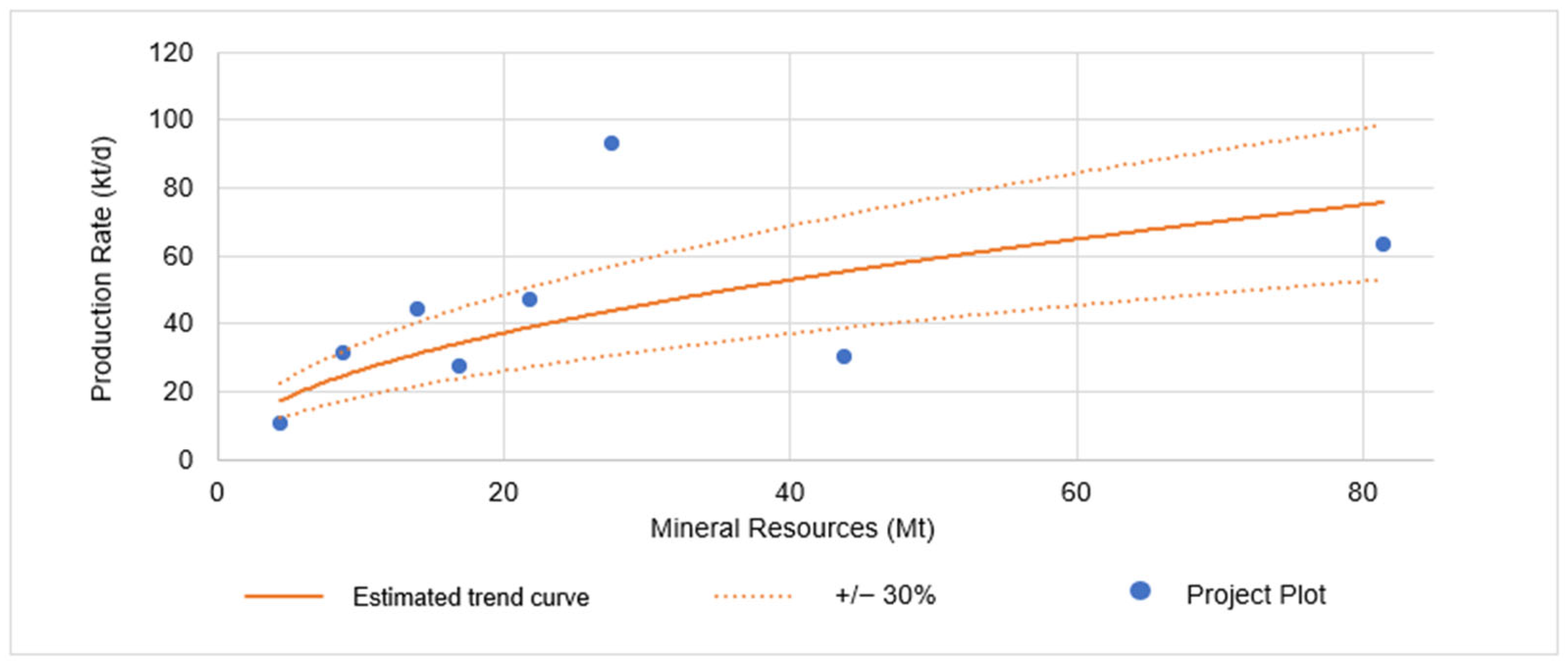
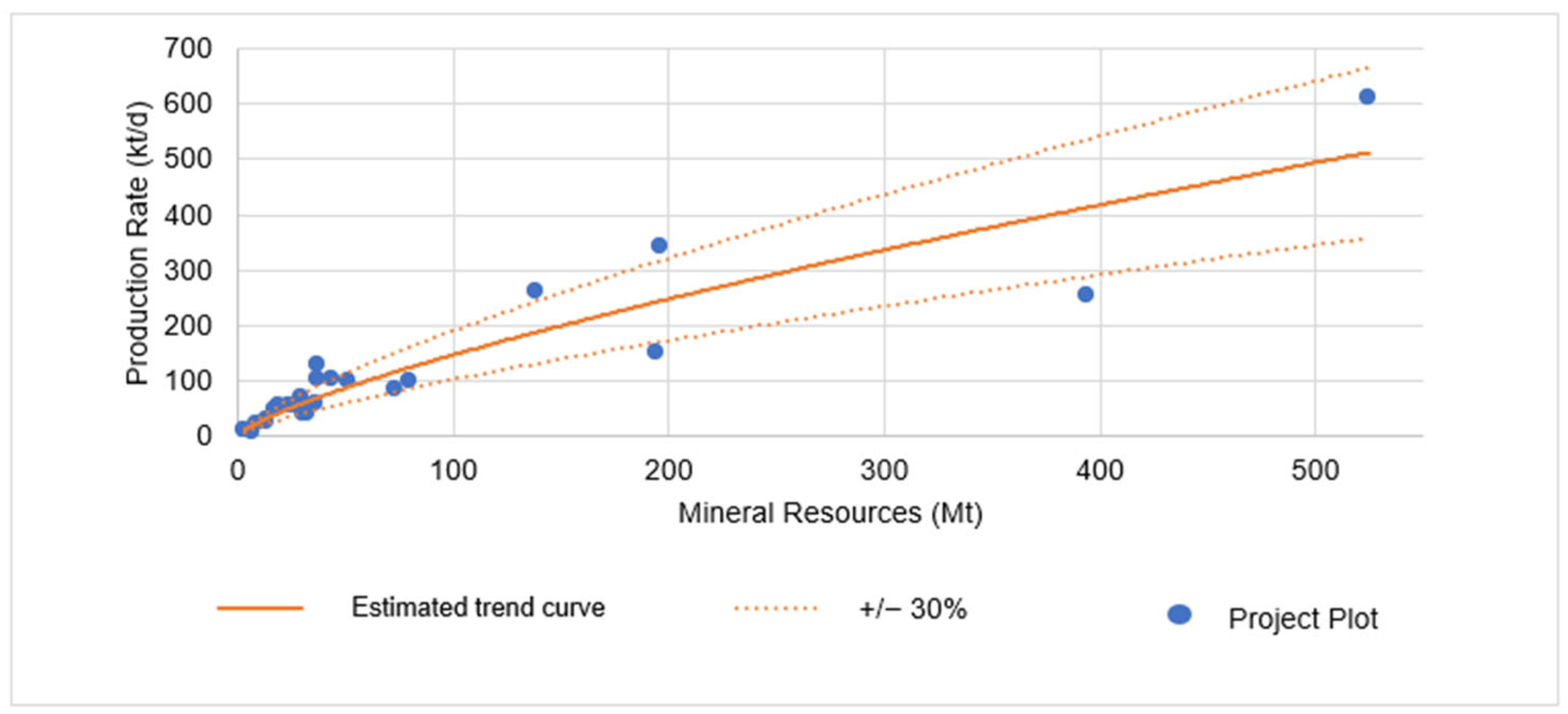
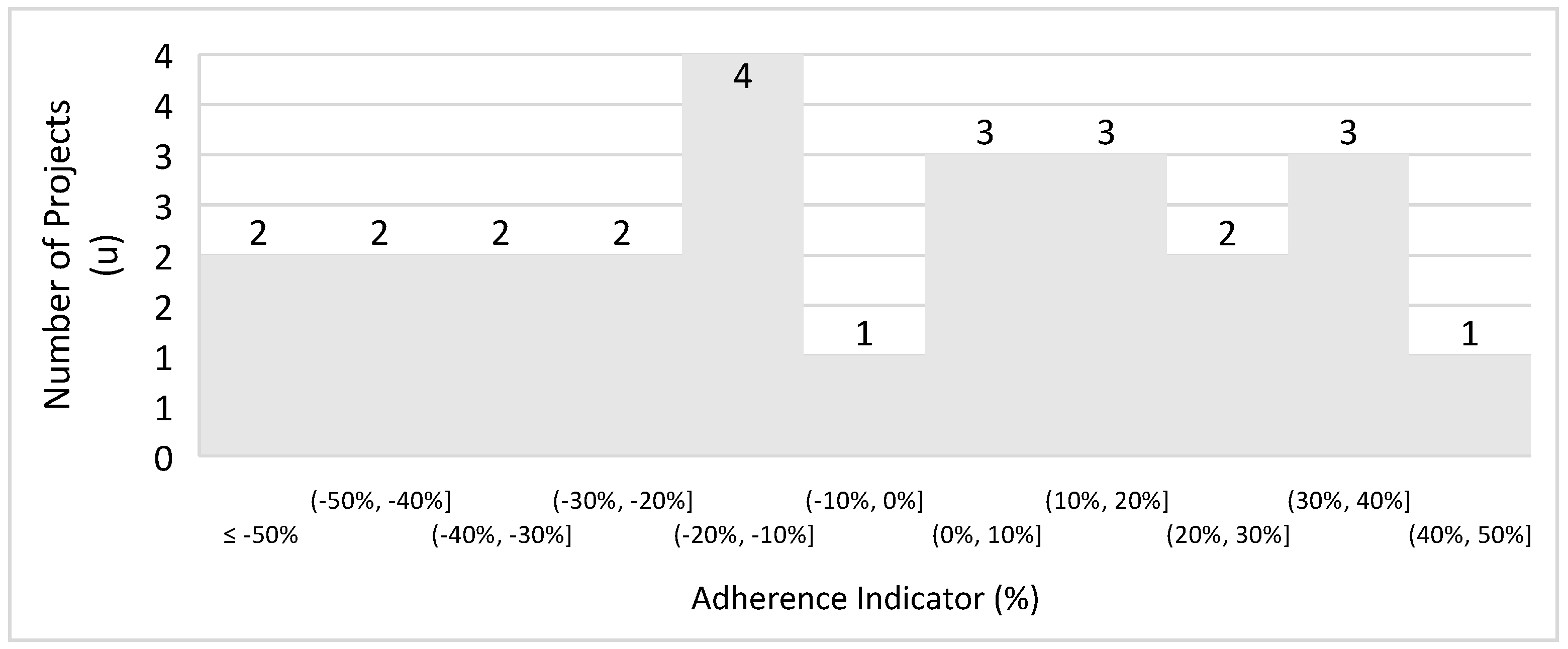
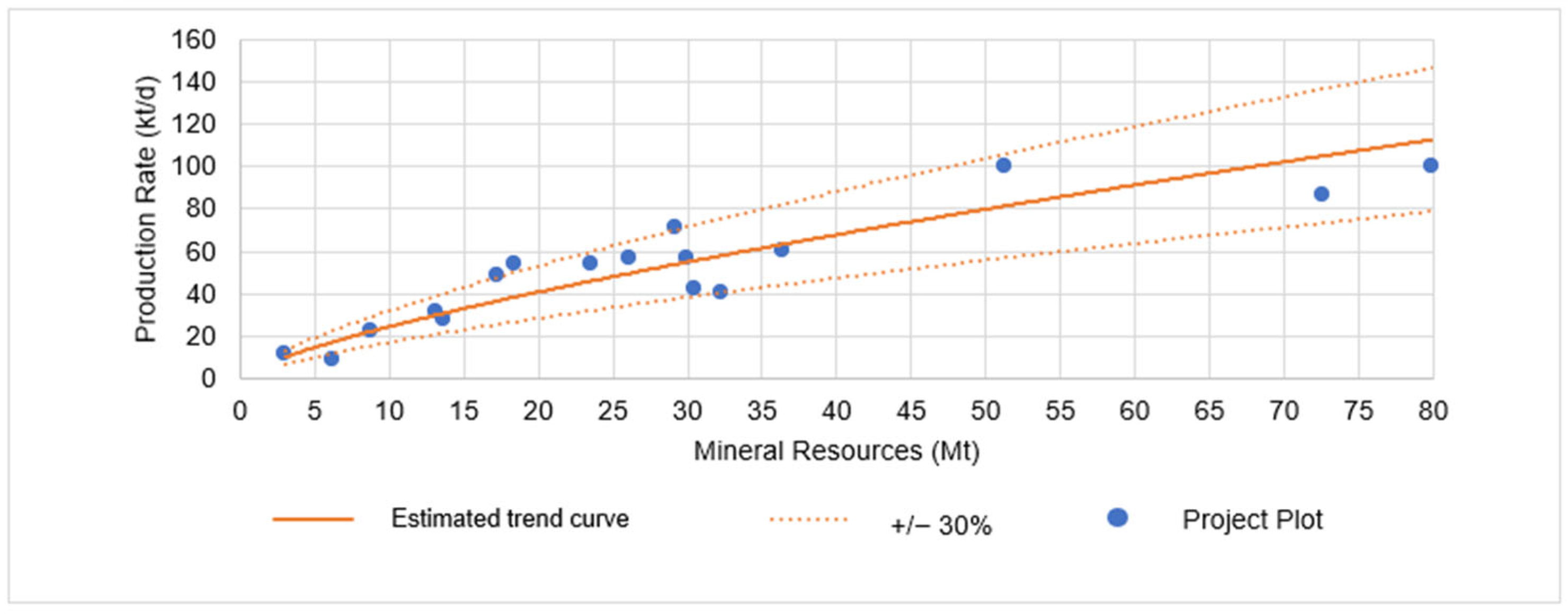
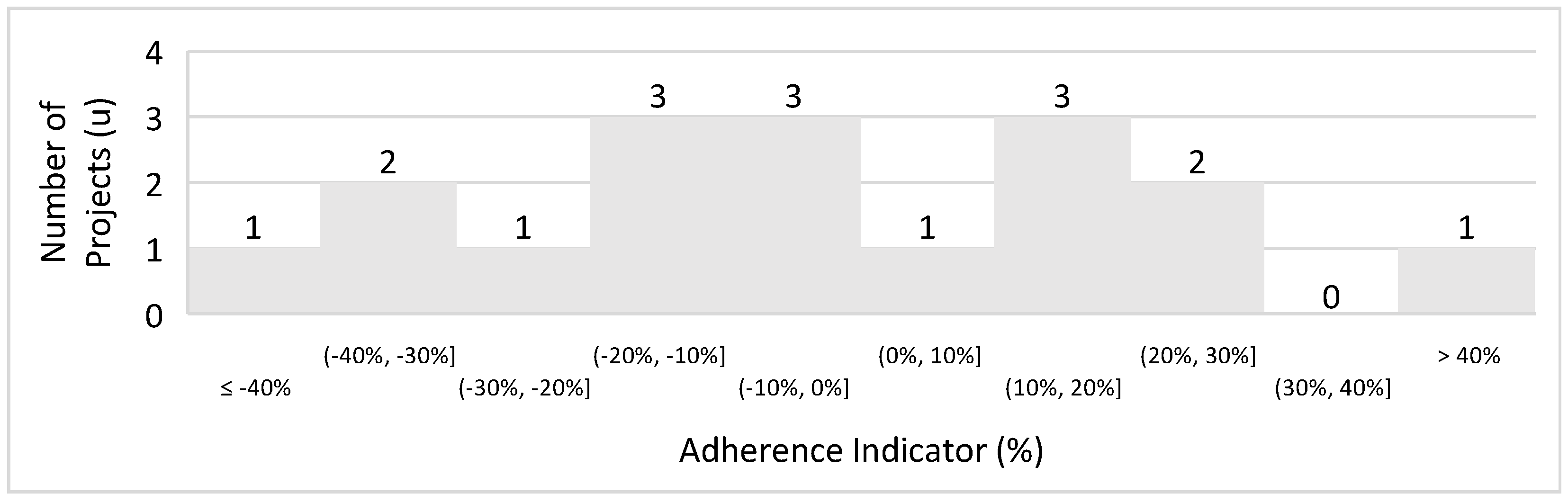
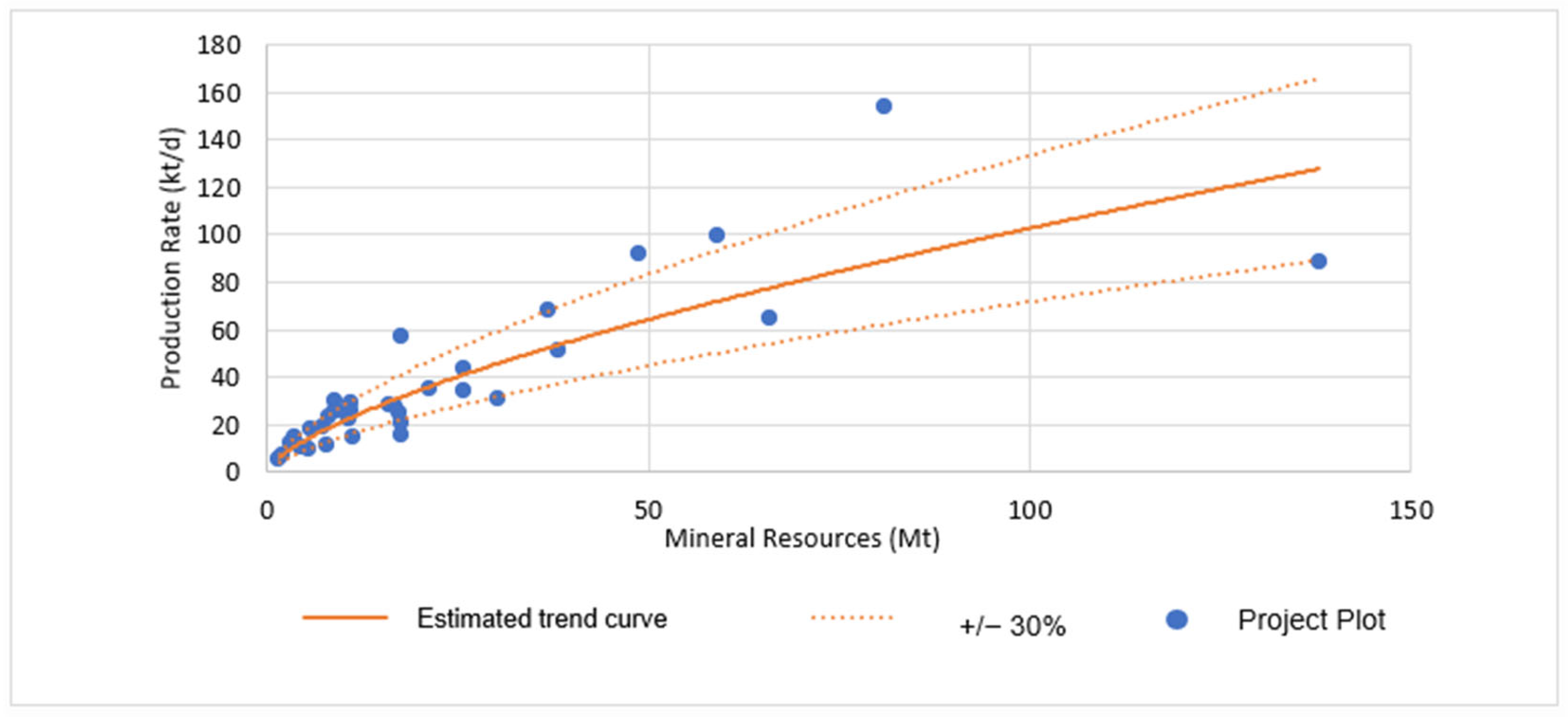
| Continent | Number of Projects | Percentage (%) |
|---|---|---|
| Africa | 8 | 5 |
| North America | 54 | 34 |
| Latin America | 52 | 33 |
| Asia | 13 | 8 |
| Europe | 15 | 9 |
| Oceania | 18 | 11 |
| Total | 160 | 100 |
| Mining Method | Average Daily Production Rate (t) |
|---|---|
| Open-pit | 20,939 |
| Underground | 3858 |
| Open-pit and underground | 4425 |
| Estimate Name | Percent Engineering | Accuracy at 90% Confidence |
|---|---|---|
| Order of magnitude (scoping) | 0–2 | ±40% (Range −50% to +100%) |
| Pre-feasibility study | 5–12 | ±25% (Range −30% to +40%) |
| Feasibility study budget | 25–40 | ±15% (Range −20% to +25%) |
| Definitive (control) | 60–80 | ±8% (Range −10% to +12%) |
| Detailed (final check/lump sum bid) | >85 | ±5% or better |
| Scoping Evaluation | Pre-Feasibility Study | Feasibility Study |
|---|---|---|
| Drilling | Drilling | Drilling |
| Sufficient for a resource, mostly RC. | Initial infill of wide spaced drilling; includes core. | Holes spaced on a grid that satisfies CRIRSCO. |
| Resource | Resource | Resource |
| Mostly inferred; | Indicated mostly, some measured, lithology map; | 80% measured and indicated; Full geological model; |
| Broad physical limits drawn. | Selected mineral samples; initial geological model. | Detailed mineralogical sampling study performed. |
| Reserve | Reserve | Reserve |
| No reserves. | Preliminary tons and grade meet Nl 43-101, SEC S K 1300 initial assessment quality requirements. | Mine plan 80% proven for Nl 43-101 SEC S-K 1300. |
| Mining | Mining | Mining |
| Generic mining method assigned; | Mining method selection based on geological data; | Detailed mining methods and mine plans configured; |
| Few or no data to support. | Rudimentary geotechnical and hydrology data. | Site-specific geotechnical and hydrogeological data. |
| Metallurgy | Metallurgy | Metallurgy |
| Minimal testing, recoveries estimated. | Core sampling, recoveries based on bench tests. | Test suite and pilot plant confirm recoveries and process. |
| Engineering and Process Design | Engineering and Process Design | Engineering and Process Design |
| Preliminary, based on similar plants; | Conceptual design initial plot plans, simple GAs; | Drawings/specs complete for full definition of scope; |
| Throughput capacity estimated; | Probable flowsheet, preliminary production rates; | Layout established, process frozen, production set; |
| Infrastructure allowance; | Trade-offs conducted, and critical infrastructure defined; | Trade-offs complete, infrastructure finalized; |
| Recommended total engineering ~1%. | 3D CADD model initiated, total engineering +7%. | Basic engineering +85%, total engineering +30%. |
| Environment/Permits/Social | Environment/Permits/Social | Environment/Permits/Social |
| Review of existing data; environmental, permit and social concerns investigated. | Initiate gathering of requisite baseline data; List permits; Assess social; Preliminary Environmental Management Plan (EMP) created. | Baseline data complete; Permits prepped; Social strategy complete; EMP finalized |
| Field Construction | Field Construction | Field Construction |
| No material knowledge of construction issues. | Some geotechnical drilling undertaken. | Geotechnical data sufficiently complete for construction. |
| Contingency | Contingency | Contingency |
| Generic average +40%, range 30–70%. | Broad evaluation delivers +22%, range 15% to 30%. | Detail undertaken yields +15%, range 12% to 18%. |
| Accuracy at 90% Confidence | Accuracy at 90% Confidence | Accuracy at 90% Confidence |
| At best +40%; range +100% to −50%. | At best ±25%; range is from +40% to −30%. | Goal should be ±15%, although historial range is +25% to −20%. |
| Sources (Year) | Developed Equation | Type of Mine/Mining Method | Number of Evaluated Mines |
|---|---|---|---|
| Taylor (1977) [1] | Cst = 0.0143 × Tst0.75 | Unknown | 30 |
| Camm (1991) [23] | Cst = Tst/Dwy × L | Unknown | - |
| Singer, Menzie, and Long (1998) [3] | Cst = 0.4159 × Tst0.5874 | Open-pit (gold and silver) | 46 |
| Singer, Menzie, and Long (2000) [2] | Cst = 0.0248 × Tst0.704 | Underground (large sulfide deposits) | 28 |
| Long and Singer (2001) [4] | Cst = 0.0236 × Tst0.74 | Open-pit (copper) | 45 |
| Long (2009) [22] | C = 0.123 × T0.649 | Open-pit and block caving | 342 |
| Long (2009) [22] | C = 0.297 × T0.563 | Underground (except block caving) | 197 |
| Source (Year) | Equation | Mining Method | Number of Evaluated Projects | Adherence (%) | Standard Deviation |
|---|---|---|---|---|---|
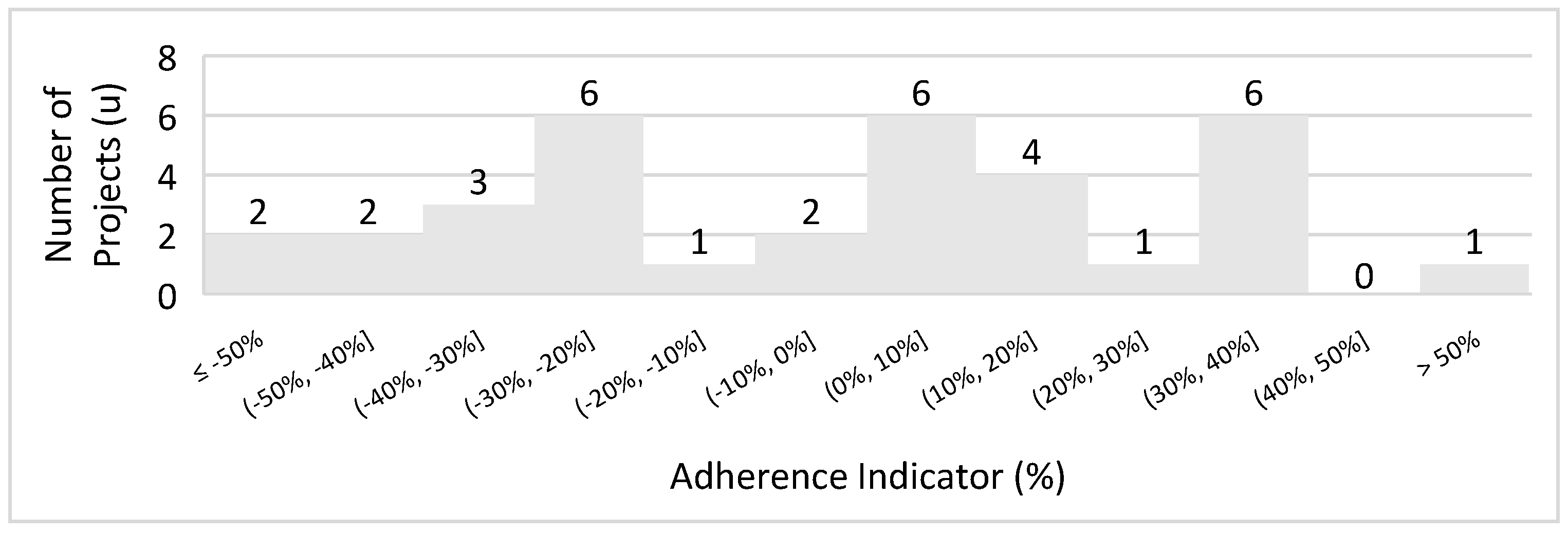
| Long and Singer (2001) [4] | Cst = 0.0236 × Tst0.74 | Open-pit (copper) | 63 | 59% | 33% |
| Long (2009) [22] | C = 0.123 × T0.649 | Open-pit/block caving | 88 | 53% | 38% |
| Long (2009) [22] | C = 0.297 × T0.563 | Underground (except block caving) | 51 | 47% | 67% |
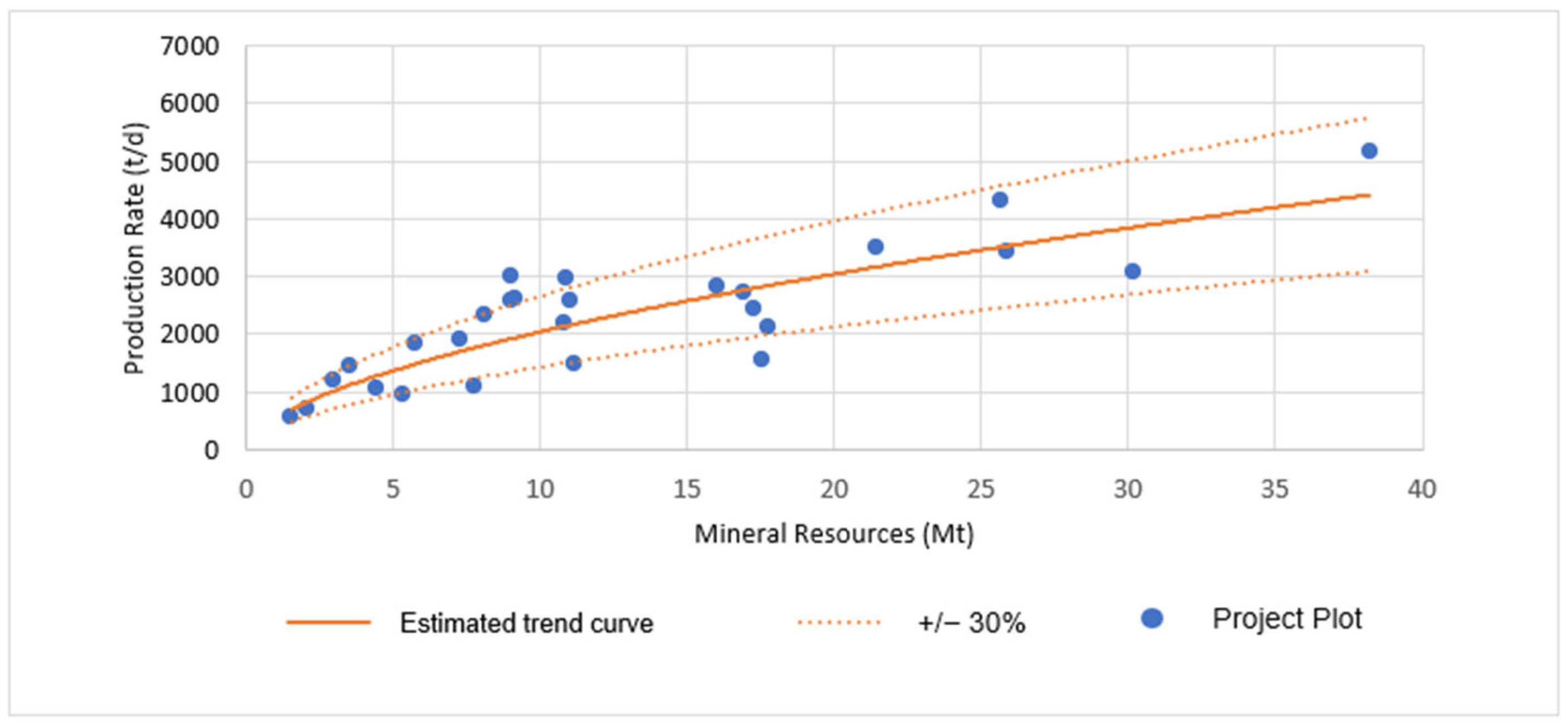
| Developed Equation | Mining Method | Number of Evaluated Projects | Coefficient of Determination (R2) | Adherence (%) | Standard Deviation |
|---|---|---|---|---|---|
| C = 0.1449 × T0.639 | Open-pit (copper) | 63 | 0.5978 | 56% | 40% |
| C = 0.2691 × T0.6056 | Open-pit (copper) up to 140 ktons/day | 55 | 0.5762 | 51% | 35% |
| C = 0.4736 × T0.5492 | Underground (copper) | 17 | 0.656 | 41% | 78% |
| C = 0.7741 × T0.5044 | Underground (copper) up to 10 ktons/day | 8 | 0.27 | 50% | 52% |
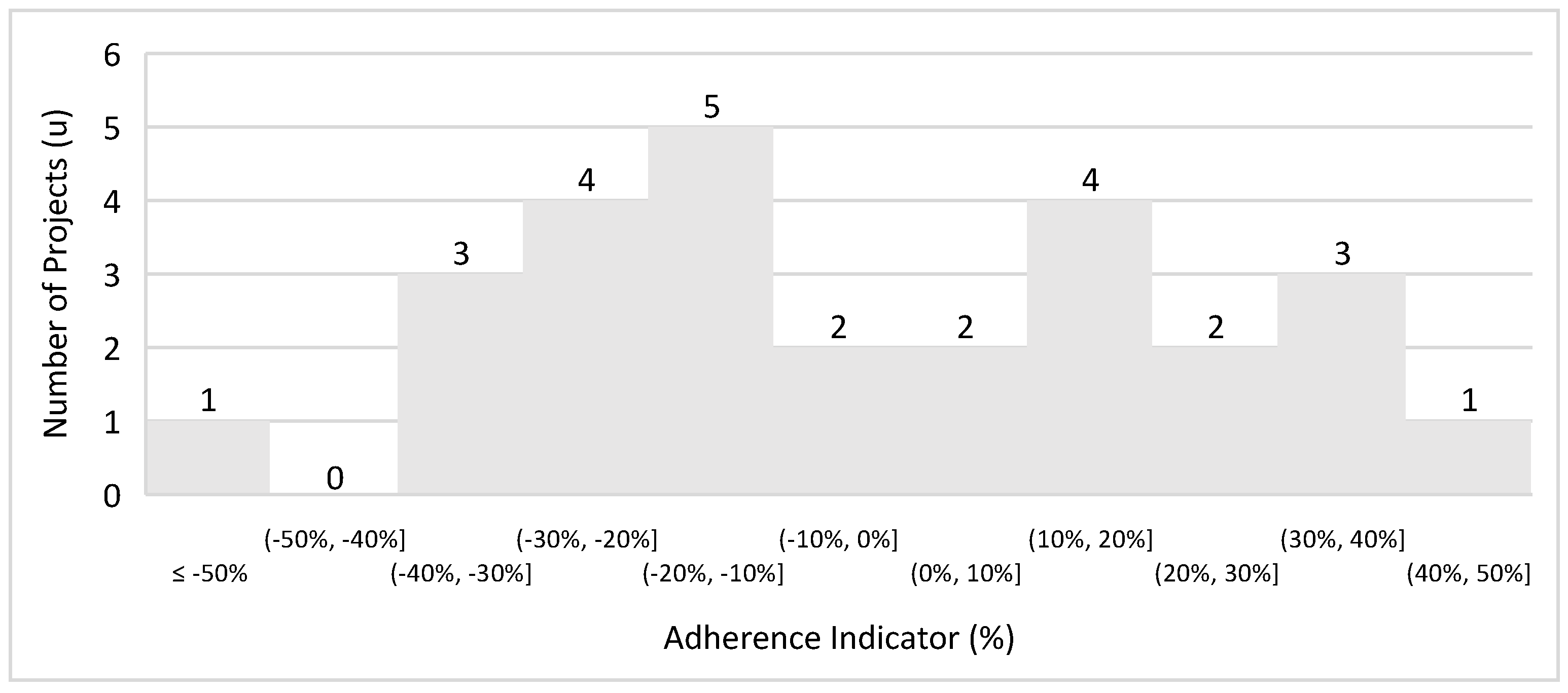
| Developed Equation | Mining Method | Number of Evaluated Projects | Coefficient of Determination (R2) | Adherence (%) | Standard Deviation |
|---|---|---|---|---|---|
| Cst = 0.0141 × Tst0.7523 | Open-pit (zinc and lead) | 25 | 0.8426 | 60% | 33% |
| C = 0.0191 × T0.7302 | Open-pit (zinc and lead) up to 10 ktons/day | 17 | 0.8296 | 76% | 24% |
| C = 0.0408 × T0.6751 | Underground (zinc and lead) | 34 | 0.722 | 59% | 33% |
| C = 0.1954 × T0.5743 | Underground (zinc and lead) up to 5.2 ktons/day | 27 | 0.7184 | 70% | 26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, L.Z.; Ayres da Silva, A.L.M. Strategic Approaches to Define the Production Rate in Conceptual Projects of Critical Raw Materials. Resources 2025, 14, 11. https://doi.org/10.3390/resources14010011
Silva LZ, Ayres da Silva ALM. Strategic Approaches to Define the Production Rate in Conceptual Projects of Critical Raw Materials. Resources. 2025; 14(1):11. https://doi.org/10.3390/resources14010011
Chicago/Turabian StyleSilva, Lucas Zucchi, and Anna Luiza Marques Ayres da Silva. 2025. "Strategic Approaches to Define the Production Rate in Conceptual Projects of Critical Raw Materials" Resources 14, no. 1: 11. https://doi.org/10.3390/resources14010011
APA StyleSilva, L. Z., & Ayres da Silva, A. L. M. (2025). Strategic Approaches to Define the Production Rate in Conceptual Projects of Critical Raw Materials. Resources, 14(1), 11. https://doi.org/10.3390/resources14010011






