Energy, Exergy, and Exergo-Sustainability Analysis of a Brayton S-CO2/Kalina Operating in Araçuaí, Brazil, Using Solar Energy as a Thermal Source
Abstract
:1. Introduction
2. Methodology
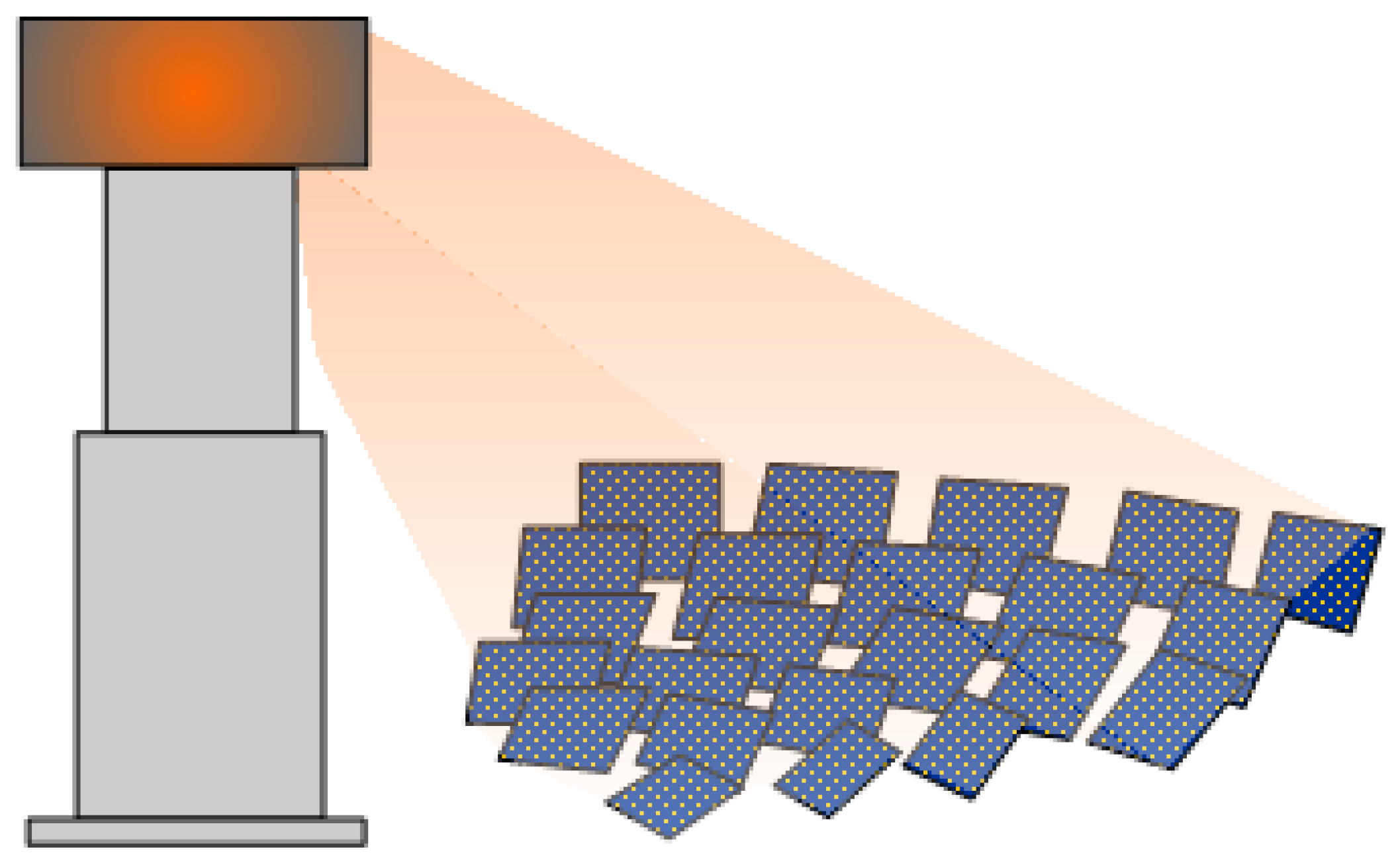
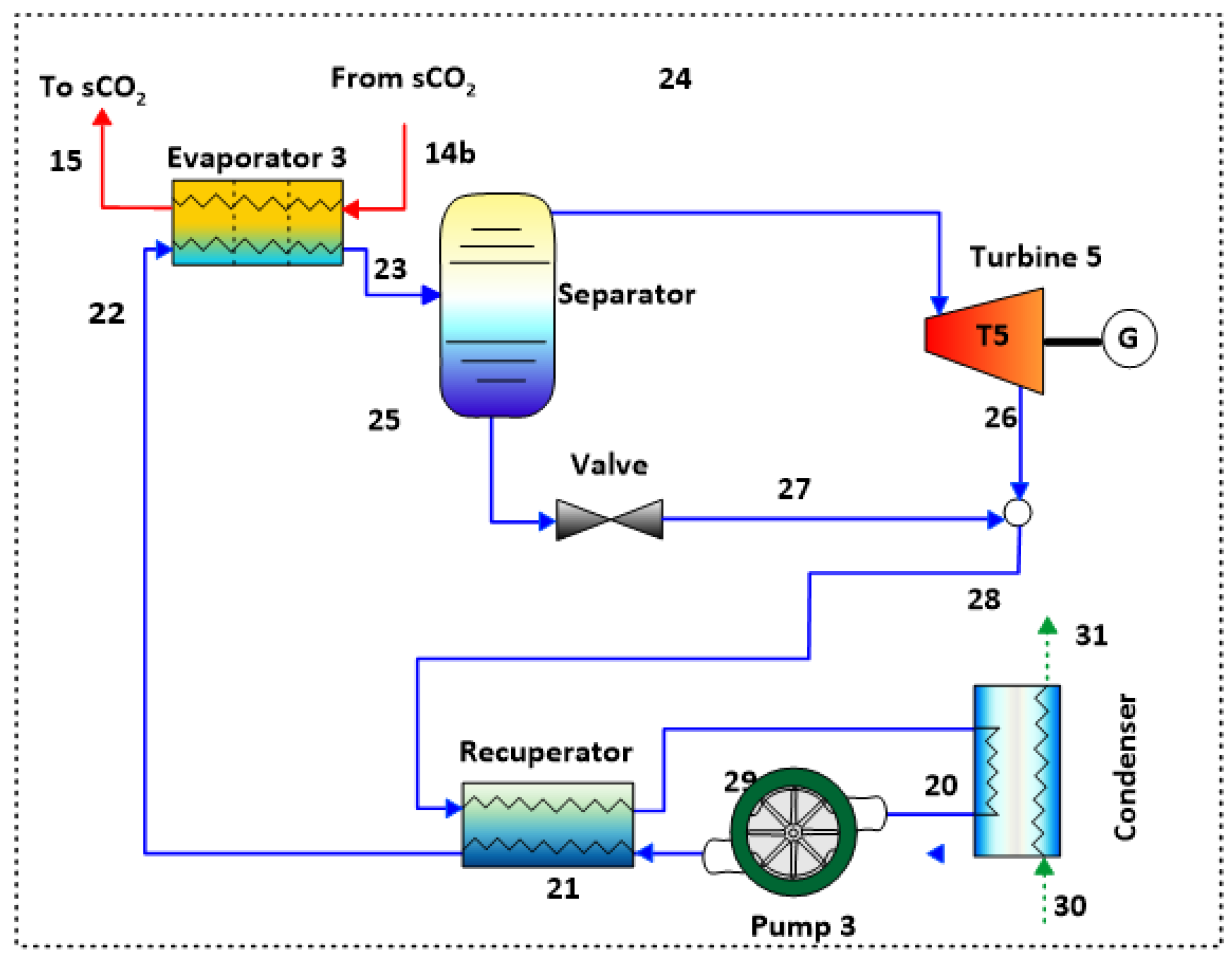
2.1. System Description
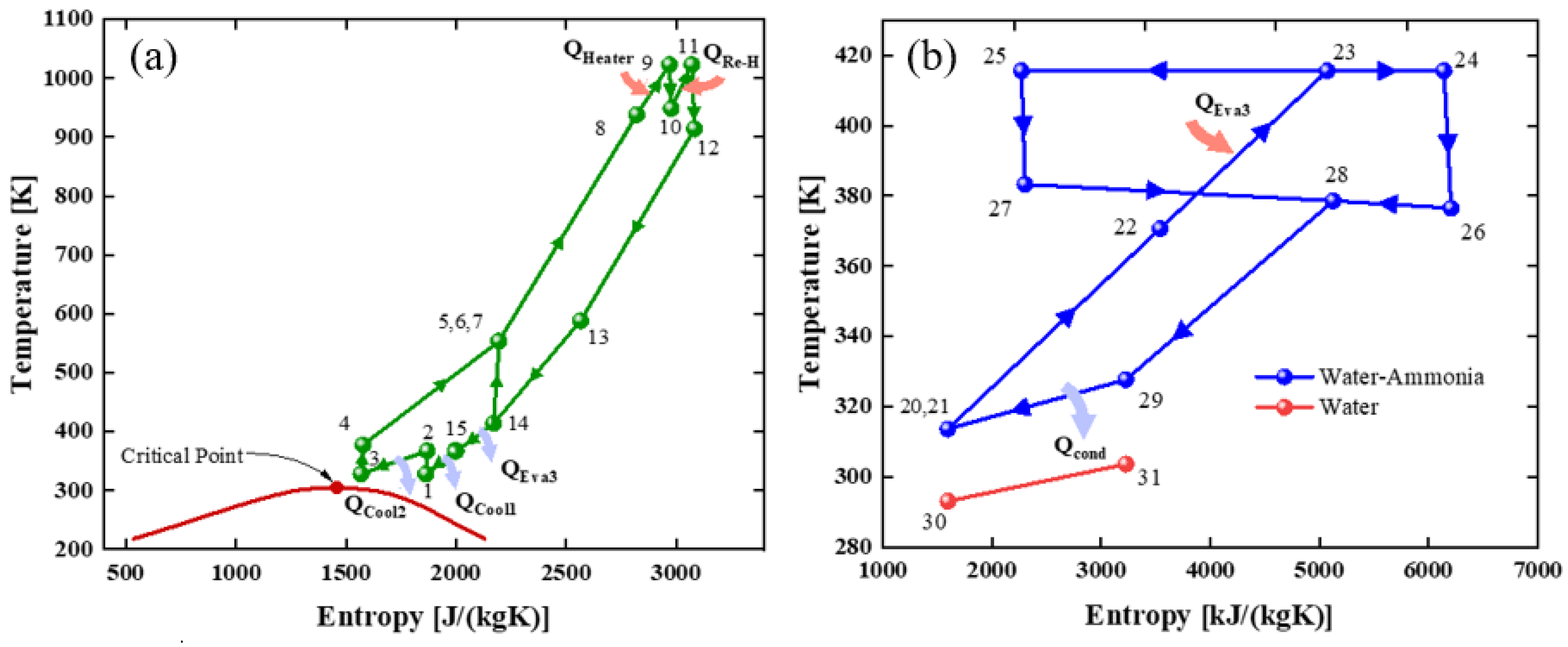
2.2. Thermodynamic Modeling
Energy and Exergy Balance
- Pressure drops in piping and heat exchangers were considered negligible.
- Changes in potential and kinetic energy were considered negligible, as were losses due to friction.
- Each component was worked as an open system operating at steady-state conditions.
- There are no fluid losses in the cycle.
- Heat losses in the solar field and receiver were included.
- The valves are isentropic.
- According to Equations (1) and (2), mass and energy balances were performed for each component.
2.3. Exergo-Sustainability Indicators
2.4. Model Validation
3. Results and Discussion
3.1. Energy and Exergy Analysis of the Proposed System
3.1.1. Effect of Solar Radiation on the System Performance
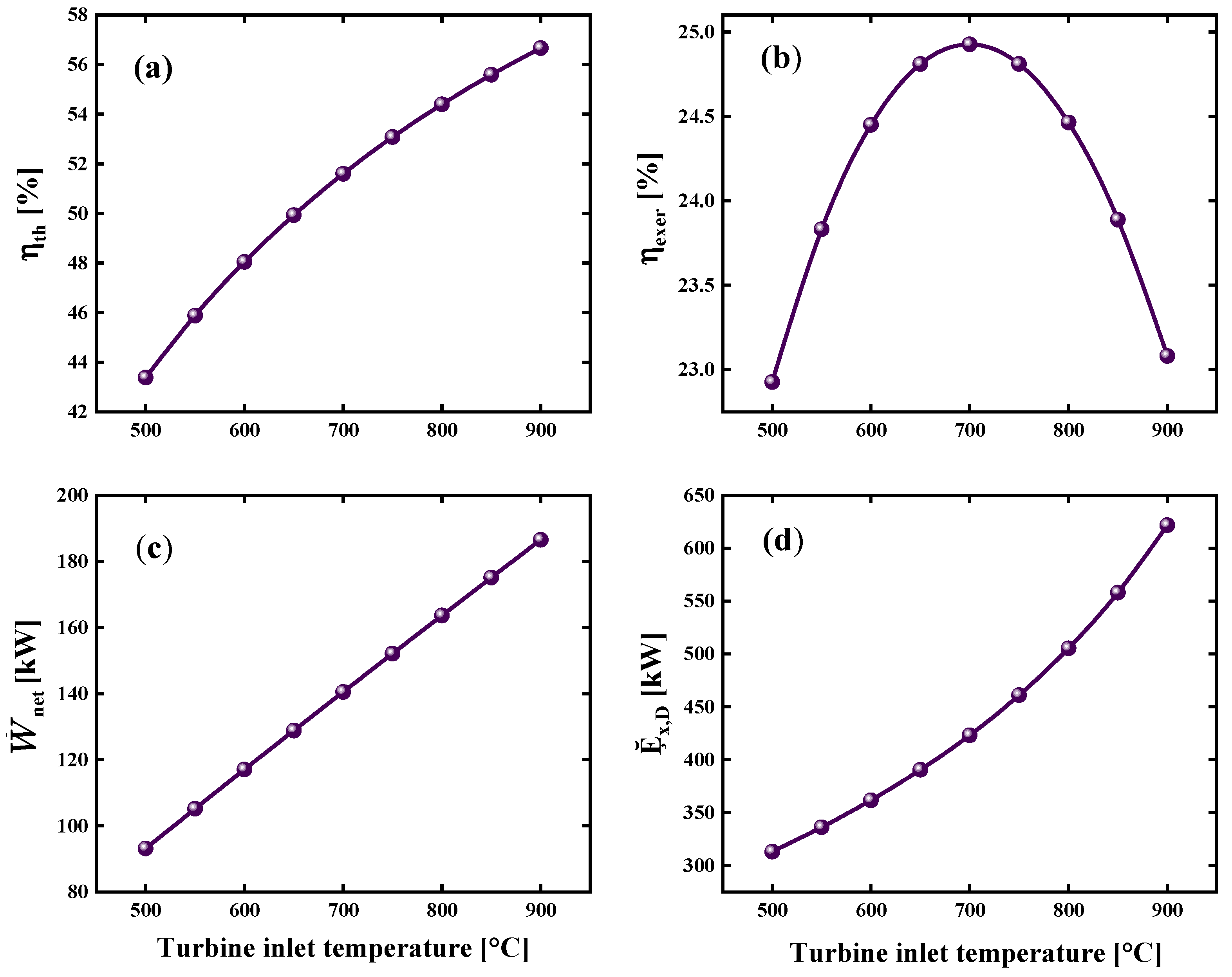
3.1.2. Effect of Turbine Inlet Temperature on System Performance
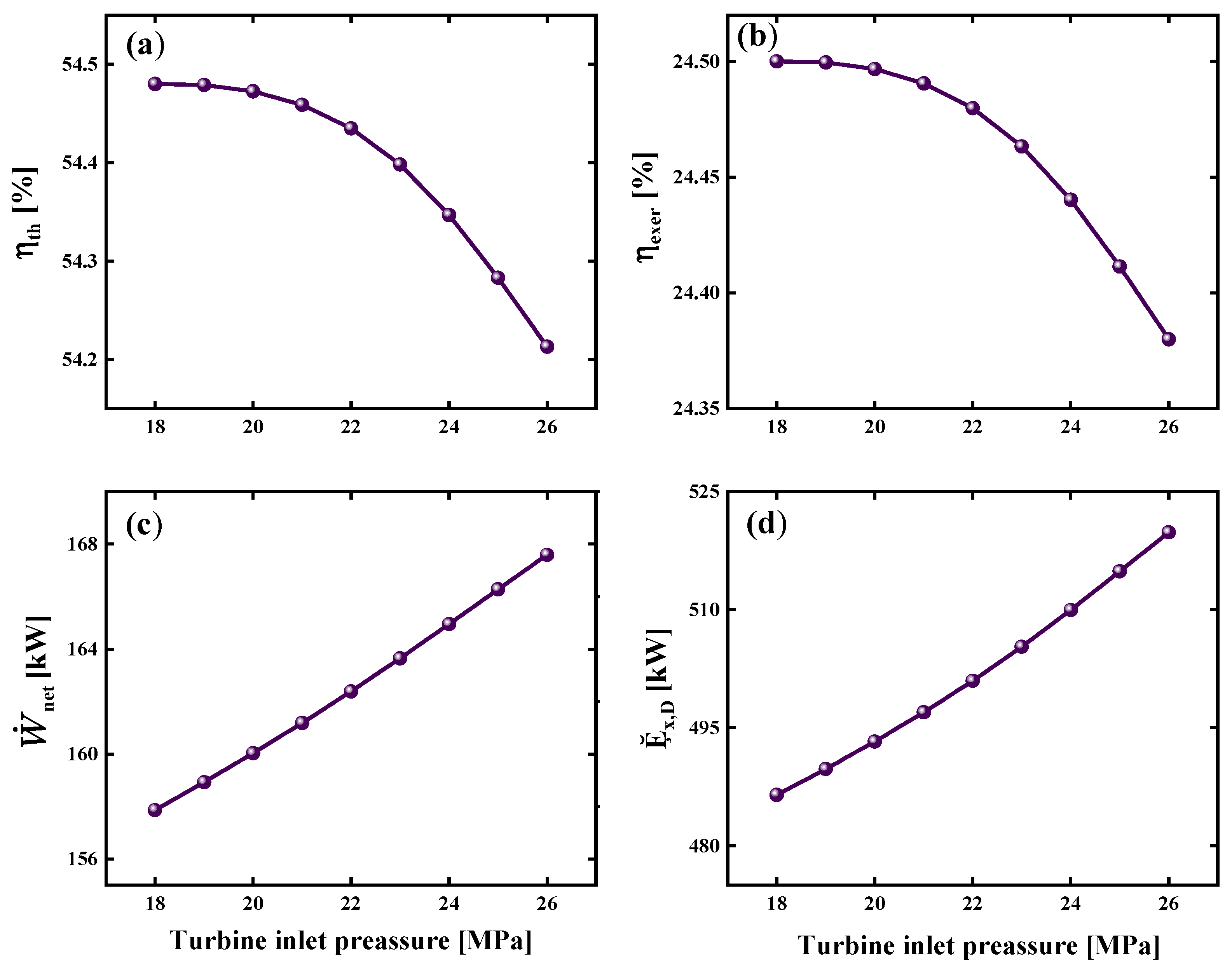
3.1.3. Effect of Turbine Inlet Pressure on the System Performance
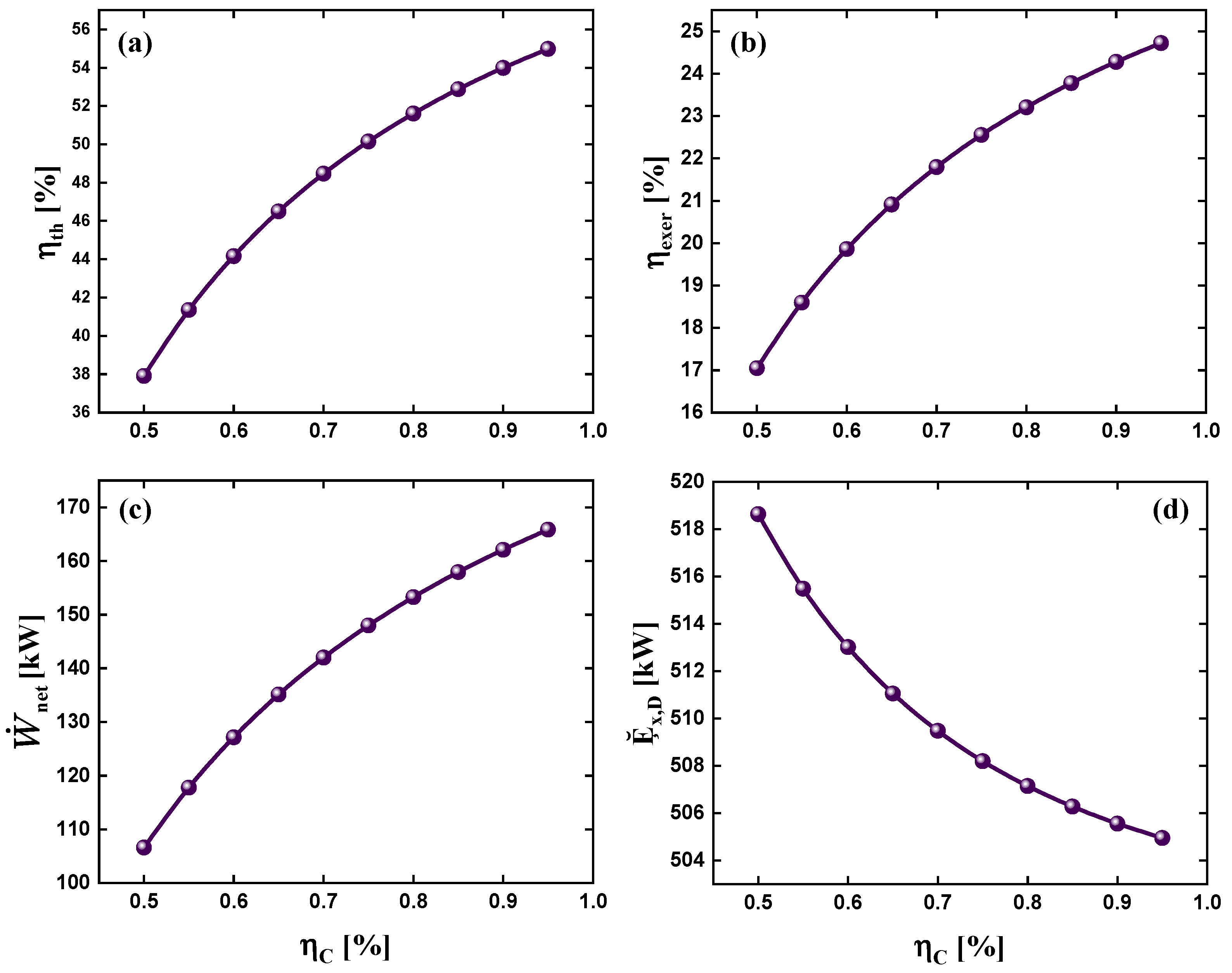
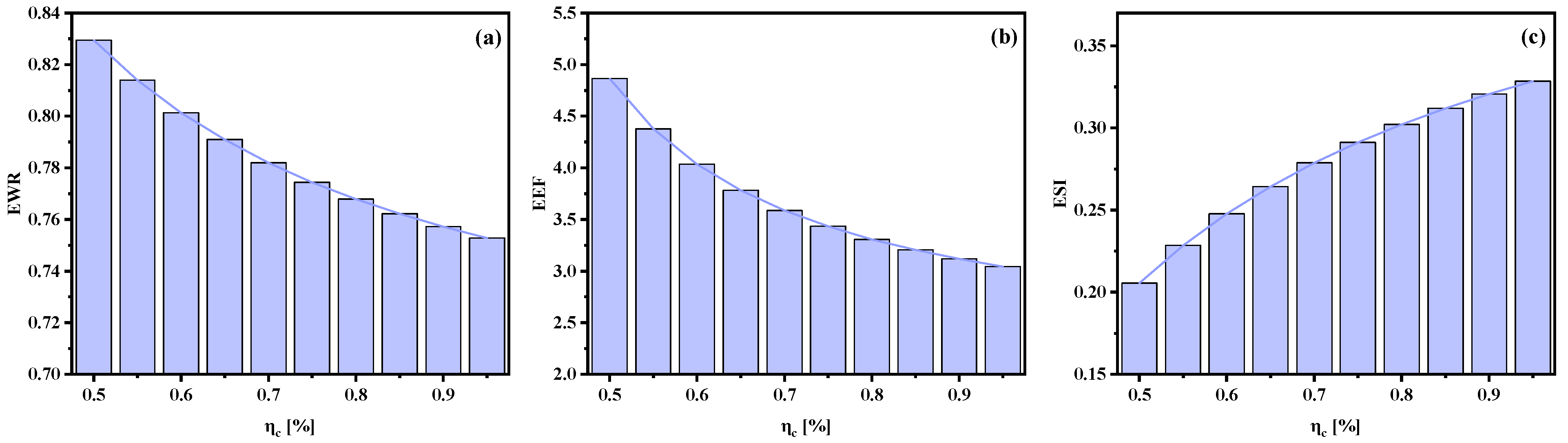
3.1.4. Effect of Compressor Efficiency on System Performance
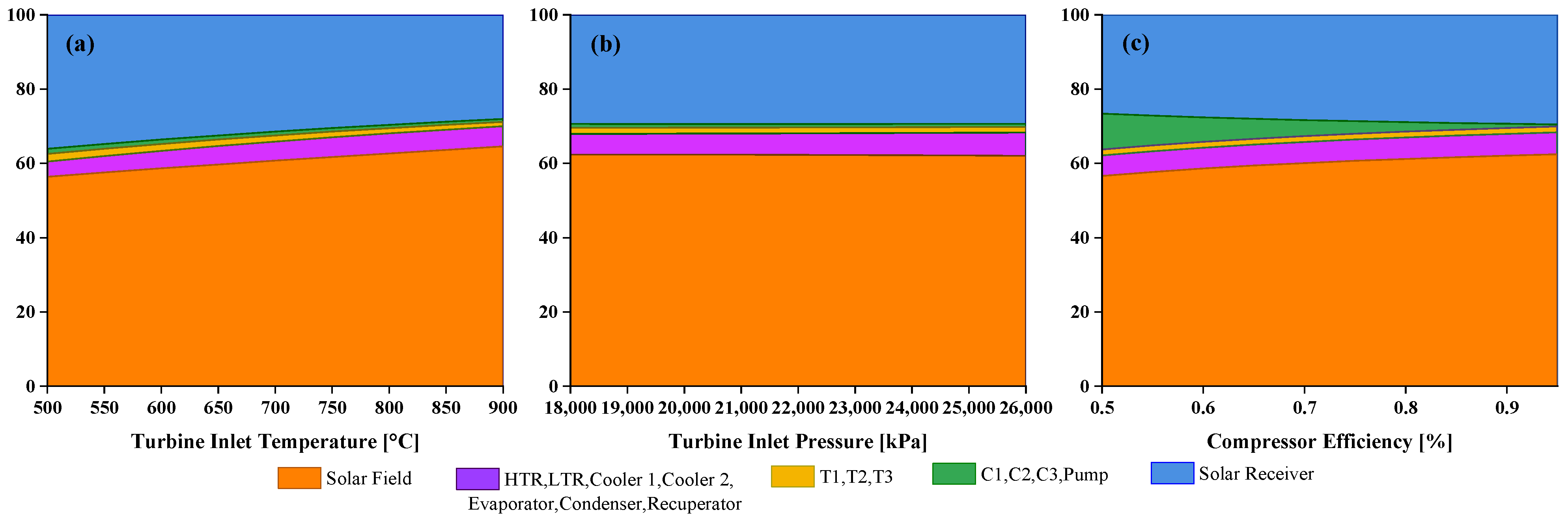
3.2. Exergy Destruction Study
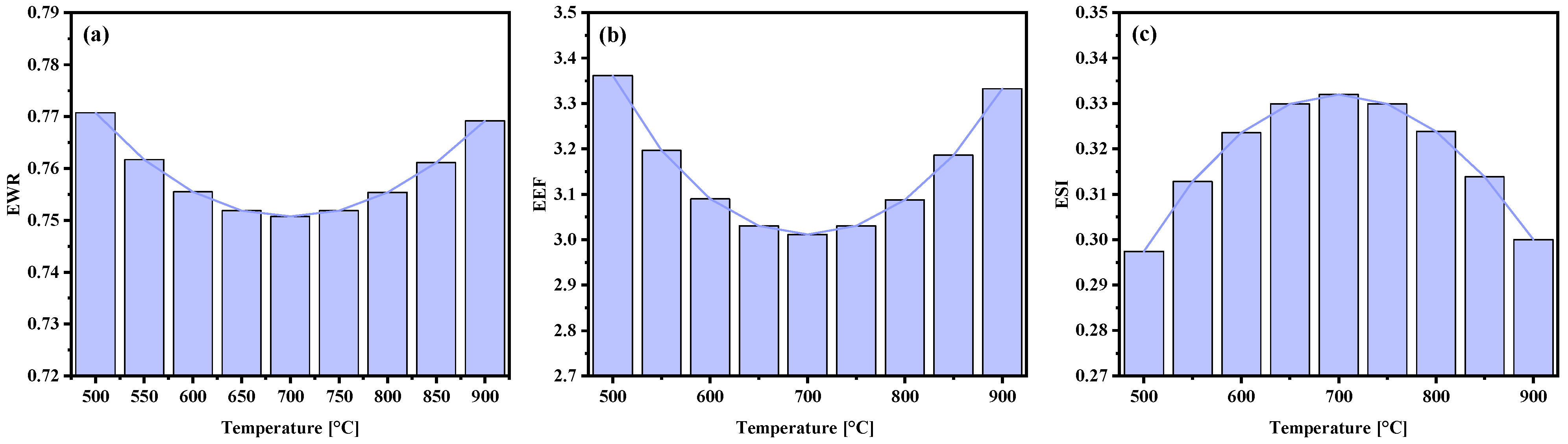
3.3. Exergo-Sustainability
4. Conclusions
- How can the solar receiver design be optimized to reduce thermal losses and increase the energy efficiency of the system?
- What materials could improve the absorption of solar energy in the receiver and its resistance to high temperatures?
- What operation and maintenance strategies could minimize deterioration and maximize the service life of the solar field and receiver components?
- What is the relationship between operating conditions and capital, operating, and maintenance costs to maximize the economic viability of the Brayton and S-CO2/Kalina cycle in CSP systems?
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbass, K.; Qasim, M.Z.; Song, H.; Murshed, M.; Mahmood, H.; Younis, I. A review of the global climate change impacts, adaptation, and sustainable mitigation measures. Environ. Sci. Pollut. Res. 2022, 29, 42539–42559. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, R.; Dahlman, L. Climate Change: Global Temperature; NOAA Climate: Silver Spring, MD, USA, 2024; pp. 1–5. [Google Scholar]
- Guamán, V.J.; Espinoza, E.E. Educación para el cambio climático. Rev. Metrop. Cienc. Apl. 2022, 5, 17–24. Available online: https://www.redalyc.org/pdf/7217/721778114003.pdf (accessed on 14 November 2024). [CrossRef]
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Holechek, J.L.; Geli, H.M.E.; Sawalhah, M.N.; Valdez, R. A Global Assessment: Can Renewable Energy Replace Fossil Fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Leme, J.V.; Casaca, W.; Colnago, M.; Dias, M.A. Towards Assessing the Electricity Demand in Brazil: Data-Driven Analysis and Ensemble Learning Models. Energies 2020, 13, 1407. [Google Scholar] [CrossRef]
- UNFCCC. Federative Republic of Brazil Nationally Determined Contribution (NDC) to the Paris Agreement Under the UNFCC; UNFCCC: Brasilia, Brazil, 2023; Available online: https://unfccc.int/sites/default/files/NDC/2023-11/Brazil%20First%20NDC%202023%20adjustment.pdf (accessed on 14 November 2024).
- Balanço Energético Nacional 2024. Epe: Empresa de Pesquisa Energética. Available online: https://www.epe.gov.br/pt/publicacoes-dados-abertos/publicacoes/balanco-energetico-nacional-2024 (accessed on 14 November 2024).
- Arias, M.E.; Farinosi, F.; Lee, E.; Livino, A.; Briscoe, J.; Moorcroft, P.R. Impacts of climate change and deforestation on hydropower planning in the Brazilian Amazon. Nat. Sustain. 2020, 3, 430–436. [Google Scholar] [CrossRef]
- da Silva, B.C.; Virgílio, R.M.; Nogueira, L.A.H.; Silva, P.D.N.; Passos, F.O.; Welerson, C.C. Assessment of Climate Change Impact on Hydropower Generation: A Case Study for Três Marias Power Plant in Brazil. Climate 2023, 11, 201. [Google Scholar] [CrossRef]
- da Silva, H.M.F.; Araújo, F.J.C. Energia solar fotovoltaica no Brasil: Uma revisao bibliográfica. Rev. Ibero-Am. Humanidades Ciências Educ. 2022, 8, 859–869. [Google Scholar] [CrossRef]
- Bernadete, M.; Gutierrez, S. Governance for the Transition to a Sustainable Energy Sector in Brazil: Integrating Energy and Climate Change Policies. International Association for Energy Economics, 2021. Available online: https://iaee2021online.org/download/contribution/fullpaper/433/433_fullpaper_20210601_222348.pdf (accessed on 14 November 2024).
- de Andrade Santos, J.A.F.; de Jong, P.; da Costa, C.A.; Torres, E.A. Combining wind and solar energy sources: Potential for hybrid power generation in Brazil. Util. Policy 2020, 67, 101084. [Google Scholar] [CrossRef]
- Paraschiv, L.S.; Paraschiv, S. Contribution of renewable energy (hydro, wind, solar and biomass) to decarbonization and transformation of the electricity generation sector for sustainable development. Energy Rep. 2023, 9, 535–544. [Google Scholar] [CrossRef]
- Boletim Agroclimatológico Mensual; Instituto Nacional de Meteorología: Nampula, Mozambique, 2025. Available online: https://portal.inmet.gov.br/boletinsagro# (accessed on 14 November 2024).
- Zhai, R.; Chen, Y.; Li, J.; Du, M.; Yang, Y. Intelligent construction and optimization based on the heatsep method of a supercritical CO2 brayton cycle driven by a solar power tower system. Sol. Energy Mater. Sol. Cells 2024, 276, 113075. [Google Scholar] [CrossRef]
- Li, M.-J.; Li, M.-J.; Jiang, R.; Du, S.; Li, X.-Y. Study on the dynamic characteristics of a concentrated solar power plant with the supercritical CO2 Brayton cycle coupled with different thermal energy storage methods. Energy 2024, 288, 129628. [Google Scholar] [CrossRef]
- Chowdhury, A.S.; Ehsan, M.M. A Critical Overview of Working Fluids in Organic Rankine, Supercritical Rankine, and Supercritical Brayton Cycles Under Various Heat Grade Sources. Int. J. Thermofluids 2023, 20, 100426. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, C.; Wang, X.; Wang, S.; Xu, X.; Li, Q.; Li, X. Life cycle assessment of the solar thermal power plant integrated with air-cooled supercritical CO2 Brayton cycle. Renew Energy 2022, 182, 119–133. [Google Scholar] [CrossRef]
- Palomino, M.H.; Pacheco, E.C.; Forero, J.D.; Lascano, A.F.; Padilla, R.V. Análisis exergético de un ciclo Brayton supercrítico con dióxido de carbono como fluido de trabajo. Inge Cuc 2018, 14, 159–170. [Google Scholar] [CrossRef]
- Nihaj, A.N.M.; Shan, U. A Review of Kalina Cycle. 2020. Available online: https://setee.globalpublisher.org/article_180394_21e49de16f7d8798550e581a3d3fb57d.pdf (accessed on 14 November 2024).
- Fan, G.; Dai, Y. Thermo-economic optimization and part-load analysis of the combined supercritical CO2 and Kalina cycle. Energy Convers. Manag. 2021, 245, 114572. [Google Scholar] [CrossRef]
- Omar, A.; Saghafifar, M.; Mohammadi, K.; Alashkar, A.; Gadalla, M. A review of unconventional bottoming cycles for waste heat recovery: Part II–Applications. Energy Convers. Manag. 2019, 180, 559–583. [Google Scholar] [CrossRef]
- Mahmoudi, S.S.; Akbari, A.D.; Rosen, M. Thermoeconomic Analysis and Optimization of a New Combined Supercritical Carbon Dioxide Recompression Brayton/Kalina Cycle. Sustainability 2016, 8, 1079. [Google Scholar] [CrossRef]
- Yousef, M.S.; Santana, D. Thermodynamic and Exergoeconomic Analysis of Utilizing a Modified Kalina Cycle for a Recompression Supercritical CO2 Cycle Waste Heat Recovery. In Proceedings of the 2023 6th International Conference on Electrical Engineering and Green Energy (CEEGE), Grimstad, Norway, 6–9 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 253–259. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Luo, Y.; Zhao, S. Comparative and optimal study of energy, exergy, and exergoeconomic performance in supercritical CO2 recompression combined cycles with organic rankine, trans-critical CO2, and kalina cycle. Energy 2024, 311, 133347. [Google Scholar] [CrossRef]
- Tovar, J.M.; Ochoa, G.V.; Casseres, D.M. Thermodynamic and environmental comparative analysis of a dual loop ORC and Kalina as bottoming cycle of a solar Brayton sCO2. Int. J. Thermofluids 2024, 24, 100895. [Google Scholar] [CrossRef]
- Hassan, R.; Barua, H.; Das, B.K. Energy, exergy, exergo-environmental, and exergetic sustainability analyses of a gas engine-based CHP system. Energy Sci. Eng. 2021, 9, 2232–2251. [Google Scholar] [CrossRef]
- Yu, A.; Su, W.; Lin, X.; Zhou, N. Recent trends of supercritical CO2 Brayton cycle: Bibliometric analysis and research review. Nucl. Eng. Technol. 2021, 53, 699–714. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Pantaleo, A.M.; Camporeale, S.M.; Sorrentino, A.; Miliozzi, A.; Shah, N.; Markides, C.N. Hybrid solar-biomass combined Brayton/organic Rankine-cycle plants integrated with thermal storage: Techno-economic feasibility in selected Mediterranean areas. Renew. Energy 2020, 147, 2913–2931. [Google Scholar] [CrossRef]
- Abam, F.I.; Okon, B.B.; Edem, I.F.; Ndukwu, M.C.; Ekpo, E.B.; Diemuodeke, O.E. Environmental assessment and CO2 emissions of Brayton cycle configurations based on exergo-sustainability, economic and ecological efficiency using multi-criteria optimization technique. Future Technol. 2024, 3, 1–12. [Google Scholar] [CrossRef]
- Padilla, R.V.; Too, Y.C.S.; Benito, R.; Stein, W. Exergetic analysis of supercritical CO2 Brayton cycles integrated with solar central receivers. Appl. Energy 2015, 148, 348–365. [Google Scholar] [CrossRef]
- Yari, M.; Mehr, A.S.; Zare, V.; Mahmoudi, S.M.S.; Rosen, M.A. Exergoeconomic comparison of TLC (trilateral Rankine cycle), ORC (organic Rankine cycle) and Kalina cycle using a low grade heat source. Energy 2015, 83, 712–722. [Google Scholar] [CrossRef]
- Padilla, R.V.; Too, Y.C.S.; Benito, R.; McNaughton, R.; Stein, W. Multi-objective thermodynamic optimisation of supercritical CO2 Brayton cycles integrated with solar central receivers. Int. J. Sustain. Energy 2018, 37, 1–20. [Google Scholar] [CrossRef]
- Merchán, R.P.; Santos, M.J.; Medina, A.; Hernández, A.C. High temperature central tower plants for concentrated solar power: 2021 overview. Renew. Sustain. Energy Rev. 2022, 155, 111828. [Google Scholar] [CrossRef]
- Jennings, T.; Parsons, L. Concentrated Solar Power-Focusing the Sun’s Energy for Large-Scale Power Generation; Environmental and Energy Study Institute: Washington, DC, USA, 2009; pp. 1–4. [Google Scholar]
- Li, H.; Wang, M.; Wang, J.; Dai, Y. Exergoeconomic Analysis and Optimization of a Supercritical CO2 Cycle Coupled with a Kalina Cycle. J. Energy Eng. 2017, 143, 04016055. [Google Scholar] [CrossRef]
- Yousef, M.S.; Santana, D. Novel supercritical CO2-Based Low-Carbon multige-neration System: Multi-Objective optimization for combined Power, Cooling, Heating, and desalination. Energy Convers. Manag. X 2024, 23, 100649. [Google Scholar] [CrossRef]
- Luo, Y.; Su, Z.; Li, Z.; Zheng, N.; Wei, J. Off-design performance analysis of super-critical CO2 mixture Brayton cycle with floating critical points. Sol. Energy 2024, 276, 112665. [Google Scholar] [CrossRef]
- Shokrkar, M.H.; Dehghan, A.; Ghasemi, H.; Ameri, M. Simultaneous optimizati-on of combined supercritical CO2 Brayton cycle and organic Rankine cycle integrated with concentrated solar power system. Energy 2020, 213, 118791. [Google Scholar] [CrossRef]
- Stand, L.M.; Ochoa, G.V.; Forero, J.D. Energy and exergy as-sessment of a combined supercritical Brayton cycle-orc hybrid system using solar radia-tion and coconut shell biomass as energy source. Renew. Energy 2021, 175, 119–142. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Li, H.; Yang, Y.; Bai, W.; Zhang, C.; Zhang, X.; Yao, M. Thermo-economic and environmental analyses of supercritical car-bon dioxide Brayton cycle for high temperature gas-cooled reactor. Prog. Nucl. Energy 2024, 177, 105461. [Google Scholar] [CrossRef]




| Cycle | Component | Ẇ | Q | Ḝx,D |
|---|---|---|---|---|
| Brayton S-CO2 | Turbine 1 | ṁ9·(h9 − h10) | - | (Ḝx,9 − Ḝx,10) − ẆT1 |
| Turbine 2 | ṁ11·(h11 − h12) | - | (Ḝx,11 − Ḝx,12) − ẆT2 | |
| Compressor 1 | ṁ1·(h2 − h1) | - | ẆC1 − (Ḝx,2 − Ḝx,1) | |
| Compressor 2 | ṁ3·(h4 − h3) | - | ẆC2 − (Ḝx,4 − Ḝx,3) | |
| Compressor 3 | ṁ14a·(h6 − h14) | - | ẆC3 − (Ḝx,6 − Ḝx,14a) | |
| HTR | - | ṁ12·(h12 − h13) | (Ḝ12 − Ḝ13) − (Ḝx,8 − Ḝx,7) | |
| LTR | - | ṁ13·(h13 − h14) | (Ḝ13 − Ḝ14) − (Ḝx,5 − Ḝx,4) | |
| Cooler 1 | - | ṁ16·(h15 − h1) | (Ḝx,15 − Ḝx,1) − (Ḝx,17 − Ḝx,16) | |
| Cooler 2 | - | ṁ2·(h2 − h3) | (Ḝx,2 − Ḝx,3) − (Ḝx,20 − Ḝx,19) | |
| Heater | - | ṁ8·(h8 − h9) | Equation (17) | |
| Reheater | - | ṁ10·(h10 − h11) | ||
| K C | Turbina 3 | ṁ24·(h24 − h26) | - | (Ḝ24 − Ḝ26) − ẆT5 |
| Pump | ṁwf·(h20 − h21) | - | ẆB3 − (Ḝ21 − Ḝ20) | |
| Evaporator | - | ṁwf·(h23 − h22) | (Ḝ14b − Ḝ15) − (Ḝ23 − Ḝ22) | |
| Condenser | - | ṁwf·(h29 − h20) | (Ḝ29 − Ḝ30) − (Ḝ31 − Ḝ30) | |
| Recuperator | - | ṁwf·(h28 − h29) | (Ḝ28 − Ḝ29) − (Ḝ22 − Ḝ21) | |
| Valve | - | - | Ḝ25 − Ḝ27 |
| Parameters | Unit | Value |
|---|---|---|
| Annual heliostat field efficiency, ηf, | - | 0.60 |
| The equivalent temperature of the sun, Ts | K | 6073.15 |
| Cone angle of the sun, ϕ | Rad | 0.05 |
| Absorption, ϑ | - | 0.95 |
| Thermal Emittance, κ | - | 0.85 |
| View factor, β | - | 1 |
| Convective heat loss factor, Fcon | - | 1 |
| Convective heat transfer coefficient, hcon | W/(m2·K) | 10 |
| Solar receiver temperature approach, δTrec | K | 423.15 |
| Concentration ratio, θ | - | 900 |
| Brayton S-CO2 Parameters | Value | Ref. | Kalina Parameters | Value | Ref. |
|---|---|---|---|---|---|
| Turbine inlet temperature | 500–850 °C (773.15–1123.15 K) | [33] | Thermal source temperature | 120 °C (393.15 K) | [34] |
| High cycle pressure | 25 Mpa | Thermal source pressure | 0.2 MPa | ||
| Turbine efficiency | 93% | Thermal source mass flow | 100 kg/s | ||
| Compressor efficiency | 90% | Condensation pressure | 1.4 MPa | ||
| Pinch temperature difference | 5 °C (278.15 K) | Evaporation pressure | 24–40 Bar (2.4–4 MPa) | ||
| Effectiveness of exchangers | 95% | Turbine efficiency | 85% | ||
| CO2 mass flow rate | 1 kg/s | Pump efficiency | 85% | ||
| Ammonia concentration | 0.9% |
| Brayton S-CO2 Parameters | Value | Refs. | Kalina Parameters | Value | Ref. |
|---|---|---|---|---|---|
| Pressure ratio 1, | 1.66 | [35] | Optimum ammonia concentration | 75% | [34] |
| Pressure ratio 2, | 3.57 | [35] | Evaporating pressure | 30 bar (3 MPa) | [34] |
| Pressure ratio 3, | 2.57 | [35] | Condensing temperature, | 40 °C (313.15 K) | [34] |
| Cooling temperature, | 50 °C (323.15 K) | [31,36] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Córdoba, J.; Valencia, G.; Molina, B. Energy, Exergy, and Exergo-Sustainability Analysis of a Brayton S-CO2/Kalina Operating in Araçuaí, Brazil, Using Solar Energy as a Thermal Source. Resources 2025, 14, 31. https://doi.org/10.3390/resources14020031
Córdoba J, Valencia G, Molina B. Energy, Exergy, and Exergo-Sustainability Analysis of a Brayton S-CO2/Kalina Operating in Araçuaí, Brazil, Using Solar Energy as a Thermal Source. Resources. 2025; 14(2):31. https://doi.org/10.3390/resources14020031
Chicago/Turabian StyleCórdoba, Juan, Guillermo Valencia, and Branda Molina. 2025. "Energy, Exergy, and Exergo-Sustainability Analysis of a Brayton S-CO2/Kalina Operating in Araçuaí, Brazil, Using Solar Energy as a Thermal Source" Resources 14, no. 2: 31. https://doi.org/10.3390/resources14020031
APA StyleCórdoba, J., Valencia, G., & Molina, B. (2025). Energy, Exergy, and Exergo-Sustainability Analysis of a Brayton S-CO2/Kalina Operating in Araçuaí, Brazil, Using Solar Energy as a Thermal Source. Resources, 14(2), 31. https://doi.org/10.3390/resources14020031







