Theoretical Substantiation of Risk Assessment Directions in the Development of Fields with Hard-to-Recover Hydrocarbon Reserves
Abstract
:1. Introduction
2. Literature Review
2.1. Classification of Hard-to-Recover Hydrocarbon Reserves
2.2. List of Classical Methods and Techniques for Risk Assessment and Analysis
2.3. Modern Methods of Risk Assessment and Analysis in the Oil and Gas Industry
- Crude oil price: Laplace distribution.
- Crack spread for gasoline and LPG: ExtValueMin distribution.
- Crack spread for diesel fuel and jet fuel: logistic distribution.
- Refinery utilization rate: uniform distribution.
- P(Uw), P(Hs), P(Vc), P(Ht), P(Δ), P(Ei): probabilities of impacts from corresponding environmental parameters—wind speed, wave height, current velocity, tsunami height, sea level changes, and other factors.
- P(TA): probability of an incident due to vessel movement.
- P(Qi): probability of an oil spill.
- Qi: volume of the spill.
- A, B—calibration coefficients for different risk levels.
- Probability: likelihood of the event occurring,
- Severity: degree of consequences.
2.4. Analysis of Methodological Gaps in the Scientific Literature and Justification of the Proposed Methodology
3. Materials and Methods
3.1. Risk Categorization and Selection
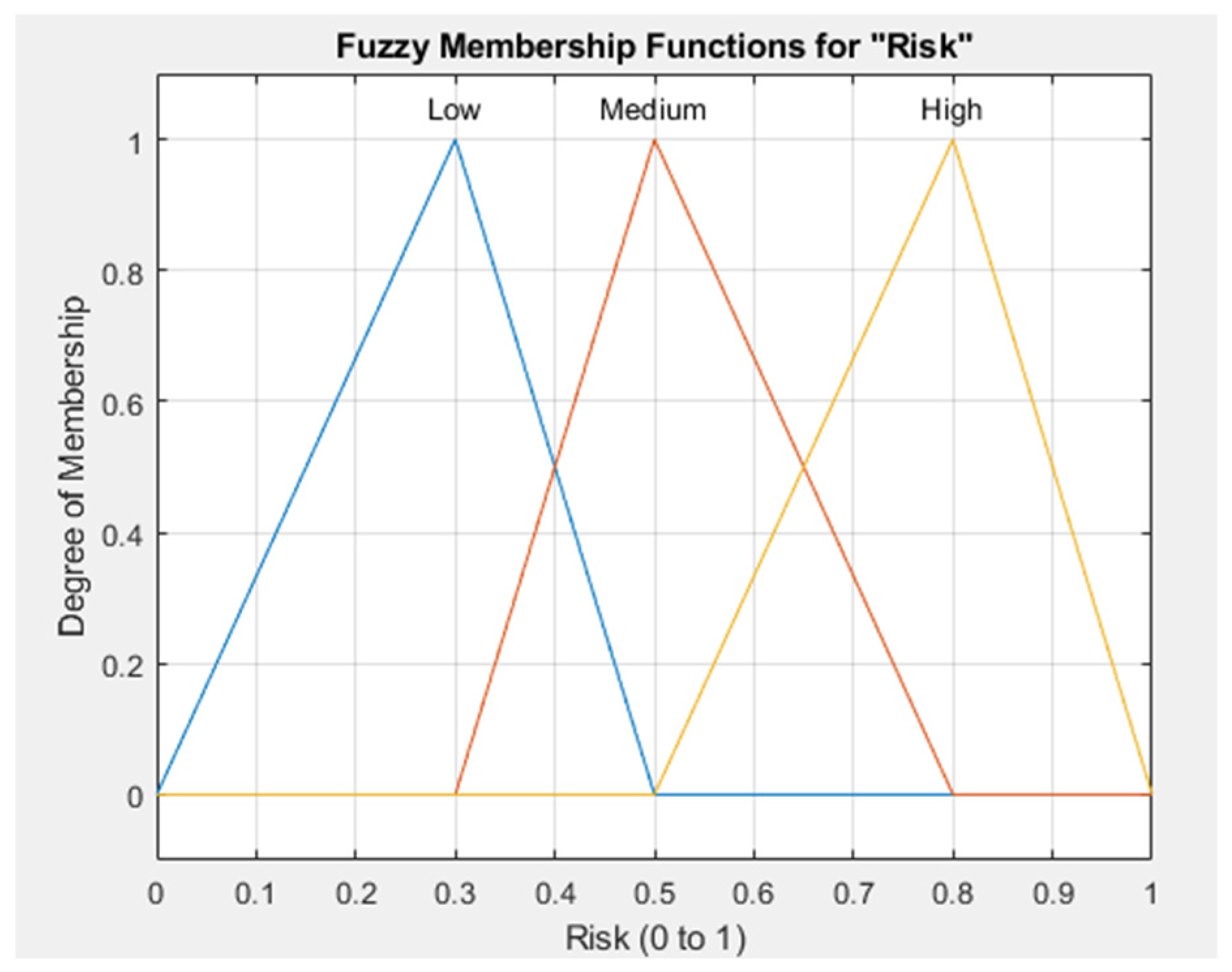
3.2. Fuzzy Logic for Qualitative Risk Analysis
3.3. Monte Carlo Simulation for Quantitative Risk Integration
3.4. Framework for Comprehensive Risk Assessment
3.5. Methodology Summary
4. Results
4.1. Comprehensive Risk Classification in the Development of Hard-to-Recover Reserves
4.2. Methodological Foundations of Stochastic Modeling Using Monte Carlo Simulation
4.3. Application of Fuzzy Logic for Qualitative Risk Assessment
4.4. Development of an Integrated Methodology Combining Monte Carlo and Fuzzy Logic
- Geological risk (Rgeo): {Low, Medium, High}.
- Environmental risk (Renv): {Low, Medium, High}.
- Technological risk (Rtech): {Low, Medium, High}.
- Political–regulatory risk (Rreg): {Low, Medium, High}.
- Social risk (Rsoc): {Low, Medium, High}.
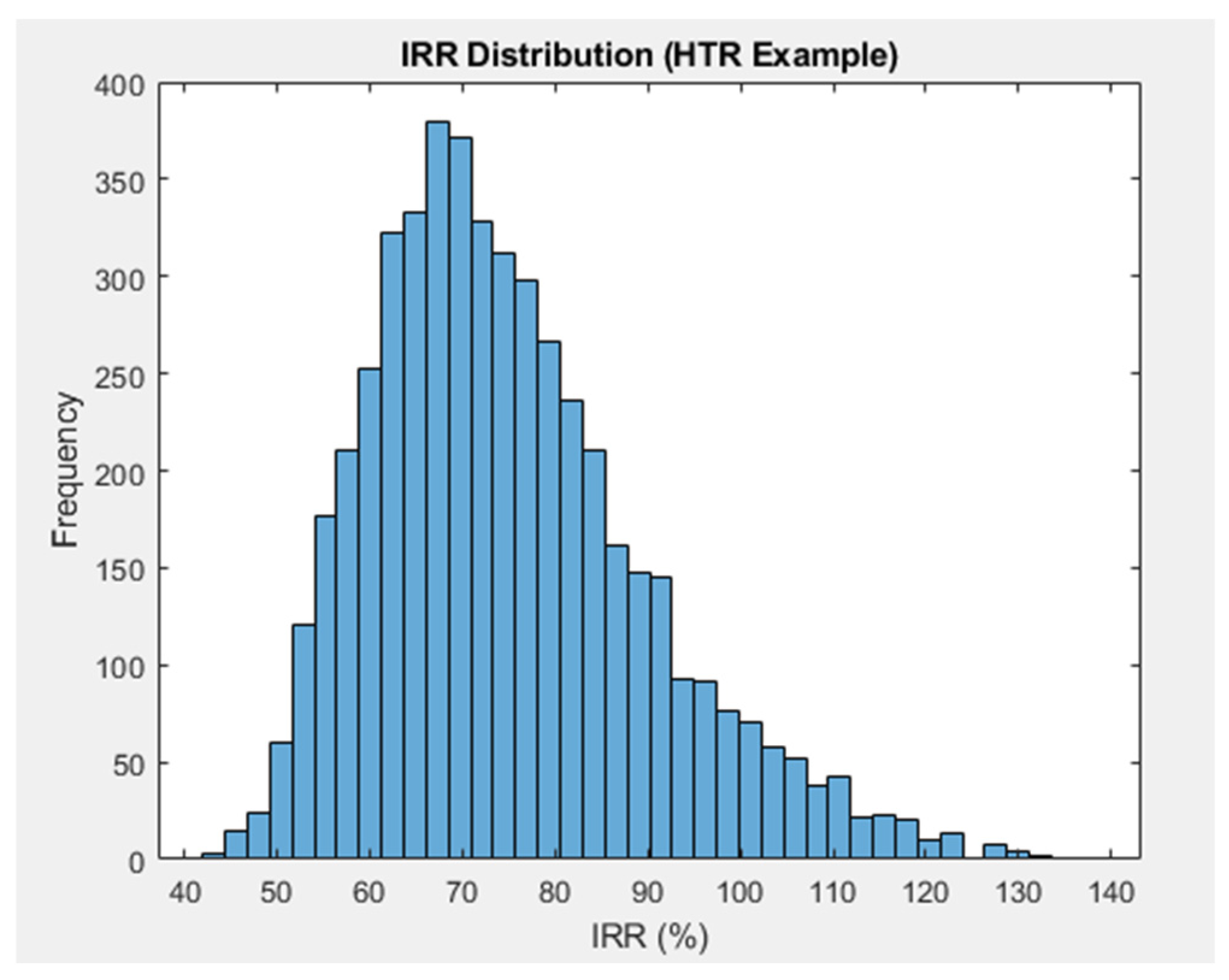
4.5. Practical Application of the Developed Methodology
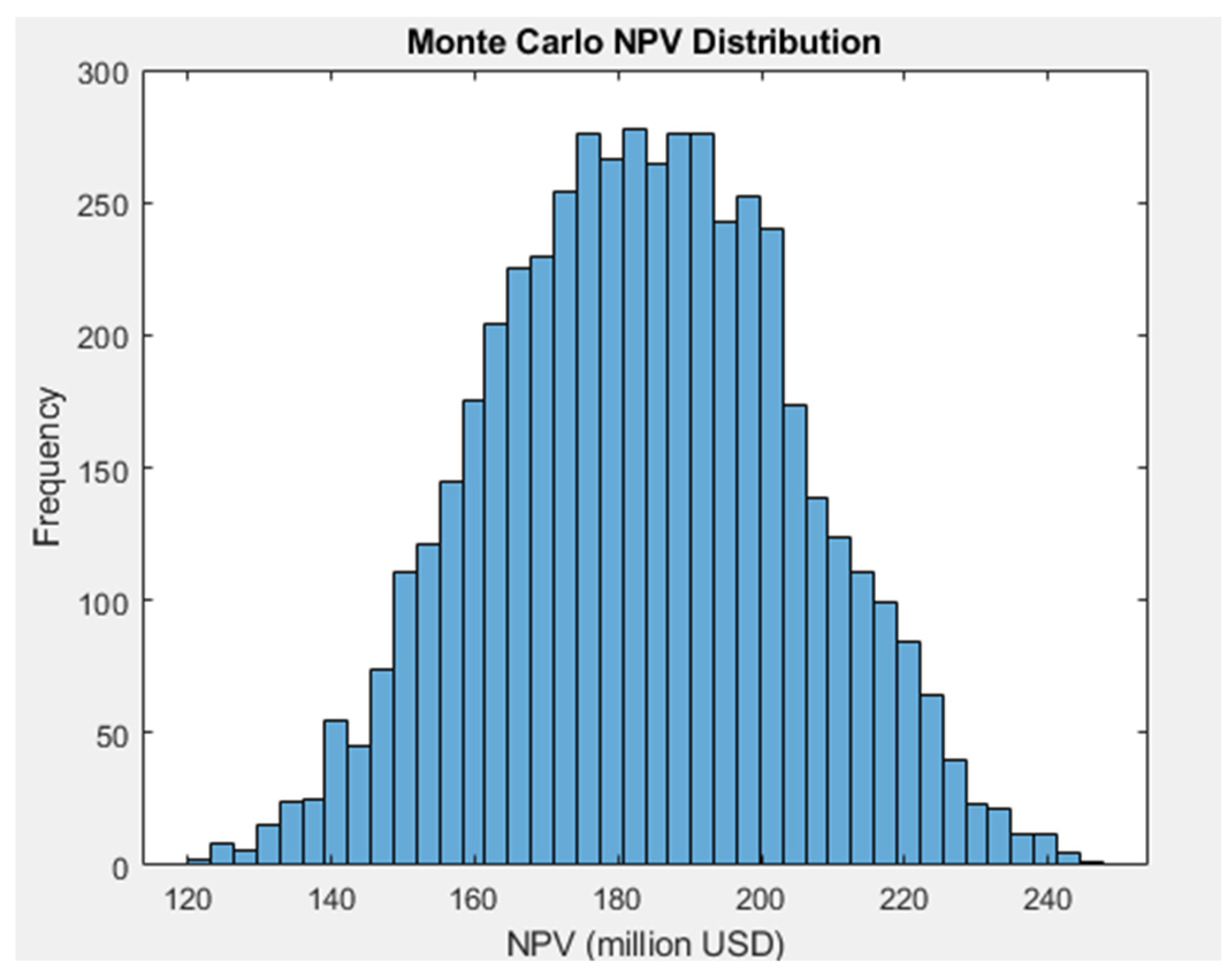
- Mean (average) NPV: USD 280 million
- Median (P50): USD 270 million
- P10 (optimistic 10th percentile): USD 450 million
- P90 (pessimistic 90th percentile): USD 100 million
- Probability of negative NPV: ~7%
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HTR | Hard-to-recover |
| CBM | Coalbed methane |
| EOR | Enhanced oil recovery |
| MSF | Multi-stage hydraulic fracturing |
| NPV | Net present value |
| IRR | Internal rate of return |
| PI | Profitability index |
Appendix A
Monte Carlo MATLAB Script
References
- Lushpeev, V.A.; Sokolov, A.N.; Galtseva, O.A.; Salimgareeva, E.M. Methodological Framework for Tight Reserve Provement for a Carbonate Reservoir. Actual Probl. Oil Gas 2023, 2, 201–215. [Google Scholar] [CrossRef]
- Kryukov, V.A.; Tokarev, A.N. Creation of Conditions for the Development of Hard-to-Recover Oil Reserves: Regional Aspects. Econ. Reg. 2022, 18, 755–769. [Google Scholar] [CrossRef]
- Ankudinov, A.A.; Arkhipov, V.N.; Starikov, M.A. Features of Technological Solutions for Developing TRIZ Reservoirs with Ultra-Low Permeability and Abnormally High Formation Pressure. Expoziya Neft I Gaz 2022, 8, 70–74. [Google Scholar] [CrossRef]
- Bizhani, M.; Ardakani, O.H.; Hawthorne, S.B.; Cesar, J.; Kurz, B.; Percival, J.B. CO2-Enhanced Oil Recovery Mechanism in Canadian Bakken Shale. Minerals 2022, 12, 779. [Google Scholar] [CrossRef]
- Mehana, M.; Kang, Q.; Viswanathan, H. Molecular-Scale Considerations of Enhanced Oil Recovery in Shale. Energies 2020, 13, 6619. [Google Scholar] [CrossRef]
- Mukhina, E.; Cheremisin, A.; Khakimova, L.; Garipova, A.; Dvoretskaya, E.; Zvada, M.; Kalacheva, D.; Prochukhan, K.; Kasyanenko, A.; Cheremisin, A. Enhanced Oil Recovery Method Selection for Shale Oil Based on Numerical Simulations. ACS Omega 2021, 6, 23731–23741. [Google Scholar] [CrossRef] [PubMed]
- Agishev, E.R.; Andreev, V.E.; Mukhametshin, V.S.; Kotenev, A.Y.; Stepanova, R.R.; Davydov, A.Y.; Malyshev, P.M. Improving the Efficiency of Putting Oil Deposits with Hard-to-Recover Reserves of Western Siberia into Development. In SOCAR Proceedings; Oil Gas Scientific Research Project Institute: Baku, Azerbaijan, 2023; pp. 78–88. [Google Scholar]
- Grishchenko, V.A.; Gareev, R.R.; Tsiklis, I.M.; Mukhametshin, V.V.; Yakupov, R.F. Expanding the Amount of Preferential Royalty Facilities with Hard-To-Recover Oil Reserves. SOCAR Proc. 2021, 2021, 8–17. [Google Scholar] [CrossRef]
- Yuan, B.; Wood, D.A. A Holistic Review of Geosystem Damage during Unconventional Oil, Gas and Geothermal Energy Recovery. Fuel 2018, 227, 99–110. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, J.; Zhang, Z.; Qin, H.; Wang, C.; Zhu, J.; Chen, A.; Chen, L.; Liu, P.; Yang, W.; et al. Research Progress and Prospects of Oil Saturation Evaluation Methods in Shale Oil Reservoirs. Processes 2024, 12, 2421. [Google Scholar] [CrossRef]
- Gu, T.; Yu, X.; Zhang, L.; Su, X.; Wu, Y.; Jie, Y.; Wang, H.; Zhou, D. A Study on the Influence of Natural Fractures in Tight Sandstone Reservoirs on Hydraulic Fracture Propagation Behavior and Post-Fracture Productivity. Processes 2024, 12, 2813. [Google Scholar] [CrossRef]
- Male, F.; Duncan, I.J. The Paradox of Increasing Initial Oil Production but Faster Decline Rates in Fracking the Bakken Shale: Implications for Long Term Productivity of Tight Oil Plays. J. Pet. Sci. Eng. 2021, 208, 109406. [Google Scholar] [CrossRef]
- Saputra, W.; Kirati, W.; Patzek, T. Forecast of Economic Tight Oil and Gas Production in Permian Basin. Energies 2022, 15, 43. [Google Scholar] [CrossRef]
- Prischepa, O.; Nefedov, Y.; Nikiforova, V.; Ruiming, X. Raw Material Base of Russia’s Unconventional Oil and Gas Reserves (Hydrocarbons Shale Strata). Front. Earth Sci. 2022, 10, 1–22. [Google Scholar] [CrossRef]
- Yu, W.; Lashgari, H.R.; Wu, K.; Sepehrnoori, K. CO2 Injection for Enhanced Oil Recovery in Bakken Tight Oil Reservoirs. Fuel 2015, 159, 354–363. [Google Scholar] [CrossRef]
- Rafati, R.; Smith, S.R.; Sharifi Haddad, A.; Novara, R.; Hamidi, H. Effect of Nanoparticles on the Modifications of Drilling Fluids Properties: A Review of Recent Advances. J. Pet. Sci. Eng. 2018, 161, 61–76. [Google Scholar] [CrossRef]
- Li, A.; Guo, H.; Peng, W.; Yu, L.; Liang, H.; Sun, Y.; Wang, D.; Guo, Y.; Ouyang, M. Application of Resistance Ring Array Sensors for Oil–Water Two-Phase Flow Water Holdup Imaging in Horizontal Wells. Coatings 2024, 14, 1535. [Google Scholar] [CrossRef]
- Conrad, C.L.; Ben Yin, Y.; Hanna, T.; Atkinson, A.J.; Alvarez, P.J.J.; Tekavec, T.N.; Reynolds, M.A.; Wong, M.S. Fit-for-Purpose Treatment Goals for Produced Waters in Shale Oil and Gas Fields. Water Res. 2020, 173, 115467. [Google Scholar] [CrossRef]
- Zinchenko, I.A.; Sharipov, B.I.; Krutoi, A.A.; Perlova, E.V.; Leonov, S.A. Unconventional Gas Resources and Reserves in Russia and Gazprom. Oil Gas Geol. = Geol. Neft. i Gaza 2018, 4s, 87–92. [Google Scholar] [CrossRef]
- Guo, T.; Wang, L.; Meng, X.; Shafiq, M.U.; Ci, J.; Lei, W. Layered Massive Fracturing of Carrier Beds Commercially Unveils the Deep Tight Sandstone Gas Reserves in Sichuan Basin. Fuel 2025, 379, 133084. [Google Scholar] [CrossRef]
- Egypt Oil&Gas Group. BP Raises Saudi Oil Reserve Estimitates by 12%. Available online: https://egyptoil-gas.com/news/bp-raises-saudi-oil-reserve-estimitates-by-12/ (accessed on 4 March 2025).
- S&P Global. Venezuela Faces Uphill Battle to Revive Oil Industry Even If Opposition Wins Presidential Election. Available online: www.spglobal.com/commodity-insights/en/news-research/latest-news/crude-oil/072624-venezuela-faces-uphill-battle-to-revive-oil-industry-even-if-opposition-wins-presidential-election (accessed on 4 March 2025).
- EnergiMedia. Existing Projects Largely Responsible for Continued Production Growth from Alberta Oil Sands. Available online: https://energi.media/news/existing-projects-largely-responsible-for-continued-production-growth-from-alberta-oil-sands (accessed on 4 March 2025).
- Alberta. Oil Sands Facts and Statistics. Available online: https://www.alberta.ca/oil-sands-facts-and-statistics (accessed on 4 March 2025).
- Institute of Energy Research. U.S. Miles Ahead in Global Shale Race. Available online: www.instituteforenergyresearch.org/fossil-fuels/gas-and-oil/only-four-countries-produce-shale-oilgas/ (accessed on 4 March 2025).
- DW Energy Group. Global Giants: A Guide to the World’s Leading Shale Oil and Gas Reserves. Available online: https://www.dwenergygroup.com/global-giants-a-guide-to-the-worlds-leading-shale-oil-and-gas-reserves/ (accessed on 4 March 2025).
- EIA. Frequently Asked Questions (FAQs). Available online: https://www.eia.gov/tools/faqs/ (accessed on 4 March 2025).
- Center for Sustainable Systems—University of Michigan. Unconventional Fossil Fuels Factsheet. Available online: https://css.umich.edu/publications/factsheets/energy/unconventional-fossil-fuels-factsheet (accessed on 4 March 2025).
- CMM Global Overview. Global Methan Initiative. Russian Federation. Available online: https://www.globalmethane.org/documents/toolsres_coal_overview_ch30_updated2020.pdf (accessed on 5 March 2025).
- NAO&GS. Sinopec Puts 1.3 Billion Barrels of Shale Oil Reserves on the Books. Available online: https://nangs.org/news/upstream/sinopec-postavila-na-balans-zapasy-slantsevoj-nefti-na-1-3-mlrd-barrelej (accessed on 4 March 2025).
- CMM Global Overview. Global Methan Initiative. China. Available online: https://www.globalmethane.org/documents/toolsres_coal_overview_ch7_updated2020.pdf (accessed on 5 March 2025).
- EIA. China Extracts Commercially Viable Natural Gas from Deeper Shale Formations. Available online: http://www.eia.gov/todayinenergy/detail.cfm?id=25372 (accessed on 8 October 2024).
- Reuters. Argentina’s Vaca Muerta Region Hits Record Oil Production in Q3, Rystad Says. Available online: https://www.reuters.com/markets/commodities/argentinas-vaca-muerta-region-hits-record-oil-production-q3-rystad-says-2024-11-29/ (accessed on 4 March 2025).
- USGS. Natural Gas Hydrates—Vast Resource, Uncertain Future. Available online: https://pubs.usgs.gov/fs/fs021-01/fs021-01.pdf (accessed on 5 March 2025).
- Semenova, T.; Martínez Santoyo, J.Y. Increasing the Sustainability of the Strategic Development of Oil Producing Companies in Mexico. Resources 2024, 13, 108. [Google Scholar] [CrossRef]
- Australian Government. Australia’s Energy Commodity Resources 2024 Overview. Available online: https://www.ga.gov.au/aecr2024/overview (accessed on 14 December 2024).
- Australian Energy Resource Assessment. Geoscience Australia. Available online: https://arena.gov.au/assets/2018/08/australian-energy-resource-assessment.pdf (accessed on 12 October 2020).
- Qi, Y.; Luo, S.; Tang, S.; Ruan, J.; Gao, D.; Liu, Q.; Li, S. Prediction of Carbonate Reservoir Porosity Based on CNN-BiLSTM-Transformer. Appl. Sci. 2025, 15, 3443. [Google Scholar] [CrossRef]
- Guo, T.; Xiong, L.; Ye, S.; Dong, X.; Wei, L.; Yang, Y. Theory and Practice of Unconventional Gas Exploration in Carrier Beds: Insight from the Breakthrough of New Type of Shale Gas and Tight Gas in Sichuan Basin, SW China. Pet. Explor. Dev. 2023, 50, 27–42. [Google Scholar] [CrossRef]
- Raoufi, M.; Fayek, A.R. Fuzzy Monte Carlo Agent-Based Simulation of Construction Crew Performance. J. Constr. Eng. Manag. 2020, 146, 337–348. [Google Scholar] [CrossRef]
- Sadeghi, N.; Fayek, A.R.; Pedrycz, W. Fuzzy Monte Carlo Simulation and Risk Assessment in Construction. Comput. Civ. Infrastruct. Eng. 2010, 25, 238–252. [Google Scholar] [CrossRef]
- Marinina, O.; Malikov, A.; Lyubek, Y.; Pasternak, S.; Reshneva, E.; Stolbovskaya, N. Selection of Enhanced Oil Recovery Method on the Basis of Clustering Wells. Processes 2024, 12, 2082. [Google Scholar] [CrossRef]
- Alekseev, A.D.; Zhukov, V.V.; Strizhnev, K.V.; Cherevko, S.A. Research of Hard-to-Recovery and Unconventional Oil-Bearing Formations According to the Principle «in-Situ Reservoir Fabric». J. Min. Inst. 2017, 228, 695–704. [Google Scholar] [CrossRef]
- Zhao, W.; Hu, S.; Hou, L.; Yang, T.; Li, X.; Guo, B.; Yang, Z. Types and Resource Potential of Continental Shale Oil in China and Its Boundary with Tight Oil. Pet. Explor. Dev. 2020, 47, 1–11. [Google Scholar] [CrossRef]
- Chizhov, A.P.; Rabaev, R.U.; Andreev, V.E.; Chibisov, A.V.; Kuangaliev, Z.A.; Efimov, E.R.; Ivanov, D.V. Theoretical Features of Improving the Oil Recovery Efficiency from Carbonate Reservoirs in the Volga-Ural Province. SOCAR Proc. 2020, 4, 9–14. [Google Scholar] [CrossRef]
- Mokheimer, E.M.A.; Hamdy, M.; Abubakar, Z.; Shakeel, M.R.; Habib, M.A.; Mahmoud, M. A Comprehensive Review of Thermal Enhanced Oil Recovery: Techniques Evaluation. J. Energy Resour. Technol. Trans. ASME 2019, 141, 030801. [Google Scholar] [CrossRef]
- Guo, X.; Aibaibu, A.; Wu, Y.; Chen, B.; Zhou, H.; Zhu, B.; Zhao, X. Numerical Modeling of Hydraulic Fracturing Interference in Multi-Layer Shale Oil Wells. Processes 2024, 12, 2370. [Google Scholar] [CrossRef]
- Reynolds, D.B.; Umekwe, M.P. Shale-Oil Development Prospects: The Role of Shale-Gas in Developing Shale-Oil. Energies 2019, 12, 3331. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, K.; Gao, X.; Li, Q. Tight Oil Well Productivity Prediction Model Based on Neural Network. Processes 2024, 12, 2088. [Google Scholar] [CrossRef]
- Chudinova, D.Y.; Atse, Y.D.B.; Minniakhmetova, R.M.; Kotenev, M.Y. Classification of Residual Oil Reserves and Methods of Its Recovery. In SOCAR Proceedings; Oil Gas Scientific Research Project Institute: Baku, Azerbaijan, 2021; pp. 26–33. [Google Scholar]
- Cano-Londono, N.A.; Médina, O.E.; Mozo, I.; Céspedes, S.; Franco, C.A.; Cortés, F.B. Viability of the Steam-Based Extraction of Extra-Heavy Crude Oil Using Nanoparticles: Exergy and Life-Cycle Assessment. Energy 2024, 304, 131929. [Google Scholar] [CrossRef]
- Ruble, I. The U.S. Crude Oil Refining Industry: Recent Developments, Upcoming Challenges and Prospects for Exports. J. Econ. Asymmetries 2019, 20, e00132. [Google Scholar] [CrossRef]
- Palyanitsina, A.; Safiullina, E.; Byazrov, R.; Podoprigora, D.; Alekseenko, A. Environmentally Safe Technology to Increase Efficiency of High-Viscosity Oil Production for the Objects with Advanced Water Cut. Energies 2022, 15, 753. [Google Scholar] [CrossRef]
- Dvoynikov, M.V.; Sidorkin, D.I.; Yurtaev, S.L.; Grokhotov, E.I.; Ulyanov, D.S. Drilling of Deep and Ultra-Deep Wells for Prospecting and Exploration of New Raw Mineral Fields. J. Min. Inst. 2022, 258, 945–955. [Google Scholar] [CrossRef]
- Burkhanov, R.N.; Lutfullin, A.A.; Raupov, I.R.; Maksyutin, A.V.; Valiullin, I.V.; Farrakhov, I.M.; Shvydenko, M.V. Localization and Involvement in Development of Residual Recoverable Reserves of a Multilayer Oil Field. J. Min. Inst. 2024, 268, 599–612. [Google Scholar]
- Wu, M.; Li, B.; Ruan, L.; Zhang, C.; Tang, Y.; Li, Z. Effect of CO2 Concentration on the Performance of Polymer-Enhanced Foam at the Steam Front. Polymers 2024, 16, 2726. [Google Scholar] [CrossRef]
- Dou, X.; Qian, M.; Zhao, X.; Wang, A.; Lei, Z.; Guo, E.; Chen, Y. Fluid Flow Behavior in Nanometer-Scale Pores and Its Impact on Shale Oil Recovery Efficiency. Energies 2024, 17, 4677. [Google Scholar] [CrossRef]
- Sleptsov, A.; Medvedeva, L.; Marinina, O.; Savenok, O. Feasibility Study on the Applicability of Intelligent Well Completion. Processes 2024, 12, 1565. [Google Scholar] [CrossRef]
- Khuzin, R.R.; Andreev, V.E.; Mukhametshin, V.V.; Kuleshova, L.S.; Dubinskiy, G.S.; Safiullina, A.R. Influence of Hydraulic Compression on Porosity and Permeability Properties of Reservoirs. J. Min. Inst. 2021, 251, 688–697. [Google Scholar] [CrossRef]
- Sui, Y.; Cao, G.; Tian, Y.; Guo, T.; Xiao, Z.; Yao, L. Application, Progress, and Trend of Thickened Acid Fracturing in Carbonate Rock Reservoir Development. Processes 2024, 12, 2269. [Google Scholar] [CrossRef]
- Cooper, M. Structural Style and Hydrocarbon Prospectivity in Fold and Thrust Belts: A Global Review. Geol. Soc. Spec. Publ. 2007, 272, 447–472. [Google Scholar] [CrossRef]
- Goffey, G.P.; Craig, J.; Needham, T.; Scott, R. Fold-Thrust Belts: Overlooked Provinces or Justifiably Avoided? Geol. Soc. Spec. Publ. 2010, 348, 1–6. [Google Scholar] [CrossRef]
- Kendall, J.; Vergés, J.; Koshnaw, R.; Louterbach, M. Petroleum Tectonic Comparison of Fold and Thrust Belts: The Zagros of Iraq and Iran, the Pyrenees of Spain, the Sevier of Western USA and the Beni Sub-Andean of Bolivia. Geol. Soc. Spec. Publ. 2020, 490, 79–103. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, R.; Ma, L.; Feng, X. Uncertainty Quantification in Rate Transient Analysis of Multi-Fractured Tight Gas Wells Exhibiting Gas–Water Two-Phase Flow. Water 2024, 16, 2744. [Google Scholar] [CrossRef]
- ISO. 2018 ISO 31000:2018—Risk Management—Guidelines; ISO: Geneva, Switzerland, 2018; ISBN 2831889189. [Google Scholar]
- IEC. 2019 IEC 31010:2019 Risk Management—Risk Assessment Techniques; IEC: London, UK, 2019; Volume 2, ISBN 2831886376. [Google Scholar]
- Stroykov, G.A.; Babyr, N.V.; Ilin, I.V.; Marchenko, R.S. System of Comprehensive Assessment of Project Risks in Energy Industry. Int. J. Eng. Trans. A Basics 2021, 34, 1778–1784. [Google Scholar] [CrossRef]
- Korshunov, G.I.; Kabanov, E.I.; Cehlár, M. Occupational Risk Management in a Mining Enterprise with the Aid of an Improved Matrix Method for Risk Assessment. Acta Montan. Slovaca 2020, 25, 289–301. [Google Scholar] [CrossRef]
- Shokouhi, M.R.; Khademvatani, A.; Beiky, F. Analyzing Economic and Financial Risk Factors Affecting Profitability of Oil Refinery Investment Projects: A Case Study from an Iranian Oil Refinery. Energy Strateg. Rev. 2024, 52, 101348. [Google Scholar] [CrossRef]
- Balas, E.A. A Hybrid Monte Carlo Simulation Risk Model for Oil Exploration Projects. Mar. Pollut. Bull. 2023, 194, 115270. [Google Scholar] [CrossRef]
- Wang, C.; Cai, B.; Shao, X.; Zhao, L.; Sui, Z.; Liu, K.; Khan, J.A.; Gao, L. Dynamic Risk Assessment Methodology of Operation Process for Deepwater Oil and Gas Equipment. Reliab. Eng. Syst. Saf. 2023, 239, 109538. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, Y.G. Progress of Technological Innovation of the United States’ Shale Petroleum Industry Based on Patent Data Association Rules. Sustainability 2020, 12, 6628. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Niu, Z. Geopolitical Risks and Crude Oil Futures Volatility: Evidence from Machine Learning. Resour. Policy 2024, 98, 105374. [Google Scholar] [CrossRef]
- Al-Mhdawi, M.K.S.; O’Connor, A.; Qazi, A. Structural Equation Modeling and Fuzzy Set Theory: Advancing Risk Assessment in Oil and Gas Construction Projects. Environ. Impact Assess. Rev. 2024, 109, 107622. [Google Scholar] [CrossRef]
- Abid, K.; Velasquez, A.F.B.; Sharma, A.; McSheridan, A.N.; Srivastava, S.; Teodoriu, C. Risk Assessment through Feature, Event, and Process for Repurposing Suspended Oil and Gas Wells for Geothermal Purposes. Renew. Energy 2024, 237, 121720. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, Z.; Qin, Y. A Hybrid BWM–CRITIC–VIKOR Approach for Assessing Oil and Gas Risk Scenarios in Probabilistic Linguistic Term Set. Heliyon 2024, 10, e38514. [Google Scholar] [CrossRef]
- Kovshov, S.V.; Tingnting, S. Application of Computer Modeling for the Accident Rate Assessment on Separate Sites of the Mohe–Daqing Oil Pipeline in Permafrost Conditions. Transp. Infrastruct. Geotechnol. 2020, 7, 605–617. [Google Scholar] [CrossRef]
- Kovshov, S.V.; Alimhanova, T.A.; Kitsis, V.M. Ranking of the Sections of East Siberia–Pacific Ocean Main Pipeline by Accident Probability Using Bow-Tie Method and Checklist Support Tool. J. Pipeline Syst. Eng. Pract. 2020, 11, 05020003. [Google Scholar] [CrossRef]
- Ilyas, M.; Jin, Z.; Ullah, I.; Almujibah, H. A Fuzzy Logic-Based Risk Assessment Framework for the Crude Oil Transportation Supply Chain. Ocean Eng. 2024, 311, 118997. [Google Scholar] [CrossRef]
- Kang, J.; Al Masry, Z.; Varnier, C.; Mosallam, A.; Zerhouni, N. A Data Quality Management Framework for Equipment Failure Risk Estimation: Application to the Oil and Gas Industry. Eng. Appl. Artif. Intell. 2024, 136, 108834. [Google Scholar] [CrossRef]
- Wan, K.; Liu, B.Y.; Fan, Y.; Ikonnikova, S.A. Modelling and Assessing Dynamic Energy Supply Resilience to Disruption Events: An Oil Supply Disruption Case in China. Energy Econ. 2024, 140, 108013. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, W. Oil Price Disaster Risk, Macroeconomic Dynamics and Monetary Policy. Int. Rev. Financ. Anal. 2024, 96, 103574. [Google Scholar] [CrossRef]
- Wang, K.; Wen, F.; Gong, X. Oil Prices and Systemic Financial Risk: A Complex Network Analysis. Energy 2024, 293, 130672. [Google Scholar] [CrossRef]
- Caporin, M.; Fontini, F.; Panzica, R. The Systemic Risk of US Oil and Natural Gas Companies. Energy Econ. 2023, 121, 106650. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, Y.; Gao, K.; Luo, C. How Geopolitical Risk and Economic Policy Uncertainty Impact Coal, Natural Gas, and Oil Rent? Evidence from China. Resour. Policy 2024, 88, 104393. [Google Scholar] [CrossRef]
- Babyr, N.; Babyr, K. To Improve the Contact Adaptability of Mechanical Roof Support. In Proceedings of the E3S Web of Conferences, EDP Sciences, Saint Petersburg, Russia, 31 May–6 June 2021; Volume 266. [Google Scholar]
- Chen, X.; Liu, S.; Liu, R.W.; Wu, H.; Han, B.; Zhao, J. Quantifying Arctic Oil Spilling Event Risk by Integrating an Analytic Network Process and a Fuzzy Comprehensive Evaluation Model. Ocean Coast. Manag. 2022, 228, 106326. [Google Scholar] [CrossRef]
- Nevskaya, M.A.; Belyaev, V.V.; Pasternak, S.N.; Vinogradova, V.V.; Shagidulina, D.I. Accidental oil spills in the arctic: An assessment of potential soil damage. Sev. Rynok Form. Ekon. Porad. 2024, 27, 107–122. [Google Scholar] [CrossRef]
- Katysheva, E.G. The Role of the Russian Arctic Gas Industry in the Northern Sea Route Development. IOP Conf. Ser. Earth Environ. Sci. 2020, 539, 012075. [Google Scholar] [CrossRef]
- Carayannis, E.G.; Ilinova, A.; Cherepovitsyn, A. The Future of Energy and the Case of the Arctic Offshore: The Role of Strategic Management. J. Mar. Sci. Eng. 2021, 9, 134. [Google Scholar] [CrossRef]
- Torres, L.; Yadav, O.P.; Khan, E. A Review on Risk Assessment Techniques for Hydraulic Fracturing Water and Produced Water Management Implemented in Onshore Unconventional Oil and Gas Production. Sci. Total Environ. 2016, 539, 478–493. [Google Scholar] [CrossRef]
- Fedorov, S.; Lavrutich, M.; Hagspiel, V.; Lerdahl, T. Risk and Benefit Sharing Schemes in Oil Exploration and Production. Energy Econ. 2022, 116, 106401. [Google Scholar] [CrossRef]
- Zhong, W.; Cai, J.; Song, Y.; Liang, T.; Zhang, J.; Gao, Z. Risk Evolution of Crude Oil Pipeline under Periodic Maintenance Based on Dynamic Bayesian Network. J. Loss Prev. Process Ind. 2024, 87, 105229. [Google Scholar] [CrossRef]
- Choi, K.H.; Nekhili, R.; Mensi, W.; Boubaker, F.Z.; Yoon, S.M. Systemic Risk-Sharing between Natural Gas, Oil, and Stock Markets in Top Energy Producer and Consumer Countries. Int. Rev. Econ. Financ. 2024, 96, 103515. [Google Scholar] [CrossRef]
- Afshan, S.; Leong, K.Y.; Najmi, A.; Razi, U.; Lelchumanan, B.; Cheong, C.W.H. Fintech Advancements for Financial Resilience: Analysing Exchange Rates and Digital Currencies during Oil and Financial Risk. Resour. Policy 2024, 88, 104432. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Shakeri, H.; Zohrehvandi, S. Risk Identification and Assessment with the Fuzzy DEMATEL-ANP Method in Oil and Gas Projects under Uncertainty. Procedia Comput. Sci. 2021, 181, 277–284. [Google Scholar] [CrossRef]
- Ilyushin, Y.; Talanov, N. Development of Methods and Models for Assessing Technical Condition of Mines and Underground Structures. Int. J. Eng. 2025, 38, 1659–1666. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, Z.; Xie, L.; Wang, Y.; Zhang, X.; Chen, N.; Hu, Y. Prediction of Shale Gas Well Productivity Based on a Cuckoo-Optimized Neural Network. Mathematics 2024, 12, 2948. [Google Scholar] [CrossRef]
- Li, H.; Sun, R.; Lee, W.J.; Dong, K.; Guo, R. Assessing Risk in Chinese Shale Gas Investments Abroad: Modelling and Policy Recommendations. Sustainability 2016, 8, 708. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Yong, Z.; Qu, X. The Differential Enrichment Law of Tight Sandstone Gas in the Eighth Member of Shihezi Formation in the North and South of Ordos Basin. Energies 2024, 17, 5978. [Google Scholar] [CrossRef]
- Burton, G.A.; Basu, N.; Ellis, B.R.; Kapo, K.E.; Entrekin, S.; Nadelhoffer, K. Hydraulic “Fracking”: Are Surface Water Impacts an Ecological Concern? Environ. Toxicol. Chem. 2014, 33, 1679–1689. [Google Scholar] [CrossRef]
- Du, F.; Nojabaei, B. A Review of Gas Injection in Shale Reservoirs: Enhanced Oil/Gas Recovery Approaches and Greenhouse Gas Control. Energies 2019, 12, 2355. [Google Scholar] [CrossRef]
- Wang, K.; Vredenburg, H.; Wang, T.; Feng, L. Financial Return and Energy Return on Investment Analysis of Oil Sands, Shale Oil and Shale Gas Operations. J. Clean. Prod. 2019, 223, 826–836. [Google Scholar] [CrossRef]
- Uzun, O.; Kazemi, H. Assessment of Enhanced Oil Recovery by Osmotic Pressure in Unconventional Reservoirs: Application to Niobrara Chalk and Codell Sandstone. Fuel 2021, 306, 121270. [Google Scholar] [CrossRef]
- Yan, M.; Ai, C.; Zhang, J.; Lu, W.; Gao, R. Study on Near-Wellbore Fracture Initiation and Propagation with Fixed-Plane Perforation in Horizontal Well for Unconventional Reservoirs. Processes 2024, 12, 2280. [Google Scholar] [CrossRef]
- Jia, B.; Su, J. Advancements and Environmental Implications in Oil Shale Exploration and Processing. Appl. Sci. 2023, 13, 7657. [Google Scholar] [CrossRef]
- Golovina, E.; Karennik, K. Modern Trends in the Field of Solving Transboundary Problems in Groundwater Extraction. Resources 2021, 10, 107. [Google Scholar] [CrossRef]
- Golovina, E.I.; Tselmeg, B. Cost estimate as a tool for managing fresh groundwater resources in the russian federation. Geol. Miner. Resour. Sib. 2023, 4, 81–91. [Google Scholar] [CrossRef]
- Yao, Q.; Yang, B.; Zhang, Q. Dynamic Uncertain Causality Graph Applied to the Intelligent Evaluation of a Shale-Gas Sweet Spot. Energies 2021, 14, 5228. [Google Scholar] [CrossRef]
- Katysheva, E. Analysis of the Interconnected Development Potential of the Oil, Gas and Transport Industries in the Russian Arctic. Energies 2023, 16, 3124. [Google Scholar] [CrossRef]
- Salygin, V.; Guliev, I.; Chernysheva, N.; Sokolova, E.; Toropova, N.; Egorova, L. Global Shale Revolution: Successes, Challenges, and Prospects. Sustainability 2019, 11, 1627. [Google Scholar] [CrossRef]
- Aziz, A.; Suzon, M.M.; Hasan, R. A Fuzzy Logic-Based Risk Evaluation and Precaution Level Estimation of Explosive, Flammable, and Toxic Chemicals for Preventing Damages. Heliyon 2025, 11, e41216. [Google Scholar] [CrossRef] [PubMed]
- Ohia, N.P.; Paul, C.; Asolo, E.; Adewa, T.A.; Chukwu, C.F.; Ubi, P.A.; Itam, D.H.; Nnaji, D.U. Artificial Intelligence-Driven Fuzzy Logic Approach for Optimal Well Selection in Gas Lift Design: A Brown Field Case Study; Elsevier: Amsterdam, The Netherlands, 2025; ISBN 0009000708732. [Google Scholar]





| Country | Reserves of Unconventional Oil (Billion Barrels) (as of 2024) | Production of Unconventional Oil (Million Barrels per Year) (as of 2024) | Reserves of Unconventional Gas (Trillion Cubic Feet) (as of 2024) | Production of Unconventional Gas (Billion Cubic Feet per Year) (for the Period 2023–2024) | References |
|---|---|---|---|---|---|
| Venezuela | 303 | 290 | N/A | N/A | [21,22] |
| Canada | 168 | 1260 | 573 | 100 | [21,23,24,25] |
| USA | 78.2 | 3040 | 665 | 850 | [25,26,27,28] |
| Russia | 74.6 | N/A | 285 | N/A | [19,26,29] |
| China | 32.2 | 7.5 | 1115 | 30 | [25,26,30,31,32] |
| Argentina | 27 | 146 | 802 | 27.5 | [25,26,33] |
| Libya | 26.1 | N/A | N/A | N/A | [26] |
| Algeria | N/A | N/A | 707 | 1.8 | [25,34] |
| Mexico | N/A | N/A | 545 | N/A | [25,35] |
| Australia | N/A | N/A | 437 | 40 | [25,36,37] |
| Reservoir Type | Key Characteristics | Examples |
|---|---|---|
| Shale Oil | Low permeability and porosity, confined pore structures; requires hydraulic fracturing and CO₂ injection. | Bakken, Eagle Ford |
| Heavy Oil Reservoirs | Dense matrices with high viscosity; dependent on thermal methods, such as steam injection and in situ combustion. | Athabasca |
| Carbonate Reservoirs | High clay content, dense formations, restricted fluid mobility; requires acid stimulation to enhance permeability. | Volga-Ural Region |
| Thinly Layered Reservoirs | Geologically complex with low permeability; requires horizontal drilling and multi-stage hydraulic fracturing for effective extraction. | Achimov and Bazhenov formations |
| Coalbed Methane Reservoirs | Methane trapped in coal seams, low permeability; requires advanced stimulation techniques. | Powder River Basin |
| Deep Tight Gas Reservoirs | Extremely low permeability; hydraulic fracturing necessary for flow stimulation. | Block WZ in Beibu Gulf |
| Multi-layered Shales | Heterogeneous stress and layer properties; prone to hydraulic fracturing interference. | Eagle Ford, Bakken |
| Type of Residual Oil | Recommended Extraction Methods | Mechanism |
|---|---|---|
| Low-permeability zones not reached by water injection | Hydrodynamic EOR, cyclic water flooding, pressure modification in injection well | Redistributes reservoir pressure and mobilizes oil in low-permeability zones |
| Stagnant zones in homogeneous formations | Blocking water-bearing intervals, selective plugging of high-permeability zones | Expands reservoir sweep, controls water breakthrough |
| Lens-shaped and undrained accumulations | Forced fluid production, inclined/horizontal well drilling | Enhances oil inflow by reducing bottomhole pressure, expands development area |
| Capillary-bound oil in hydrophilic media | Polymer flooding, wettability alteration methods | Reduces interfacial tension and improves filtration in small pores |
| Film oil in hydrophobic reservoirs | Hydraulic fracturing, elastic wave stimulation | Applies physical forces to release trapped oil |
| Residual oil in isolated pores and micro-heterogeneous zones | Advanced extraction methods targeting micro-heterogeneous zones | Mobilizes oil in complex pore structures using physical or chemical methods |
| Residual oil due to unstable water displacement | Water injection control to stabilize displacement front | Reduces channeling effects to improve oil recovery |
| Method/Technique | Description | Advantages | Limitations in HTR Context |
|---|---|---|---|
| Monte Carlo Simulation | Uses random sampling to model probability distributions of outcomes through multiple iterations. | Flexible for complex models; effectively accounts for uncertainty; supports probabilistic results. | Geological heterogeneity complicates stable distribution definitions; data often sparse or variable, increasing model uncertainty; non-stationary reservoir properties hamper iterative sampling. |
| Bayesian Analysis | Combines prior information with new data to update probability estimates. | Considers both subjective and empirical data; supports dynamic updates. | Determining suitable priors is difficult if similar HTR references are lacking; limited high-quality field data yield large posterior uncertainty; rapid technological or economic shifts can invalidate priors mid-project. |
| Bayesian Networks | Uses a graphical model to represent dependencies and calculate probabilities of outcomes. | Effective for causal analysis; suitable for scenarios with complex interdependencies. | HTR usually has multiple interlinked variables; obtaining reliable conditional probabilities is hard when reservoir physics are poorly understood; risk of overfitting if data are sparse. |
| Event Tree Analysis (ETA) | Displays possible outcomes following an initial event and calculates probabilities. | Clearly defines sequential event outcomes; allows assessment of overall probabilities. | Many HTR risks are correlated (e.g., fracturing failure and environmental release); “unknown unknowns” inflate scenario branches; updating the tree for new geological data is time-consuming. |
| Fault Tree Analysis (FTA) | Identifies root causes of system failures and evaluates their probabilities. | Suitable for technical systems with defined failure modes; provides quantitative probability assessment. | HTR reserves have overlapping failure modes (equipment, well integrity, fracturing leaks); building a fault tree for multilayer geology is complex; lacks direct handling of feedback loops. |
| Cause-and-Effect Analysis | Combines ETA and FTA to consider both causes and effects of risks. | Integrates multiple analytical approaches. | HTR cause-and-effect pathways can be highly nonlinear; initial data often insufficient; emergent reservoir behaviors may be missed as technology evolves. |
| Markov Analysis | Models state transitions in a system over time to calculate probabilities. | Accounts for dynamic system behavior; provides clear state transition insights. | Reservoir properties can rapidly change with production; Markov chains require recalibration to track evolving conditions; some short-lived states (e.g., fracturing stages) are uncertain. |
| Value at Risk (VaR) | A financial measure to assess potential losses with a given confidence level over a specific period. | Widely used in finance to quantify risks. | Price shocks in HTR reserves can be severe, so tail events are poorly captured; key risks (geological and operational) may dwarf simple price volatility. |
| Conditional Value at Risk (CVaR) | Extends VaR by considering expected losses beyond the VaR threshold. | Overcomes VaR limitations for tail risk evaluation. | High uncertainty and limited data hamper tail modeling; robust extreme-scenario data for novel or geologically complex HTR plays rarely exist. |
| Toxicological Risk Assessment | Assesses risks to humans/ecosystems from chemical exposure. | Applicable for specific medical and environmental risk contexts. | HTR fracturing fluids/additives vary widely; lab toxicity data do not always match in situ conditions; actual exposure pathways can be hard to monitor. |
| S-Curves (Cumulative Distributions) | Displays cumulative probabilities relative to consequences for risk visualization. | Provides clear visual representation; useful for communicating risk profiles. | HTR reservoir outcomes often deviate from normal or triangular distributions; S-curves can mislead if underlying distribution is poorly known; complex geology may shift the curve unexpectedly. |
| Method/Technique | Description | Advantages | Limitations in HTR Context |
|---|---|---|---|
| Brainstorming | Group idea generation for risk identification. | Encourages creativity; considers diverse perspectives. | Technical experts may dominate if social/environmental participants are fewer; unstructured format may overlook subtle geological or engineering issues specific to HTR reserves. |
| Delphi Method | Consensus building through anonymous expert evaluations over multiple rounds. | Reduces groupthink; ensures anonymity. | HTR reserve specialists can be few, leading to narrow perspectives; fundamental geological uncertainties may block convergence; repeated rounds can stall. |
| Fuzzy Logic | Processes imprecise or ambiguous data for qualitative risk assessment. | Useful with incomplete data; allows flexible modeling of uncertainty. | HTR geology often yields conflicting or vague assessments; designing membership functions for high heterogeneity is difficult; calibrating fuzzy rules under uncertain reservoir data is challenging. |
| Scenario Analysis | Explores hypothetical future scenarios and their risk implications. | Stimulates strategic thinking; identifies a broad range of risks. | HTR economics and operations can swing drastically; multiple unknown parameters (fracture success and reservoir performance) lead to scenario explosion; balancing breadth vs. depth is tough. |
| Risk Register | Systematic documentation of identified risks, including their context and impacts. | Centralized tracking tool; facilitates communication among participants. | HTR reserve data evolve quickly (new well logs and fracturing results); a static register becomes outdated fast; interactions of geologic/technical/social factors not always visible in a simple register. |
| SWIFT (Structured What-If) | Explores deviations from norms using structured questions. | Easy to use; effective for analyzing deviations; useful across teams. | HTR “what-if” queries often require deep reservoir or fracturing knowledge; many potential off-nominal conditions remain unspecified if the team has partial data. |
| Checklists | Predetermined lists of potential risks to simplify assessments. | Easy to use; ensures consistent analysis. | Rapid changes in HTR technology can outdate the checklist; unique geological challenges for each reservoir may be absent from standard lists. |
| Fishbone Diagrams (Ishikawa) | Visual representation of causes leading to risky outcomes. | Excellent for root cause analysis; useful for identifying factors. | HTR processes can have multiple interwoven causal chains; intangible or unknown geologic drivers hamper a single fishbone approach; real-time data shifts can invalidate the diagram. |
| Bow-Tie Analysis | Visual tool combining fault trees (causes) and event trees (consequences). | Clear representation of preventive and reactive measures. | HTR reserves may have multiple “central” hazards (geologic, operational, and social), each needing a separate bow-tie; updating diagrams as new reservoir info emerges is laborious. |
| Consequence/Probability Matrix | Combines qualitative probability and impact assessments into a visual grid. | Quick risk prioritization; intuitive and easy to use. | Probability/impact rating for HTR reserves can be very uncertain; synergy among geologic, social, and economic factors is not well represented in a 2D matrix; wide uncertainty intervals hamper meaningful categorization. |
| Nominal Group Technique | Group discussion method for ranking and prioritizing risks. | Encourages equal participation; produces ordered results. | Large HTR ventures have varied stakeholders (geoscientists, engineers, and local authorities); forging consensus on high-uncertainty issues is difficult; time-consuming for multi-stage geology or fracturing issues. |
| Causal Mapping | Visually represents interdependencies and causal links between risk factors. | Helps understand complex interrelationships. | HTR fields often exhibit dynamic feedback loops (fracturing affects pressure, which affects well stability); enumerating all geologic, technical, and social connections can be unwieldy without advanced tools. |
| Method | Application | Description |
|---|---|---|
| Monte Carlo Simulation | Risk assessment in energy projects | Simulates parameter variability, such as costs and prices, through thousands of iterations, integrating qualitative data where statistical data are unavailable. |
| 3D Computer Modeling | Pipeline risk assessment in permafrost conditions | Combines SolidWorks for 3D modeling and ANSYS for thermal and structural analysis, focusing on thermal stresses and ‘soil–pipeline’ interactions. |
| Enhanced Matrix Method | Professional risk management in mining enterprises | Uses regression models and continuous scaling for detailed and objective risk categorization. |
| Bow-Tie Analysis | Accident probability assessment for pipelines | Visually links risk causes to consequences, supported by a checklist adapted to regional conditions like Siberia. |
| Dynamic Bayesian Networks (DBN) | Operational risks in deepwater oil equipment | Dynamically models failure processes with parameters such as degradation states and probabilistic dependencies, enhanced by Markov processes. |
| FEP Method (Features, Events, Processes) | Repurposing oil and gas wells for geothermal energy | Evaluates risks by combining static characteristics, dynamic processes, and potentially destructive events, supported by interaction matrices and cause–effect diagrams. |
| Fuzzy DEMATEL–ANP | Risk prioritization in oil and gas exploration projects | Integrates expert-driven fuzzy logic to identify and rank risks, considering interdependencies. |
| ANP–Fuzzy Comprehensive Evaluation (FCE) | Oil spill risk assessment in the Arctic | Combines an analytic network process with fuzzy logic to evaluate risks affecting the environment, economy, society, and recovery mechanisms. |
| Structural Equation Modeling (SEM) | Risk assessment in oil and gas construction | Analyzes risk impacts using SEM combined with fuzzy set theory for quantitative evaluation and ranking of critical risks. |
| Hybrid BWM–CRITIC–VIKOR Approach | Risk scenarios in the oil and gas industry | Combines subjective and objective weighting methods to prioritize scenarios using probabilistic linguistic term sets. |
| Wavelet Analysis | Financial risk dynamics related to oil prices | Explores temporal and frequency relationships between variables, such as oil price volatility, financial risks, and digital currencies, using advanced wavelet techniques. |
| M-SDIIM (Dynamic Inoperability Model) | Resilience analysis for oil supply disruptions | Quantifies industry disruptions and suggests strategies, such as reserve releases, to improve system resilience. |
| Hybrid Monte Carlo and HYDROTAM-3D Model | Offshore oil exploration projects | Simulates environmental risks, including tsunamis and currents, using probabilistic and hydrodynamic modeling. |
| Fuzzy TOPSIS | Risk assessment in crude oil transportation supply chains | Optimizes logistics by addressing uncertainties using fuzzy logic and prioritizing ideal transportation routes. |
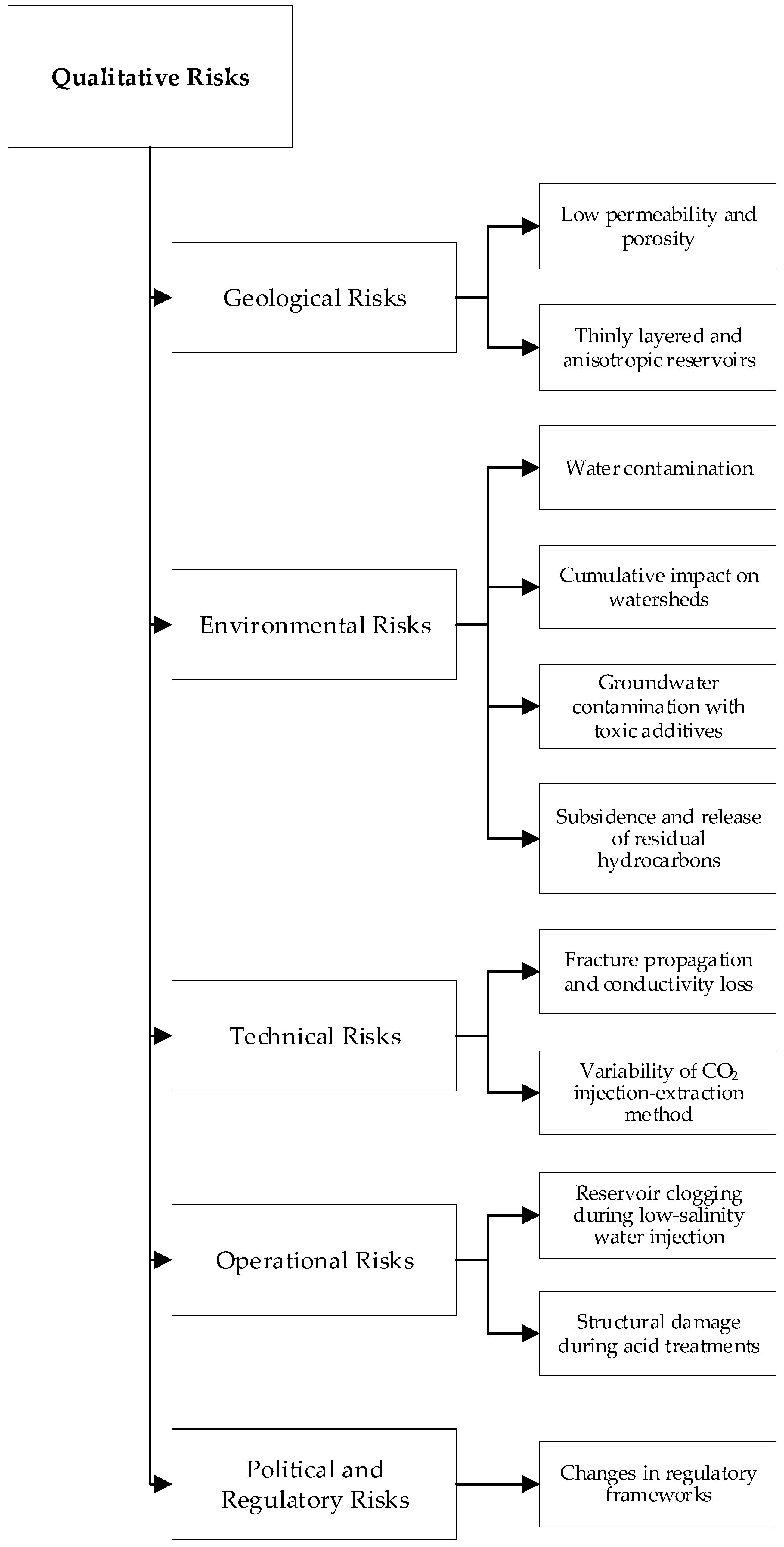
| Risk Category | Specific Risks | Description |
|---|---|---|
| Geological Risks | Low permeability and porosity | Fluid movement issues require advanced methods, such as hydraulic fracturing. |
| Thinly layered and anisotropic reservoirs | Complex reservoir structures hinder efficient resource extraction. | |
| Environmental Risks | Water contamination | Hydraulic fracturing fluids and chemicals pose threats to water sources. |
| Cumulative impact on watersheds | High well density affects watershed ecosystems. | |
| Groundwater contamination with toxic additives | Toxic substances in fracturing fluids threaten groundwater safety. | |
| Subsidence and release of residual hydrocarbons | Prolonged production leads to geological and structural instability. | |
| Technical Risks | Fracture propagation and conductivity loss | Increased stress on proppant reduces fracture efficiency. |
| Variability of CO₂ injection–extraction method | Effectiveness varies depending on reservoir heterogeneity and fracture network. | |
| Economic Risks | High initial production costs | Significant early-stage expenses and technology implementation costs. |
| Global market price volatility | Market fluctuations impact the financial viability of operations. | |
| Lack of long-term market stability | Global supply–demand shifts, geopolitical factors, and renewable energy transitions destabilize forecasts. | |
| Insufficient infrastructure investment | Inadequate pipeline networks, processing capacities, and transportation solutions increase operational costs and limit market access. | |
| Rising capital costs due to technological advances | Complex extraction technologies require high upfront investments, not always justified by returns. | |
| Tax policy and fiscal changes | Unpredictable changes in taxation, royalties, and subsidies negatively impact long-term profitability, especially in politically unstable regions. | |
| Insufficient diversification of financial risks | Heavy reliance on a single income source or market increases vulnerability to sectoral declines. | |
| Operational Risks | Reservoir clogging during low-salinity water injection | Injection of low-salinity water can cause scaling and blockages. |
| Structural damage during acid treatments | Improper pressure management can damage well structures. | |
| Political and Regulatory Risks | Changes in regulatory frameworks | Policy changes and lack of incentives create financial instability. |
| Rgeo | Renv | Rtech | Rreg | Rsoc | Rqual |
|---|---|---|---|---|---|
| Low | Low | Low | Low | Low | Low |
| Low | Low | Low | - | - | Low |
| - | Low | Low | - | Low | Low |
| Low | - | - | Low | - | Low |
| Medium | Medium | Low | Low | Low | Medium |
| High | Low | Low | Low | Low | Medium |
| - | Medium | Medium | - | Medium | Medium |
| - | Low | High | Low | Medium | Medium |
| Low | High | Low | Low | Low | Medium |
| - | Medium | High | - | High | High |
| High | Low | Low | - | High | High |
| High | High | High | - | - | High |
| - | - | - | High | High | High |
| Medium | Medium | Medium | High | High | High |
| Name of the Risk Category | Definition | Expert Assessment |
|---|---|---|
| Geological Risk (Rgeo) | Uncertainty around heterogeneous layers, uncertain fracturing efficiency. | Medium (geological data confirm complexity, but suitable MSF design might stabilize production). |
| Technological Risk (Rtech) | Likelihood of equipment failures, complexity of multi-stage fracturing, potential lack of local technical expertise. | Medium (MSF is partly proven, but some specialized competencies may be missing). |
| Social Risk (Rsoc) | Possible public opposition to fracturing, local environmental requirements, workforce shortages. | Low (sparsely populated remote region, initial agreements with local authorities in place, no current protests). |
| Environmental Risk (Renv) | Threat of contaminating surface water during fracturing, greenhouse gas emissions, waste disposal concerns (e.g., drill cuttings). | Low (no protected areas nearby; the operator follows standard environmental protocols). |
| Political–Regulatory Risk (Rreg) | Potential changes in taxation rates, stricter environmental regulations, sanctions restricting equipment imports. | Medium (rumors of higher tax rates for new fields exist, but no official law yet). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semenova, T.; Sokolov, I. Theoretical Substantiation of Risk Assessment Directions in the Development of Fields with Hard-to-Recover Hydrocarbon Reserves. Resources 2025, 14, 64. https://doi.org/10.3390/resources14040064
Semenova T, Sokolov I. Theoretical Substantiation of Risk Assessment Directions in the Development of Fields with Hard-to-Recover Hydrocarbon Reserves. Resources. 2025; 14(4):64. https://doi.org/10.3390/resources14040064
Chicago/Turabian StyleSemenova, Tatyana, and Iaroslav Sokolov. 2025. "Theoretical Substantiation of Risk Assessment Directions in the Development of Fields with Hard-to-Recover Hydrocarbon Reserves" Resources 14, no. 4: 64. https://doi.org/10.3390/resources14040064
APA StyleSemenova, T., & Sokolov, I. (2025). Theoretical Substantiation of Risk Assessment Directions in the Development of Fields with Hard-to-Recover Hydrocarbon Reserves. Resources, 14(4), 64. https://doi.org/10.3390/resources14040064







