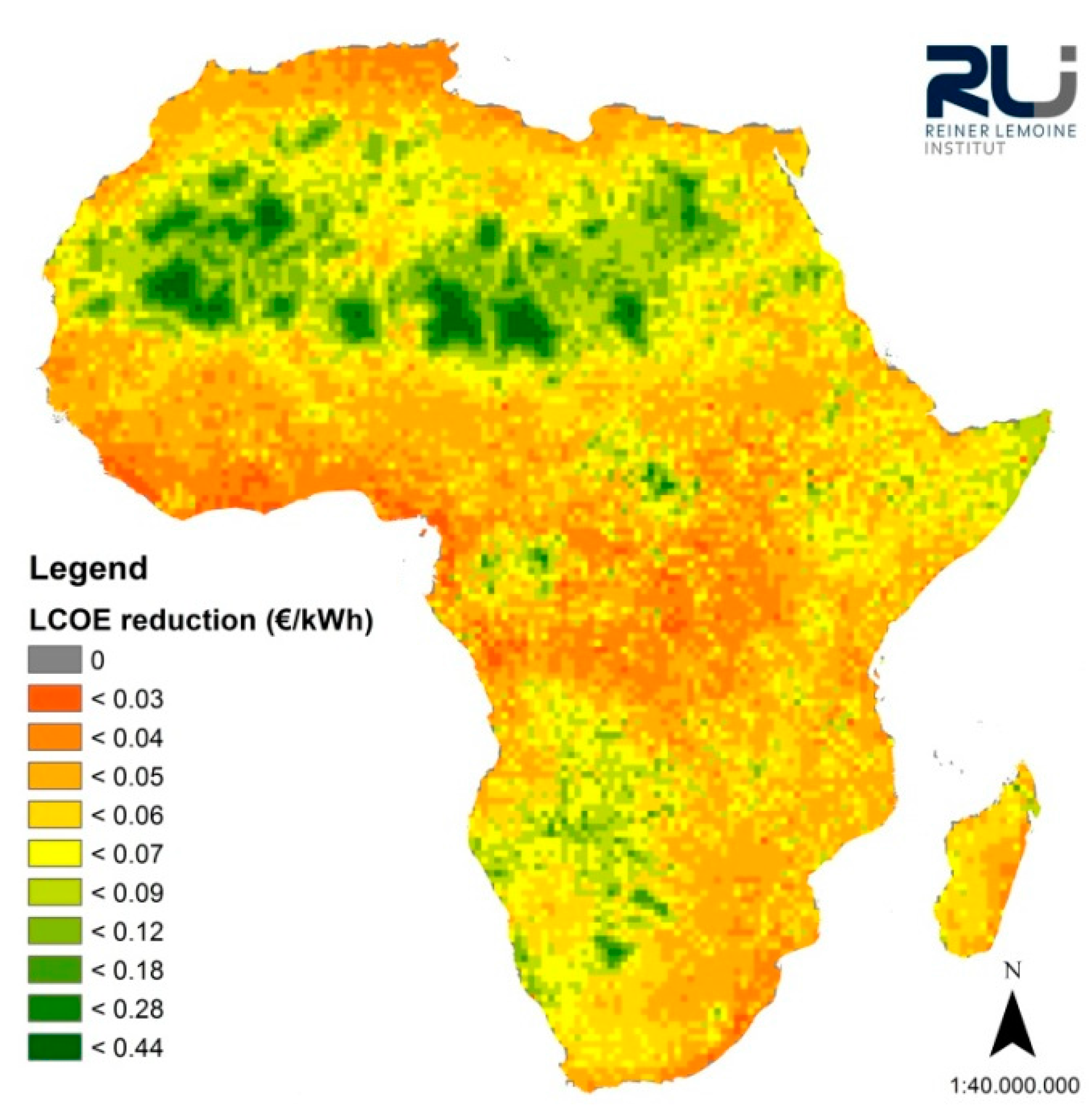
The purpose of this study is to quantify the techno-economic potential for decentralized PV power for the African continent by comparing the power generation costs of decentralized diesel-based systems to PV-based hybrid systems. Due to the generic character of this study decentralized power generation is assumed for each location in Africa. Certainly, this is partly not reflecting the reality as a central power generation infrastructure is in place in many countries and centralized power generation presents the most-cost effective electrification and energy supply option in many areas [
11]. Nevertheless, the African continent is predestined for studying the potential for decentralized power generation with renewable energies as literally “thousands” of diesel-based mini-grids are in place with largely high power generation costs [
13,
14]. Furthermore, the low developed central power infrastructure, vast distances, and sparse population are decreasing the cost-effectiveness of central power generation systems and favor small decentralized energy systems. Furthermore, decentralized renewable systems can largely contribute to rural electrification. The International Energy Agency (IEA) assumes that, globally, new electrification has to be provided by 40% through decentralized mini-grids till 2030 [
15].
2.3. Energy System Modelling
Secondly, an energy system modelling tool developed at the RLI was applied in order to study the economic feasibility of decentralized PV systems compared to diesel systems. The general approach of the model and relevant results have been published in [
19]. This model is able to simulate an energy system in hourly time steps over one reference year regarding the fossil and solar resources, as well as technical, economic, and load data to define the most economical configuration of RE-based hybrid systems. It describes energy flows between system components and their resulting costs (
Figure 2).
Within the energy simulation model capital and operational expenditures for each component, as well as local fuel costs, are considered. Diesel generator capital expenditures were set to zero, assuming that the diesel power generation infrastructure is already in place. The cost data form the baseline for calculating the system’s overall levelized cost of electricity (LCOE) [
20] (Equations (1) and (2)) for one reference year. The results provide the cost-optimized system configurations for a project period of 20 years.
Equation (1): Levelized cost of electricity (
LCOE) for power systems. Abbreviations stand for: Capital expenditures (
Capex); capital recovery factor (
CRF); weighted average cost of capital (
WACC); project lifetime (
N); operation and maintenance expenditures per year (
Opex); cost of diesel per liter (
); consumed diesel per year (Fuel), consumed electricity per year (
).
Equation (2): Capital recovery factor (
CRF). CRF is set according to weighted average cost of capital (
WACC) and project lifetime (
N).
Figure 2.
Renewable-based hybrid energy system. Diesel generator, PV module, battery storage, and load are the considered parts. Arrows indicate direction of power flows and resources.
Figure 2.
Renewable-based hybrid energy system. Diesel generator, PV module, battery storage, and load are the considered parts. Arrows indicate direction of power flows and resources.
Two energy supply options are considered: a diesel system consisting of diesel generators only and a hybrid system consisting of crystalline-silicon PV modules, lead-acid battery storage systems, and a diesel generator (
Figure 2). For diesel generators no capital expenditures are applied as we assume that diesel generators are already in place and are extended by renewable energies. The configuration of the components in the hybrid system is optimized in order to minimize the LCOE. For every time step of the simulated period the load has to be fully covered. In a first step, renewables feed into the network. Two cases may then occur: either a power surplus exists, which can be stored by the battery or a lack of power has to be filled first by a battery discharge and/or by diesel power. A spinning reserve of 10% of the current load has to be provided in every time step. This spinning reserve can be seen as the needed amount of grid-forming devices within the system to meet all stability criteria (e.g., frequency stabilization, voltage stabilization, short circuit power). The spinning reserve can either be supplied by the battery, if its state of charge is sufficient, or by the diesel generator, in order to guarantee the stability of the system. If not enough spinning reserve is provided, additional power has to be generated by the generator leading to power surpluses. Additionally, due to maintenance reasons, diesel generators have a minimal loading which is reflected in the model as a minimal operation of 20% of the maximal load of the entire year which can also lead to power surpluses. In a last step, generated power surpluses may release the discharge or even charge the battery, respectively (
Figure 3).
Figure 3.
Dispatch strategy applied in the energy system modelling tool.
Figure 3.
Dispatch strategy applied in the energy system modelling tool.
The simulation model was fed with the site-specific input parameters derived from the spatial analysis supplemented by the general input parameters for each reference point (
Table 2). Resource data are comprised by the diesel base price, diesel transport costs, diesel price increase, and PV yield. For assessing the local diesel price transport costs, as defined in the spatial analysis, were added to the average diesel world market price of 2013 of 0.58 €/L [
21] in Scenario I, or the respective national diesel prices [
22,
23] in Scenario II (
Table A1). On the national basis, diesel fuel costs were researched individually and, in some cases, it was necessary to estimate diesel fuel costs as no reliable sources were available. Generally, national diesel costs refer to retail prices rather than to pump prices for diesel. An annual diesel price increase of 3% is applied and, for the simulation model, the average diesel costs over the project period of 20 years were used. Finally, the PV yield as described in the spatial analysis was applied.
All technologies (PV power plant, diesel generator, and battery system) are characterized by CAPEX, OPEX, life time, and conversion efficiency. The OPEX are reflected as a percentage of the CAPEX for PV and as fixed values per kWh for diesel generator and battery system. The battery system is, furthermore, described by its round cycle efficiency and maximal depth of discharge. For this study the technological parameters of lead-acid batteries were applied [
24].
Table 2.
Simulation input parameters.
Table 2.
Simulation input parameters.
| Input parameter | Parameter value |
|---|
| Resource data |
| Diesel base price | Scenario I: 0.58 €/L world market base price |
| Scenario II: according to national retail price |
| Diesel transport costs | Transportation costs according to [8,16] |
| Diesel price increase | 3% annual increase |
| PV yield | Varies according to geographic location (in kWh/kWp/a) [12,13] |
| Technical data |
| Diesel generator efficiency | 30% |
| Battery round cycle efficiency | 85% |
| Battery max. depth of discharge | 50% |
| Battery life time | 10 years |
| Battery C-rate | 1:6 kW/kWh |
| Economic data |
| CAPEX diesel generator | 0 €/kW |
| OPEX diesel generator—variable | 0.01 €/kWh |
| CAPEX PV | 1,600 €/kWp |
| OPEX PV—fixed | 2% of Capex/year |
| CAPEX battery | 350 €/kWh |
| OPEX battery—fixed | 10 €/kWh/year |
| Project duration | 20 years |
| WACC | 10% |
A typical load curve was assumed for all locations in order to estimate the energy demand (
Figure 4). The selected load curve shows a maximum load more than three times higher than the minimum load, including a significant peak load in the evening hours. This load curve was derived from a real load curve of a Tanzanian village and reflects the energy demand profile of a typical rural settlement, the focus object of the analysis [
25]. The load curve reflects the primary use of electricity for lighting purposes and small residential appliances. This daily load curve was converted to a yearly load curve by repeating it 365 times.
Figure 4.
Typical load curve of a rural village [
25]. This daily load curve was converted to a yearly load curve by repeating it 365 times.
Figure 4.
Typical load curve of a rural village [
25]. This daily load curve was converted to a yearly load curve by repeating it 365 times.