Improving the Hydro-Morpho Dynamics of A River Confluence by Using Vanes
Abstract
:1. Introduction
2. Materials and Methods
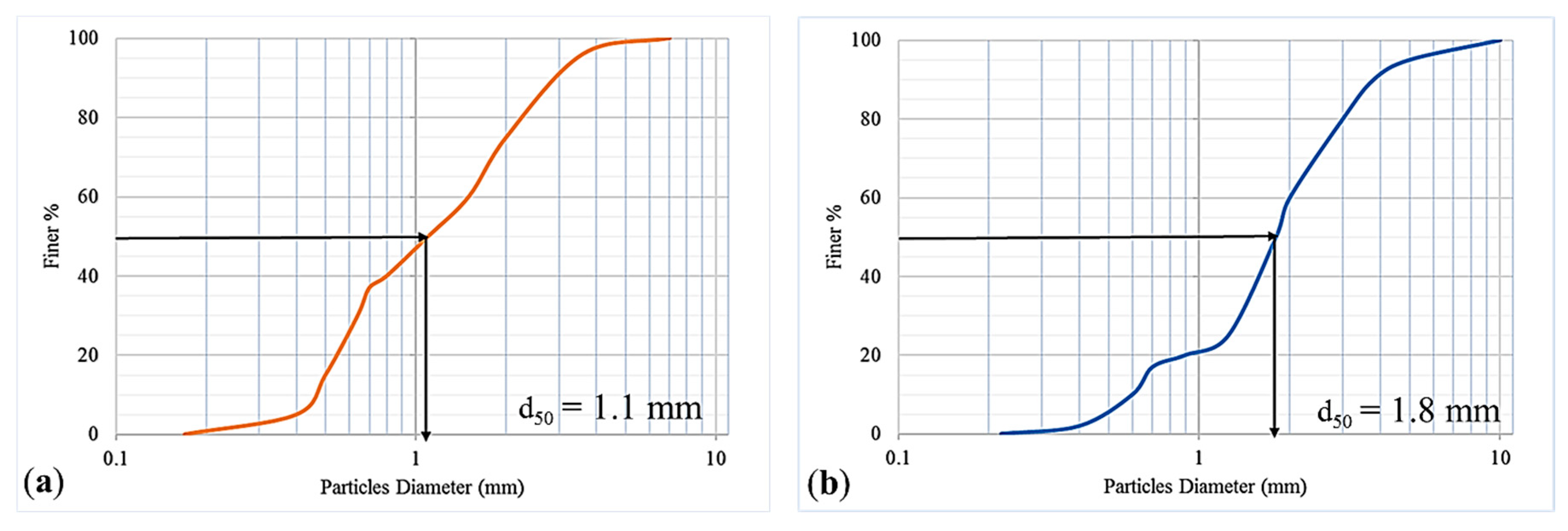
2.1. Study Area and Data Acquisition
2.2. Critical Velocity of Sediment Inception Motion
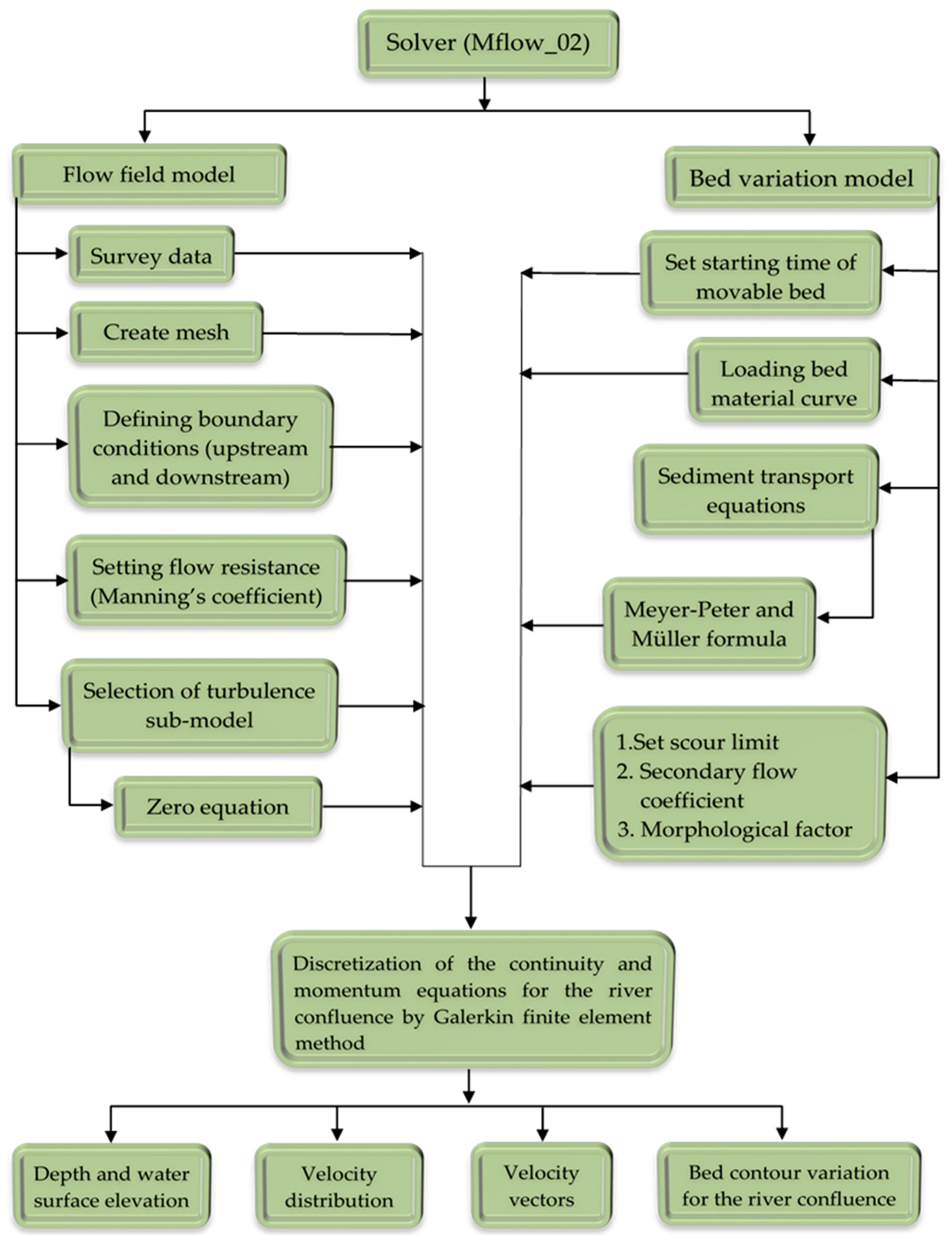
2.3. Solver Background, Structure, and Characteristics
2.3.1. Flow Field Model
- A Galerkin finite element sub-model (a type of weighted residual method) is used to discretize continuity and momentum equations.
- Open boundary conditions (upstream and downstream boundaries, etc.), enable the setting up of various conditions, such as time series of flow discharge, time series of water level, and water level discharge.
- The friction of the river bed can be set by using the Manning roughness coefficient. This coefficient can be represented in the model as a polygon for the entire area or for each element (cell), thus providing spatial distribution of roughness.
- Three sub-models are available for computing the turbulence field (flows with large and small eddies). These are the zero equation sub-model, simple k-ε, and direct input of kinematic eddy viscosity. In this study, the zero equation sub-model was selected because of its stability in calculating large and small eddies. The kinematic eddy viscosity, υ, is expressed by using the von Kàrmàn coefficient with (0.40).where : bottom friction velocity.
- 5.
- Other effects, such as the effect of wind on the water surface and of vegetation on flow, are available in this solver but were disregarded in this study.
2.3.2. Riverbed Variation Model
- The riverbed variation associated with the flow field model is calculated. This model can calculate the flow field only or together with riverbed variation.
- The riverbed material can be selected from uniform and mixed grain diameters. If a mixed grain diameter is selected, then a variation in grain distribution can be assumed for deep directions and multiple layers.
- Three methods for calculating the total bed load of depth-averaged flow velocity are available in the Mflow_02 solver, and these are the Meyer-Peter and Müller formula [51], Ashida and Michiue formula [52], and Engelund-Hansen formula [53]. In this study, the Meyer-Peter and Müller formula was adopted for computing the total bed load.
- 4.
- The scour limit of the riverbed, secondary flow coefficient, and morphological factor can be set accordingly.
2.4. Model Implementation and Boundary Conditions
2.5. Hydraulic Performance of the Proposed Vanes Used in The River Confluence
- Single row of the vanes with a length of 1 m and a spacing of 6 m between vanes
- Single row of the vanes with a length of 2 m and a spacing of 5 m between vanes
- Single vane a length of with 10 m
2.6. Statistical Indices
3. Results and Discussion
3.1. Model Calibration
3.2. Model Validation
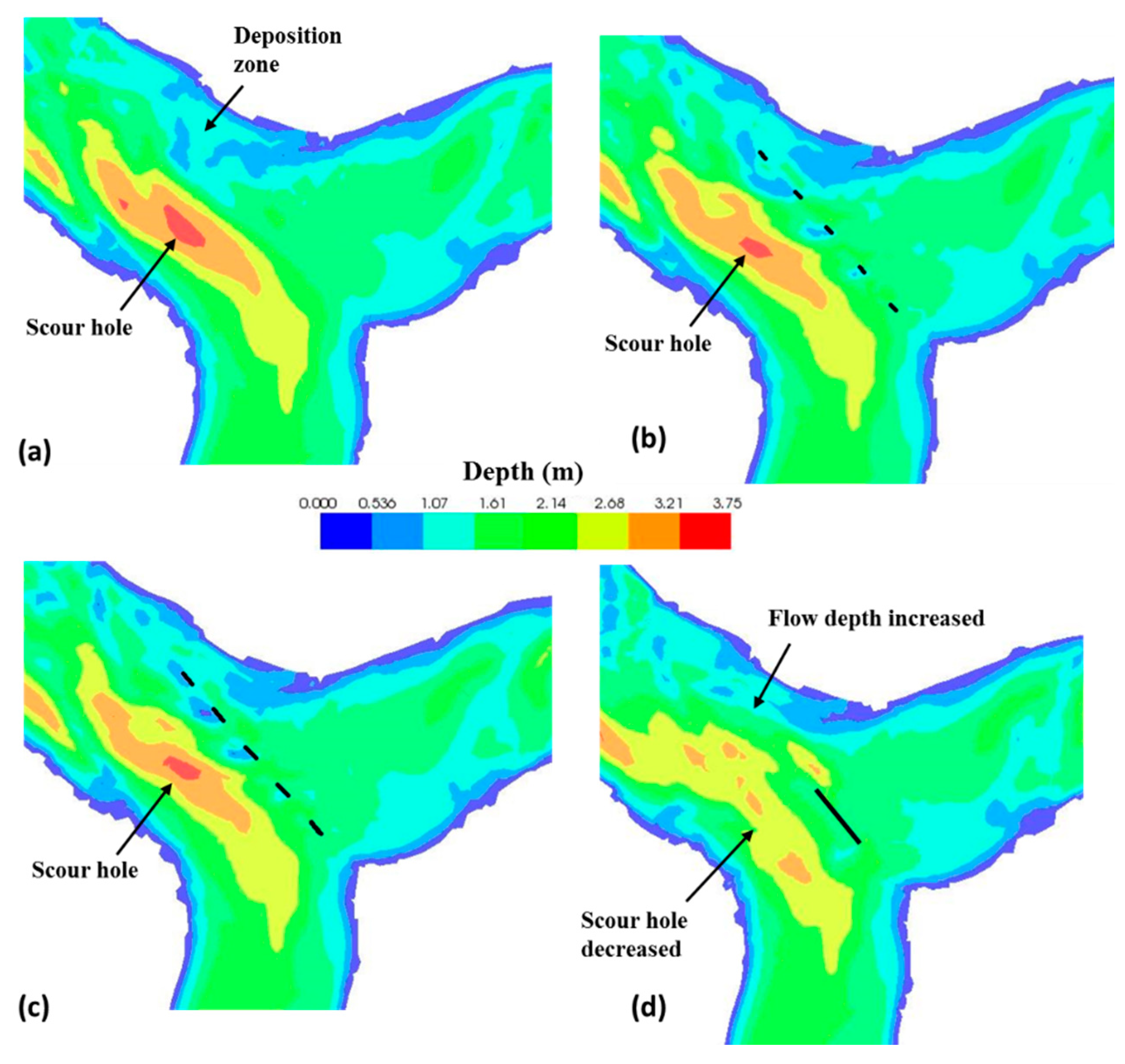
3.3. Evaluation of Hydraulic Performance of the Proposed Vanes Used in the River Confluence
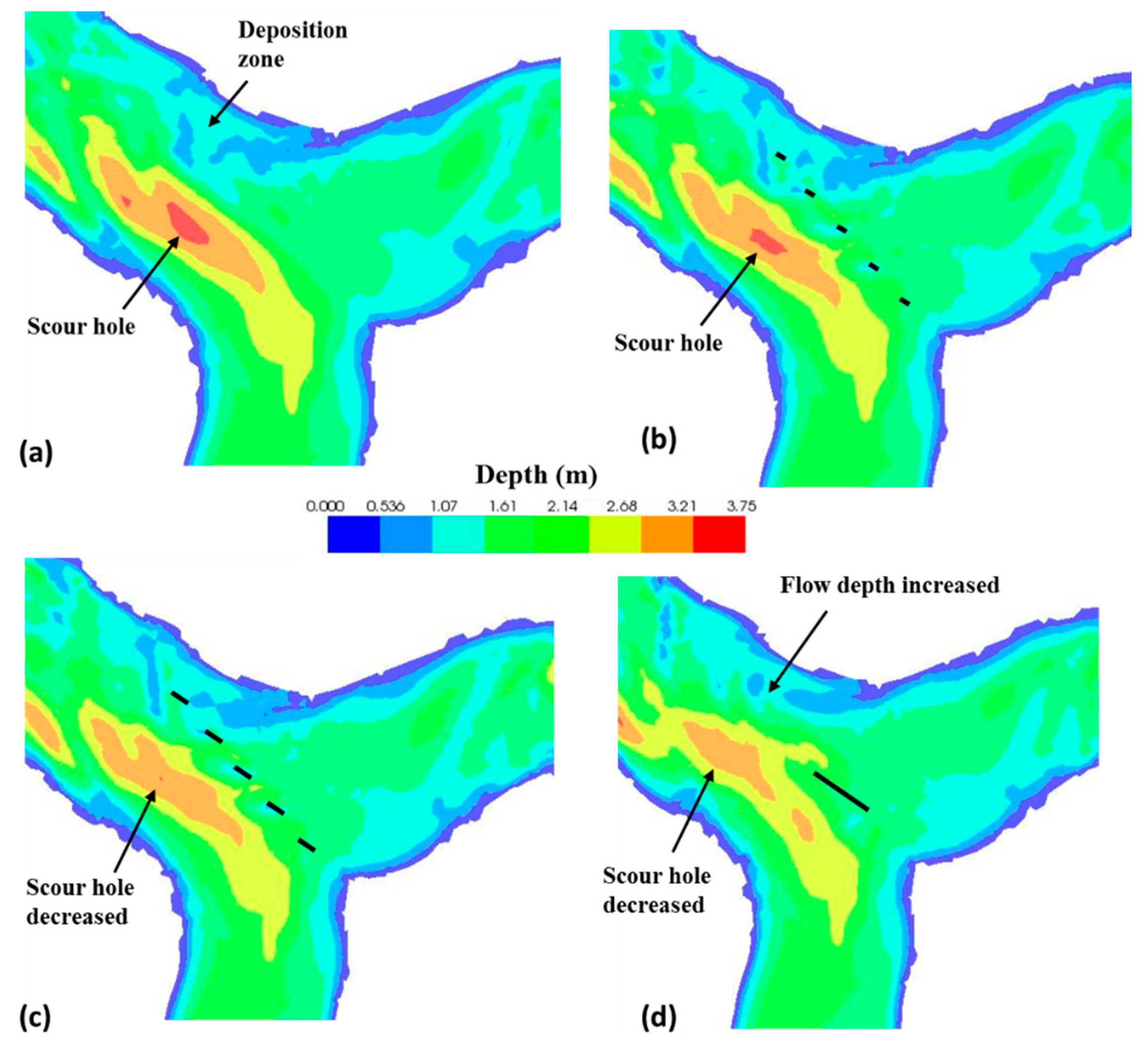
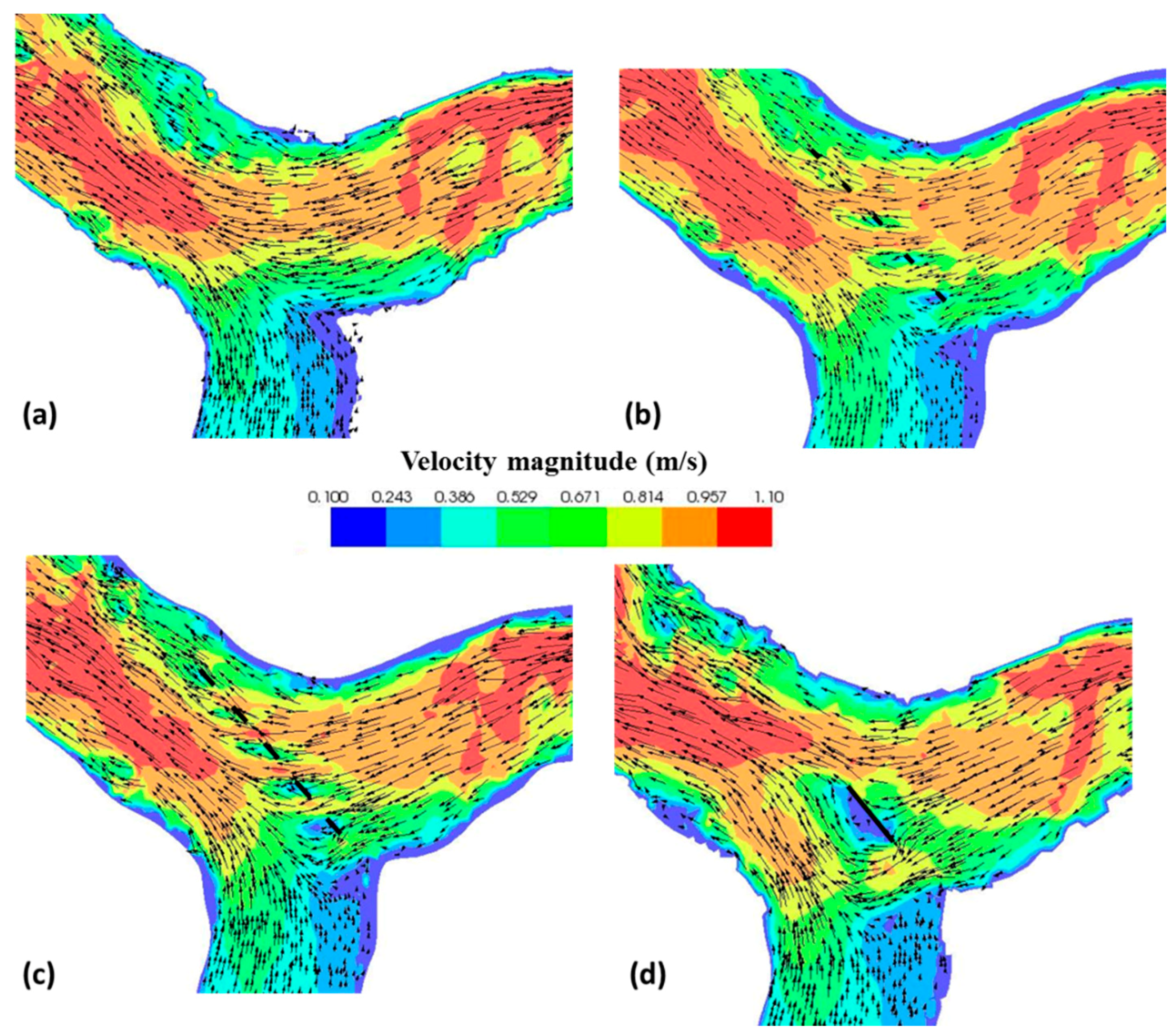
3.3.1. First Scenario: Single Row of the Vanes with a Length of 1 m
3.3.2. Second Scenario: Single Row of Vanes with a Length of 2 m
3.3.3. Third Scenario: Single Vane with a Length of 10 m
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riley, J.D.; Rhoads, B.L.; Parsons, D.R.; Johnson, K.K. Influence of junction angle on three-dimensional flow structure and bed morphology at confluent meander bends during different hydrological conditions. Earth Surf. Process. Landforms 2014, 40, 252–271. [Google Scholar] [CrossRef]
- Ashmore, P.; Parker, G. Confluence scour in coarse braided streams. Water Resour. Res. 1983, 19, 392–402. [Google Scholar] [CrossRef] [Green Version]
- Guillén-Ludeña, S.; Franca, M.J.; Cardoso, A.H.; Schleiss, A.J. Evolution of the hydromorphodynamics of mountain rivesr confluences for varying discharge ratios and junction angles. Geomorphology 2016, 255, 1–15. [Google Scholar] [CrossRef]
- Rhoads, B.L. Mean structure of transport-effective flows at an asymmetrical confluence when the main stream is dominant. In Coherent Flow Structures in Open Channels; Ashworth, P.J., Bennett, J.S.J., Best, L., McLelland, S.J., Eds.; Wiley: Chichester, UK, 1996; pp. 491–517. [Google Scholar]
- Rice, S.P.; Roy, A.G.; Rhoads, B.L. River Confluences, Tributaries and the Fluvial Network; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar] [CrossRef]
- Best, J.L. The Morphology of River Channel Confluences. Prog. Phys. Geogr. 1986, 10, 157–174. [Google Scholar] [CrossRef]
- Best, J.L. Flow Dynamics at River Channel Confluences: Implications for Sediment Transport and Bed Morphology. In Recent Developments in Fluvial Sedimentology; SEPM (Society for Sedimentary Geology): Tulsa, OK, USA, 1987; pp. 27–35. [Google Scholar] [CrossRef]
- Best, J.L. Sediment transport and bed morphology at river channel confluences. Sedimentology 1988, 35, 481–498. [Google Scholar] [CrossRef]
- Best, J.L.; Reid, I. Separation Zone at Open-Channel Junctions. J. Hydraul. Eng. 1984, 110, 1588–1594. [Google Scholar] [CrossRef]
- Biron, P.; Best, J.L.; Roy, A.G. Effects of Bed Discordance on Flow Dynamics at Open Channel Confluences. J. Hydraul. Eng. 1996, 122, 676–682. [Google Scholar] [CrossRef]
- Liu, T.; Fan, B.; Lu, J. Sediment–flow interactions at channel confluences: A flume study. Adv. Mech. Eng. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Mosley, M. An experimental study of channel confluences. J. Geol. 1976, 84, 535–562. [Google Scholar] [CrossRef]
- Yuan, S.; Tang, H.; Xiao, Y.; Qiu, X.; Zhang, H.; Yu, D. Turbulent flow structure at a 90-degree open channel confluence: Accounting for the distortion of the shear layer. J. Hydro-Environ. Res. 2016, 12, 130–147. [Google Scholar] [CrossRef]
- Ashmore, P.E.; Ferguson, R.I.; Prestegaard, K.L.; Ashworth, P.J.; Paola, C. Secondary flow in anabranch confluences of a braided, gravel-bed stream. Earth Surf. Process. Landforms 1992, 17, 299–311. [Google Scholar] [CrossRef]
- Boyer, C.; Roy, A.G.; Best, J.L. Dynamics of a river channel confluence with discordant beds: Flow turbulence, bed load sediment transport, and bed morphology. J. Geophys. Res. Earth Surf. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Lane, S.N.; Kostaschuk, R.A.; Hardy, R.J.; Orfeo, O. Large river channel confluences. In River Confluences, Tributaries and the Fluvial Network; Rice, S.P., Rhoads, B.L., Roy, A.G., Eds.; John Wiley & Sons: Chichester, UK, 2008; pp. 73–91. ISBN 9780470026724. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Riley, J.D.; Mayer, D.R. Geomorphology Response of bed morphology and bed material texture to hydrological conditions at an asymmetrical stream confluence. Geomorphology 2009, 109, 161–173. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Sukhodolov, A.N. Lateral momentum flux and the spatial evolution of flow within a confluence mixing interface. Water Resour. Res. 2008, 44, W08440. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Sukhodolov, A.N. Field investigation of three-dimensional flow structure. Water Resour. Res. 2001, 37, 2393–2410. [Google Scholar] [CrossRef]
- Roy, A.G.; Roy, R.; Bergeron, N. Hydraulic geometry and changes in flow velocity at a river confluence with coarse bed material. Earth Surf. Process. Landforms 1988, 13, 583–598. [Google Scholar] [CrossRef]
- Szupiany, R.N.; Amsler, M.L.; Parsons, D.R.; Best, J.L. Morphology, flow structure, and suspended bed sediment transport at two large braid-bar confluences. Water Resour. Res. 2009, 45, W05415. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Biron, P.M.; Lane, S.N.; Richards, K.S.; Roy, A.G. Investigation of controls on secondary circulation in a simple confluence geometry using a three dimensional numerical model. Hydrol. Process. 1998, 12, 1371–1396. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S. Numerical simulation of three-dimensional, time-averaged flow structure at river channel confluences. Water Resour. Res. 2000, 36, 2731–2746. [Google Scholar] [CrossRef] [Green Version]
- Schindfessel, L.; Creëlle, S.; De Mulder, T. Flow patterns in an open channel confluence with increasingly dominant tributary inflow. Water 2015, 7, 4724–4751. [Google Scholar] [CrossRef]
- Shakibainia, A.; Reza, M.; Tabatabai, M.; Zarrati, A.R. Three-dimensional numerical study of flow structure in channel confluences. Canadian J. Civ. Eng. 2010, 37, 772–781. [Google Scholar] [CrossRef]
- Song, C.G.; Seo, I.W.; Kim, Y. Do. Analysis of secondary current effect in the modeling of shallow flow in open channels. Adv. Water Resour. 2012, 41, 29–48. [Google Scholar] [CrossRef]
- Ashmore, P.; Gardner, J.T. Unconfined Confluences in Braided Rivers. In River Confluences, Tributaries and the Fluvial Network; Rice, S., Roy, A., Rhoads, B., Eds.; John Wiley and Sons: Chichester, UK, 2008. [Google Scholar]
- Leite Ribeiro, M.; Blanckaert, K.; Roy, A.G.; Schleiss, A.J. Flow and sediment dynamics in channel confluences. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Birjukova, O.; Guillen, S.; Alegria, F.; Cardoso, A. Three Dimensional Flow Field at Confluent Fixed-Bed Open Channels. In River Flow. Available online: http://infoscience.epfl.ch/record/202026/files/2014-989 (accessed on 29 December 2018).
- Thanh, M.; Kimura, I.; Shimizu, Y.; Hosoda, T. Depth-averaged 2D models with effects of secondary currents for computation of flow at a channel confluence. In Proceedings of the International Conference on Fluvial Hydraulics (River Flow’10), Braunschweig, Germany, 8–10 September 2010; pp. 137–144. [Google Scholar]
- Benda, L.; Andras, K.; Miller, D.; Bigelow, P. Confluence effects in rivers: Interactions of basin scale, network geometry, and disturbance regimes. Water Resour. Res. 2004, 40, 1–15. [Google Scholar] [CrossRef]
- Leite Ribeiro, M.; Blanckaert, K.; Roy, A.G.; Schleiss, A.J. Hydromorphological implications of local tributary widening for river rehabilitation. Water Resour. Res. 2012, 48, W10528. [Google Scholar] [CrossRef]
- Julien, P.Y.; Ghani, A.A.; Zakaria, N.A.; Abdullah, R.; Chang, C.K. Case Study: Flood Mitigation of the Muda River, Malaysia. J. Hydraul. Eng. 2010, 136, 251–261. [Google Scholar] [CrossRef]
- Mohammed, T.A.; Al-Hassoun, S.; Ghazali, A.H. Prediction of flood levels along a stretch of the langat river with insufficient hydrological data. Pertanika J. Sci. Technol. 2011, 19, 237–248. [Google Scholar]
- Sinnakaudan, S.K.; Ab Ghani, A.; Ahmad, M.S.S.; Zakaria, N.A. Flood risk mapping for Pari River incorporating sediment transport. Environ. Model. Softw. 2003, 18, 119–130. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Yan, X.; Liu, X.; Duan, H.F. Experimental Study on the Hydrodynamic Influence of River Flow Confluences to the Open Channel Stage—Discharge Relationship. Preprints 2016. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Wang, Y. Sediment management with submerged vanes. I: Theory. J. Hydraul. Eng. 1991, 117, 267. [Google Scholar] [CrossRef]
- Wuppukondur, A.; Chandra, V. Control of Bed Erosion at 60° River Confluence Using Vanes and Piles. Int. J. Civ. Eng. 2017, 16, 619–627. [Google Scholar] [CrossRef]
- Wuppukondur, A.; Chandra, V. Methods to control bed erosion at 90° river confluence: An experimental study. Int. J. River Basin Manag. 2017, 15, 297–307. [Google Scholar] [CrossRef]
- Sirdari, Z.Z.; Ab Ghani, A.; Hassan, Z.A. Bedload transport of small rivers in Malaysia. Int. J. Sediment Res. 2014, 29, 481–490. [Google Scholar] [CrossRef]
- Hamidun, N. Integrated River Basin Management (IRBM): Simulation Modelling System for Kurau River. Master’s Thesis, Universiti Sains Malaysia, Penang, Malaysia, 2010. [Google Scholar]
- Karmaker, T.; Dutta, S. Prediction of short-term morphological change in large braided river using 2D numerical model. J. Hydraul. Eng. 2016, 142, 04016039. [Google Scholar] [CrossRef]
- USACE (U.S. Army Corps of Engineers). Upper Mississippi River Restoration Environmental Management Program, Environmental Design Handbook; The U.S. Army Corps of Engineers: Rock Island, IL, USA, 2012; Available online: http://www.mvr.usace.army.mil/Portals/48/docs/Environmental/EMP/HREP/EMP_Documents/2012%20UMRR%20EMP%20Environmental%20Design%20Handbook%20-%20FINAL.pdf (accessed on 29 December 2018).
- Bhuiyan, F.; Hey, R.D.; Wormleaton, P.R. Bank-attached vanes for bank erosion control and restoration of river meanders. J. Hydraul. Eng. 2010, 136, 583–596. [Google Scholar] [CrossRef]
- Sirdari, Z.Z.; Ghani, A.A.; Hasan, Z.A. Application of 3D Numerical Model in Bedload Transport and Bed Morphology of River Channel Confluence. In Proceedings of the 35th IAHR World Congress: The Wise Find Pleasure in Water, Chengdu, China, 8–13 September.
- Sirdari, Z.Z. Bedload Transport for Small Rivers in Malaysia. Ph.D. Thesis, Universiti Sains Malaysia, Penang, Malaysia, 2013. Available online: https://www.academia.edu/4147500/Bed_Load_Transport_of_Small_Rivers_in_Malaysia (accessed on 29 December 2018).
- Alomari, N.K.; Yusuf, B.; Mohammad, T.A.; Ghazali, A.H. Experimental investigation of scour at a channel junctions of different diversion angles and bed width ratios. CATENA 2018, 166, 10–20. [Google Scholar] [CrossRef]
- Simons, D.B.; Şentürk, F. Sediment Transport Tec)nology: Water and Sediment Dynamics; Water Resources Publication: Littleton, CO, USA, 1992. [Google Scholar]
- Tomidokoro, G.; Araki, M.; Yoshida, H. Three-Dimensional Analysis of Open Channel Flows. Annu. J. Hydraul. Eng. 1985, 29, 727–732. [Google Scholar] [Green Version]
- iRIC. Mflow_02 Solver Manual. Produced by Mineyuki Gamou. Available online: http://i-ric.org/en/software/?c=19 (accessed on 10 July 2014).
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Stockholm, Sweden, 7 June 1948; pp. 39–64. [Google Scholar]
- Ashida, K.; Michiue, M. Study on hydraulic resistance and bedload transport rate in alluvial streams. Transcr. Jpn. Soc. Civ. Eng. 1972, 1972, 59–69. [Google Scholar] [CrossRef]
- Engelund, F. Flow and bed topography in channel bends. J. Hydraul. Div. 1974, 100, 1631–1648. [Google Scholar]
- Iwagaki, Y. Hydrodynamical Study on Critical Tractive Force. J. Jpn. Soc. Civ. Eng. 1956, 41, 1–21. [Google Scholar] [CrossRef]
- Watanabe, A.; Fukuoka, S.; Yasutake, Y.; Kawaguchi, H. Method for Arranging Vegetation Groins at Bends for Control of Bed Variation. Collect. Pap. River Eng. 2001, 7, 285–290. [Google Scholar]
- Hasegawa, K. Hydraulic Study on Alluvial Meandering Channel Planes and Bedform Topography-Affected Flows. Ph.D. Thesis, Hokkaido University, Hokkaido, Japan, 1984; pp. 1–184. [Google Scholar]
- Teo, F.Y.; Noh, M.N.M.; Ghani, A.A.; Zakaria, N.A. River Sand Mining Capacity in Malaysia. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017; pp. 538–546. [Google Scholar]
- Papanicolaou, A.N.; Elhakeem, M.; Dermisis, D.; Young, N. Evaluation of the Missouri River shallow water habitat using a 2D-hydrodynamic model. River Res. Appl. 2011, 27, 157–167. [Google Scholar] [CrossRef]
- Pinto, L.; Fortunato, A.; Freire, P. Sensitivity analysis of non-cohesive sediment transport formulae. Cont. Shelf Res. 2006, 26, 1826–1839. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Elhakeem, M.; Wardman, B. Calibration and verification of a 2D-hydrodynamic model for simulating flow around bendway weir structures. J. Hydr. Eng. 2010, 137, 75–89. [Google Scholar] [CrossRef]
- Papanicolaou, A.T.N.; Elhakeem, M.; Krallis, G.; Prakash, S.; Edinger, J. Sediment transport modeling review—Current and future developments. J. Hydraul. Eng. 2008, 134, 1–14. [Google Scholar] [CrossRef]
- Allahyonesi, H.; Omid, M.H.; Haghiabi, A.H. A study of the effects of the longitudinal arrangement sediment behavior near intake structures. J. Hydraul. Res. 2008, 46, 814–819. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Spoljaric, A. Sediment control by submerged vanes. J. Hydraul. Eng. 1986, 112, 1164–1180. [Google Scholar] [CrossRef]
- Barkdoll, B.D.; Ettema, R.; Odgaard, A.J. Sediment control at lateral diversions: Limits and enhancements to vane use. J. Hydraul. Eng. 1999, 125, 862–870. [Google Scholar] [CrossRef]










| No. | Cross Sections | Simulated Mean Velocity (m/s) | Mean Velocity Measured | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 h | 2 h | 3 h | 6 h | 12 h | 18 h | 24 h | Mean | |||
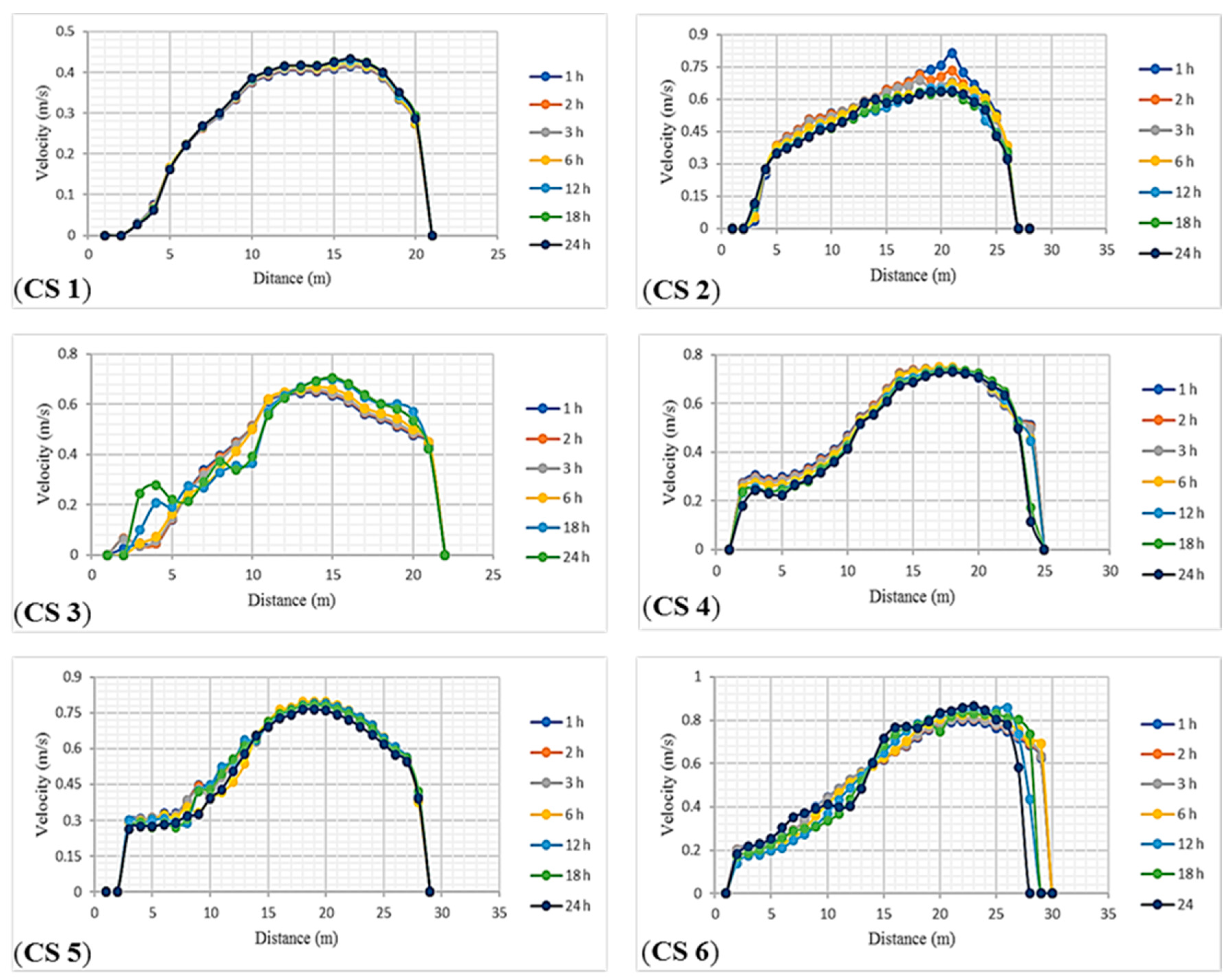
| 1 | CS 1 | 0.310 | 0.312 | 0.312 | 0.315 | 0.317 | 0.320 | 0.319 | 0.315 | 0.319 |
| 2 | CS 2 | 0.574 | 0.562 | 0.549 | 0.538 | 0.509 | 0.508 | 0.512 | 0.536 | 0.582 |
| 3 | CS 3 | 0.494 | 0.497 | 0.497 | 0.498 | 0.459 | 0.486 | 0.476 | 0.487 | 0.586 |
| 4 | CS 4 | 0.533 | 0.531 | 0.528 | 0.518 | 0.507 | 0.495 | 0.482 | 0.513 | 0.572 |
| 5 | CS 5 | 0.569 | 0.569 | 0.566 | 0.557 | 0.567 | 0.558 | 0.537 | 0.560 | 0.580 |
| 6 | CS 6 | 0.631 | 0.605 | 0.608 | 0.610 | 0.600 | 0.593 | 0.585 | 0.605 | 0.699 |
| Cross-Section | Average Velocity (m/s) | Error M-S | Absolute Value of Errors | Square of Error | Absolute Values of Errors Divided by Measured | Results of Different Statistical Indices | ||
|---|---|---|---|---|---|---|---|---|
| Measured (M) | Simulated (S) | |||||||
| CS 1 | 0.582 | 0.536 | 0.046 | 0.046 | 0.002 | 0.079 | MAD | 0.054 |
| CS 2 | 0.319 | 0.315 | 0.004 | 0.004 | 2 × 10−5 | 0.013 | MSE | 0.004 |
| CS 3 | 0.586 | 0.487 | 0.099 | 0.099 | 0.01 | 0.169 | RMSE | 0.064 |
| CS 4 | 0.572 | 0.513 | 0.059 | 0.059 | 0.003 | 0.103 | MAPE | 8.877 |
| CS 5 | 0.58 | 0.56 | 0.02 | 0.02 | 4 × 10−4 | 0.034 | ||
| CS 6 | 0.699 | 0.605 | 0.094 | 0.094 | 0.009 | 0.134 | ||
| Sum. | 0.322 | 0.025 | 0.533 | |||||
| Location of Measuring Water Surface Elevation | Measured (m) a.m.s.l | Simulated (m) a.m.s.l | Error M-S | Absolute Value of Error | Square of Error | Absolute Value of Error Divided by Measured |
|---|---|---|---|---|---|---|
| Kurau 1 | 16.476 | 16.441 | 0.035 | 0.035 | 0.0012 | 0.0021 |
| Kurau 2 | 16.423 | 16.432 | −0.009 | 0.009 | 8 × 10−5 | 0.0005 |
| Ara 1 | 16.528 | 16.578 | −0.05 | 0.05 | 0.0025 | 0.003 |
| Ara 2 | 16.475 | 16.514 | −0.039 | 0.039 | 0.0015 | 0.0024 |
| Ara 3 | 16.423 | 16.44 | −0.017 | 0.017 | 0.0003 | 0.001 |
| Main Kurau 1 | 16.371 | 16.386 | −0.015 | 0.015 | 0.0002 | 0.0009 |
| Main Kurau 2 | 16.318 | 16.33 | −0.012 | 0.012 | 0.0001 | 0.0007 |
| Main Kurau 3 | 16.266 | 16.278 | −0.012 | 0.012 | 0.0001 | 0.0007 |
| Sum. | 0.189 | 0.0061 | 0.0115 |
| No. | Time (s) | Discharge (m3/s) | Total Discharge (m3/s) | Water Levels at Downstream of Main Kurau River (m) | |
|---|---|---|---|---|---|
| Kurau River | Ara River | ||||
| 1 | 0 | 5 | 4 | 9 | 16.21 |
| 2 | 86,400 | 8 | 7 | 15 | 16.25 |
| 3 | 172,800 | 14 | 17 | 31 | 16.75 |
| 4 | 259,200 | 15 | 28 | 43 | 17.1 |
| 5 | 345,600 | 12 | 23 | 35 | 16.9 |
| 6 | 432,000 | 10 | 15 | 25 | 16.6 |
| 7 | 518,400 | 7 | 6 | 13 | 16.2 |
| Transect Name | Water Level | Results of Different Statistical Indices | Average Flow Depth (m) | Results of Different Statistical Indices | ||||
|---|---|---|---|---|---|---|---|---|
| Measured | Simulated | Measured | Simulated | |||||
| CS 1 | 16.44 | 16.48 | MAD | 0.032 | 1.17 | 1.12 | MAD | 0.04 |
| CS 2 | 16.45 | 16.49 | MSE | 0.001 | 0.58 | 0.59 | MSE | 0.002 |
| CS 3 | 16.42 | 16.45 | RMSE | 0.034 | 0.94 | 0.98 | RMSE | 0.044 |
| CS 5 | 16.38 | 16.4 | MAPE | 0.198 | 0.78 | 0.84 | MAPE | 4.486 |
| Transect Name | Water Level | Results of Different Statistical Indices | Average Flow Depth (m) | Results of Different Statistical Indices | ||||
|---|---|---|---|---|---|---|---|---|
| Measured | Simulated | Measured | Simulated | |||||
| CS 1 | 17.29 | 17.35 | MAD | 0.083 | 1.91 | 1.92 | MAD | 0.075 |
| CS 2 | 17.3 | 17.37 | MSE | 0.008 | 1.48 | 1.37 | MSE | 0.008 |
| CS 3 | 17.213 | 17.34 | RMSE | 0.087 | 1.83 | 1.77 | RMSE | 0.087 |
| CS 5 | 17.193 | 17.27 | MAPE | 0.484 | 1.58 | 1.7 | MAPE | 4.707 |
| River Name | Discharge (m3/s) | Average Velocity (m/s) | Confluence Status | Momentum Ratio (Mr) * | |
|---|---|---|---|---|---|
| Measured | Simulated | ||||
| Ara | 7 | 0.49 | 0.52 | 15 (m3/s) | 0.9 |
| Kurau | 8 | 0.5 | 0.431 | ||
| Ara | 28 | 0.85 | 0.752 | 43 (m3/s) | 2.6 |
| Kurau | 15 | 0.6 | 0.44 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, H.L.; Yusuf, B.; Mohammed, T.A.; Shimizu, Y.; Ab Razak, M.S.; Rehan, B.M. Improving the Hydro-Morpho Dynamics of A River Confluence by Using Vanes. Resources 2019, 8, 9. https://doi.org/10.3390/resources8010009
Ali HL, Yusuf B, Mohammed TA, Shimizu Y, Ab Razak MS, Rehan BM. Improving the Hydro-Morpho Dynamics of A River Confluence by Using Vanes. Resources. 2019; 8(1):9. https://doi.org/10.3390/resources8010009
Chicago/Turabian StyleAli, Hydar Lafta, Badronnisa Yusuf, Thamer Ahamed Mohammed, Yasuyuki Shimizu, Mohd Shahrizal Ab Razak, and Balqis Mohamed Rehan. 2019. "Improving the Hydro-Morpho Dynamics of A River Confluence by Using Vanes" Resources 8, no. 1: 9. https://doi.org/10.3390/resources8010009
APA StyleAli, H. L., Yusuf, B., Mohammed, T. A., Shimizu, Y., Ab Razak, M. S., & Rehan, B. M. (2019). Improving the Hydro-Morpho Dynamics of A River Confluence by Using Vanes. Resources, 8(1), 9. https://doi.org/10.3390/resources8010009





