Adaptive Large Neighborhood Search for a Production Planning Problem Arising in Pig Farming
Abstract
:1. Introduction
2. Literature Review
3. Definitions of the Problem and Mathematical Construction
3.1. Problem Definitions
3.2. Mathematical Construction
| i | illustrates the number of pig farms i = 1, 2, …, I |
| t | illustrates the time taken to feed pigs t = 1, 2, …, T |
| k | illustrates the workers which is used k = 1, 2, …, K |
| Pi | The income from matured pigs of farm i (baht/pigs) |
| C | Cost of producing mature pigs (baht/pig) |
| Fi | Fixed cost of farm i (baht) |
| Number of new born pigs that can feed on the farm i | |
| Worker experience level k | |
| Daily worker wages k | |
| M | big-M coefficient |
| Dt | Demand for pigs in period t |
| L | Lead time to produce pigs |
| Duration of pigs in new born stage | |
| Duration of pigs in growing stage | |
| Duration of pigs in mature stage | |
| Minimum workers required for pigs in new born stage | |
| Minimum workers required for pigs in growing stage | |
| Minimum workers required for pigs in mature stage | |
| Size of farm i |
| Yit | |
| Xit | |
| Oi | |
| Nkit | |
4. The Proposed Methods
4.1. Construct Initial Solution
| Algorithm 1. Procedure to construct the initial solution. |
| Input Number of farms (N), Number of workers (M), Number of planning period (T), Demand of pigs in each period (Dt) |
| Output: Farm production planning. |
| Begins: Generate vector that has dimension of 1*N and call it has value in vector. Generate vector that has dimension of 1*W and call it has value in vector. Sort each vector according to the value in each position of the vector obtained (list of farms i in position n) and (list of workers k in position w) |
| Set t=1; while t ≤ T Do set g=1; = Dt while ≥ 0 |
| Do open farm i according to calculate when Update slack; = Update g=g+1; |
| End do Update t=t+1; |
| End. do |
4.2. Destroy Operators
4.2.1. d-Random Removal Farm (d-RRF)
4.2.2. d-Random Removal Worker (d-RRW)
4.2.3. d-Worst Farm Removal (d-WFR)
4.2.4. d-Worst Worker Removal (d-WWR)
4.2.5. d-Related Farms Removal (d-RFR):
4.2.6. d-Relate Worker Removal (d-RWR)
4.2.7. d-ACO—ALNS Farm Removal (d-AAFR)
4.2.8. d-ACO—ALNS Worker Removal (d-AAWR)
4.3. Repair Operator
4.3.1. d-Random Farm Insert Repair (d-RFIR)
4.3.2. d-Random Workers Insert Repair (d-RWIR)
4.3.3. d-ACO—ALNS Farm Insertion (d-AAFR)
4.3.4. d-ACO—ALNS Worker Insertion (d-AAWR)
4.4. Update Heuristics Information
4.4.1. The Best Solution Update
4.4.2. Update Heuristics Information: The Destroy and Repair Method Weight Adjustment
| Algorithm 2. Procedure of the proposed algorithm |
| Input End customer demand, number customers, farm capacity, number of workers, the skill of the workers. |
| Output: Farm production planning. |
| Begins: Generated initial solution (Section 4.1). |
| While termination condition does not meet. |
| Do Select the destroy method and perform |
| Select the repair method. |
| Update heuristics information. |
| End do |
| End. |
5. Computational Framework and Result
6. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Srivarapongse, T.; Pijitbanjong, P. Solving a special case of the generalized assignment problem using the modified differential evolution algorithms: A case study in sugarcane harvesting. J. Open Innov. Technol. Mark. Complex. 2019, 5, 5. [Google Scholar] [CrossRef]
- Al-Yakoob, S.; Sherali, H. A column generation mathematical model for a teaching assistant workload assignment problem. Informatica 2017, 28, 583–608. [Google Scholar] [CrossRef]
- De Werra, D.; Asratian, A.S.; Durand, S. Complexity of some special types of timetabling problems. J. Sched. 2002, 5, 171–183. [Google Scholar] [CrossRef]
- Eikelder, H.M.; Willemen, R.J. Some complexity aspects of secondary school timetabling problems. In Practice and Theory of Automated Timetabling III; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2079, pp. 18–27. [Google Scholar]
- Even, S.; Itai, A.; Shamir, A. On the complexity of timetable and multi-commodity flow problems. Siam J. Sci. Comput. 1976, 4, 691–703. [Google Scholar] [CrossRef]
- Ross, G.T.; Soland, R.M. A branch and bound algorithm for the generalized Assignment problem. Math. Program 1975, 8, 91–103. [Google Scholar] [CrossRef]
- Fisher, M.L.; Jaikumar, R. A generalized assignment heuristic for vehicle routing. Networks 1981, 11, 109–124. [Google Scholar] [CrossRef]
- Chu, P.C.; Beasley, J.E. A genetic algorithm for the generalized assignment problem. Comput. Oper. Res. 1997, 24, 17–23. [Google Scholar] [CrossRef]
- Osorio, M.A.; Laguna, M. Logic cuts for multi-level generalized assignment problems. Eur. J. Oper. Res. 2003, 151, 238–246. [Google Scholar] [CrossRef]
- Alfares, H.K. Optimum work force scheduling under the (14,21) days-off timetable. Adv. Decis. Sci. 2002, 6, 191–199. [Google Scholar]
- Elshafei, M.; Alfares, H.K. A dynamic programming algorithm for days-off scheduling with sequence dependent labor costs. J. Sched. 2008, 11, 85–93. [Google Scholar] [CrossRef]
- Laguna, M.; Kelly, J.P.; Gonzalez Velarde, J.L.; Glover, F. Tabu search for the multilevel generalized assignment problem. Eur. J. Oper. Res. 1995, 82, 176–189. [Google Scholar] [CrossRef]
- Maenhout, B.; Vanhoucke, M. A perturbation metaheuristic for the integrated personnel shift and task re-scheduling problem. Eur. J. Oper. Res. 2018, 3, 806–823. [Google Scholar] [CrossRef]
- Aksen, D.; Kaya, O.; Salman, F.S.; Tüncel, Ö. An adaptive large neighborhood search algorithm for a selective and periodic inventory routing problem. Eur. J. Oper. Res. 2014, 239, 413–426. [Google Scholar] [CrossRef]
- Gutjahr, W.J.; Rauner, M.S. An ACO algorithm for a dynamic regional nurse scheduling problem in Austria. Comput. Oper. Res. 2007, 3, 66–642. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 4, 341–359. [Google Scholar] [CrossRef]
- Şahin, C.; Kuvvetli, Y. Differential evolution based meta-heuristic algorithm for dynamic continuous berth allocation problem. Appl. Math. Model. 2016, 40, 10679–10688. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Shaw, P. Using constraint programming and local search methods to solve vehicle routing problems. Princ. Pract. Constraint Program. 1998, 1520, 417–431. [Google Scholar]
- Toklu, N.E.; Gambardella, L.M.; Montemanni, R. A multiple ant colony system for a vehicle routing problem with time windows and uncertain travel times. J. Traff. Logis. Eng. 2014, 2, 52–58. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Mett, F.; Nardin, A.; Pulaj, J. Integrating LP-guided variable fixing with MIP heuristics in the robust design of hybrid wired-wireless FTTx access networks. Appl. Soft Comput. 2017, 61, 1074–1087. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Nardin, A. Towards the fast and robust optimal design of wireless body area networks. Appl. Soft Comput. 2015, 37, 971–982. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Montemanni, R.; Weyland, D. Coupling ant colony systems with strong local searches. Eur. J. Oper. Res. 2012, 220, 831–843. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transp. Sci. 2006, 4, 455–472. [Google Scholar] [CrossRef]
- Mancini, S. A real-life multi depot multi period vehicle routing problem with a heterogeneous fleet: Formulation and adaptive large neighborhood search based matheuristic. Transp. Res. Part. C Emerg. Technol. 2006, 70, 100–112. [Google Scholar] [CrossRef]
- Muller, L.F. An adaptive large neighborhood search algorithm for the multi-mode RCPSP. DTU Manag. Eng. 2011, 3, 25. [Google Scholar]
- Monroy-Licht, M.; Amaya, C.A.; Langevin, A. Adaptive large neighborhood search algorithm for the rural postman problem with time windows. Networks 2017, 1, 44–59. [Google Scholar] [CrossRef]
- Stenger, A.; Vigo, D.; Enz, S.; Schwind, M. An adaptive variable neighborhood search algorithm for a vehicle routing problem arising in small package shipping. Transp. Sci. 2013, 1, 64–80. [Google Scholar] [CrossRef]
- Li, J.; Pardalos, P.M.; Sun, H.; Pei, J.; Zhang, Y. Iterated local search embedded adaptive neighborhood selection approach for the multi-depot vehicle routing problem with simultaneous deliveries and pickups. Expert Syst. Appl. 2015, 7, 3551–3561. [Google Scholar] [CrossRef]
- Sze, J.F.; Salhi, S.; Wassan, N. A hybridisation of adaptive variable neighbourhood search and large neighbourhood search: Application to the vehicle routing problem. Expert Syst. Appl. 2016, 65, 383–397. [Google Scholar] [CrossRef]
- Žulj, I.; Kramer, S.; Schneider, M. A hybrid of adaptive large neighborhood search and tabu search for the order-batching problem. Eur. J. Oper. Res. 2018, 2, 653–664. [Google Scholar] [CrossRef]
- Qu, Y.; Bard, J.F. A GRASP with adaptive large neighborhood search for pickup and delivery problems with transshipment. Comput. Oper. Res. 2012, 10, 2439–2456. [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.C.; Sun, H.X.; Li, J.H. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Ma, Y.; Gong, Y.; Xiao, C.; Gao, Y.; Zhang, J. Path Planning for Autonomous Underwater Vehicles: An Ant Colony Algorithm Incorporating Alarm Pheromone. IEEE Trans. Veh. Technol. 2019, 68, 141–154. [Google Scholar] [CrossRef]
- Yang, J.; Xu, M.; Zhao, W.; Xu, B. A Multipath Routing Protocol Based on Clustering and Ant Colony Optimization for Wireless Sensor Networks. Sensors 2010, 10, 4521–4540. [Google Scholar] [CrossRef] [PubMed]
- Stutzle, T.; Hoos, H. Max-min ant system and local search for the travelling salesman problem. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC ’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 309–314. [Google Scholar]
- Lee, M.G.; Yu, K.M. Dynamic Path Planning Based on an Improved Ant Colony Optimization with Genetic Algorithm. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP 2018), Auckland, New Zealand, 5–8 August 2018. [Google Scholar]
- Zhou, Z.; Nie, Y.; Gao, M. Enhanced Ant Colony Optimization Algorithm for Global Path Planning of Mobile Robots. In Proceedings of the 2013 International Conference on Computational and Information Sciences (ICCIS 2013), Shiyan, China, 21–23 June 2013; pp. 698–701. [Google Scholar]
- Mao, L.; Liu, S.; Yu, J. An improved ant colony algorithm for mobile robot path planning. J. East. China Univ. Sci. Technol. 2006, 32, 997–1001. [Google Scholar]
- Zhao, M.; Dai, Y. Robot Three Dimensional Space Path-planning Applying the Improved Ant Colony Optimization. Telkomnika Indones. J. Electr. Eng. Comput. Sci. 2015, 14, 304–310. [Google Scholar] [CrossRef]
- Wang, L.; Kan, J.; Guo, J.; Wang, C. Improved Ant Colony Optimization for Ground Robot 3D Path Planning. In Proceedings of the 2018 International Conference on Network-based Distributed Computing and Knowledge Discovery (Cyberc 2018), Zhengzhou, China, 18–20 October 2018. [Google Scholar]
- Zhang, Y.; Niu, X. Simulation Research on Mobile Robot Path Planning Based on Ant Colony Optimization. Comput. Simul. 2011, 28, 231–234. [Google Scholar]
- Nadal-Roig, E.; Plà, L. Multiperiod planning tool for multisite pig production systems. J. Anim. Sci. 2014, 92, 4154–4160. [Google Scholar] [CrossRef]
- Nadal-Roig, E.; Plà-Aragonès, L.M.; Alonso-Ayuso, A. Production planning of supply chains in the pig industry. Comput. Electron. Agric. 2018. [Google Scholar] [CrossRef]
- Van der Vorst, J.G.; Da Silva, C.; Trienekens, J.H. Agro-Industrial Supply Chain Management: Concepts and Applications; FAO: Rome, Italy, 2007. [Google Scholar]
- Rodríguez-Sánchez, S.V.; Plà-Aragonés, L.M.; Albornoz, V.M. Modeling tactical planning decisions through a linear optimization model in sow farms. Livest. Sci. 2012, 143, 162–171. [Google Scholar] [CrossRef]
- Taylor, D.H. Strategic considerations in the development of lean agri-food supply chains: A case study of the UK pork sector. Supply Chain Manage. Int. J. 2006, 3, 271–280. [Google Scholar] [CrossRef]
- Perez, C.; Castro, R.D.; Simons, D.; Gimenez, G. Development of lean supply chains: A case study of the Catalan pork sector. Supply Chain Manag. Int. J. 2010, 15, 55–68. [Google Scholar] [CrossRef]
- Plà, L.M.; Sandars, D.L.; Higgins, A.J. A perspective on operational research prospects for agriculture. J. Oper. Res. Soc. 2014, 65, 1078–1089. [Google Scholar] [CrossRef]
- Plà, L.M. Review of mathematical models for sow herd management. Livest. Sci. 2007, 106, 107–119. [Google Scholar] [CrossRef]
- Rodríguez, S.V.; Plà, L.M.; Faulin, J. New opportunities in operations research to improve pork supply chain efficiency. Ann. Oper. Res. 2014, 219, 5–23. [Google Scholar] [CrossRef]
- Plà, L.M.; Faulín, J.; Rodríguez, S.V. A linear programming formulation of a semi-Markov model to design pig facilities. J. Oper. Res. Soc. 2009, 60, 619–625. [Google Scholar] [CrossRef]
- Huirne, R.B.M.; Dijkhuizen, A.A.; van Beek, P.; Hendriks, T.H.B. Stochastic dynamic programming to support sow replacement decisions. Eur. J. Oper Res. 1993, 67, 161–171. [Google Scholar] [CrossRef]
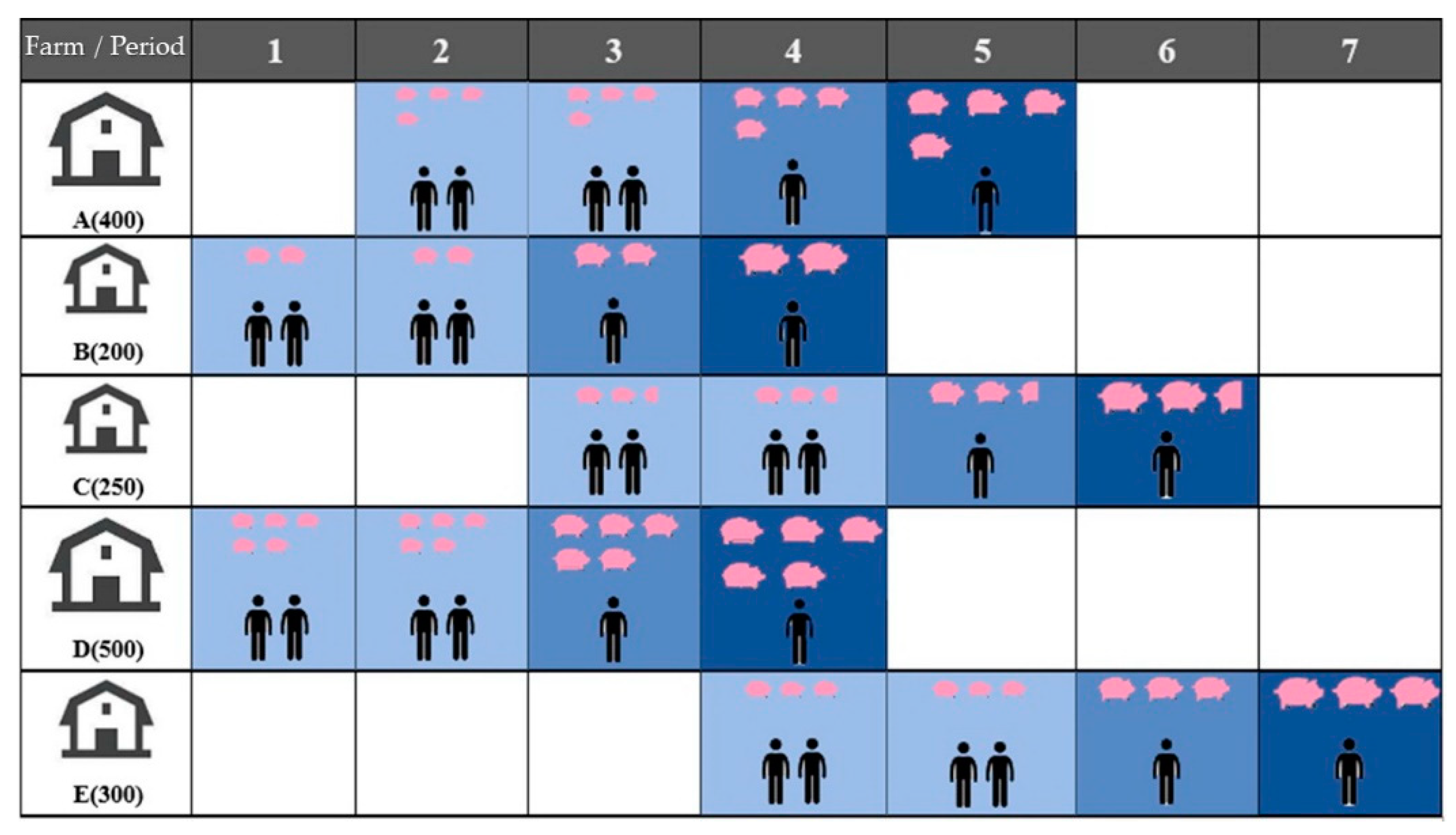
| Farm | Period | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| A (400) | 6 (400) | 6 (400) | 4 (400) | 2 (400) | ||||
| B (200) | 3 (200) | 3 (200) | 2 (200) | 1 (200) | ||||
| C (250) | 3 (200) | 3 (200) | 2 (200) | 1 | ||||
| D (500) | 3 (200) | 3 (300) | 2 (300) | 1 (300) | ||||
| E (300) | ||||||||
| #of workers | 8 | 11 | 13 | 12 | 7 | 3 | 1 | |
| Demand | (400) | (400) | (200) |
| Vector #1 Farm’s Vector | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 0.16 | 0.26 | 0.26 | 0.90 | 0.35 | 0.78 | 0.94 | 0.74 | ||||
| Vector #2 Worker’s Vector | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0.59 | 0.61 | 0.98 | 0.25 | 0.14 | 0.64 | 0.15 | 0.85 | 0.34 | 0.91 | 0.42 | 0.18 |
| Vector #1 Farm’s Vector | |||||||||||
| 1 | 2 | 3 | 5 | 8 | 6 | 4 | 7 | ||||
| 0.16 | 0.26 | 0.26 | 0.35 | 0.74 | 0.78 | 0.9 | 0.94 | ||||
| Vector #2 Worker’s Vector | |||||||||||
| 5 | 7 | 12 | 4 | 9 | 11 | 1 | 2 | 6 | 8 | 10 | 3 |
| 0.14 | 0.15 | 0.18 | 0.25 | 0.34 | 0.42 | 0.59 | 0.61 | 0.64 | 0.85 | 0.91 | 0.98 |
| Period | 1 | 2 | 3 |
|---|---|---|---|
| Farm | 1, 2, 3 | 5, 8 | 6, 4, 7 |
| 400, 500, 100 | 600, 150 | 620, 130 | |
| Total production | 1000 | 150 | 750 |
| Workers | 4 (5, 7, 12, 4) Sum exp. = 5.35 | 7 (5, 7, 12, 4, 9, 1) Sum exp. = 7.9 | 7 (5, 7, 12, 4, 9, 11) Sum exp. = 7.9 |
| demand | 1000 | 1000 | 700 |
| Destroy Method | Possible Repair Method | Destroy Method | Possible Repair Method |
|---|---|---|---|
| d-RRF | d-RFIR d-AAFR | d-RFR | d-RFIR d-AAFR |
| d-RRW | d-RWIR d-AAWR | d-RWR | d-RWIR d-AAWR |
| d-WFR | d-RFIR d-AAFR | d-AAFR | d-RFIR d-AAFR |
| d-WWR | d-RWIR d-AAWR | d-AAWR | d-RWIR d-AAWR |
| Value | Description | |
|---|---|---|
| 4 | When destroy/repair method q to find new global optimal | |
| 3 | When destroy/repair method q to generate Z(S’) that is better than Z(S) | |
| 2 | When destroy/repair method q to generate Z(S’) that is not better than Z(S) but the solution is accepted from using the formula in Section 4.4.1 | |
| 1 | When destroy/repair method q to generate Z(S’) that is not better than Z(S) |
| Size of Problem | Number of Farms | Number of Workers | Planning Horizon | Stopping Criteria |
|---|---|---|---|---|
| Small(S-1) | 4 | 80 | 2 | * |
| Small (S-2) | 4 | 90 | 2 | * |
| Small (S-3) | 7 | 90 | 2 | * |
| Small (S-4) | 7 | 100 | 2 | * |
| Small (S-5) | 8 | 100 | 2 | * |
| Medium (M-1) | 14 | 200 | 4 | * |
| Medium (M-2) | 14 | 220 | 4 | & |
| Medium (M-3) | 18 | 220 | 4 | & |
| Medium (M-4) | 18 | 240 | 4 | & |
| Medium (M-5) | 20 | 240 | 4 | & |
| Large (L-1) | 40 | 320 | 8 | & |
| Large (L-2) | 40 | 360 | 8 | & |
| Large (L-3) | 48 | 360 | 8 | & |
| Large (L-4) | 48 | 400 | 8 | & |
| Large (L-5) | 52 | 400 | 8 | & |
| Case study | 37 | 320 | 8 | & |
| Algorithms | Definition of the Proposed Heuristics |
|---|---|
| ALNS-1 | Using acceptance Formula (24) |
| ALNS-2 | Using acceptance Formula (25) |
| ALNS-3 | Using acceptance Formula (26) |
| ALNS-4 | Using acceptance Formula (27) |
| ALNS-5 | ALNS-1-without ACO |
| ALNS-6 | ALNS-2-without ACO |
| ALNS-7 | ALNS-3-without ACO |
| ALNS-8 | ALNS-4-without ACO |
| #No | Lingo v.11 | Computational Time | ||||
|---|---|---|---|---|---|---|
| Profit | Time | ALNS-1 | ALNS-2 | ALNS-3 | ALNS-4 | |
| S-1 | 2,584,951 | 9.45 | 5.08 | 4.93 | 7.40 | 7.41 |
| S-2 | 2,611,949 | 15.87 | 10.37 | 10.15 | 10.52 | 10.38 |
| S-3 | 2,638,980 | 28.08 | 8.12 | 7.86 | 5.44 | 10.19 |
| S-4 | 2,642,952 | 28.56 | 8.62 | 10.97 | 8.72 | 8.66 |
| S-5 | 2,645,992 | 30.5 | 11.24 | 5.73 | 8.77 | 5.82 |
| Average- | 22.492 | 8.686 | 7.928 | 8.17 | 8.492 | |
| %diff Opt. | 61.3 | 64.7 | 63.7 | 62.2 | ||
| #No | Lingo V.11 | Computational Time | ALNS-1 | ALNS-2 | ALNS-3 | ALNS-4 |
|---|---|---|---|---|---|---|
| Profit | 60 m | 60 | 60 | 60 | ||
| Upper Bound | Profit | Profit | Profit | Profit | ||
| M-1 | 10,807,920 | 480 | 10,789,954 | 10,807,920 | 10,798,920 | 10,798,920 |
| M-2 | 10,987,275 | 480 | 10,807,920 | 10,880,920 | 10,825,920 | 10,864,920 |
| M-3 | 10,934,581 | 480 | 10,825,920 | 10,898,984 | 10,869,945 | 10,899,683 |
| M-4 | 10,944,129 | 480 | 10,807,920 | 10,838,989 | 10,876,953 | 10,884,931 |
| M-5 | 10,925,920 | 480 | 10,825,976 | 10,847,956 | 10,865,978 | 10,875,999 |
| L-1 | 33,239,045 | 620 | 32,720,760 | 32,765,902 | 32,893,458 | 32,994,514 |
| L-2 | 33,182,125 | 620 | 32,809,450 | 32,923,891 | 32,991,768 | 33,018,913 |
| L-3 | 32,998,282 | 620 | 32,873,768 | 32,883,778 | 32,890,123 | 32,993,459 |
| L-4 | 33,289,197 | 620 | 32,998,192 | 33,001,209 | 33,098,412 | 33,198,138 |
| L-5 | 33,208,592 | 620 | 32,988,123 | 32,998,156 | 33,009,134 | 33,114,595 |
| Case study | 32,887,185 | 620 | 32,693,760 | 32,676,748 | 32,779,093 | 32,810,945 |
| % diff UB | 0.92 | 0.72 | 0.67 | 0.48 | ||
| ALNS-1 | ALNS-2 | ALNS-3 | ALNS-4 | |
|---|---|---|---|---|
| Obj.bound | 0.0004 | 0.00064 | 0.00044 | 0.00194 |
| ALNS-1 | 0.0134 | 0.0028 | 0.00112 | |
| ALNS-2 | 0.0784 | 0.0096 | ||
| ALNS-3 | 0.0037 |
| #No | % diff P | |||
|---|---|---|---|---|
| ALNS-1 vs. ALNS-5 | ALNS-2 vs. ALNS-6 | ALNS-3 vs. ALNS-7 | ALNS-4 vs. ALNS-8 | |
| M-1 | 0.00 | 0.00 | 0.00 | 0.00 |
| M-2 | 0.00 | 0.00 | 0.00 | 0.00 |
| M-3 | 0.00 | 0.00 | 0.00 | 0.00 |
| M-4 | 0.00 | 0.00 | 0.00 | 0.00 |
| M-5 | 0.00 | 0.00 | 0.00 | 0.00 |
| L-1 | 1.08 | 1.01 | 1.20 | 1.01 |
| L-2 | 2.02 | 2.60 | 2.09 | 2.34 |
| L-3 | 2.10 | 2.53 | 2.12 | 2.33 |
| L-4 | 2.04 | 1.29 | 1.27 | 1.25 |
| L-5 | 2.00 | 2.16 | 2.09 | 2.09 |
| Case study | 1.60 | 1.82 | 1.81 | 2.32 |
| average | 0.985455 | 1.037273 | 0.961818 | 1.030909 |
| Type of Method | Proposed Method | |||
|---|---|---|---|---|
| defender | ALNS-1 | ALNS-2 | ALNS-3 | ALNS-4 |
| Challenger | ALNS-5 | ALNS-6 | ALNS-7 | ALNS-8 |
| p-value | 0.00388 | 0.00388 | 0.00388 | 0.00388 |
| #Farm | Period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Q | Cap |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 500 | 500 | ||||||||
| 2 | 1500 | 1500 | 1500 | ||||||||
| 3 | 500 | 500 | 500 | ||||||||
| 4 | 1500 | 1500 | 1500 | ||||||||
| 5 | 1400 | 1400 | 1400 | ||||||||
| 6 | 1000 | 1000 | 1000 | ||||||||
| 7 | 900 | 900 | 900 | ||||||||
| 8 | 0 | 1500 | |||||||||
| 9 | 1400 | 1400 | 1500 | ||||||||
| 10 | 1000 | 1000 | 1000 | ||||||||
| 11 | 1000 | 1000 | 1000 | ||||||||
| 12 | 1300 | 1300 | 1400 | ||||||||
| 13 | 1200 | 1200 | 1300 | ||||||||
| 14 | 1000 | 1000 | 1200 | ||||||||
| 15 | 500 | 500 | 500 | ||||||||
| 16 | 1000 | 1000 | 1200 | ||||||||
| 17 | 650 | 650 | 650 | ||||||||
| 18 | 0 | 1500 | |||||||||
| 19 | 1000 | 1000 | 1000 | ||||||||
| 20 | 1100 | 1100 | 1100 | ||||||||
| 21 | 1300 | 1300 | 1300 | ||||||||
| 22 | 1000 | 1000 | 1000 | ||||||||
| 23 | 1000 | 1000 | 1000 | ||||||||
| 24 | 1300 | 1300 | 1500 | ||||||||
| 25 | 500 | 500 | 500 | ||||||||
| 26 | 500 | 500 | 500 | ||||||||
| 27 | 650 | 650 | 650 | ||||||||
| 28 | 1300 | 1300 | 1500 | ||||||||
| 29 | 800 | 800 | 1000 | ||||||||
| 30 | 1500 | 1500 | 1500 | ||||||||
| 31 | 1200 | 1200 | 1350 | ||||||||
| 32 | 1400 | 1400 | 1400 | ||||||||
| 33 | 800 | 800 | 1000 | ||||||||
| 34 | 0 | 500 | |||||||||
| 35 | 500 | 500 | 500 | ||||||||
| 36 | 0 | 1000 | |||||||||
| 37 | 800 | 800 | 1500 | ||||||||
| 5200 | 5000 | 3950 | 3300 | 4400 | 3250 | 4500 | 3500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praseeratasang, N.; Pitakaso, R.; Sethanan, K.; Kaewman, S.; Golinska-Dawson, P. Adaptive Large Neighborhood Search for a Production Planning Problem Arising in Pig Farming. J. Open Innov. Technol. Mark. Complex. 2019, 5, 26. https://doi.org/10.3390/joitmc5020026
Praseeratasang N, Pitakaso R, Sethanan K, Kaewman S, Golinska-Dawson P. Adaptive Large Neighborhood Search for a Production Planning Problem Arising in Pig Farming. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(2):26. https://doi.org/10.3390/joitmc5020026
Chicago/Turabian StylePraseeratasang, Nat, Rapeepan Pitakaso, Kanchana Sethanan, Sasitorn Kaewman, and Paulina Golinska-Dawson. 2019. "Adaptive Large Neighborhood Search for a Production Planning Problem Arising in Pig Farming" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 2: 26. https://doi.org/10.3390/joitmc5020026
APA StylePraseeratasang, N., Pitakaso, R., Sethanan, K., Kaewman, S., & Golinska-Dawson, P. (2019). Adaptive Large Neighborhood Search for a Production Planning Problem Arising in Pig Farming. Journal of Open Innovation: Technology, Market, and Complexity, 5(2), 26. https://doi.org/10.3390/joitmc5020026






