1. Introduction
The impact Elliptic Curve Cryptography (ECC) has made as an approach to Public-Key Cryptography is profound, mainly by offering various digital signature, key agreement and certificate schemes. These solutions have been deployed in a wide variety of applications, which range from high-performance computing systems to low-end IoT and embedded devices.
A goal when developing an implementation of this kind should be a flexible and adaptable solution. In practice, this means that alongside high computational performance, efficient resource management is essential in cases where the execution environments might be resource constrained. By exploiting this approach, the suitable hardware-accelerated operations should be selected with the premise that they can provide the best trade-off between performance improvements and flexibility. In the majority of ECC-based implementations [
1,
2,
3], the main computational barrier is related to the scalar multiplication operation, mainly realized through a series of point addition and point doubling operations. This fact makes it an ideal point of interest for optimization improvements in most ECC-based implementations, especially those targeted towards embedded systems. Literature confirms this fact, with extensive studies focusing on the optimization of the EC scalar multiplication and its arithmetic operations on Finite Fields in terms of speed, resources and power consumption improvements [
4,
5].
Despite the obvious aspects of flexibility and performance enhancement that need to be addressed during the design phase, another crucial consideration should be made in regard to the multiplier’s Side Channel attack (SCA) resistance. As a side channel attack, we define the attempt of an adversary to extract sensitive information during an algorithmic execution. This information can be accessed through the implementation’s side channels (power consumption, electromagnetic radiation, timing characteristics, etc.) and through extensive statistical analysis it can potentially reveal the hidden secret. Thus, the need for resistance against these attacks has been addressed in literature [
6,
7], denoting the wide range of side channel attacks that can be executed on these multiplier implementations. Both the aspects of performance enhancements and side channel attack resistance are in direct influence of the adopted scalar multiplication algorithm and the overall multiplier architecture.
The most powerful form of side channel attacks have traditionally been Template Attacks, proposed in [
8]. They belong in the family of profiling side channel attacks, in which a profile for a given device/cryptographic primitive is generated, mapping the behavior during the execution of the primitive. This process, however, requires the use of a system identical with the device under attack, in order to capture the target’s execution behavior (EM or Power Analysis) and generate the profile. In recent research efforts, there has been a shift towards performing machine learning and neural-network based analysis, since the essence of this type of attack is the profiling of the device under attack [
9,
10]. This attempt has been mainly focused on implementations of symmetric cryptography (DES, AES) and RSA when referring to public-key cryptography. Regarding Elliptic Curve Cryptography (ECC), there are works evaluating popular machine learning classification algorithms [
11], with the trend being the further use of Deep Learning techniques.
Being motivated by the above, this paper initially describes the SCA landscape for Elliptic Curve cryptography, and the potential of profiling attacks such as TA and ML-based SCAs is highlighted. Using the formulation of the above description, the paper offers the following contributions on the topic:
A scalar multiplier design strategy is proposed; the fine-graining of decomposition operations in the SM computations enables the introduction of SCA countermeasures that are hard to bypass for an attacker. Given that the MPL Scalar multiplication algorithm’s EC point operations (point addition and doubling) in each round can be parallelized, we decompose them into their underlying finite field operations and propose their merging in a unified SM round computation flow with parallel stages. In each of those stages, SCA countermeasures can be introduced.
An example use case of a scalar multiplier for a Binary Extension field is provided, so as to showcase the practicality of the design approach. In addition, in line with the proposed design strategy, an advanced side channel attack resistance enhancement roadmap is provided. This enhancement relies on the re-randomization of the point operation projective coordinates results in each MPL round. This is achievable by performing a finite field multiplication of each round’s generated coordinates with a unique per-round random number.
We describe a simple ML SCA roadmap showing how to attack the proposed use-case implementation (that follows the paper’s design strategy and SCA countermeasure proposal) using simple ML algorithms that require small/medium sized number of leakage traces. The mounted attacks employ three ML models (Random Forest, SVM and MLP algorithms). We demonstrate actual simple ML-based SCAs mounted on two use case SM implementations, an unprotected one (GF operation MPL parallelism exploitation with no projective coordinate randomization) and a protected one (GF operation MPL parallelism exploitation with projective coordinate randomization), and we validate the resistance of the proposed design approach (with SCA countermeasures) as this is applied in the use case BEC scalar multiplier. The results show that the protected implementation is highly resistant against simple ML-based SCAs using any of the three modeling approaches.
The rest of the paper is organized as follows.
Section 2 briefly describes the underlying mathematical foundation of ECC;
Section 3 presents an overview of SCA on Elliptic Curve Cryptography and possible countermeasures;
Section 4 describes the proposed fine-grained GF unification model and design strategy, as well as its expansion to support SCA countermeasures on the MPL architecture;
Section 5 describes the machine learning algorithms applied in this work;
Section 6 analyzes the experimental process that was followed and
Section 7 discusses the outcome of the analysis executed on the impact of countermeasures.
Section 8 concludes the work.
3. ECC Side Channel Attacks and Countermeasures
Scalar Multiplication (SM) constitutes the main attack point of SCAs in Elliptic Curve Cryptography algorithms since the involved operations have a strong correlation with the secret scalar. The types of SCA attacks on SM that exist today can vary between simple or advanced on one hand and vertical or horizontal on the other, as seen in [
17,
18,
19]. For the collection of the leakage traces/observations
to be realized in the vertical method, sets of same or different inputs are utilized at each time
t (
) in the SM implementation within the total
p times. Each observation is associated with the
execution of the implementation for an operation
i. For the horizontal procedure, just a single execution is sufficient to capture the leakage traces of the unit under attack. In this case, a distinct time period is represented by each collected trace during the time frame of the execution [
17].
If the double-and-add algorithmic option is followed in SM, the probability of simple SCAs being deployed in the implementation is increased substantially. These attacks are usually horizontal in nature, able to be mounted by only a distinct leakage trace. A straightforward counter against these type of SCAs is the utilization of SM algorithms that are highly regular, i.e., the scalar bit that is being processed in each round does not appear to have a link to the round’s operations (e.g., MPL or Double and Always Add) [
16]. Nevertheless, there exist some SCAs that have the ability to thwart this regularity, mainly by altering the EC base point used as an input of the SM [
20]. For this objective, Comparative SCAs were introduced (initially based on Power Attacks but adapted to Electromagnetic Emission attacks as well). In such attacks the adversary is able to control the SM input, provide a few inputs (usually two) that are arithmetically related (e.g., Point
P and
), collect the SM leakage traces and compare them using some statistical tool. Most widely known such attacks that manage to defeat many regular/balanced SM algorithms are the doubling attack (collision based attack) [
21] (DA) and its variant, the relative doubling attack (RDA) [
22], or the chosen plaintext attack in [
23] (also known as the 2-Torsion Attack (2-TorA) for ECC). The above comparative attacks can be further refined by using special input points as is the case in Zero PA (ZPA) or Refined PA (RPA). In the former, an exceptional EC point
(which can induce a zero
P coordinate at round
i) is loaded to the implementation, thus allowing scalar bit recovery by exploiting the vulnerability at the
ith round.
Besides the attacks already mentioned, there exist other advanced SCAs that can be executed with either one or many collected leakage traces on EC SM. One of the most dominant types in this category are the Differential Side Channel Attacks (DSCAs), initially introduced by Kocher in [
24], that depend on power consumption characteristics. DSCAs follow the hypothesis test principle [
18,
25], where a series of hypotheses
on the secret
e (or part of the secret, for example some bit of the scalar
e) are made for many
p inputs
, where
are used in some leaky internal operation of the algorithm along with some other known values (derived from each
, e.g., the plaintext or the ciphertext). The hypothetical result leakage is then estimated using some prediction model. The predicted leakages (for all predictions and all inputs
) are compared against all real leakage traces by using a suitable distinguisher
for all inputs
, in order to choose which hypotheses are correct. There are various distinguishers that have been used in literature, leading to sophisticated DSCAs. Most notably, the Correlation SCA demands less traces in order to recover a secret value when compared to the DSCA [
26], and the Collision Correlation Attack [
27,
28,
29] has the ability to be executed even if an adversary is unable to freely influence the inputs that the SM implementation demands [
17]. Apart from vertical attacks, there is a broad range of horizontal advanced SCAs exploiting the fact that each
operation, when performed in off-the-shelf hardware, is partitioned into a succession of simpler operations (e.g., word-based field multiplications) that are all related to the scalar bit. In this case, a process similar to a vertical differential SCA is mounted using leakage partitions from a single trace. Attacks such as these are the Horizontal Correlation Analysis attack (HCA) [
30], the Big Mac Attack [
31], or the Horizontal Collision Correlation Attack (HCCA) [
18,
19].
Advanced SCAs can follow various leakage models and may take many forms [
32], but in general they fit the above description that assumes a leakage
from an intermediate computation
at round
i of the SM algorithm can be modeled by taking into account the computational and storage leakage
under the presence of noise, as shown in the following equation:
where
is noise intrinsically associated with the device being tested and is independent of
. In the above equation,
t corresponds to the time variable within the timeslot that
is active.
Traditionally, countermeasures can fit into two different classes, leakage masking and leakage hiding [
1,
14]. When applying the hiding method, suitable logic is included in the computation flow of the SM in order to make the leakage of the device independent from both the operations executed and their intermediate values. This can be achieved either by implementing cryptographic algorithms in such a way that the power consumption is random, or by implementing cryptographic operations that consume an equal amount of power for all operations and for all data values [
14]. In practice, information hiding is realized by the implementation of suitable circuits that can add noise to the monitored side channel. These mainly include components that offer power scrambling redundancy or power consumption balancing (dual rail). A similar outcome can be achieved in the algorithmic level of the EC SM by introducing dummy calculations, or by modifying the algorithm so that
appears similar to
(where
is a different SM intermediate operation) for all
t within a given timeslot that each one of the operations are active. The MPL algorithm, in conjunction with the nature of BECs, offers great conditions for developing such countermeasures. On one hand, a designer is able to parallelize multiple operations in the time domain with the help of the MPL; on the other, BECs further contribute to the aforementioned hiding procedure with their completeness and uniformity. Many realizations of the above SCA protection approach cannot effectively thwart some Advanced SCAs or, in addition, some Comparative SCAs, including the Doubling Attack (DA) group, i.e., normal and Relative (RDA) [
21,
22].
The goal of masking is the decoupling of sensitive data from their corresponding leakage trace. Crucial for this method is the existence of some randomization technique (multiplicative or additive) upon the secret information that has a sensitivity to leakage
[
20]. Three well-established EC SM masking techniques have been used in practice (appearing in several variations), originally proposed by Coron in [
33]. The values that are the targets of randomization by those countermeasures are the EC input point
P (i.e., base point blinding), the projective coordinates in the
domain of the same point and the EC scalar vector (Algorithm 1
e) of the SM. These mentioned randomization methods have been extended in ECC with several forms after their introduction in literature. In terms of applicability, though, the two latter ones (projective coordinate and scalar blinding) are easier to implement. This is due to the fact that the first described method, point blinding technique, demands the inclusion and storage overhead of an additional random point that is generated in every multiplication round, which introduces additional complexity [
34].
Profiling Attacks
The above existing SCA research (especially univariate Differential SCAs) creates momentum for the description of a generic DSCA mechanism that will be able to utilize a generic-compatible distinguisher that uses a generic leakage model on a generic device for which no information is provided. However, such a generic case is not realistic, as analyzed in [
35], and it is concluded that existing DSCAs (with a specific distinguisher, model and insight on the device under test and the implemented SM algorithm) may be less effective than anticipated. Whitnall et al. [
35] indicate that another type of SCA can be considerably more potent than DSCAs, i.e., profiling attacks. The most widely used profiling attack is the template attack (TA); it requires two identical devices, which we refer to as the profiling and the attacked device. In the profiling device, a profiling phase occurs, where the attacker identifies the operation that produces information leakage (
) and provides as input to the device all possible values (ideally) of a secret value portion (e.g., one byte or one bit) that influences
. This will produce all possible different states of this operation for which the attacker collects the leakage
. During the profiling phase of a TA on SM, the scalar bit can act as the TA input, and the point addition or point doubling operation values associated with the scalar bit value can act as
. The collected traces, along with the associated input values are used, in order to estimate a leakage model (by calculating the parameters of a leakage Probability Density Function (PDF)) which is considered the TA’s template (or profile in general). In the second TA phase (attack phase), an attacker uses an attacked device with an unknown secret (i.e., secret scalar) and collects leakage traces of
for various inputs
t using the same trace-collection mechanism and parameters as in the previous case. Using some discriminator, the attacker tries to identify from the template an appropriate leakage trace that has the highest probability of matching the unknown secret leakages, and then retrieves the secret in the template associated with the selected leakage trace. The attack exists in several variations [
36,
37], with various PDF estimators and even in online form (Online TA) where the profile is created during the collection of the traces on the device under attack [
38].
The concept of creating a leakage model based on labeled leakage traces has been further researched in academia by adopting Machine Learning (ML) techniques in order to create an ML-produced leakage model. With ML, an adversary does not need to create a perfect leakage model (using all possible inputs of a secret value block) but instead allows an ML model to be built with a non-exhaustive series of leakage traces (that can only be corresponded to specific, instead of all, secret block values). As the leakage becomes more noisy (either due to the hiding or the masking countermeasures implemented), more accurate results can be extracted by applying an approach based on ML profiling [
9,
10,
20].
The analysis carried out above leads us to the conclusion that an SM implementation cannot be considered secure if it does not incorporate methods to protect against a varied range of SCAs. As several researchers point out [
36,
38,
39], Profiling SCAs can overcome several of the existing countermeasures. Thus, the necessity of a more advanced randomization implementation is highlighted for the entirety of the computation flow during an SM.
4. Proposed SCA Countermeatures on MPL
The analysis in the previous section indicates that the MPL SM algorithm is not sufficient to thwart many of the existing Advanced SCAs, including the formidable profiling attacks. Thus, SM MPL should be infused with advanced countermeasures based on masking and/or hiding (using randomization). However, MPL has some interesting features that can be exploited in order to make ASCAs difficult. These features stem from the regularity of each SM round. Each MPL round always performs point addition and doubling. Moreover, the order of execution of these operations within an SM round is not important so the two operations can be performed in parallel. Given the fact that most of the SM SCAs focus on the leakage of a single point operation (usually point doubling), merging point doubling with point addition by performing them in parallel can potentially make an attacker’s work harder. In fact, this parallelism approach forces the attacker to change the leakage observation operation from point addition or doubling to one full MPL round. Given that the leakage of each point operation has an associated intrinsic noise level, the leakage of two combined operations will potentially increase this integrated noise. The identification of each one of point operations is, thus, very hard to pinpoint, making attacks harder to mount. So, assuming that
is the point addition operation and
is the doubling operation in a single MPL round, the MPL round leakage for a certain round
i would be
. For the sake of simplicity, we can exclude, from this point onwards, the parameter of time in the above equation, assuming a constant time slot
T for each MPL round and considering the leakage at an MPL round instead of a single time instance within the round. In addition, note that
and
correspond to the noise associated with point addition and point doubling, respectively. Unfortunately,
could potentially have non-trivial information leakage of the SM secret value (i.e., the scalar bit on a given SM MPL round) on a single
or
. The issue can be mitigated by a design approach that more deeply fuses
and
, i.e., on the EC underlying Finite Field operation level.In textbook point addition and doubling design and implementation, EC points are represented in the projective space (EC point projective coordinate), and
or
can be partitioned into many finite field multiplications and additions/subtractions that need to be executed in discrete time instances within the MPL round execution time slot
T. The
and
operations that are performed in parallel within the MPL round could be considered a unified round operation, with inputs and outputs that can be point addition and point doubling coordinate results. This unified round operation can then be fine-grained into a complex sequence of finite field operations that will collectively contribute to the point addition and point doubling result of an MPL round. These GF operations can be synchronized with the time units of the MPL round’s time slot
T, based on their data dependence and the capabilities of the underlying computing device. The latter constraint concerns the number of GF operations that can be performed in parallel on a given hardware architecture which has a finite number of operating units (finite field multipliers and adders/subtractors) within the SM architectural design (the typical case in hardware SM implementation and some software ones).To identify which GF operations can be performed in parallel in a given time slot of
T, a Data Flow Graph analysis of the GF multiplication and addition sequence is realized. This analysis is performed for a single unified MPL round computation while also assuming a specific finite number of parallel processing units (for finite field multiplication and addition) exist. Such analysis can reveal that the computation can be partitioned into
z parallel stages (corresponding to a single time slot of
T) where each stage performs
p concurrent GF operations while processing for both
and
. Assuming that the
GF operation within the
parallel-processing stage is denoted by
, leakage
(the leakage within round
i for the time
of the
jth parallel stage) becomes:
where
corresponds to the noise that exists during the computation of leakage round
i for the time
of the
jth parallel stage. This noise is related to both point addition and doubling computations. Thus, the overall leakage of a single
ith MPL round, where
and
are merged into unified computations and decomposed into GF operations in each time point
for all
j values inside
T, will be the following:
From the above equation and relevant analysis, it can be remarked that the MPL SM round computation has now been shifted from a processing model closely related to the scalar bit operation (related to or ) to a processing model of regularly executed autonomous, unified stages of parallel operations that are associated with both or , and loosely relate the the scalar bit at round i. Using the proposed fine-grained GF unification stages approach, the and are processed in a unified way.
Without any additional countermeasure, in general, the BEC MPL implementations suffer from MPL’s lack of resistance against Advanced SCAs (ASCAs), including Differential SCAs, Correlation SCAs, etc. [
1], but–most importantly–against Profiling Attacks [
7,
39]. The inclusion of the fine-grained GF unification stages approach could potentially reduce the MPL leakage. However, t-test leakage assessment results performed in [
34], where a similar approach is used, reveal that there is still enough leakage associated with the base point and the secret scalar to reveal the secret. This is an expected result, since
does not model only the computation leakage during a single parallel stage, but also the intermediate values’ storage leakage at this stage. Specifically, for power consumption side channels where dynamic power consumption is leaking information, the register storage operations form a distinct leakage pattern for scalar bit
or
when all
are included. However, no actual attack is performed in [
34] to show if this leakage can be exploited, especially for potent Profiling SCAs. The aforementioned fine-grained GF unification stages approach, as modeled in Equations (
3) and (
4), relies on the intrinsic scrabbling of the implementation parallelism to hide the leaked information. To enhance this information hiding with masking, an additional source of randomness can be introduced in the computation process of each MPL round
i. This can be achieved by including some random computation in some of the
operations included in a parallel stage.
For the sake of efficiency, it suffices to include random operations within only a few parallel stages of each MPL round and to let the randomness propagate to the remaining stages. The choice one needs to make in order to identify the best-possible stage to add the random operation is dependent on three parameters. The first parameter is the available parallel computation units that the implementation can support (e.g., the number of parallel finite field multipliers and adders). Secondly, the number of units that are in an idle stage (i.e., awaiting correct inputs from another computation) and lastly, the data dependency that exists between the different parallel stages in the executed MPL round. Furthermore, the inclusion of random operations in some parallel stages should not lead to a false computation result of the MPL round. In some cases, the same outcome can be achieved by including additional parallel stages, so that the randomly injected information per round is handled correctly.
The above masking mechanism can be realized by appropriately adapting existing randomization techniques in the research literature. Coron’s countermeasures [
33] constitute the basis of many algorithmic SCA-resistance solutions. Among them, projective coordinates randomization may be the most easy to deploy (and simultaneously one of the most efficient to deploy). In this approach, the input point
is randomized by multiplying its coordinates with a randomly generated number
h, thus, forming
. At first glance, this point seems to be a different one than the original, when viewed in projective coordinates; however, in reality it is the same point in affine coordinates. Coordinate randomization is applied once in the MPL. Before the first round of the algorithm, however, this approach provides no protection against RPAs. Adopting and adapting the coordinate randomization countermeasure to the proposed fine-grained GF unification stages mechanism and enhancing its potency, we propose the inclusion, in some parallel stages of each MPL round’s
i, a different multiplicative randomization of all the round’s projective coordinate point outcomes (both point addition and doubling results), using a round’s random number
.
Instantiating the Complete SCA Resistance Mechanism Based on the Proposed Approach
The above proposed SCA resistance approach can be instantiated both in hardware and software implementations that support parallelism in their computation flow. It is expected that the application of the proposed approach in software implementations that have high level of device noise (
) due to parallel processing of unrelated processes (e.g., Operating System functions), will considerably increase the noise level. Such noise, in combination with the proposed added random operations per parallel computation stage, will make the Signal-to-Noise (SNR) ratio significant enough to make SCAs difficult to mount [
39]. In hardware implementations though, where the noise is only related to the ASIC or FPGA chip’s hardware resources, the impact of noise is small, and SCA resistance relies mostly on the potency of the proposed solution. For the above reason, in the remainder of the paper, the analysis is focused on hardware implementations of the proposed SCA resistance mechanism in BEC ECCs.The explicit formulas for point addition and point doubling that are defined in [
13] can be decomposed into the single
operations presented in
Table 1. Based on those operations, a possible realization of the proposed fine-grained GF unification stages technique can be presented in
Table 2 [
34]. In this table, each row corresponds to a parallelism stage; thus, one MPL round is concluded in 13 stages (
). In the last two stages of the MPL round
i, random operations have been included (marked in the table with a different cell color). In these operations, the projective coordinates of all output BEC points are multiplicatively randomized using a unique random value
in each round (each coordinate is multiplied with
). The hardware design adopts the hardware architecture described in [
34]. Each parallelism stage in the hardware architecture includes three finite field multipliers (M1 to M3) and three adders (Ad1 to Ad3) that can operate in parallel.
In
Table 2, it is revealed that the parallel operations of each stage that appears in
Table 1 for an MPL round, are associated with both point operation (addition or doubling) in this round. Moreover, two extra stages have been introduced in the table in line with the leakage model of Equation (
3) (no random operations in parallel stages). Those stages (marked in blue in the table) add SCA resistance following the hiding resistance approach. This hiding countermeasure introduces a timing and computing overhead of approximately 7.69%, which can be considered a satisfactory trade-off. Despite the fact that for all
z stages the processing that occurs in each round has high regularity in regards to the scalar bit value, the storage leakage footprint might be different depending on the scalar bit. This can be observed from Algorithm 1 steps 2a or 2b, where the point addition and point doubling results are stored in R1 and R0, respectively, for
and in R0 and R1, respectively, for
. This storage in different registers, which is related to
, is not masked/hidden when the proposed fine-grained GF unification stages approach is adopted without the random operations in each parallel stage, which hide the values stored in the implementations’ registers. Despite the fact that this information might not be exploitable in traditional SCAs/ASCAs, it may provide significant benefit in profiling attacks where the attacker has the ability to create a concrete profile of the device. In the following sections, we perform analytic practical evaluation of the proposed SCA countermeasure as is implemented in a BEC scalar multiplier, following the computation flow of
Table 2. The analysis is focused on simple ML-based SCAs that do not require a huge number of leakage traces for training and validation.
6. Experimental Process
The evaluation process requires the collection of a series of traces. The collection of the required traces was achieved in a controlled environment as previously described in [
34]. The SAKURA-X board [
45], featuring a Kintex-7 cryptographic FPGA chip, is regarded as a widely used tool for its low-noise trace collection characteristics. The trace collection mechanism described and implemented in [
46] has been utilized for leakage trace sampling, irregardless of the underlying executed implementation (AES, ECC, etc.). Thus, in our process it was used as the control loop of the conducted leakage assessment mechanism, enabling the collection of waveforms for the two versions (protected and unprotected). In order to capture the generated traces, a PicoScope 5000D Series Oscilloscope with a sampling rate of 1 GS/s was connected through a pre-amplifier to a resistor onboard the SAKURA-X, in order to measure the power consumption.
6.1. Sample Trace Formation
In contrast to the approach used in [
34], each collected trace, which corresponds to a full scalar multiplier, is split into trace blocks, each of them representing a Scalar Multiplication round for a known random scalar bit. Given the clear visual pattern of each round (as it can be seen in [
34]) in the collected traces, we were able to accurately identify the timeslot
T corresponding to a single SM round. Given that each round in the MPL algorithm takes constant time, each collected trace was divided into
n timeslots
T, where
n is the number of MPL rounds or, in other words, the number of scalar bits. Moreover, given that each round performs the necessary processing for a single scalar bit, and also given that in the trace-collection process known scalars were used, each trace block (corresponding to a single round for a known scalar bit) was labeled as a processing of ‘0’ or ‘1’, respectively. Using this splitting strategy for the traces, with each block representing a single bit, we were able to quickly and efficiently collect a vast amount of samples without wasting a lot of time. The above process constitutes the profiling phase, where the attacker has full access on the device and is operating using a known secret scalar
e.
Figure 2 and Figure 4 show the waveforms captured during the execution of one round in the unprotected SM implementation, labeled as processing of scalar bit ‘0’ or ‘1’, respectively. Likewise,
Figure 3 and Figure 5 show the waveforms for a single round in the protected SM version of the accelerator, with the randomization countermeasure rounds shown in detail. Note that there are 11 clearly visible patterns in
Figure 2 and
Figure 4 corresponding to the 11 stages of
Table 2’s unprotected approach. Similarly, in
Figure 3 and
Figure 5, there are 13 patterns that indicate the stages of the protected implementation of
Table 2.
The low-noise captured traces can be considered as very well aligned, without the need for averaging or post-acquisition alignment, due to the combination of the SAKURA-X, the collection mechanism and the PicoScope 5000D. In total, 1000 full Scalar Multiplications were captured, which upon further splitting amounted to a maximum of
different sample block traces labeled ‘0’ and ‘1’. These raw sample traces consist of 33,750 sampling points each, ready to be analyzed for feature generation. In order to train the different models, the Scikit-Learn library [
47] was utilized, offering a fast and simple development environment with good functionality. Characterizing a dataset as small or medium sized for ML-based side channel analysis is considerably dependent on the targeted cryptography algorithm (and relevant implementation) on which the attack is intended. Typically, simple Machine Learning algorithms use small- to medium-size datasets while Deep Learning algorithms (e.g., Neural Networks) use larger datasets for training. In the research literature, the few public SCA raw trace datasets that exist can provide an indication of the dataset size characterization. In the ASCAD database (one of the well-used public databases of DL SCA models for symmetric key algorithms) [
48] the authors collect around 100,000 traces to build the DL models. Similarly, in the study of [
49], the authors study DL models for symmetric key using 500,000 traces. When constructing models for public key cryptography algorithms, the needed number of traces to train a model can increase even further. Thus, the number of traces needed to train SCA models of size more than 100,000 can be considered a large dataset. In simple ML SCAs for ECC, such as the work of [
11] which is focused on an unprotected ECC FPGA implementation, a reasonably sized dataset of 14,000 traces has been used. While in our paper we have collected a large number of traces (1000 scalar multiplications have been captured with 233 bits of the scalar processed in each one of them, thus resulting in 232,233 traces), we only needed to use 5000 traces for our models, which is considerably less than the dataset size used in other works (e.g., 14,000 traces in [
11]). For this reason, our traces dataset can be considered of small or medium size. It should be noted that increasing the dataset size in the ML training did not improve the accuracy of the models.
6.2. Feature Generation
An important and crucial step to take into account when training any machine learning or neural network model is choosing the features of the dataset most capable of delivering as high prediction accuracy as possible. In this effort, targeting efficient model generation and training time, we adopted the strategy depicted in [
11,
50], where signal properties of the collected traces are used as features. Based on the recommendation in these papers, the following signal properties for every trace were measured to be used as features:
Mean of Absolute Value
Kurtosis
Median Frequency
Mean Frequency
Slope Sign Change
The computation of these signal properties was achieved through the usage of already-available toolsets implemented in a MATLAB environment, as well as in-house built Python scripts, verifying with two different implementations, the correctness of our feature generation process. A preliminary observation on the values of the features, indicates that Kurtosis and Slope Sign Change might have the highest contribution regarding the final classification decision each model makes. After generating the appropriate values, the formation of the feature array is completed, appropriately assigning the correct labels to each feature value of the collected traces. This means that for each captured trace, such as those shown in
Figure 2,
Figure 3,
Figure 4 and
Figure 5, the raw 33,750 signal data points are now reduced to a five-value array containing the computed features.
It is a prevalent conclusion that this feature generation process, in which signal properties are used as features rather than raw signal data, allows for a significant decrease in input data amount necessary to train the different ML models. The training time is, thus, greatly shortened for the majority of the models, allowing for quick evaluation and assessment of the implemented countermeasures, as well as of the impact each tuned parameter has on the accuracy of the trained model.
6.3. Feature Extraction
Noise is considered one of the biggest obstacles when attempting a successful side channel attack. In order to overcome this barrier, it has been shown [
51] that using statistical methods such as Principal Component Analysis (PCA) as a pre-processing method has the potential to lead to a reduction in noise in the leaked side channel data. This fact elevates techniques such as PCA into potentially valuable feature extraction mechanisms. During this process, the data that are evaluated to be redundant and not able to provide any contribution to the critical leakage are then removed from the finalized feature set. In our case and in similarity with the above feature generation procedure, PCA was applied on the raw signal traces containing all the collected information. This leads to a significant reduction in needed data to just two computed Principal Components. These values are then labeled correctly before being fed as input data into our models. As mentioned above, this additional way of reducing the training portion of the data can lead to shortened training time and better classification accuracy. Out of the three machine learning algorithms described in
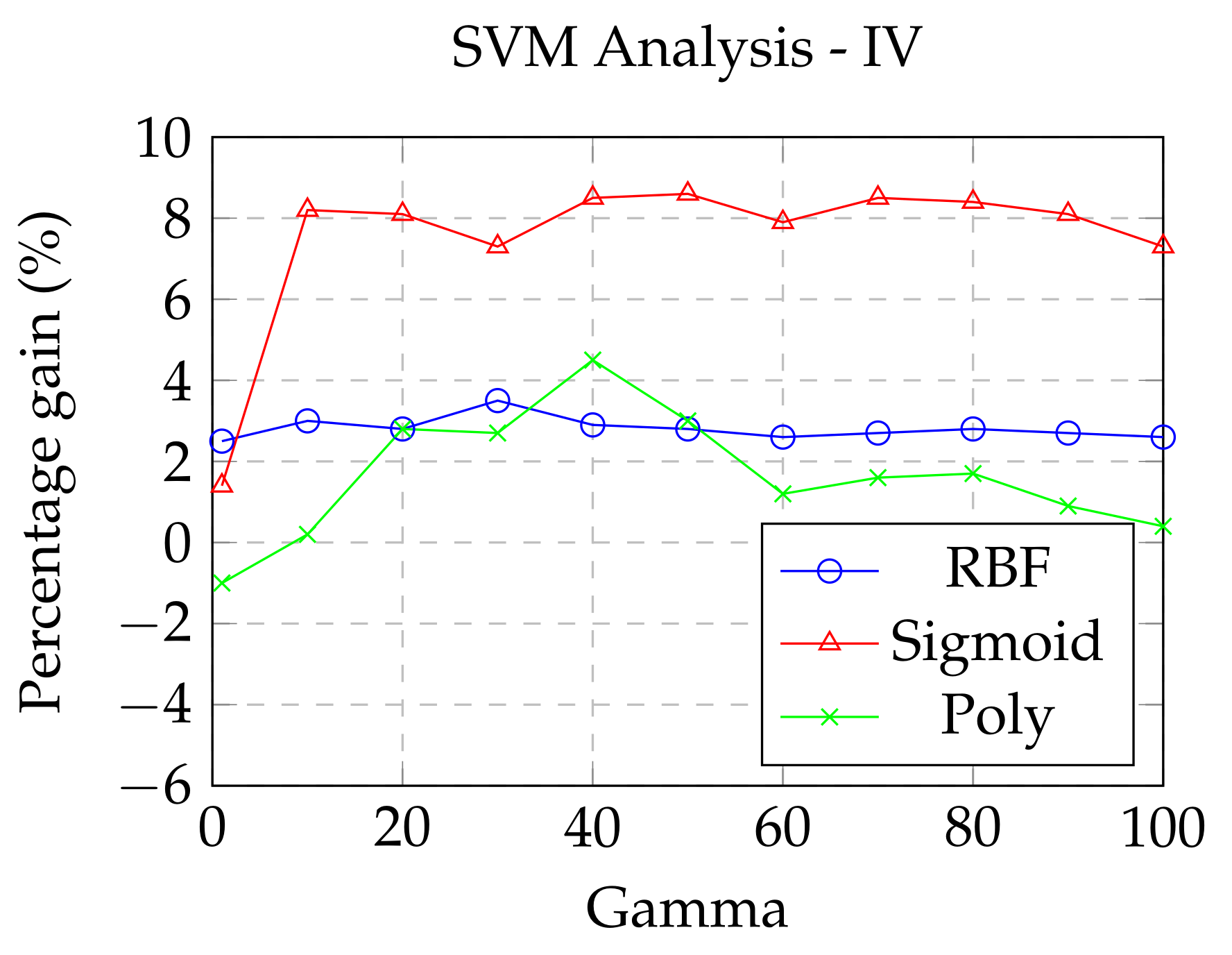
Section 5, Support Vector Machines seem to provide better performance, compared to the other algorithms, when using PCA pre-processing, due to their high-dimensionality characteristic.
6.4. Validation
Caution during the training of any Machine Learning model should be exercised in order to avoid the effects of underfitting and overfitting. Underfitting happens in cases where the dataset is excessively large or there are errors in the input data. The model then cannot correctly train on the available dataset, producing wrong classification results. On the other side of the spectrum, when the trained model can predict the training data with incredibly high accuracy, this is a sign of overfitting, as the model cannot generalize its predictions to new input data. To overcome these effects, the K-Fold Cross Validation technique has been adopted. More specifically, the input dataset that has been generated with the signal properties as features is divided into training and testing data portions. For our model, the training portion of the data is 20% of the total samples collected. As is apparent, the training of the model is completed using the training portion of the data, while the testing portion is only used to assess the classification accuracy without any impact during the model training phase (holdout method). The whole dataset is then subjected to the same procedure K-1 times, where in each iteration a different percentage of datapoints reflects the training set and the testing set, respectively. The model is, thus, trained K times using a different pair of subsets, after which the final classification accuracy is considered the mean value of each iteration. The cross validation process ensures that the training of the model does not lean heavily into one-dimensional learning of the dataset, which causes inaccuracy in new testing subsets.
8. Conclusions
In this paper, the current landscape on simple and advanced SCAs for EC scalar multipliers was described and the potential of profiling attacks, such as TA and ML-based SCAs, was highlighted. Moreover, a fine-grained GF unification stages model and overall design approach was proposed, and relevant leakage models were presented. The proposal relies on the MPL algorithm’s ability to perform all point operations in parallel within a computation round. This led to a decomposition of the point operations in their underlying finite field operations and the redistribution of those operations in parallel stages that concurrently implement finite field operations for both point operations on an MPL round. The approach is further enhanced by the injection, in some parallel stage, of finite field operations that perform multiplicative randomization. This process extends the projective coordinate randomization countermeasure found in relevant literature, showcasing the transparent migration of randomization inside the parallel stages of the proposed fine-grained GF unification stages approach. This randomization is performed for each MPL round with a different random value per round. Furthermore, in the paper, the proposed fine-grained GF unification stages approach was practically evaluated against ML-based SCAs that utilize three ML models (Random Forest, SVM and MLP). A detailed roadmap on how to mount such attacks on MPL-based SM was made using an existing implementation that follows the proposed fine-grained GF unification stages approach. Actual ML-based SCAs were mounted onto two SM implementations, an unprotected one and a protected one (that latter using our proposed approach with projective coordinate re-randomization).
Analyzing the data resulting from the implemented attacks on the fine-grained GF unification stages based SM implementations, using different and popular SCA applications with simple Machine Learning algorithms (that do not require a significant amount of leakage traces, as traditionally needed in deep learning approaches), we can safely conclude the effectiveness of the applied countermeasures. For all the tested models, the unprotected version of the scalar multiplier did not manage to conceal important information from the attempts to recover the key bits, reaching up to accuracy in some cases. This means that the provided leakage model reveals a significant amount of secret scalar information to an attacker, regardless of the GF unification in each round, and is not appropriate for ML-based SCA resistance. On the contrary, after applying the re-randomization countermeasure, the ML models were unable to achieve an accuracy that can be considered satisfactory in order to reveal the secret key bits. Thus, the masking mechanism of random operation within the MPL round’s parallel stages, which can be easily included in the proposed design approach, seems to be potent enough to thwart several different ML-based SCAs, such as the ones described in this paper.