UAV-Assisted Cooperative NOMA and OFDM Communication Systems: Analysis and Optimization
Abstract
:1. Introduction
1.1. Related Work
1.2. Main Contributions
- We have proposed a model for leveraging UAV-assisted ground communication in specialized communication scenarios where data stations are deployed in complex terrains without direct connectivity to the base station. Our objective is to devise optimal algorithms for the operation of UAVs and ground stations to achieve the maximum system capacity for two scenarios employing NOMA and OFDMA, under constraints of energy, travelling time of the UAV, and required total data from further users;
- We formulated optimization problems to maximize the system sum data rate for both NOMA and OFDMA scenarios. Since these problems are not convex, we transformed them into equivalent forms that can be readily solved using block-coordinate gradient descent (BCGD) and successive convex optimization (SCO) techniques to find the optimal parameter set. We demonstrated that our proposed algorithm guarantees convergence and significantly improves the system sum data rate metric.
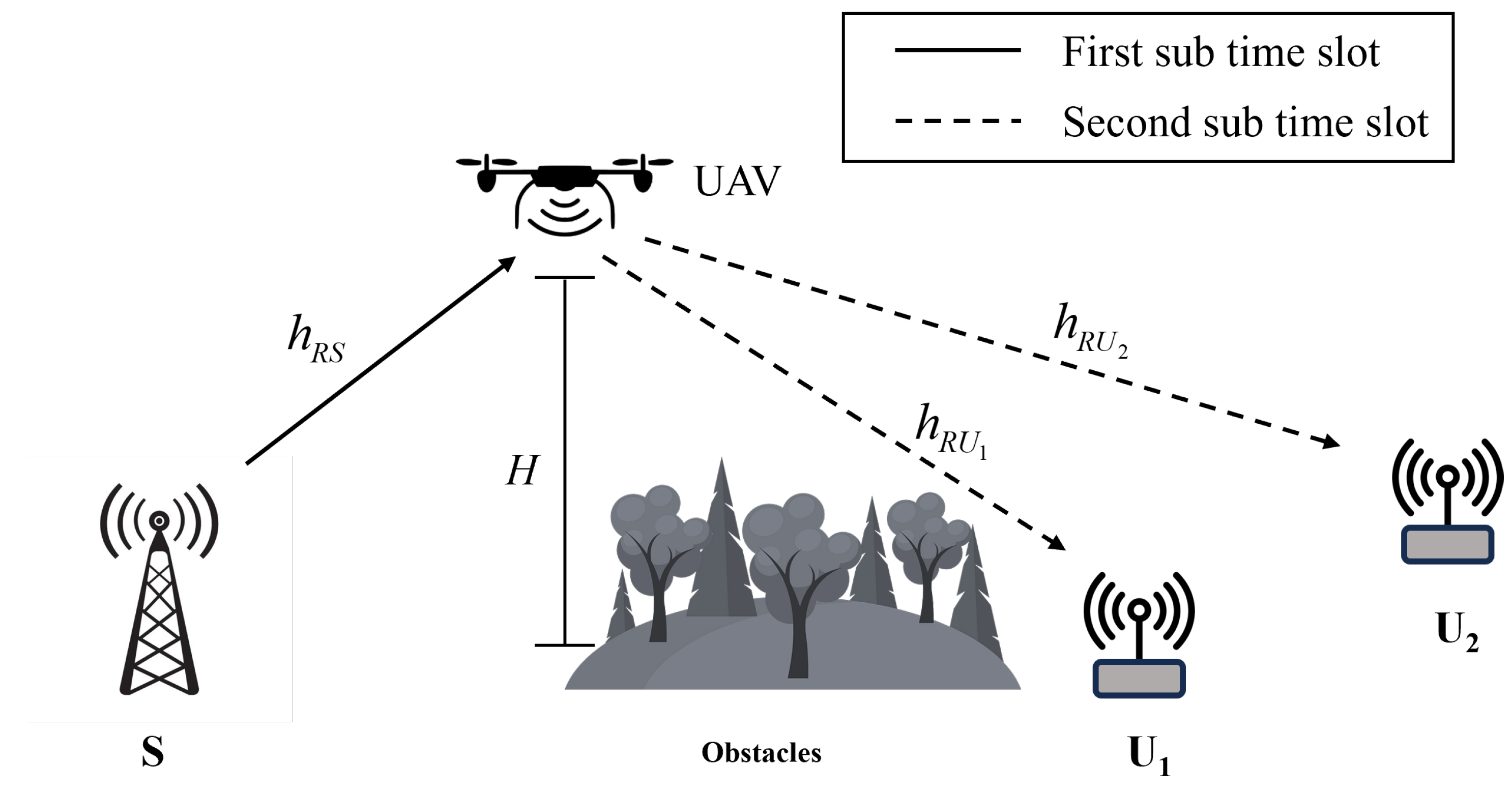
2. System Model
3. Preliminary Results and Sum-Rate Optimization Problem Formulation
3.1. Preliminary Results
3.1.1. OFDMA-Based UAV Relaying Protocol
3.1.2. NOMA-Based UAV Relaying Protocol
3.2. Sum-Rate Optimization Problem Formulation
4. Proposed Alternative Optimization Problem
4.1. UAV Trajectory Optimization (TO)
4.1.1. TO in OFDMA-Based UAV Relaying Protocol
4.1.2. TO in NOMA-Based UAV Relaying Protocol
4.2. Transmit Power Optimization (TPO)
4.2.1. TPO in OFDMA-Based UAV Relaying Protocol
4.2.2. TPO in NOMA-Based UAV Relaying Protocol
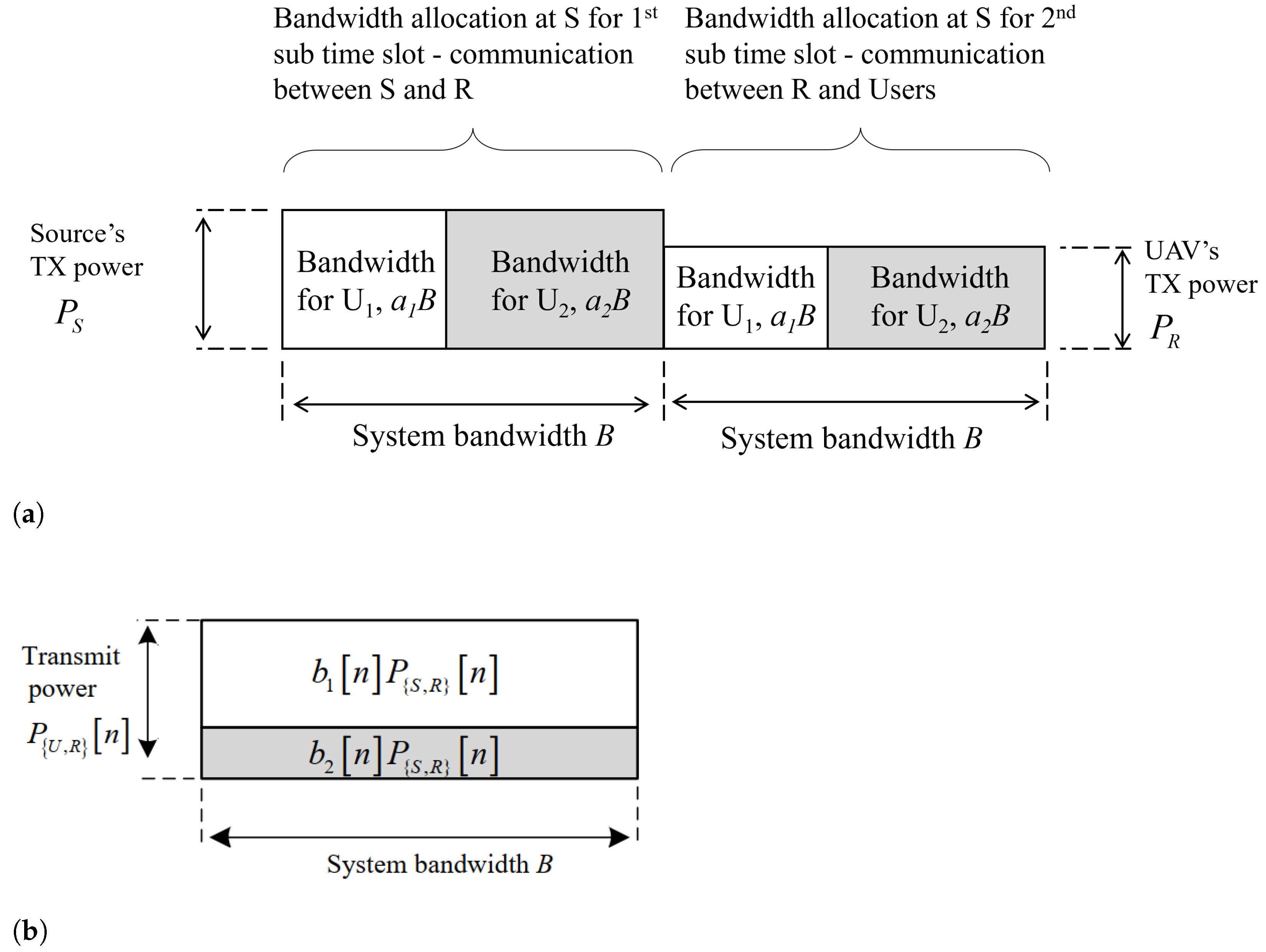
4.3. Optimizing the Resource Allocation (ORA)
4.3.1. ORA in OFDMA-Based UAV Relaying Protocol
4.3.2. ORA in NOMA-Based UAV Relaying Protocol
5. Proposed Comprehensive Algorithm
| Algorithm 1 The Sum-Rate Maximization Algorithm for OFDMA–/NOMA–UAVR Protocols. |
|
| Algorithm 2 The Initialization Scheme for Algorithm 1. |
|
5.1. Overall Algorithm
5.2. Initialization Scheme
6. Simulation Results
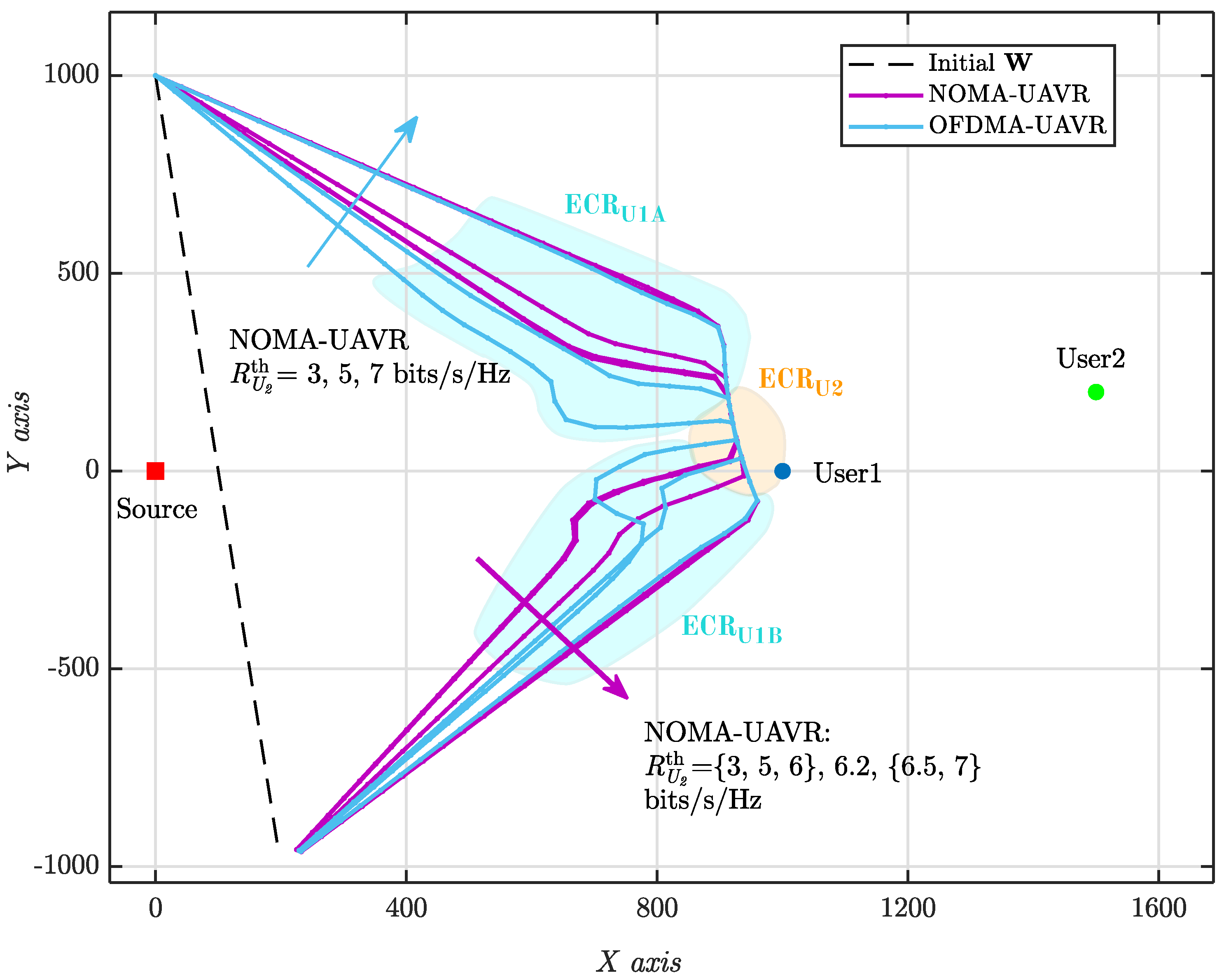
6.1. UAV’s Fight Trajectory and Velocity Analysis
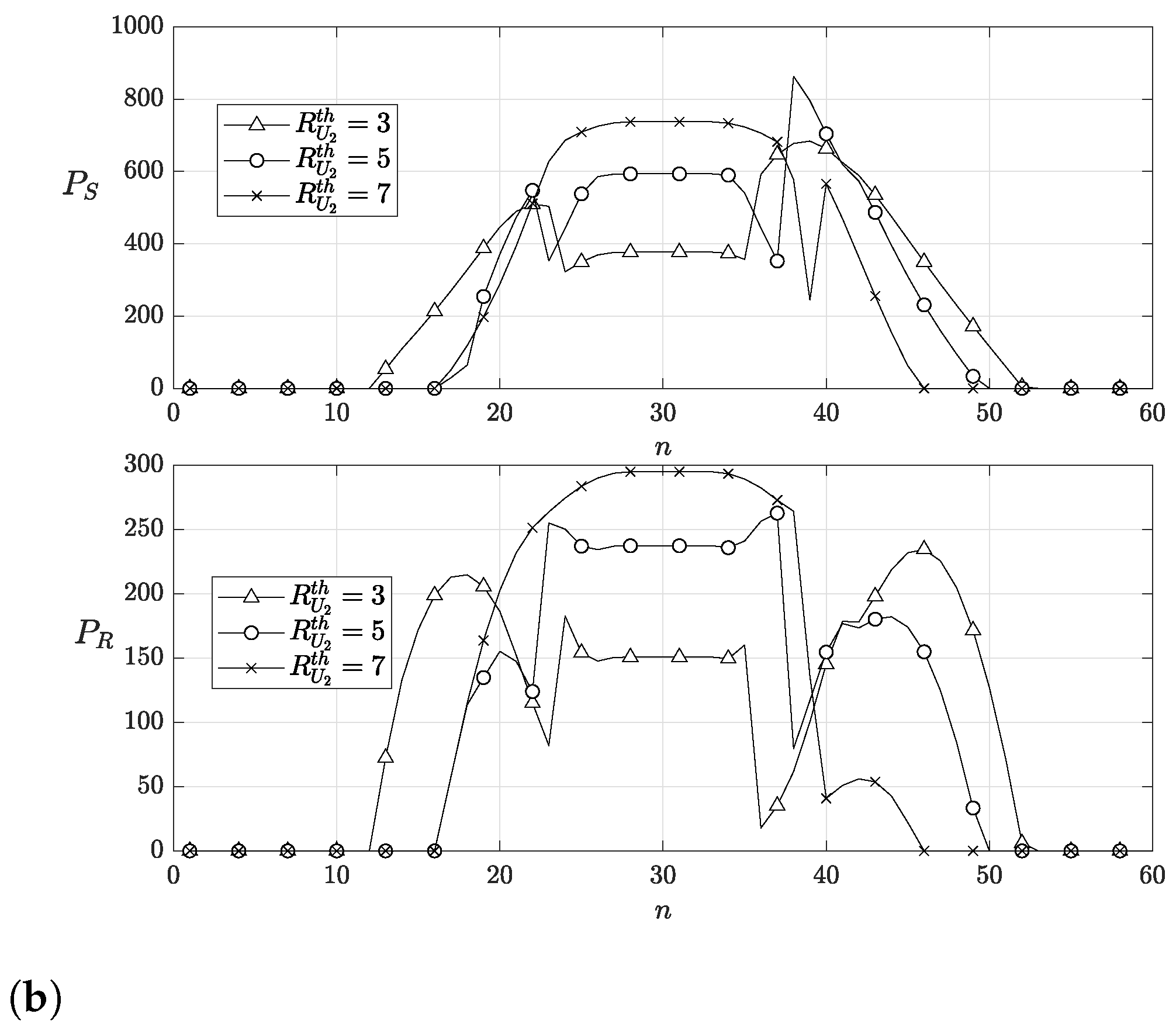
6.2. Transmission Powers and Resource Allocation Analysis
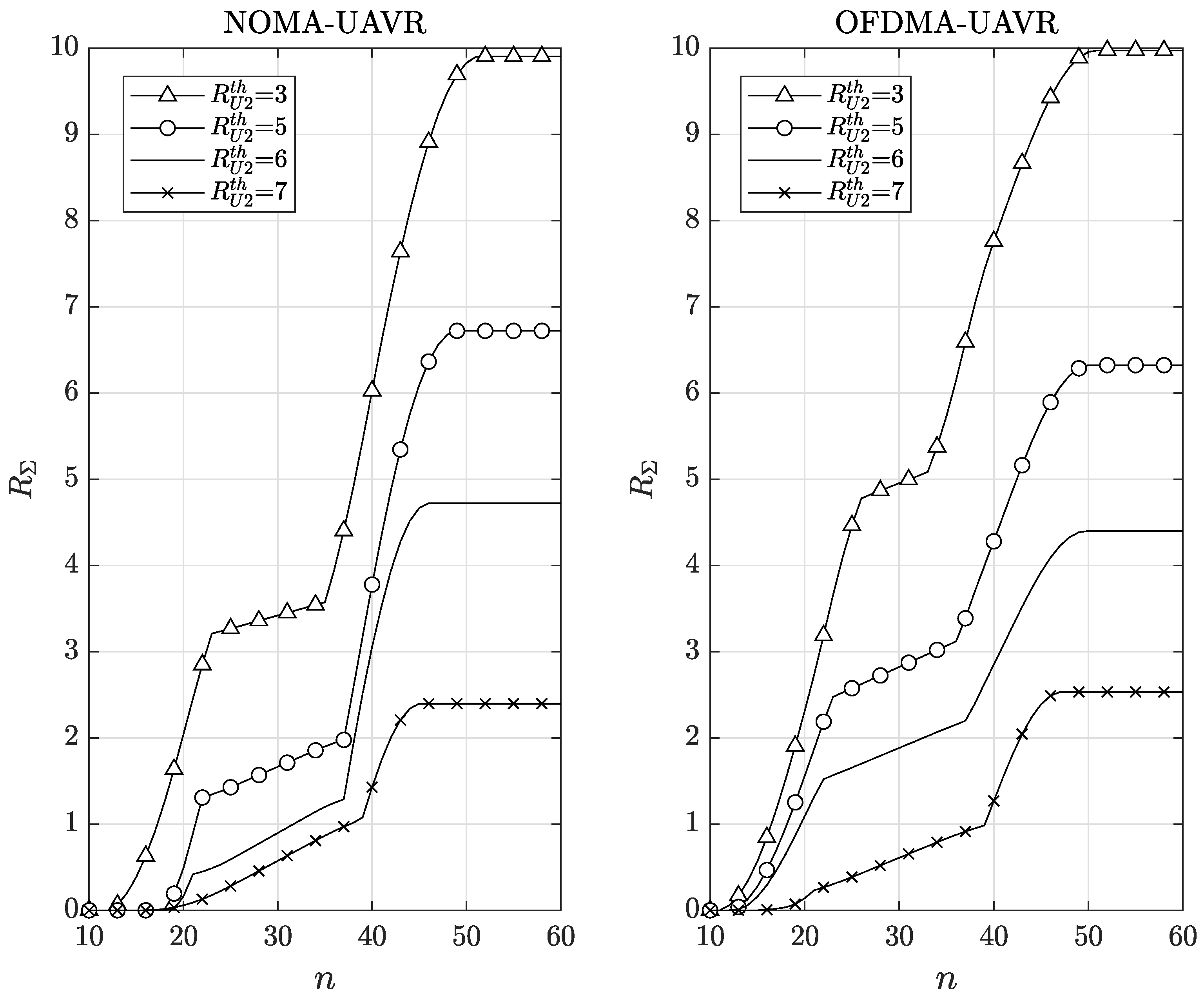
6.3. Analysis of Instantaneous Rate and Sum Data Rate of Each User
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BCGD | Block-coordinate gradient descent |
| DU | Destination user |
| GBS | Round base station |
| OMA | Orthogonal multiple access |
| OFDMA | Orthogonal frequency division multiple access |
| ORA | Optimizing the resource allocation |
| NOMA | Non-orthogonal multiple access |
| SCO | Successive convex optimization |
| SIC | Successive interference cancellation |
| SINR | Signal-to-interference and noise ratio |
| TPO | Transmit power optimization |
| UAV | Unmanned aerial vehicles |
| UAVR | UAV relaying |
| UAVWC | UAV-assisted wireless communication |
References
- Vinogradov, E.; Sallouha, H.; De Bast, S.; Azari, M.M.; Pollin, S. Tutorial on UAV: A blue sky view on wireless communication. arXiv 2019, preprint. arXiv:1901.02306. [Google Scholar]
- Shen, T.; Ochiai, H. A UAV-Enabled Wireless Powered Sensor Network Based on NOMA and Cooperative Relaying with Altitude Optimization. IEEE Open J. Commun. Soc. 2021, 2, 21–34. [Google Scholar] [CrossRef]
- Michailidis, E.T.; Maliatsos, K.; Skoutas, D.N.; Vouyioukas, D.; Skianis, C. Secure UAV-aided mobile edge computing for IoT: A review. IEEE Access 2022, 10, 86353–86383. [Google Scholar] [CrossRef]
- Duong, T.Q.; Kim, K.J.; Kaleem, Z.; Bui, M.P.; Vo, N.S. UAV caching in 6G networks: A Survey on models, techniques, and applications. Phys. Commun. 2022, 51, 101532. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wang, J.; Chen, J.; Yao, K.; Wu, Q.; Anpalagan, A. Opportunistic UAV utilization in wireless networks: Motivations, applications, and challenges. IEEE Commun. Mag. 2020, 58, 62–68. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, P. The Effectiveness of Unmanned Aerial Vehicle (UAV) on Farmlands with Artificial Intelligence (AI) System. In Proceedings of the 2022 7th International Conference on Financial Innovation and Economic Development (ICFIED 2022), Harbin, China, 21–23 January 2022; Atlantis Press: Dordrecht, The Netherlands, 2022; pp. 1664–1669. [Google Scholar]
- Thi Tam, D.; Cao Nguyen, B.; Manh Hoang, T.; The Dung, L.; Vinh, N.V.; Kim, T.; Lee, W. Combining FD-UAV and NOMA technologies in IoT sensor network with millimeter-wave communications. Int. J. Commun. Syst. 2023, e5492. [Google Scholar] [CrossRef]
- Greenberg, E.; Bar, A.; Klodzh, E. Los classification of UAV-to-ground links in built-up areas. In Proceedings of the 2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel, 4–6 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Cui, Z.; Briso-Rodríguez, C.; Guan, K.; Güvenç, I.; Zhong, Z. Wideband air-to-ground channel characterization for multiple propagation environments. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1634–1638. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, L. Fast deployment of UAV networks for optimal wireless coverage. IEEE Trans. Mob. Comput. 2018, 18, 588–601. [Google Scholar] [CrossRef]
- Shahzadi, R.; Ali, M.; Khan, H.Z.; Naeem, M. UAV assisted 5G and beyond wireless networks: A survey. J. Netw. Comput. Appl. 2021, 189, 103114. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, T.; Wang, S. Location optimization and user association for unmanned aerial vehicles assisted mobile networks. IEEE Trans. Veh. Technol. 2019, 68, 10056–10065. [Google Scholar] [CrossRef]
- Khan, S.K.; Naseem, U.; Sattar, A.; Waheed, N.; Mir, A.; Qazi, A.; Ismail, M. UAV-aided 5G network in suburban, urban, dense urban, and high-rise urban environments. In Proceedings of the 2020 IEEE 19th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 24–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Liu, Y.; Yi, W.; Ding, Z.; Liu, X.; Dobre, O.; Al-Dhahir, N. Application of NOMA in 6G networks: Future vision and research opportunities for next generation multiple access. arXiv 2021, preprint. arXiv:2103.02334. [Google Scholar]
- Khan, W.U.; Jameel, F.; Jamshed, M.A.; Pervaiz, H.; Khan, S.; Liu, J. Efficient power allocation for NOMA-enabled IoT networks in 6G era. Phys. Commun. 2020, 39, 101043. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, W.; Ding, Z.; Liu, X.; Dobre, O.A.; Al-Dhahir, N. Developing NOMA to Next Generation Multiple Access: Future Vision and Research Opportunities. IEEE Wirel. Commun. 2022, 29, 120–127. [Google Scholar] [CrossRef]
- Le, T.A.; Kong, H.Y. Evaluating the performance of cooperative NOMA with energy harvesting under physical layer security. Wirel. Pers. Commun. 2019, 108, 1037–1054. [Google Scholar] [CrossRef]
- Makki, B.; Chitti, K.; Behravan, A.; Alouini, M.S. A survey of NOMA: Current status and open research challenges. IEEE Open J. Commun. Soc. 2020, 1, 179–189. [Google Scholar] [CrossRef]
- Xiong, C.; Li, G.Y.; Zhang, S.; Chen, Y.; Xu, S. Energy-efficient resource allocation in OFDMA networks. IEEE Trans. Commun. 2012, 60, 3767–3778. [Google Scholar] [CrossRef]
- New, W.K.; Leow, C.Y.; Navaie, K.; Sun, Y.; Ding, Z. Application of NOMA for cellular-connected UAVs: Opportunities and challenges. Sci. China Inf. Sci. 2021, 64, 1–14. [Google Scholar] [CrossRef]
- Do, D.T.; Nguyen, T.T.T.; Nguyen, T.N.; Li, X.; Voznak, M. Uplink and downlink NOMA transmission using full-duplex UAV. IEEE Access 2020, 8, 164347–164364. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, Z. The full-duplex device-to-device security communication under the coverage of unmanned aerial vehicle. KSII Trans. Internet Inf. Syst. (TIIS) 2019, 13, 1941–1960. [Google Scholar]
- Kumar, V.; Ding, Z.; Flanagan, M.F. On the Effective Rate of NOMA in Underlay Spectrum Sharing. IEEE Trans. Veh. Technol. 2021, 70, 12220–12225. [Google Scholar] [CrossRef]
- Van Phu, T.; Kong, H.Y. Secrecy sum rate maximization for UAV-aided NOMA communication systems. Ann. Telecommun. 2022, 77, 127–138. [Google Scholar] [CrossRef]
- Wang, N.; Li, F.; Chen, D.; Liu, L.; Bao, Z. NOMA-based Energy-Efficiency optimization for UAV enabled space-air-ground integrated relay networks. IEEE Trans. Veh. Technol. 2022, 71, 4129–4141. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Liu, X.; Liu, Y.; Chen, Y.; Cui, S.; Poor, H.V. AI-driven UAV-NOMA-MEC in next generation wireless networks. IEEE Wirel. Commun. 2021, 28, 66–73. [Google Scholar] [CrossRef]
- Hariz, H.M.; Sheikhzadeh, S.; Mokari, N.; Javan, M.R.; Abbasi-Arand, B.; Jorswieck, E.A. Ai-based radio resource management and trajectory design for pd-noma communication in irs-uav assisted networks. arXiv 2021, preprint. arXiv:2111.03869. [Google Scholar]
- Senadhira, N.; Durrani, S.; Zhou, X.; Yang, N.; Ding, M. Uplink NOMA for Cellular-Connected UAV: Impact of UAV Trajectories and Altitude. IEEE Trans. Commun. 2020, 68, 5242–5258. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K.; Jiang, C.; Guizani, M. Joint Resource Allocation and Trajectory Optimization with QoS in UAV-Based NOMA Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 6343–6355. [Google Scholar] [CrossRef]
- Yamazaki, I.; Nooshabadi, S.; Tomov, S.; Dongarra, J. Structure-aware linear solver for realtime convex optimization for embedded systems. IEEE Embed. Syst. Lett. 2017, 9, 61–64. [Google Scholar] [CrossRef]
- Alshammari, F.; El-Refaie, A. Time-Varying Optimization-Based Consensus Control for Microgrid’s Secondary Control. In Proceedings of the 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]




| Previous Works | System Models | Operation Type | Primary Findings |
|---|---|---|---|
| [20] | UAV—downlink NOMA, multiple terrestrial BSs, terrestrial users, aerial users | Ground-to-air connections: modeling, analyzing, and simulating via two metrics as coverage probability and average user rate | Balanced performance between system throughput and fairness, and reduced delay |
| [21] | UAV—uplink and downlink NOMA | Full-duplex and half-duplex schemes over Nakagami-m channel: modeling, analyzing, and simulating via main metric as outage probability (OP) | Exploiting the benefits of UAV as a relay, save bandwidth, improving the data transmission efficiency, deriving closed-form expressions for OP |
| [25] | UAV with phased-array antennas and NOMA scheme | Modeling, analyzing, optimizing, and simulating via main metrics such as energy efficiency (EE), trajectory, NOMA scheduling, and NOMA power allocation | Their proposed system achieves high EE, and NOMA was shown to outperform OMA in UAV EE. |
| [26] | UAV—NOMA with AI | Proposing some AI techniques that can apply for UAV communication, using NOMA to serve terrestrial mobile users: analysis and presentation | Main techniques such as federated learning and reinforcement learning (RL) to address the intelligent task offloading and computing resource allocation |
| [27] | UAV with the uplink PD-NOMA and IRS | Multi IRS–UAV with ground BS and NOMA users: modeling, analyzing, optimizing, and simulating | Two different RL-based algorithms (DDQN and PPO) to minimize the average age of information of user |
| [28] | UAV and power-domain aerial–terrestrial NOMA (uplink scheme) | Concurrent uplink transmission of the aerial user (AU) and terrestrial user (TU) in uplink to UAV: modeling, analytical framework, simulating via the probability of achievable data rate | Determining the minimum height that AU needs to fly, enhancing the quality of services and showing the importance of modeling AU trajectory in UAV system |
| [29] | UAV—downlink NOMA | Optimizing joint resource allocation and UAV trajectory to maximize the total EE: using heuristic algorithm and logarithmic approximation | Improving the total energy efficiency and transmit power allocation, data rate, and computational complexity |
| No. | Symbol | Description |
|---|---|---|
| 1 | P | Transmit power |
| 2 | B | Bandwidth |
| 3 | H | Fixed altitude |
| 4 | Initial location | |
| 5 | Final location | |
| 6 | T | Length of time |
| 7 | N | Time slots |
| 8 | Channel gain | |
| 9 | Bandwidth allocation factor in OFDM | |
| 10 | R | Instantaneous rate |
| 11 | Required sum rate | |
| 12 | Additive white Gaussian noise | |
| 13 | Power allocation factor of NOMA | |
| 14 | Power budget | |
| 15 | Maximum transmit power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kieu-Xuan, T.; Le-Thi, A. UAV-Assisted Cooperative NOMA and OFDM Communication Systems: Analysis and Optimization. J. Sens. Actuator Netw. 2024, 13, 18. https://doi.org/10.3390/jsan13010018
Kieu-Xuan T, Le-Thi A. UAV-Assisted Cooperative NOMA and OFDM Communication Systems: Analysis and Optimization. Journal of Sensor and Actuator Networks. 2024; 13(1):18. https://doi.org/10.3390/jsan13010018
Chicago/Turabian StyleKieu-Xuan, Thuc, and Anh Le-Thi. 2024. "UAV-Assisted Cooperative NOMA and OFDM Communication Systems: Analysis and Optimization" Journal of Sensor and Actuator Networks 13, no. 1: 18. https://doi.org/10.3390/jsan13010018
APA StyleKieu-Xuan, T., & Le-Thi, A. (2024). UAV-Assisted Cooperative NOMA and OFDM Communication Systems: Analysis and Optimization. Journal of Sensor and Actuator Networks, 13(1), 18. https://doi.org/10.3390/jsan13010018






