Real-Time Damage Detection and Localization on Aerospace Structures Using Graph Neural Networks
Abstract
1. Introduction
2. Theoretical Background
2.1. Automated Operational Modal Analysis
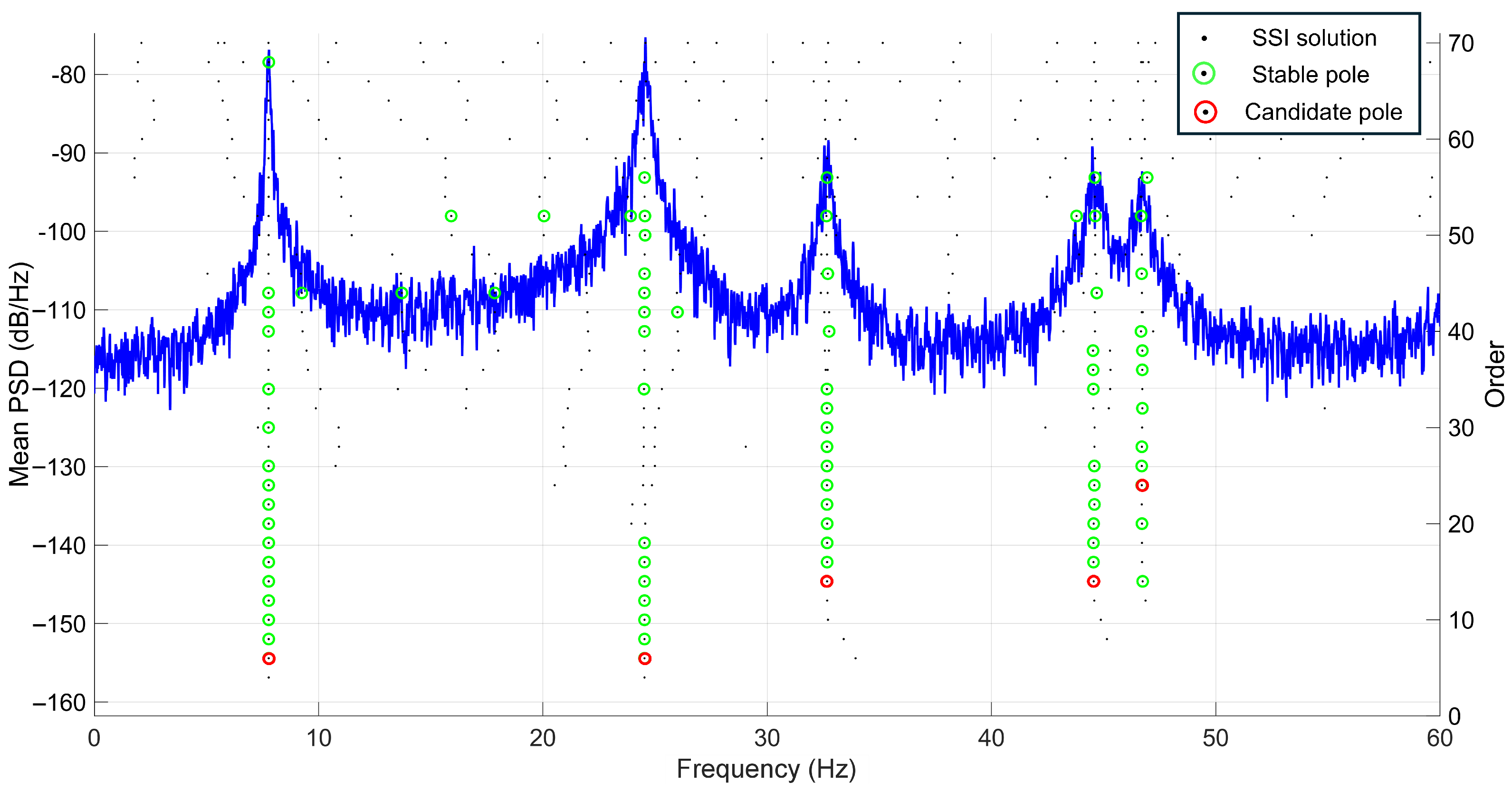
2.1.1. Stochastic Subspace Identification
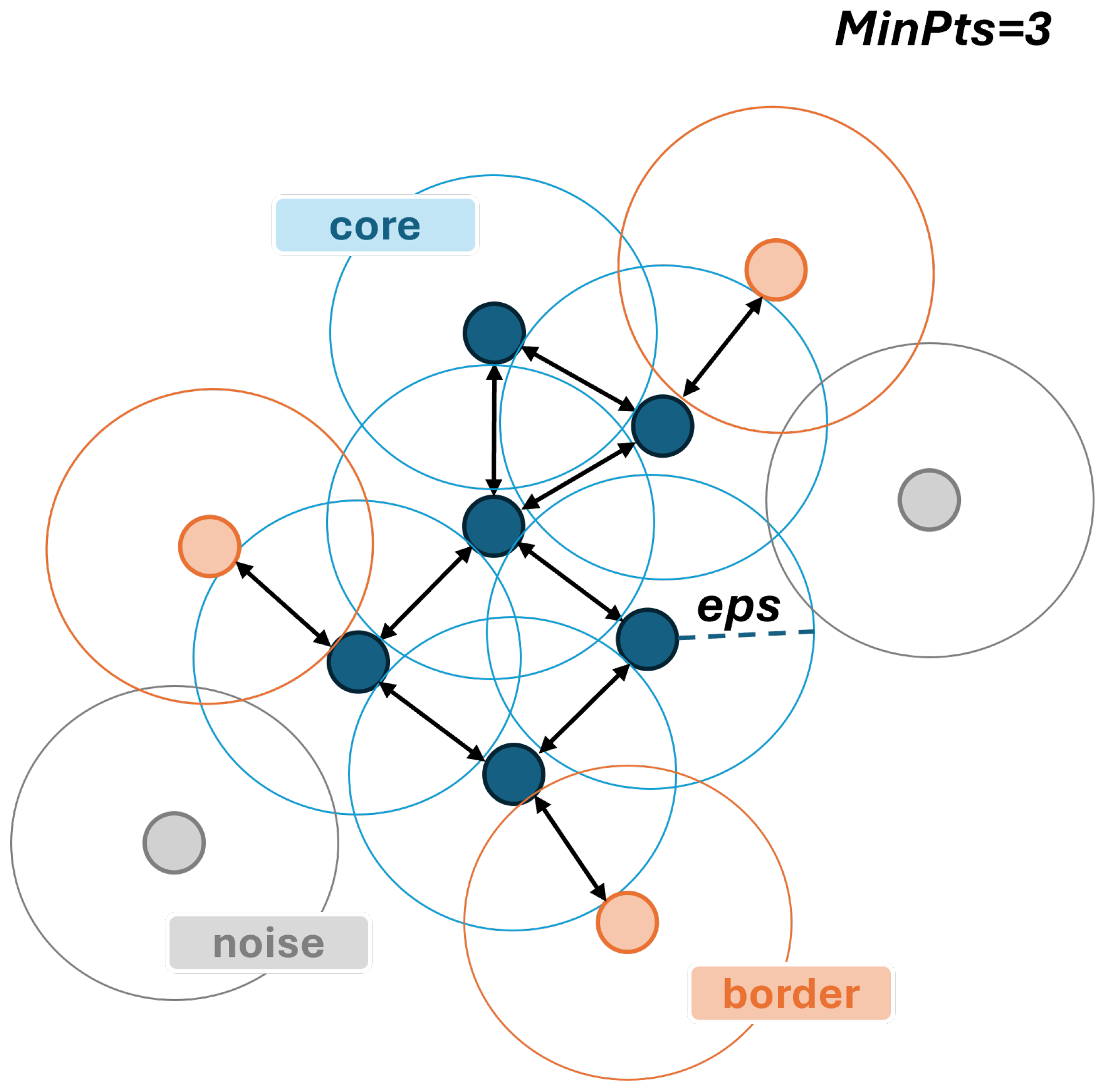
2.1.2. Automatic Selection of Poles
- If is a core point, a new cluster is initiated. All points that are density-reachable from (i.e., connected through a chain of neighboring core points) are then included in the cluster.
- If the number of neighboring points is less than , the point is classified as a border point if it lies within the neighborhood of a core point, or as an outlier point otherwise.
2.2. Graph Neural Networks
2.2.1. Graph Fundamentals
- is the set of nodes (or vertices);
- is the set of edges, which encode relationships between nodes.
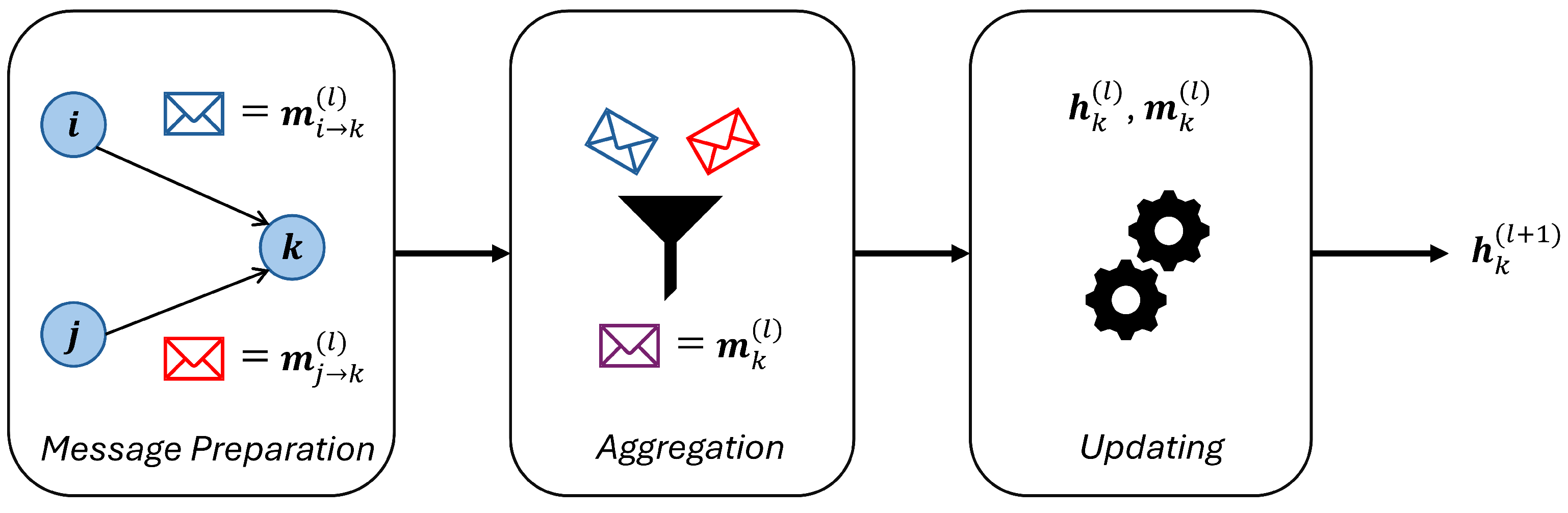
2.2.2. Graph Convolutional Networks
- Message preparation: Each neighboring node generates a message to send to node v, which is typically a function of the source and target node embeddings, and optionally edge attributes:
- Aggregation: Node v collects the messages coming from all its neighbors and combines them using a permutation-invariant aggregation function (e.g., sum and max):
- Update: The node updates its own embedding by combining its previous state with the aggregated message
- is the matrix of node features at layer l ( number of node features);
- is the adjacency matrix with self-loops;
- is the degree matrix corresponding to
- is a trainable weight matrix;
- is a non-linear activation function.
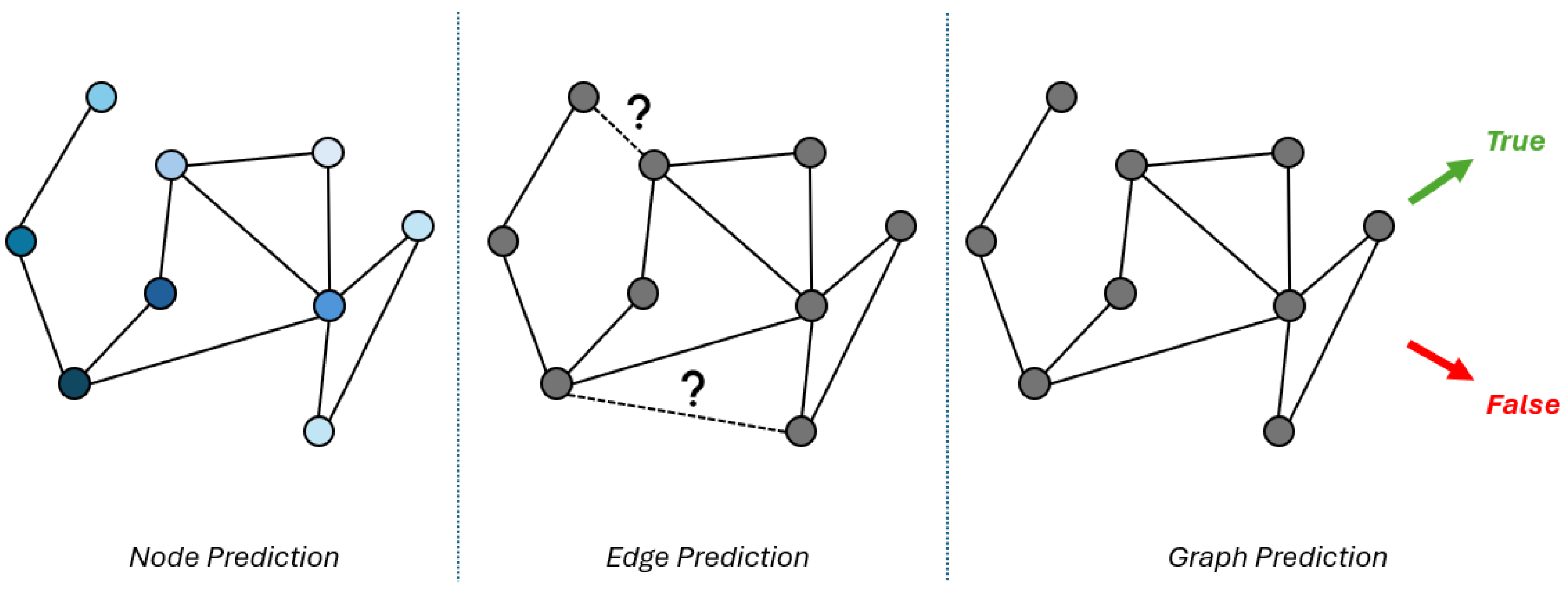
- Node-level prediction: estimate the node embedding for each individual node in a graph;
- Edge-level prediction: understand the relationship between entities in graphs and predict if two entities have a connection;
- Graph-level prediction: predict a value associated with the entire graph.
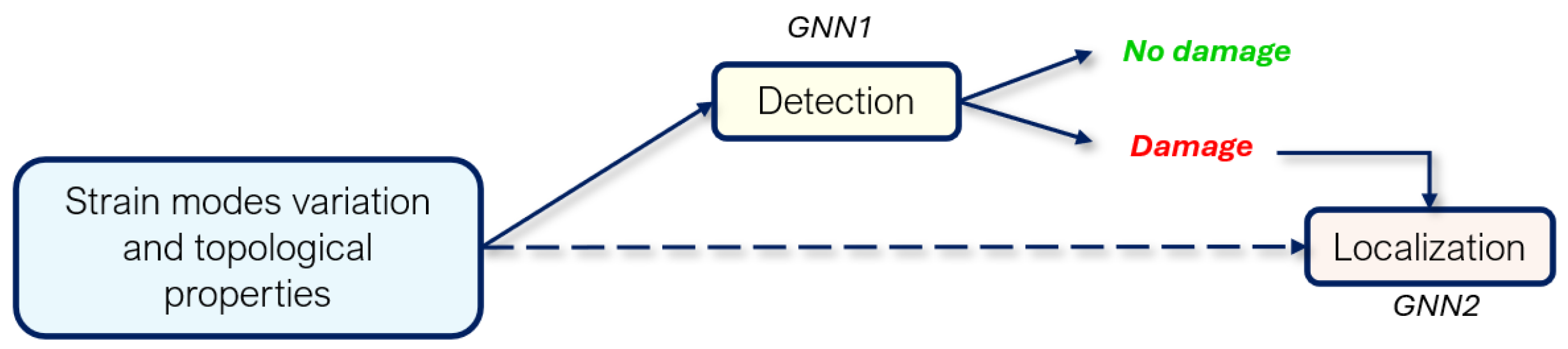
3. Methodology
- Damage Detection: a graph-level prediction task in which the GNN classifies the entire structure as damaged or undamaged, based on the input node features.
- Damage Localization: a node-level prediction task where the GNN estimates a probability distribution over the nodes, indicating the most likely locations of damage across the structure.
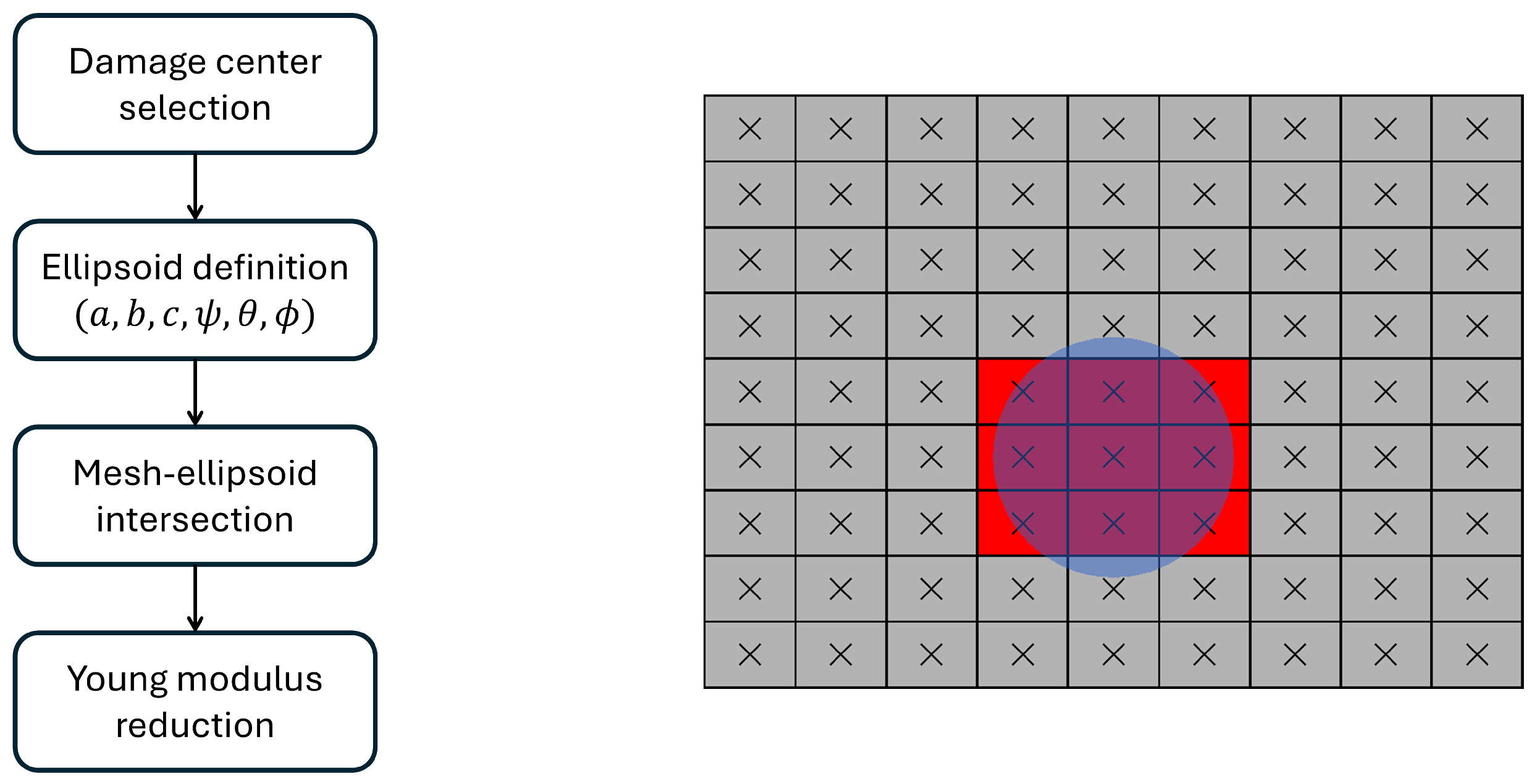
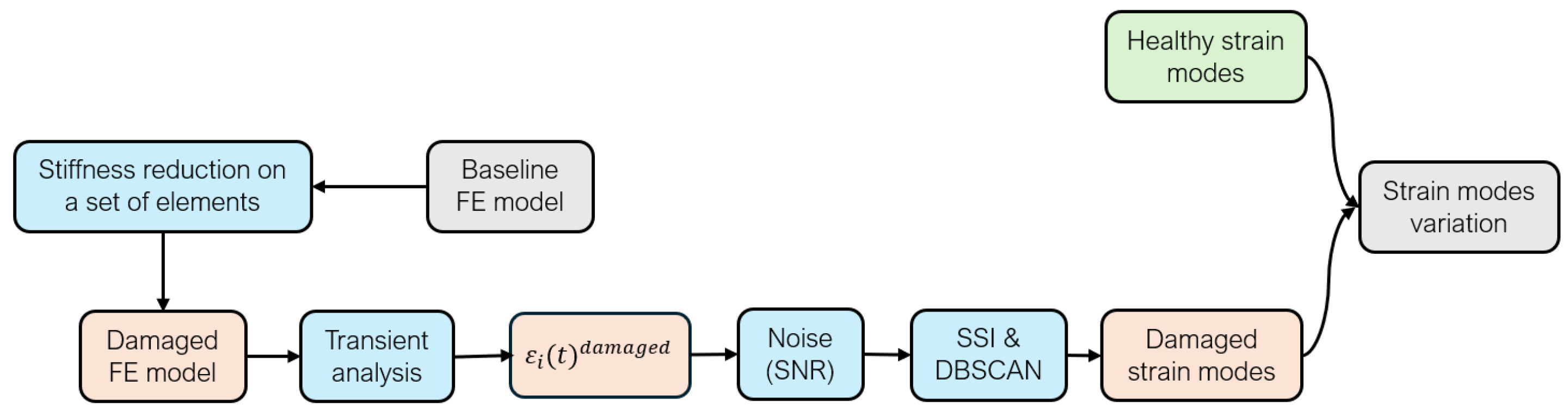
3.1. Dataset Generation
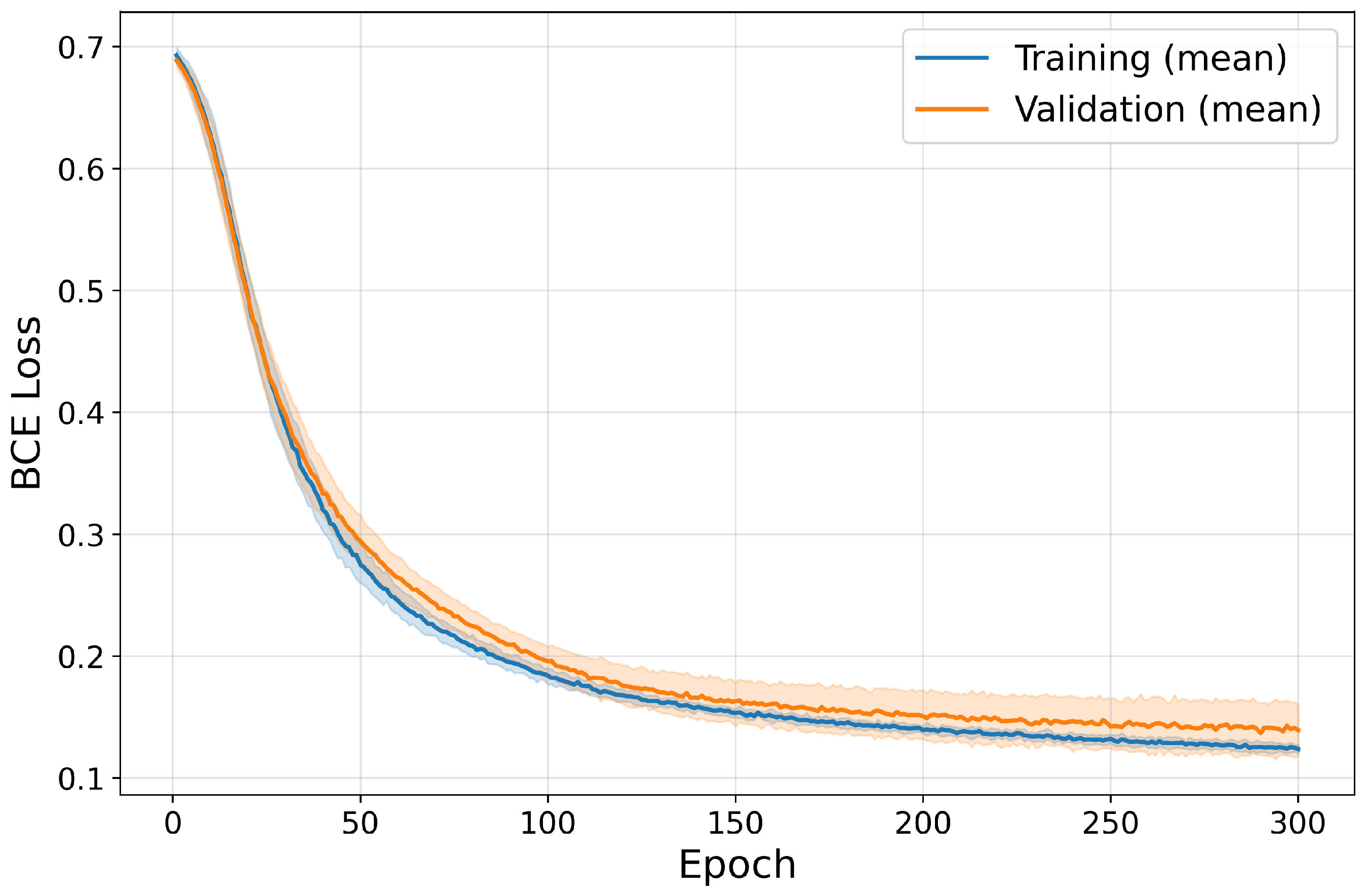
3.2. Detection GNN
3.3. Localization GNN
4. Results
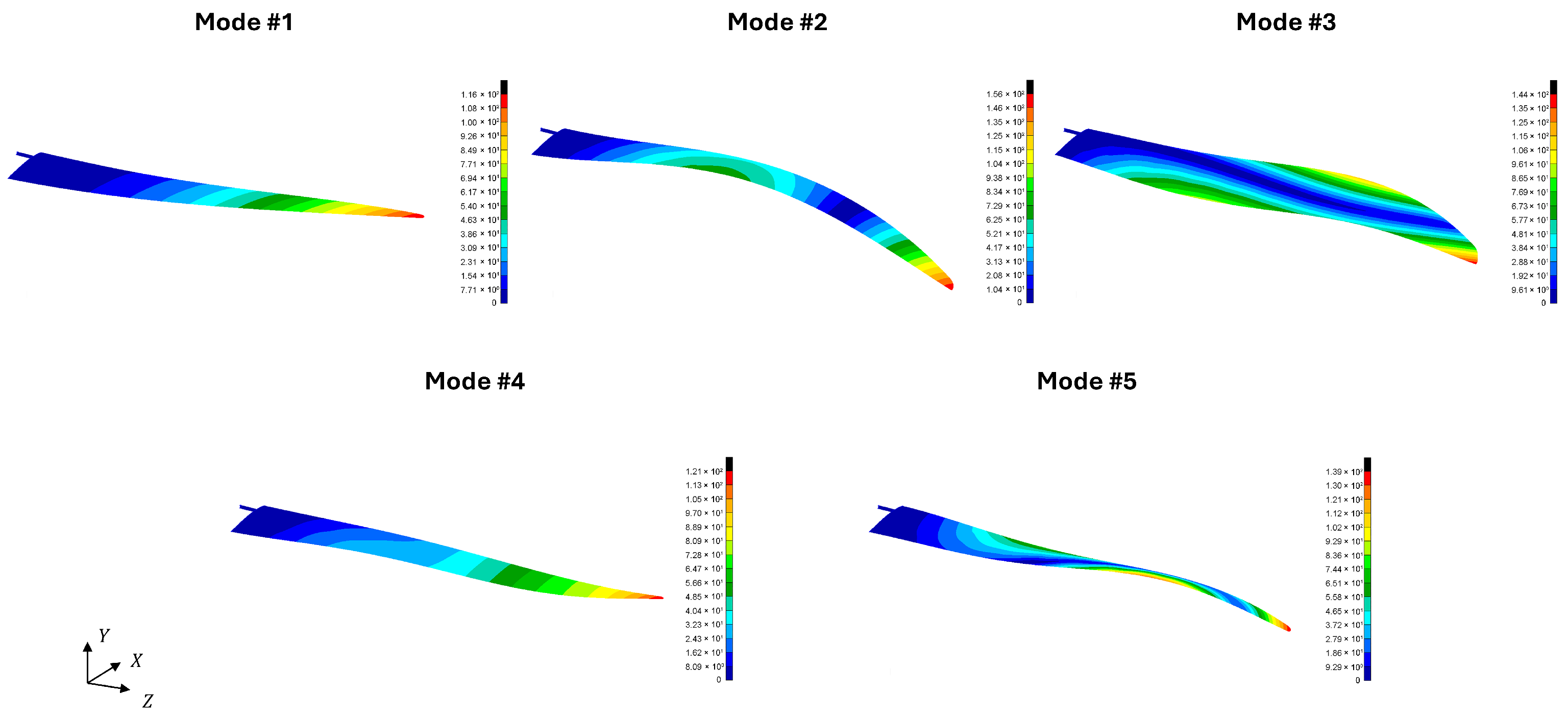
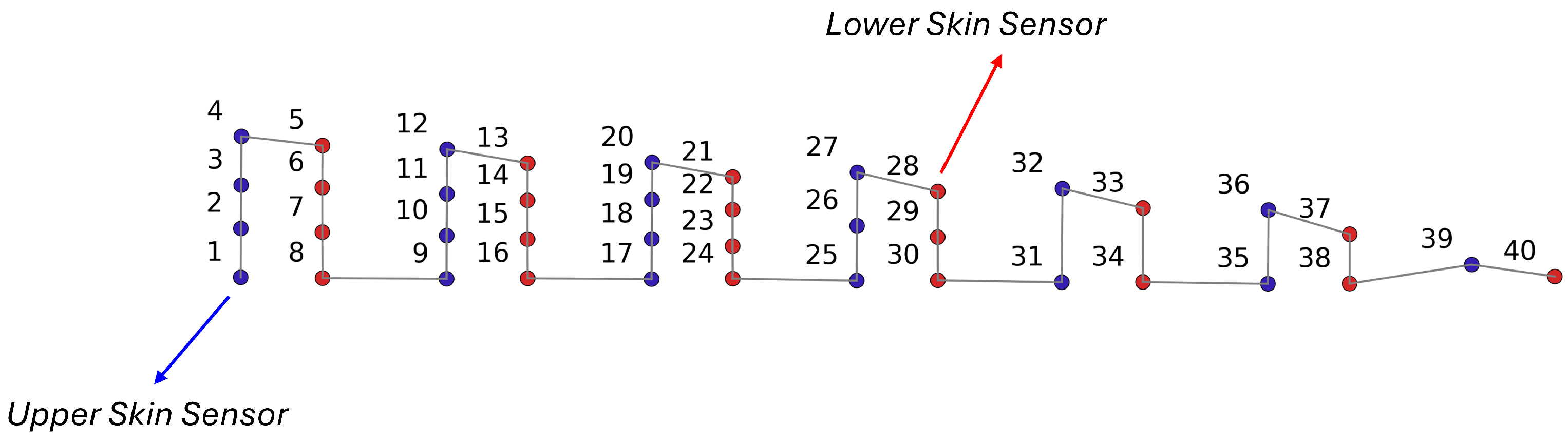
4.1. Case Study
- A number of spanwise sections is selected, seven for both the upper and lower skins, staggered along the wingspan;
- A variable number of sensors is positioned on each section, decreasing from four near the wing root to one near the tip, reflecting the tapering of the wing’s cross-section.
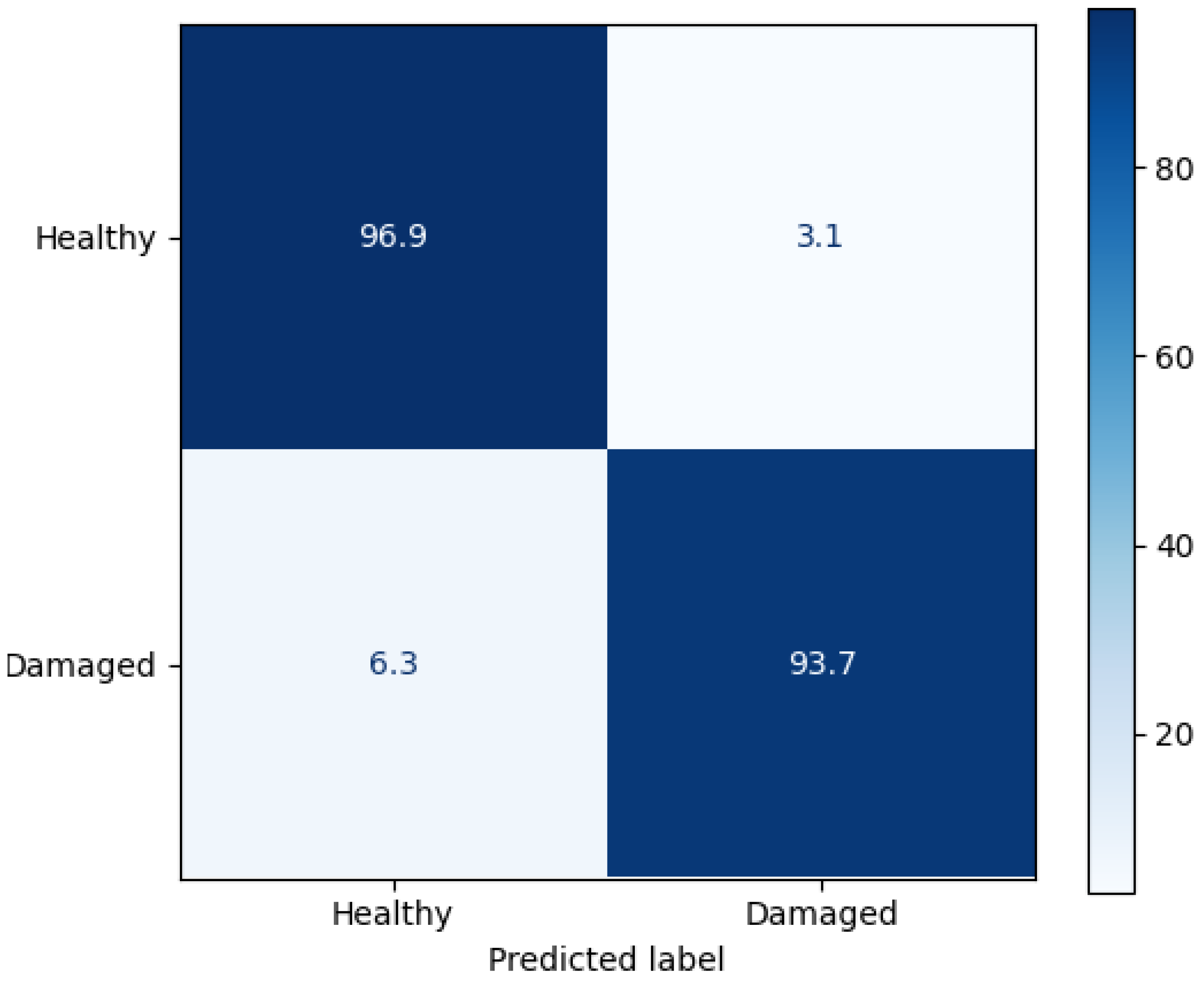
4.2. Detection Results
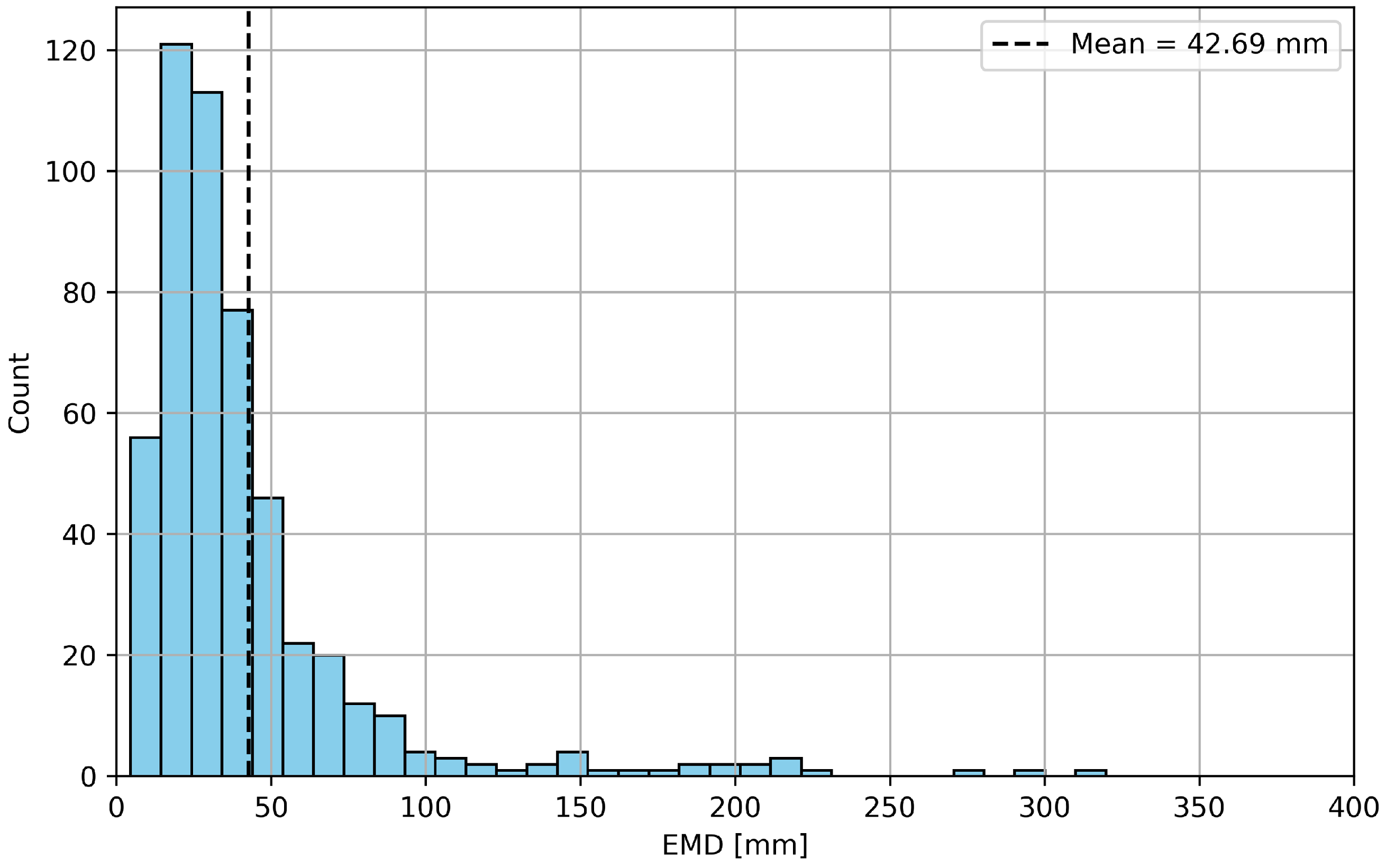
4.3. Localization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giurgiutiu, V.; Soutis, C. Enhanced composites integrity through structural health monitoring. Appl. Compos. Mater. 2012, 19, 813–829. [Google Scholar] [CrossRef]
- Dong, T.; Kim, N.H. Cost-effectiveness of structural health monitoring in fuselage maintenance of the civil aviation industry. Aerospace 2018, 5, 87. [Google Scholar] [CrossRef]
- Barazanchy, D.; Martinez, M.; Rocha, B.; Yanishevsky, M. A hybrid structural health monitoring system for the detection and localization of damage in composite structures. J. Sensors 2014, 2014, 109403. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Pagani, A.; Enea, M. Displacement and strain data-driven damage detection in multi-component and heterogeneous composite structures. Mech. Adv. Mater. Struct. 2024, 31, 2053–2068. [Google Scholar] [CrossRef]
- Sonker, M.; Shanker, R. Enhanced diagnostic approach for multiple damage detection and severity evaluation through EMI-based sensing and artificial neural network model. Asian J. Civ. Eng. 2025, 26, 747–760. [Google Scholar] [CrossRef]
- Facciotto, N.; Martinez, M.; Troiani, E. Source identification and classification of acoustic emission signals by a SHAZAM-inspired Pattern Recognition Algorithm. In Proceedings of the International Workshop on Structural Health Monitoring (IWSHM 2017), Palo Alto, CA, USA, 12–14 September 2017; Volume 12783. [Google Scholar]
- De Fenza, A.; Sorrentino, A.; Vitiello, P. Application of Artificial Neural Networks and Probability Ellipse methods for damage detection using Lamb waves. Compos. Struct. 2015, 133, 390–403. [Google Scholar] [CrossRef]
- Pirrotta, C.; Gueli, A.M.; Trigona, C.; Imposa, S. Coherence Analysis for Vibration Monitoring Under High Variability Conditions: Constraints for Cultural Heritage Preventive Conservation. J. Sens. Actuator Netw. 2025, 14, 45. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.Z.; Wu, J.; Wang, Y. Zero-faulty sample machinery fault detection via relation network with out-of-distribution data augmentation. Eng. Appl. Artif. Intell. 2025, 141, 109753. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.Z.; Deng, Z.; Wu, J. Shrinkage mamba relation network with out-of-distribution data augmentation for rotating machinery fault detection and localization under zero-faulty data. Mech. Syst. Signal Process. 2025, 224, 112145. [Google Scholar] [CrossRef]
- Sahin, M.; Shenoi, R. Quantification and localisation of damage in beam-like structures by using artificial neural networks with experimental validation. Eng. Struct. 2003, 25, 1785–1802. [Google Scholar] [CrossRef]
- Pagani, A.; Enea, M.; Carrera, E. Component-wise damage detection by neural networks and refined FEs training. J. Sound Vib. 2021, 509, 116255. [Google Scholar] [CrossRef]
- Rao, P.S.; Mahendra, N. Vibration based damage identification method for cantilever beam using artificial neural network. In Proceedings of the International Conference on Experimental Vibration Analysis for Civil Engineering Structures, La Jolla, CA, USA, 12–14 July 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–93. [Google Scholar]
- Padil, K.H.; Bakhary, N.; Abdulkareem, M.; Li, J.; Hao, H. Non-probabilistic method to consider uncertainties in frequency response function for vibration-based damage detection using Artificial Neural Network. J. Sound Vib. 2020, 467, 115069. [Google Scholar] [CrossRef]
- Zhong, K.; Teng, S.; Liu, G.; Chen, G.; Cui, F. Structural damage features extracted by convolutional neural networks from mode shapes. Appl. Sci. 2020, 10, 4247. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Wahab, M.A. Damage detection in slab structures based on two-dimensional curvature mode shape method and Faster R-CNN. Adv. Eng. Softw. 2023, 176, 103371. [Google Scholar] [CrossRef]
- Duran, B.; Emory, D.; Azam, Y.E.; Linzell, D.G. A novel CNN architecture for robust structural damage identification via strain measurements and its validation via full-scale experiments. Measurement 2025, 239, 115393. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Miele, E.S.; Bonacina, F.; Corsini, A. Deep anomaly detection in horizontal axis wind turbines using graph convolutional autoencoders for multivariate time series. Energy AI 2022, 8, 100145. [Google Scholar] [CrossRef]
- Kim, M.; Song, J.; Kim, C.W. Near-real-time damage identification under vehicle loads using dynamic graph neural network based on proper orthogonal decomposition. Mech. Syst. Signal Process. 2025, 224, 112175. [Google Scholar] [CrossRef]
- Son, H.; Pham, V.T.; Jang, Y.; Kim, S.E. Damage localization and severity assessment of a cable-stayed bridge using a message passing neural network. Sensors 2021, 21, 3118. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Chen, N.Z. G-Twin: Graph neural network-based digital twin for real-time and high-fidelity structural health monitoring for offshore wind turbines. Mar. Struct. 2025, 103, 103813. [Google Scholar] [CrossRef]
- Pollet, M.; Shepherd, P.; Hawkins, W.; Costa, E. Fast Structural Analysis of Concrete Thin-Shells Using Deep Learning. Preprint 2025. [Google Scholar] [CrossRef]
- Cui, H.; Du, H.; Zhao, F.; Hong, M. Damage identification in a plate structure based on a cross-direction strain measurement method. Measurement 2020, 158, 107714. [Google Scholar] [CrossRef]
- Peeters, B.; De Troyer, T.; Guillaume, P.; Van der Auweraer, H. In-flight modal analysis-a comparison between sweep and turbulence excitation. In Proceedings of the ISMA2006: International Conference on Noise and Vibration Engineering, Heverlee, Belgium, 18–20 September 2006; pp. 1627–1641. [Google Scholar]
- Brincker, R.; Andersen, P. Understanding stochastic subspace identification. In Proceedings of the IMAC-XXIV: A Conference & Exposition on Structural Dynamics, St Louis, MI, USA, 30 January–2 February 2006; Society for Experimental Mechanics: Bethel, CT, USA, 2006. [Google Scholar]
- Civera, M.; Sibille, L.; Fragonara, L.Z.; Ceravolo, R. A DBSCAN-based automated operational modal analysis algorithm for bridge monitoring. Measurement 2023, 208, 112451. [Google Scholar] [CrossRef]
- Wu, C.; Liu, H.; Qin, X.; Wang, J. Stabilization diagrams to distinguish physical modes and spurious modes for structural parameter identification. J. Vibroengineering 2017, 19, 2777–2794. [Google Scholar] [CrossRef]
- McLachlan, G.; Ng, S.; Peel, D. On clustering by mixture models. In Exploratory Data Analysis in Empirical Research, Proceedings of the 25th Annual Conference of the Gesellschaft für Klassifikation eV, Munich, Germany, 14–16 March 2001; Springer: Berlin/Heidelberg, Germany, 2003; pp. 141–148. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Bessadok, A.; Mahjoub, M.A.; Rekik, I. Graph neural networks in network neuroscience. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5833–5848. [Google Scholar] [CrossRef]
- Corso, G.; Stark, H.; Jegelka, S.; Jaakkola, T.; Barzilay, R. Graph neural networks. Nat. Rev. Methods Prim. 2024, 4, 17. [Google Scholar] [CrossRef]
- Wang, T. Poisson-disk sampling: Theory and applications. In Encyclopedia of Computer Graphics and Games; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1424–1431. [Google Scholar]
- Ruby, U.; Yendapalli, V. Binary cross entropy with deep learning technique for image classification. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 5393–5397. [Google Scholar] [CrossRef]
- Fuglede, B.; Topsoe, F. Jensen-Shannon divergence and Hilbert space embedding. In Proceedings of the International Symposium on Information Theory, ISIT, Washington, DC, USA, 27 June–2 July 2004; p. 31. [Google Scholar]
- Sbarra, R.G.; Del Priore, E.; Coppotelli, G.; Lampani, L.; Pasquali, M. On the Use of Fiber Optic Sensors and Operational Modal Analysis for Structural Health Monitoring in Aerospace Structures. In Proceedings of the ISMA 2024—International Conference on Noise and Vibration Engineering and USD 2024—International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 9–11 September 2024; pp. 2346–2358. [Google Scholar]
- Llugsi, R.; El Yacoubi, S.; Fontaine, A.; Lupera, P. Comparison between Adam, AdaMax and Adam W optimizers to implement a Weather Forecast based on Neural Networks for the Andean city of Quito. In Proceedings of the 2021 IEEE Fifth Ecuador Technical Chapters Meeting (ETCM), Cuenca, Ecuador, 12 October 2021; pp. 1–6. [Google Scholar]
- Michelucci, U.; Venturini, F. Estimating neural network’s performance with bootstrap: A tutorial. Mach. Learn. Knowl. Extr. 2021, 3, 357–373. [Google Scholar] [CrossRef]
- Shahbazi, M. An Efficient Virtual Testing Framework to Simulate the Progression of Damage in Notched Composite Laminates. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2017. [Google Scholar]









| Material | [MPa] | [MPa] | [MPa] | Density [kg/mm3] | |
|---|---|---|---|---|---|
| Twill | 47,000 | 47,000 | 3420 | 0.062 | |
| Unidirectional | 141,000 | 11,000 | 5500 | 0.280 |
| Mode # | Frequency [Hz] |
|---|---|
| 1 | 12.25 |
| 2 | 49.65 |
| 3 | 91.79 |
| 4 | 105.51 |
| 5 | 111.40 |
| Metric | Value | 95% CI |
|---|---|---|
| Accuracy | 0.954 | [0.934, 0.969] |
| Precision | 0.963 | [0.921, 0.978] |
| Recall | 0.937 | [0.916, 0.966] |
| F1 Score | 0.945 | [0.922, 0.963] |
| Input Features | AUC | 95% CI |
|---|---|---|
| Modal + Geometric | 0.970 | [0.954, 0.982] |
| Modal only | 0.958 | [0.936, 0.975] |
| Configuration | Mean [mm] | Standard Deviation [mm] | 95% CI [mm] |
|---|---|---|---|
| Modal + Geometric | 42.69 | 44.83 | [39.15, 46.44] |
| Modal only | 88.41 | 66.21 | [83.38, 93.54] |
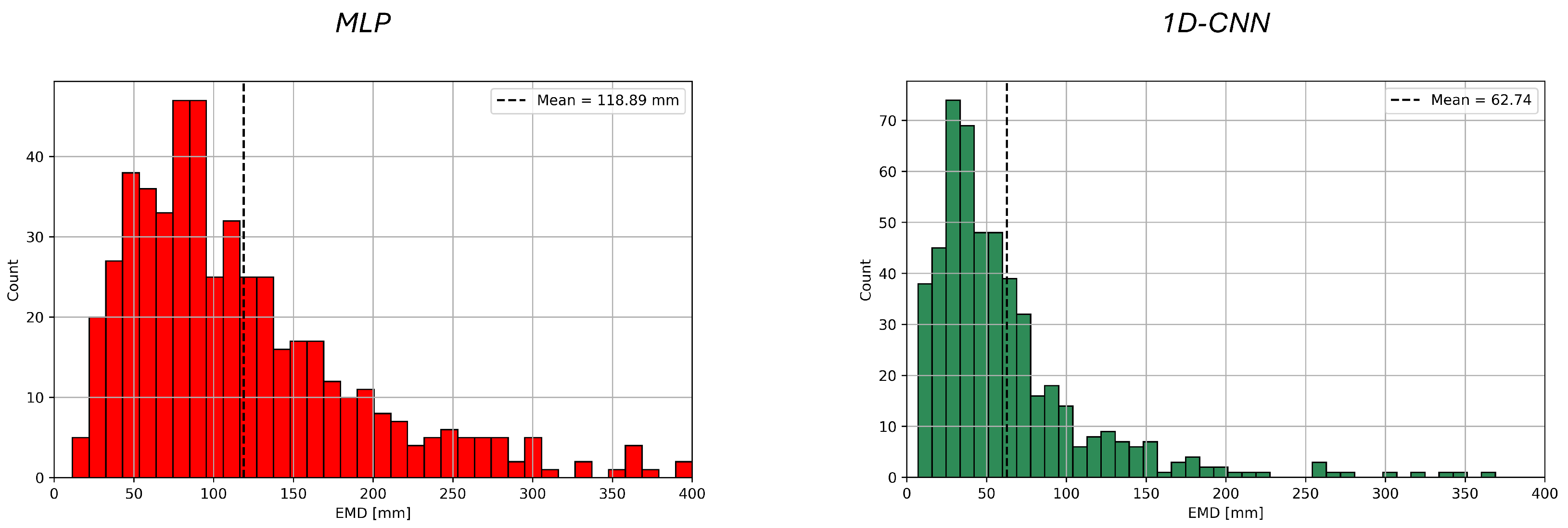
| Model | Mean [mm] | Standard Deviation [mm] | 95% CI [mm] |
|---|---|---|---|
| GNN | 42.69 | 44.83 | [39.15, 46.44] |
| MLP | 118.89 | 79.39 | [112.11, 125.78] |
| 1D-CNN | 62.74 | 54.77 | [58.09, 67.58] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Priore, E.; Lampani, L. Real-Time Damage Detection and Localization on Aerospace Structures Using Graph Neural Networks. J. Sens. Actuator Netw. 2025, 14, 89. https://doi.org/10.3390/jsan14050089
Del Priore E, Lampani L. Real-Time Damage Detection and Localization on Aerospace Structures Using Graph Neural Networks. Journal of Sensor and Actuator Networks. 2025; 14(5):89. https://doi.org/10.3390/jsan14050089
Chicago/Turabian StyleDel Priore, Emiliano, and Luca Lampani. 2025. "Real-Time Damage Detection and Localization on Aerospace Structures Using Graph Neural Networks" Journal of Sensor and Actuator Networks 14, no. 5: 89. https://doi.org/10.3390/jsan14050089
APA StyleDel Priore, E., & Lampani, L. (2025). Real-Time Damage Detection and Localization on Aerospace Structures Using Graph Neural Networks. Journal of Sensor and Actuator Networks, 14(5), 89. https://doi.org/10.3390/jsan14050089






