The Age–Period–Cohort Problem in Hedonic House Prices Models
Abstract
:1. Introduction
2. Literature Review
3. Research Design
4. Empirical Data and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | There is no consensus among scholars as to who first introduced the hedonic regression. Most of the scholars agree that it was Court (1939) using hedonic pricing method to explain the weighting of the relative importance of the various components of automobile and presented the automobile price indices for 1920 to 1939, whereas another group of scholars pioneered by Colwell and Dilmore (1999) demonstrate that Haas (1922) conducted a hedonic study seventeen years prior to Court (1939) despite the term ‘hedonic’ had never been used. |
| 2 | https://www.sfu.ca/~pendakur/teaching/buec333/Multicollinearity%20and%20Endogeneity.pdf, accessed on 4 November 2021. |
| 3 | Cohort analysis is a technique used in various areas of science (e.g., demography, epidemiology, sociology, and biostatistics) in which statistical attempts are made to partition (variance in) the outcome on an independent variable into the unique components attributable to APC effects. Vintage analysis can be viewed as a variant of cohort analysis, which is commonly used in real estate research. Subtle differences may exist between these two terms, but they are used interchangeably in this study. |
| 4 | O’Brien (2011, pp. 1431–32, Table 1 and Table 2) presents a cohort table for the case of 4 periods and 4 age groups that elucidate both problems. |
| 5 | The proportion of houses cohorts in the neighbourhood is such external information (constraints) imposed on the estimation. |
| 6 | Rehm et al. (2019), on the other hand, take repair works on the leaky housing cohorts as a proxy variable for a particular cohort effect. |
| 7 | Bathrooms effect ranges from 3.7% to 7.3%, Bedrooms effect ranges from 7.9% to 14.0%, Floor Area effect ranges from 6.31 × 10−5% to 1.12 × 10−4%, Land Area effect ranges from −6.49 × 10−4% to −2.02 × 10−3%, Wide Water View effect (relative to Moderate Other View) ranges from 32.3% to 38.1%, Wide Other View effect (relative to Moderate Other View) ranges from 4.7% to 6.1%, Moderate Water View effect (relative to Moderate Other View) ranges from 12.5% to 14.3%, and Slight or No View (relative to Moderate Other View) ranges from −4.1% to −3.1%. |
References
- Bosman, Merijn. 2012. The Potential of Cohort Analysis for Vintage Analysis: An Exploration. Master’s thesis, University of Twente, Enschede, The Netherlands, January 23. [Google Scholar]
- Cannaday, Roger E., Henry J. Munneke, and Tyler T. Yang. 2005. A Multivariate Repeat-Sales Model for Estimating House Price Indices. Journal of Urban Economics 57: 320–42. [Google Scholar] [CrossRef]
- Chau, Kwong Wing, Siu Kei Wong, and Chung Yim Yiu. 2005. Adjusting for Non-Linear Age Effects in the Repeat Sales Index. Journal of Real Estate Finance and Economics 31: 137–54. [Google Scholar] [CrossRef] [Green Version]
- Cheung, Ka Shing, and Chung Yim Edward Yiu. 2022. The Economics of Architectural Aesthetics: Identifying Price Effect of Urban Ambiences by Different House Cohorts. Environment and Planning B: Urban Analytics and City Science. forthcoming. [Google Scholar]
- Chinloy, Peter T. 1977. Hedonic Price and Depreciation Indexes for Residential Housing: A Longitudinal Approach. Journal of Urban Economics 4: 469–82. [Google Scholar] [CrossRef]
- Clapp, John M., and Carmelo Giaccotto. 1998. Residential Hedonic Models: A Rational Expectations Approach to Age Effects. Journal of Urban Economics 44: 415–37. [Google Scholar] [CrossRef]
- Colwell, Peter F., and Gene Dilmore. 1999. Who was first? An examination of an early hedonic study. Land Economics 75: 620–26. [Google Scholar] [CrossRef]
- Coulson, N. Edward, and Daniel P. McMillen. 2008. Estimating time, age and vintage effects in housing prices. Journal of Housing Economics 17: 138–51. [Google Scholar] [CrossRef]
- Court, Andrew. 1939. Hedonic Price Indexes with Automotive Examples. New York: The Dynamics of Automobile Demand, General Motors, pp. 98–119. [Google Scholar]
- de Vaus, David A. 2001. Research Design in Social Research. London: Sage Publications. [Google Scholar]
- Denton, Frank T., Denton C. Mountain, and Byron G. Spencer. 1999. Age, trend, and cohort effects in a macro model of Canadian expenditure patterns. Journal of Business and Economic Statistics 17: 430–43. [Google Scholar]
- Englund, Peter, John M. Quigley, and Christian L. Redfearn. 1998. Improved Price Indexes for Real Estate: Measuring the Course of Swedish Housing Prices. Journal of Urban Economics 44: 171–96. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, Mario A. 2019. A Review of Applications of Hedonic Pricing Models in the New Zealand Housing Market. Auckland: Auckland Council. [Google Scholar]
- Francke, Marc K., and Alex M. van de Minne. 2017. Land, structure and depreciation. Real Estate Economics 45: 415–51. [Google Scholar] [CrossRef]
- Gallimore, Paul, Michael Fletcher, and Matthew Carter. 1996. Modelling the Influence of Location on Value. Journal of Property Valuation and Investment 14: 6–19. [Google Scholar] [CrossRef]
- Goodman, Allen C., and Thomas G. Thibodeau. 1995. Age-related heteroskedasticity in hedonic house price equations. Journal of Housing Research 6: 25–42. [Google Scholar]
- Haas, George Casper. 1922. A Statistical Analysis of Farm Sales in Blue Earth County, Minnesota, as a Basis for Farm Land Appraisal (No. 1693-2016-137481). Available online: https://ageconsearch.umn.edu/record/184329/files/Haas1.pdf (accessed on 13 October 2021).
- Hall, Robert E. 1971. The Measurement of Quality Change from Vintage Price Data. In Price Indexes and Quality Change: Studies in New Methods of Measurement. Edited by Zvi Griliches. Cambridge: Harvard University Press. [Google Scholar]
- Hencher, S. R., J. T. Tyson, and P. Hutchinson. 2005. Investigating substandard piles in Hong Kong. In Forensic Engineering: The Investigation of Failures. Edited by Brian S. Neale. London: Institute of Civil Engineers. [Google Scholar]
- Hobcraft, John, Jane Menken, and Samuel Preston. 1985. Using Longitudinal Data to Estimate Age, Period and Cohort Effects in Earnings Equations. In Cohort Analysis in Social Research: Beyond the Identification Problem. Edited by William M. Mason and Stephen E. Fienberg. New York: Springer. [Google Scholar]
- Intriligator, Michael D., Ronald G. Bodkin, and Cheng Hsiao. 1996. Econometric Models, Techniques and Applications, 2nd ed. Upper Saddle River: Prentice-Hall. [Google Scholar]
- Kennedy, Peter. 2003. A Guide to Econometrics, 5th ed. Cambridge: MIT Press. [Google Scholar]
- Keyes, Katherine M., Rebecca L. Utz, Whitney Robinson, and Guohua Li. 2010. What is a cohort effect? Comparison of Three Statistical Methods for Modeling Cohort Effects in Obesity Prevalence in the United States, 1971–2006. Social Science & Medicine 70: 1100–8. [Google Scholar]
- Mason, William M., and Nicholas H. Wolfinger. 2001. Cohort Analysis. In International Encyclopaedia of the Social and Behavioural Sciences. Edited by Neil J. Smelser and Paul B. Baltes. Oxford: Elsevier Science, pp. 151–228. [Google Scholar]
- McKenzie, David J. 2006. Disentangling Age, Cohort and Time Effects in the Additive Model. Oxford Bulletin of Economics and Statistics 68: 473–95. [Google Scholar] [CrossRef]
- O’Brien, Robert M. 2011. The age–period–cohort conundrum as two fundamental problems. Quality & Quantity 45: 1429–44. [Google Scholar]
- Palmquist, Raymond B. 1979. Hedonic Price and Depreciation Indexes for Residential Housing: A Comment. Journal of Urban Economics 6: 267–71. [Google Scholar] [CrossRef]
- PricewaterhouseCoopers. 2009. Weathertightness—Estimating the Cost, for the Department of Building and Housing. London: PricewaterhouseCoopers (PwC), Available online: https://www.interest.co.nz/sites/default/files/PWC-leaky%20homes%20report.pdf (accessed on 13 October 2021).
- Quigley, John M. 1995. A Simple Hybrid Model for Estimating Real Estate Price Indices. Journal of Housing Economics 4: 1–12. [Google Scholar] [CrossRef] [Green Version]
- Randolph, William C. 1988. Housing Depreciation and Aging Bias in the Consumer Price Index. Journal of Business and Economic Statistics 6: 359–71. [Google Scholar]
- Rehm, Michael, Ka Shing Cheung, Olga Filippova, and Dipesh Patel. 2019. Stigma, risk perception and the remediation of leaky homes in New Zealand. New Zealand Economic Papers 54: 89–105. [Google Scholar] [CrossRef]
- Rodgers, Willard L. 1982a. Estimable Functions of Age, Period and Cohort Effects. American Sociological Review 47: 774–87. [Google Scholar] [CrossRef]
- Rosen, Sherwin. 1974. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. Journal of Political Economy 82: 34–55. [Google Scholar] [CrossRef]
- Rubin, Geoffrey M. 1993. Is Housing Age a Commodity? Hedonic Price Estimates of Unit Age. Journal of Housing Research 4: 165–84. [Google Scholar]
- Sirmans, G. Stacy, Lynn Macdonald, David A. Macpherson, and Emily Norman Zietz. 2006. The Value of Housing Characteristics: A Meta Analysis. The Journal of Real Estate Finance and Economics 33: 215–40. [Google Scholar] [CrossRef]
- Smith, Herbert L. 2008. Advances in age-period-cohort analysis. Sociological Methods & Research 36: 287–96. [Google Scholar]
- Waddell, Paul, Brian J. L. Berry, and Kyoun Sup Chung. 1996. Variations in Housing Price Depreciation: The “Taste for Newness” Across Heterogeneous Submarkets. Urban Geography 17: 269–80. [Google Scholar] [CrossRef]
- Yang, Yang. 2010. Aging, Cohorts, and Methods. In Handbook of Aging and the Social Sciences. Edited by Robert H. Binstock and Linda K. George. London: Elsevier Academic Press, pp. 17–29. [Google Scholar]
- Yang, Yang, and Kenneth C. Land. 2008. Age-Period-Cohort Analysis of Repeated Cross-Section Surveys: Fixed or Random Effects? Sociological Methods & Research 36: 297. [Google Scholar]
- Yiu, Chung Yim. 2009. Disentanglement of Age, Time, and Vintage Effects on Housing Price by Forward Contracts. Journal of Real Estate Literature 17: 273–91. [Google Scholar] [CrossRef]
- Yiu, Chung Yim Edward, and Ka Shing Cheung. 2021. A housing price index with the improvement-value adjusted repeated sales (IVARS) method. International Journal of Housing Markets and Analysis. [Google Scholar] [CrossRef]
| Panel A | Mean | SD. | Min | Max |
| 490,575.90 | 446,307.30 | 11,000.00 | 9,985,000.00 | |
| 33.25 | 26.25 | 0.00 | 119.00 | |
| Improvement Value (NZ$) | 191,378.00 | 156,458.00 | 0.00 | 5,710,000.00 |
| Panel B | Count | Percent | Desc: COHORTS | |
| 8193 | 1.52 | Houses built in the 1900s | ||
| 16,455 | 3.06 | Houses built in the 1910s | ||
| 26,369 | 4.90 | Houses built in the 1920s | ||
| 13,461 | 2.50 | Houses built in the 1930s | ||
| 20,307 | 3.78 | Houses built in the 1940s | ||
| 56,916 | 10.59 | Houses built in the 1950s | ||
| 75,927 | 14.12 | Houses built in the 1960s | ||
| 75,895 | 14.12 | Houses built in the 1970s | ||
| 77,216 | 14.36 | Houses built in the 1980s | ||
| 98,176 | 18.26 | Houses built in the 1990s | ||
| 68,764 | 12.79 | Houses built in the 2000s | ||
| Fixed Effects | Count | |||
| 265 | Suburbs in the Auckland Region | |||
| 360 | January 1990–December 2019 | |||
| Equations | Equation (6) | Equation (7) | Equation (8) | Equation (9) |
|---|---|---|---|---|
| Dep. Var. | ln | |||
| Variables | Coefficients (t-stat) | |||
| Age-in-years, | 0.0019 (0.0002) | −0.0013 (−10.375) *** | −0.0003 (−18.520) *** | - |
| Period-in-year, | - | - | - | - |
| Cohort year, | 0.0023 (0.0002) | - | - | - |
| Dummies of | ||||
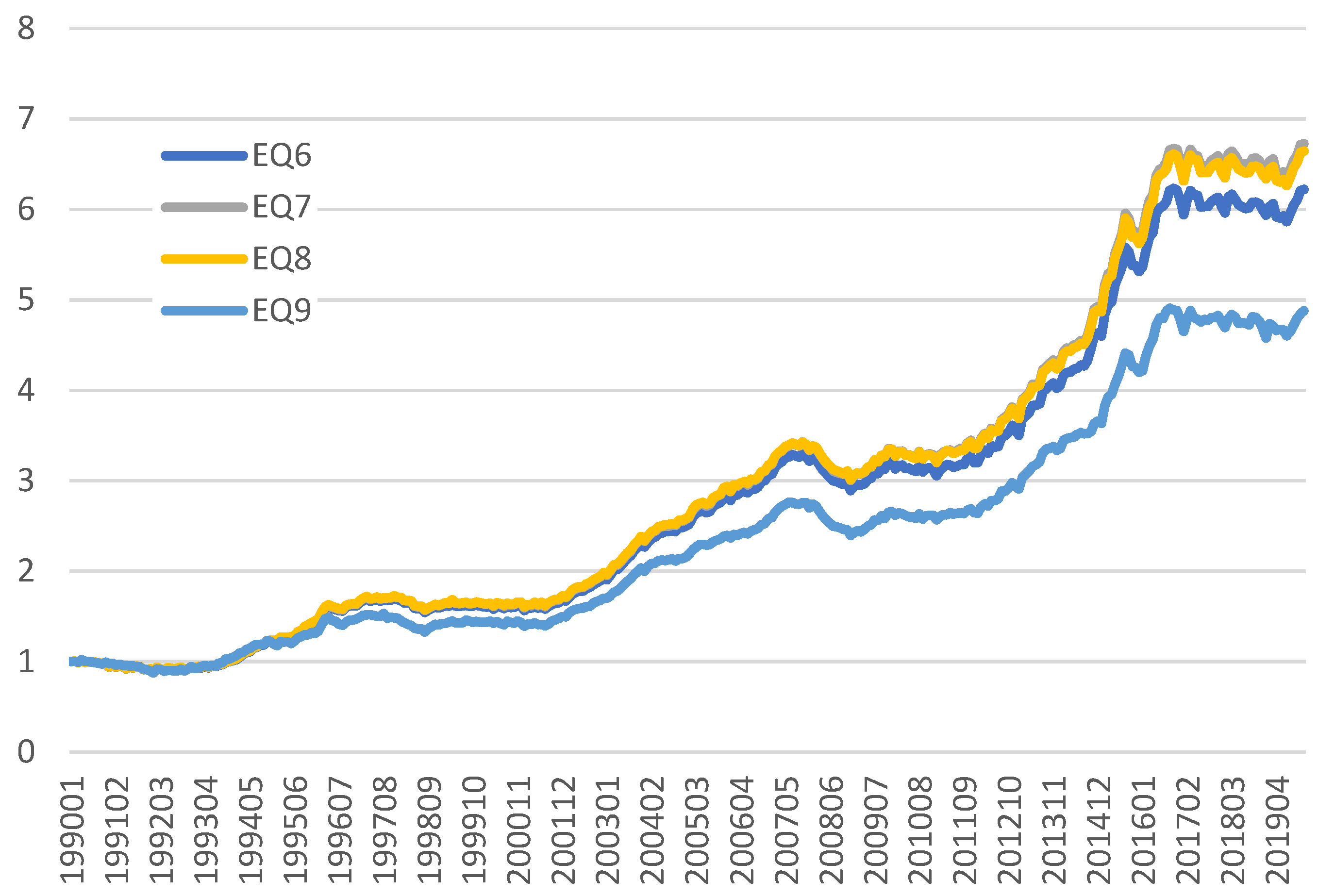
| Period-in-month, | Figure 1 (Mostly Insign.) | Figure 1 (Mostly sign.) | Figure 1 (Mostly sign.) | Figure 1 (Mostly sign.) |
| Cohort-in-decade | ||||
| - | 0.173 (13.180) | - | 0.145 (45.239) *** | |
| - | 0.174 (14.828) *** | - | 0.162 (66.048) *** | |
| - | 0.089 (8.722) *** | - | 0.120 (60.181) *** | |
| - | 0.051 (5.607) ** | - | 0.119 (48.667) *** | |
| - | −0.041 (−5.187) *** | - | 0.081 (38.486) *** | |
| - | −0.058 (−9.086) *** | - | 0.057 (36.513) *** | |
| - | −0.071 (−13.803) *** | - | 0.034 (23.220) *** | |
| - | −0.085 (−21.512) *** | - | 0.008 (5.246) *** | |
| - | −0.085 (−30.962) *** | - | −0.020 (−14.054) *** | |
| - | −0.029 (−16.700) *** | - | −0.013 (−9.980) *** | |
| ln | - | - | - | 0.307 (357.027) *** |
| Centred VIF for Age Variable | UICM | 92.018 > 10 | 1.724 < 10 | |
| Centred VIF for Period Variables | UICM | 1.612–4.228 All < 10 | 1.596–4.089 All < 10 | 1.675–7.020 All < 10 |
| Centered VIF for Cohort Variables | UICM | 3.763–41.183 80% > 10 | 1.376–2.540 All < 10 | |
| 2.639 < 10 | ||||
| No. of Obs. | 536,858 | 536,858 | 536,858 | 427,646 |
| Adj. R-Squared | 0.871 | 0.875 | 0.871 | 0.898 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yiu, C.-Y.; Cheung, K.-S. The Age–Period–Cohort Problem in Hedonic House Prices Models. Econometrics 2022, 10, 4. https://doi.org/10.3390/econometrics10010004
Yiu C-Y, Cheung K-S. The Age–Period–Cohort Problem in Hedonic House Prices Models. Econometrics. 2022; 10(1):4. https://doi.org/10.3390/econometrics10010004
Chicago/Turabian StyleYiu, Chung-Yim, and Ka-Shing Cheung. 2022. "The Age–Period–Cohort Problem in Hedonic House Prices Models" Econometrics 10, no. 1: 4. https://doi.org/10.3390/econometrics10010004
APA StyleYiu, C.-Y., & Cheung, K.-S. (2022). The Age–Period–Cohort Problem in Hedonic House Prices Models. Econometrics, 10(1), 4. https://doi.org/10.3390/econometrics10010004





_Cheung.jpeg)

