Inference of Impulse Responses via Bayesian Graphical Structural VAR Models
Abstract
:1. Introduction
2. SVAR and Impulse Response Analysis
2.1. SVAR Model
2.2. Impulse Response Analysis via VAR
2.2.1. Orthogonalized Impulse Response—OIR
2.2.2. Generalized Impulse Response—GIR
2.3. Graphical Structural VAR (GSVAR)
3. Bayesian Graphical SVAR Model Estimation
3.1. Prior on Network Parameters
3.2. Posterior Inference of Network Parameters
- Sample via a Metropolis-within-Gibbs by the following:
- (a)
- Sampling from the marginal distribution: .
- (b)
- Sampling from the conditional distribution: .
- Estimate given and Z following the conventional normal-inverse Wishart prior distribution for a seemingly unrelated regression (SUR). The posterior expectations of and are as follows:where is the -th row and -columns of , is that number of elements in , corresponds the dependent variable, and and are the lag predictors of according to . is the estimate of the reduced-form error for the -th equation. is the -th row and -columns of , corresponds to the predictors of according to , and is a diagonal matrix of the prior covariance. The posterior of is Wishart distributed with degrees of freedom.
4. Modeling Macroeconomic Time Series
4.1. Data
4.2. Model Specification
- Estimate : Regress on using OLS to obtain , and compute the residuals .
- Estimate and : Regress each residual component on the remaining residuals (i.e., all U excluding ) to obtain and .
- (i)
- DGP-1: Sparse ()−Sparse ();
- (ii)
- DGP-2: Sparse ()−Dense ();
- (iii)
- DGP-3: Dense ()−Sparse ();
- (iv)
- DGP-4: Dense ()−Dense ().
4.3. Methods Compared and Evaluation Criteria
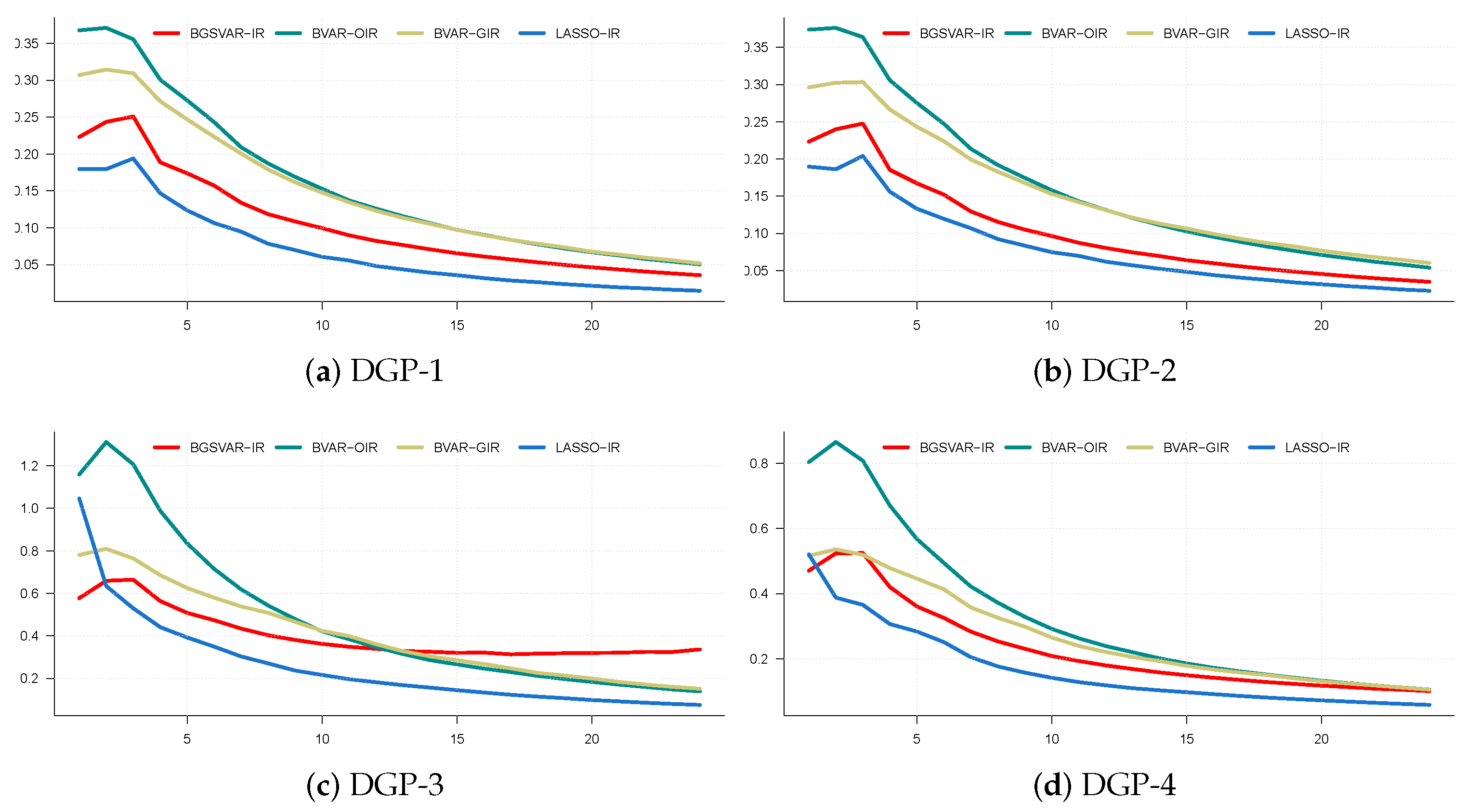
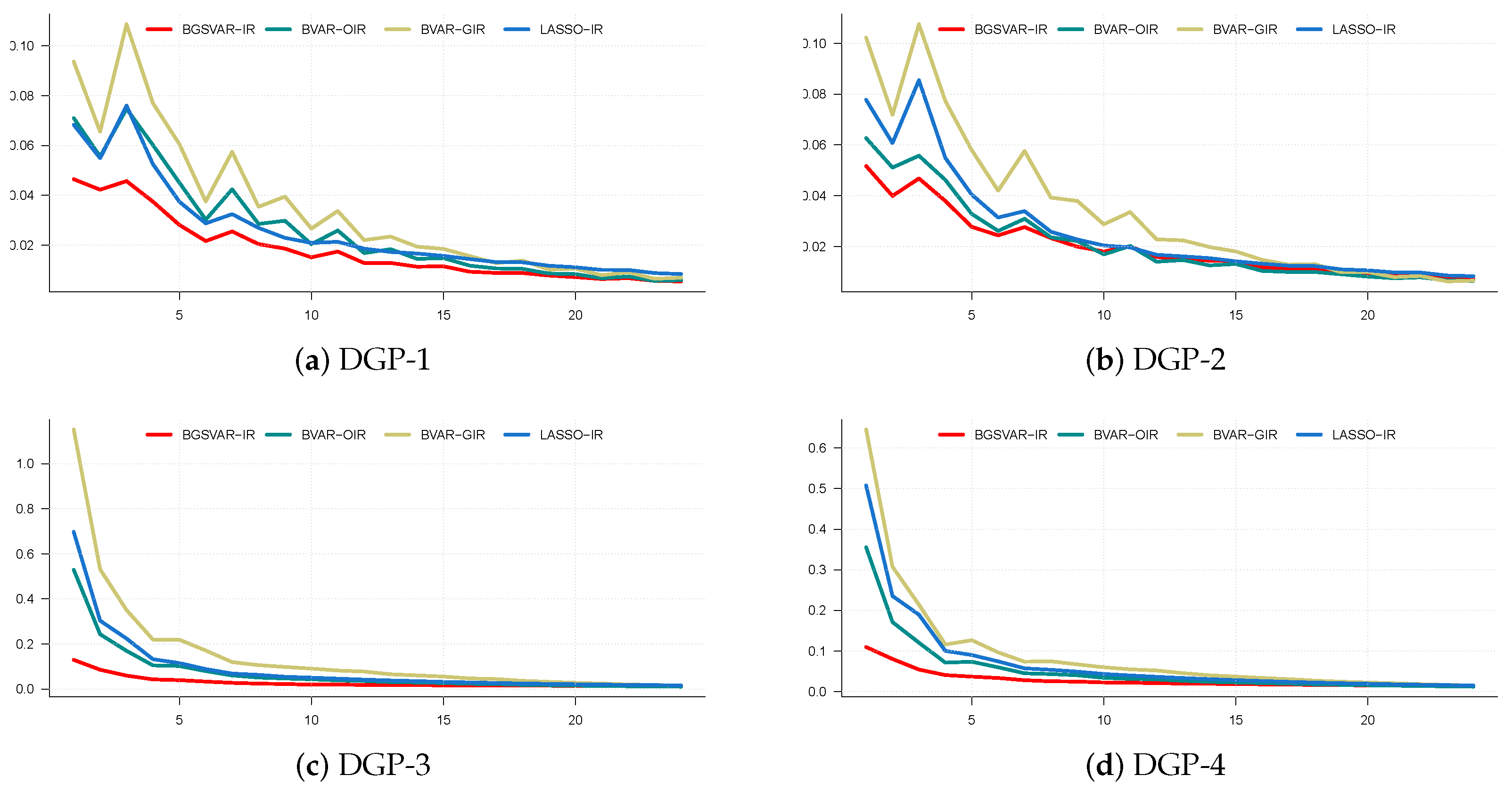
4.4. Simulation Results
4.4.1. VAR Slope Coefficient Matrix
4.4.2. Shock Matrix
4.4.3. Impulse Response Performance
5. Conclusions
Limitations and Future Work
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahelegbey, D. F., Billio, M., & Casarin, R. (2016a). Bayesian graphical models for structural vector autoregressive processes. Journal of Applied Econometrics, 31(2), 357–386. [Google Scholar] [CrossRef]
- Ahelegbey, D. F., Billio, M., & Casarin, R. (2016b). Sparse graphical vector autoregression: A bayesian approach. Annals of Economics and Statistics, 123/124, 333–361. [Google Scholar] [CrossRef]
- Ahelegbey, D. F., & Giudici, P. (2022). NetVIX—A network volatility index of financial markets. Physica A: Statistical Mechanics and Its Applications, 594, 127017. [Google Scholar] [CrossRef]
- Ahelegbey, D. F., Giudici, P., & Hashem, S. Q. (2021). Network VAR models to measure financial contagion. The North American Journal of Economics and Finance, 55, 101318. [Google Scholar] [CrossRef]
- Bai, J., & Ng, S. (2002). Determining the number of factors in approximate factor models. Econometrica, 70(1), 191–221. [Google Scholar] [CrossRef]
- Banbura, M., Giannone, D., & Reichlin, L. (2010). Large bayesian vector autoregressions. Journal of Applied Econometrics, 25, 71–92. [Google Scholar] [CrossRef]
- Bassetti, F., Casarin, R., & Leisen, F. (2014). Beta-product dependent pitman–Yor processes for bayesian inference. Journal of Econometrics, 180(1), 49–72. [Google Scholar] [CrossRef]
- Basu, S., & Michailidis, G. (2015). Regularized estimation in sparse high-dimensional time series models. The Annals of Statistics, 43(4), 1535–1567. [Google Scholar]
- Bernanke, B. S., Boivin, J., & Eliasz, P. S. (2005). Measuring the effects of monetary policy: A factor-augmented vector autoregressive (FAVAR) approach. The Quarterly Journal of Economics, 120(1), 387–422. [Google Scholar] [CrossRef]
- Bernanke, B. S., & Mihov, I. (1998). Measuring monetary policy. The Quarterly Journal of Economics, 113(3), 869–902. [Google Scholar]
- Billio, M., Casarin, R., & Rossini, L. (2019). Bayesian nonparametric sparse var models. Journal of Econometrics, 212(1), 97–115. [Google Scholar] [CrossRef]
- Blanchard, O. J., & Quah, D. (1989). The dynamic effects of aggregate demand and supply disturbances. The American Economic Review, 79(4), 655–673. [Google Scholar]
- Canova, F., & Ciccarelli, M. (2004). Forecasting and turning point predictions in a bayesian panel VAR model. Journal of Econometrics, 120(2), 327–359. [Google Scholar] [CrossRef]
- Canova, F., & De Nicolo, G. (2002). Monetary disturbances matter for business fluctuations in the G-7. Journal of Monetary Economics, 49(6), 1131–1159. [Google Scholar] [CrossRef]
- Casarin, R., Iacopini, M., Molina, G., Ter Horst, E., Espinasa, R., Sucre, C., & Rigobon, R. (2020). Multilayer network analysis of oil linkages. The Econometrics Journal, 23(2), 269–296. [Google Scholar] [CrossRef]
- Celani, A., Pagnottoni, P., & Jones, G. (2024). Bayesian variable selection for matrix autoregressive models. Statistics and Computing, 34(2), 91. [Google Scholar] [CrossRef]
- Choi, C.-Y., & Chudik, A. (2019). Estimating impulse response functions when the shock series is observed. Economics Letters, 180, 71–75. [Google Scholar] [CrossRef]
- Christiano, L. J., Eichenbaum, M., & Evans, C. L. (1999). Monetary policy shocks: What have we learned and to what end? In J. B. Taylor, & M. Woodford (Eds.), Handbook of macroeconomics (Vol. 1, pp. 65–148). Elsevier. [Google Scholar]
- Cimadomo, J., Giannone, D., Lenza, M., Monti, F., & Sokol, A. (2022). Nowcasting with large bayesian vector autoregressions. Journal of Econometrics, 231(2), 500–519. [Google Scholar] [CrossRef]
- Corander, J., & Villani, M. (2006). A Bayesian approach to modelling graphical vector autoregressions. Journal of Time Series Analysis, 27(1), 141–156. [Google Scholar] [CrossRef]
- Davis, R. A., Zang, P., & Zheng, T. (2016). Sparse vector autoregressive modeling. Journal of Computational and Graphical Statistics, 25(4), 1077–1096. [Google Scholar] [CrossRef]
- Demiralp, S., & Hoover, K. D. (2003). Searching for the causal structure of a vector autoregression. Oxford Bulletin of Economics and Statistics, 65, 745–767. [Google Scholar] [CrossRef]
- Diebold, F., & Yilmaz, K. (2014). On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics, 182(1), 119–134. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting, 28(1), 57–66. [Google Scholar] [CrossRef]
- Eichenbaum, M., & Evans, C. L. (1995). Some empirical evidence on the effects of shocks to monetary policy on exchange rates. The Quarterly Journal of Economics, 110(4), 975–1009. [Google Scholar] [CrossRef]
- Eichler, M. (2007). Granger causality and path diagrams for multivariate time series. Journal of Econometrics, 137(2), 334–353. [Google Scholar] [CrossRef]
- Faust, J. (1998). The robustness of identified VAR conclusions about money. In Carnegie-rochester conference series on public policy (Vol. 49, pp. 207–244). North-Holland. [Google Scholar]
- Forni, M., Hallin, M., Lippi, M., & Reichlin, L. (2005). The generalized dynamic factor model: One-Sided estimation and forecasting. Journal of the American Statistical Association, 100(471), 830. [Google Scholar] [CrossRef]
- Gefang, D. (2014). Bayesian doubly adaptive elastic-net lasso for VAR shrinkage. International Journal of Forecasting, 30(1), 1–11. [Google Scholar] [CrossRef]
- Geiger, D., & Heckerman, D. (2002). Parameter priors for directed acyclic graphical models and the characterization of several probability distributions. Annals of Statistics, 30(5), 1412–1440. [Google Scholar] [CrossRef]
- Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences, (with discussion). Statistical Science, 7, 457–511. [Google Scholar] [CrossRef]
- Jordà, Ò. (2005). Estimation and inference of impulse responses by local projections. American Economic Review, 95(1), 161–182. [Google Scholar] [CrossRef]
- Jordà, Ò. (2023). Local projections for applied economics. Annual Review of Economics, 15(1), 607–631. [Google Scholar] [CrossRef]
- Jordà, Ò., & Taylor, A. M. (2025). Local projections. Journal of Economic Literature, 63(1), 59–110. [Google Scholar]
- Kalli, M., & Griffin, J. E. (2018). Bayesian nonparametric vector autoregressive models. Journal of Econometrics, 203(2), 267–282. [Google Scholar] [CrossRef]
- Karlsson, S. (2013). Forecasting with bayesian vector autoregressions. In G. Elliott, & A. Timmermann (Eds.), Handbook of economic forecasting (Vol. 2, pp. 689–1324). Elsevier. [Google Scholar]
- Kilian, L. (2009). Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market. American Economic Review, 99(3), 1053–1069. [Google Scholar] [CrossRef]
- Kilian, L. (2013). Structural vector autoregressions. In N. Hashimzade, & M. Thornton (Eds.), Handbook of research methods and applications in empirical macroeconomics (pp. 515–554). Edward Elgar Publishing. [Google Scholar]
- Kilian, L., & Kim, Y. J. (2011). How reliable are local projection estimators of impulse responses? Review of Economics and Statistics, 93(4), 1460–1466. [Google Scholar] [CrossRef]
- King, R. G., Plosser, C. I., Stock, J. H., & Watson, M. W. (1991). Stochastic trends and economic fluctuations. American Economic Review, 81, 819–840. [Google Scholar]
- Kock, A. B., & Callot, L. (2015). Oracle inequalities for high dimensional vector autoregressions. Journal of Econometrics, 186(2), 325–344. [Google Scholar] [CrossRef]
- Koop, G., & Korobilis, D. (2016). Model uncertainty in panel vector autoregressive models. European Economic Review, 81, 115–131. [Google Scholar] [CrossRef]
- Koop, G., Korobilis, D., & Pettenuzzo, D. (2019). Bayesian compressed vector autoregressions. Journal of Econometrics, 210(1), 135–154. [Google Scholar] [CrossRef]
- Koop, G., Pesaran, M. H., & Potter, S. M. (1996). Impulse response analysis in nonlinear multivariate models. Journal of Econometrics, 74(1), 119–147. [Google Scholar] [CrossRef]
- Korobilis, D. (2013). VAR forecasting using bayesian variable selection. Journal of Applied Econometrics, 28(2), 204–230. [Google Scholar] [CrossRef]
- Korobilis, D. (2022). A new algorithm for structural restrictions in bayesian vector autoregressions. European Economic Review, 148, 104241. [Google Scholar] [CrossRef]
- Li, D., Plagborg-Møller, M., & Wolf, C. K. (2024). Local projections vs. VARs: Lessons from thousands of DGPs. Journal of Econometrics, 244(2), 105722. [Google Scholar] [CrossRef]
- Lopes, H. F., & Carvalho, C. M. (2007). Factor stochastic volatility with time varying loadings and markov switching regimes. Journal of Statistical Planning and Inference, 137(10), 3082–3091. [Google Scholar] [CrossRef]
- Medeiros, M. C., & Mendes, E. F. (2016). L1-regularization of high-dimensional time-series models with non-gaussian and heteroskedastic errors. Journal of Econometrics, 191(1), 255–271. [Google Scholar] [CrossRef]
- Pesaran, H. H., & Shin, Y. (1998). Generalized impulse response analysis in linear multivariate models. Economics Letters, 58(1), 17–29. [Google Scholar] [CrossRef]
- Pesaran, M. H., Schuermann, T., & Weiner, S. M. (2004). Modelling regional interdependencies using a global error-correcting macroeconometric model. Journal of Business and Economic Statistics, 22(2), 129–162. [Google Scholar] [CrossRef]
- Plagborg-Møller, M., & Wolf, C. K. (2021). Local projections and VARs estimate the same impulse responses. Econometrica, 89(2), 955–980. [Google Scholar] [CrossRef]
- Sims, C. A. (1980). Macroeconomics and reality. Econometrica, Econometric Society, 48(1), 1–48. [Google Scholar] [CrossRef]
- Stock, J. H., & Watson, M. W. (2002). Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association, 97(460), 1167–1179. [Google Scholar] [CrossRef]
- Stock, J. H., & Watson, M. W. (2018). Identification and estimation of dynamic causal effects in macroeconomics using external instruments. The Economic Journal, 128(610), 917–948. [Google Scholar] [CrossRef]
- Suppes, P. (1970). A probabilistic theory of causality. North-Holland Pub. Co. [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288. [Google Scholar] [CrossRef]
- Uhlig, H. (2005). What are the effects of monetary policy on output? Results from an agnostic identification procedure. Journal of Monetary Economics, 52(2), 381–419. [Google Scholar] [CrossRef]
- Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2), 301–320. [Google Scholar] [CrossRef]






| No. | Variable | Transformation | FRED Id | Code |
|---|---|---|---|---|
| 1 | Economic policy uncertainty | USEPUINDXM | EPU | |
| 2 | Employment | PAYEMS | EMP | |
| 3 | Unemployment rate | UNRATE | UNR | |
| 4 | Avg. weekly hours | AWHNONAG | HRS | |
| 5 | Industrial production | INDPRO | IP | |
| 6 | CPI inflation | CPIAUCSL | CPI | |
| 7 | Loans | BUSLOANS | LOA | |
| 8 | Housing starts | HOUST | HS | |
| 9 | Private consumption | PCE | PC | |
| 10 | PCE price index | PCEPI | PCE | |
| 11 | Real disp. personal income | DSPIC96 | DPI | |
| 12 | Fed. funds rate | FEDFUNDS | FF | |
| 13 | Credit spread | BAA10YM | BAA | |
| 14 | Total reserves | TOTRESNS | TRS | |
| 15 | Real M1 money stock | M1REAL | M1 |
| # | Model | Description | Structural Assumptions |
|---|---|---|---|
| 1 | BGSVAR-IR | BGSVAR + IR | Sparse ()−Sparse () |
| 2 | BVAR-OIR | BVAR + OIRF | Dense ()−Cholesky () |
| 3 | BVAR-GIR | BVAR + GIRF | Dense ()−Dense () |
| 4 | LASSO-IR | LASSO-VAR + IRF | Sparse ()−Sparse () |
| h | BGSVAR-IR | BVAR-OIR | BVAR-GIR | LASSO-IR | |
|---|---|---|---|---|---|
| DGP-1 | 1.4758 | 2.2833 | 2.0968 | 1 | |
| 1.7044 | 2.6109 | 2.5530 | 1 | ||
| 2.4368 | 3.4333 | 3.5384 | 1 | ||
| DGP-2 | 1.2719 | 2.0683 | 1.8724 | 1 | |
| 1.2974 | 2.122 | 2.1174 | 1 | ||
| 1.5215 | 2.3536 | 2.6283 | 1 | ||
| DGP-3 | 1.3558 | 2.0467 | 1.6591 | 1 | |
| 1.8660 | 1.9078 | 1.9866 | 1 | ||
| 4.4813 | 1.8479 | 2.0159 | 1 | ||
| DGP-4 | 1.2959 | 1.9693 | 1.6462 | 1 | |
| 1.5176 | 2.0208 | 1.8672 | 1 | ||
| 1.7328 | 1.8186 | 1.8118 | 1 |
| h | BGSVAR-IR | BVAR-OIR | BVAR-GIR | LASSO-IR | |
|---|---|---|---|---|---|
| DGP-1 | 1 | 1.3950 | 1.7341 | 1.3277 | |
| 1 | 1.3108 | 1.7150 | 1.4481 | ||
| 1 | 1.0909 | 1.2723 | 1.5377 | ||
| DGP-2 | 1 | 1.0721 | 1.7214 | 1.2878 | |
| 1.1327 | 1 | 1.6255 | 1.1929 | ||
| 1.0967 | 1 | 1.0162 | 1.2814 | ||
| DGP-3 | 1 | 2.4003 | 5.1577 | 2.6716 | |
| 1 | 1.9571 | 4.2454 | 2.2892 | ||
| 1.1822 | 1 | 1.4845 | 1.5540 | ||
| DGP-4 | 1 | 1.7935 | 2.9006 | 2.2331 | |
| 1 | 1.4542 | 2.5316 | 1.7729 | ||
| 1.0865 | 1 | 1.2464 | 1.2447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahelegbey, D.F. Inference of Impulse Responses via Bayesian Graphical Structural VAR Models. Econometrics 2025, 13, 15. https://doi.org/10.3390/econometrics13020015
Ahelegbey DF. Inference of Impulse Responses via Bayesian Graphical Structural VAR Models. Econometrics. 2025; 13(2):15. https://doi.org/10.3390/econometrics13020015
Chicago/Turabian StyleAhelegbey, Daniel Felix. 2025. "Inference of Impulse Responses via Bayesian Graphical Structural VAR Models" Econometrics 13, no. 2: 15. https://doi.org/10.3390/econometrics13020015
APA StyleAhelegbey, D. F. (2025). Inference of Impulse Responses via Bayesian Graphical Structural VAR Models. Econometrics, 13(2), 15. https://doi.org/10.3390/econometrics13020015






