Forecasting Asset Returns Using Nelson–Siegel Factors Estimated from the US Yield Curve
Abstract
1. Introduction
2. Methodology
2.1. Fitting the Nelson–Siegel Model to the US Yield Curve
2.2. Yield Curve Forecasting
2.2.1. AR(1) Model
2.2.2. Joint VAR(1) Model
2.2.3. Random Walk Model for Yields
2.2.4. AR(1) Model for Yields
2.2.5. Slope Regression Model
2.2.6. VAR(1) Model for Yields
2.2.7. VAR(1) Model for Yield Changes
2.2.8. AR(1) Model for Principal Components
2.3. Returns Forecasting
2.4. Measuring and Testing (Equal) Predictive Accuracy
2.5. Combination Forecasts With and Without NS Factors
- Dividend–Price Ratio (log), D/P: The logarithmic difference between total dividends paid on the S&P 500 index and the index’s price level, where dividends are aggregated over a rolling one-year period.
- Dividend Yield (log), D/Y: The log of dividends minus the log of lagged S&P 500 prices.
- Earnings–Price Ratio (log), E/P: The difference between the logarithm of S&P 500 earnings (measured over a trailing 12-month period) and the log of stock prices.
- Dividend–Earnings Ratio (log), D/E: Logarithmic gap between dividend payments and earnings on the S&P 500 index.
- Stock Variance, SVAR: The cumulative sum of squared daily returns on the S&P 500 index over a given month.
- Book-to-Market Ratio, B/M: The ratio between book value and market capitalization of the Dow Jones Industrial Average firms.
- Net Equity Issuance, NTIS: The ratio of 12-month cumulative net stock issuance by NYSE-listed firms to their total year-end market value.
- Treasury Bill Rate, TBL: Yield on three-month U.S. Treasury bills traded in the secondary market.
- Long-Term Yield, LTY: Yield on long-term government bonds.
- Long-Term Return, LTR: Realized return from investing in long-term government bonds.
- Term Spread, TMS: The difference between long-term government bond yields and short-term Treasury bill rates.
- Default Yield Spread, DFY: The yield spread between BAA-rated and AAA-rated corporate bonds.
- Default Return Spread, DFR: The difference in returns between long-term corporate and long-term government bonds.
- Inflation, INFL: Computed using the Consumer Price Index (CPI) for urban consumers. Following Welch and Goyal (2008), inflation is lagged by one month to account for release timing and used as in the regressions.
3. Data Description
3.1. US Treasury Yields
3.2. US Treasury Returns
3.3. US Equity Returns
3.4. US REIT Returns
3.5. US Corporate Bond Returns
3.6. Commodity Returns
3.7. Summary Statistics
4. Empirical Results
4.1. Yield Curve Forecasting
4.2. Forecasting Treasury Returns
4.3. Forecasting Equity Portfolio Returns
4.4. Forecasting REIT Returns
4.5. Forecasting Corporate Bond Returns
4.6. Forecasting Commodity Returns
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Diebold–Mariano and Model Confidence Set Tests
Appendix B. Summary Statistics
| Panel A: Treasury Rates | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| 3 Months | 372 | 2.692 | 2.225 | 0.000 | 8.070 | 2.286 | 0.341 |
| 6 Months | 372 | 2.818 | 2.360 | 0.030 | 8.440 | 2.320 | 0.324 |
| 1 Year | 372 | 2.943 | 2.475 | 0.090 | 8.580 | 2.326 | 0.303 |
| 2 Years | 372 | 3.230 | 2.865 | 0.110 | 8.960 | 2.354 | 0.289 |
| 3 Years | 372 | 3.441 | 3.130 | 0.110 | 9.050 | 2.312 | 0.276 |
| 5 Years | 372 | 3.831 | 3.710 | 0.210 | 9.040 | 2.203 | 0.248 |
| 7 Years | 372 | 4.135 | 4.015 | 0.390 | 9.060 | 2.115 | 0.243 |
| 10 Years | 372 | 4.370 | 4.335 | 0.550 | 9.040 | 2.012 | 0.238 |
| Panel B: Treasury Returns | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| 3 Months | 371 | 0.226 | 0.193 | −0.017 | 0.698 | 0.195 | 0.377 |
| 6 Months | 371 | 0.242 | 0.197 | −0.060 | 0.876 | 0.217 | 0.556 |
| 1 Year | 371 | 0.445 | 0.205 | −5.024 | 12.214 | 1.985 | 1.326 |
| 2 Years | 371 | 0.483 | 0.336 | −6.957 | 9.110 | 2.327 | 0.355 |
| 3 Years | 371 | 0.505 | 0.398 | −8.362 | 8.550 | 2.480 | 0.065 |
| 5 Years | 371 | 0.534 | 0.485 | −8.637 | 9.317 | 2.542 | −0.025 |
| 7 Years | 371 | 0.551 | 0.480 | −8.611 | 9.892 | 2.481 | −0.064 |
| 10 Years | 371 | 0.562 | 0.413 | −8.346 | 11.054 | 2.380 | 0.085 |
| Panel C | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| Fama and French Factor Portfolios | |||||||
| SMB | 370 | 0.092 | 0.115 | −16.720 | 21.130 | 3.143 | 0.633 |
| HML | 370 | 0.191 | −0.050 | −9.050 | 14.110 | 3.074 | 0.761 |
| Mkt | 370 | 0.891 | 1.385 | −17.150 | 13.650 | 4.352 | −0.641 |
| Industry Portfolios | |||||||
| Food | 371 | 0.913 | 1.020 | −14.560 | 15.140 | 3.962 | −0.286 |
| Mines | 371 | 0.846 | 0.740 | −32.740 | 22.450 | 7.919 | −0.284 |
| Oil | 371 | 0.701 | 0.670 | −34.810 | 32.820 | 6.280 | 0.003 |
| Textiles | 371 | 1.040 | 1.280 | −22.140 | 23.270 | 6.150 | −0.216 |
| Consumer Durables | 371 | 0.808 | 1.070 | −25.770 | 29.240 | 5.777 | −0.217 |
| Chemicals | 371 | 0.897 | 1.240 | −21.930 | 22.300 | 5.886 | −0.193 |
| Consumer | 371 | 1.001 | 1.380 | −10.130 | 15.630 | 4.156 | −0.179 |
| Construction | 371 | 1.137 | 1.510 | −20.200 | 17.920 | 5.871 | −0.248 |
| Steel | 371 | 0.669 | 0.710 | −32.910 | 30.670 | 8.333 | −0.230 |
| Fabricated Products | 371 | 1.033 | 1.360 | −23.030 | 18.820 | 5.473 | −0.496 |
| Machinery | 371 | 1.178 | 1.670 | −28.320 | 19.320 | 6.938 | −0.514 |
| Cars | 371 | 1.097 | 0.980 | −28.430 | 38.710 | 7.194 | 0.536 |
| Transportation | 371 | 1.023 | 1.510 | −22.680 | 19.700 | 5.196 | −0.621 |
| Utilities | 371 | 0.799 | 1.230 | −13.020 | 11.720 | 3.965 | −0.645 |
| Retail Stores | 371 | 1.080 | 1.010 | −14.590 | 18.240 | 4.776 | −0.070 |
| Financials | 371 | 0.973 | 1.590 | −22.100 | 17.100 | 5.647 | −0.623 |
| Other | 371 | 0.918 | 1.600 | −17.790 | 15.310 | 4.941 | −0.489 |
| Size and Value | |||||||
| Ptf 1 | 370 | 0.500 | 0.937 | −27.845 | 38.321 | 7.982 | 0.209 |
| Ptf 2 | 370 | 1.080 | 1.454 | −21.521 | 42.421 | 7.013 | 0.442 |
| Ptf 3 | 370 | 0.982 | 1.370 | −21.929 | 21.057 | 5.740 | −0.344 |
| Ptf 4 | 370 | 1.159 | 1.470 | −26.786 | 26.369 | 5.615 | −0.344 |
| Ptf 5 | 370 | 1.166 | 1.330 | −27.820 | 16.381 | 5.801 | −0.721 |
| Ptf 6 | 370 | 0.875 | 1.527 | −25.775 | 28.115 | 7.024 | −0.308 |
| Ptf 7 | 370 | 1.045 | 1.581 | −23.116 | 18.785 | 5.775 | −0.518 |
| Ptf 8 | 370 | 1.042 | 1.529 | −21.257 | 16.062 | 5.191 | −0.661 |
| Ptf 9 | 370 | 0.974 | 1.788 | −23.772 | 16.193 | 5.295 | −0.822 |
| Ptf 10 | 370 | 1.025 | 1.771 | −32.144 | 26.019 | 6.333 | −0.776 |
| Ptf 11 | 370 | 0.929 | 1.721 | −23.097 | 23.130 | 6.485 | −0.436 |
| Ptf 12 | 370 | 1.091 | 1.454 | −21.509 | 18.969 | 5.335 | −0.418 |
| Ptf 13 | 370 | 0.978 | 1.465 | −17.847 | 16.757 | 4.879 | −0.555 |
| Ptf 14 | 370 | 1.077 | 1.522 | −26.854 | 16.936 | 5.168 | −0.752 |
| Ptf 15 | 370 | 1.055 | 1.382 | −31.175 | 19.058 | 5.885 | −0.815 |
| Ptf 16 | 370 | 1.116 | 1.380 | −20.840 | 26.044 | 5.816 | −0.175 |
| Ptf 17 | 370 | 1.054 | 1.364 | −20.165 | 15.899 | 4.873 | −0.713 |
| Ptf 18 | 370 | 0.931 | 1.462 | −25.327 | 15.515 | 5.010 | −0.867 |
| Ptf 19 | 370 | 1.002 | 1.604 | −31.427 | 16.233 | 5.025 | −1.128 |
| Ptf 20 | 370 | 0.899 | 1.832 | −32.802 | 18.336 | 5.830 | −0.961 |
| Ptf 21 | 370 | 1.013 | 1.078 | −14.776 | 15.356 | 4.437 | −0.298 |
| Ptf 22 | 370 | 0.911 | 1.313 | −17.049 | 13.691 | 4.168 | −0.540 |
| Ptf 23 | 370 | 0.931 | 1.469 | −17.308 | 12.570 | 4.246 | −0.623 |
| Ptf 24 | 370 | 0.605 | 1.151 | −27.164 | 15.878 | 5.025 | −1.209 |
| Ptf 25 | 370 | 0.846 | 1.330 | −28.401 | 21.494 | 6.218 | −0.572 |
| Operating Profits and Investments | |||||||
| Ptf 26 | 371 | 0.929 | 1.305 | −25.258 | 27.048 | 6.967 | −0.085 |
| Ptf 27 | 371 | 0.629 | 1.009 | −25.572 | 15.998 | 5.420 | −0.599 |
| Ptf 28 | 371 | 0.970 | 1.266 | −31.152 | 18.713 | 5.712 | −0.764 |
| Ptf 29 | 371 | 0.924 | 1.884 | −26.366 | 18.620 | 6.106 | −0.711 |
| Operating Profits and Investments | |||||||
| Ptf 30 | 371 | 0.485 | 1.201 | −27.414 | 18.763 | 6.832 | −0.598 |
| Ptf 31 | 371 | 0.945 | 1.098 | −19.474 | 21.352 | 5.180 | −0.238 |
| Ptf 32 | 371 | 1.010 | 1.486 | −20.912 | 17.886 | 4.983 | −0.383 |
| Ptf 33 | 371 | 0.824 | 1.244 | −24.368 | 18.783 | 5.243 | −0.920 |
| Ptf 34 | 371 | 1.004 | 1.255 | −20.014 | 23.141 | 5.258 | −0.163 |
| Ptf 35 | 371 | 0.822 | 1.189 | −20.749 | 27.256 | 5.612 | −0.180 |
| Ptf 36 | 371 | 0.932 | 1.393 | −23.239 | 15.767 | 5.105 | −0.572 |
| Ptf 37 | 371 | 1.032 | 1.269 | −22.021 | 16.520 | 4.746 | −0.522 |
| Ptf 38 | 371 | 0.990 | 1.433 | −20.939 | 13.858 | 4.505 | −0.781 |
| Ptf 39 | 371 | 0.975 | 1.296 | −21.704 | 16.741 | 4.745 | −0.643 |
| Ptf 40 | 371 | 0.863 | 1.700 | −24.746 | 16.446 | 5.825 | −0.714 |
| Ptf 41 | 371 | 1.241 | 1.599 | −21.235 | 15.446 | 4.563 | −0.449 |
| Ptf 42 | 371 | 1.034 | 1.227 | −13.247 | 15.350 | 3.826 | −0.171 |
| Ptf 43 | 371 | 0.947 | 1.201 | −14.485 | 12.952 | 4.242 | −0.413 |
| Ptf 44 | 371 | 1.077 | 1.569 | −17.855 | 18.125 | 4.613 | −0.447 |
| Ptf 45 | 371 | 1.103 | 1.342 | −23.784 | 18.896 | 5.565 | −0.412 |
| Ptf 46 | 371 | 1.184 | 1.534 | −17.225 | 15.081 | 4.588 | −0.258 |
| Ptf 47 | 371 | 0.973 | 1.292 | −19.068 | 17.008 | 4.364 | −0.356 |
| Ptf 48 | 371 | 0.914 | 1.142 | −17.249 | 17.431 | 4.253 | −0.354 |
| Ptf 49 | 371 | 1.103 | 1.233 | −16.588 | 12.851 | 4.537 | −0.352 |
| Size and Cash flow | |||||||
| Ptf 50 | 371 | 1.170 | 1.349 | −20.308 | 20.017 | 5.884 | −0.332 |
| Ptf 51 | 371 | 0.992 | 1.690 | −21.650 | 19.520 | 5.876 | −0.375 |
| Ptf 52 | 371 | 1.125 | 1.720 | −22.920 | 16.670 | 4.961 | −0.709 |
| Ptf 53 | 371 | 1.122 | 1.690 | −31.130 | 21.000 | 5.663 | −0.816 |
| Ptf 54 | 371 | 1.024 | 1.390 | −15.670 | 14.360 | 4.522 | −0.355 |
| Size and Dividend yield | |||||||
| Ptf 55 | 371 | 0.898 | 1.350 | −15.380 | 12.570 | 4.139 | −0.573 |
| Ptf 56 | 371 | 0.935 | 1.350 | −23.610 | 15.190 | 4.594 | −0.816 |
| Ptf 57 | 371 | 1.103 | 1.800 | −20.890 | 15.930 | 5.180 | −0.646 |
| Ptf 58 | 371 | 1.010 | 1.560 | −20.440 | 16.210 | 4.821 | −0.633 |
| Ptf 59 | 371 | 0.992 | 1.320 | −23.460 | 21.840 | 4.644 | −0.608 |
| Size and Price to Earnings ratio | |||||||
| Ptf 60 | 371 | 0.894 | 1.210 | −20.310 | 16.100 | 4.861 | −0.492 |
| Ptf 61 | 371 | 0.968 | 1.230 | −15.550 | 12.900 | 4.063 | −0.555 |
| Ptf 62 | 371 | 0.868 | 1.030 | −16.750 | 14.960 | 4.072 | −0.661 |
| Ptf 63 | 371 | 1.000 | 1.700 | −22.510 | 18.860 | 5.928 | −0.415 |
| Ptf 64 | 371 | 1.097 | 1.660 | −22.890 | 17.030 | 4.873 | −0.679 |
| Ptf 65 | 371 | 1.138 | 1.640 | −30.890 | 20.050 | 5.536 | −0.844 |
| Ptf 66 | 371 | 0.955 | 1.230 | −15.940 | 13.800 | 4.451 | −0.375 |
| Ptf 67 | 371 | 0.930 | 1.250 | −15.470 | 13.100 | 4.104 | −0.511 |
| Ptf 68 | 371 | 1.046 | 1.580 | −23.590 | 15.950 | 4.788 | −0.829 |
| Ptf 69 | 371 | 0.573 | 0.610 | −29.210 | 47.520 | 8.846 | 0.858 |
| Ptf 70 | 371 | 0.897 | 1.280 | −23.550 | 27.550 | 5.758 | −0.308 |
| Ptf 71 | 371 | 1.137 | 1.670 | −23.430 | 22.480 | 5.190 | −0.538 |
| Ptf 72 | 371 | 1.333 | 1.690 | −24.340 | 20.730 | 5.157 | −0.548 |
| Ptf 73 | 371 | 1.606 | 2.190 | −22.830 | 31.850 | 6.619 | −0.132 |
| Ptf 74 | 371 | 0.737 | 0.760 | −27.730 | 55.850 | 8.728 | 0.607 |
| Ptf 75 | 371 | 1.037 | 1.480 | −25.210 | 33.740 | 6.095 | −0.156 |
| Ptf 76 | 371 | 1.122 | 1.620 | −22.280 | 18.670 | 5.156 | −0.607 |
| Ptf 77 | 371 | 1.218 | 1.630 | −23.070 | 17.670 | 5.183 | −0.565 |
| Ptf 78 | 371 | 1.404 | 1.780 | −25.600 | 30.160 | 6.799 | −0.132 |
| Ptf 79 | 371 | 0.790 | 0.890 | −27.530 | 44.280 | 8.438 | 0.417 |
| Ptf 80 | 371 | 0.970 | 1.440 | −25.020 | 27.060 | 5.820 | −0.350 |
| Ptf 81 | 371 | 1.047 | 1.350 | −22.200 | 23.520 | 5.012 | −0.482 |
| Ptf 82 | 371 | 1.035 | 1.490 | −22.110 | 16.620 | 4.808 | −0.637 |
| Size and Momentum | |||||||
| Ptf 83 | 371 | 1.297 | 1.640 | −21.460 | 26.390 | 6.215 | −0.267 |
| Ptf 84 | 371 | 0.649 | 0.620 | −38.490 | 46.420 | 8.554 | 0.133 |
| Ptf 85 | 371 | 1.016 | 1.420 | −23.550 | 28.880 | 5.738 | −0.161 |
| Ptf 86 | 371 | 1.092 | 1.610 | −22.240 | 17.480 | 4.802 | −0.580 |
| Ptf 87 | 371 | 1.075 | 1.410 | −19.390 | 12.980 | 4.378 | −0.719 |
| Ptf 88 | 371 | 1.245 | 1.430 | −22.170 | 25.080 | 5.631 | −0.338 |
| Ptf 89 | 371 | 0.600 | 0.620 | −31.450 | 30.950 | 7.720 | 0.163 |
| Ptf 90 | 371 | 0.871 | 0.930 | −20.640 | 24.370 | 5.144 | −0.003 |
| Ptf 91 | 371 | 0.899 | 1.130 | −16.890 | 17.540 | 4.211 | −0.329 |
| Ptf 92 | 371 | 0.964 | 1.210 | −14.190 | 15.800 | 4.019 | −0.263 |
| Ptf 93 | 371 | 1.111 | 1.630 | −19.610 | 18.520 | 4.920 | −0.381 |
| Panel D | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| Diversified | 321 | 0.699 | 1.262 | −31.960 | 39.687 | 6.181 | −0.575 |
| Industrial | 321 | 1.232 | 1.528 | −56.188 | 70.483 | 8.254 | 0.264 |
| Lodging/Resorts | 321 | 0.570 | 0.590 | −36.555 | 67.525 | 8.710 | 0.638 |
| Office | 321 | 0.895 | 1.480 | −31.796 | 32.458 | 6.077 | −0.487 |
| Residential | 321 | 1.013 | 1.362 | −26.656 | 22.242 | 5.501 | −0.833 |
| Retail | 321 | 0.846 | 1.086 | −42.678 | 43.516 | 6.701 | −0.985 |
| Self Storage | 321 | 1.326 | 1.616 | −22.244 | 21.928 | 5.584 | −0.364 |
| All REITs | 321 | 0.888 | 1.194 | −30.226 | 27.975 | 5.296 | −0.959 |
| Mortgage REITs | 321 | 0.642 | 1.595 | −53.753 | 19.411 | 6.551 | −2.455 |
| Panel E | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| AAA | 372 | 0.536 | 0.586 | −6.544 | 6.391 | 1.473 | −0.185 |
| AA | 372 | 0.586 | 0.565 | −5.774 | 5.357 | 1.339 | −0.258 |
| BBB | 372 | 0.531 | 0.671 | −10.996 | 6.286 | 1.668 | −1.575 |
| A | 372 | 0.565 | 0.649 | −9.672 | 6.750 | 1.524 | −1.063 |
| Panel F | Observations | Mean | Median | Minimum | Maximum | St. Dev | Skewness |
| Gold | 372 | 0.533 | 0.115 | −18.005 | 16.458 | 4.430 | 0.174 |
| Silver | 372 | 0.866 | 0.235 | −27.958 | 30.462 | 8.371 | 0.199 |
| Platinum | 372 | 0.417 | 0.309 | −42.004 | 24.112 | 6.286 | −0.854 |
| Copper | 372 | 0.582 | 0.421 | −36.150 | 34.064 | 7.181 | 0.044 |
| Brent Crude | 372 | 0.660 | 0.829 | −54.988 | 40.074 | 9.540 | −0.361 |
| Gasoil | 372 | 0.557 | 0.566 | −33.617 | 31.172 | 9.286 | −0.092 |
| Light crude oil | 372 | 0.703 | 0.924 | −54.245 | 88.376 | 10.485 | 1.198 |
| Natural Gas | 372 | 1.132 | 0.512 | −41.616 | 62.613 | 15.197 | 0.568 |
| Cotton | 372 | 0.385 | 0.511 | −36.116 | 24.749 | 8.492 | −0.222 |
| Cocoa | 372 | 0.585 | 0.201 | −28.083 | 34.565 | 8.921 | 0.457 |
| Coffee | 372 | 0.638 | −0.727 | −30.391 | 50.595 | 10.622 | 1.007 |
| Corn | 372 | 0.565 | 0.081 | −31.380 | 22.190 | 7.976 | −0.185 |
| Lumber | 372 | 1.091 | 0.485 | −34.030 | 58.416 | 11.205 | 0.674 |
| Soybean Oil | 372 | 0.444 | 0.242 | −24.461 | 26.862 | 6.933 | 0.039 |
| Soybeans | 372 | 0.485 | 0.434 | −32.867 | 19.573 | 7.010 | −0.491 |
| Wheat | 372 | 0.637 | 0.204 | −25.248 | 42.335 | 8.608 | 0.516 |
| Live Cattle | 372 | 0.264 | 0.017 | −25.565 | 40.342 | 5.652 | 0.437 |
Appendix C. Diebold–Mariano Test on Asset Return Series
| Panel A—Diebold–Mariano test comparing AR(1) on NS to listed models | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| 3 Months | 7.283 | 1.736 | 1.517 | −1.826 | −2.140 | −1.875 | −17.772 | −5.762 | −3.419 |
| 6 Months | 6.760 | 2.771 | 2.077 | −0.786 | −4.413 | −2.878 | −16.321 | −5.688 | −3.373 |
| 1 Year | 4.887 | 2.489 | 1.046 | 0.940 | −0.026 | −0.082 | −0.331 | −0.054 | −0.089 |
| 2 Years | 4.056 | 2.256 | 1.130 | 0.903 | 0.405 | −0.026 | 0.384 | 0.402 | −0.021 |
| 3 Years | 3.059 | 1.628 | 0.786 | 0.529 | 0.328 | −0.195 | 0.323 | 0.325 | −0.193 |
| 5 Years | 1.391 | 0.374 | −0.185 | −0.294 | −0.041 | −0.677 | −0.323 | −0.045 | −0.664 |
| 7 Years | 0.559 | −0.208 | −0.630 | −0.595 | −0.177 | −0.924 | −0.810 | −0.186 | −0.896 |
| 10 Years | −0.335 | −0.749 | −0.967 | −0.909 | −0.143 | −0.975 | −1.353 | −0.162 | −0.945 |
| Panel B—Diebold–Mariano test comparing AR(1) on NS vs. listed models | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| SMB | 0.126 | −0.542 | −1.039 | −0.245 | 0.006 | −0.113 | −1.137 | 0.025 | −0.059 |
| HML | 1.314 | 1.387 | 1.107 | −1.489 | −1.039 | −2.176 | −2.247 | −1.869 | −1.048 |
| Mkt | 0.472 | 1.218 | 1.220 | −1.922 | 2.333 | 1.606 | −1.395 | 0.745 | 2.549 |
| Food | 2.698 | 2.504 | 1.742 | 0.930 | 1.613 | 1.606 | 0.945 | 1.679 | 1.659 |
| Mines | −2.193 | −1.363 | −1.399 | 1.068 | 2.369 | 2.022 | 1.184 | 2.364 | 2.030 |
| Oil | −1.573 | −1.955 | −0.684 | 0.192 | 0.460 | 0.935 | −1.081 | −0.519 | 1.048 |
| Textiles | 2.530 | 2.341 | 1.697 | −0.368 | 1.777 | 1.735 | 0.442 | 1.759 | 1.835 |
| Consumer Durables | −2.381 | −1.343 | 0.545 | 0.592 | 1.017 | 1.302 | −0.038 | 1.077 | 1.366 |
| Chemicals | 1.407 | 1.458 | 1.039 | −0.490 | 0.644 | 1.001 | −0.351 | −0.675 | 1.085 |
| Steel | 1.068 | 1.902 | −1.839 | −2.504 | 0.554 | 1.156 | −0.902 | −1.129 | −0.678 |
| Consumer | 0.826 | −0.061 | −0.094 | 0.592 | 1.017 | 1.302 | −0.038 | 1.077 | 1.366 |
| Construction | 0.826 | −0.061 | −0.094 | 0.592 | 1.017 | 1.302 | −0.038 | 1.077 | 1.366 |
| Steel | 1.474 | 1.525 | 0.807 | −0.435 | 1.696 | 2.370 | −0.848 | −1.662 | 2.197 |
| Fabricated Products | −1.408 | −1.357 | −1.381 | −2.364 | 1.399 | 1.588 | −0.957 | 1.496 | −1.670 |
| Machinery | 1.263 | 1.027 | 0.209 | −0.567 | 1.386 | 1.364 | −0.723 | −1.931 | −1.384 |
| Cars | −1.498 | −1.579 | −1.417 | −1.068 | 1.227 | 1.525 | −1.566 | 1.249 | 1.544 |
| Transportation | 1.397 | 1.282 | 1.070 | −1.066 | 1.209 | 1.756 | −0.686 | 1.235 | 1.904 |
| Utilities | −0.712 | −1.517 | −2.243 | −2.775 | 1.277 | 1.254 | −2.444 | −1.877 | −1.087 |
| Retail Stores | 1.269 | 1.430 | 1.833 | −2.512 | 1.234 | 1.634 | −1.742 | 1.092 | 1.643 |
| Financials | 2.085 | 2.302 | 2.081 | 0.210 | 1.304 | 1.724 | 0.293 | 1.322 | 1.770 |
| Other | −0.728 | −0.042 | 0.631 | −2.162 | −0.607 | 1.300 | −2.668 | −1.443 | 1.034 |
| Ptf 1 | −1.042 | −0.875 | −0.369 | −1.516 | 0.655 | 2.206 | −3.251 | 0.537 | 2.125 |
| Ptf 2 | −0.800 | −0.970 | −1.421 | −2.910 | 0.702 | 1.622 | −1.624 | −0.732 | 1.718 |
| Ptf 3 | −0.656 | −0.750 | −0.769 | −2.638 | 0.126 | 0.981 | −1.943 | 0.170 | 1.060 |
| Ptf 4 | −1.106 | −1.035 | −0.711 | −2.329 | −0.243 | 0.221 | −0.944 | −0.208 | 0.267 |
| Ptf 5 | −1.107 | −1.126 | −0.897 | −1.974 | −0.305 | 0.234 | −1.870 | −0.259 | 0.292 |
| Ptf 6 | −1.461 | −0.863 | −0.715 | −2.311 | 1.153 | 2.646 | −2.678 | 1.091 | 2.213 |
| Ptf 7 | 0.410 | 0.578 | −0.046 | −1.534 | 1.470 | 0.902 | −2.169 | 1.388 | 0.773 |
| Ptf 8 | −0.857 | −0.637 | −0.116 | −1.807 | 0.067 | 0.541 | −1.868 | 0.145 | 0.608 |
| Ptf 9 | −0.988 | −0.958 | −0.691 | −2.272 | −0.424 | 0.112 | −1.144 | −0.375 | 0.175 |
| Ptf 10 | −0.353 | −0.442 | −0.515 | −2.196 | −0.125 | 0.724 | −1.203 | −0.047 | −0.885 |
| Ptf 11 | −1.282 | −1.189 | −1.529 | −1.493 | 1.198 | 2.775 | −1.886 | 1.228 | 3.369 |
| Ptf 12 | −1.243 | −0.533 | 0.027 | −1.797 | 0.654 | 1.309 | −0.895 | −0.715 | 1.448 |
| Ptf 13 | −0.337 | 0.038 | −0.277 | −2.253 | −0.058 | 0.709 | −1.799 | 0.074 | 0.939 |
| Ptf 14 | −0.742 | 0.196 | 0.490 | −1.419 | 0.375 | 0.770 | −0.525 | −0.438 | 0.845 |
| Ptf 15 | 0.046 | 0.156 | −0.111 | −2.848 | −1.122 | −0.557 | −1.719 | −1.055 | −0.499 |
| Ptf 16 | −1.201 | −0.746 | −0.997 | −1.978 | 0.854 | 3.021 | −2.192 | 0.790 | 3.791 |
| Ptf 17 | −0.422 | −0.352 | −0.067 | −1.749 | 1.401 | 1.541 | −2.793 | 1.246 | 3.655 |
| Ptf 18 | −0.454 | 0.568 | 0.206 | −1.764 | 0.678 | 1.827 | −1.337 | 0.824 | 2.230 |
| Ptf 19 | −0.992 | −1.519 | −0.867 | −2.611 | −0.730 | −0.021 | −1.821 | −0.659 | 0.083 |
| Ptf 20 | 0.626 | 1.153 | 1.022 | −1.359 | 0.453 | 0.976 | −0.596 | 0.479 | 1.059 |
| Ptf 21 | 1.473 | 2.740 | 1.991 | −1.669 | 0.307 | 1.786 | −1.669 | 0.151 | 1.706 |
| Ptf 22 | 1.714 | 2.310 | 1.483 | 0.170 | 1.420 | 1.812 | −0.092 | 1.425 | 1.888 |
| Ptf 23 | 0.421 | 0.096 | 0.251 | −2.148 | 0.134 | 1.715 | −1.478 | −0.205 | 2.009 |
| Ptf 24 | 1.251 | 0.664 | 0.471 | −0.743 | 0.895 | 1.388 | −0.368 | 0.930 | 1.471 |
| Ptf 25 | 1.097 | 0.768 | 0.838 | −0.521 | 0.824 | 1.455 | −1.851 | 0.833 | 1.509 |
| Ptf 26 | −1.036 | −0.979 | −0.027 | −1.200 | 1.202 | 1.594 | −2.065 | 1.148 | 1.483 |
| Ptf 27 | −0.432 | 0.398 | 2.164 | −0.917 | 0.701 | 1.209 | −0.667 | 0.712 | 1.280 |
| Ptf 28 | 2.111 | 1.729 | 1.234 | −0.718 | 0.782 | 1.019 | −0.104 | 0.798 | 1.033 |
| Ptf 29 | −0.572 | −1.026 | −1.557 | −2.588 | 0.352 | 2.803 | −2.962 | −0.285 | 3.126 |
| Ptf 30 | −1.391 | −0.508 | −0.470 | −1.806 | −0.693 | −0.189 | −2.648 | −0.842 | 0.287 |
| Ptf 31 | 0.110 | 0.357 | −0.005 | −2.030 | −4.420 | −0.751 | −1.676 | −4.702 | −0.713 |
| Ptf 32 | −1.084 | −3.046 | −1.119 | −1.280 | −0.560 | 0.632 | −1.904 | −0.519 | 0.783 |
| Ptf 33 | −0.158 | −0.226 | −0.373 | −1.210 | −0.088 | 0.400 | −2.192 | −0.157 | 0.329 |
| Ptf 34 | 0.295 | 0.865 | 2.266 | −1.154 | 1.115 | 3.148 | −1.695 | 1.112 | 2.939 |
| Ptf 35 | −1.499 | −2.748 | −2.188 | −1.455 | 0.147 | 1.578 | −1.325 | −0.009 | 1.453 |
| Ptf 36 | −0.679 | 0.379 | 1.114 | −1.394 | 1.406 | 5.678 | −1.915 | 1.463 | 5.460 |
| Ptf 37 | 0.714 | 0.615 | 0.486 | −0.812 | −0.246 | 0.248 | −0.835 | −0.175 | 0.323 |
| Ptf 38 | −0.758 | 0.455 | 0.382 | −1.869 | 1.210 | 2.144 | −2.526 | 1.017 | 1.870 |
| Ptf 39 | 3.157 | 2.732 | 2.057 | 1.301 | 2.064 | 2.237 | 0.951 | 2.083 | 2.283 |
| Ptf 40 | −0.319 | −0.968 | −1.168 | −1.693 | −0.805 | −0.052 | −2.180 | −0.830 | −0.082 |
| Ptf 41 | 0.392 | 0.942 | 0.603 | −0.603 | 1.098 | 1.149 | −0.908 | 1.090 | 1.157 |
| Ptf 42 | −0.727 | −0.543 | −0.174 | −0.974 | 0.595 | 2.561 | −2.044 | 0.647 | 2.729 |
| Ptf 43 | 0.655 | 0.174 | 0.421 | −0.637 | 0.600 | 1.712 | −1.266 | 0.662 | 1.985 |
| Ptf 44 | −0.799 | −0.273 | 0.239 | −2.300 | 0.876 | 3.570 | −2.645 | 0.884 | 3.764 |
| Ptf 45 | −1.234 | −3.087 | −2.192 | −0.644 | 0.666 | 4.135 | −2.237 | 0.497 | 4.996 |
| Ptf 46 | 3.401 | 2.968 | 2.602 | 1.590 | 2.107 | 2.423 | 1.252 | 2.167 | 2.472 |
| Ptf 47 | 3.901 | 4.542 | 4.220 | 1.632 | 2.609 | 4.120 | 1.646 | 2.599 | 4.209 |
| Ptf 48 | 0.423 | −0.003 | 0.120 | −1.838 | 0.876 | 1.364 | −1.862 | 0.951 | 1.551 |
| Ptf 49 | −0.191 | 0.074 | 0.414 | −1.104 | 0.831 | 1.579 | −2.720 | 0.824 | 1.669 |
| Ptf 50 | 0.864 | 1.174 | 1.042 | −1.441 | 1.772 | 2.319 | −2.431 | 1.672 | 2.646 |
| Ptf 51 | −0.816 | −0.897 | −1.052 | −2.446 | 0.652 | 2.013 | −1.861 | −0.720 | 2.253 |
| Ptf 52 | −0.717 | −0.617 | −0.611 | −2.865 | −0.231 | 0.326 | −1.236 | −0.147 | 0.430 |
| Ptf 53 | −0.167 | 0.094 | −0.064 | −2.077 | −0.404 | 0.179 | −1.763 | −0.310 | 0.343 |
| Ptf 54 | 1.091 | 1.944 | 1.818 | −1.892 | 0.284 | 1.620 | −1.835 | 0.180 | 1.602 |
| Ptf 55 | 1.830 | 1.968 | 1.374 | −0.031 | 1.395 | 2.055 | −0.017 | 1.402 | 2.163 |
| Ptf 56 | 0.528 | −0.106 | −0.019 | −1.314 | 0.217 | 1.081 | −1.004 | −0.282 | 1.233 |
| Ptf 57 | −0.742 | −0.627 | −0.521 | −2.514 | 0.073 | 0.750 | −1.260 | 0.169 | 0.909 |
| Ptf 58 | −1.143 | −1.136 | −0.893 | −2.518 | 0.196 | 0.710 | −1.842 | 0.247 | 0.803 |
| Ptf 59 | −1.942 | −1.436 | −0.650 | −1.676 | 0.544 | 0.743 | −0.240 | 0.588 | 0.804 |
| Ptf 60 | 1.476 | 1.782 | 1.649 | −0.716 | 1.099 | 1.806 | −0.519 | 1.107 | 1.867 |
| Ptf 61 | 1.224 | 1.042 | 0.967 | −0.076 | 1.001 | 2.157 | −0.760 | 0.993 | 2.301 |
| Ptf 62 | 1.042 | 0.545 | 0.204 | −1.845 | 0.227 | 0.948 | −0.677 | 0.299 | 1.075 |
| Ptf 63 | −0.498 | −0.570 | −0.923 | −2.505 | 0.496 | 1.956 | −1.849 | 0.581 | 2.327 |
| Ptf 64 | −0.762 | −0.562 | −0.491 | −2.937 | −0.079 | 0.564 | −1.298 | −0.008 | 0.686 |
| Ptf 65 | −0.581 | −0.445 | −0.451 | −2.253 | −0.397 | 0.174 | −1.930 | −0.335 | 0.297 |
| Ptf 66 | 1.324 | 2.013 | 1.910 | −1.603 | 0.824 | 1.848 | −1.250 | 0.780 | 1.887 |
| Ptf 67 | 1.307 | 1.409 | 1.063 | −0.253 | 0.990 | 2.175 | −0.610 | 0.981 | 2.323 |
| Ptf 68 | 1.101 | 0.817 | 0.638 | −0.777 | 0.521 | 1.096 | −0.655 | 0.568 | 1.188 |
| Ptf 69 | −0.111 | −0.283 | −0.398 | −1.807 | 1.030 | 1.494 | −1.932 | 0.972 | 1.371 |
| Ptf 70 | −1.116 | −1.208 | −0.735 | −2.382 | 0.443 | 0.752 | −0.774 | 0.443 | 0.793 |
| Ptf 71 | −1.498 | −1.899 | −1.178 | −2.323 | 0.621 | 1.462 | −0.584 | 0.641 | 1.559 |
| Ptf 72 | −0.960 | −1.210 | −1.001 | −2.172 | −0.268 | 0.414 | −1.021 | −0.199 | 0.490 |
| Ptf 73 | −2.198 | −1.564 | −1.096 | −0.993 | 0.388 | 0.758 | −0.202 | −0.426 | 0.801 |
| Ptf 74 | 1.744 | 1.638 | 0.936 | −1.151 | 1.580 | 1.435 | 0.165 | 1.518 | 1.379 |
| Ptf 75 | 1.075 | 1.237 | 0.719 | −1.727 | 1.224 | 0.937 | −0.869 | 1.169 | 0.873 |
| Ptf 76 | −0.516 | −0.138 | −0.254 | −2.455 | 0.233 | 1.672 | −1.551 | 0.312 | 1.951 |
| Ptf 77 | −0.949 | −0.871 | −0.824 | −2.308 | −0.142 | 0.409 | −1.901 | −0.050 | 0.495 |
| Ptf 78 | −1.170 | −0.932 | −1.037 | −1.031 | 0.166 | 0.830 | −0.831 | 0.252 | 0.914 |
| Ptf 79 | 0.737 | 0.563 | 0.128 | −1.576 | 1.334 | 1.634 | −1.342 | 1.294 | 1.475 |
| Ptf 80 | −0.205 | 0.183 | −0.011 | −2.024 | 0.023 | 1.820 | −2.325 | −0.008 | 1.401 |
| Ptf 81 | 1.066 | 1.040 | 1.062 | −1.871 | 0.422 | 0.783 | −0.637 | −0.483 | 0.881 |
| Ptf 82 | −1.342 | 0.049 | 0.451 | −0.290 | 0.493 | 0.730 | −0.198 | 0.563 | 0.796 |
| Ptf 83 | −1.518 | 1.009 | 0.683 | −0.075 | 0.674 | 1.261 | −0.195 | 0.745 | 1.317 |
| Ptf 84 | −1.058 | −0.955 | −1.135 | −1.717 | 0.655 | 1.411 | −1.820 | 0.708 | 1.592 |
| Ptf 85 | −0.515 | 0.147 | 0.219 | −2.104 | 0.307 | 1.354 | −1.506 | 0.307 | 1.562 |
| Ptf 86 | 0.602 | 0.387 | 0.536 | −1.522 | 0.612 | 1.581 | −1.261 | 0.674 | 1.862 |
| Ptf 87 | 0.364 | 0.160 | 0.322 | −1.500 | 0.592 | 1.944 | −1.749 | −0.687 | 2.414 |
| Ptf 88 | −1.199 | −0.564 | −0.862 | −0.562 | 0.636 | 1.475 | −0.749 | 0.707 | 1.565 |
| Ptf 89 | 1.467 | 1.768 | 1.516 | −1.580 | 1.298 | 2.332 | −0.615 | 1.291 | 2.392 |
| Ptf 90 | −0.536 | −0.323 | 0.125 | −1.901 | 0.022 | 1.081 | −2.532 | −0.022 | 1.036 |
| Ptf 91 | 0.895 | 1.284 | 1.055 | −2.489 | 0.151 | 2.307 | −2.666 | −0.143 | 2.191 |
| Ptf 92 | 0.170 | 0.218 | 0.617 | −0.508 | 0.246 | 1.882 | −1.812 | −0.232 | 2.093 |
| Ptf 93 | 1.514 | 2.127 | 1.807 | 0.048 | 1.230 | 1.880 | −0.436 | 1.257 | 1.981 |
| Panel C—Diebold–Mariano test comparing AR(1) on NS vs. listed models | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| Diversified | −0.669 | −0.527 | 1.117 | −2.594 | −0.534 | −1.274 | −1.973 | −0.515 | −1.269 |
| Industrial | −0.576 | 0.370 | 1.847 | −0.371 | 0.349 | 0.390 | −1.499 | −0.353 | 0.375 |
| Lodging/Resorts | −0.994 | 0.204 | 0.710 | −1.736 | −0.142 | −0.337 | −1.824 | −0.139 | −0.323 |
| Office | −0.885 | −0.057 | −0.064 | −2.286 | −1.595 | −0.803 | −1.701 | −1.598 | −0.774 |
| Residential | −0.204 | −0.116 | 0.449 | −1.676 | −0.698 | −1.058 | −2.513 | −0.666 | −1.054 |
| Retail | −1.580 | −0.668 | −0.362 | −1.893 | −0.883 | −1.768 | −1.178 | −0.877 | −1.586 |
| Self Storage | −0.363 | 0.963 | 0.036 | −0.131 | 0.058 | −0.457 | −2.379 | −0.063 | −0.425 |
| All REITs | −0.572 | 0.158 | 1.728 | −2.790 | 0.506 | −0.974 | −1.824 | 0.539 | −0.916 |
| Mortgage REITs | 0.243 | 0.850 | 1.405 | 0.992 | 0.973 | 0.267 | 0.091 | 1.107 | 0.290 |
| Panel D—Diebold–Mariano test comparing AR(1) vs. NS to listed models | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| AAA | 0.720 | 0.357 | 0.386 | −1.169 | −0.076 | −0.314 | −1.117 | −0.072 | −0.290 |
| AA | 1.832 | 0.472 | −0.236 | −1.113 | −0.364 | −0.850 | −0.430 | −0.354 | −0.829 |
| BBB | 1.482 | 0.178 | −0.169 | −0.954 | 0.012 | −0.350 | −0.217 | 0.020 | −0.302 |
| A | 1.505 | 0.219 | −0.340 | −1.884 | −0.291 | −0.710 | −0.484 | −0.289 | −0.683 |
| Panel E—Diebold–Mariano test comparing AR(1) on NS vs. listed models | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| Gold | −1.159 | −1.594 | −1.839 | 0.787 | 1.858 | 1.572 | 0.607 | 1.683 | 1.570 |
| Silver | −0.100 | −1.614 | −1.032 | 0.152 | 5.875 | 2.313 | −0.136 | 3.118 | 2.166 |
| Platinum | 2.183 | 2.147 | 2.748 | 1.460 | 2.563 | 5.188 | 1.893 | 2.549 | 4.752 |
| Copper | −0.346 | −0.214 | −0.283 | 0.515 | 2.712 | 2.393 | 1.747 | 2.605 | 2.412 |
| Brent Crude | 0.785 | 0.171 | −0.004 | 1.339 | 2.513 | 2.538 | 0.729 | 2.498 | 2.458 |
| Gasoil | 0.660 | 0.081 | −0.104 | 1.745 | 1.892 | 2.567 | 0.907 | 1.725 | 2.438 |
| Light crude oil | 0.704 | 0.036 | -0.063 | 0.863 | 2.292 | 3.414 | 0.238 | 2.386 | 2.919 |
| Natural Gas | 0.662 | −1.216 | 0.131 | 0.205 | −1.102 | 1.434 | −0.059 | −1.539 | 1.604 |
| Cotton | −1.218 | −1.386 | −0.857 | 1.402 | 1.283 | 3.114 | 1.158 | 1.201 | 3.421 |
| Cocoa | 0.451 | −0.007 | −0.206 | 1.821 | −0.763 | 0.437 | −0.362 | −0.871 | 0.535 |
| Coffee | −2.830 | −1.829 | −0.898 | 0.068 | 0.411 | 1.632 | −0.295 | 0.104 | 1.685 |
| Corn | −0.061 | 0.470 | 3.181 | 0.325 | −0.647 | 1.662 | −1.077 | −1.144 | 1.776 |
| Lumber | 0.123 | 0.540 | 1.536 | −0.377 | −0.213 | 2.186 | −0.795 | −0.544 | 2.015 |
| Soybean Oil | −0.660 | −0.299 | −0.354 | 1.144 | 1.306 | 2.033 | 0.226 | 0.501 | 1.983 |
| Soybeans | 0.085 | 0.303 | 1.393 | 0.191 | −0.439 | 1.861 | −0.521 | −0.683 | 2.062 |
| Wheat | 0.460 | −0.752 | −0.351 | 0.926 | −0.848 | 2.093 | −0.802 | −0.918 | 2.059 |
| Live Cattle | 0.923 | 0.986 | −0.020 | 1.339 | 0.746 | 1.791 | 0.410 | 0.525 | 1.882 |
| Panel F—Summary of Diebold–Mariano test results | |||||||||
| VAR(1) on NS | AR(1) for Returns | Historical Average | |||||||
| h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | h = 1 | h = 6 | h = 12 | |
| Equity | 4 | 5 | 4 | 52 | 1 | 1 | 49 | 4 | 0 |
| Treasuries | 0 | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 |
| REITs | 1 | 0 | 0 | 6 | 0 | 1 | 6 | 0 | 0 |
| Corporate Bonds | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Commodities | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Model | RMSE (h = 1) | RMSE (h = 6) | RMSE (h = 12) |
|---|---|---|---|
| VAR(1) on NS | 1.88 | 0.22 | 0.03 |
| AR(1) on Yields | 9.30 | 0.93 | 0.44 |
| VAR(1) on Yield Changes | 14.44 | 1.56 | 0.77 |
| Random Walk | 8.07 | 1.03 | 0.54 |
| Slope Regression | 12.75 | 0.60 | 0.84 |
| VAR(1) on Yields | 10.88 | 21.90 | 0.77 |
| Regression on Principal Components | 177.89 | 24.79 | 0.77 |
Appendix D. Combining Forecast with Goyal and Welch Predictors
| Yield Curve | Treasury Returns | Equity Returns | ||||||
| Maturity | GW Predictors | GW + NS Factor | Maturity | GW Predictors | GW + NS Factor | Sector | GW Predictors | GW + NS Factor |
| 3 M | 3.24 *** | 4.77 *** | 3 M | 0.71 *** | 5.77 *** | Mkt | 0.25 ** | 0.13 * |
| 1 Y | 3.32 *** | 4.88 *** | 6 M | 3.38 *** | 5.66 *** | Food | 0.25 | 0.09 |
| 5 Y | 2.54 *** | 3.28 *** | 1 Y | 0.87 *** | 0.95 *** | Mines | 0.06 | 0.13 * |
| 10 Y | 2.25 *** | 3.03 *** | 2 Y | 0.14 | 0.66 ** | Oil | −0.09 | −0.11 |
| 3 Y | 0.08 | 0.32 * | Textiles | 0.25 | 0.06 | |||
| 5 Y | −0.01 | 1.52 ** | Consumer Durables | 0.53 *** | 0.31 * | |||
| 7 Y | 0.04 | 0.08 | Chemicals | 0.14 | 0.09 | |||
| 10 Y | 0.14 | 0.24 | Consumer | 0.45 ** | 0.40 ** | |||
| Construction | 0.21 * | 0.14 | ||||||
| Steel | 0.03 | 0.01 | ||||||
| Fabricated Products | 0.13 | 0.26 * | ||||||
| Machinery | 0.03 | 0.01 | ||||||
| Cars | 0.31 ** | −0.01 | ||||||
| Transportation | 0.16 * | 0.01 | ||||||
| Utilities | −0.09 | −0.17 | ||||||
| Retail Stores | 0.08 | 0.13 | ||||||
| Financials | 0.38 ** | 0.26 * | ||||||
| Other | 0.52 *** | 0.53 ** | ||||||
| REITs | Corporate Bonds | Commodities | ||||||
| Sector | GW Predictors | GW + NS Factor | Rating | GW Predictors | GW + NS Factor | Commodity | GW Predictors | GW + NS Factor |
| Diversified | −0.18 | −0.27 | AAAA | 0.12 | 0.16 | Gold | 0.13 | 0.19 |
| Industrial | −0.09 | −0.79 | AA | 0.45 * | 0.55 * | Silver | 0.10 | 0.04 |
| Lodging/Resorts | 0.33 | 0.32 | BBB | 0.46 * | 0.33 | Platinum | −0.34 | −0.39 |
| Office | −0.21 | −0.23 | A | 0.85 ** | 0.74 * | Copper | −0.30 | −0.33 |
| Residential | −0.07 | −0.23 | Brent Crude | −0.12 | −0.21 | |||
| Retail | −0.17 | −0.07 | Gasoil | −0.26 | −0.35 | |||
| Self Storage | −0.19 | −0.07 | Light crude oil | −0.17 | 0.16 | |||
| All REITs | −0.23 | −0.04 | Natural Gas | 0.01 | 0.20 | |||
| Mortgage REITs | 0.15 * | 0.03 | Cotton | 0.35 ** | 0.09 | |||
| Cocoa | −0.03 | −0.02 | ||||||
| Coffee | −0.15 | −0.18 | ||||||
| Corn | −0.09 | −0.17 | ||||||
| Lumber | 0.38 *** | 0.24 ** | ||||||
| Soybean Oil | −0.06 | −0.20 | ||||||
| Soybeans | −0.09 | −0.15 | ||||||
| Wheat | −0.04 | −0.03 | ||||||
| Live Cattle | −0.04 | −0.11 | ||||||
| 1 | The stochastic discount factor, also called the pricing kernel, is a random variable used in asset pricing to discount future payoffs. It ensures that the expected discounted payoffs equal current asset prices. The SDF captures time value, risk preferences, and market conditions. |
| 2 | Fixing allows us to avoid estimating the baseline NS specification using nonlinear least squares, enhancing the simplicity and robustness of the forecasts obtained from the model. In fact, Diebold et al. (2006) emphasized that NLS estimation can encounter issues such as local minima or convergence failures. |
| 3 | In Equation (4) and in all subsequent forecasting models, we use a caret to denote the final predictions (of factors and yields) that we assign an economic meaning to and that we use to assess the forecast accuracy of the different models. A tilde is used to indicate intermediate-step parameter estimates that are instrumental in computing the final predictions. |
| 4 | In unreported tests, we tried to perform formal model specification searches concerning the number of VAR lags, and in particular investigated the performance for the yield series of a VAR(2) model, finding a similar or uniformly worse predictive performance. |
| 5 | The use of cointegrated VAR models for interest rate forecasting does not consistently outperform other methods. The inclusion of many yields increases model complexity, which can lead to overfitting and poor out-of-sample predictions. Despite improvements like cubic splines and ECM approaches, these models often overlook the fact that bond prices (yields) reflect all available information about future interest rates, limiting their forecasting effectiveness (Duffee, 2013). |
| 6 | In the case of Treasury data, even though an obvious (yet non linear) relationship exists between (the changes in ex ante) yields and (ex post, realized) returns, even when the NS factors are used, the forecast results obtained for returns are not presumed to be the same as the ones obtainable for yields. |
| 7 | Some literature labels this third predictive benchmark as a ”random walk”, which obviously is at odds with the restriction applied to Equation (15). The label derives from the fact that restricting in one obtains the model in (15) with . |
| 8 | These predictors are available at Goyal’s personal site: https://sites.google.com/view/agoyal145/home?authuser=0, accessed on 20 March 2025. |
| 9 | Negative yields, which may arise due to the low interest rate environment or specific technical market factors, such as cash and repurchase agreements in US Treasury markets, were excluded from the CMT calculation. This ensures that the dataset included only positive and economically meaningful yields. |
| 10 | Maturities such as the 1-month, 2-month, 20-year, and 30-year constant maturity rates, which were discontinued during the study period, were excluded. |
| 11 | https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/index.html, accessed on 20 March 2025. |
| 12 | To qualify for inclusion, bonds had to have an investment-grade rating (based on an average of Moody’s, S&P, and Fitch) and meet specific criteria regarding maturity (a remaining maturity of at least one year at the time of inclusion in the index), a fixed coupon schedule (i.e., zero coupon bonds are excluded), and minimum amount outstanding (USD 250 million). The index was capitalization-weighted based on the outstanding amount of each security at the end of each month. |
| 13 | Nonetheless, this is considered partially unrealistic, also in light of the recent results in Kim and Choi (2017). |
| 14 | The sample autocorrelation in the forecast errors further supports these findings, with errors from the AR(1) and VAR(1) models for yields being serially correlated for most maturities and horizons, except for longer maturities (3-, 5-, 7-, and 10-year yields) at one-step-ahead horizons. |
| 15 | Because the results for MCS test are starker and allow us to draw sharper conclusions, in the main text, we present the tables documenting the findings from the MCS methodology and report in an Appendix those from the simpler, but intuitive DM tests. |
| 16 | While the two test statistics used in the MCS procedure, TMax and TR, produced similar results, they differed in the total number of models excluded from the superior set. The TMax statistic tended to exclude fewer models from M* across all forecasting horizons compared to the TR statistic. Using the TMax statistic, we excluded 187, 62, and 181 models from M* across all return series for the one-step-ahead, six-step-ahead, and 12-step-ahead forecasts, respectively. Using the TR statistic, we excluded 229, 76, and 188 models from M* for the same horizons. In the case of the return series, we observed the opposite of what was found for the bond yield series, with the TMax test appearing less selective than the TR statistic. This difference was likely due to the fact that only four models were compared when forecasting returns, whereas up to eight models were compared when forecasting bond yields, making pairwise comparisons based on the TR statistic more powerful than the multivariate comparisons used by the TMax statistic. |
| 17 | As a sub-question, we also explored whether an AR(1) or a VAR(1) model based on (predicted) NS factors could be preferable in forecasting returns. Although no definitive conclusion emerged, our analysis suggested that the two types of models did not exhibit equivalent performance across different asset classes and forecast horizons. In overall terms, the VAR(1) NS tended to outperform the AR(1) NS, particularly in the case of Treasury securities, equities, and corporate bonds. However, the AR(1) NS returned a slightly superior performance in the prediction of REIT returns. As far as the forecast horizon is concerned, the AR(1) NS performance relative to the VAR(1) improved as the horizon lengthened, especially for US Treasuries and corporate bonds. Conversely, the VAR(1) model proved more effective in forecasting REIT returns. |
References
- Campbell, J. Y., & Thompson, S. B. (2008). Predicting excess stock returns out of sample: Can anything beat the historical average? The Review of Financial Studies, 21(4), 1509–1531. [Google Scholar] [CrossRef]
- Chen, Y., & Niu, L. (2014). Adaptive dynamic Nelson–Siegel term structure model with applications. Journal of Econometrics, 180(1), 98–115. [Google Scholar] [CrossRef]
- Christensen, J. H. E., Diebold, F. X., & Rudebusch, G. D. (2011). The affine arbitrage-free class of Nelson–Siegel term structure models. Journal of Econometrics, 164(1), 4–20. [Google Scholar] [CrossRef]
- Clark, T. E., & West, K. D. (2007). Approximately normal tests for equal predictive accuracy in nested models. Journal of Econometrics, 138(1), 291–311. [Google Scholar] [CrossRef]
- Diebold, F. X., & Li, C. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 130(2), 337–364. [Google Scholar] [CrossRef]
- Diebold, F. X., & Mariano, R. S. (2002). Comparing predictive accuracy. Journal of Business & Economic Statistics, 20(1), 134–144. [Google Scholar]
- Diebold, F. X., & Rudebusch, G. D. (2013). Yield curve modeling and forecasting: The dynamic Nelson-Siegel approach. Princeton University Press. [Google Scholar]
- Diebold, F. X., Rudebusch, G. D., & Aruoba, S. B. (2006). The macroeconomy and the yield curve: A dynamic latent factor approach. Journal of Econometrics, 131(1–2), 309–338. [Google Scholar]
- Drobetz, W., Stürmer, S., & Zimmermann, H. (2002). Conditional asset pricing in emerging stock markets. Swiss Journal of Economics and Statistics (SJES), 138(IV), 507–526. [Google Scholar]
- Duffee, G. (2013). Forecasting interest rates. In G. Elliott, & A. Timmermann (Eds.), Handbook of economic forecasting (Vol. 2, pp. 385–426). North Holland. [Google Scholar]
- Favero, C. A., Niu, L., & Sala, L. (2012). Term structure forecasting: No-arbitrage restrictions versus large information set. Journal of Forecasting, 31(2), 124–156. [Google Scholar] [CrossRef]
- Fernandes, M., & Vieira, F. (2019). A dynamic Nelson–Siegel model with forward-looking macroeconomic factors for the yield curve in the US. Journal of Economic Dynamics and Control, 106, 103720. [Google Scholar] [CrossRef]
- Frankel, J. A. (2008). The effect of monetary policy on real commodity prices. In Asset prices and monetary policy (pp. 291–333). University of Chicago Press. [Google Scholar]
- Guidolin, M., McMillan, D. G., & Wohar, M. E. (2013). Time varying stock return predictability: Evidence from US sectors. Finance Research Letters, 10(1), 34–40. [Google Scholar] [CrossRef]
- Guidolin, M., & Pedio, M. (2019). Forecasting and trading monetary policy effects on the riskless yield curve with regime switching Nelson–Siegel models. Journal of Economic Dynamics and Control, 107, 103723. [Google Scholar]
- Hansen, P. R., Lunde, A., & Nason, J. M. (2011). The model confidence set. Econometrica, 79(2), 453–497. [Google Scholar] [CrossRef]
- Hillebrand, E., Huang, H., Lee, T.-H., & Li, C. (2018). Using the entire yield curve in forecasting output and inflation. Econometrics, 6(3), 40. [Google Scholar] [CrossRef]
- Holmström, B., & Tirole, J. (2001). LAPM: A liquidity-based asset pricing model. The Journal of Finance, 56(5), 1837–1867. [Google Scholar] [CrossRef]
- Kim, J. H., & Choi, I. (2017). Unit roots in economic and financial time series: A re-evaluation at the decision-based significance levels. Econometrics, 5(3), 41. [Google Scholar] [CrossRef]
- Nelson, C. R., & Siegel, A. F. (1987). Parsimonious modeling of yield curves. Journal of Business, 473–489. [Google Scholar] [CrossRef]
- Nymand-Andersen, P. (2018). Yield curve modelling and a conceptual framework for estimating yield curves: Evidence from the European Central Bank’s yield curves. In ECB statistics paper. European Central Bank. [Google Scholar]
- Pesando, J. E. (1979). On the random walk characteristics of short-and long-term interest rates in an efficient market. Journal of Money, Credit and Banking, 11(4), 457–466. [Google Scholar] [CrossRef]
- Potì, V. (2018). A new tight and general bound on return predictability. Economics Letters, 162, 140–145. [Google Scholar]
- Rapach, D., Strauss, J., & Zhou, G. (2010). Out-of-sample equity premium prediction: Consistently beating the historical average. Review of Financial Studies, 23(2), 821–862. [Google Scholar] [CrossRef]
- Rapach, D., & Zhou, G. (2013). Forecasting stock returns. In Handbook of economic forecasting (Vol. 2, pp. 328–383). Elsevier Science & Technology. [Google Scholar]
- Steeley, J. M. (2014). Forecasting the term structure when short-term rates are near zero. Journal of Forecasting, 33(5), 350–363. [Google Scholar] [CrossRef]
- Toczydlowska, D., & Peters, G. W. (2018). Financial big data solutions for state space panel regression in interest rate dynamics. Econometrics, 6(3), 34. [Google Scholar] [CrossRef]
- Welch, I., & Goyal, A. (2008). A comprehensive look at the empirical performance of equity premium prediction. The Review of Financial Studies, 21(4), 1455–1508. [Google Scholar] [CrossRef]
- Xiang, J., & Zhu, X. (2013). A regime-switching Nelson–Siegel term structure model and interest rate forecasts. Journal of Financial Econometrics, 11(3), 522–555. [Google Scholar] [CrossRef]
- Yu, W.-C., & Zivot, E. (2011). Forecasting the term structures of Treasury and corporate yields using dynamic Nelson-Siegel models. International Journal of Forecasting, 27(2), 579–591. [Google Scholar] [CrossRef]

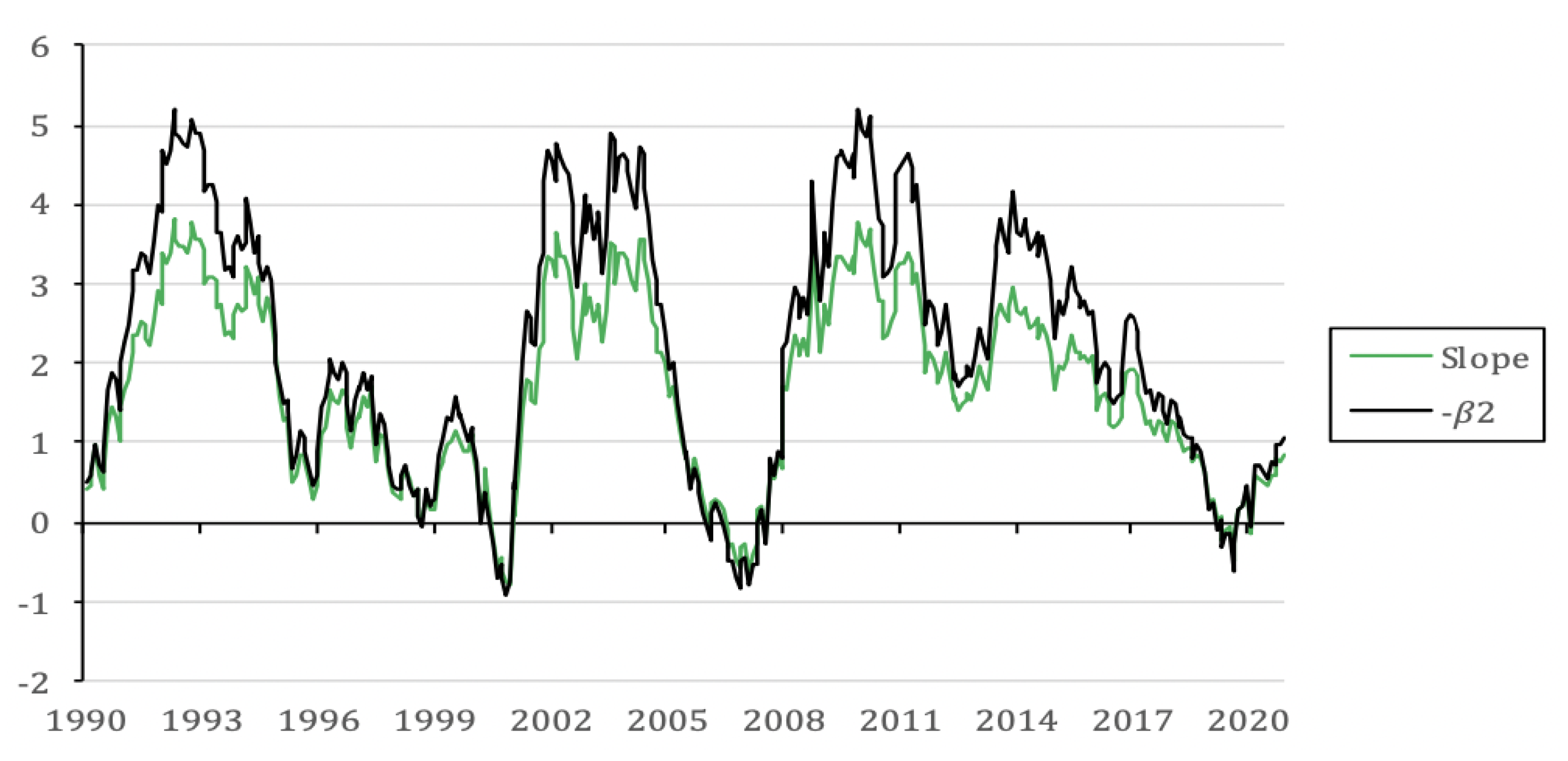
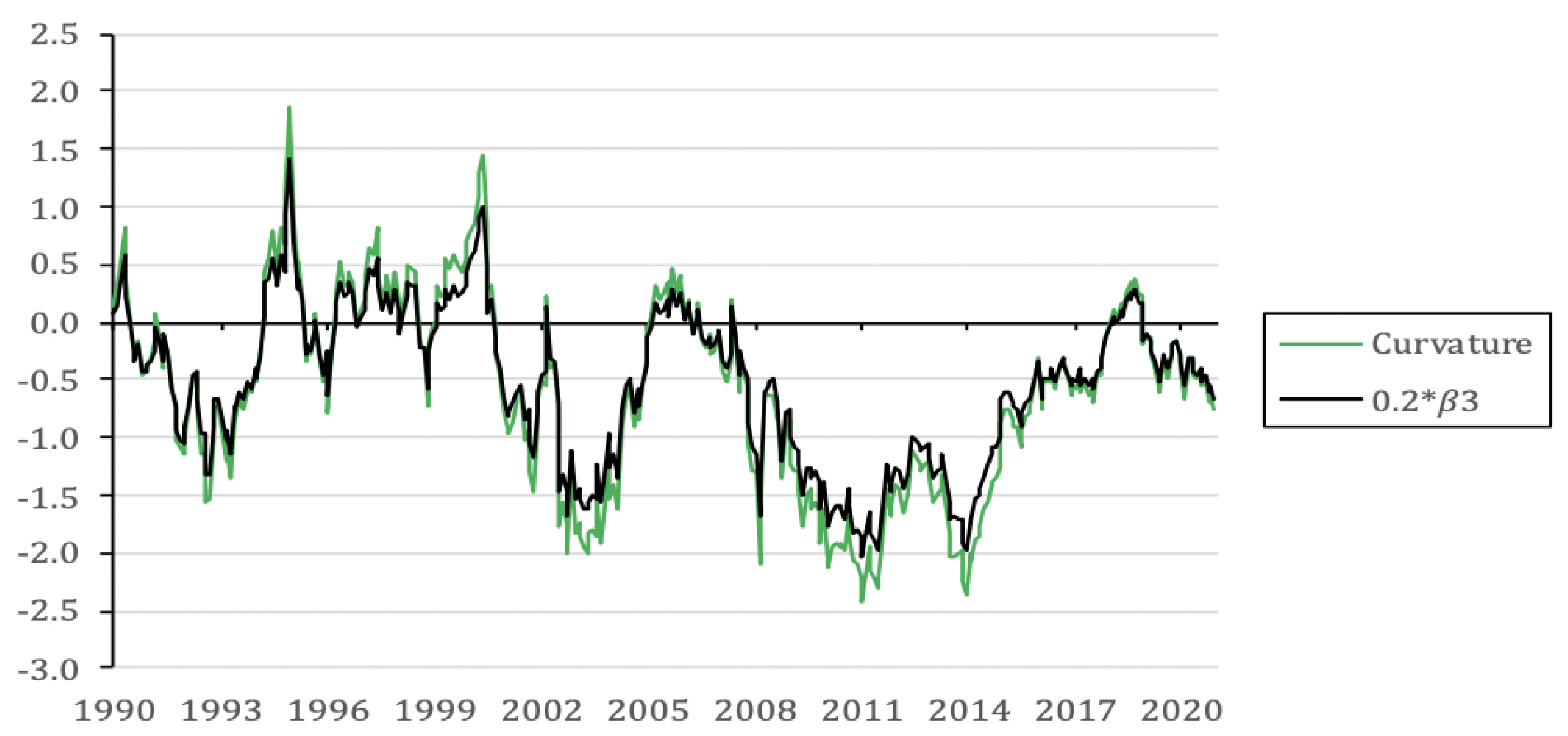
| Factor | Mean | Std. Dev. | Minimum | Maximum | ADF | |||
|---|---|---|---|---|---|---|---|---|
| 4.893 | 1.955 | 0.747 | 9.267 | 0.980 | 0.776 | 0.616 | −1.398 | |
| −2.205 | 1.582 | −5.214 | 0.980 | 0.973 | 0.523 | −0.163 | −2.235 | |
| −1.801 | 2.226 | −6.796 | 4.704 | 0.954 | 0.582 | 0.200 | −2.984 |
| Yield Maturity | h = 1 | h = 6 | h = 12 |
|---|---|---|---|
| VAR(1) on NS | |||
| 3 Months | −2.052 | −0.552 | 0.059 |
| 1 Y | 0.835 | 0.156 | 0.210 |
| 5 Y | −1.538 | 0.631 | 0.249 |
| 10 Y | 0.501 | 0.389 | 0.137 |
| AR(1) on Yields | |||
| 3 Months | 2.504 | 0.733 | 0.273 |
| 1 Y | 4.614 | 0.306 | 0.080 |
| 5 Y | 2.801 | 1.435 | 0.926 |
| 10 Y | 1.335 | 1.424 | 1.176 |
| VAR(1) on Yield Changes | |||
| 3 Months | 2.623 | 0.430 | −0.081 |
| 1 Y | 3.431 | 0.111 | −0.188 |
| 5 Y | 2.135 | 1.325 | 0.839 |
| 10 Y | 2.062 | 1.424 | 1.176 |
| Random Walk | |||
| 3 Months | 2.221 | 0.440 | −0.050 |
| 1 Y | 4.314 | 0.125 | −0.156 |
| 5 Y | 2.527 | 1.351 | 0.850 |
| 10 Y | 1.535 | 1.444 | 1.188 |
| Slope Regression | |||
| 3 Months | n.a. | n.a. | n.a. |
| 1 Y | 5.408 | −0.411 | −1.364 |
| 5 Y | 2.268 | 0.931 | 0.440 |
| 10 Y | 1.967 | 0.878 | 0.695 |
| VAR(1) on Yields | |||
| 3 Months | 3.692 | −4.433 | −3.406 |
| 1 Y | 4.358 | −1.976 | −1.057 |
| 5 Y | 2.963 | −3.564 | −1.825 |
| 10 Y | 1.458 | −7.165 | −3.938 |
| Predictive Regression on Principal Components | |||
| 3 Months | −6.097 | −1.564 | −0.975 |
| 1 Y | −6.379 | −2.379 | −2.780 |
| 5 Y | −14.848 | −5.825 | −3.533 |
| 10 Y | −20.328 | −7.557 | −2.278 |
| Panel A—MCS test results for 1-step-ahead forecasts using the TMax test statistic | |||||||||
| Rankings | Summary | ||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | excluded | excluded | excluded | 7 | AR(1) on NS | 3 | - | - | 1 |
| VAR(1) on NS | excluded | excluded | excluded | 6 | VAR(1) on NS | 3 | - | 1 | 1 |
| Slope Regression | excluded | 3 | 2 | 1 | Slope Regression | 1 | 3 | - | - |
| AR on Yields | 3 | 4 | 4 | excluded | AR on Yields | - | 1 | 3 | - |
| VAR(1) on Yields | 2 | 1 | 1 | 4 | VAR(1) on Yields | - | 3 | 1 | - |
| VAR(1) on Yield Changes | 1 | 2 | 3 | 2 | VAR(1) on Yield Changes | - | 4 | - | - |
| Principal Components | excluded | excluded | excluded | excluded | Principal Components | 4 | - | - | - |
| Random Walk | 4 | 5 | 5 | 3 | Random Walk | - | 1 | 3 | - |
| Panel B—MCS test results for 6-step-ahead forecasts using the TMax test statistic | |||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | 4 | 5 | 5 | 6 | AR(1) on NS | - | - | 4 | - |
| VAR(1) on NS | 5 | 2 | 5 | 4 | VAR(1) on NS | - | 1 | 3 | - |
| Slope Regression | excluded | 6 | 4 | 3 | Slope Regression | 1 | 1 | 2 | - |
| AR on Yields | 1 | 1 | 1 | 5 | AR on Yields | - | 3 | 1 | - |
| VAR(1) on Yields | 2 | 1 | 1 | 4 | VAR(1) on Yields | - | 3 | 1 | - |
| VAR(1) on Yield Changes | 3 | 4 | 3 | 2 | VAR(1) on Yield Changes | - | 3 | 1 | - |
| Principal Components | excluded | excluded | excluded | excluded | Principal Components | 4 | - | - | - |
| Random Walk | 2 | 3 | 2 | 1 | Random Walk | - | 4 | - | - |
| Panel C—MCS test results for 12-step-ahead forecasts using the TMax test statistic | |||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | 5 | 2 | 6 | 6 | AR(1) on NS | - | 1 | 3 | - |
| VAR(1) on NS | 4 | 3 | 5 | 5 | VAR(1) on NS | - | 1 | 3 | - |
| Slope Regression | excluded | 6 | 4 | 3 | Slope Regression | 1 | 1 | 2 | - |
| AR on Yields | 1 | 1 | 1 | 4 | AR on Yields | - | 3 | 1 | - |
| VAR(1) on Yields | excluded | 7 | excluded | excluded | VAR(1) on Yields | 3 | - | - | 1 |
| VAR(1) on Yield Changes | 3 | 4 | 3 | 2 | VAR(1) on Yield Changes | - | 4 | 1 | - |
| Principal Components | 6 | excluded | excluded | excluded | Principal Components | 3 | - | 1 | - |
| Random Walk | 2 | 5 | 2 | 1 | Random Walk | - | 2 | 1 | - |
| Panel D—MCS test results for 1-step-ahead forecasts using the TR test statistic | |||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | excluded | excluded | excluded | 7 | AR(1) on NS | 3 | - | - | 1 |
| VAR(1) on NS | excluded | excluded | excluded | 6 | VAR(1) on NS | 3 | - | 1 | - |
| Slope Regression | excluded | 3 | 2 | 1 | Slope Regression | 1 | 3 | - | - |
| AR on Yields | 3 | 4 | 4 | 5 | AR on Yields | - | 2 | 2 | - |
| VAR(1) on Yields | 2 | 1 | 1 | 4 | VAR(1) on Yields | - | 3 | 1 | - |
| VAR(1) on Yield Changes | 1 | 2 | 3 | 2 | VAR(1) on Yield Changes | - | 4 | - | - |
| Principal Components | excluded | excluded | excluded | excluded | Principal Components | 4 | - | - | - |
| Random Walk | 4 | 5 | 5 | 3 | Random Walk | - | - | 4 | - |
| Panel E—MCS test results for 6-step-ahead forecasts using the TR test statistic | |||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | 4 | 4 | 6 | 6 | AR(1) on NS | - | 2 | 2 | - |
| VAR(1) on NS | 5 | 5 | 5 | 4 | VAR(1) on NS | - | 1 | 3 | - |
| Slope Regression | excluded | 6 | 4 | 3 | Slope Regression | 1 | 2 | 1 | - |
| AR on Yields | 1 | 1 | 1 | 5 | AR on Yields | - | 2 | 2 | - |
| VAR(1) on Yields | excluded | 7 | excluded | excluded | VAR(1) on Yields | 3 | - | 1 | - |
| VAR(1) on Yield Changes | 3 | 2 | 3 | 2 | VAR(1) on Yield Changes | - | 2 | ||
| Principal Components | 6 | 8 | excluded | excluded | Principal Components | 2 | - | 1 | 1 |
| Random Walk | 2 | 3 | 2 | 1 | Random Walk | - | 3 | 1 | - |
| Panel F—MCS test results for 12-step-ahead forecasts using the TR test statistic | |||||||||
| Model | 3 Mo | 1 Y | 5 Y | 10 Y | Model | Excluded | 1st to 3rd | 4th to 6th | 7th to 8th |
| AR(1) on NS | 5 | 2 | 6 | 6 | AR(1) on NS | - | 2 | 2 | - |
| VAR(1) on NS | 4 | 4 | 5 | 5 | VAR(1) on NS | - | 2 | 2 | - |
| Slope Regression | excluded | 6 | 4 | 3 | Slope Regression | 1 | 1 | 2 | - |
| AR on Yields | 1 | 1 | 1 | 4 | AR on Yields | - | 3 | 1 | - |
| VAR(1) on Yields | excluded | 7 | excluded | excluded | VAR(1) on Yields | 3 | - | 1 | - |
| VAR(1) on Yield Changes | 3 | 3 | 3 | 2 | VAR(1) on Yield Changes | - | 2 | 1 | 1 |
| Principal Components | 6 | excluded | excluded | excluded | Principal Components | - | 2 | 1 | - |
| Random Walk | 2 | 5 | 2 | 1 | Random Walk | - | 2 | 1 | - |
| Panel A—MCS test results for 1-step-ahead forecasts using the TMax test statistic (h = 1) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| Equities (113) | ||||||||||
| AR(1) on NS | 9 | 60 | 34 | 8 | 2 | 8% | 53% | 30% | 7% | 2% |
| VAR(1) on NS | 8 | 43 | 56 | 4 | 2 | 7% | 38% | 50% | 4% | 2% |
| AR(1) for returns | 69 | 7 | 4 | 17 | 16 | 61% | 6% | 4% | 15% | 14% |
| Historical Average | 61 | 3 | 7 | 29 | 13 | 54% | 3% | 6% | 26% | 12% |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 1 | 0 | 4 | 1 | 2 | 13% | 0% | 50% | 13% | 25% |
| VAR(1) on NS | 0 | 5 | 3 | 0 | 0 | 0% | 63% | 38% | 0% | 0% |
| AR(1) for returns | 1 | 3 | 0 | 3 | 1 | 13% | 38% | 0% | 38% | 13% |
| Historical Average | 3 | 0 | 0 | 3 | 2 | 38% | 0% | 0% | 38% | 25% |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 8 | 0 | 1 | 0 | 0% | 89% | 0% | 11% | 0% |
| VAR(1) on NS | 1 | 0 | 7 | 0 | 1 | 11% | 0% | 78% | 0% | 11% |
| AR(1) for returns | 6 | 1 | 0 | 2 | 0 | 67% | 11% | 0% | 22% | 0% |
| Historical Average | 7 | 0 | 1 | 1 | 0 | 78% | 0% | 11% | 11% | 0% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 0 | 0 | 4 | 0 | 0 | 0% | 0% | 100% | 0% | 0% |
| VAR(1) on NS | 0 | 4 | 0 | 0 | 0 | 0% | 100% | 0% | 0% | 0% |
| AR(1) for returns | 3 | 0 | 0 | 0 | 1 | 75% | 0% | 0% | 0% | 25% |
| Historical Average | 1 | 0 | 0 | 3 | 0 | 25% | 0% | 0% | 75% | 0% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 5 | 1 | 3 | 6 | 2 | 29% | 6% | 18% | 35% | 12% |
| VAR(1) on NS | 5 | 0 | 4 | 5 | 3 | 29% | 0% | 24% | 29% | 18% |
| AR(1) for returns | 2 | 14 | 0 | 1 | 0 | 12% | 82% | 0% | 6% | 0% |
| Historical Average | 5 | 2 | 5 | 0 | 5 | 29% | 12% | 29% | 0% | 29% |
| Equities (113) | ||||||||||
| AR(1) on NS | 21 | 18 | 4 | 35 | 33 | 19% | 16% | 4% | 31% | 31% |
| VAR(1) on NS | 14 | 10 | 9 | 38 | 42 | 12% | 9% | 8% | 34% | 37% |
| AR(1) for returns | 1 | 28 | 63 | 11 | 10 | 1% | 25% | 56% | 10% | 9% |
| Historical Average | 1 | 57 | 37 | 15 | 3 | 1% | 50% | 33% | 13% | 3% |
| Panel B—MCS test results for 6-step-ahead forecasts using the TMax test statistic (h = 6) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 2 | 2 | 2 | 0 | 2 | 25% | 25% | 25% | 0% | 25% |
| VAR(1) on NS | 0 | 6 | 0 | 0 | 2 | 0% | 75% | 0% | 0% | 25% |
| AR(1) for returns | 2 | 0 | 4 | 2 | 0 | 25% | 0% | 50% | 25% | 0% |
| Historical Average | 2 | 0 | 0 | 4 | 2 | 25% | 0% | 0% | 50% | 25% |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 4 | 1 | 0 | 4 | 0% | 44% | 11% | 0% | 44% |
| VAR(1) on NS | 0 | 2 | 4 | 3 | 0 | 0% | 22% | 44% | 33% | 0% |
| AR(1) for returns | 1 | 0 | 3 | 1 | 4 | 11% | 0% | 33% | 11% | 44% |
| Historical Average | 0 | 3 | 1 | 5 | 0 | 0% | 33% | 11% | 56% | 0% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 0 | 0 | 3 | 0 | 1 | 0% | 0% | 0% | 75% | 0% |
| VAR(1) on NS | 0 | 4 | 0 | 0 | 0 | 0% | 100% | 0% | 0% | 0% |
| AR(1) for returns | 0 | 0 | 0 | 2 | 2 | 0% | 0% | 0% | 50% | 50% |
| Historical Average | 0 | 0 | 1 | 2 | 1 | 0% | 0% | 25% | 50% | 25% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 5 | 2 | 4 | 5 | 1 | 29% | 12% | 24% | 29% | 6% |
| VAR(1) on NS | 8 | 4 | 2 | 1 | 2 | 47% | 24% | 12% | 6% | 12% |
| AR(1) for returns | 0 | 11 | 0 | 6 | 0 | 0% | 65% | 0% | 35% | 0% |
| Historical Average | 5 | 0 | 7 | 0 | 5 | 29% | 0% | 41% | 0% | 29% |
| Panel C—MCS test results for 12-step-ahead forecasts using the TMax test statistic (h = 12) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| Equities (113) | ||||||||||
| AR(1) on NS | 68 | 5 | 2 | 22 | 16 | 60% | 4% | 2% | 19% | 14% |
| VAR(1) on NS | 62 | 3 | 3 | 24 | 21 | 55% | 3% | 3% | 21% | 19% |
| AR(1) for returns | 2 | 51 | 54 | 4 | 2 | 2% | 45% | 48% | 4% | 2% |
| Historical Average | 3 | 54 | 49 | 5 | 2 | 3% | 48% | 43% | 4% | 2% |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 2 | 2 | 4 | 0 | 0 | 25% | 25% | 50% | 0% | 0% |
| VAR(1) on NS | 0 | 6 | 1 | 0 | 1 | 0% | 75% | 13% | 0% | 13% |
| AR(1) for returns | 2 | 0 | 0 | 2 | 4 | 25% | 0% | 0% | 25% | 50% |
| Historical Average | 2 | 0 | 1 | 4 | 1 | 25% | 0% | 13% | 50% | 13% |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 2 | 5 | 0 | 2 | 0% | 22% | 56% | 0% | 22% |
| VAR(1) on NS | 0 | 6 | 2 | 1 | 0 | 0% | 67% | 22% | 11% | 0% |
| AR(1) for returns | 2 | 0 | 2 | 0 | 5 | 22% | 0% | 22% | 0% | 56% |
| Historical Average | 2 | 1 | 0 | 6 | 0 | 22% | 11% | 0% | 67% | 0% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 0 | 0 | 4 | 0 | 0 | 0% | 0% | 100% | 0% | 0% |
| VAR(1) on NS | 0 | 4 | 0 | 0 | 0 | 0% | 100% | 0% | 0% | 0% |
| AR(1) for returns | 0 | 0 | 0 | 0 | 4 | 0% | 0% | 0% | 0% | 100% |
| Historical Average | 0 | 0 | 0 | 4 | 0 | 0% | 0% | 0% | 100% | 0% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 16 | 0 | 0 | 1 | 0 | 94% | 0% | 0% | 6% | 0% |
| VAR(1) on NS | 16 | 0 | 0 | 0 | 1 | 94% | 0% | 0% | 0% | 6% |
| AR(1) for returns | 3 | 7 | 7 | 0 | 0 | 18% | 41% | 41% | 0% | 0% |
| Historical Average | 1 | 10 | 6 | 0 | 0 | 6% | 59% | 35% | 0% | 0% |
| Equities (113) | ||||||||||
| AR(1) on NS | 22 | 59 | 22 | 5 | 5 | 19% | 52% | 19% | 4% | 4% |
| VAR(1) on NS | 20 | 44 | 38 | 7 | 4 | 18% | 39% | 34% | 6% | 4% |
| AR(1) for returns | 73 | 6 | 13 | 18 | 3 | 65% | 5% | 12% | 16% | 3% |
| Historical Average | 64 | 25 | 17 | 3 | 3 | 57% | 4% | 22% | 15% | 3% |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 6 | 1 | 1 | 0 | 0 | 75% | 13% | 13% | 0% | 0% |
| VAR(1) on NS | 0 | 4 | 4 | 0 | 0 | 0% | 50% | 50% | 0% | 0% |
| AR(1) for returns | 2 | 3 | 0 | 3 | 0 | 25% | 38% | 0% | 38% | 0% |
| Historical Average | 2 | 0 | 1 | 3 | 2 | 25% | 0% | 13% | 38% | 25% |
| Panel D—MCS test results for 1-step-ahead forecasts using the TR test statistic (h = 1) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 8 | 0 | 1 | 0 | 0% | 89% | 0% | 11% | 0% |
| VAR(1) on NS | 1 | 0 | 5 | 2 | 1 | 11% | 0% | 56% | 22% | 11% |
| AR(1) for returns | 6 | 1 | 2 | 0 | 0 | 67% | 11% | 22% | 0% | 0% |
| Historical Average | 7 | 0 | 1 | 1 | 0 | 78% | 0% | 11% | 11% | 0% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 2 | 0 | 1 | 0 | 1 | 50% | 0% | 25% | 0% | 25% |
| VAR(1) on NS | 0 | 4 | 0 | 0 | 0 | 0% | 100% | 0% | 0% | 0% |
| AR(1) for returns | 3 | 0 | 0 | 1 | 0 | 75% | 0% | 0% | 25% | 0% |
| Historical Average | 1 | 0 | 0 | 0 | 0 | 25% | 0% | 75% | 0% | 0% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 5 | 0 | 4 | 7 | 1 | 29% | 0% | 24% | 41% | 6% |
| VAR(1) on NS | 6 | 1 | 5 | 3 | 2 | 35% | 6% | 29% | 18% | 12% |
| AR(1) for returns | 2 | 14 | 0 | 1 | 0 | 12% | 82% | 0% | 6% | 0% |
| Historical Average | 7 | 2 | 3 | 0 | 5 | 41% | 12% | 18% | 0% | 29% |
| Panel E—MCS test results for 6-step-ahead forecasts using the TR test statistic (h = 6) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| Equities (113) | ||||||||||
| AR(1) on NS | 21 | 14 | 20 | 28 | 30 | 19% | 12% | 18% | 25% | 27% |
| VAR(1) on NS | 11 | 12 | 13 | 48 | 29 | 10% | 11% | 12% | 42% | 26% |
| AR(1) for returns | 2 | 33 | 41 | 16 | 21 | 2% | 29% | 36% | 14% | 19% |
| Historical Average | 2 | 54 | 38 | 14 | 5 | 2% | 48% | 34% | 12% | 4% |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 5 | 2 | 1 | 0 | 0 | 63% | 25% | 13% | 0% | 0% |
| VAR(1) on NS | 0 | 6 | 0 | 1 | 1 | 0% | 75% | 0% | 13% | 13% |
| AR(1) for returns | 5 | 0 | 2 | 1 | 0 | 63% | 0% | 25% | 13% | 0% |
| Historical Average | 5 | 0 | 0 | 1 | 2 | 63% | 0% | 0% | 13% | 25% |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 4 | 0 | 1 | 4 | 0% | 44% | 0% | 11% | 44% |
| VAR(1) on NS | 0 | 2 | 6 | 1 | 0 | 0% | 22% | 67% | 11% | 0% |
| AR(1) for returns | 0 | 0 | 1 | 3 | 5 | 0% | 0% | 11% | 33% | 56% |
| Historical Average | 0 | 3 | 2 | 4 | 0 | 0% | 33% | 22% | 44% | 0% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 0 | 0 | 3 | 1 | 0 | 0% | 0% | 75% | 25% | 0% |
| VAR(1) on NS | 0 | 4 | 0 | 0 | 0 | 0% | 100% | 0% | 0% | 0% |
| AR(1) for returns | 0 | 0 | 0 | 3 | 1 | 0% | 0% | 0% | 75% | 25% |
| Historical Average | 0 | 0 | 1 | 0 | 3 | 0% | 0% | 25% | 0% | 75% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 6 | 3 | 5 | 3 | 0 | 35% | 18% | 29% | 18% | 0% |
| VAR(1) on NS | 8 | 3 | 4 | 1 | 1 | 47% | 18% | 24% | 6% | 6% |
| AR(1) for returns | 0 | 11 | 1 | 5 | 0 | 0% | 65% | 6% | 29% | 0% |
| Historical Average | 11 | 0 | 2 | 1 | 3 | 65% | 0% | 12% | 6% | 18% |
| Equities (113) | ||||||||||
| AR(1) on NS | 69 | 5 | 13 | 13 | 13 | 61% | 4% | 12% | 12% | 12% |
| VAR(1) on NS | 66 | 3 | 8 | 27 | 9 | 58% | 3% | 7% | 24% | 8% |
| AR(1) for returns | 2 | 45 | 49 | 4 | 13 | 2% | 40% | 43% | 4% | 12% |
| Historical Average | 3 | 60 | 40 | 9 | 1 | 3% | 53% | 35% | 8% | 1% |
| Treasuries (8) | ||||||||||
| AR(1) on NS | 4 | 3 | 1 | 0 | 0 | 50% | 38% | 13% | 0% | 0% |
| VAR(1) on NS | 0 | 5 | 2 | 0 | 1 | 0% | 63% | 25% | 0% | 13% |
| AR(1) for returns | 5 | 0 | 0 | 1 | 2 | 63% | 0% | 0% | 13% | 25% |
| Historical Average | 5 | 0 | 1 | 2 | 0 | 63% | 0% | 13% | 25% | 0% |
| Panel F—MCS test results for 12-step-ahead forecasts using the TR test statistic (h = 12) | ||||||||||
| Excl. | 1st | 2nd | 3rd | 4th | Excl. | 1st | 2nd | 3rd | 4th | |
| REITs (9) | ||||||||||
| AR(1) on NS | 0 | 2 | 3 | 0 | 4 | 0% | 22% | 33% | 0% | 44% |
| VAR(1) on NS | 0 | 6 | 3 | 0 | 0 | 0% | 67% | 33% | 0% | 0% |
| AR(1) for returns | 0 | 0 | 1 | 5 | 3 | 0% | 0% | 11% | 56% | 33% |
| Historical Average | 0 | 1 | 2 | 4 | 2 | 0% | 11% | 22% | 44% | 22% |
| Corporate Bonds (4) | ||||||||||
| AR(1) on NS | 0 | 3 | 1 | 0 | 0 | 0% | 75% | 25% | 0% | 0% |
| VAR(1) on NS | 0 | 1 | 3 | 0 | 0 | 0% | 25% | 75% | 0% | 0% |
| AR(1) for returns | 0 | 0 | 0 | 0 | 4 | 0% | 0% | 0% | 0% | 100% |
| Historical Average | 0 | 0 | 0 | 4 | 0 | 0% | 0% | 0% | 100% | 0% |
| Commodities (17) | ||||||||||
| AR(1) on NS | 15 | 0 | 1 | 0 | 1 | 88% | 0% | 6% | 0% | 6% |
| VAR(1) on NS | 15 | 0 | 0 | 1 | 1 | 88% | 0% | 0% | 6% | 6% |
| AR(1) for returns | 3 | 7 | 6 | 1 | 0 | 18% | 41% | 35% | 6% | 0% |
| Historical Average | 1 | 10 | 6 | 0 | 0 | 6% | 59% | 35% | 0% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guidolin, M.; Ionta, S. Forecasting Asset Returns Using Nelson–Siegel Factors Estimated from the US Yield Curve. Econometrics 2025, 13, 17. https://doi.org/10.3390/econometrics13020017
Guidolin M, Ionta S. Forecasting Asset Returns Using Nelson–Siegel Factors Estimated from the US Yield Curve. Econometrics. 2025; 13(2):17. https://doi.org/10.3390/econometrics13020017
Chicago/Turabian StyleGuidolin, Massimo, and Serena Ionta. 2025. "Forecasting Asset Returns Using Nelson–Siegel Factors Estimated from the US Yield Curve" Econometrics 13, no. 2: 17. https://doi.org/10.3390/econometrics13020017
APA StyleGuidolin, M., & Ionta, S. (2025). Forecasting Asset Returns Using Nelson–Siegel Factors Estimated from the US Yield Curve. Econometrics, 13(2), 17. https://doi.org/10.3390/econometrics13020017







