Demonstrating That the Autoregressive Distributed Lag Bounds Test Can Detect a Long-Run Levels Relationship When the Dependent Variable Is I(0)
Abstract
1. Introduction
2. The ARDL Bounds Test Method When the Dependent Variable Is I(0)
3. Simulation Methods and Results
3.1. Simulations Without an Equilibrium
3.2. Simulations with an Equilibrium
4. Empirical Application with Results and Discussion
4.1. PPP Literature Review
4.2. Empirical Results and Discussion
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADF | Augmented Dickey-Fuller |
| AIC | Akaike information criterion |
| ARCH | Autoregressive conditional heteroscedasticity |
| ARDL | Autoregressive distributed lag |
| CPI | Consumer price index |
| DF-GLS | Generalised least squares detrended Dickey-Fuller |
| DGP | Data generating process |
| GLS | Generalised least squares |
| Integrated of order zero | |
| Integrated of order one | |
| Integrated of order two | |
| KPSS | Kwiatkowski et al. (1992) |
| LOP | Law of one price |
| MA | Moving average |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MSG | McNown et al. (2018) |
| OLS | Ordinary least squares |
| PP | Phillips-Perron |
| PPP | Purchasing power parity |
| PSS | Pesaran et al. (2001) |
| RER | Real exchange rate |
| SALOP | Strong absolute law of one price |
| WALOP | Weak absolute law of one price |
| 1 | Cho et al. (2023) survey the broad ARDL approach that may be split into two categories: techniques that estimate an equilibrium assuming a long-run relation exists and methods that test for an equilibrium and, if one exists, estimates it. The PSS method falls into the latter category. Several extensions of the ARDL approach are surveyed, including those allowing for nonlinearity, quantile regression, panel data, and spatio-temporal models. |
| 2 | An equilibrium can occur when the dependent variable is if it is significantly correlated with all the regressors. A long-run relation can also exist if any regressors form linear combination(s) that are significantly correlated with the dependent variable. |
| 3 | See PSS pp. 291–295 for further discussion of the assumptions. |
| 4 | In applications, the alternative hypothesis of is , given that left-sided critical values are reported by PSS, even if is the alternative hypothesis for (see PSS p. 296). |
| 5 | and can also be rejected when and significantly correlated with at least one regressor so there is cointegration. |
| 6 | As explained in the main text, it is this possibility that we argue the PSS tests (augmented with a third test) can detect that is not currently (explicitly) recognised in the literature. |
| 7 | McNown et al. (2018) use a bootstrap method to produce critical values for the three tests such that upper and lower bounds are not needed. This has two advantages. First, the critical values are based on the specific integration properties of the data being used, and second, it removes the situation where a test can yield no decision, being when the test statistic lies between the upper and lower bound critical values. Kripfganz and Schneider (2020, p. 1479), suggest that by “… leaving the process for the long-run forcing regressors unrestricted, McNown et al. (2018) avoid the potential problem of inconclusive evidence when the integration order of the regressors is a priori unknown. A shortcoming of the bootstrap procedure is that residuals for each variable in the underlying VAR model need to be estimated and resampled, not just for the single-equation EC model of interest. Eventually, there is still a lack of comprehensive evidence about the relative performance of the bootstrap, in particular when there are many variables in the model and the sample size is small.” They also highlight the computational burden as a drawback of McNown et al.’s (2018) bootstrap method. |
| 8 | Sam et al. (2019) provide the asymptotic theory as well as asymptotic and small sample critical values for the test for cases 1, 3, and 5. |
| 9 | The following quotes are further examples from McNown et al. (2018, p. 1510), indicating their contention that PSS assume . “PSS rules out another degenerate case by assuming the dependent variable is integrated of order 1.” “Instead of assuming the dependent variable to be in order to rule out the degenerate case, we propose an explicit test on the lagged level of the independent variable(s) to have a full picture of the cointegration status between the dependent and independent variables.” The following quote from Sam et al. (2019, p. 130) is another example where they explicitly state that PSS assume . “Nevertheless, PSS made some assumptions in developing the bounds testing approach. These include the exogeneity of the independent variables, the dependent variable must be , and the absence of degenerate cases.” |
| 10 | While McNown et al. (2018) and Sam et al. (2019) contend that PSS assume to rule out the lagged independent variable degenerate case, PSS allow when this degenerate case occurs. PSS (p. 291) state that “… Assumption 1 permits the elements of to be purely , purely or cointegrated …”, where . |
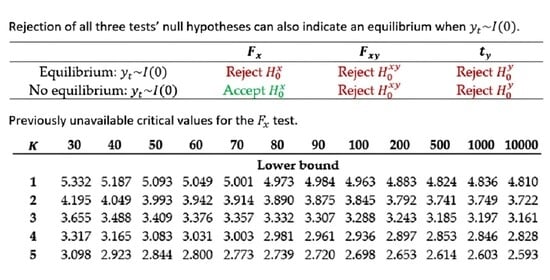
| 11 | When an equilibrium exists through cointegration with , all three tests’ null hypotheses should be rejected, and this is indicated in row 3 of Table 1. |
| 12 | When some of the level regressors can be and others and can still be consistent with an equilibrium, provided all regressors (with non-zero coefficients) cointegrate with each other such that their linear combination is . This yields a balanced long-run levels relation where both sides of the equation have the same order of integration. Hence, theoretical models that specify equilibrium relationships between and variables can be accommodated in the three-test ARDL method. For example, consider the absolute PPP model that relaxes the proportionality and symmetry restrictions, thus . Where , , and are the natural logarithms of the exchange rate, domestic price level, and foreign price level, respectively. Assume as exchange rates are not necessarily nonstationary and and as prices are arguably intrinsically nonstationary. Hence, the dependent variable in the above PPP specification is while both regressors are . This can still have a long-run levels relationship if and cointegrate such that the linear combination . Imposing the symmetry restriction on the above three variable PPP model yields the following two variable PPP model such that both the dependent variable and regressor are and the model is a balanced regression. If is (significantly) different from zero, the variables are correlated, and there is an equilibrium solely among variables. This also implies that the three variable PPP model should represent a valid equilibrium. Following a reviewer’s helpful suggestion, we now assume the following four variable model , and it is known that , , and . In this case, the coefficient would be expected to be zero to ensure a balanced regression. A t-test of the null hypothesis can be applied on the long-run model, and the null should not be rejected. |
| 13 | When no long-run levels relation exists, all level regressors’ coefficients should be insignificantly different from zero and the ARDL test Equation (2) becomes a generalised ADF test equation for the null hypothesis that , which will be rejected when . |
| 14 | When no equilibrium exists (no regressor is correlated with ) and , all three tests’ null hypotheses cannot be rejected (see row 4 of Table 1). |
| 15 | Kripfganz and Schneider (2023, p. 993) suggest that should still be applied (first) because it requires less restrictive assumptions for the data generation process than . |
| 16 | Pesaran and Shin (1998) demonstrate that, regardless of whether the variables are or , the ARDL approach yields consistent estimates for the long-run coefficients that have an asymptotically normal distribution. |
| 17 | Critical values for cases 2 and 4 of the test at the 1%, 2.5%, 5%, and 10% significance levels are available in the online Supplementary Materials. |
| 18 | Equation (13) reflects the likely practice of tending to over-specify the lag order of regressors in the ARDL test equation to help ensure is free from evident autocorrelation. |
| 19 | The test is not undersized because the critical values used generate as under the null hypothesis, whereas the simulations in Table 4 specify . As a reviewer points out, if it is known that all variables are , standard methods designed for variables could be used, and the ARDL method would not be required. However, when there is uncertainty over whether some or all variables in the model are or , standard methods designed for all variables being will be inappropriate if any of the variables are , as this will cause spurious regression or spurious significance. In contrast, the ARDL method is appropriate when there is uncertainty over the variables’ orders of integration. This is the situation we are concerned with, and the results in Table 4 reflect this. |
| 20 | The previous literature has focused on all three ARDL tests rejecting their respective null hypotheses when to infer an equilibrium exists when there is a long-run levels relationship. This situation is depicted in row 3 of Table 1. |
| 21 | When over differencing (in the sense that differencing is not required to induce stationarity) can cause a moving average (MA) error process and possibly violate the invertibility condition (we are grateful to a reviewer for raising this point). Adding sufficient lags of the dependent variable in the ARDL test equation should ensure that the over differencing of is modelled and does not induce an MA error process. |
| 22 | We follow the literature (see, for example, Nagayasu, 1998; Pedroni, 2001; and Robertson et al., 2014) in using the terminology strong PPP for the following model and weak PPP to refer to the equation . |
| 23 | See Proposition 1 in Pelagatti and Colombo (2015, p. 909). |
| 24 | See Greene (2012, pp. 108–110) on using the delta method to calculate long-run coefficient covariances. Such covariances facilitate F/Wald tests of on multiple long-run coefficients. |
| 25 | The Bulgaria–Denmark exchange rate is calculated as the ratio of the Bulgarian-euro and Danish-euro exchange rates. |
| 26 | Data prior to the euro’s launch in January 1999 is not used. |
| 27 | While this is so for the case 3 Denmark-euro models there may be structural instability for the case 4 Denmark-euro specifications (inference on this is ambiguous). These case 4 models’ bounds test results are reported for completeness and comparison purposes, although they should be treated with caution. |
| 28 | The Bulgaria–Denmark ARDL(1,1) specifications without ARCH effects exhibit evident ARCH effects and heteroscedasticity. While we use White’s covariance matrix for hypothesis tests, the evident ARCH effects mean that inference from these models should be treated with caution. These models’ results are reported for completeness and for comparison with the ARDL(1,1) specifications with ARCH(5) processes for which the results are deemed valid. Since all estimated ARCH coefficients are non-negative and the sums of ARCH coefficients are strictly below unity, these stability conditions for a valid ARCH process are not violated. |
| 29 | We are grateful to a reviewer for pointing out that, in practice, it may be desirable to ascertain whether it is necessary to consider test results for case 2 or case 4 instead of case 3, effectively choosing a single deterministic specification for inference. While we recognise this may generally be how empirical ARDL testing would be implemented in practice, we choose to consider test results for case 2 and 4 (in addition to case 3) to illustrate ARDL testing applications that are relevant to the test critical values that we produce and report for cases 2 and 4 in this paper. Following a reviewer’s suggestion, we also note that, in small sample applications, it may be worthwhile recalibrating the ARDL tests’ critical values using, for example, bootstrap methods to ameliorate any small-sample distortions. |
| 30 | Provided and reject their null hypotheses, t- and/or F-tests of can be applied using conventional t and F distributions, respectively, and importantly, there is no indecision region. |
| 31 | Our simulations reported in Table 6 provide information on the power of the test when all variables are for deterministic cases 2 and 4. While they correspond to the estimated models we report in many respects and should provide some useful reference points for other applied researchers using the ARDL bounds test they do not match our estimated models in all respects. As a reviewer points out, to more closely consider the impact of sample size on power for our models requires the use of data calibrated simulations (based on the sample sizes, lag structures, error processes, deterministic terms, and estimated parameters employed in our empirical application). This should be borne in mind when the results on the power of the test reported in Table 6 are used as a point of reference and for guidance. |
References
- Bahmani-Oskooee, M., Chang, T., Cheng, S. C., & Tzeng, H. (2017). Revisiting purchasing power parity in Eastern European countries: Quantile unit root tests. Empirical Economics, 52, 463–483. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., Chang, T., Cheng, S. C., & Wu, T. (2015a). Revisiting purchasing power parity in major oil-exporting countries. Macroeconomics and Finance in Emerging Market Economies, 8(1–2), 108–116. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., Chang, T., & Hung, K. (2013). Revisiting purchasing power parity in Latin America: Sequential panel selection method. Applied Economics, 45, 4584–4590. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., Chang, T., & Liu, W. (2014a). Revisiting purchasing power parity in 34 OECD countries: Sequential panel selection method. Applied Economics Letters, 21(20), 1283–1287. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., Chang, T., & Wu, T. (2014b). Revisiting purchasing power parity in African countries: Panel stationary test with sharp and smooth breaks. Applied Financial Economics, 24(20), 1429–1438. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., Chang, T., & Wu, T. (2015b). Purchasing power parity in transition countries: Panel stationary test with smooth and sharp breaks. International Journal of Financial Studies, 3, 153–161. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, M., & Hegerty, S. H. (2009). Purchasing power parity in less-developed and transition economies: A review paper. Journal of Economic Surveys, 23(4), 617–658. [Google Scholar] [CrossRef]
- Bahramian, P., & Saliminezhad, A. (2021). Revisiting purchasing power parity in the ASEAN-5 countries: Evidence from the Fourier quantile unit root test. Applied Economics Letters, 28(8), 1104–1109. [Google Scholar] [CrossRef]
- Bergin, P. R., Glick, R., & Wu, J. L. (2013). The micro-macro disconnect of purchasing power parity. The Review of Economics and Statistics, 95(3), 798–812. [Google Scholar] [CrossRef]
- Bollerslev, T., & Wooldridge, J. M. (1992). Quasi maximum likelihood estimation and inference in dynamic models with time-varying covariances. Econometric Reviews, 11(2), 143–172. [Google Scholar] [CrossRef]
- Boundi-Chraki, F., & Mateo Tomé, J. P. (2022). The purchasing power parity hypothesis tested once again. New empirical evidence for 28 OECD countries. Investigación Económica, 81(322), 3–26. [Google Scholar] [CrossRef]
- Cho, J. S., Greenwood-Nimmo, M., & Shin, Y. (2023). Recent developments of the autoregressive distributed lag modelling framework. Journal of Economic Surveys, 37, 7–32. [Google Scholar] [CrossRef]
- Cho, J. S., Kin, T., & Shin, Y. (2015). Quantile cointegration in the autoregressive distributed-lag modelling framework. Journal of Econometrics, 188, 281–300. [Google Scholar] [CrossRef]
- Crownover, C., Pippenger, J., & Steigerwald, D. G. (1996). Testing for absolute purchasing power parity. Journal of International Money and Finance, 15, 783–796. [Google Scholar] [CrossRef]
- Crucini, M., & Shintani, M. (2008). Persistence in law of one price deviations: Evidence from micro-data. Journal of Monetary Economics, 55, 629–644. [Google Scholar] [CrossRef]
- De Villiers, D., & Phiri, A. (2022). Towards resolving the purchasing power parity (PPP) ‘Puzzle’ in newly industrialized countries (NIC’s). The Journal of International Trade & Economic Development, 31(2), 161–180. [Google Scholar]
- Dornbusch, R. (1976). Expectations and exchange rate dynamics. The Journal of Political Economy, 84(4), 1161–1176. [Google Scholar] [CrossRef]
- Greene, W. H. (2012). Econometric analysis (7th ed.). Pearson. [Google Scholar]
- Huang, C. H., & Yang, C. Y. (2015). European exchange rate regimes and purchasing power parity: An empirical study on eleven eurozone countries. International Review of Economics and Finance, 35, 100–109. [Google Scholar] [CrossRef]
- Imbs, J., Mumtaz, H., Ravn, M., & Rey, H. (2005). PPP strikes back: Aggregation and the real exchange rate. Quarterly Journal of Economics, 120, 1–43. [Google Scholar]
- Kripfganz, S., & Schneider, D. C. (2020). Response surface regressions for critical value bounds and approximate p-values in equilibrium correction models. Oxford Bulletin of Economics and Statistics, 82(6), 1456–1481. [Google Scholar] [CrossRef]
- Kripfganz, S., & Schneider, D. C. (2023). ardl: Estimating autoregressive distributed lag and equilibrium correction models. The Stata Journal, 23(4), 983–1019. [Google Scholar]
- Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54, 159–178. [Google Scholar] [CrossRef]
- McNown, R., Sam, C. Y., & Goh, S. K. (2018). Bootstrapping the autoregressive distributed lag test for cointegration. Applied Economics, 50, 1509–1521. [Google Scholar]
- Nagayasu, J. (1998). Does the long-run PPP hypothesis hold for Africa? Evidence from panel co-integration study. IMF Working Paper, WP/98/123. International Monetary Fund.
- Pedroni, P. (2001). Purchasing power parity tests in cointegrated panels. The Review of Economics and Statistics, 83(4), 727–731. [Google Scholar] [CrossRef]
- Pelagatti, M., & Colombo, E. (2015). On the empirical failure of purchasing power parity tests. Journal of Applied Econometrics, 30, 904–923. [Google Scholar]
- Pesaran, M. H., & Shin, Y. (1997). An autoregressive distributed lag modelling approach to cointegration analysis [Unpublished manuscript]. Cambridge University. [Google Scholar]
- Pesaran, M. H., & Shin, Y. (1998). An autoregressive distributed lag modelling approach to cointegration analysis. In S. Strom (Ed.), Econometrics and economic theory: The Ragnar Frisch centennial symposium, econometric society monographs (pp. 371–413). Cambridge University Press. [Google Scholar]
- Pesaran, M. H., Shin, Y., & Smith, R. J. (2001). Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics, 16, 289–326. [Google Scholar] [CrossRef]
- Robertson, R., Kumar, A., & Dutkowsky, D. H. (2014). Weak-form and strong-form purchasing power parity between the US and Mexico: A panel cointegration investigation. Journal of Macroeconomics, 42, 241–262. [Google Scholar]
- Rogoff, K. (1996). The purchasing power parity puzzle. Journal of Economic Literature, 34, 647–668. [Google Scholar]
- Sam, C. Y., McNown, R., & Goh, S. K. (2019). An augmented autoregressive distributed lag bounds test for cointegration. Economic Modelling, 80, 130–141. [Google Scholar] [CrossRef]
- She, F., Zakaria, M., Khan, M., & Wen, J. (2021). Purchasing power parity in Pakistan: Evidence from Fourier unit root tests. Emerging Markets Finance and Trade, 57(8), 3835–3854. [Google Scholar]
- Stewart, C. (2023). Law of one price data for the paper entitled “the autoregressive distributed lag bounds test generalised to consider a long-run levels relationship when all levels variables are I(0)”. GARDL_data(.xlsx). Kingston University. [Google Scholar] [CrossRef]
- Taylor, A. M. (2002). A century of purchasing power parity. The Review of Economics and Statistics, 84, 139–150. [Google Scholar] [CrossRef]
- Taylor, A. M., & Taylor, M. P. (2004). The purchasing power parity debate. Journal of Economic Perspectives, 18(4), 135–158. [Google Scholar] [CrossRef]
- Taylor, M. P. (2009). Long-run purchasing power parity and real exchange rates: Introduction and overview. Applied Economics Letters, 16, 1–4. [Google Scholar] [CrossRef]
- Wu, T., Bahmani-Oskooee, M., & Chang, T. (2018). Revisiting purchasing power parity in G6 countries: An application of smooth time-varying cointegration approach. Empirica, 45, 187–196. [Google Scholar] [CrossRef]
- Yilanci, V., Ursavas, U., & Mike, F. (2024). Revisiting purchasing power parity in emerging-7 countries: A powerful unit root test. Investigacion Economica, 83(328), 32–54. [Google Scholar] [CrossRef]
- Zhang, Z. (2024). Is there a rule of thumb for absolute purchasing power parity to hold? Applied Economics, 56(7), 851–860. [Google Scholar] [CrossRef]
| Row | ||||
|---|---|---|---|---|
| 1 | Equilibrium: | Reject | Reject | Reject |
| 2 | No equilibrium: | Accept | Reject | Reject |
| 3 | Equilibrium: | Reject | Reject | Reject |
| 4 | No equilibrium: | Accept | Accept | Accept |
| Sample Size (T) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 500 | 1000 | 10,000 |
| Lower bound | ||||||||||||
| 1 | 5.332 | 5.187 | 5.093 | 5.049 | 5.001 | 4.973 | 4.984 | 4.963 | 4.883 | 4.824 | 4.836 | 4.810 |
| 2 | 4.195 | 4.049 | 3.993 | 3.942 | 3.914 | 3.890 | 3.875 | 3.845 | 3.792 | 3.741 | 3.749 | 3.722 |
| 3 | 3.655 | 3.488 | 3.409 | 3.376 | 3.357 | 3.332 | 3.307 | 3.288 | 3.243 | 3.185 | 3.197 | 3.161 |
| 4 | 3.317 | 3.165 | 3.083 | 3.031 | 3.003 | 2.981 | 2.961 | 2.936 | 2.897 | 2.853 | 2.846 | 2.828 |
| 5 | 3.098 | 2.923 | 2.844 | 2.800 | 2.773 | 2.739 | 2.720 | 2.698 | 2.653 | 2.614 | 2.603 | 2.593 |
| 6 | 2.949 | 2.761 | 2.691 | 2.638 | 2.603 | 2.571 | 2.561 | 2.530 | 2.477 | 2.446 | 2.436 | 2.416 |
| 7 | 2.844 | 2.648 | 2.565 | 2.504 | 2.470 | 2.437 | 2.424 | 2.400 | 2.349 | 2.313 | 2.301 | 2.287 |
| 8 | 2.787 | 2.557 | 2.453 | 2.403 | 2.367 | 2.345 | 2.321 | 2.299 | 2.249 | 2.212 | 2.202 | 2.190 |
| 9 | 2.740 | 2.488 | 2.376 | 2.323 | 2.293 | 2.259 | 2.239 | 2.213 | 2.161 | 2.128 | 2.113 | 2.103 |
| 10 | 2.699 | 2.427 | 2.318 | 2.258 | 2.223 | 2.198 | 2.175 | 2.144 | 2.086 | 2.055 | 2.049 | 2.033 |
| 11 | 2.677 | 2.389 | 2.266 | 2.205 | 2.169 | 2.140 | 2.119 | 2.095 | 2.030 | 1.996 | 1.986 | 1.973 |
| 12 | 2.676 | 2.355 | 2.223 | 2.162 | 2.128 | 2.092 | 2.071 | 2.046 | 1.981 | 1.944 | 1.936 | 1.920 |
| Upper bound | ||||||||||||
| 1 | 6.329 | 6.098 | 6.015 | 5.948 | 5.884 | 5.863 | 5.836 | 5.811 | 5.726 | 5.667 | 5.641 | 5.619 |
| 2 | 5.457 | 5.230 | 5.130 | 5.072 | 4.998 | 4.951 | 4.946 | 4.926 | 4.836 | 4.784 | 4.775 | 4.727 |
| 3 | 5.003 | 4.767 | 4.649 | 4.582 | 4.528 | 4.498 | 4.452 | 4.436 | 4.374 | 4.306 | 4.303 | 4.247 |
| 4 | 4.738 | 4.490 | 4.367 | 4.276 | 4.221 | 4.195 | 4.163 | 4.156 | 4.050 | 4.008 | 4.015 | 3.959 |
| 5 | 4.583 | 4.313 | 4.165 | 4.077 | 4.024 | 3.983 | 3.956 | 3.948 | 3.832 | 3.788 | 3.801 | 3.750 |
| 6 | 4.470 | 4.174 | 4.025 | 3.951 | 3.879 | 3.850 | 3.814 | 3.797 | 3.683 | 3.624 | 3.625 | 3.594 |
| 7 | 4.416 | 4.091 | 3.926 | 3.833 | 3.776 | 3.733 | 3.703 | 3.684 | 3.555 | 3.499 | 3.493 | 3.468 |
| 8 | 4.369 | 4.011 | 3.842 | 3.748 | 3.685 | 3.639 | 3.602 | 3.589 | 3.459 | 3.399 | 3.384 | 3.374 |
| 9 | 4.356 | 3.963 | 3.779 | 3.679 | 3.607 | 3.559 | 3.526 | 3.506 | 3.377 | 3.309 | 3.299 | 3.285 |
| 10 | 4.379 | 3.925 | 3.729 | 3.612 | 3.547 | 3.501 | 3.458 | 3.441 | 3.315 | 3.237 | 3.226 | 3.209 |
| 11 | 4.397 | 3.900 | 3.682 | 3.572 | 3.495 | 3.443 | 3.404 | 3.381 | 3.255 | 3.176 | 3.168 | 3.146 |
| 12 | 4.432 | 3.901 | 3.670 | 3.536 | 3.457 | 3.411 | 3.371 | 3.347 | 3.202 | 3.125 | 3.113 | 3.092 |
| Sample Size (T) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 500 | 1000 | 10,000 |
| Lower bound | ||||||||||||
| 1 | 6.108 | 5.979 | 5.904 | 5.834 | 5.768 | 5.771 | 5.721 | 5.709 | 5.646 | 5.596 | 5.570 | 5.579 |
| 2 | 4.732 | 4.585 | 4.502 | 4.423 | 4.379 | 4.367 | 4.331 | 4.326 | 4.265 | 4.217 | 4.182 | 4.212 |
| 3 | 4.051 | 3.851 | 3.787 | 3.723 | 3.681 | 3.674 | 3.644 | 3.641 | 3.567 | 3.512 | 3.504 | 3.510 |
| 4 | 3.621 | 3.433 | 3.364 | 3.294 | 3.261 | 3.242 | 3.208 | 3.204 | 3.137 | 3.097 | 3.086 | 3.087 |
| 5 | 3.366 | 3.157 | 3.073 | 3.026 | 2.983 | 2.947 | 2.918 | 2.914 | 2.846 | 2.810 | 2.795 | 2.795 |
| 6 | 3.177 | 2.965 | 2.882 | 2.825 | 2.782 | 2.755 | 2.721 | 2.718 | 2.646 | 2.611 | 2.596 | 2.592 |
| 7 | 3.042 | 2.820 | 2.732 | 2.665 | 2.628 | 2.595 | 2.565 | 2.565 | 2.487 | 2.460 | 2.441 | 2.441 |
| 8 | 2.949 | 2.709 | 2.608 | 2.548 | 2.504 | 2.477 | 2.440 | 2.437 | 2.370 | 2.328 | 2.317 | 2.311 |
| 9 | 2.873 | 2.628 | 2.519 | 2.451 | 2.406 | 2.381 | 2.345 | 2.335 | 2.271 | 2.230 | 2.216 | 2.213 |
| 10 | 2.841 | 2.563 | 2.443 | 2.366 | 2.327 | 2.300 | 2.263 | 2.251 | 2.193 | 2.145 | 2.130 | 2.130 |
| 11 | 2.815 | 2.515 | 2.378 | 2.303 | 2.258 | 2.232 | 2.201 | 2.186 | 2.128 | 2.080 | 2.065 | 2.062 |
| 12 | 2.811 | 2.470 | 2.324 | 2.249 | 2.205 | 2.176 | 2.146 | 2.129 | 2.066 | 2.022 | 2.006 | 2.002 |
| Upper bound | ||||||||||||
| 1 | 7.030 | 6.848 | 6.745 | 6.671 | 6.608 | 6.547 | 6.559 | 6.535 | 6.428 | 6.376 | 6.332 | 6.373 |
| 2 | 5.889 | 5.667 | 5.561 | 5.497 | 5.442 | 5.414 | 5.368 | 5.369 | 5.276 | 5.223 | 5.187 | 5.220 |
| 3 | 5.292 | 5.113 | 4.963 | 4.890 | 4.836 | 4.801 | 4.786 | 4.772 | 4.669 | 4.600 | 4.577 | 4.593 |
| 4 | 4.971 | 4.717 | 4.600 | 4.532 | 4.479 | 4.425 | 4.401 | 4.381 | 4.305 | 4.220 | 4.187 | 4.216 |
| 5 | 4.738 | 4.463 | 4.342 | 4.265 | 4.207 | 4.166 | 4.149 | 4.136 | 4.040 | 3.954 | 3.931 | 3.941 |
| 6 | 4.616 | 4.306 | 4.169 | 4.076 | 4.024 | 3.984 | 3.954 | 3.930 | 3.840 | 3.762 | 3.750 | 3.747 |
| 7 | 4.518 | 4.192 | 4.040 | 3.951 | 3.877 | 3.841 | 3.808 | 3.795 | 3.694 | 3.619 | 3.588 | 3.595 |
| 8 | 4.457 | 4.102 | 3.939 | 3.838 | 3.761 | 3.719 | 3.697 | 3.679 | 3.568 | 3.497 | 3.476 | 3.475 |
| 9 | 4.446 | 4.051 | 3.867 | 3.753 | 3.669 | 3.634 | 3.604 | 3.586 | 3.475 | 3.408 | 3.379 | 3.371 |
| 10 | 4.437 | 4.003 | 3.809 | 3.684 | 3.610 | 3.551 | 3.528 | 3.507 | 3.392 | 3.324 | 3.299 | 3.290 |
| 11 | 4.486 | 3.971 | 3.761 | 3.629 | 3.552 | 3.493 | 3.459 | 3.434 | 3.324 | 3.255 | 3.228 | 3.226 |
| 12 | 4.547 | 3.942 | 3.727 | 3.594 | 3.502 | 3.445 | 3.405 | 3.378 | 3.264 | 3.203 | 3.170 | 3.166 |
| Sample Size (T) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 30 | 50 | 80 | 100 | 200 | 500 | 30 | 50 | 80 | 100 | 200 | 500 |
| Case 2 using lower bound critical values | Case 2 using upper bound critical values | |||||||||||
| 1 | 0.01064 | 0.00977 | 0.00937 | 0.00848 | 0.00828 | 0.00843 | 0.00544 | 0.00444 | 0.00417 | 0.00412 | 0.00383 | 0.00372 |
| 2 | 0.01489 | 0.01240 | 0.01193 | 0.01197 | 0.01103 | 0.01103 | 0.00429 | 0.00364 | 0.00316 | 0.00311 | 0.00265 | 0.00270 |
| 3 | 0.01738 | 0.01512 | 0.01377 | 0.01404 | 0.01378 | 0.01329 | 0.00411 | 0.00284 | 0.00249 | 0.00217 | 0.00190 | 0.00197 |
| 4 | 0.02103 | 0.01748 | 0.01517 | 0.01585 | 0.01506 | 0.01493 | 0.00398 | 0.00260 | 0.00188 | 0.00161 | 0.00140 | 0.00147 |
| 5 | 0.02376 | 0.01876 | 0.01776 | 0.01788 | 0.01605 | 0.01625 | 0.00401 | 0.00229 | 0.00173 | 0.00144 | 0.00127 | 0.00098 |
| 6 | 0.02808 | 0.01958 | 0.01846 | 0.01847 | 0.01808 | 0.01680 | 0.00435 | 0.00204 | 0.00138 | 0.00123 | 0.00101 | 0.00086 |
| 7 | 0.03399 | 0.02151 | 0.02007 | 0.01984 | 0.01860 | 0.01856 | 0.00555 | 0.00145 | 0.00087 | 0.00082 | 0.00064 | 0.00060 |
| 8 | 0.04021 | 0.02437 | 0.02116 | 0.02121 | 0.01952 | 0.02007 | 0.00779 | 0.00182 | 0.00091 | 0.00069 | 0.00058 | 0.00053 |
| 9 | 0.05105 | 0.02689 | 0.02206 | 0.02218 | 0.02036 | 0.02034 | 0.01162 | 0.00168 | 0.00065 | 0.00051 | 0.00045 | 0.00032 |
| 10 | 0.06826 | 0.02795 | 0.02122 | 0.02155 | 0.02048 | 0.02110 | 0.01735 | 0.00183 | 0.00070 | 0.00048 | 0.00023 | 0.00030 |
| 11 | 0.09862 | 0.03124 | 0.02374 | 0.02367 | 0.02216 | 0.02223 | 0.03295 | 0.00153 | 0.00057 | 0.00030 | 0.00028 | 0.00019 |
| 12 | 0.15387 | 0.03366 | 0.02369 | 0.02301 | 0.02160 | 0.02346 | 0.06967 | 0.00184 | 0.00057 | 0.00032 | 0.00019 | 0.00011 |
| Case 4 using lower bound critical values | Case 4 using upper bound critical values | |||||||||||
| 1 | 0.00761 | 0.00585 | 0.00489 | 0.00521 | 0.00413 | 0.00384 | 0.00430 | 0.00280 | 0.00231 | 0.00230 | 0.00226 | 0.00177 |
| 2 | 0.01084 | 0.00806 | 0.00739 | 0.00707 | 0.00618 | 0.00575 | 0.00421 | 0.00280 | 0.00201 | 0.00188 | 0.00178 | 0.00158 |
| 3 | 0.01399 | 0.01049 | 0.00923 | 0.00853 | 0.00749 | 0.00741 | 0.00400 | 0.00231 | 0.00207 | 0.00167 | 0.00150 | 0.00107 |
| 4 | 0.01731 | 0.01268 | 0.01113 | 0.01080 | 0.00987 | 0.00876 | 0.00406 | 0.00217 | 0.00145 | 0.00116 | 0.00113 | 0.00104 |
| 5 | 0.02128 | 0.01530 | 0.01286 | 0.01211 | 0.01092 | 0.01076 | 0.00504 | 0.00200 | 0.00133 | 0.00105 | 0.00061 | 0.00061 |
| 6 | 0.02635 | 0.01686 | 0.01419 | 0.01317 | 0.01220 | 0.01099 | 0.00568 | 0.00164 | 0.00108 | 0.00078 | 0.00069 | 0.00045 |
| 7 | 0.03360 | 0.01886 | 0.01556 | 0.01427 | 0.01421 | 0.01288 | 0.00754 | 0.00168 | 0.00077 | 0.00061 | 0.00041 | 0.00046 |
| 8 | 0.04269 | 0.02056 | 0.01589 | 0.01520 | 0.01416 | 0.01435 | 0.00989 | 0.00164 | 0.00077 | 0.00057 | 0.00032 | 0.00046 |
| 9 | 0.05727 | 0.02262 | 0.01684 | 0.01687 | 0.01569 | 0.01555 | 0.01588 | 0.00175 | 0.00061 | 0.00043 | 0.00026 | 0.00025 |
| 10 | 0.08010 | 0.02423 | 0.01839 | 0.01799 | 0.01594 | 0.01572 | 0.02631 | 0.00176 | 0.00081 | 0.00043 | 0.00022 | 0.00020 |
| 11 | 0.11959 | 0.02746 | 0.01962 | 0.01948 | 0.01554 | 0.01669 | 0.05017 | 0.00211 | 0.00050 | 0.00039 | 0.00019 | 0.00014 |
| 12 | 0.20218 | 0.03194 | 0.02054 | 0.01957 | 0.01763 | 0.01680 | 0.10938 | 0.00222 | 0.00050 | 0.00043 | 0.00009 | 0.00016 |
| DGP 1 and 7 | 0.07 | 0.90 | 0.03 | 0.10 | −0.10 | 10.00 | 0.10 | 1.00 |
| DGP 2 and 8 | 0.20 | 0.75 | 0.05 | 0.25 | −0.25 | 4.00 | 0.04 | 1.00 |
| DGP 3 and 9 | 0.30 | 0.50 | 0.20 | 0.50 | −0.50 | 2.00 | 0.02 | 1.00 |
| DGP 4 and 10 | 0.15 | 0.90 | −0.05 | 0.10 | −0.10 | 10.00 | 0.10 | 1.00 |
| DGP 5 and 11 | 0.30 | 0.75 | −0.05 | 0.25 | −0.25 | 4.00 | 0.04 | 1.00 |
| DGP 6 and 12 | 1.00 | 0.50 | −0.50 | 0.50 | −0.50 | 2.00 | 0.02 | 1.00 |
| Sample Size (T) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DGP | 30 | 50 | 80 | 100 | 200 | 500 | 30 | 50 | 80 | 100 | 200 | 500 |
| Case 2 using lower bound critical values | Case 2 using upper bound critical values | |||||||||||
| 1 | 0.08267 | 0.12618 | 0.22688 | 0.31123 | 0.81175 | 1.00000 | 0.04457 | 0.07077 | 0.13709 | 0.20055 | 0.66720 | 1.00000 |
| 2 | 0.34798 | 0.65055 | 0.92905 | 0.98479 | 1.00000 | 1.00000 | 0.19524 | 0.44571 | 0.81156 | 0.93482 | 1.00000 | 1.00000 |
| 3 | 0.81880 | 0.98924 | 0.99997 | 1.00000 | 1.00000 | 1.00000 | 0.62618 | 0.95167 | 0.99955 | 0.99998 | 1.00000 | 1.00000 |
| 4 | 0.26552 | 0.40174 | 0.60217 | 0.72783 | 0.98695 | 1.00000 | 0.11525 | 0.19189 | 0.34202 | 0.45354 | 0.91319 | 1.00000 |
| 5 | 0.53890 | 0.84428 | 0.98672 | 0.99852 | 1.00000 | 1.00000 | 0.27413 | 0.59343 | 0.91108 | 0.97908 | 1.00000 | 1.00000 |
| 6 | 0.80913 | 0.98982 | 0.99995 | 1.00000 | 1.00000 | 1.00000 | 0.52375 | 0.92550 | 0.99932 | 0.99999 | 1.00000 | 1.00000 |
| 7 | 0.36685 | 0.53756 | 0.75025 | 0.85151 | 0.99712 | 1.00000 | 0.14992 | 0.26348 | 0.44621 | 0.57413 | 0.96159 | 1.00000 |
| 8 | 0.63652 | 0.91384 | 0.99574 | 0.99970 | 1.00000 | 1.00000 | 0.33854 | 0.69123 | 0.95197 | 0.99135 | 1.00000 | 1.00000 |
| 9 | 0.92448 | 0.99875 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 0.72723 | 0.98320 | 0.99991 | 1.00000 | 1.00000 | 1.00000 |
| 10 | 0.39359 | 0.59700 | 0.80098 | 0.89239 | 0.99874 | 1.00000 | 0.15143 | 0.29297 | 0.49083 | 0.62171 | 0.97289 | 1.00000 |
| 11 | 0.64779 | 0.92979 | 0.99705 | 0.99981 | 1.00000 | 1.00000 | 0.31747 | 0.69949 | 0.95753 | 0.99300 | 1.00000 | 1.00000 |
| 12 | 0.86382 | 0.99688 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 0.55233 | 0.95311 | 0.99988 | 1.00000 | 1.00000 | 1.00000 |
| Case 4 using lower bound critical values | Case 4 using upper bound critical values | |||||||||||
| 1 | 0.04717 | 0.05978 | 0.11763 | 0.18147 | 0.69006 | 0.99998 | 0.02945 | 0.03678 | 0.07635 | 0.11833 | 0.56051 | 0.99997 |
| 2 | 0.09941 | 0.16688 | 0.39248 | 0.60868 | 0.99983 | 1.00000 | 0.05571 | 0.09871 | 0.26313 | 0.45907 | 0.99893 | 1.00000 |
| 3 | 0.29196 | 0.53306 | 0.84703 | 0.95615 | 1.00000 | 1.00000 | 0.18011 | 0.38219 | 0.73822 | 0.90310 | 1.00000 | 1.00000 |
| 4 | 0.18250 | 0.25176 | 0.42410 | 0.56510 | 0.97356 | 1.00000 | 0.08764 | 0.12720 | 0.23841 | 0.34539 | 0.87972 | 1.00000 |
| 5 | 0.20723 | 0.33136 | 0.61661 | 0.80837 | 0.99999 | 1.00000 | 0.10060 | 0.18191 | 0.41374 | 0.62929 | 0.99981 | 1.00000 |
| 6 | 0.35509 | 0.58214 | 0.85614 | 0.95493 | 1.00000 | 1.00000 | 0.19277 | 0.38245 | 0.70533 | 0.87622 | 1.00000 | 1.00000 |
| 7 | 0.26433 | 0.36151 | 0.56685 | 0.70888 | 0.99268 | 1.00000 | 0.12344 | 0.18490 | 0.33415 | 0.46082 | 0.94441 | 1.00000 |
| 8 | 0.27615 | 0.43460 | 0.72576 | 0.88647 | 1.00000 | 1.00000 | 0.13349 | 0.24667 | 0.52331 | 0.73580 | 0.99999 | 1.00000 |
| 9 | 0.49778 | 0.76589 | 0.95654 | 0.99173 | 1.00000 | 1.00000 | 0.29465 | 0.57778 | 0.88242 | 0.96847 | 1.00000 | 1.00000 |
| 10 | 0.29258 | 0.41499 | 0.62800 | 0.76942 | 0.99628 | 1.00000 | 0.13015 | 0.20873 | 0.37876 | 0.51199 | 0.96300 | 1.00000 |
| 11 | 0.30009 | 0.47762 | 0.76393 | 0.90787 | 1.00000 | 1.00000 | 0.13400 | 0.26801 | 0.55033 | 0.75565 | 0.99996 | 1.00000 |
| 12 | 0.45528 | 0.72499 | 0.93450 | 0.98370 | 1.00000 | 1.00000 | 0.22459 | 0.49470 | 0.81873 | 0.93793 | 1.00000 | 1.00000 |
| Currency | Bulgaria–Denmark | |||||
| Variable | LS_BD | LRP_PH_BD | ||||
| Hypotheses | ||||||
| ADF | −3.427 * | −18.602 * | −3.858 * | −2.762 | ||
| PP | −4.656 * | −20.285 * | −5.579 * | −15.163 * | ||
| DF-GLS | −1.897 | −3.418 * | 0.282 | −2.791 * | ||
| KPSS | 0.231 | 0.051 | 0.900 * | 0.685 * | ||
| Currency | Denmark-Euro | |||||
| Variable | LS_DE | LRP_HT_DE | LRP_RR_DE | |||
| Hypotheses | ||||||
| ADF | −3.737 * | −17.828 * | −1.477 | −24.412 * | −0.136 | −12.564 * |
| PP | −3.733 * | −17.917 * | −6.864 * | −48.650 * | −1.326 | −23.863 * |
| DF-GLS | −2.617 * | −3.487 * | −1.457 | −0.648 | 3.135 | −12.241 * |
| KPSS | 0.213 | 0.028 | 0.442 | 0.171 | 2.048 * | 0.126 |
| Currency | Bulgaria–Denmark | Denmark-Euro | ||
|---|---|---|---|---|
| Regressor | LRP_PH_BD | LRP_PH_BD | LRP_HT_DE | LRP_RR_DE |
| Model | ARDL(1,1) | ARDL(1,1) ARCH(5) | ARDL(1,3) | ARDL(1,1) |
| Case 2 and Case 3 | ||||
| −5.635 {−2.868*, −3.224 *} | −6.008 {−2.868 *, −3.224 *} | −4.077 {−2.865 *, −3.226 *} | −3.662 {−2.869 *, −3.224 *} | |
| Case 2 | ||||
| 10.830 {3.636 *, 4.158 *} | 12.346 {3.636 *, 4.158 *} | 5.651 {3.629 *, 4.163 *} | 4.490 {3.638 *, 4.155 *} | |
| 15.964 {4.866 *, 5.683 *} | 18.316 {4.866 *, 5.683 *} | 8.442 {4.847 *, 5.685 *} | 6.720 {4.859 *, 5.674 *} | |
| 16,373,960.207 [0.000] * | 19,065,236.642 [0.000] * | 18,588,586.026 [0.000] * | 11,858,472.960 [0.000] * | |
| Case 3 | ||||
| 15.960 {4.948 *, 5.758 *} | 18.312 {4.948 *, 5.758 *} | 8.441 {4.933 *, 5.761 *} | 6.721 {4.945 *, 5.749 *} | |
| 5.615 {3.924 *, 7.179} | 8.498 {3.924 *, 7.179 *} | 2.072 {4.013, 7.194} | 0.185 {3.914, 7.164} | |
| 6.384 [0.012] * | 12.699 [0.000] * | 2.599 [0.108] | 0.190 [0.663] | |
| Case 4 | ||||
| −5.712 {−3.424 *, −3.704 *} | −6.653 {−3.424 *, −3.704 *} | −4.069 {−3.416 *, −3.703 *} | −3.642 {−3.422 *, −3.702} | |
| 11.020 {4.733 *, 5.226 *} | 17.011 {4.733 *, 5.226 *} | 5.615 {4.712 *, 5.223 *} | 4.467 {4.724 *, 5.214} | |
| 3.004 {5.611 *, 6.418} | 7.138 {5.611 *, 6.418} | 1.042 {5.607, 6.423} | 0.096 {5.608, 6.410} | |
| 3.383 [0.035] * | 9.892 [0.000] * | 1.312 [0.271] | 0.098 [0.907] | |
| Observations | 282 | 282 | 291 | 293 |
| Currency | Bulgaria–Denmark | Denmark-Euro | ||
|---|---|---|---|---|
| Regressor | LRP_PH_BD | LRP_PH_BD | LRP_HT_DE | LRP_RR_DE |
| Model | ARDL(1,1) | ARDL(1,1) ARCH(5) | ARDL(1,3) | ARDL(1,1) |
| Case 2 and Case 3 | ||||
| Adjustment | −0.191 | −0.171 | −0.109 | −0.089 |
| Intercept | −1.338 (−5439.383) * | −1.338 (−5040.970) * | 2.009 (3227.496) * | 2.008 (4556.664) * |
| () | 0.005 (2.527) * | 0.010 (3.564) * | 0.021 (1.612) | 0.003 (0.436) |
| Proportionality | −540.152 [0.000] * | −358.013 [0.000] * | −73.850 [0.000] * | −171.328 [0.000] * |
| Case 4 | ||||
| Adjustment | −0.193 | −0.185 | −0.110 | −0.089 |
| Trend | 10−6 (0.542) | 10−6 (2.163) * | 10−7 (0.141) | 10−6 (−0.082) |
| () | 0.004 (2.066) * | 0.008 (3.179) * | 0.021 (1.548) | 0.006 (0.143) |
| Proportionality | −492.832 [0.000] * | −390.455 [0.000] * | −72.276 [0.000] * | −24.267 [0.000] * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stewart, C. Demonstrating That the Autoregressive Distributed Lag Bounds Test Can Detect a Long-Run Levels Relationship When the Dependent Variable Is I(0). Econometrics 2025, 13, 39. https://doi.org/10.3390/econometrics13040039
Stewart C. Demonstrating That the Autoregressive Distributed Lag Bounds Test Can Detect a Long-Run Levels Relationship When the Dependent Variable Is I(0). Econometrics. 2025; 13(4):39. https://doi.org/10.3390/econometrics13040039
Chicago/Turabian StyleStewart, Chris. 2025. "Demonstrating That the Autoregressive Distributed Lag Bounds Test Can Detect a Long-Run Levels Relationship When the Dependent Variable Is I(0)" Econometrics 13, no. 4: 39. https://doi.org/10.3390/econometrics13040039
APA StyleStewart, C. (2025). Demonstrating That the Autoregressive Distributed Lag Bounds Test Can Detect a Long-Run Levels Relationship When the Dependent Variable Is I(0). Econometrics, 13(4), 39. https://doi.org/10.3390/econometrics13040039