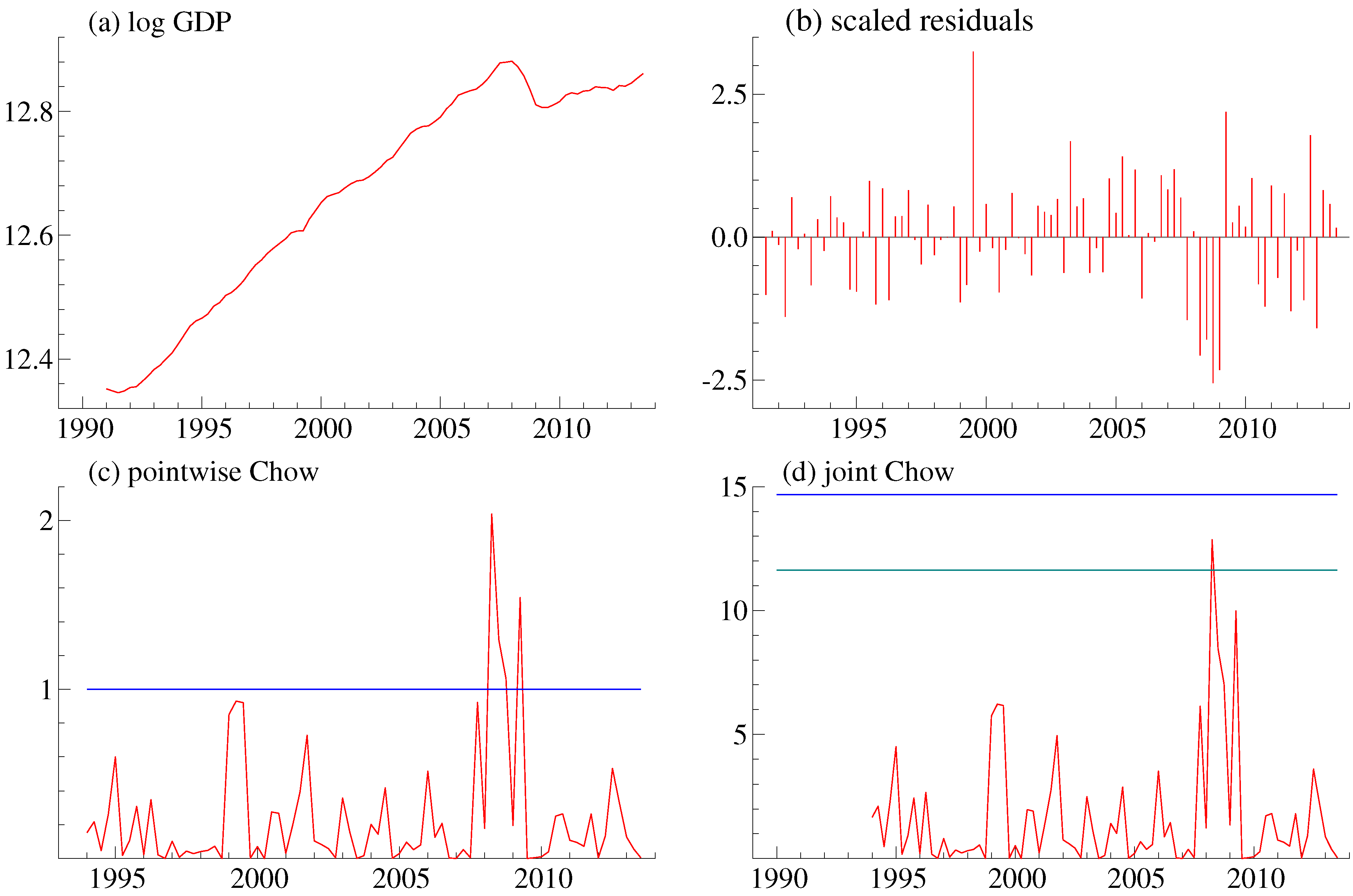
6.1. Autoregressive Data-Generating Process
Consider the following data-generating process:
Where not otherwise stated, we set
and
. The number of Monte Carlo repetitions and the implied Monte Carlo standard error,
, are indicated in table captions.
The regression model is that of an first order autoregression. It includes an intercept unless otherwise stated. The five tests computed and presented in the tables are: the asymptotic sup-Chow test (
); the corrected sup-Chow test (
); the [
13] sup-F test (
); an outlier test based on the OLS residuals (
); and the [
32]
test for normality (Φ). The nominal size is
unless otherwise stated.
The two sup-Chow tests are described in Theorem 10 and Equation (
28), respectively; for the function
, we use
. The sup-F test is a linear regression form of Andrews’ sup-W (Wald) test with 15% trimming, as used for the simulations in [
33] and implemented in EViews 7 by the command ubreak. It is the maximum of the Chow F-tests calculated over break points
, such that for each break point
λ, under the alternative, the model is estimated separately for each subsample (
and
…T), whereas under the hypothesis, the model is estimated for the full sample. The null distribution is given by asymptotic approximation to a non-standard distribution with simulated critical values given in [
15]. The sup-
test examines the maximum of the squared full-sample OLS residuals, externally studentised as in ([
34] s. 2.2.9); that is, residual
t is normalised using an estimate of the error variance that excludes residual
t itself. These squared statistics are
distributed under normality of the errors, but not independent; hence, the use of the Bonferroni inequality to find significance levels is recommended by [
34]. We find in simulation that, despite dependence, the exact maximal distribution of
T independent
random variables is a reasonable choice for the sample sizes and processes we consider, except those that are near-unit-root. Finally, in experiments where we wish to evaluate the performance of the sup-Chow test conditional on residuals having satisfied a normality test, we use the [
32]
test of the OLS residuals.
In the first experiment (
Table 1), we vary the autoregressive parameter through the stationary, unit-root and explosive regions and consider the effect of either including or excluding an intercept from the model. As noted above, the
test is uniformly oversized. The
test is correctly sized and approximately similar, with simulated size varying very little across the parameter space. There is some tendency towards inflated sizes under near-unit-root processes when an intercept is included in the model, but the extent of this is quite limited (7% simulated size). The key consequence of this result is that it is not necessary to know
a priori where the autoregressive parameter lies to effectively apply the
test, avoiding a potential circularity in model construction.
In simulations that are not reported here, we also investigated the test. This test is not valid in the non-stationary case. Thus, the same patterns were seen, albeit with a larger effect. The simulated size is as high as 44% in the unit root case.
Table 1.
Simulated rejection frequency for
and
under the Gaussian autoregression in Equation (
29). 200,000 repetitions,
.
Table 1.
Simulated rejection frequency for and under the Gaussian autoregression in Equation (29). 200,000 repetitions, .
| T | | Autoregressive Coefficient (α) |
|---|
| | −1.03 | −1.00 | −0.50 | 0.00 | 0.50 | 0.90 | 1.00 | 1.03 |
|---|
| 5% Nominal Size |
| Intercept included in model (M1) |
| 25 | | 14.52 | 14.44 | 13.92 | 14.40 | 15.82 | 19.28 | 19.86 | 20.21 |
| 5.30 | 5.26 | 5.01 | 5.24 | 5.78 | 7.28 | 7.59 | 7.75 |
| 50 | | 12.80 | 12.72 | 12.32 | 12.60 | 13.50 | 16.13 | 16.97 | 17.43 |
| 5.17 | 5.15 | 4.92 | 5.05 | 5.38 | 6.52 | 7.00 | 7.27 |
| 100 | | 10.43 | 10.41 | 10.15 | 10.36 | 10.73 | 12.34 | 13.27 | 13.85 |
| 5.09 | 5.05 | 4.95 | 5.00 | 5.08 | 5.82 | 6.38 | 6.74 |
| No intercept included in model (M2) |
| 25 | | 15.28 | 15.23 | 14.51 | 14.49 | 14.62 | 15.11 | 15.33 | 15.39 |
| 5.49 | 5.46 | 5.20 | 5.19 | 5.23 | 5.44 | 5.49 | 5.53 |
| 50 | | 13.17 | 13.12 | 12.72 | 12.72 | 12.71 | 13.01 | 13.20 | 13.21 |
| 5.33 | 5.29 | 5.06 | 5.03 | 5.09 | 5.20 | 5.26 | 5.27 |
| 100 | | 10.64 | 10.60 | 10.27 | 10.31 | 10.34 | 10.42 | 10.62 | 10.63 |
| 5.17 | 5.12 | 5.02 | 4.99 | 5.01 | 5.03 | 5.13 | 5.16 |
| 1% Nominal Size |
| No intercept included in model (M1) |
| 25 | | 6.30 | 6.29 | 5.98 | 6.24 | 7.06 | 8.87 | 9.16 | 9.33 |
| 1.09 | 1.10 | 1.04 | 1.07 | 1.24 | 1.64 | 1.75 | 1.79 |
| 50 | | 4.77 | 4.77 | 4.56 | 4.70 | 5.16 | 6.44 | 6.83 | 7.04 |
| 1.08 | 1.08 | 1.02 | 1.06 | 1.15 | 1.45 | 1.57 | 1.60 |
| 100 | | 3.36 | 3.36 | 3.24 | 3.31 | 3.47 | 4.22 | 4.59 | 4.74 |
| 1.05 | 1.05 | 1.02 | 1.02 | 1.04 | 1.21 | 1.36 | 1.43 |
| No intercept included in model (M2) |
| 25 | | 6.71 | 6.69 | 6.25 | 6.22 | 6.34 | 6.59 | 6.71 | 6.73 |
| 1.16 | 1.15 | 1.06 | 1.04 | 1.06 | 1.12 | 1.18 | 1.19 |
| 50 | | 4.98 | 4.97 | 4.70 | 4.69 | 4.78 | 4.90 | 4.95 | 4.95 |
| 1.12 | 1.11 | 1.04 | 1.05 | 1.05 | 1.07 | 1.10 | 1.09 |
| 100 | | 3.41 | 3.37 | 3.24 | 3.24 | 3.25 | 3.33 | 3.39 | 3.40 |
| 1.06 | 1.05 | 1.02 | 1.01 | 1.00 | 1.00 | 1.03 | 1.04 |
The second experiment evaluates the sensitivity of the
test to failures of Assumption 5, in particular the non-normality of the errors.
Table 2 presents simulated sizes for both the
and
tests under a range of error distributions. The former is very sensitive to departures from normality, while the latter is not. In the second part of the table we consider a further scenario, in which a model builder runs the structural instability tests only if a test for normal residuals is not rejected. This yields three additional tests, the normality test Φ and the
and
tests, each conditional on the normality hypothesis having not been rejected. We also consider joint tests
and
that first tests normality and then tests for break if normality cannot be rejected. As the table illustrates, some size distortion remains, but the inflation of the unconditional test is largely controlled in the conditional case. As noted in
Section 8 below, we recommend using the test in this way if the normality of the errors cannot be safely assumed.
Table 2.
Simulated rejection frequency for
and
, possibly combined with normality test Φ, under autoregression in Equation (
29) with various error distributions. 50,000 repetitions,
.
Table 2.
Simulated rejection frequency for and , possibly combined with normality test Φ, under autoregression in Equation (29) with various error distributions. 50,000 repetitions, .
| T | | Error Distribution |
|---|
| | Φ | | | | |
|---|
| Unconditional tests |
| 50 | | 5.0 | 6.6 | 15.0 | 28.8 | 40.9 |
| 6.0 | 6.0 | 6.0 | 5.9 | 6.3 |
| 100 | | 5.0 | 7.4 | 22.2 | 45.0 | 59.9 |
| 4.9 | 5.0 | 4.9 | 4.7 | 4.9 |
| Joint tests |
| 50 | Φ | 4.9 | 6.7 | 19.0 | 41.0 | 95.1 |
| 3.4 | 3.9 | 6.2 | 8.0 | * 7.4 |
| 6.0 | 6.0 | 6.1 | 6.0 | * 6.7 |
| 8.1 | 10.4 | 24.0 | 45.8 | * 95.5 |
| 10.6 | 12.3 | 23.9 | 44.6 | * 95.4 |
| 100 | Φ | 4.8 | 7.6 | 28.7 | 63.0 | 100.0 |
| 3.3 | 4.2 | 7.2 | 8.6 | |
| 5.0 | 5.0 | 5.0 | 4.9 | |
| 8.0 | 11.5 | 33.9 | 66.2 | * 100.0 |
| 9.5 | 12.2 | 32.3 | 64.8 | * 100.0 |
The third experiment considers the power of the tests against a single shift in the mean level of the process. The data generating process is:
and we allow
γ and
τ to vary as presented. The regression model remains a first order autoregression with an intercept. The level shift is therefore not modelled.
Table 3 shows simulated sizes for the unconditional tests as in the previous experiment. We note that the
test performs well for a break at mid-sample, but is outperformed by the
test for breaks occurring near the end of the sample. We also consider conditional tests as in the previous experiment. There are two main observations: firstly, the normality test is increasingly likely to reject as the break magnitude becomes large; but secondly, the
test still has power (attenuated by around one-half) to detect the break in this case.
Table 3.
Simulated rejection frequency for
and
, possibly combined with normality test Φ, under the process in Equation (
30) with a break of magnitude
γ at time
τ. 50,000 repetitions,
.
Table 3.
Simulated rejection frequency for and , possibly combined with normality test Φ, under the process in Equation (30) with a break of magnitude γ at time τ. 50,000 repetitions, .
| T | | | Break Timing (τ) |
|---|
| | | 0.5T | T-2 | T-1 |
|---|
| | | Post-Break Constant (γ) |
|---|
| | 0.0 | 2.0 | 4.0 | 2.0 | 4.0 | 2.0 | 4.0 |
|---|
| Unconditional tests |
| 25 | | 5.5 | 13.7 | 51.2 | 21.0 | 78.7 | 16.0 | 70.3 |
| 10.3 | 90.4 | 99.9 | 19.9 | 44.8 | 14.1 | 28.1 |
| 50 | | 5.2 | 17.1 | 67.6 | 18.6 | 83.2 | 13.3 | 69.9 |
| 6.0 | 99.8 | 100.0 | 10.2 | 34.5 | 7.1 | 11.5 |
| 100 | | 5.1 | 20.0 | 77.9 | 16.1 | 84.2 | 11.5 | 67.6 |
| 4.9 | 100.0 | 100.0 | 7.2 | 31.2 | 5.4 | 7.4 |
| Joint tests |
| 25 | Φ | 5.1 | 4.3 | 15.6 | 9.6 | 37.9 | 9.9 | 53.9 |
| 3.8 | 12.5 | 45.3 | 14.8 | 66.7 | 9.4 | 38.3 |
| 10.2 | 90.4 | 99.9 | 19.6 | 52.1 | 13.1 | 22.6 |
| 8.7 | 16.2 | 53.8 | 22.9 | 79.4 | 18.4 | 71.5 |
| 14.8 | 90.8 | 99.9 | 27.3 | 70.3 | 21.7 | 64.3 |
| 50 | Φ | 4.8 | 4.4 | 17.0 | 11.1 | 61.9 | 9.5 | 58.6 |
| 3.5 | 15.7 | 62.6 | 11.3 | 58.6 | 7.2 | 31.1 |
| 6.0 | 99.8 | 100.0 | 9.8 | 33.9 | 6.9 | 9.0 |
| 8.2 | 19.4 | 69.0 | 21.1 | 84.2 | 16.1 | 71.5 |
| 10.6 | 99.9 | 100.0 | 19.8 | 74.8 | 15.8 | 62.3 |
| 100 | Φ | 4.7 | 4.2 | 15.6 | 11.2 | 74.7 | 8.5 | 57.4 |
| 3.4 | 18.7 | 74.7 | 8.9 | 43.5 | 6.4 | 28.4 |
| 4.9 | 100.0 | 100.0 | 6.8 | 19.3 | 5.4 | 6.3 |
| 8.0 | 22.1 | 78.7 | 19.1 | 85.7 | 14.4 | 69.5 |
| 9.4 | 100.0 | 100.0 | 17.2 | 79.6 | 13.5 | 60.0 |
The fourth experiment (
Table 4) considers the power of the tests against a single innovation outlier at the process mid-point. The data generating process is:
and we allow
α and
δ to vary. Both tests presented have similar power in most circumstances, with an outlier larger than three-times the error standard deviation being detected with useful frequency. The OLS-based
test has slightly better power than the Chow test. The conditional evaluations show that both tests retain power in situations where the normality test is not rejected.
Table 4.
Simulated rejection frequency for
and
, possibly combined with normality test Φ, under the process in Equation (
31) with a break of magnitude
δ. 50,000 repetitions,
.
Table 4.
Simulated rejection frequency for and , possibly combined with normality test Φ, under the process in Equation (31) with a break of magnitude δ. 50,000 repetitions, .
| α | T | | Outlier Magnitude (δ) |
|---|
| | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
|---|
| Unconditional tests |
|
| 0.5 | 50 | | 5.5 | 5.8 | 10.6 | 28.7 | 58.7 | 84.9 |
| | 4.7 | 5.0 | 10.5 | 31.8 | 66.2 | 90.7 |
| 100 | | 5.2 | 5.5 | 9.8 | 28.1 | 61.1 | 87.9 |
| | 4.8 | 5.1 | 9.8 | 29.9 | 65.1 | 90.8 |
| 0.9 | 50 | | 6.6 | 7.0 | 12.0 | 30.2 | 59.7 | 85.3 |
| | 4.7 | 4.9 | 10.3 | 31.3 | 65.5 | 90.3 |
| 100 | | 5.9 | 6.3 | 10.8 | 28.9 | 61.4 | 87.9 |
| | 4.9 | 5.1 | 9.8 | 29.7 | 64.9 | 90.6 |
| Joint tests |
| 0.5 | 50 | Φ | 4.9 | 5.0 | 9.6 | 27.7 | 59.3 | 86.6 |
| | 3.8 | 4.0 | 5.8 | 10.8 | 18.0 | 25.6 |
| | 2.2 | 2.4 | 4.0 | 10.3 | 22.7 | 36.8 |
| | 8.5 | 8.8 | 14.8 | 35.5 | 66.6 | 90.0 |
| | 7.0 | 7.3 | 13.2 | 35.2 | 68.5 | 91.5 |
| | 100 | Φ | 4.8 | 5.0 | 8.7 | 25.0 | 57.1 | 86.0 |
| | 3.5 | 3.7 | 5.2 | 11.0 | 20.9 | 32.0 |
| | 2.7 | 2.8 | 4.4 | 10.9 | 24.3 | 40.0 |
| | 8.1 | 8.5 | 13.4 | 33.2 | 66.1 | 90.5 |
| | 7.3 | 7.7 | 12.7 | 33.2 | 67.5 | 91.6 |
| 0.9 | 50 | Φ | 4.9 | 5.1 | 9.4 | 27.1 | 58.6 | 85.9 |
| | 4.9 | 5.2 | 7.3 | 13.1 | 21.6 | 30.6 |
| | 2.2 | 2.3 | 4.0 | 10.3 | 22.6 | 37.5 |
| | 9.5 | 10.0 | 16.0 | 36.6 | 67.5 | 90.2 |
| | 6.9 | 7.2 | 13.0 | 34.6 | 68.0 | 91.2 |
| 100 | Φ | 4.7 | 5.0 | 8.6 | 24.7 | 56.8 | 85.8 |
| | 4.2 | 4.4 | 6.2 | 12.2 | 22.2 | 33.6 |
| | 2.7 | 2.8 | 4.4 | 10.9 | 24.2 | 39.5 |
| | 8.7 | 9.2 | 14.3 | 33.8 | 66.4 | 90.6 |
| | 7.3 | 7.6 | 12.6 | 32.9 | 67.2 | 91.4 |
6.2. Autoregressive Distributed Lag Data-Generating Process
We consider a bivariate data-generating process, written in triangular equilibrium correction form as
where
. The characteristic roots of the system are
ψ and
. When
, the model is cointegrated. When
, the model is stationary. In both cases,
is stationary.
We then fit the univariate autoregressive distributed lag model
and investigate the residuals
using the Chow statistics.
The first experiment (
Table 5) evaluates the size of the Chow tests. Here,
ψ varies, while
in the data generating process. The results are in line with those seen for the autoregressive situation in
Table 1. The second experiment is not done in this situation.
Table 5.
Simulated rejection frequency for
,
under an autoregressive distributed lag process in Equations (
32), (
33). 50,000 repetitions,
.
Table 5.
Simulated rejection frequency for , under an autoregressive distributed lag process in Equations (32), (33). 50,000 repetitions, .
| T | | Autoregressive Coefficient (ψ) |
|---|
| | | 0.25 | 1.00 | |
|---|
| 50 | | | 15.0 | 16.3 | |
| | 6.1 | 6.7 | |
| 100 | | | 11.6 | 12.2 | |
| | 5.4 | 5.8 | |
The third experiment (
Table 6) evaluates the power of the Chow tests against a single shift in the mean level. This is done by replacing
ν by
in the data generating process Equation (
32). The results are in line with those seen for the autoregressive situation in
Table 3: There is good size control. The power is nearly uniform in
ψ and comparable to the power reported in
Table 3.
The fourth experiment (
Table 7) evaluates the power of the Chow tests against a single innovation outlier at the process mid-point. This is done by replacing
ν by
in the data generating process Equation (
32). The results are in line with those seen for the autoregressive situation in
Table 4.
Table 6.
Simulated rejection frequency for
under process in Equations (
32), (
33) with a break of magnitude
ν at time
τ.
. 50,000 repetitions,
.
Table 6.
Simulated rejection frequency for under process in Equations (32), (33) with a break of magnitude ν at time τ. . 50,000 repetitions, .
| ψ | | Break Timing(τ) |
|---|
| | | 0.5T | T-2 | T-1 |
|---|
| | | Post-Break Constant (ν) |
|---|
| | 0.0 | 2.0 | 4.0 | 2.0 | 4.0 | 2.0 | 4.0 |
|---|
| 0.25 | | 6.1 | 16.3 | 64.6 | 19.7 | 83.2 | 13.8 | 68.2 |
| Φ | 4.9 | 6.8 | 34.1 | 10.9 | 61.8 | 9.1 | 54.9 |
| 4.5 | 13.4 | 51.2 | 12.7 | 58.8 | 8.4 | 33.1 |
| 9.2 | 19.3 | 67.8 | 22.2 | 84.3 | 16.7 | 69.8 |
| 1.00 | | 6.7 | 16.0 | 62.0 | 19.4 | 81.2 | 14.2 | 67.2 |
| Φ | 5.0 | 6.0 | 25.1 | 9.7 | 54.5 | 8.7 | 51.8 |
| 5.3 | 13.7 | 52.6 | 13.5 | 60.8 | 9.1 | 35.2 |
| 10.0 | 18.9 | 64.5 | 21.9 | 82.2 | 17.0 | 68.8 |
Table 7.
Simulated rejection frequency for
under process in Equations (
32), (
33) with an outlier of magnitude
ν at mid-sample.
. 50,000 repetitions,
.
Table 7.
Simulated rejection frequency for under process in Equations (32), (33) with an outlier of magnitude ν at mid-sample. . 50,000 repetitions, .
| ψ | | Outlier Magnitude (ν) |
|---|
| | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
|---|
| 0.25 | | 6.1 | 6.3 | 10.4 | 25.5 | 53.0 | 79.1 |
| | Φ | 4.9 | 5.2 | 9.1 | 25.4 | 55.4 | 83.1 |
| | | 4.5 | 4.6 | 6.3 | 10.8 | 17.5 | 24.8 |
| | | 9.2 | 9.6 | 14.8 | 33.5 | 63.2 | 87.3 |
| 1.00 | | 6.7 | 7.1 | 11.0 | 25.4 | 51.5 | 77.4 |
| | Φ | 5.0 | 5.3 | 9.3 | 25.9 | 55.9 | 83.5 |
| | | 5.3 | 5.5 | 7.1 | 11.7 | 18.5 | 26.0 |
| | | 10.0 | 10.5 | 15.7 | 34.6 | 64.1 | 87.8 |