Filters, Waves and Spectra
Abstract
:1. Introduction
2. Sinc Function Interpolation and the Sampling Theorem
2.1. Aliasing
2.2. The Sampling Theorem
2.3. Orthogonal Bases and Wavelets
3. Linear Filters
3.1. The Gain and Phase Effects
3.2. A Classical Econometric Filter
4. The Ideal Filters
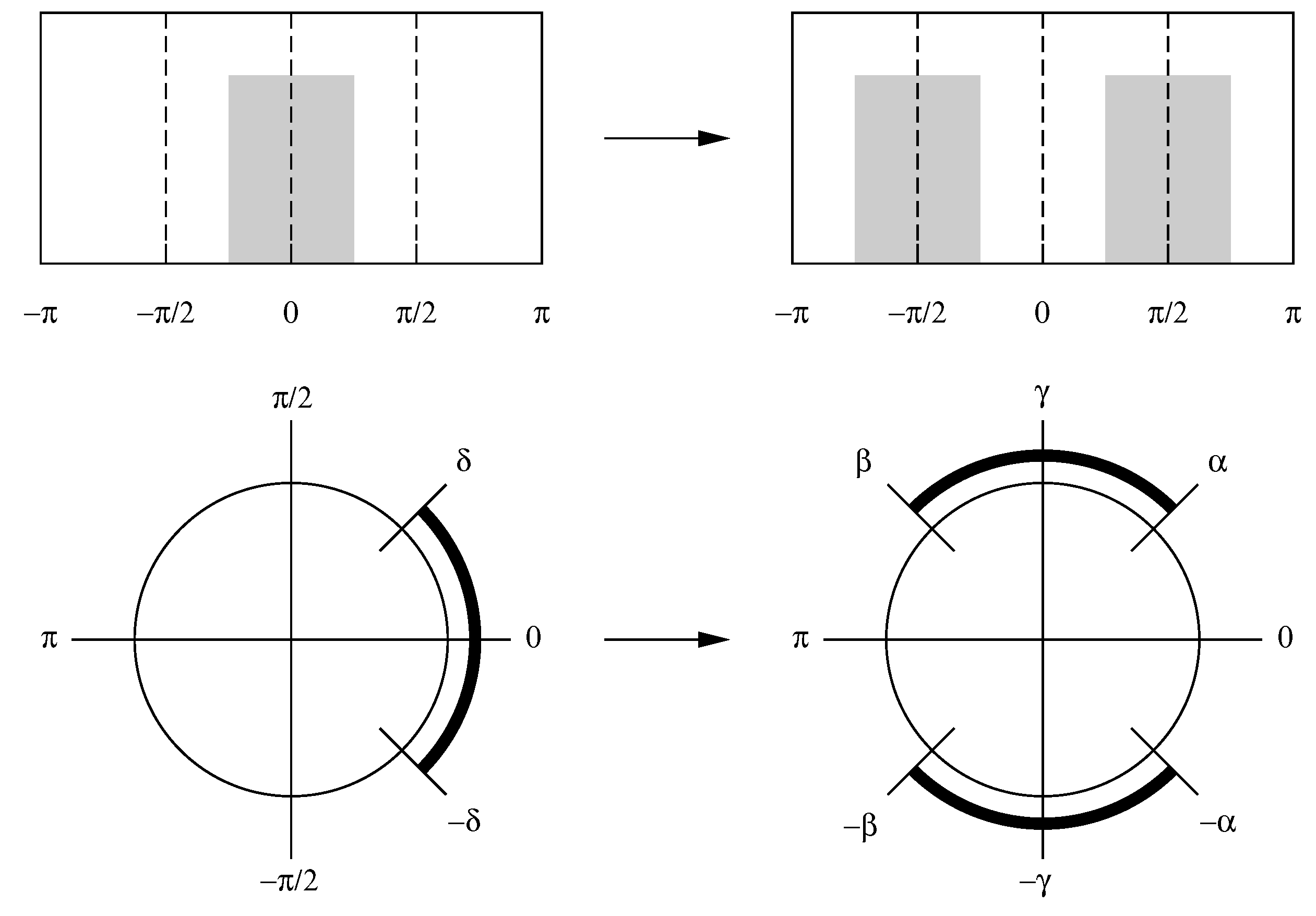
4.1. Frequency Shifting
4.2. Truncating the Filter
4.3. The Ideal Filters in the Frequency Domain
4.4. The Band pass Specification
4.5. Interpolating a Finite Data Sequence
4.6. Resampling the Data
5. Graded Filters
5.1. Gaussian Filters
5.2. The Binomial Filter
5.3. Wiener–Kolmogorov Filters and the Butterworth Filter
5.4. The Hodrick–Prescott Filter
6. Adapting the Filters to Short and Trended Data
6.1. Extrapolations of the Data
6.2. The Interpolation of a Trend Function
6.3. The Differencing and Anti-Differencing in the Time Domain
6.4. Centralised Differences
6.5. The Binomial Filter with Trended Data
6.6. The Wiener–Kolmogorov Frequency-Domain Filters with Trended Data
7. The Finite-Sample Time-Domain Wiener–Kolmogorov Filters
8. Conclusions
Funding
Conflicts of Interest
Appendix A. Fourier Transforms—Sampling and Wrapping
Appendix A.1. Euler’s Equations
Appendix A.2. The Variety of Fourier Transforms
Appendix A.3. The Wrapped Coefficients of the Ideal Lowpass Filter
References
- Abramovich, Felix, Trevor C. Bailey, and Theofanis Sapatinas. 2000. Wavelet Analysis and its Statistical Applications. Journal of the Royal Statistical Society: Series D (The Statistician) 49: 1–29. [Google Scholar] [CrossRef] [Green Version]
- Baxter, Marianne, and Robert G. King. 1999. Measuring Business Cycles: Approximate Band-Pass Filters for Economic Time Series. Review of Economics and Statistics 81: 575–93. [Google Scholar] [CrossRef]
- Burns, Arthur F., and Wesley C. Mitchell. 1946. Measuring Business Cycles. New York: National Bureau of Economic Research. [Google Scholar]
- Christiano, Lawrence J., and Terry J. Fitzgerald. 2003. The Band-pass Filter. International Economic Review 44: 435–65. [Google Scholar] [CrossRef]
- Cooley, James W., and John W. Tukey. 1965. An Algorithm for the Machine Calculation of Complex Fourier Series. Mathematics of Computation 19: 297–301. [Google Scholar] [CrossRef]
- Doherty, Mike. 2001. The Surrogate Henderson Filters in X-11. Australian and New Zealand Journal of Statistics 43: 385–92. [Google Scholar] [CrossRef]
- Fishman, George S. 1969. Spectral Methods in Econometrics. Cambridge: Harvard University Press. [Google Scholar]
- Granger, Clive William John, and Michio Hatanaka. 1964. Spectral Analysis of Economic Time Series. Princeton: Princeton University Press. [Google Scholar]
- Gray, Alistair G., and Peter J. Thomson. 2002. On a Family of Finite Moving-average Trend Filters for the Ends of Series. Journal of Forecasting 21: 125–49. [Google Scholar] [CrossRef]
- Guerlac, Henry. 1947. Radar in World War II. Volume 1 of MIT Radiation Laboratory Series; New York: McGraw-Hill. [Google Scholar]
- Hall, Henry Sinclair, and Samuel Ratcliffe Knight. 1899. Higher Algebra. London: Macmillan and Co. [Google Scholar]
- Henderson, Robert. 1916. Note on Graduation by Adjusted Average. Transactions of the Actuarial Society of America 17: 43–48. [Google Scholar]
- Henderson, Robert. 1924. A New Method of Graduation. Transactions of the Actuarial Society of America 25: 29–40. [Google Scholar]
- Hodrick, Robert J., and Edward C. Prescott. 1980. Postwar U.S. Business Cycles: An Empirical Investigation, Working Paper. Pittsburgh: Carnegie Mellon University.
- Hodrick, Robert J., and Edward C. Prescott. 1997. Postwar U.S. Business Cycles: An Empirical Investigation. Journal of Money, Credit and Banking 29: 1–16. [Google Scholar] [CrossRef]
- Henney, Keith, ed. 1953. Index, Volume 28 of MIT Radiation Laboratory Series. New York: McGraw-Hill. [Google Scholar]
- Jolly, Leonard Benjamin William. 1961. Summation of Series: Second Revised Edition. New York: Dover Publications. [Google Scholar]
- Kailath, Thomas. 1974. A View of Three Decades of Filtering Theory. IEEE Transactions on Information Theory 20: 146–81. [Google Scholar] [CrossRef]
- Kenny, Peter B., and James Durbin. 1982. Local Trend Estimation and Seasonal Adjustment of Economic and Social Time Series. Journal of the Royal Statistical Society Series A 145: 1–41. [Google Scholar] [CrossRef]
- Kolmogorov, Andrei Nikolaevitch. 1941. Stationary Sequences in a Hilbert Space. Bulletin of the Moscow State University 2: 1–40. (In Russian). [Google Scholar]
- Kolmogorov, Andrei Nikolaevitch. 1941. Interpolation and Extrapolation. Bulletin de l’Academie des Sciences de U.S.S.R Series Mathematical 5: 3–14. [Google Scholar]
- Kovačević, Jelena, Vivek K. Goyal, and Martin Vetterli. 2013. Fourier and Wavelet Signal Processing. Available online: www.fourierandwavelets.org (accessed on 23 July 2018).
- Ladiray, Dominique, and Benoit Quenneville. 2001. Seasonal Adjustment with the X-11 Method. Springer Lecture Notes in Statistics 158. Berlin: Springer Verlag. [Google Scholar]
- Laniel, Normand. 1986. Design Criteria for 13-Term Henderson End-Weights. Technical Report Working paper TSRA-86-011. Ottawa: Statistics Canada. [Google Scholar]
- Leser, C. E. V. 1961. A Simple Method of Trend Construction. Journal of the Royal Statistical Society, Series B 23: 91–107. [Google Scholar]
- Mallat, Stéphane. 1998. A Wavelet Tour of Signal Processing. San Diego: Academic Press. [Google Scholar]
- Musgrave, J. C. 1964a. A Set of End Weights to End all End Weights, Unpublished Working Paper of the U.S. Bureau of Commerce.
- Musgrave, J. C. 1964b. Alternative Sets of Weights Proposed for X-11 Seasonal Factor Curve Moving Averages, Unpublished Working Paper of the U.S. Bureau of Commerce.
- Nahin, Paul J. 2006. Dr. Euler’s Fabulous Formula. Princeton: Princeton University Press. [Google Scholar]
- Nyquist, Harry. 1928. Certain Topics in Telegraph Transmission Theory. AIEE Transactions, Series B 47: 617–44. [Google Scholar] [CrossRef]
- Oppenheim, Alan V., and Ronald W. Schafer. 1975. Digital Signal Processing. Englewood: Prentice-Hall. [Google Scholar]
- Pollock, D. Stephen G. 2007. Wiener–Kolmogorov Filtering, Frequency-Selective Filtering and Polynomial Regression. Econometric Theory 23: 71–88. [Google Scholar] [CrossRef]
- Pollock, D. Stephen G. 2008. Realisations of Finite-Sample Frequency Selective Filters. Journal of Statistical Planning and Inference 139: 1541–58. [Google Scholar] [CrossRef]
- Pollock, D. Stephen G. 2009. Statistical Signal Extraction and Filtering: A Partial Survey. In Handbook of Computational Econometrics. Edited by David Belsley and Erricos Kontoghiorges. Chichester: John Wiley and Sons, chp. 9. pp. 321–76. [Google Scholar]
- Pollock, D. Stephen G. 2014. Cycles, Syllogisms and Semantics: Examining the Idea of Spurious Cycles. Journal of Times Series Econometrics 6: 81–102. [Google Scholar] [CrossRef]
- Pollock, D. Stephen G. 2016. Econometric Filters. Computational Economics 48: 669–91. [Google Scholar] [CrossRef]
- Rabiner, Lawrence R., and Bernard Gold. 1975. Theory and Application of Digital Signal Processing. Englewood: Prentice-Hall. [Google Scholar]
- QMS. 2000. Eviews 4.0. Irvine: Quantitative Micro Software (QMS). [Google Scholar]
- Ridenour, Louis Nicot. 1947. Radar System Engineering, Volume 1 of MIT Radiation Laboratory Series. New York: McGraw-Hill. [Google Scholar]
- Shannon, Claude Elwood. 1949a. Communication in the Presence of Noise. Proceedings of the Institute of Radio Engineers 37, 10–21. Reprinted in 1998. Proceedings of the IEEE 86: 447–57. [Google Scholar] [CrossRef]
- Shannon, Claude E. 1949b. The Mathematical Theory of Communication. Urbana: University of Illinois Press, Reprinted in 1998. [Google Scholar]
- Shiskin, Julius, Allan H. Young, and John C. Musgrave. 1967. The X-11 Variant of the Census Method II Seasonal Adjustment Program; Technical Paper 15. Washington, D.C.: Bureau of the Census, U.S. Department of Commerce.
- Vetterli, Martin, Jelena Kovacčević, and Vivek K. Goyal. 2014. Foundations of Signal Processing. Available online: www.fourierandwavelets.org (accessed on 23 July 2018).
- Wallis, Kenneth F. 1981. Models for X-11 and X-11-Forecast Procedures for Preliminary and Revised Seasonal Adjustments. Paper presented at the A.S.A–Census–NBER Conference on Applied Time Series Analysis of Economic Data, Washington, D.C., US; pp. 3–11. [Google Scholar]
- Wiener, Norbert. (1941) 1949. Extrapolation, Interpolation and Smoothing of Stationary Time Series. Report on the Services Research Project DIC-6037. Published in book form. Cambridge: MIT Technology Press, New York: John Wiley and Sons. [Google Scholar]


















© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pollock, D.S.G. Filters, Waves and Spectra. Econometrics 2018, 6, 35. https://doi.org/10.3390/econometrics6030035
Pollock DSG. Filters, Waves and Spectra. Econometrics. 2018; 6(3):35. https://doi.org/10.3390/econometrics6030035
Chicago/Turabian StylePollock, D. Stephen G. 2018. "Filters, Waves and Spectra" Econometrics 6, no. 3: 35. https://doi.org/10.3390/econometrics6030035
APA StylePollock, D. S. G. (2018). Filters, Waves and Spectra. Econometrics, 6(3), 35. https://doi.org/10.3390/econometrics6030035



