Integration and Disintegration of EMU Government Bond Markets

Abstract

It is commonly found that the markets for long-term government bonds of Economic and Monetary Union (EMU) countries were integrated prior to the EMU debt crisis. Contrasting this, we show, based on the interrelation between market integration and fractional cointegration, that there were periods of integration and disintegration that coincide with bull and bear market periods in the stock market. An econometric argument about the spectral behavior of long-memory time series leads to the conclusion that there is a stronger differentiation between bonds with different default risks. This implied the possibility of macroeconomic and fiscal divergence between the EMU countries before the crisis periods.

1. Introduction

We show that even though the yields on long-term government bonds of the major EMU countries were largely co-moving prior to the crisis, the degree of market integration exhibited considerable variation over time. This time variation is related to the stock market sentiment. During bear market periods, there was no equilibrium mechanism between the yields that would have ensured the subsistence of a stable relationship.

To address the dynamics of market integration and to draw economic conclusions, we take a very different perspective from previous contributions to the literature. Instead of focusing on the shock transmission among the spreads or the relative importance of global and local factors, we test for the existence of an equilibrium among the yields themselves. To do so, our study adopts a definition of market integration that is widely used in other areas such as the analysis of commodity markets. This definition is directly based on the law of one price and closely connected to the existence of a (fractional) cointegrating relationship. Using it enables us to draw conclusions about market equilibria by applying a wide set of modern methods for the analysis of fractionally cointegrated systems.

Utilizing this direct correspondence between economic theories and statistical concepts allows us to make several major contributions. First, we establish that the EMU bond markets were integrated during bull markets but disintegrated in bear markets. This is achieved directly by testing for pairwise fractional cointegration among the yields and indirectly by considering the persistence of the yield spreads (which are the cointegrating residuals obtained by imposing the cointegrating vector ${(1,-1)}^{\prime }$ on the yields). Further insights into the dynamics of integration and disintegration in the EMU bond markets are therefore obtained from a rolling window analysis of the memory of the spreads.

The second contribution is to provide insights into the possible economic origins of the observed time variation in market integration. Standard results on the properties of linear combinations of long-memory time series from Chambers (1998) indicate that default risk is the driving component behind the changes in market integration. In addition to that, they give rise to two possible mechanisms that can generate the observed time variation. The first one is that markets expect economic and fiscal divergence within the EMU area in bear markets, whereas they are optimistic about convergence within the Eurozone in bull markets. The second possible explanation is that markets always assume that divergence is a possibility, but the default risk premium exhibits so little variation in good times that the persistence of the spreads is dominated by the liquidity premium. In contrast to that, in bad times, when risk and risk aversion are high, the persistence of the spreads is dominated by the default risk premium, due to its increased variability. These arguments lead to the conclusion that (at least in crisis times) the pricing of EMU government bonds implied the possibility of macroeconomic and fiscal divergence between the EMU countries, long prior to the EMU debt crisis. Furthermore, differences between the core and periphery countries are already visible during previous bear market periods.

This work is related to two strands of literature. The first one is concerned with the integration of EMU bond markets. Here, it is nearly universally accepted that the introduction of the Euro led to essentially complete integration of EMU bond markets that ended with the advent of the subprime mortgage crisis. This was found empirically by contributions such as Baele et al. (2004), Ehrmann et al. (2011), Pozzi and Wolswijk (2012), Christiansen (2014), and Ehrmann and Fratzscher (2017), using a range of different definitions of market integration and econometric methodologies. Similarly, Balli et al. (2019) find growing cross-border capital flows driven by a diversification motive, and Bergin and Pyun (2016) find importance of hedging potential of the regional destination of funds. EMU bond market integration is also implicitly assumed by studies on the determinants of yield spreads between government bonds in the Eurozone, such as Beber et al. (2008), or Codogno et al. (2003), and Manganelli and Wolswijk (2009), who treat the yield spreads as stationary variables. Jappelli and Pagano (2008) review some related studies and conclude that government bonds are co-moving but still not perfect substitutes. The study by Cipollini et al. (2015) also attests integration in the beginning of EMU but segmentation after 2010. Evidence against overall full integration of the EMU government bond markets is only provided by Abad et al. (2010), who define market integration in the sense of Bekaert and Harvey (1995) so that markets are not fully integrated as long as country specific risk factors are priced in the bond return.

The difference between these studies and ours is rooted in the fact that their definitions of market integration are closely tied to the co-movement of the yields. Since a common factor explains the vast majority of the variation of the yields, as shown by Bhatt et al. (2017), this leads to the conclusion that bond markets are highly integrated. While this result may be intuitive, definitions of market integration such as that of Bekaert and Harvey (1995) are not directly rooted in theoretical models. In contrast to that, our definition is based on the law of one price and it is tested whether there is an equilibrium relationship between the yields.

The second strand of literature related to this paper is concerned with the empirical relationship between stock and bond markets. There are few theoretical models that consider this relationship, but it is well documented that there are flight-to-quality effects in the dependence structure of price changes in bonds and stocks. While Shiller and Beltratti (1992) and Campbell and Ammer (1993) show that the long-run correlation between stock market and bond-price returns is slightly positive as implied by present value relations and rational expectations, they also find that there is considerable time variation that cannot be accounted for. Further studies such as those of Gulko (2002), Hartmann et al. (2004), and Connolly et al. (2005) show that there are subperiods during which the relationship turns negative. These are related to stock market crashes during which investors shift their portfolios from stocks to bonds, which leads to a negative correlation between stock returns and bond (price) returns. The effect of the EMU on the dependence between bond and stock returns is studied by Kim et al. (2006).

The literature on the determinants of flight-to-quality effects finds that macro-variables such as the business cycle and inflation expectations have some explanatory power but generally do not provide a model that explains the variation of the stock-bond correlation sufficiently well (cf. Shiller and Beltratti (1992), Yang et al. (2009), and Baele et al. (2010)). While Baele et al. (2010) stress that illiquidity seems to be one of the main factors driving the relationship, others such as Pagano and von Thadden (2004), Connolly et al. (2005), Bernoth et al. (2012), and Asgharian et al. (2016) stress the importance of market uncertainty.

Recently, Koijen et al. (2017) show that risk factors that explain variation of bond yields across maturities are also priced in the cross section of stock returns. This again stresses the importance of linkages between the asset classes that has also been pointed out by earlier studies such as Fleming et al. (1998), who study volatility linkages between asset classes. Furthermore, Longstaff and Wang (2012) consider a theoretical model that links stock and credit markets. However, none of these studies has related the stock market sentiment to the dynamics of integration in the bond market.

The rest of the paper is structured as follows. Section 2 provides a discussion of market integration and a discussion of fractional integration and cointegration. Subsequently, Section 3 describes the data set and discusses the definition of bull and bear markets. Section 4 contains the empirical analysis including formal tests for market integration separately for bull and bear markets, rolling window estimates of the persistence of the spreads, and an analysis of the drivers of the degree of market integration. Finally, Section 5 concludes.

2. Market Integration, Fractional Integration, and Fractional Cointegration

In international finance, measures for market integration are typically based on factor models for the returns. The most widely adopted approaches in recent years are those of Bekaert and Harvey (1995) and Pukthuanthong and Roll (2009). Bekaert and Harvey (1995) consider two markets to be financially integrated if their movement is completely determined by global factors, whereas local factors (that are specific to individual countries) are not priced. Similarly, Pukthuanthong and Roll (2009) consider the explanatory power of a multifactor model as a measure for market integration. While both of these measures are intuitive for asset returns, they lack a rigorous foundation in economic theory and they are not readily applicable to bond yields that are typically found to have unit roots.

Here, we therefore consider a different definition that is commonly applied to the analysis of commodity markets. According to this definition markets for different goods that are close substitutes, or markets for the same good that are spatially separated are considered to be (economically) integrated with each other if the law of one price (LOP) applies. In the strict sense, the LOP requires a correction mechanism (such as arbitrage) that enforces the stability of an equilibrium relationship, and that the form of this equilibrium is such that prices in both markets are exactly the same. The weaker definition of partial market integration only requires the existence of a stable equilibrium relationship but not exact equality of the prices.

For non-stationary prices, this definition is often tied to the concept of cointegration (cf. Ravallion (1986), Ardeni (1989)), since cointegration implies the existence of an equilibrium relationship between unit root processes. In the classical $I\left(1\right)/I\left(0\right)$ framework, deviations from this equilibrium have to be weakly persistent in the sense that they are stationary and have short memory. This, however, is an unnecessary restriction, since an equilibrium relationship only requires deviations from the mean to be transitory in the sense that they are mean reverting. We therefore consider fractional cointegration that allows for a more flexible treatment of the data as we do not need to assume that the bond data have a unit root, but we can treat the order of integration as unknown. This flexibility also applies to the residuals that do not need to be short memory but might still exhibit some persistence. In this context the degree of persistence of the cointegrating residuals is related to the strength of the equilibrium relationship, since more persistent residuals imply a slower convergence towards the equilibrium.

By using this framework we are able to cover the whole range of orders of integration and to find weaker equilibria (that however still are such). Furthermore, there are several applications in the literature showing that fractional cointegration can be better suited to model economic equilibrium relationships than the classical $I\left(1\right)/I\left(0\right)$ framework. Examples include the purchasing power parity (cf. Cheung and Lai (1993) and Baillie and Bollerslev (1994)) or the parity between implied and realized volatility (cf. Christensen and Nielsen (2006)). Cointegration analysis is also applied by Holmes and Maghrebi (2006) for asymmetries in real interest parity, and Hualde and Iacone (2017) for non-zero inflation differentials.

Hence, we allow for fractional cointegration when testing for (partial) market integration and consider a bivariate system of the form

$$\begin{array}{cc}\hfill X_{1t}& =c_1+{\xi }_1{Y}_t+{\Delta }^{-(d-b_1)}{u}_{1t}{\mathbb{1}}_{\{t>0\}}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill X_{2t}& =c_2+{\xi }_2{Y}_t+{\Delta }^{-(d-b_2)}{u}_{2t}{\mathbb{1}}_{\{t>0\}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill Y_t& ={\Delta }^{-d}{e}_t{\mathbb{1}}_{\{t>0\}},\hfill \end{array}$$

(3)

where the coefficients $c_1,c_2,{\xi }_1$, and ${\xi }_2$ are finite, $0\le b_1, b_2\le d$, L is the lag-operator, the fractional differences ${\Delta }^d{Y}_t={(1-L)}^d{Y}_t$ are defined in terms of generalized binomial coefficients such that

$$\begin{array}{cc}\hfill {(1-L)}^d& =\sum _{k=0}^{\infty }\left(\genfrac{}{}{0pt}{}{d}{k}\right){(-1)}^k{L}^k=\sum _{k=0}^{\infty }{\pi }_k{L}^k,\hfill \\ \hfill \mathrm{with}\left(\genfrac{}{}{0pt}{}{d}{k}\right)& =\frac{d(d-1)(d-2)\cdots (d-(k-1\left)\right)}{k!},\hfill \end{array}$$

and ${(e_t,u_t)}^{\prime }$ with $u_t={(u_{1t},u_{2t})}^{\prime }$ is a zero mean process with covariance matrix ${\Omega }_{e,u}$ and spectral density $f_{e,u}\left(\lambda \right)$ satisfying $f_{e,u}\left(\lambda \right)\sim G_{e,u}$ for $\lambda \to 0$. Here, the matrix $G_{e,u}$ is real, symmetric, finite, and positive definite.

In this setup, the memory of both $X_{1t}$ and $X_{2t}$ is determined by $Y_t$ so that they are integrated of the same order d (if both ${\xi }_1,{\xi }_2\ne 0$), denoted by $X_t\sim I\left(d\right)$, where $X_t={(X_{1t},X_{2t})}^{\prime }$. If one or both of the coefficients ${\xi }_1,{\xi }_2$ are zero, $X_{1t}$ and $X_{2t}$ do not share the same memory parameter, i.e., $X_t\sim I(d_1,d_2)$. Since it is assumed that $u_{1t}=u_{2t}=e_t=0$ for all $t\le 0$, the processes under consideration are fractionally integrated of type-II. For a detailed discussion of type-I and type-II processes confer Marinucci and Robinson (1999). The (pseudo) spectral density of $X_t$ can be approximated by

$$\begin{array}{cc}\hfill f_X\left(\lambda \right)& \sim \Lambda \left(D\right)G\overline{\Lambda \left(D\right)},\mathrm{as}\lambda \to 0^{+},\hfill \end{array}$$

(4)

where G is a real, symmetric, finite, and non-negative definite matrix, $\Lambda \left(D\right)=\mathrm{diag}(\Lambda \left(d_1\right),\Lambda \left(d_2\right))$ with $\Lambda \left(d_j\right)={\lambda }^{-d_j}{e}^{i\pi d_j/2}$, $j\in \{1,2\}$ is a $2\times 2$ diagonal matrix and $\overline{\Lambda \left(D\right)}$ is its complex conjugate transpose.

The two series $X_{1t}$ and $X_{2t}$ are said to be fractionally cointegrated if there exists a linear combination ${\beta }^{\prime }{X}_t=v_t,$ so that the cointegrating residuals $v_t$ are fractionally integrated of order $I(d-b)$ for some $0<b\le d$. For the model in Equations (1)–(3), this is the case for every multiple of the vector ${\left(1,-\frac{{\xi }_1}{{\xi }_2}\right)}^{\prime }$ and $b=min(b_1,b_2)$.

In the context of this model, EMU government bonds can be considered as close substitutes and their market is (partially) economically integrated if the yields are fractionally cointegrated with each other. From the definition above, this is the case if there exists an equilibrium relationship between the yields ($X_{1t}$ and $X_{2t}$) so that the persistence of deviations from the equilibrium denoted by $v_t$ is reduced compared to that of the individual series.

In the following, we will test this hypothesis in two different ways. First, we apply a number of tests for the null hypothesis of no fractional cointegration among the yields. The methods used are semiparametric and do not impose any assumptions on the short-run behavior of the series apart from mild regularity conditions. This approach has the advantage of avoiding spurious findings that might arise due to misspecifications.

The first group of tests is based on the rank of the matrix G in Equation (4) that is reduced in fractionally cointegrated systems. Robinson and Yajima (2002) and Nielsen and Shimotsu (2007) use the singularity of the G matrix in case of cointegration to propose an information criterion that is based on the eigenvalues of the estimate $\widehat{G}$. Souza et al. (2018) use the fractionally differenced process and the determinant of its spectral density that allows to estimate b via log-periodogram regression so that the hypothesis $b=0$ can be tested.

A second group of tests is residual-based using the fact that cointegrating residuals $v_t$ have reduced memory of order $d-b$ if a fractional cointegrating relationship exists. The test of Wang et al. (2015) is based on the sum over the fractionally differenced process ${\Delta }^{{\widehat{d}}_v}{X}_{2t}$, where ${\widehat{d}}_v$ is an estimate of the memory from the cointegrating residuals obtained using a consistent estimator for the cointegrating vector $\beta$ such as the narrow-band least squares estimator of Robinson (1994), Robinson and Marinucci (2003), and Christensen and Nielsen (2006), among others. In contrast to that, the test of Chen and Hurvich (2006) is directly based on ${\widehat{d}}_v$, but the cointegrating space is estimated by the eigenvectors of the averaged and tapered periodogram matrix local to the origin.

A third group of tests proposed by Marmol and Velasco (2004) and Hualde and Velasco (2008) relies on the behavior of pairs of estimators for the cointegrating vector $\beta$. These pairs include one estimator that is only consistent under the null hypothesis of no fractional cointegration and one estimator that is only consistent under fractional cointegration. While the test statistic of Marmol and Velasco (2004) has an asymptotic non-standard distribution under the null, the version of Hualde and Velasco (2008) utilizes the GLS estimates of Robinson and Hualde (2003) and results in an asymptotic chi-square distribution.

Finally, Nielsen (2010) suggests a variance ratio test. The test statistic is based on the sum of the eigenvalues of the variance-covariance matrix of the original series multiplied with the inverse of the variance-covariance matrix of the fractionally differenced series exploiting different limiting behavior of the eigenvalues from eigenvectors in (non-) cointegrating directions.

The second approach uses domain specific knowledge about the behavior of the yields in the common currency area and allows us to test for cointegration based on simple estimations of the memory parameters in the yield spreads. We denote the bonds yields of country i in period t by $y_t^i$ for $i=1,\cdots ,N$ and $t=1,\cdots ,T$. The spreads $s_t^i$ are usually formed relative to the yield of the German bonds

$$\begin{array}{cc}\hfill s_t^i& =y_t^i-y_t^{GER}.\hfill \end{array}$$

(5)

It is commonly assumed that the yields of country i can be decomposed into

$$\begin{array}{cc}\hfill y_t^i& =r_t^f+{\delta }_t^i+l_t^i,\hfill \end{array}$$

(6)

where $r_t^f$ is the risk-free interest rate, and ${\delta }_t^i$ and $l_t^i$ are the risk premiums for the default risk and liquidity risk of country i. The risk-free rate is the same across countries due to the common currency area. If Germany—the benchmark country—is assumed to have no default risk and no liquidity risk so that $y_t^{GER}=r_t^f$, it follows that

$$\begin{array}{cc}\hfill s_t^i& ={\delta }_t^i+l_t^i.\hfill \end{array}$$

(7)

Hence, the spreads equal the risk premiums associated with the liquidity and default risk of the respective country. If Germany is not assumed to be risk-free, ${\delta }_t^i$ and $l_t^i$ are interpreted as risk premium differentials between the respective country and Germany. However, if the risk of Germany and its variation are low compared to that of the respective country, the behavior of the differentials will still be dominated by the risk premiums of the country. We therefore maintain the assumption that Germany is risk-free to simplify the verbal description of results.

The risk-free interest rate $r_t^f$ in (6) is driven by expected macroeconomic factors such as GDP-growth, inflation rates, and interest rates, and it is widely found to be $I\left(1\right)$ (cf. for example Stock and Watson (1988), Mishkin (1992), Chen and Hurvich (2003) and Nielsen (2010)). That means $y_t^i$ and $y_t^{GER}$ can only be cointegrated if $r_t^f$ is removed from the linear combination ${\beta }^{\prime }{(y_t^i,y_t^{GER})}^{\prime }$, as it is the case in the spreads in (7). Forming the spreads according to (5) therefore means to impose the cointegrating vector $\beta ={(1,-1)}^{\prime }$ on the yields so that the yield spreads are the cointegrating residuals. An easy test for market integration can then be constructed by comparing the integration orders of the spreads to that of the risk-free rate. In this way, we do not impose the assumption that $r_t^f$ follows exactly a unit root and we stay in a fractional setting. We still assume that the German yield represents the risk-free rate so the hypotheses are formulated as follows

$$\begin{array}{cc}\hfill & H_0:d_{s_t^i}=d_{r_t^f}=d_{y_t^{GER}}\mathrm{versus}{H}_1:d_{s_t^i}<d_{r_t^f}=d_{y_t^{GER}}.\hfill \end{array}$$

If this hypothesis can be rejected, this is statistical evidence for market integration. A simplified version of this test is based on the assumption $d_{r_t^f}=1$, i.e.,

$$\begin{array}{cc}\hfill & H_0:d_{s_t^i}=1\mathrm{versus}{H}_1:d_{s_t^i}<1.\hfill \end{array}$$

To gain a deeper economic understanding of the mechanisms driving market integration and disintegration, reconsider the decomposition of the spreads in Equation (7). Since the spreads are the cointegrating residuals between the yields, their persistence determines whether there is an equilibrium or not. According to Equation (7), the spreads consist of two components—the liquidity risk premium $l_t^i$ and the default risk premium ${\delta }_t^i$. Since credit default swap data is not available for most of the time period before the subprime mortgage crisis, we cannot use this information to disentangle the default and liquidity risk premiums as for example in Longstaff et al. (2005).

We can, however, draw some conclusions based on properties of long-memory processes. Denote the memory of the default risk premium for country i at time t and its liquidity risk premium by $d_{{\delta }_t^i}$ and $d_{l_t^i}$, respectively. With constant unconditional mean and variance of the component series, it was shown by Chambers (1998) that the memory of a linear combination of long-memory processes is determined by the most persistent series in the combination. For two long-memory series $a_t$ and $b_t$ with memory parameters $d_a$ and $d_b$ this means that $c_t=a_t+b_t$ has long memory of order $d_c=max\{d_a,d_b\}$. The memory of the spreads $s_t^i$ is therefore either $d_{{\delta }_t^i}$, or $d_{l_t^i}$, according to which is larger.

This finding is based on the assumption that the long-run variances of $a_t$ and $b_t$ are fixed, finite, and positive. An alternative theoretical framework might be based on the ratio of the long-run variances of the short-memory components that depends on the sample size and goes to zero. This implies that in practice the estimated degree of persistence in the spreads $d_{s_t^i}$ will be a convex combination of $d_{l_t^i}$ and $d_{{\delta }_t^i}$ that depends on the relative scale of the variation of the two risk premiums. Most importantly, if the persistence of the spreads is high and that of the liquidity premium is low, the behavior of the default premium ${\delta }_t^i$ has to be the main driver of the spreads.

3. Data and Definition of Bull and Bear Markets

Our analysis is based on the daily yields of 10-year maturity benchmark government bonds of eleven EMU countries. As is customary in the literature, we refer to Spain, Italy, Portugal, Ireland, and Greece as the periphery countries. Belgium, Austria, Finland, the Netherlands, and France are called the core countries. The data set contains daily (bid) yields on benchmark bonds for these ten countries and for Germany. All series are obtained from Thomson Reuters Eikon and observed between 1 January 1999 and 8 August 2017 resulting in about 4800 data points per time series.

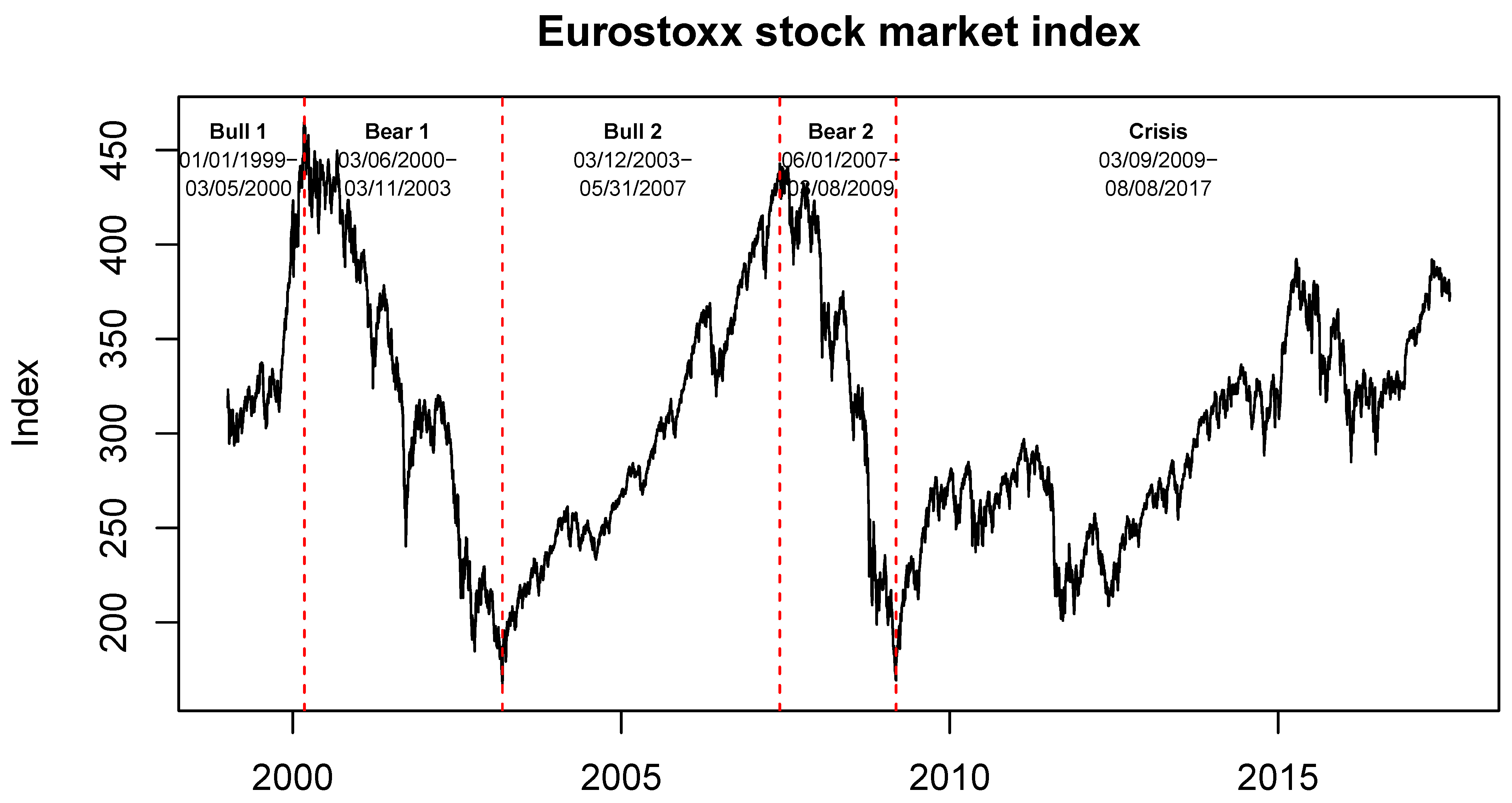
As discussed in the introduction, one of the main objectives of this paper is to show that the degree of EMU bond market integration differs between bull and bear markets. Since there is no universally accepted definition of bull and bear markets, we rely on a visual inspection of the trajectory of the Eurostoxx index. Every bull market period begins with a local minimum and every bear market period begins with a local maximum. The timing of these local extrema is indicated by vertical dashed lines in Figure 1. We are aware that this approach is somewhat arbitrary. However, the trajectory of the S&P500 index and the MSCI World index both exhibit an identical pattern with respect to highs and lows. Alternatively, we could consider market volatility which also comes with the advantage of being a nowcast instead of an ex post consideration. It can be estimated from a Markov-switching mean and variance model, where

$$\begin{array}{c}\hfill r_t={\mu }_{s_t}+{\sigma }_{s_t}{\eta }_t,\end{array}$$

(8)

with ${\eta }_t\stackrel{iid}{\sim }(0,1)$. Here $s_t\in \left\{1,2\right\}$ is a Markov chain with transition probabilities $p_{12}$ and $p_{21}$. For identification purposes, we assume ${\mu }_1>{\mu }_2$ and call regime one the “bull market regime”. When the model is applied to the Eurostoxx returns, we observe that the bull market regime is associated with a positive mean ${\widehat{\mu }}_1=0.0008$ whereas the bear market regime has a negative mean of ${\widehat{\mu }}_2=-0.0014$ and a larger standard deviation than that of the bull market. Both regimes are persistent, but the average bear market is shorter than the average bull market since the probability to remain in a bear market is smaller. The probability of a bull market at time t conditional on the observations up to time t is depicted in Figure 2. Even though the nowcast does not result in the same sharp borders as the other approach, it still confirms the pattern.

The first two periods are determined by the dot-com bubble and the subsequent crash starting on 6 March 2000. The recovery and boom thereafter lasted from 12 March 2003, until 31 May 2007, when the subprime mortgage crisis began. This bear market lasted until 8 March 2009. In the recovery after that, it could be argued that there were several shorter bull and bear market periods. However, it can be expected that the mechanisms driving the pricing of EMU government bonds changed permanently with the onset of the EMU debt crisis in October 2009 when the Greek government revised its deficit figures. This is also confirmed empirically by previous studies such as Pozzi and Wolswijk (2012), Christiansen (2014), and Ehrmann and Fratzscher (2017). We therefore focus on the previous bull and bear markets and refer to the post-2009 period as the crisis period.

Estimates of the memory parameters of the yields in each subsample are given in

Table 1. Memory estimates of the yields for different subperiods. In the Bull 2 period the standard error of the estimate for Ireland is 0.05.

	ES	IT	PT	IE	GR	BE	AT	FI	NL	FR	GER	(s.e.)
Bull 1	1.00	1.02	0.96	1.01	1.00	1.03	1.02	0.94	0.99	0.98	1.01	(0.07)
Bear 1	0.95	0.95	0.94	0.97	0.95	0.95	0.96	0.97	0.95	0.94	0.97	(0.05)
Bull 2	1.05	1.07	1.04	1.07	1.06	1.04	1.04	1.06	1.05	1.05	1.06	(0.04)
Bear 2	0.99	0.91	0.93	1.01	0.91	0.94	0.88	0.95	0.97	0.97	1.01	(0.06)
Crisis	0.89	0.92	0.97	1.02	0.95	0.95	1.00	0.97	0.99	0.99	0.95	(0.03)
Full sample	0.99	1.03	0.96	1.00	0.93	0.93	0.99	1.05	0.98	0.96	1.00	(0.02)

. Here and hereafter, all memory parameters are estimated using the exact local Whittle estimator of Shimotsu (2010) and a bandwidth of $m=\lfloor T^{0.7}\rfloor$. The estimator is a direct extension of that suggested in Shimotsu and Philips (2005), but allowing for non-zero means. Those can be treated in the following ways: If $d<0.5$, classical demeaning by the arithmetic mean $\overline{X}$ is recommended. If $d\ge 0.5$, demeaning is not necessary although some correction in finite samples is sensible in order to cope with possibly large $\mu$. To do so, $\mu$ can be estimated by the initial value $X_1$. Simulations by Shimotsu (2010) show that this kind of correction leads to a lower bias in non-stationary data than arithmetic mean correction. The third suggestion is a weighted combination of both demeaning versions that requires a two-step estimation procedure. Our own simulations suggest that the best choice between these alternatives depends on the persistence of the data.

The estimator is given by

$$\begin{array}{cc}\hfill {\widehat{d}}_{ELW}& ={argmin}_{-1<d<3.5}\left\{log{\widehat{G}}_m\left(d\right)-d\left(\frac{2}{m}\sum _{j=1}^{m}log{\lambda }_j\right)\right\},\hfill \end{array}$$

where ${\lambda }_j=2\pi j/T$, ${\widehat{G}}_m\left(d\right)=m^{-1}{\sum }_{j=1}^m{I}_{{\Delta }^{d}x}\left({\lambda }_j\right)$, and $I_{{\Delta }^{d}x}\left(\lambda \right)$ denotes the periodogram of the fractionally differenced process ${(1-L)}^d(X_t-X_1)$. As our data is very persistent we choose the initial value correction $X_t-X_1$. Under mild regularity conditions Shimotsu (2010) show that $\sqrt{m}\left({\widehat{d}}_{ELW}-d\right)\stackrel{d}{\to }N(0,1/4)$. As can be seen in Table 1, the estimated memory parameters are statistically indistinguishable from one, so that it is reasonable to assume that the bond yields follow a stochastic trend. This is also supported by formal tests.

4. Empirical Analysis

Using the methods and data presented in the previous sections, we analyze the dynamics of integration and disintegration in EMU government bond markets. First, we test for fractional cointegration among the yields separately for bull and bear markets. Second, we test in a rolling window whether the order of integration in the spreads is equal to one, so that we do not impose any restrictions on the timing of periods of integration and disintegration. Finally, we look into the persistence of default and liquidity premium.

4.1. Testing for Market Integration Among the Yields

As discussed in Section 2, integration in the market for EMU government bonds requires the yields to be pairwise fractionally cointegrated. Since the German government bonds are considered to be the most liquid and essentially risk free, it is customary to use Germany as the base country and to analyze the pairwise relationship of each country with Germany. We therefore adopt this approach and start our analysis by applying tests for the null hypothesis of no fractional cointegration on these pairs in each of the subsamples. The results of this exercise are given in

Table 2. Memory of the fractional cointegrating residuals (${\widehat{d}}_{v^i}$) of the relation between the yields of bonds of the respective country and the German yield, and ${}^{*}$ memory reduction (${\widehat{b}}^i$) in the case of SRFB18. In the Bull 2 period the standard error of the estimate for Ireland is 0.05 (except for test SRFB18).

		ES	IT	PT	IE	GR	BE	AT	FI	NL	FR	(s.e.)
Bull 1	NS07	0.42	0.63	0.58	0.59		0.42	0.42	0.24	0.30	0.26	(0.07)
	SRFB18 *	0.47	0.29	0.45	0.45		0.41	0.59	0.86	0.59	0.71	(0.14)
	MV04	0.42	0.63	0.55	0.49		0.42	0.32	0.24	0.31	0.30	(0.07)
	WWC15	0.42	0.63	0.55	0.49	0.97	0.42	0.32	0.24	0.31	0.30	(0.07)
	CH06	0.48	0.64	0.55	0.55		0.42	0.33	0.24	0.30	0.31	(0.07)
	HV08	0.42	0.63	0.55	0.49		0.42	0.32	0.24	0.31	0.30	(0.07)
	N10			0.55	0.52		0.46	0.32	0.36	0.34		(0.07)
	Nbr. Obs.	304	303	304	299	285	304	293	298	304	304
Bear 1	NS07	0.81	0.90	0.84	0.83	0.71	0.80	0.82	0.62	0.75	0.61	(0.05)
	SRFB18 *	0.32		0.29	0.29			0.30	0.43	0.29	0.39	(0.10)
	MV04				0.82				0.61	0.80	0.64	(0.05)
	WWC15	0.86			0.82		0.87		0.61	0.80	0.64	(0.05)
	CH06	0.83						0.83	0.62	0.75	0.60	(0.05)
	HV08				0.82				0.61	0.80	0.64	(0.05)
	N10
	Nbr. Obs.	779	778	777	751	767	777	779	773	780	782
Bull 2	NS07	0.56	0.94	0.68	0.61	0.68	0.86	0.59	0.62	0.59	0.76	(0.04)
	SRFB18 *	0.45		0.28	0.43	0.34	0.19	0.36	0.18	0.29	0.28	(0.09)
	MV04	0.56		0.68	0.59	0.68	0.87	0.60	0.59	0.59	0.77	(0.04)
	WWC15	0.56		0.68	0.59	0.68	0.87	0.60	0.59	0.59	0.77	(0.04)
	CH06	0.57	0.92	0.68	0.59	0.68	0.85	0.62	0.60	0.59	0.76	(0.04)
	HV08	0.56		0.68	0.59	0.68	0.87	0.60	0.59	0.59	0.77	(0.04)
	N10	0.56			0.61			0.59	0.62	0.59	0.77	(0.04)
	Nbr. Obs.	1078	1081	1081	738	1068	1084	1074	1081	1083	1083
Bear 2	NS07	0.90	0.83	0.96			0.95	0.92	0.78	0.86	0.81	(0.06)
	SRFB18 *							0.26	0.34	0.28		(0.12)
	MV04		0.82				0.90	0.80	0.77	0.83	0.77	(0.06)
	WWC15		0.82					0.80	0.77	0.83	0.77	(0.06)
	CH06		0.80						0.74	0.81	0.76	(0.06)
	HV08							0.80	0.77	0.83	0.77	(0.06)
	N10
	Nbr. Obs.	448	448	444	432	445	448	361	446	448	448
Crisis	NS07							0.92	0.87	0.84	0.89	(0.03)
	SRFB18 *
	MV04								0.87	0.84		(0.03)
	WWC15
	CH06								0.87	0.84		(0.03)
	HV08									0.84		(0.03)
	N10
	Nbr. Obs.	2145	2139	2145	2122	2099	2145	2089	2115	2145	2142

. Empty fields indicate the absence of a significant fractional cointegrating relationship at the 5%-level. Non-empty fields give an estimate of $d_{v^i}$, where smaller values of $d_{v^i}$ lead to larger values of $b^i$ that again indicate stronger cointegrating relations.

The tests from Section 2 are abbreviated by the authors’ names and the year of publication. The test of Wang et al. (2015) was originally restricted to stationary data, but our implementation is based on the narrow-band least squares and exact local Whittle estimators that are able to deal with non-stationarity, and the test performed well under non-stationarity in simulations by Leschinski et al. (2020). The tests by Marmol and Velasco (2004) and Nielsen (2010) are able to deal with non-stationarity, but the asymptotic properties are derived based on non-stationary and stationary residuals, respectively. Our cointegrating residuals are neither strictly one or the other, but again finite sample behavior shows robustness. The tests require several decisions on bandwidth where we generally follow the recommendations by Leschinski et al. (2020). The most crucial choice concerns the bandwidth m for estimating d. As stated before, we use $m=\lfloor T^{0.7}\rfloor$.

Overall the results show that the majority of bond yields were indeed cointegrated with the German rate during the bull market periods but not during the bear market periods. A notable exception is Greece in the first bull market, since it only joined the EMU in 2001 which is during our first bear market period. Evidence for the existence of an equilibrium relationship during the bear market periods is mainly found for the core countries. Furthermore, when comparing the strength of the cointegrating relationships that persist during bull and bear markets, we can observe that the strength declines in bear market periods. If we consider Netherlands, for example, deviations from the equilibrium have a memory of approximately ${\widehat{d}}_{v^{NL}}=0.3$ in the first bull market. This increases to nearly $0.8$ in the first bear market, before dropping to $0.6$ in the second bull market, and rising again to about $0.8$ in the second bear market.

When we consider the results for the EMU crisis period, we find that there is no evidence for the existence of an equilibrium relationship for the periphery countries anymore. Among the core countries some weak evidence is found, but mostly for the Netherlands and Finland. The overwhelming majority of the tests are unable to detect any evidence for market integration during this period.

Taken together, we find more evidence of financial integration in the pre-crisis period. As described by Bhatt et al. (2017), this could be explained by the importance of a global factor. However, we already find tendencies of decoupling during bear markets before the crisis. We also observe stronger market integration between the core countries than between the core and the periphery during bear markets. Finally, we observe a full decoupling of the yields for all countries during the crisis. Considering the behavior of the Eurostoxx, the EMU crisis could be regarded as a bull market period, which usually is a period of integration. The cyclical relationship with periods of integration and disintegration therefore breaks down with the advent of the EMU debt crisis.

For robustness, we did the analysis with other bandwidth choices m as well. Taking into account the usually applied range, we considered $m=\lfloor T^{0.65}\rfloor$ and $m=\lfloor T^{0.75}\rfloor$. For the first option, we obtained fewer rejections and for the latter it resulted in slightly more rejections. Overall however, the test decisions and the estimates of $d_{v^i}$ are very similar irrespective of the bandwidth choice.

An obvious extension of our analysis would be to model the system as a whole and to determine the number of common trends driving it. However, this is econometrically challenging. Methods to determine the cointegrating rank tend to become more unstable as the dimension of the system increases, when the cointegrating strength decreases, and when the correlation of the short memory components increases. Since we are dealing with a system of 11 strongly correlated series that appears to be weakly cointegrated, such an analysis is unlikely to produce reliable results.

4.2. Testing for Market Integration among the Yield Spreads

As discussed in Section 2, a second approach to test for fractional cointegration is to consider the persistence of the spreads directly.

First, we compare the orders of integration of the spreads and the risk-free (German) rate in the same pre-defined subsamples as before.

Table 3. p-values of test $H_0$: $d_{s_t^i}=d_{y_t^{GER}}$ versus $H_1$: $d_{s_t^i}<d_{y_t^{GER}}$.

	ES	IT	PT	IE	GR	BE	AT	FI	NL	FR
Bull 1	0.000	0.005	0.003	0.003	0.159	0.000	0.000	0.000	0.000	0.000
Bear 1	0.050	0.229	0.102	0.088	0.003	0.053	0.052	0.001	0.020	0.000
Bull 2	0.000	0.093	0.000	0.000	0.000	0.014	0.000	0.000	0.000	0.001
Bear 2	0.149	0.052	0.322	0.333	0.445	0.297	0.211	0.014	0.086	0.029
Crisis	0.157	0.274	0.492	0.407	0.472	0.179	0.329	0.112	0.066	0.204

contains p-values of the test for equal memory parameters introduced by Robinson and Yajima (2002) that is robust under cointegration. We observe a similar pattern of cointegration in the bull market periods and non in the bear market periods without imposing any assumptions on the specific values for the orders of integration.

However, with respect to persistence of spreads we no longer need to impose specific time periods that are defined to be bull or bear markets. Hence we trade the flexible treatment of $d_{r_t^f}$ for a flexible treatment with respect to time so that we can gain further insights into the dynamics of economic integration and disintegration among the bond yields in the Eurozone by testing for $d_{s_t^i}=1$ in a rolling window. The window size is set to 250 observations which corresponds to one year and provides a good tradeoff between bias and sampling variation of the estimate.

The results are shown in Figure 3 for the core countries and in Figure 4 for the periphery countries. Each point represents the estimated memory parameter ${\widehat{d}}_{s_t^i}$ from the window that ends on this date. The horizontal dashed lines are 95% confidence bands centered around $d_{s_t^i}=1$, based on $1.96/\left(2\sqrt{{\sum }_{j=1}^m{\nu }_j^2}\right)$, where ${\nu }_j=log{\lambda }_j-m^{-1}{\sum }_{j=1}^{m}log{\lambda }_j$ and ${\lambda }_j=2\pi j/250$. This is the typical finite sample correction for the variance of the estimator that is based on its Hessian (cf. Hurvich and Beltrao (1994), Lemma 1). It is well known that these tests remain liberal even despite the correction. We therefore might reject the hypothesis of no fractional cointegration too often. As before, the vertical dashed lines mark the start and endpoints of the bull and bear market periods defined as before.

Considering the results for the core countries in Figure 3, we can make several observations. When we move from a bull market period to a bear market period, the estimated memory parameter increases as new observations enter the estimation window. Conversely, when we enter a bull market after a bear market, the new observations entering the estimation window tend to decrease the estimated memory parameter.

A similar pattern can be observed for the periphery countries in Figure 4 although they are a bit less homogeneous. Around the end of the first bear market in 2003, there is an extended period during which the estimated memory parameters indicate the absence of a fractional cointegrating relationship and thus no evidence for market integration.

In both groups there are some deviations from the general pattern. Among the core countries the persistence of the Belgian and French spreads keeps increasing in the initial phase of the second bull market. This is in line with the higher values of ${\widehat{d}}_{v^{FR}}$ and ${\widehat{d}}_{v^{BE}}$, i.e., weaker cointegrating relations, in bull 2 in the previous sections. Similarly, the persistence of the Greek and Italian spreads remains high in the same period. Referring back to the cointegration tests again, this matches the rejections for the Italian-German cointegrating relation in bull 2. Finally, Ireland shows a somewhat different behavior during the first bull and bear market.

After the second bear market—with the advent of the EMU debt crisis—the relationship breaks down. The estimates of the $d_{s_t^i}$ are close to 1, and well within the confidence bands, indicating that there is no equilibrium relationship. A notable exception is a short dip in the level of the persistence after April, 2010 when the European Financial Stability Facility (EFSF) was first established. Here, the estimated memory parameters are close to the lower confidence band. However, this period ended quickly thereafter, which implies that the EFSF as a policy measure was not sufficient to effectively calm the market and re-establish an equilibrium.

Overall, the results are clearly in line with those in the previous section that show that there are periods of integration and periods of decoupling that are related to bull markets and bear markets.

4.3. Drivers of Market Integration and Disintegration

Following the discussion in Section 2 on how the order of integration in a linear combination can be derived from its single components, the persistence of the spreads may be driven by that of the default risk premium or that of the liquidity risk premium. Unfortunately, credit default swaps are only available from 2008 onwards so that we cannot draw any direct conclusions about the memory of the default risk premium during our period of interest. However, we can consider the bid-ask spreads of the benchmark bonds ($b{a}_{it}$), as for example Fleming (2001) refer to them as a good measure of liquidity. Estimates of their memory parameters are provided in

Table 4. Memory estimates for the yield spreads $s_t^i$ and the bid-ask spreads $b{a}_{it}$. The estimation is carried out for the period from 1 December 2001–8 March 2009. The standard error of the estimate for the bid-ask spread of Ireland is 0.05.

	ES	IT	PT	IE	GR	BE	AT	FI	NL	FR	(s.e.)
${\widehat{d}}_{s_t^i}$	0.90	0.88	0.94	1.03	0.95	0.94	0.90	0.84	0.85	0.90	(0.04)
$\widehat{d}\left(b{a}_{it}\right)$	0.27	0.29	0.06	0.55	0.24	0.09	0.41	0.24	0.13	0.26	(0.04)

along with estimates of the memory in the yield spreads for the same period. It can be observed that the level of persistence in the bid-ask spreads is much lower than that in the yield spreads. From the theoretical results on the memory of linear combinations discussed above, the persistence of the spreads and thus the periods of integration and disintegration could not have been caused by changes in the persistence of the liquidity risk premium. Instead, the persistence of the bid-ask spreads has to be caused by changes of the persistence or relative variability of the default risk premium which is in line with findings of Codogno et al. (2003) and Pagano and von Thadden (2004). Of course, default risk is probably not the only factor for the observed decoupling. Transient market frictions like illiquidity certainly also contribute to this phenomenon. Nonetheless, this is not revealed by our spectral argument about persistence that rather identifies default risk as the driving factor.

Hence, it seems reasonable to assume that $d_{{\delta }_t^i}\ge d_{l_t^i}$ for all $i=1,\cdots ,N$ and $t=1,\cdots ,T$ giving rise to two possible mechanisms that generate the observed time variation in the memory of the spreads: (i) breaks in $d_{{\delta }_t^i}$ from $d_{{\delta }_t^i}<1$ to $d_{{\delta }_t^i}=1$ and vice versa, or (ii) $d_{{\delta }_t^i}=1$, for all t, but the relative scale of variations in ${\delta }_t^i$ compared to $l_t^i$ differs for bull and bear markets.

Default risk is driven by macroeconomic and fiscal conditions in the respective country so that its persistence translates to possible convergence or divergence between the countries. The conclusion in situation (i) would therefore be that market participants considered the possibility of economic and fiscal divergence within the EMU area in bear markets, whereas they expected economic convergence within the currency area in bull markets. In situation (ii), market participants would permanently anticipate the possibility of economic and fiscal divergence between the EMU countries, but the level and variability of the default risk premium is so low during bull markets that the memory properties are dominated by those of the less persistent liquidity risk premium. Conversely, during bear markets risk and risk aversion are high so that the variability of the default risk premium increases relative to that of the liquidity risk premium and the persistence of the spreads is dominated by that of the default risk premium.

Nonetheless, both arguments ((i) and (ii)) lead to the conclusion that (at least in crisis times) the pricing of EMU government bonds implied the possibility of macroeconomic and fiscal divergence between the EMU countries.

5. Conclusions

The analysis in this paper is based on the application of a wide array of modern methods for the analysis of fractionally cointegrated time series, coupled with a careful consideration of the interrelations between the dynamics driving long-term bond yields and yield spreads, the persistence of these series, and the implications of the relationships for the existence or non-existence of equilibria in the EMU government bond market.

Contrary to previous results in the literature, we find that EMU government bond markets are not continually integrated prior to the EMU debt crisis. This roots in the fact that there were periods during which the spreads became unit root processes so that there was no correction mechanism that would drive the yields back to their equilibrium relationship. This is a critical component of the law of one price that was therefore not fulfilled. These periods of decoupling tended to coincide with bear market periods, whereas EMU bond markets tended to be economically integrated when stock markets were bullish. Furthermore, the integration among the core countries used to be more intense than that among the periphery countries or among periphery and core.

Altogether, these results imply that investors do not only shift their portfolios from (comparatively) risky stocks to safer bonds in bear markets as described by flight-to-quality effects, there is also a stronger differentiation between sovereign default risks during these periods. As discussed in the previous section, the nature of this differentiation between the default risks of the different countries implies that at least in bear markets investors did consider the possibility of macroeconomic and fiscal divergence between the EMU countries, even though the low magnitude of the spreads shows that this was considered very unlikely.