Interdependency Pattern Recognition in Econometrics: A Penalized Regularization Antidote
Abstract
:1. Introduction
A Motivating Example
2. Literature Review
2.1. Review of Multicollinearity Measures
3. Elastic Information Criterion
3.1. Review of the Regularization Methods
3.2. The Penalized Regularization Antidote
- k is the total number of regressors (explanatory variables),
- is the optimal alpha emerging from the Elastic Net procedure and corresponds to the modelling of the variable,
- is the intercept term in Equation (13),
- is the penalized coefficient of the regressor in Equation (13),
- is the of the variable as predictor regressed against all other regressors.
| Algorithm 1 Pseudocode for EIC implementation in R. |
| Input: A matrix, namely A, containing the dataset with each column representing a variable. Output: A data frame containing the EIC value for each variable indicating the level of multicollinearity.
|
3.3. Data-Driven Threshold
| Algorithm 2 Pseudocode for the threshold of EIC in R. |
| Input: A matrix, namely A, containing the dataset with each column representing a variable. Output: A single number which serves as for ruling about the existence of multicollinearity.
|
4. Numerical Applications
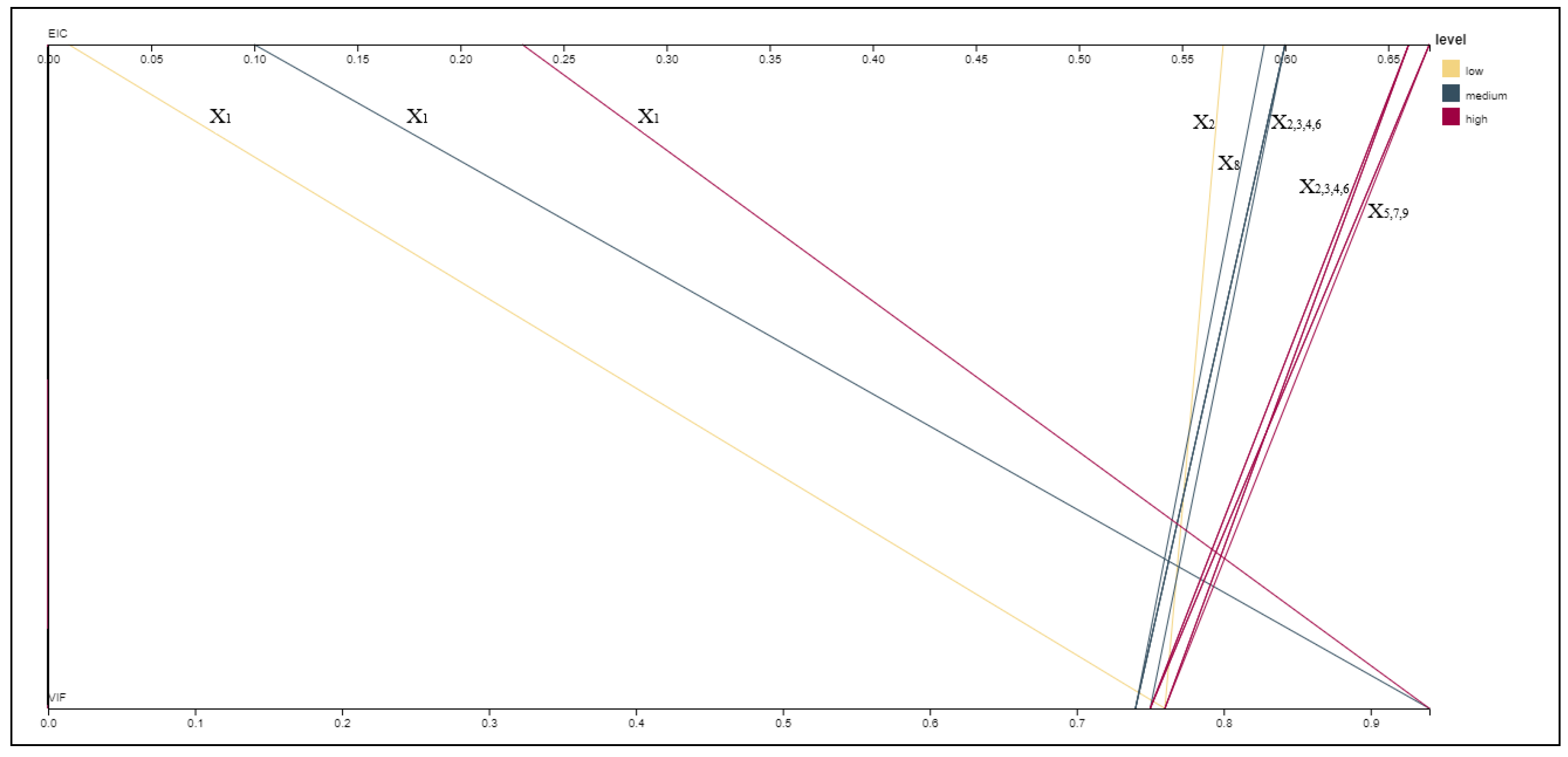
4.1. Real Case Study
4.2. Simulation Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bayer, Sebastian. 2018. Combining Value-at-Risk Forecasts using Penalized Quantile Regressions. Econometrics and Statistics 8: 56–77. [Google Scholar] [CrossRef]
- Belsley, David A. 1991. A Guide to Using the Collinearity Diagnostics. Computer Science in Economics and Management 4: 33–50. [Google Scholar]
- Dumitrescu, Bogdan Andrei, Dedu Vasile, and Enciu Adrian. 2009. The Correlation Between Unemployment and Real GDP Growth. A Study Case on Romania. Annals of Faculty of Economics 2: 317–22. [Google Scholar]
- Farrar, Donald, and Robert Glauber. 1967. Multicollinearity in Regression Analysis: The Problem Revisited. The Review of Economics and Statistics 49: 92–107. [Google Scholar] [CrossRef]
- Fried, Joel, and Peter Howitt. 1983. The Effects of Inflation on Real Interest Rates. The American Economic Review 73: 968–80. [Google Scholar]
- Geary, Robert Charles, and Conrad Emanuel Victor Leser. 1968. Significance Tests in Multiple Regression. The American Statistician 22: 20–21. [Google Scholar]
- Greene, William H. 2002. Econometric Analysis, 5th ed. Hoboken: Prentice Hall. [Google Scholar]
- Gujarati, Damodar N., and Dawn C. Porter. 2008. Basic Econometrics, 5th ed. New York: Mc-Graw Hill. [Google Scholar]
- Hair, Joseph F., William C. Black, Barry J. Babin, and Rolph E. Anderson. 2010. Advanced Diagnostics for Multiple Regression: A Supplement to Multivariate Data Analysis, 7th ed. Upper Saddle River: Pearson Education. [Google Scholar]
- Halkos, George, and Kyriaki Tsilika. 2018. Programming Correlation Criteria with free CAS Software. Computational Economics 52: 299–311. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome H. Friedman. 2001. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer. [Google Scholar]
- Imdadullah, Muhammad, Muhammad Aslam, and Saima Altaf. 2016. mctest: An R Package for Detection of Collinearity among Regressors. The R Journal 8: 495–505. [Google Scholar] [CrossRef]
- Kendall, Maurice G. 1957. A Course in Multivariate Analysis. New York: Hafner Pub. [Google Scholar]
- Klein, Lawrence R. 1962. An Introduction to Econometrics. Englewood Cliffs: Prentice Hall. [Google Scholar]
- Kovács, Péter, Tibor Petres, and László Tóth. 2005. A New Measure of Multicollinearity in Linear Regression Models. International Statistical Review/Revue Internationale de Statistique 73: 405–12. [Google Scholar] [CrossRef]
- Lindner, Thomas, Jonas Puck, and Alain Verbeke. 2020. Misconceptions about Multicollinearity in International Business Research: Identification, Consequences, and Remedies. Journal of International Business Studies 51: 283–98. [Google Scholar] [CrossRef] [Green Version]
- Liu, Wenya, and Qi Li. 2017. An Efficient Elastic Net with Regression Coefficients Method for Variable Selection of Spectrum Data. PLOS ONE 12: e0171122. [Google Scholar] [CrossRef] [PubMed]
- Mauri, Michele, Tommaso Elli, Giorgio Caviglia, Giorgio Uboldi, and Matteo Azzi. 2017. RAWGraphs: A Visualisation Platform to Create Open Outputs. In Proceedings of the 12th Biannual Conference on Italian SIGCHI Chapter. Association for Computing Machinery. New York: Association for Computing Machinery. [Google Scholar]
- Ntotsis, Kimon, and Alex Karagrigoriou. 2021. The Impact of Multicollinearity on Big Data Multivariate Analysis Modeling. In Applied Modeling Techniques and Data Analysis. London: iSTE Ltd., pp. 187–202. [Google Scholar]
- Ntotsis, Kimon, Emmanouil N. Kalligeris, and Alex Karagrigoriou. 2020. A Comparative Study of Multivariate Analysis Techniques for Highly Correlated Variable Identification and Management. International Journal of Mathematical, Engineering and Management Sciences 5: 45–55. [Google Scholar] [CrossRef]
- Oner, Ceyda. 2020. Unemployment: The Curse of Joblessness. International Monetary Fund. Available online: www.imf.org/external/pubs/ft/fandd/basics/unemploy.htm (accessed on 29 November 2021).
- Organisation for Economic Co-operation and Development. 2021. OECD Main Economic Indicators (MEI). Available online: https://www.oecd.org/sdd/oecdmaineconomicindicatorsmei.htm (accessed on 10 August 2021).
- Perez-Melo, Sergio, and B. M. Golam Kibria. 2020. On Some Test Statistics for Testing the Regression Coefficients in Presence of Multicollinearity: A Simulation Study. Stats 3: 40–55. [Google Scholar] [CrossRef] [Green Version]
- Silvey, Samuel D. 1969. Multicollinearity and Imprecise Estimation. Journal of the Royal Statistical Society. Series B 31: 539–52. [Google Scholar] [CrossRef]
- Theil, Henri. 1971. Principles of Econometrics. New York: John Wiley & Sons. [Google Scholar]
- Tibshirani, Robert. 1996. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B 58: 267–88. [Google Scholar] [CrossRef]
- Tikhonov, Andrei Nikolajevits. 1943. On the Stability of Inverse Problems. Doklady Akademii Nauk SSSR 39: 195–98. [Google Scholar]
- Tikhonov, Andrei Nikolajevits. 1963. Solution of Incorrectly Formulated Problems and the Regularization Method. Soviet Mathematics 4: 1035–38. [Google Scholar]
- Trading Economics. 2021. Main Indicators. Available online: https://tradingeconomics.com/indicators (accessed on 7 November 2021).
- Ueki, Masao, and Yoshinori Kawasaki. 2013. Multiple Choice from Competing Regression Models under Multicollinearity based on Standardized Update. Computational Statistics and Data Analysis 63: 31–41. [Google Scholar] [CrossRef]
- Ullah, Muhammad, Muhammad Aslam, Saima Altaf, and Munir Ahmed. 2019. Some New Diagnostics of Multicollinearity in Linear Regression Model. Sains Malaysiana 48: 2051–60. [Google Scholar] [CrossRef]
- Weisburd, David, and Chester Britt. 2013. Statistics in Criminal Justice. Berlin/Heidelberg: Springer Science and Business Media. [Google Scholar]
- Wooldridge, Jeffrey M. 2014. Introduction to econometrics: Europe, Middle East and Africa Edition. Boston: Cengage Learning. [Google Scholar]
- World Bank Open Data. 2021. Available online: data.worldbank.org (accessed on 15 August 2021).
- Yue, Lili, Gaorong Li, Heng Lian, and Xiang Wan. 2019. Regression Adjustment for Treatment Effect with Multicollinearity in High Dimensions. Computational Statistics and Data Analysis 134: 17–35. [Google Scholar] [CrossRef]
- Zou, Hui, and Trevor Hastie. 2005. Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society, Series B 67: 301–20. [Google Scholar] [CrossRef] [Green Version]
- Zou, Hui, Trevor Hastie, and Robert Tibshirani. 2006. Sparse Principal Component Analysis. Journal of Computational and Graphical Statistics 15: 265–86. [Google Scholar] [CrossRef] [Green Version]

| Measure | EIC | VIF | Correlation Range | |
|---|---|---|---|---|
| [u,] | ||||
| [2,0.2] | 45% | 0% | [0.98, 1] | |
| [2,0.5] | 40% | 0% | [0.94, 0.98] | |
| [2,1] | 24% | 1% | [0.78, 0.94] | |
| [2,2] | 16% | - | [0.46, 0.83] | |
| [2,5] | 7% | - | [−0.1, 0.59] | |
| [5,0.2] | 50% | 0% | [0.99, 1] | |
| [5,0.5] | 67% | 0% | [0.98, 1] | |
| [5,1] | 72% | 0% | [0.96, 0.99] | |
| [5,2] | 70% | 0.1% | [0.86, 0.96] | |
| [5,5] | 35% | - | [0.45, 0.83] | |
| Individual Multicollinearity Diagnostic Measures | |||||||
|---|---|---|---|---|---|---|---|
| EIC | VIF | TOL | CI | F-G wj | Leamer | IND1 | |
| BoT | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| GovDebt | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| GDP | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Inf | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| Int | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| Unem | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntotsis, K.; Karagrigoriou, A.; Artemiou, A. Interdependency Pattern Recognition in Econometrics: A Penalized Regularization Antidote. Econometrics 2021, 9, 44. https://doi.org/10.3390/econometrics9040044
Ntotsis K, Karagrigoriou A, Artemiou A. Interdependency Pattern Recognition in Econometrics: A Penalized Regularization Antidote. Econometrics. 2021; 9(4):44. https://doi.org/10.3390/econometrics9040044
Chicago/Turabian StyleNtotsis, Kimon, Alex Karagrigoriou, and Andreas Artemiou. 2021. "Interdependency Pattern Recognition in Econometrics: A Penalized Regularization Antidote" Econometrics 9, no. 4: 44. https://doi.org/10.3390/econometrics9040044
APA StyleNtotsis, K., Karagrigoriou, A., & Artemiou, A. (2021). Interdependency Pattern Recognition in Econometrics: A Penalized Regularization Antidote. Econometrics, 9(4), 44. https://doi.org/10.3390/econometrics9040044








