Remote Learning in Transnational Education: Relationship between Virtual Learning Engagement and Student Academic Performance in BSc Pharmaceutical Biotechnology
Abstract
:1. Introduction
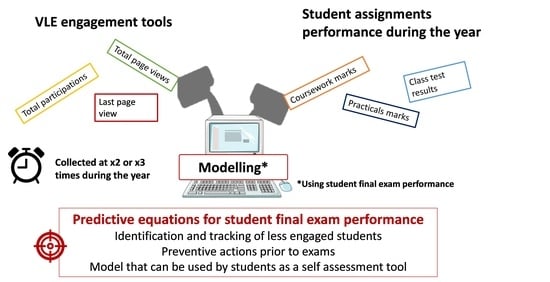
2. Materials and Methods
2.1. Study Participants and Studied Course
2.2. Study Design
2.3. Data Modelling and Analysis
2.4. Data Storage and Accessibility
3. Results
3.1. Effect of Outliers on Individual Indicators Relationship to Exam Marks
3.2. Modelling Using All Variables
3.3. Modelling Using E, F, G and H Variables
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weller, M. Virtual Learning Environments: Using, Choosing and Developing Your VLE; Routledge: London, UK, 2007. [Google Scholar]
- O’Mahony, J. Enhancing Student Learning and Teacher Development in Transnational Education; Higher Education Academy: York, UK, 2014. [Google Scholar]
- Wolff, A.; Zdrahal, Z.; Nikolov, A.; Pantucek, M. Improving Retention: Predicting at-Risk Students by Analysing Clicking Behaviour in a Virtual Learning Environment. In Proceedings of the Third International Conference on Learning Analytics and Knowledge, Leuven, Belgium, 8–12 April 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 145–149. [Google Scholar] [CrossRef]
- Kuh, G.D.; Cruce, T.M.; Shoup, R.; Kinzie, J.; Gonyea, R.M. Unmasking the Effects of Student Engagement on First-Year College Grades and Persistence. J. High. Educ. 2008, 79, 540–563. Available online: http://www.jstor.org/stable/25144692 (accessed on 29 November 2021).
- Axelson, R.D.; Flick, A. Defining Student Engagement. Change Mag. High. Learn. 2011, 43, 38–43. [Google Scholar] [CrossRef]
- Casuso-Holgado, M.J.; Cuesta-Vargas, A.I.; Moreno-Morales, N.; Labajos-Manzanares, M.T.; Barón-López, F.J.; Vega-Cuesta, M. The association between academic engagement and achievement in health sciences students. BMC Med. Educ. 2013, 13, 33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamane, A. Student Engagement in an Online Course and Its Impact on Student Success. Ph.D. Thesis, Pepperdine University, Malibu, CA, USA, 2014. Available online: https://digitalcommons.pepperdine.edu/etd/428 (accessed on 20 September 2021).
- Boud, D.; Lawson, R.; Thompson, D.G. Does student engagement in self-assessment calibrate their judgement over time? Assess. Eval. High. Educ. 2013, 38, 941–956. [Google Scholar] [CrossRef]
- Boud, D.; Falchikov, N. Developing assessment for informing judgement. In Rethinking Assessment in Higher Education; Routledge: Oxfordshire, UK, 2007; pp. 191–207. [Google Scholar]
- Boud, D. Enhancing Learning through Self-Assessment; Routledge: London, UK, 2013. [Google Scholar]
- Grossi, M.G.R.; Elias, M.; Chamon, C.M.; Leal, D. The educational potentialities of the virtual learning environments moodle and canvas: A comparative study. Int. J. Inf. Educ. Technol. 2018, 8, 514–519. [Google Scholar] [CrossRef] [Green Version]
- Endozo, A.N.; Oluyinka, S.; Daenos, R.G. Teachers’ Experiences towards Usage of Learning Management System: CANVAS. In Proceedings of the 2019 11th International Conference on Education Technology and Computers; Association for Computing Machinery: New York, NY, USA, 2019; pp. 91–95. [Google Scholar]
- al Khoeri, A.F.; Nuraini, W.; Ramdani, R.; Agum, S. The implementation of Canvas to enhance English teaching and learning. In International Conference on Education of Suryakancana (IConnects Proceedings); Suryakancana University: Jawa Barat, Indonesia, 2021. [Google Scholar]
- MathWorks—Makers of MATLAB and Simulink—MATLAB & Simulink, (n.d.). Available online: https://uk.mathworks.com/ (accessed on 28 October 2021).
- Audet, C.; Hare, W. Derivative-Free and Blackbox Optimization; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Walfish, S. A review of statistical outlier methods. Pharm. Technol. 2006, 30, 82. [Google Scholar]
- Raja, R.; Nagasubramani, P.C. Impact of modern technology in education. J. Appl. Adv. Res. 2018, 3, 33–35. [Google Scholar] [CrossRef] [Green Version]
- William, W.; Higson, H.E.; Dey, P.K.; Xu, X.; Bahsoon, R. Measuring performance of virtual learning environment system in higher education. Qual. Assur. Educ. 2009, 17, 6–29. [Google Scholar] [CrossRef] [Green Version]
- Blizak, D.; Blizak, S.; Bouchenak, O.; Yahiaoui, K. Students’ Perceptions Regarding the Abrupt Transition to Online Learning During the COVID-19 Pandemic: Case of Faculty of Chemistry and Hydrocarbons at the University of Boumerdes—Algeria. J. Chem. Educ. 2020, 97, 2466–2471. [Google Scholar] [CrossRef]
- Alzubaidi, H.; Jirjees, F.J.; Franson, K.L.; Saidawi, W.; Othman, A.M.; Rabeeah, Z.H.; Al-Obaidi, H.J.; Hatahet, T.; Caliph, S. A global assessment of distance pharmacy education amid COVID-19: Teaching, assessment and experiential training. Int. J. Pharm. Pract. 2021, 29, 633–641. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Shehata, M.; Hassanien, M. Emerging Faculty Needs for Enhancing Student Engagement on a Virtual Platform. MedEdPublish 2020, 9, 75. [Google Scholar] [CrossRef] [Green Version]
- Maltby, A.; Mackie, S. Virtual learning environments–help or hindrance for the ‘disengaged’student? ALT-J 2009, 17, 49–62. [Google Scholar] [CrossRef]
- Al-Azawei, A.; Al-Azawei, A.; Al-Masoudy, M. Predicting Learners’ Performance in Virtual Learning Environment (VLE) based on Demographic, Behavioral and Engagement Antecedents. Int. J. Emerg. Technol. Learn. 2020, 15, 60–75. [Google Scholar] [CrossRef]
- Hussain, M.; Zhu, W.; Zhang, W.; Abidi, S.M.R. Student Engagement Predictions in an e-Learning System and Their Impact on Student Course Assessment Scores. Comput. Intell. Neurosci. 2018, 2018, 6347186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mogus, A.M.; Djurdjevic, I.; Suvak, N. The impact of student activity in a virtual learning environment on their final mark. Act. Learn. High. Educ. 2012, 13, 177–189. [Google Scholar] [CrossRef]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education; Routledge: London, UK, 2013. [Google Scholar]
- Lee, M.-G. Profiling students’ adaptation styles in Web-based learning. Comput. Educ. 2001, 36, 121–132. [Google Scholar] [CrossRef]
- Understanding Grades|Imperial students|Imperial College London, (n.d.). Available online: https://www.imperial.ac.uk/students/success-guide/ug/assessments-and-feedback/improving-through-feedback/understanding-grades/ (accessed on 20 September 2021).
- Jackson, L.A.; Biocca, F.A.; von Eye, A.; Fitzgerald, H.E.; Barbatsis, G.; Zhao, Y.; Ware, D. Motivational, affective and cognitive factors and Internet use: A model to explain the racial digital divide and the Internet paradox. In WebNet World Conference on the WWW and Internet; Association for the Advancement of Computing in Education (AACE): Waynesville, NC, USA, 2000; pp. 736–737. [Google Scholar]
- Dawson, S. The impact of institutional surveillance technologies on student behavior. Surveill. Soc. 2006, 4, 69–84. [Google Scholar]




| Modelling Type | Equation Number | Equation |
|---|---|---|
| All Variables Are in Court | ||
| With Outliers | ||
| Simple linear regression model without optimization | (1) | |
| Simple linear regression with a new predictor (adjusting variable X) | (2) | |
| Without Outliers | ||
| Simple linear regression model without optimization | (3) | |
| Simple linear regression with a new predictor (adjusting variable X) | (4) | |
| E, F, G and H Variables Are in Court | ||
| With Outliers | ||
| Simple linear regression model without optimization | (5) | |
| Simple linear regression with a new predictor (adjusting variable X) | (6) | |
| Without Outliers | ||
| Simple linear regression model without optimization | (7) | |
| Simple linear regression with a new predictor (adjusting variable X) | (8) | |
| Modelling Type | Equation Number | Number of Observation Error Degrees of Freedom | Root Mean Squared Error | Pearson Correlation Coefficient R2 Adjusted R2 | p-Value |
|---|---|---|---|---|---|
| All Variables Are in Court | |||||
| With Outliers | |||||
| Simple linear regression model without optimization | (1) | 55 46 | 14.1 | 0.600 0.350 0.237 | 7.01 × 10−3 ** |
| Simple linear regression with a new predictor (adjusting variable X) | (2) | 55 45 | 0.0656 | 1 1 | 2.98 × 10−6 *** |
| Without Outliers | |||||
| Simple linear regression model without optimization | (3) | 47 38 | 12.4 | 0.724 0.524 0.424 | 1.89 × 10−4 *** |
| Simple linear regression with a new predictor (adjusting variable X) | (4) | 47 37 | 0.276 | 1 1 | 1.77 × 10−64 *** |
| D, E, G and H Variables Are in Court | |||||
| With Outliers | |||||
| Simple linear regression model without optimization | (5) | 55 50 | 13.6 | 0.585 0.342 0.289 | 2.72 × 10−4 *** |
| Simple linear regression with a new predictor (adjusting variable X) | (6) | 55 49 | 0.264 | 1 1 | 3.18 × 10−87 *** |
| Without Outliers | |||||
| Simple linear regression model without optimization | (7) | 47 42 | 12.1 | 0.700 0.493 0.445 | 7.28 × 10−6 *** |
| Simple linear regression with a new predictor (adjusting variable X) | (8) | 47 41 | 0.106 | 1 1 | 1.36 × 10−89 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatahet, T.; Mohamed, A.A.R.; Malekigorji, M.; Kerry, E.K. Remote Learning in Transnational Education: Relationship between Virtual Learning Engagement and Student Academic Performance in BSc Pharmaceutical Biotechnology. Pharmacy 2022, 10, 4. https://doi.org/10.3390/pharmacy10010004
Hatahet T, Mohamed AAR, Malekigorji M, Kerry EK. Remote Learning in Transnational Education: Relationship between Virtual Learning Engagement and Student Academic Performance in BSc Pharmaceutical Biotechnology. Pharmacy. 2022; 10(1):4. https://doi.org/10.3390/pharmacy10010004
Chicago/Turabian StyleHatahet, Taher, Ahmed A.Raouf Mohamed, Maryam Malekigorji, and Emma K. Kerry. 2022. "Remote Learning in Transnational Education: Relationship between Virtual Learning Engagement and Student Academic Performance in BSc Pharmaceutical Biotechnology" Pharmacy 10, no. 1: 4. https://doi.org/10.3390/pharmacy10010004
APA StyleHatahet, T., Mohamed, A. A. R., Malekigorji, M., & Kerry, E. K. (2022). Remote Learning in Transnational Education: Relationship between Virtual Learning Engagement and Student Academic Performance in BSc Pharmaceutical Biotechnology. Pharmacy, 10(1), 4. https://doi.org/10.3390/pharmacy10010004