Study of Joint Symmetry in Gait Evolution for Quadrupedal Robots Using a Neural Network
Abstract
:1. Introduction
2. Methodology
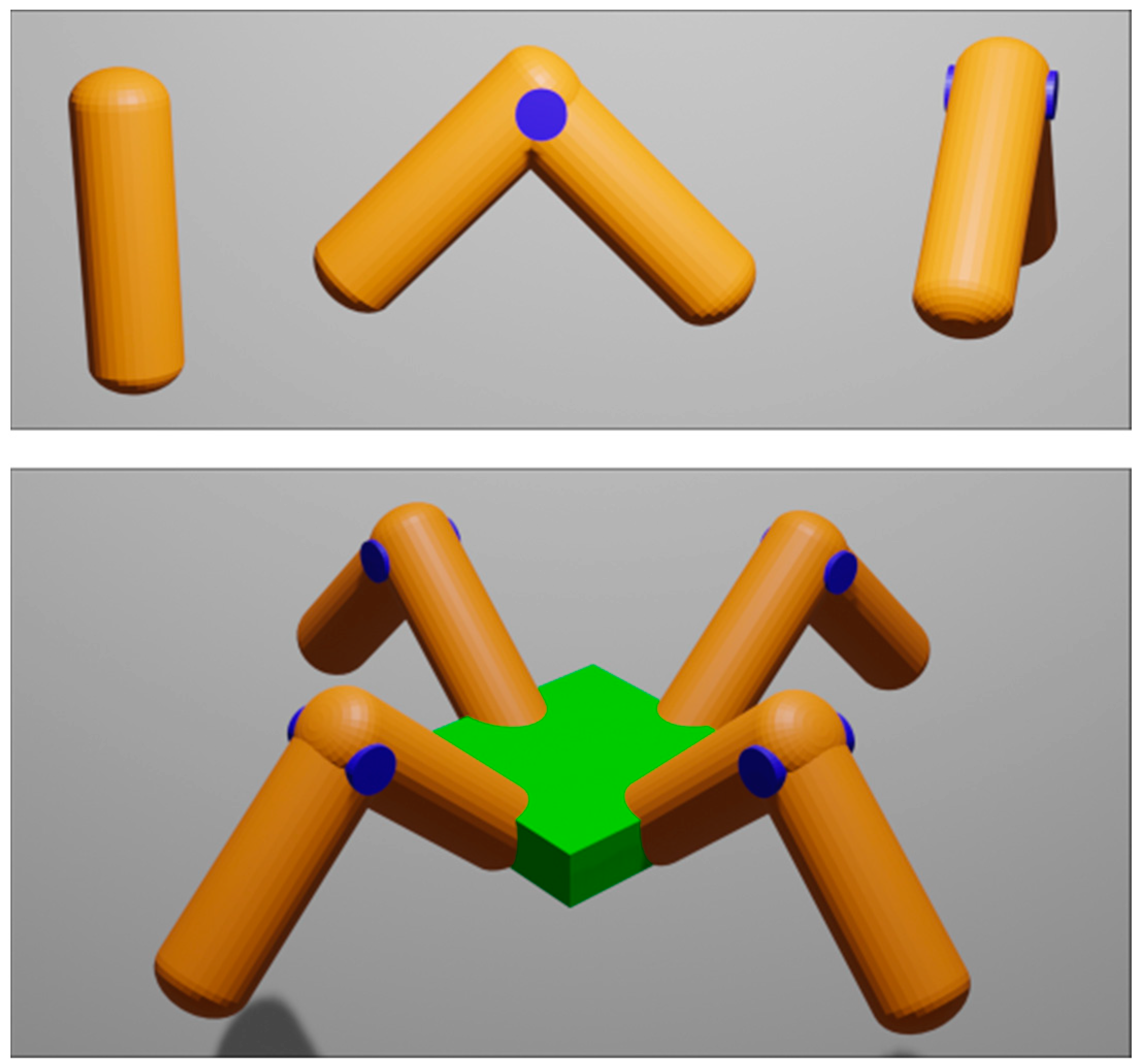
2.1. Simulation
2.2. Controller
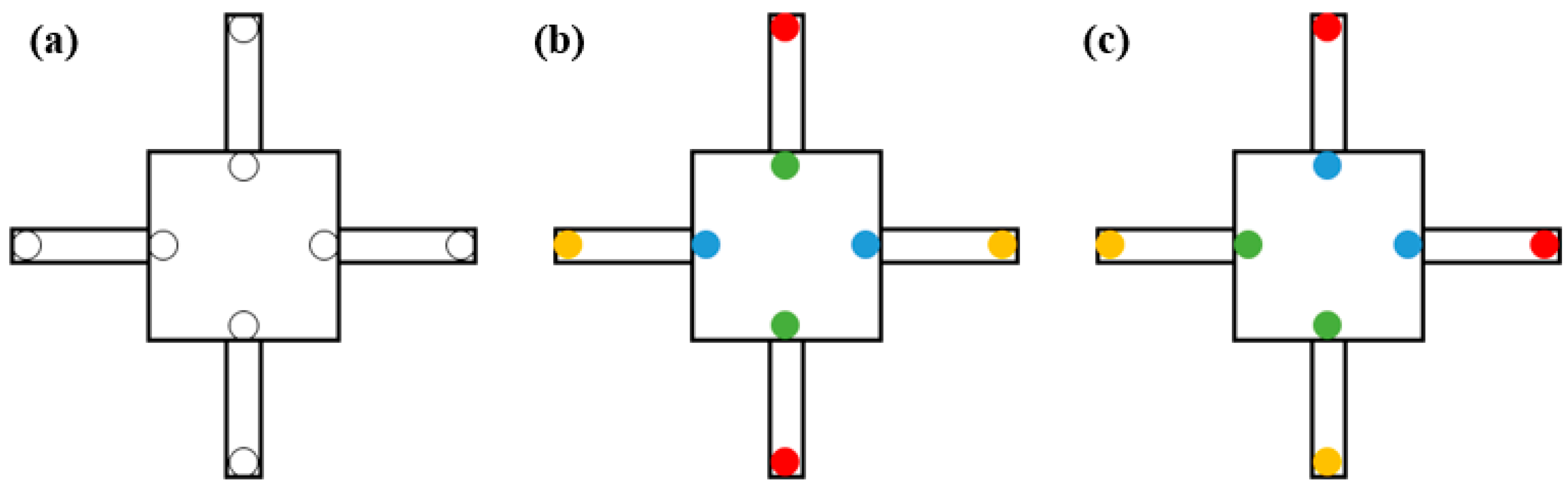
2.2.1. Diagonal Joint Symmetry
2.2.2. Adjacent Joint Symmetry
2.2.3. Diagonal Joint Reverse Symmetry
2.2.4. Adjacent Joint Reverse Symmetry
2.2.5. Joint Asymmetry or Random Joint Movement
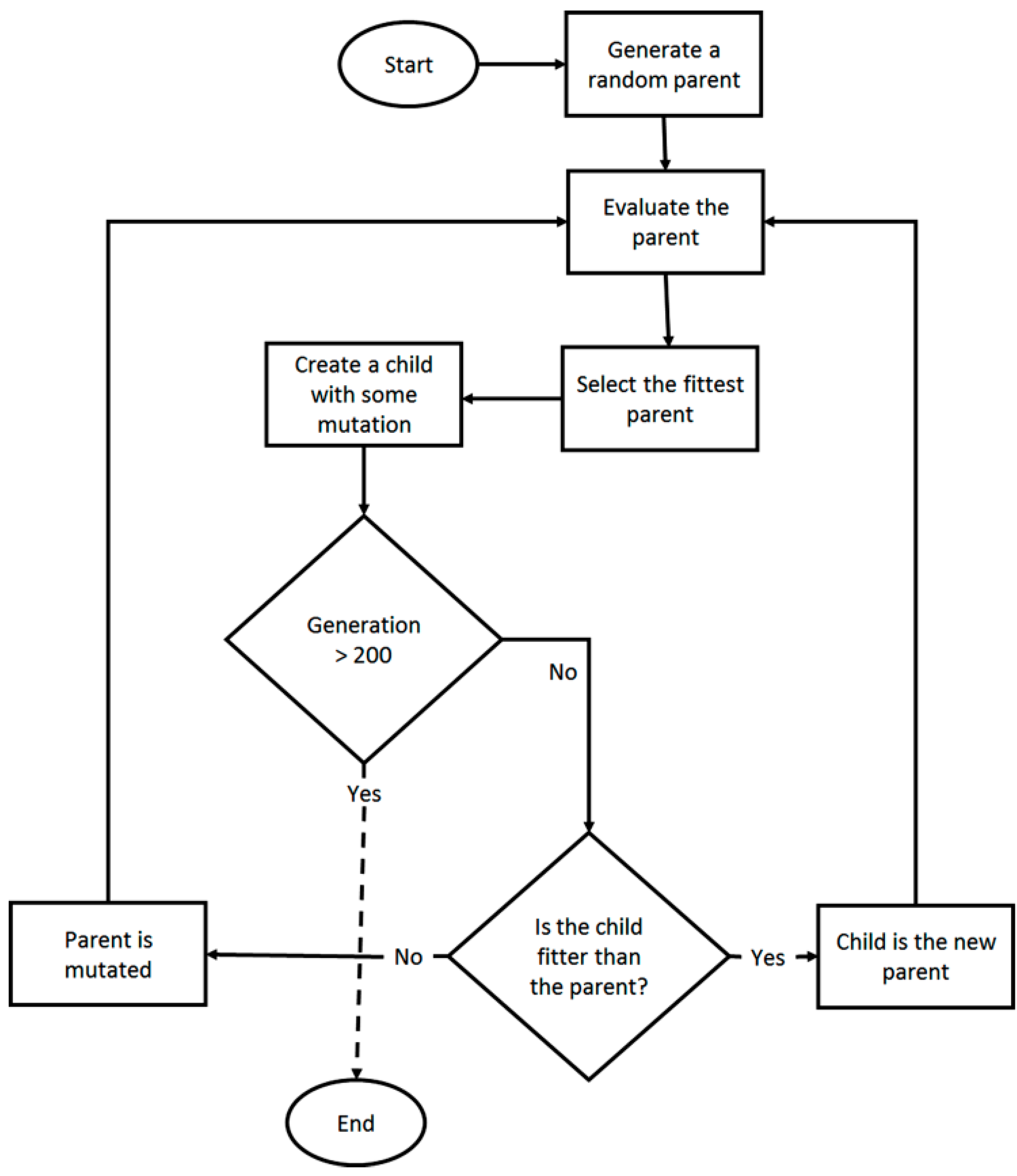
2.3. Algorithm
2.4. Selection Criteria
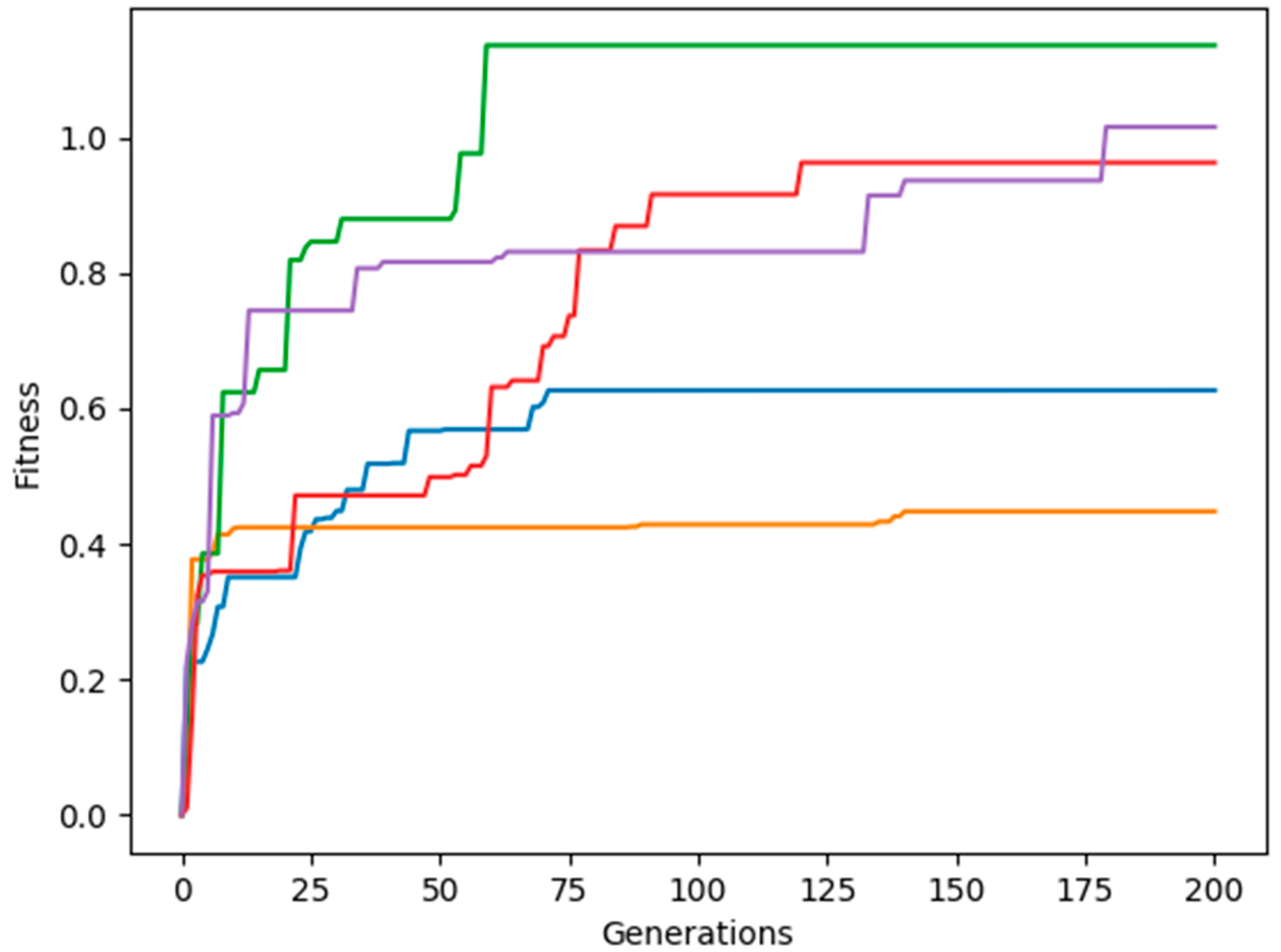
3. Results and Discussion
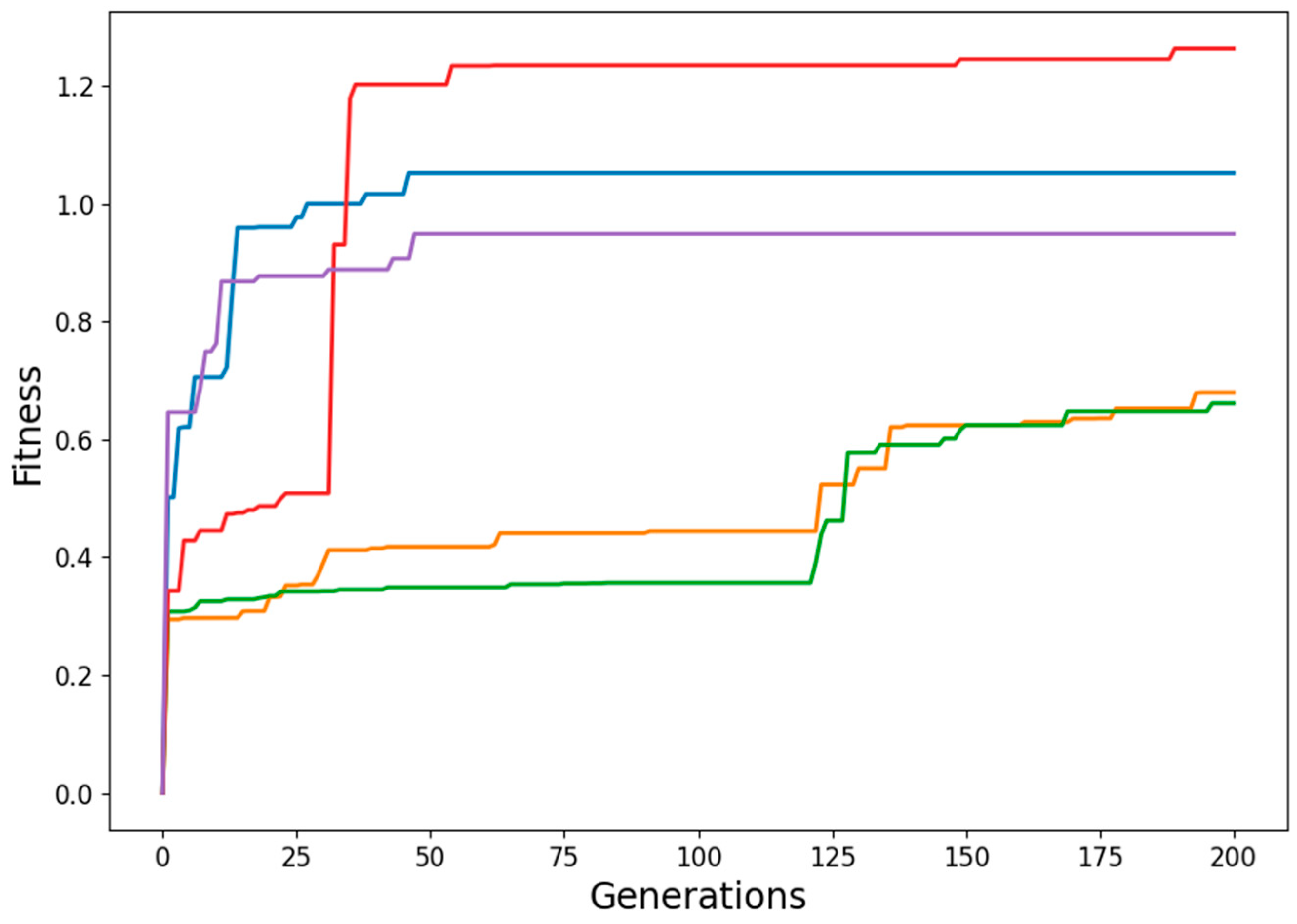
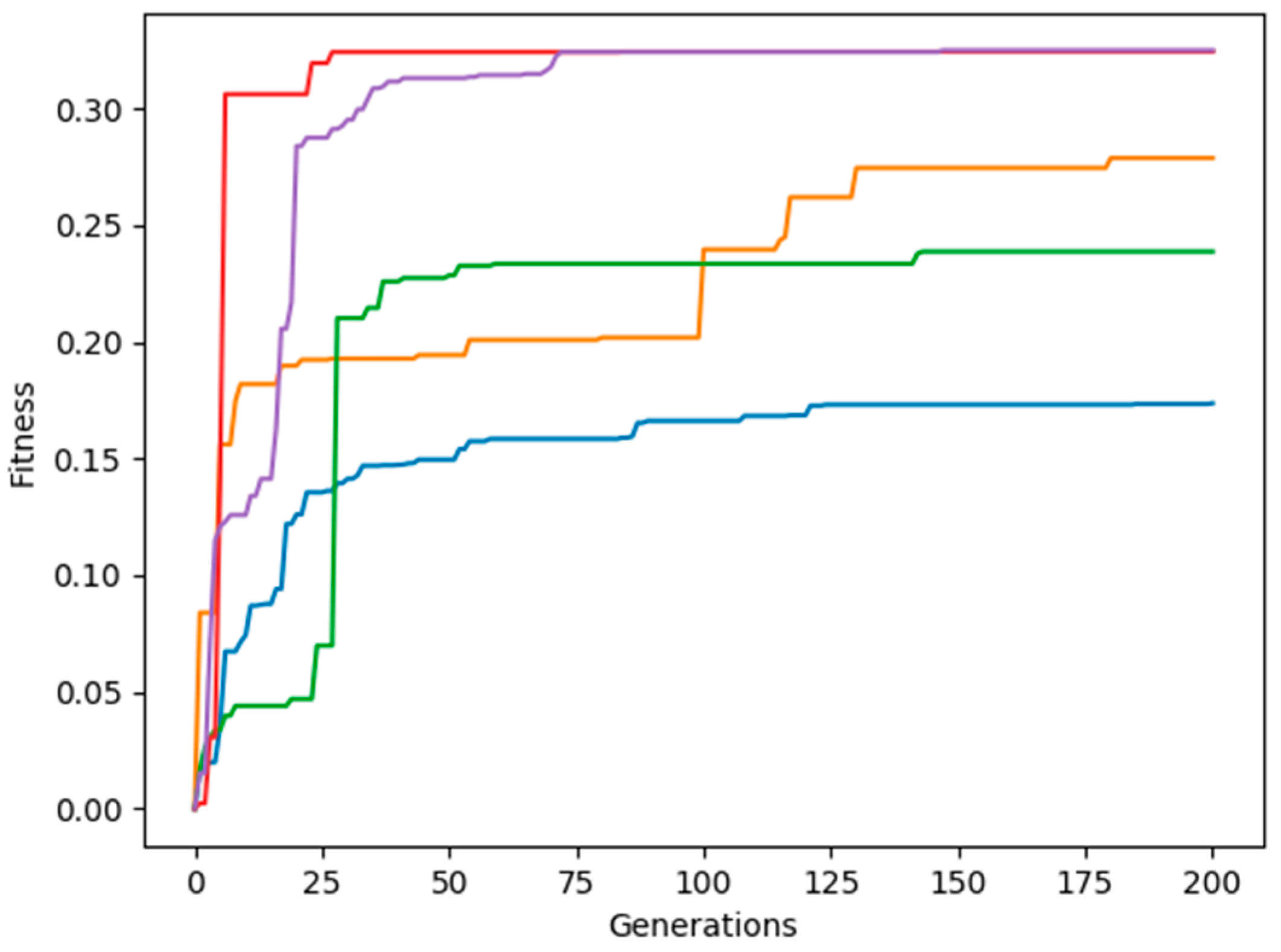
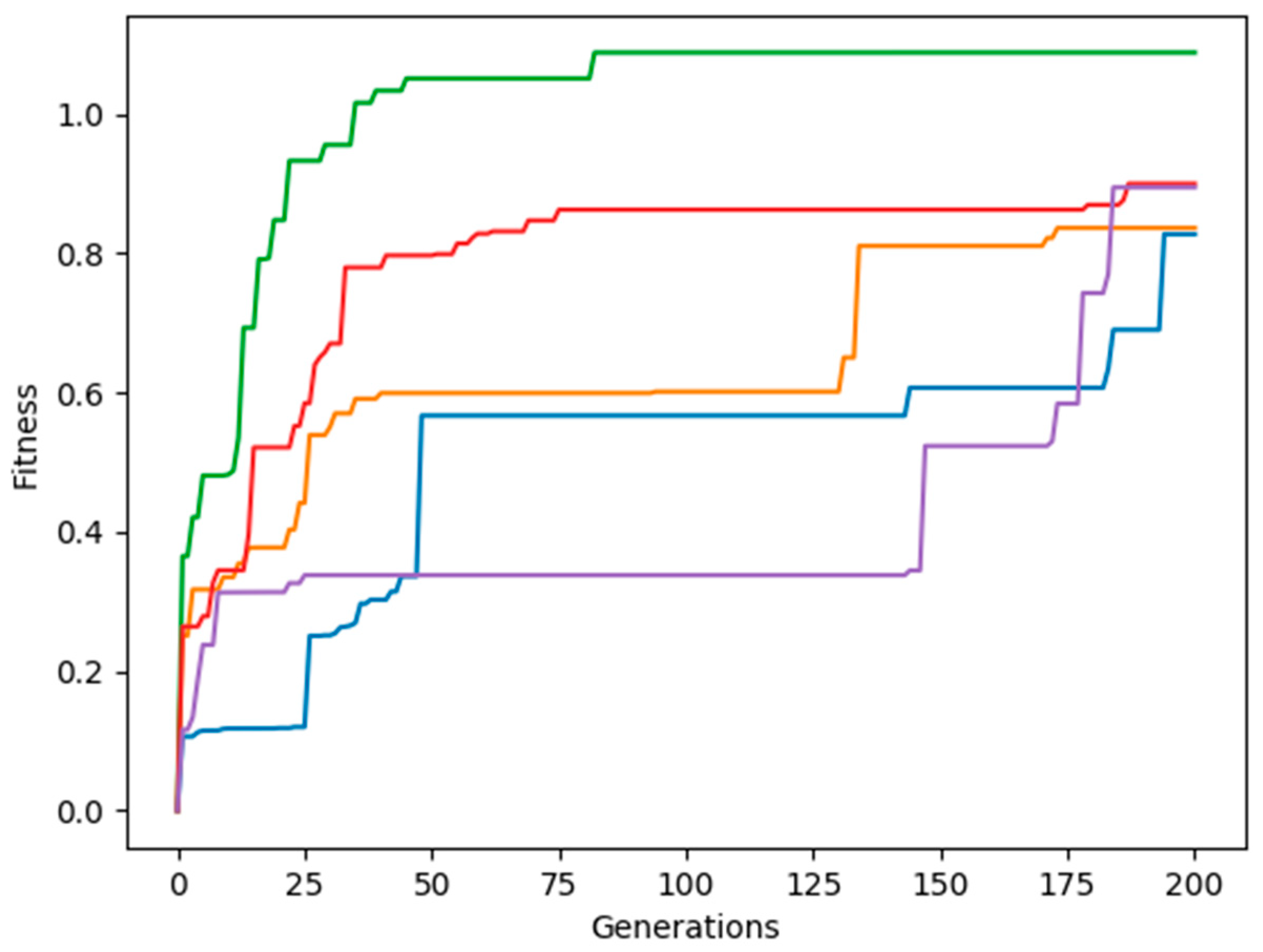
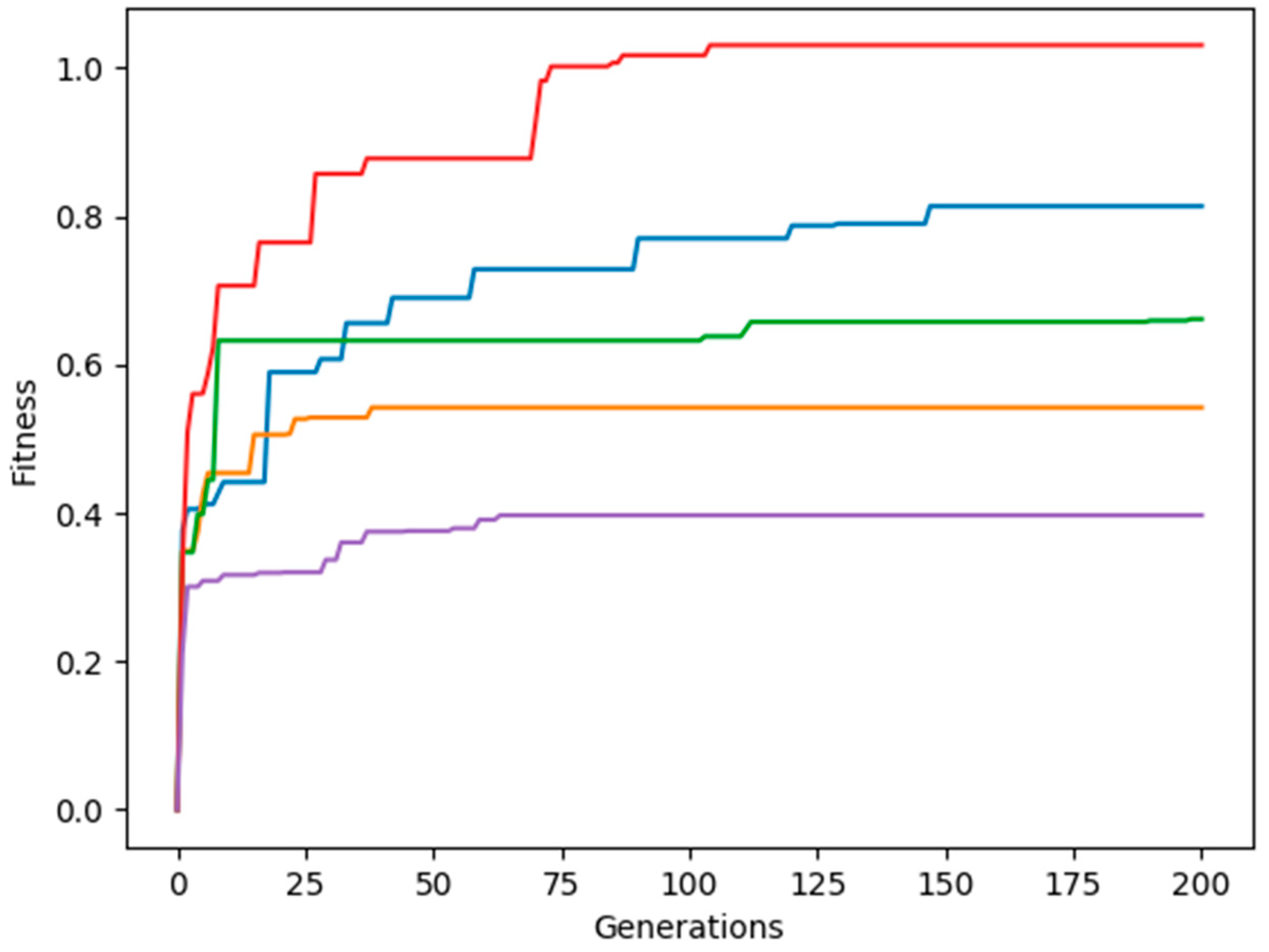
3.1. Adjacent Joint Symmetry and Reverse Symmetry
3.2. Diagonal Joint Symmetry and Reverse Symmetry
3.3. Random Joint Movement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pfeifer, R.; Bongard, J. How the Body Shapes the Way We Think: A New View of Intelligence; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Bongard, J.C. Evolutionary robotics. Commun. ACM 2013, 56, 74–83. [Google Scholar] [CrossRef] [Green Version]
- Eckert, P.; Ijspeert, A.J. Benchmarking agility for multilegged terrestrial robots. IEEE Trans. Robot. 2019, 35, 529–535. [Google Scholar] [CrossRef]
- Carpentier, J.; Wieber, P.B. Recent progress in legged robots locomotion control. Curr. Robot. Rep. 2021, 2, 231–238. [Google Scholar] [CrossRef]
- Zhao, A.; Xu, J.; Konaković-Luković, M.; Hughes, J.; Spielberg, A.; Rus, D.; Matusik, W. Robogrammar: Graph grammar for terrain-optimized robot design. ACM Trans. Graphics (TOG) 2020, 39, 1–6. [Google Scholar] [CrossRef]
- Hauert, S.; Zufferey, J.C.; Floreano, D. Reverse-engineering of artificially evolved controllers for swarms of robots. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 55–61. [Google Scholar]
- De Santos, P.G.; Garcia, E.; Estremera, J. Quadrupedal locomotion: An Introduction to the Control of Four-Legged Robots; Springer: London, UK, 2006. [Google Scholar]
- Goswami, A.; Thuilot, B.; Espiau, B. A study of the passive gait of a compass-like biped robot: Symmetry and chaos. Int. J. Robot. Res. 1998, 17, 1282–1301. [Google Scholar] [CrossRef]
- Zanotto, D.; Stegall, P.; Agrawal, S.K. Adaptive assist-as-needed controller to improve gait symmetry in robot-assisted gait training. In Proceedings of the 2014 IEEE international conference on robotics and automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 724–729. [Google Scholar]
- RunBin, C.; YangZhen, C.; WenQi, H.; Jiang, W.; HongXu, M. Trotting gait of a quadruped robot based on the time-pose control method. Int. J. Adv. Robot. Syst. 2013, 10, 148. [Google Scholar] [CrossRef] [Green Version]
- Wong, L.H.; Sivanesan, S.; Faisol, M.F.; Othman, W.A.; Wahab, A.A.; Alhady, S.S. Development of quadruped walking robot with passive compliance legs using XL4005 buck converter. J. Phys. Conf. Ser. 2021, 1969, 012003. [Google Scholar] [CrossRef]
- He, D. An Optimal Initial Foot Position for Quadruped Robots in Trot Gait. J. Phys. Conf. Ser. 2020, 1624, 052015. [Google Scholar] [CrossRef]
- Kamimura, T.; Aoi, S.; Higurashi, Y.; Wada, N.; Tsuchiya, K.; Matsuno, F. Dynamical determinants enabling two different types of flight in cheetah gallop to enhance speed through spine movement. Sci. Rep. 2021, 11, 9631. [Google Scholar] [CrossRef] [PubMed]
- Poulakakis, I.; Smith, J.A.; Buehler, M. Modeling and experiments of untethered quadrupedal running with a bounding gait: The Scout II robot. Int. J. Robot. Res. 2005, 24, 239–256. [Google Scholar] [CrossRef] [Green Version]
- Pongas, D.; Mistry, M.; Schaal, S. A robust quadruped walking gait for traversing rough terrain. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1474–1479. [Google Scholar]
- Chen, J.P.; San, H.J.; Wu, X.; Xiong, B.Z. Structural design and gait research of a new bionic quadruped robot. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 0954405421995663. [Google Scholar] [CrossRef]
- Havoutis, I.; Semini, C.; Buchli, J.; Caldwell, D.G. Quadrupedal trotting with active compliance. In Proceedings of the 2013 IEEE International Conference on Mechatronics (ICM), Vicenza, Italy, 27–28 February 2013; pp. 610–616. [Google Scholar]
- Zhai, K.; Li, C.A.; Rosendo, A. Scaffolded Learning of In-place Trotting Gait for a Quadruped Robot with Bayesian Optimization. In Proceedings of the International Conference on Intelligent Autonomous Systems, Singapore, 22–25 June 2021; Springer: Cham, Switzerland; pp. 365–373. [Google Scholar]
- Dini, N.; Majd, V.J. An MPC-based two-dimensional push recovery of a quadruped robot in trotting gait using its reduced virtual model. Mech. Mach. Theory 2020, 146, 103737. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Wang, P.; Sun, L. Running and turning control of a quadruped robot with compliant legs in bounding gait. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 511–518. [Google Scholar]
- Owaki, D.; Ishiguro, A. A quadruped robot exhibiting spontaneous gait transitions from walking to trotting to galloping. Sci. Rep. 2017, 7, 277. [Google Scholar] [CrossRef] [PubMed]
- Billard, A.; Ijspeert, A.J. Biologically inspired neural controllers for motor control in a quadruped robot. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000; Volume 6, pp. 637–641. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Garcia, T.B.; Coronado-Mendoza, A.; Domínguez-Navarro, J.A. Artificial neural networks in microgrids: A review. Eng. Appl. Artif. Intell. 2020, 95, 103894. [Google Scholar] [CrossRef]
- McHale, G.; Husbands, P. Quadrupedal locomotion: GasNets, CTRNNs and hybrid CTRNN/PNNs compared. In Proceedings of the 9th International Conference on the Simulation and Synthesis of Living Systems (ALIFE IX), Boston, MA, USA, 12–15 September 2004; MIT Press: Cambridge, MA, USA; pp. 106–112. [Google Scholar]
- Yosinski, J.; Clune, J.; Hidalgo, D.; Nguyen, S.; Zagal, J.C.; Lipson, H. Evolving robot gaits in hardware: The HyperNEAT generative encoding vs. parameter optimization. In Proceedings of the ECAL, Paris, France, 8–12 August 2011; pp. 890–897. [Google Scholar]
- Glette, K.; Klaus, G.; Zagal, J.C.; Torresen, J. Evolution of locomotion in a simulated quadruped robot and transferral to reality. In Proceedings of the Seventeenth International Symposium on Artificial Life and Robotics, Beppu, Japan, 19–21 January 2012; pp. 1–4. [Google Scholar]
- Kim, J.; Ba, D.X.; Yeom, H.; Bae, J. Gait optimization of a quadruped robot using evolutionary computation. J. Bionic Eng. 2021, 18, 306–318. [Google Scholar] [CrossRef]
- Bongard, J. GitHub-Jbongard/Pyrosim: A Python Robot Simulator. Available online: https://github.com/jbongard/pyrosim (accessed on 14 February 2022).
- Smith, R. Open Dynamics Engine. 2005, p. 84. Available online: http://ode.org/ (accessed on 25 April 2022).
- Phillips, A.; du Plessis, M. Towards the incorporation of proprioception in evolutionary robotics controllers. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 226–229. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Gagliano, S. Imperfections in Integrated Devices Allow the Emergence of Unexpected Strange Attractors in Electronic Circuits. IEEE Access 2021, 9, 29573–29583. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Rizzo, A. Dynamical network interactions in distributed control of robots. Chaos 2006, 16, 015116. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Symbol | Value |
|---|---|---|
| Robot body length | l | 0.2 m |
| Robot body width | w | 0.2 m |
| Robot body height | h | 0.05 m |
| Length of cylinder | cL | 0.2 m |
| Radius of cylinder | cR | 0.02 m |
| Mass of each robot body part in the simulation | m | 1 kg |
| Gravity | g | −9.8 ms−2 |
| Number of joints | J | 8 |
| Number of motors | M | 8 |
| Motor impulse | τ | 0.15 |
| Simulation world step time | dt | 0.05 |
| Total number of timesteps for the simulation | T | 1000 |
| ANN recall interval timesteps | Rc | 60 |
| ANN inputs | I | 9 |
| ANN outputs | O | 8 |
| Number of individuals in the population | P | 10 |
| Number of generations | G | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Z.; Naseer, F.; Khan, Y.; Bilal, M.; Butt, M.A. Study of Joint Symmetry in Gait Evolution for Quadrupedal Robots Using a Neural Network. Technologies 2022, 10, 64. https://doi.org/10.3390/technologies10030064
Khan Z, Naseer F, Khan Y, Bilal M, Butt MA. Study of Joint Symmetry in Gait Evolution for Quadrupedal Robots Using a Neural Network. Technologies. 2022; 10(3):64. https://doi.org/10.3390/technologies10030064
Chicago/Turabian StyleKhan, Zainullah, Farhat Naseer, Yousuf Khan, Muhammad Bilal, and Muhammad A. Butt. 2022. "Study of Joint Symmetry in Gait Evolution for Quadrupedal Robots Using a Neural Network" Technologies 10, no. 3: 64. https://doi.org/10.3390/technologies10030064
APA StyleKhan, Z., Naseer, F., Khan, Y., Bilal, M., & Butt, M. A. (2022). Study of Joint Symmetry in Gait Evolution for Quadrupedal Robots Using a Neural Network. Technologies, 10(3), 64. https://doi.org/10.3390/technologies10030064







