Detecting Airborne Pathogens: A Computational Approach Utilizing Surface Acoustic Wave Sensors for Microorganism Detection
Abstract
:1. Introduction
2. Materials and Methods
2.1. Airborne Pathogen Characterization
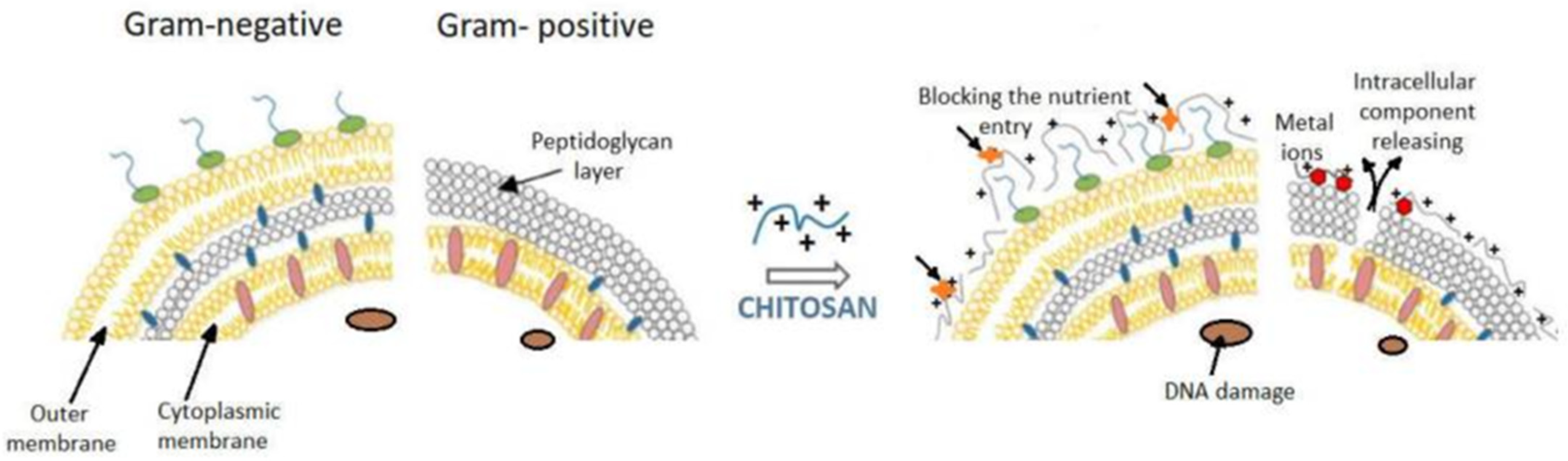
2.2. Sensing Layer Selection:
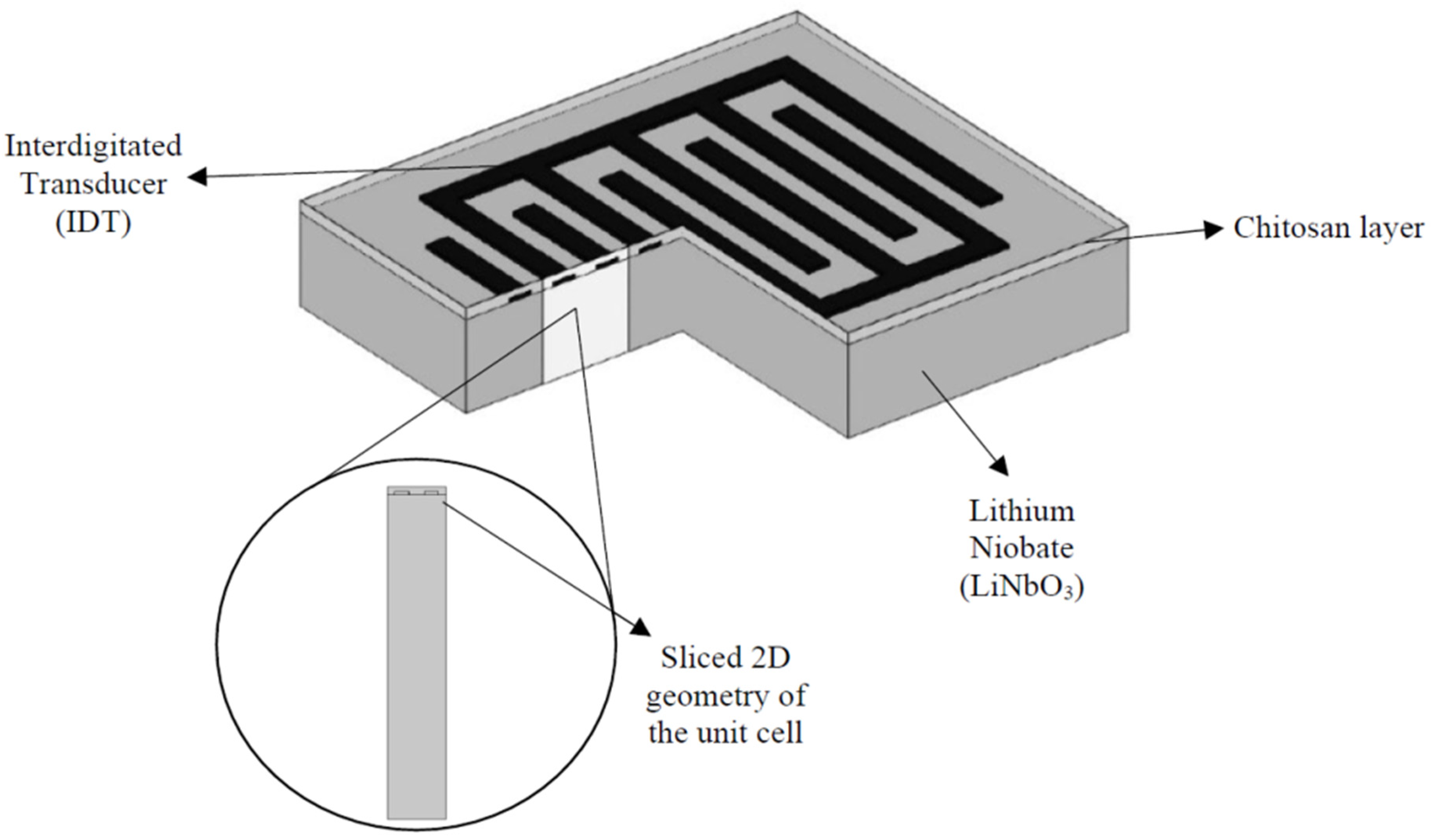
2.3. Substrate Selection—Lithium Niobate (LiNbO3)
2.4. Inter-Digital Transducers (IDTs)—A1 Electrodes
2.5. Multi-Physics Simulation Using COMSOL Multiphysics
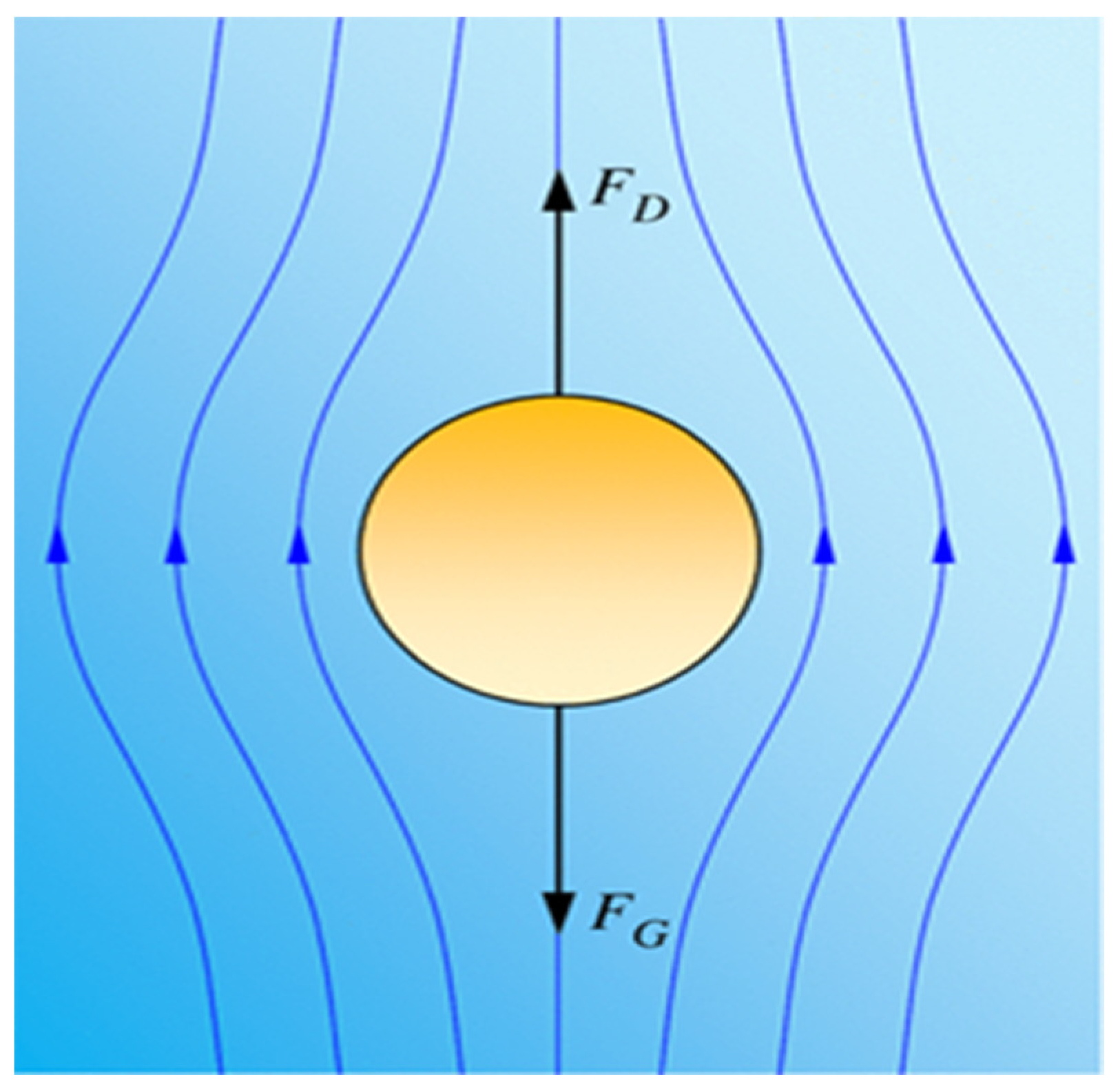
2.6. Mathematical Model for Air Microbe Detection
2.7. Proposed Surface Acoustic Sensing Method
2.8. FEM Simulation
3. Results and Discussion
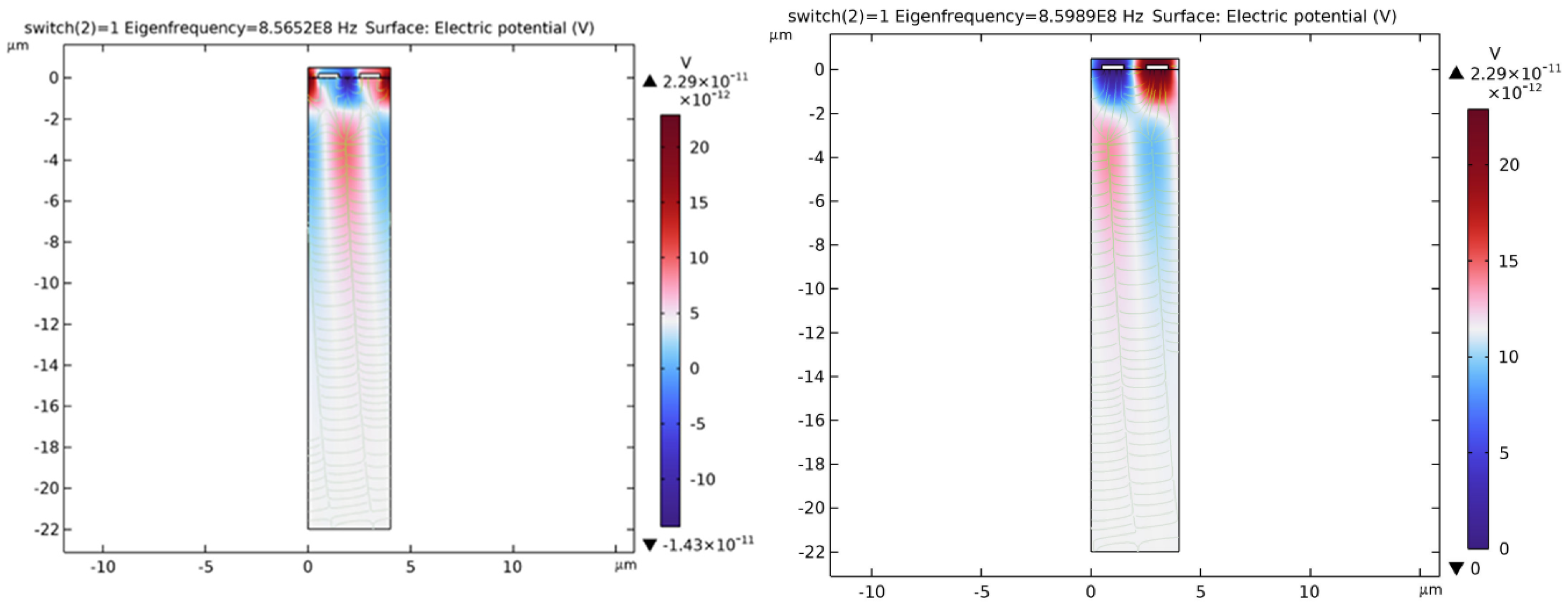
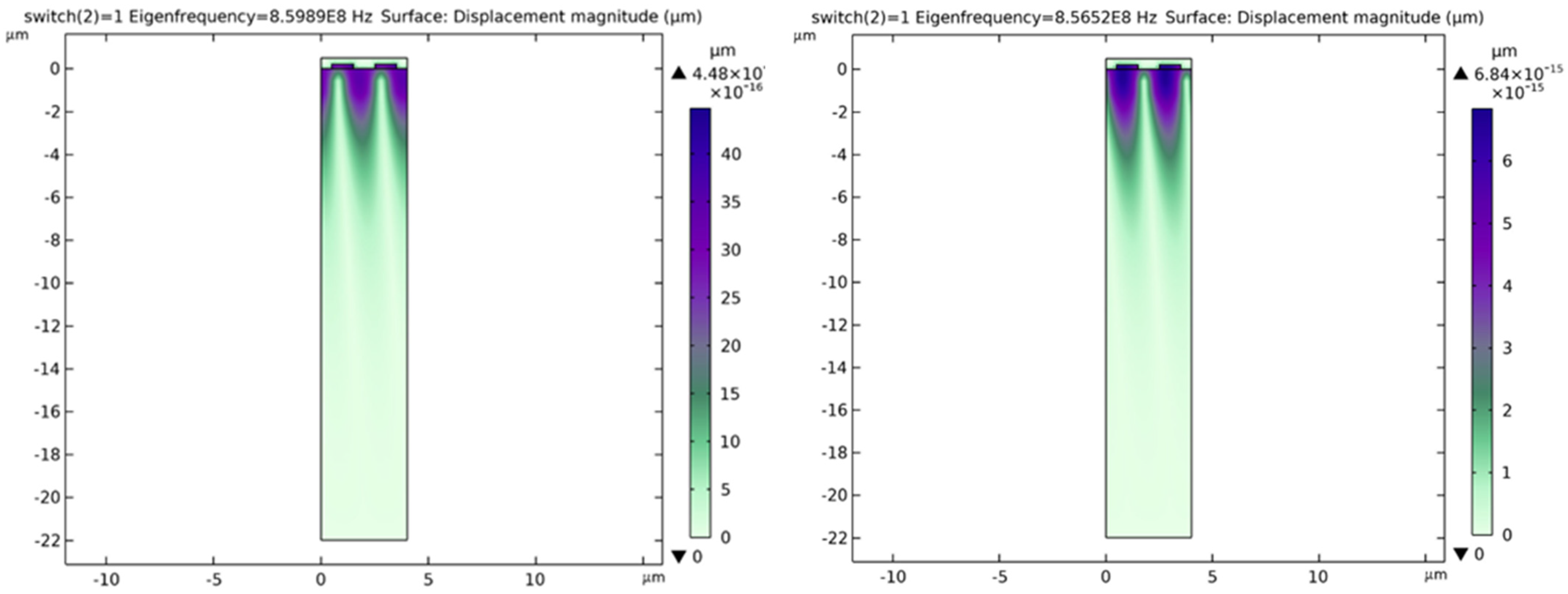
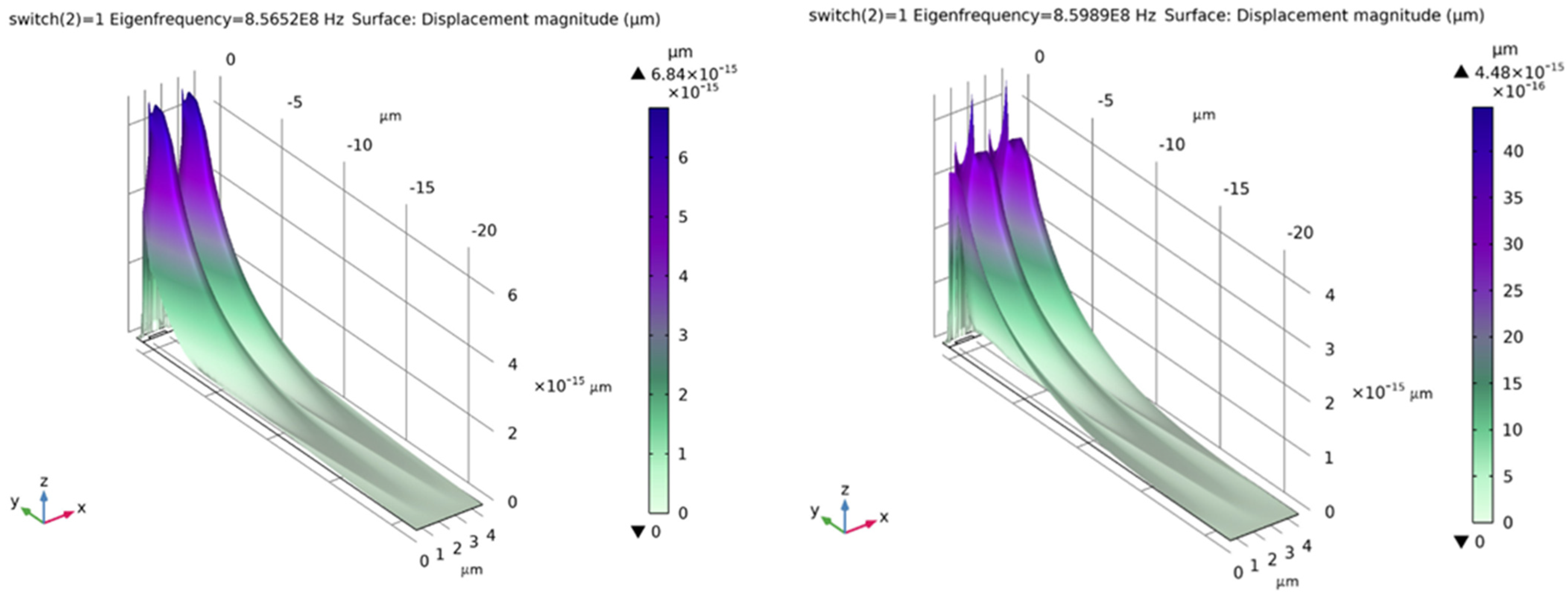
- Case 1: switch = 0: no adsorbed microbes on the chitosan film
- Case 2: switch = 1: presence of adsorbed microbes on the chitosan film
4. Conclusions: Advancing SAW Sensor Simulation and Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dillon, C.F.; Dillon, M.B. Multi-Scale Airborne Infectious Disease Transmission. Appl. Env. Environ. Microbiol. 2021, 87, e02314-20. [Google Scholar] [CrossRef]
- Ma, J.; Du, M.; Wang, C.; Xie, X.; Wang, H.; Zhang, Q. Advances in airborne microorganisms detection using biosensors: A critical review. Front. Environ. Sci. Eng. 2021, 15, 47. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, N.; Jolly, P.; Formisano, N.; Estrela, P. Introduction to biosensors. Essays Biochem. 2016, 60, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Sharma, A.; Ahmed, A.; Sundramoorthy, A.K.; Furukawa, H.; Arya, S.; Khosla, A. Recent Advances in Electrochemical Biosensors: Applications, Challenges, and Future Scope. Biosensors 2021, 11, 336. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, R.; Lee, N.Y. Recent advances in airborne pathogen detection using optical and electrochemical biosensors. Anal. Chim. Acta 2022, 1234, 340297. [Google Scholar] [CrossRef] [PubMed]
- Banks, J.M.; Capistrano, K.; Thakkar, P.; Ranade, H.; Soni, V.; Datta, M.; Naqvi, A.R. Chapter 3-Current molecular diagnostics assays for SARS-CoV-2 and emerging variants. In Methods in Microbiology; Pavia, C.S., Gurtler, V., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 50, pp. 83–121. ISSN 0580-9517. ISBN 9780323850612. [Google Scholar] [CrossRef]
- Ramanathan, K.; Rank, M.; Svitel, J.; Dzgoev, A.; Danielsson, B. The development and applications of thermal biosensors for bioprocess monitoring. Trends Biotechnol. 1999, 17, 499–505. [Google Scholar] [CrossRef] [PubMed]
- Pohanka, M. Overview of Piezoelectric Biosensors, Immunosensors and DNA Sensors and Their Applications. Materials 2018, 11, 448. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, S.J. Amperometric Biosensors. In Encyclopedia of Biophysics; Roberts, G.C.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Yunus, S.; Jonas, A.M.; Lakard, B. Potentiometric Biosensors. In Encyclopedia of Biophysics; Roberts, G.C.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Dzyadevych, S.; Jaffrezic-Renault, N. 6-Conductometric biosensors. In Biological Identification; Schaudies, R.P., Ed.; Woodhead Publishing: Sawston, UK, 2014; pp. 153–193. ISBN 9780857095015. [Google Scholar] [CrossRef]
- Naresh, V.; Lee, N. A Review on Biosensors and Recent Development of Nanostructured Materials-Enabled Biosensors. Sensors 2021, 21, 1109. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.; Hu, J.; Lu, F. Aptamers used for biosensors and targeted therapy. Biomed. Pharmacother. Biomed. Pharmacother. 2020, 132, 110902. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Das, P.K.; Bhethanabotla, V.R. Surface acoustic waves in biosensing applications. Sens. Actuators Rep. 2021, 3, 100041. [Google Scholar] [CrossRef]
- Du, J.; Harding, G.L.; Ogilvy, J.A.; Dencher, P.R.; Lake, M. A study of Love-wave acoustic sensors. Sens. Actuators A Phys. 1996, 56, 211–219. [Google Scholar] [CrossRef]
- Rocha-Gaso, M.I.; March-Iborra, C.; Montoya-Baides, Á.; Arnau-Vives, A. Surface Generated Acoustic Wave Biosensors for the Detection of Pathogens: A Review. Sensors 2009, 9, 5740–5769. [Google Scholar] [CrossRef] [PubMed]
- Pepper, I.L.; Gerba, C.P. Aeromicrobiology. In Environmental Microbiology; Academic Press: Cambridge, MA, USA, 2015; pp. 89–110. [Google Scholar] [CrossRef]
- Dulbecco, D.; Ginsberg, E. Bacterial Physiology: Microbiology, 2nd ed.; Harper and Row: MD, New York, USA, 1973; pp. 96–97. [Google Scholar]
- Ardean, C.; Davidescu, C.M.; Nemeş, N.S.; Negrea, A.; Ciopec, M.; Duteanu, N.; Negrea, P.; Duda-Seiman, D.; Musta, V. Factors Influencing the Antibacterial Activity of Chitosan and Chitosan Modified by Functionalization. Int. J. Mol. Sci. 2021, 22, 7449. [Google Scholar] [CrossRef] [PubMed]
- Kravanja, G.; Primožič, M.; Knez, Ž.; Leitgeb, M. Chitosan-based (Nano)materials for Novel Biomedical Applications. Molecules 2019, 24, 1960. [Google Scholar] [CrossRef] [PubMed]
- Mushi, N.E.; Utsel, S.; Berglund, L.A. Nanostructured biocomposite films of high toughness based on native chitin nanofibers and chitosan. Front. Chem. 2014, 2, 99. [Google Scholar] [CrossRef] [PubMed]
- Le, H.R.; Qu, S.; Mackay, R.E.; Rothwell, R. Fabrication and mechanical properties of chitosan composite membrane containing hydroxyapatite particles. J. Adv. Ceram. 2012, 1, 66–71. [Google Scholar] [CrossRef]
- Aryaei, A.; Jayatissa, A.H.; Jayasuriya, A.C. Nano and micro mechanical properties of uncross-linked and cross-linked chitosan films. J. Mech. Behav. Biomed. Mater. 2012, 5, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Lima, C.G.A.; De Oliveira, R.S.; Figueiró, S.D.; Wehmann, C.F.; Góes, J.C.; Sombra, A.S.B. DC conductivity and dielectric permittivity of collagen–chitosan films. Mater. Chem. Phys. 2006, 99, 284–288. [Google Scholar] [CrossRef]
- Available online: https://www.comsol.com/model/surface-acoustic-wave-gas-sensor-2129 (accessed on 21 July 2023).
- Mamishev, A.V.; Sundara-Rajan, K.; Yang, F.; Du, Y.; Zahn, M. Interdigital sensors and transducers. Proc. IEEE 2004, 92, 808–845. [Google Scholar] [CrossRef]
- Gregersen, E. Stoke’s Law. Encyclopedia Britannica. Available online: https://www.britannica.com/science/Stokess-law (accessed on 9 April 2021).
- Subhasish, D.; Zeeshan, A.S.; Ellora, P. Terminal fall velocity: The legacy of Stokes from the perspective of fluvial hydraulics. Proc. R. Soc. A 2019, 475, 20190277. [Google Scholar]

| Ref. | Properties | Values |
|---|---|---|
| [21] | Density | 1.425 g/cm3 |
| [22] | Young’s Modulus (cross-linked) | 7.06 MPa |
| [23] | Poisson’s Ratio | 1.3 |
| [24] | Relative Permittivity (1 GHz) | 2.71 |
| Name | Expression | Value | Description |
|---|---|---|---|
| A | 31.4 cm2 | 0.00314 m2 | Cross-sectional area of volume of air |
| D | 0.1 µm | 1 × 10−7 m | Diameter of microbe |
| V | 628 cm3 | 6.28 × 10−4 m3 | Volume of air |
| e_chsan | 0.007 GPa | 7 × 106 Pa | Young’s modulus of chitosan |
| eps_chsan | 2.91 | 2.91 | Relative permittivity of chitosan [850 MHz] |
| nu_chsan | 1.3 | 1.3 | Poisson’s Ratio of chitosan |
| t_chsan | 0.5 µm | 5 × 10−7 m | Chitosan thickness |
| g | 9.81 m/s2 | 9.81 m/s2 | Acceleration due to gravity |
| 1.849 × 10−5 µ | 3.0703 × 10−32 kg | Dynamic Viscosity of air (25 °C) | |
| 1.83 × 10−4 poise | 1.83 × 10−5 kg/(m·s) | Density of air through which particle is falling | |
| 1.91 fg/pl | 0.00191 kg/m3 | Density of microbe | |
| 1.425 g/cm3 | 1425 kg/m3 | Density of chitosan | |
| Vs | m/s | 3.3579 × 1016 | Velocity of fall of microbes onto the chitosan layer |
| C | Vs × A/V microbes/m3 | 1.6789 × 1017 | Concentration of microbe in chitosan (microbes/m3) |
| switch | 0, 1 | 1 | Switch for adding microbe density |
| + switch × C microbes/m3 | 1425 | Adsorption of microbes in chitosan | |
| height | 23 µm | 2.3 × 10−5 m | Height of unit cell |
| width | 4 µm | 4 × 10−6 m | Width of unit cell |
| vR | 3488 m/s | 3488 m/s | Rayleigh wave velocity |
| f0 | vR/width | 8.72 × 108 1/s | Estimated SAW frequency |
| No. of Microbes/Density | Eigen Frequency (Hz) | Switch = 0, Frequency (Hz) | Switch = 1, Frequency (Hz) |
|---|---|---|---|
| 1 | 8.565194884964089 × 108 | 8.565194884964089 × 108 | 8.565194884964098 × 108 |
| 8.598910950429227 × 108 | 8.598910950429227 × 108 | 8.598910950429237 × 108 | |
| 10 | 8.565194884964098 × 108 | 8.565194884964098 × 108 | 8.565194884964089 × 108 |
| 8.598910950429237 × 108 | 8.598910950429237 × 108 | 8.598910950429227 × 108 | |
| 100 | 8.565194884964089 × 108 | 8.565194884964089 × 108 | 8.565194884964089 × 108 |
| 8.598910950429229 × 108 | 8.598910950429229 × 108 | 8.598910950429227 × 108 | |
| 1000 | 8.565194884964098 × 108 | 8.565194884964098 × 108 | 8.565194884964089 × 108 |
| 8.598910950429237 × 108 | 8.598910950429237 × 108 | 8.598910950429229 × 108 | |
| 10,000 | 8.565194884964098 × 108 | 8.565194884964098 × 108 | 8.565194884964089 × 108 |
| 8.598910950429237 × 108 | 8.598910950429237 × 108 | 8.598910950429229 × 108 | |
| 100,000 | 8.565194884964089 × 108 | 8.565194884964089 × 108 | 8.565194884964089 × 108 |
| 8.598910950429229 × 108 | 8.598910950429229 × 108 | 8.598910950429229 × 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varughese, S.P.; Raj, S.M.G.; Joel, T.J.; Gautam, S. Detecting Airborne Pathogens: A Computational Approach Utilizing Surface Acoustic Wave Sensors for Microorganism Detection. Technologies 2023, 11, 135. https://doi.org/10.3390/technologies11050135
Varughese SP, Raj SMG, Joel TJ, Gautam S. Detecting Airborne Pathogens: A Computational Approach Utilizing Surface Acoustic Wave Sensors for Microorganism Detection. Technologies. 2023; 11(5):135. https://doi.org/10.3390/technologies11050135
Chicago/Turabian StyleVarughese, Sharon P., S. Merlin Gilbert Raj, T. Jesse Joel, and Sneha Gautam. 2023. "Detecting Airborne Pathogens: A Computational Approach Utilizing Surface Acoustic Wave Sensors for Microorganism Detection" Technologies 11, no. 5: 135. https://doi.org/10.3390/technologies11050135
APA StyleVarughese, S. P., Raj, S. M. G., Joel, T. J., & Gautam, S. (2023). Detecting Airborne Pathogens: A Computational Approach Utilizing Surface Acoustic Wave Sensors for Microorganism Detection. Technologies, 11(5), 135. https://doi.org/10.3390/technologies11050135






