Enhanced Energy Transfer Efficiency for IoT-Enabled Cyber-Physical Systems in 6G Edge Networks with WPT-MIMO-NOMA
Abstract
1. Introduction
- This work proposes a UE–BS connection model to assign each UE to a single BS for WPT in order to mitigate CCI during the wireless charging phase;
- This study developed an energy-efficient resource allocation scheme that integrates the UE–BS connection approach with joint optimization of transmit power, time allocation, antenna selection, and subcarrier assignment;
- This work derived a non-convex mixed integer optimization problem for EE maximization and applied some techniques such as relaxation and approximation to transform it into a more tractable form;
- The study further applied the Alternating Direction Method of Multipliers (ADMM) to efficiently solve the resource allocation problem in a distributed manner.
2. Related Works
2.1. Massive MIMO–NOMA Networks
2.2. Wireless Power Transfer
- Directional beamforming techniques like maximum ratio transmission focus the radiated wireless energy toward the energy harvester’s location;
- Waveform and transmit optimization to maximize the DC power extracted by the energy harvester circuitry;
- Sensitive antenna designs and low-power electronics to improve the RF-to-DC conversion efficiency.
2.3. Co-Channel Interference in WPT
3. Proposed UE–BS Connection Model
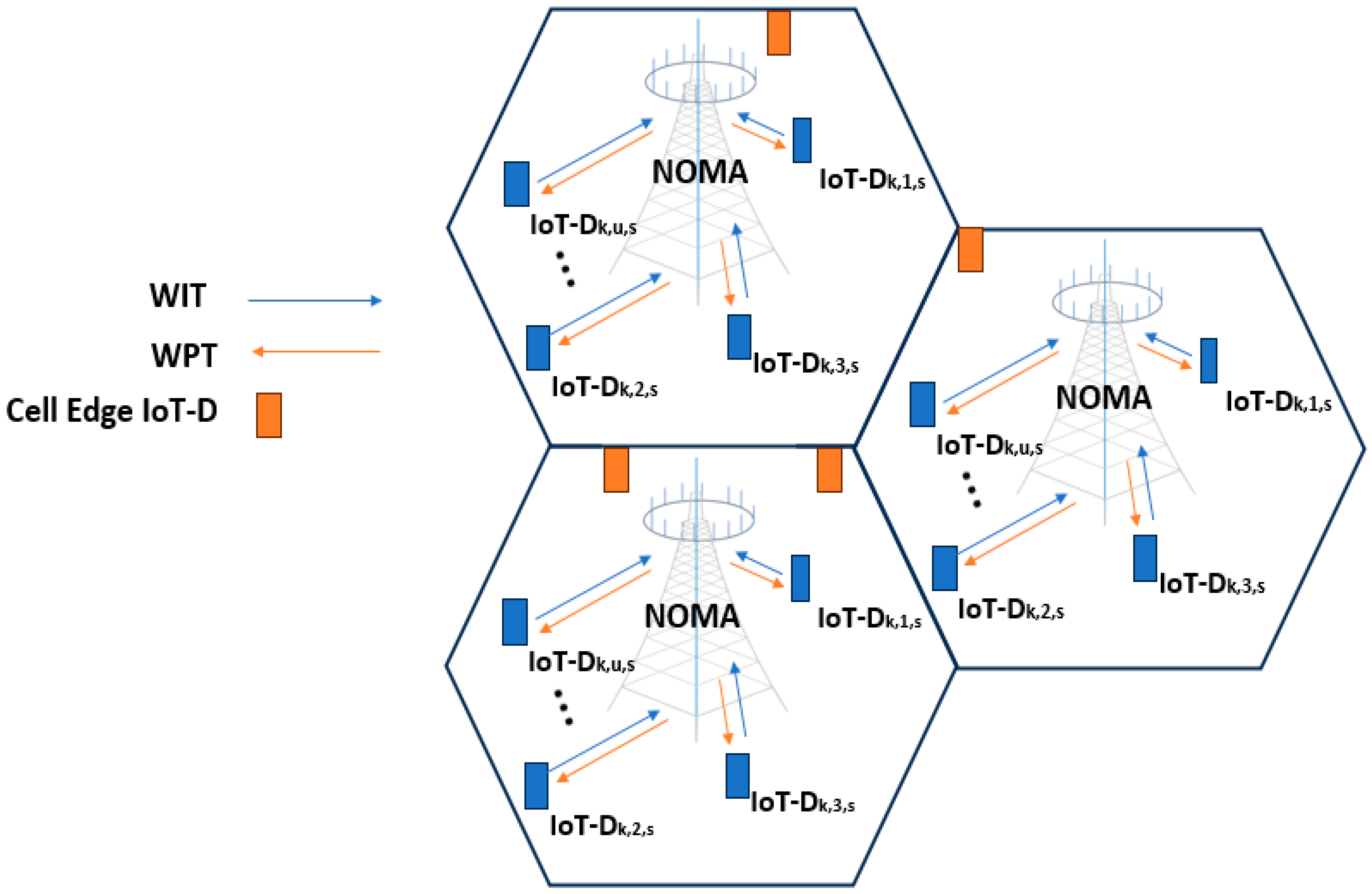
3.1. System Model
3.2. UE–BS Connection Matrix
| Algorithm 1: UE–BS Connection Model |
| 1: Input: K, U, M, h, and N 2: Output: x 3: Initialize UE–BS connection matrix x to zeros 4: Estimate channel gains hk,u,s 5: Select optimal antennas Nk,u,s based on channel gains 6: Initialize antenna connection matrix Zk,u,s 7: for u = 1 to U do 8: for k = 1 to K do 9: for m = 1 to M do 10: if Nk,u,s = m then 11: Zk,u,s = 1 12: else 13: Zk,u,s = 0 14: end if 15: end for 16: end for 17: end for 18: Establish UE–BS connections: 19: for u = 1 to U do 20: k* = arg maxk(Zu,k,1:M) 21: xu,k* = 1 22: end for 23: Limit each UE to 1 BS: 24: for u = 1 to U do 25: if (xu,1:K) > 1 then 26: k = arg maxk(Zu,k,1:M) 27: xu,k = 1 28: xu,1:K\k = 0 29: end if 30: end for 31: return x |
4. Energy-Efficient Resource Allocation Scheme
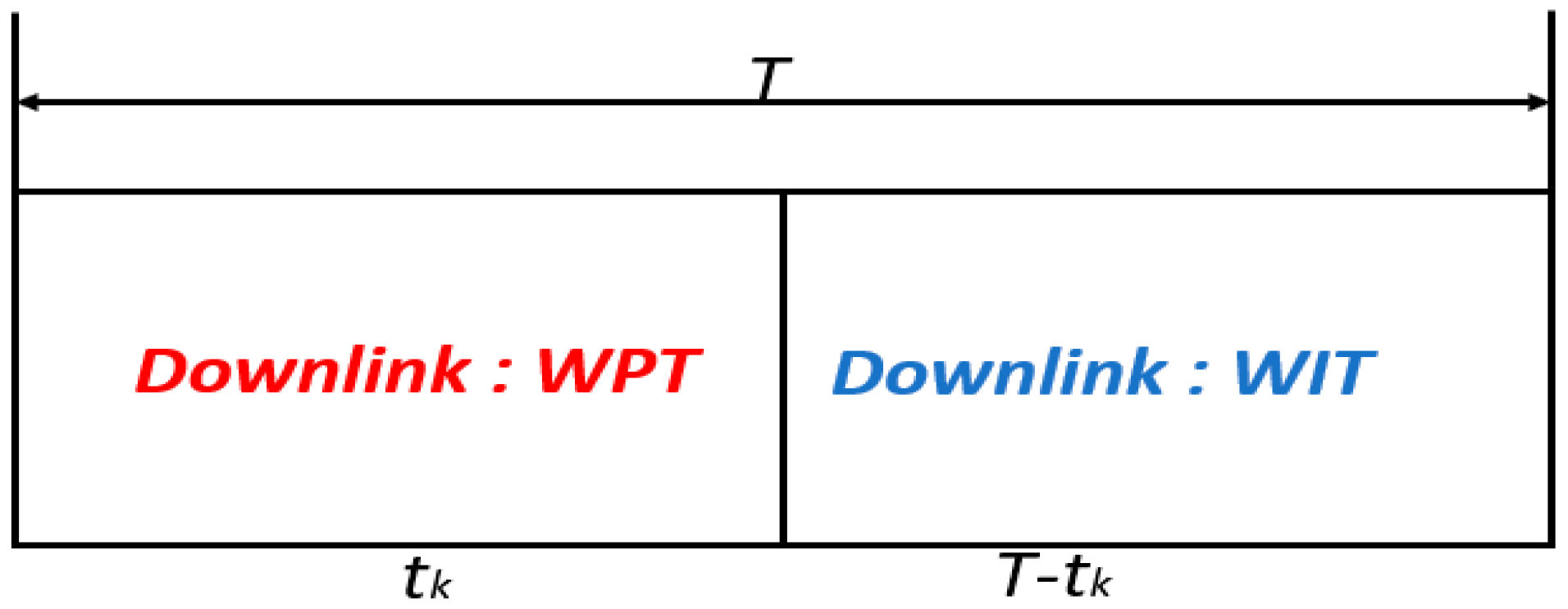
4.1. Problem Formulation
4.2. Non-Linear Optimization
| Algorithm 2: Energy Efficient Resource Allocation Scheme. |
| Input: K, U, M, S, h, X, Pmax, Pbs, Puser, T, Rmin, Pbs,max, Puser,max, αk,u, and ηEE Output: x, P, t, N, and C 1. Initialize x, P, t, N, and C 2. Calculate channel rates Rk,u,s based on h, P, and N 3. while not converged do 4. Update X to optimize UE–BS connections 5. Update P to maximize EE under Pmax constraint 6. Update t to allocate WPT and WIT time 7. Update N for optimal antenna selection 8. Update C for subcarrier assignment 9. Calculate UE rates Rk,u,s based on current P, t, N, and C 10. end while return x, P, t, N, and C |
4.3. Distributed ADMM Approach
| Algorithm 3: Energy-Efficient Resource Allocation with Distributed ADMM |
| 1: Objective: Maximize system energy efficiency (EE) |
| 2: Input: |
| 3: Local CSI: |
| 4: hk—Local channel gain matrix at BS k |
| 5: Nk—Local antenna selection at BS k |
| 6: Rk—Local UE rate matrix at BS k |
| 7: Resource constraints: |
| 8: Pmax, tmin, tmax, Rmin, and Cmax—Local max connections per subcarrier |
| 9: 1. Initialization: |
| 10: Initialize local copies of optimization variables at each BS k and local dual variables |
| 11: xk = 0 |
| 12: Pk = Pmax/K |
| 13: tk = T/2 |
| 14: Nk = M/K |
| 15: Ck = S/K |
| 16: // For consensus on global UE–BS connections x |
| 17: // For consensus on global power allocation P |
| 18: // For consensus on global energy efficiency EE |
| 19: 2. Repeat until convergence: |
| 20: 3. Each BS k updates local variables to maximize local EE |
| 21: xk = arg max EE(xk, Pk, tk, Nk, and Ck) s.t. local constraints |
| 22: Pk = arg max EE(xk, Pk, tk, Nk, and Ck) |
| 23: tk = arg max EE(xk, Pk, tk, Nk, and Ck) |
| 24: Nk = arg max EE(xk, Pk, tk, Nk, and Ck) |
| 25: Ck = arg max EE(xk, Pk, tk, Nk, and Ck) |
| 26: 4. Update local dual variables |
| 27: = + ρΔ |
| 28: = + ρΔ |
| 29: + ρΔ |
| 30: 5. Exchange updates with neighbors |
| 31: Share xk, Pk, , and |
| 32: 6. Master node reaches consensus |
| 33: |
| 34: |
| 35: 7. Broadcast consensus to BSs |
| 36: Send xk, Pk to all BSs |
| 37: 8. Until convergence criteria met |
| 38: return Optimized x, P, t, N, and C |
Overview of the Computational Complexity of Distributed ADMM
- Mitigates co-channel interference during the wireless charging phase;
- Introduces an energy-efficient resource allocation scheme;
- Integrates the UE–BS connection model for joint optimization;
- Addresses additional constraints related to UE–BS connections (C7).
5. Performance Evaluation
5.1. Simulation Setup
5.2. Results and Discussion
- Impact of UE–BS connection on system EE;
- Performance under imperfect CSI;
- Trends with the number of BS antennas;
- Convergence of the distributed ADMM algorithm.
5.2.1. UE–BS Connection and EE
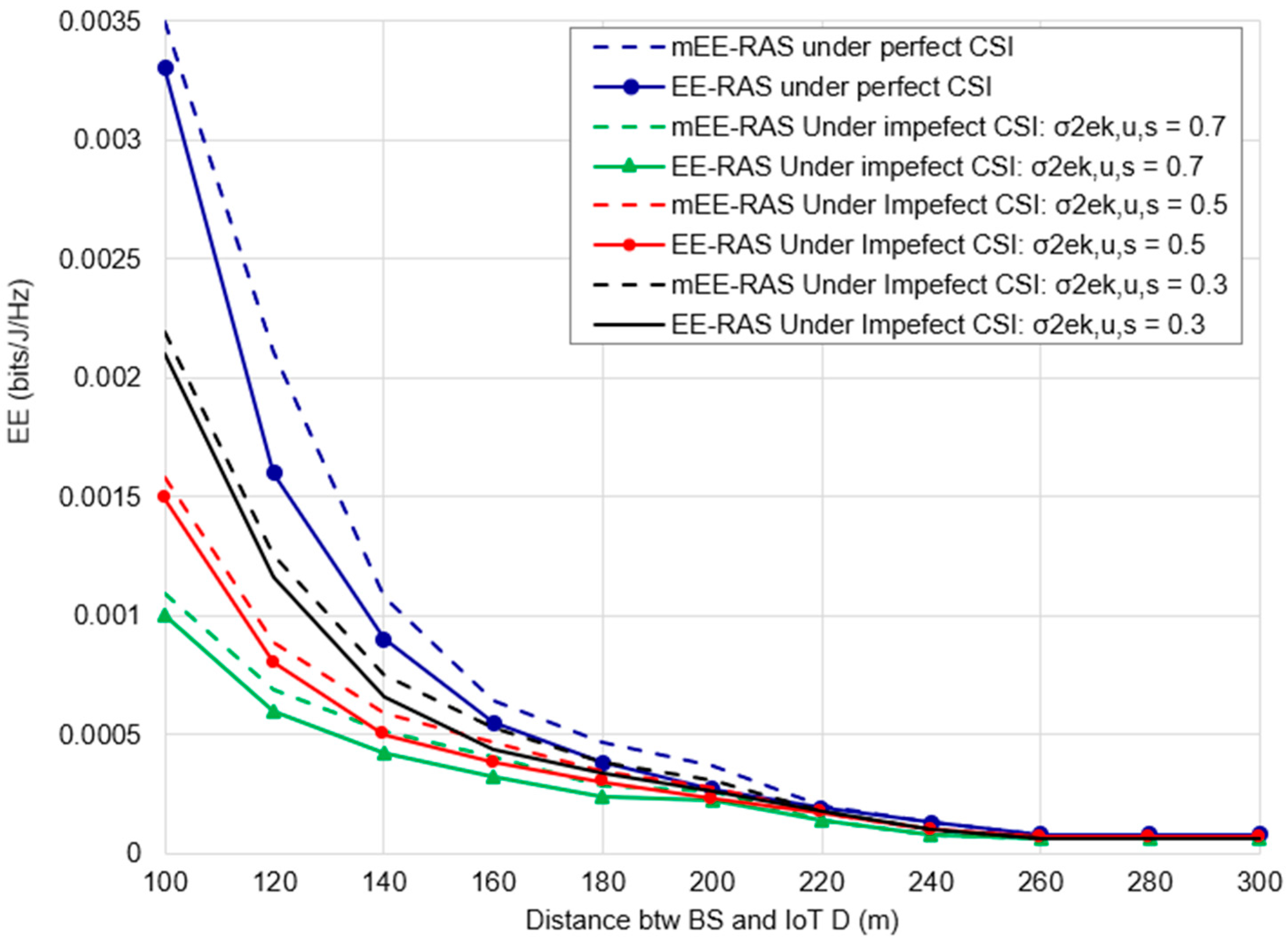
5.2.2. Imperfect CSI Impact on EE
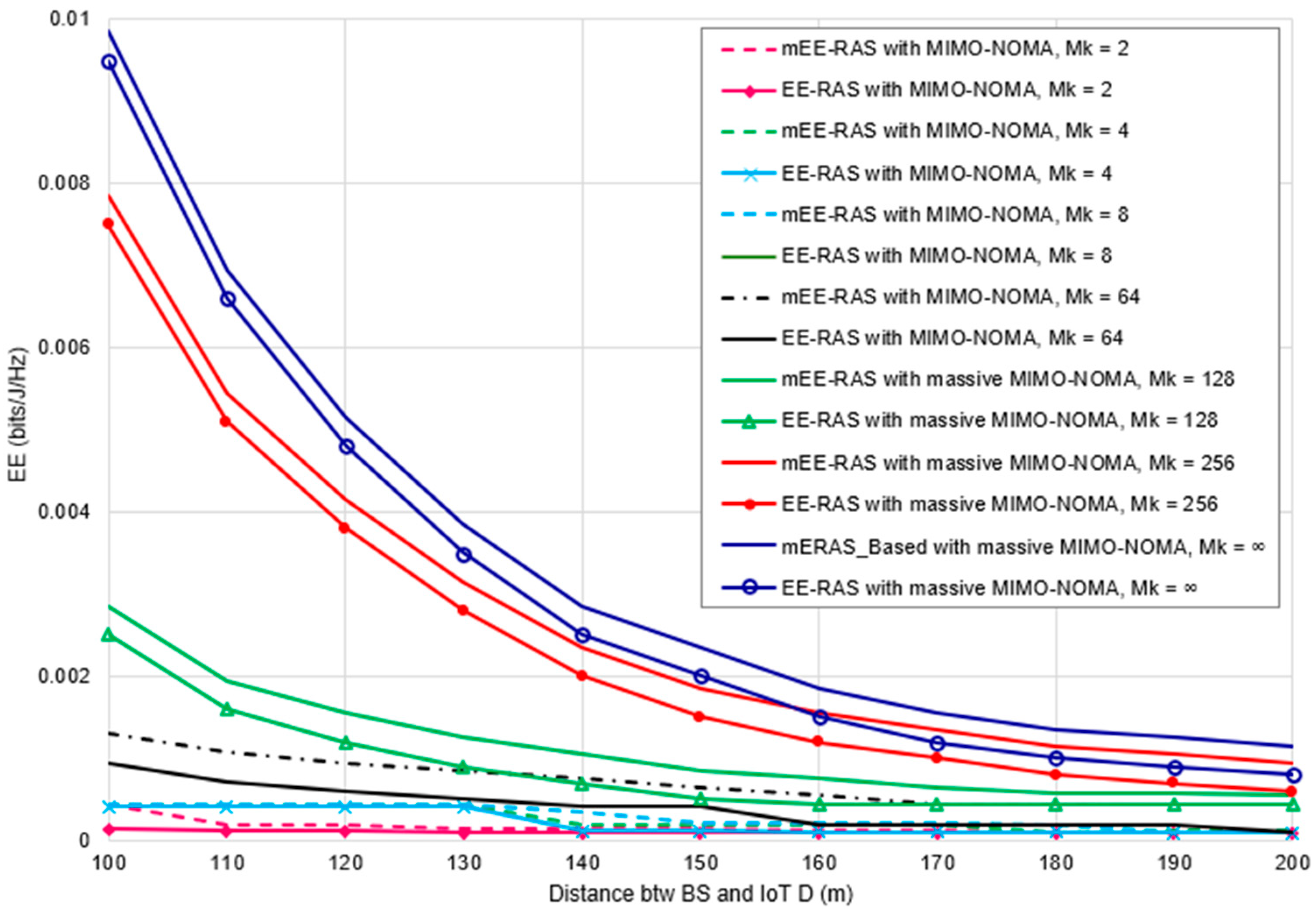
5.2.3. EE vs. Number of Antennas (MIMO and Massive MIMO)
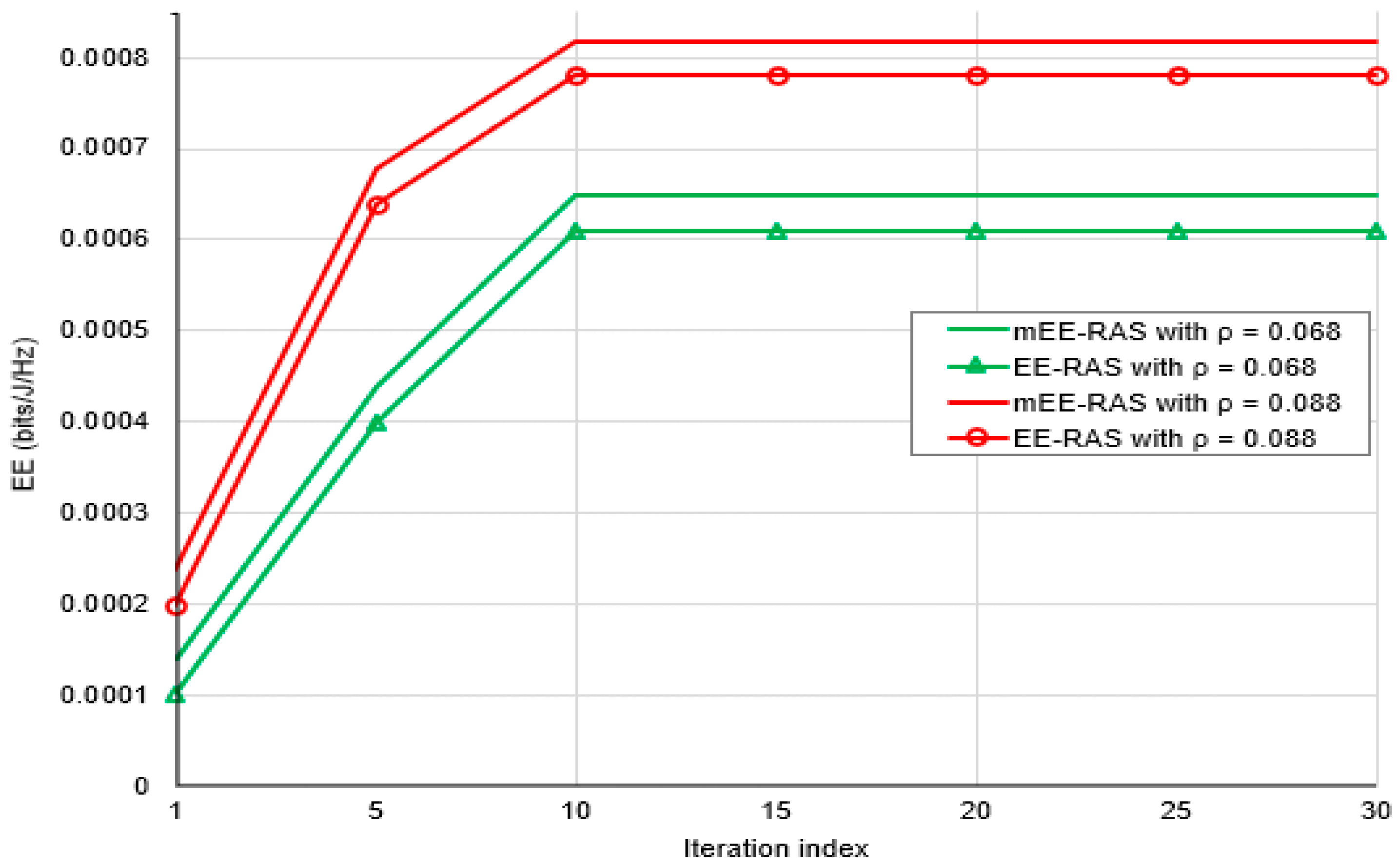
5.2.4. Convergence Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gandotra, P.; Jha, R.K. A survey on green communication and security challenges in 5G wireless communication networks. J. Netw. Comput. Appl. 2017, 96, 39–61. [Google Scholar] [CrossRef]
- Shahraki, A.; Abbasi, M.; Piran, M.J.; Taherkordi, A. A comprehensive survey on 6G networks: Applications, core services, enabling technologies, and future challenges. arXiv 2021, arXiv:2101.12475. [Google Scholar]
- Patzold, M. Countdown for the full-scale development of 5G new radio [mobile radio]. IEEE Veh. Technol. Mag. 2018, 13, 7–13. [Google Scholar] [CrossRef]
- Hao, W.; Chu, Z.; Zhou, F.; Yang, S.; Sun, G.; Wong, K.-K. Green communication for NOMA-based CRAN. IEEE Internet Things J. 2018, 6, 666–678. [Google Scholar] [CrossRef]
- Mai, T.C.; Ngo, H.Q.; Duong, T.Q. Uplink spectral efficiency of cell-free massive MIMO with multi-antenna users. In Proceedings of the 2019 3rd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Hanoi, Vietnam, 21–22 March 2019; pp. 126–129. [Google Scholar]
- Ding, Z.; Fan, P.; Poor, H.V. Impact of user pairing on 5G Non-Orthogonal Multiple Access. arXiv 2014, arXiv:1412.2799. [Google Scholar]
- Zewde, T.A.; Gursoy, M.C. NOMA-based energy-efficient wireless powered communications. IEEE Trans. Green Commun. Netw. 2018, 2, 679–692. [Google Scholar] [CrossRef]
- Chen, L.; Hu, B.; Xu, G.; Chen, S. Energy-efficient power allocation and splitting for mmWave beamspace MIMO-NOMA with SWIPT. IEEE Sens. J. 2021, 21, 16381–16394. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, W.; Pan, Y.; Pan, C.; Chen, M. Energy-efficient resource allocation in machine-to-machine communications with multiple access and energy harvesting for IoT. IEEE Internet Things J. 2018, 5, 229–245. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Z.; Lv, T.; Ni, W. Energy-efficient resource allocation in massive MIMO-NOMA networks with wireless power transfer: A distributed ADMM approach. IEEE Internet Things J. 2021, 8, 14232–14247. [Google Scholar] [CrossRef]
- Guo, N.; Yuan, X.; Hu, Y.; Schmeink, A. Fairness-aware resource allocation in multi-source WPCN in the finite blocklength regime. IEEE Access 2023, 11, 32348–32364. [Google Scholar] [CrossRef]
- Li, J.; Jiang, H. Research on the SWIPT system throughput based on interference signal energy collecting. KSII Trans. Internet Inf. Syst. 2023, 17, 2170. [Google Scholar]
- Le, A.T.; Tran, D.H.; Le, C.B.; Tin, P.T.; Nguyen, T.N.; Ding, Z.; Poor, H.V.; Voznak, M. Power beacon and NOMA-assisted cooperative IoT networks with co-channel interference: Performance analysis and deep learning evaluation. IEEE Trans. Mob. Comput. 2023, 23, 7270–7283. [Google Scholar] [CrossRef]
- Wang, Y.; Li, P.; Tan, D.; Zhang, J.; Duan, X.; Chen, Y.; Zhao, D. A game-based computation offloading method in vehicular multiaccess edge computing networks. IEEE Internet Things J. 2020, 7, 4987–4996. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Zhang, M.; Li, Y.; Wang, R.; He, Y. A game-based computing resource allocation scheme of edge server in vehicular edge computing networks considering diverse task offloading modes. Sensors 2023, 24, 69. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Yan, M.; Dai, L.; Yang, P. Joint communication and computation resource scheduling of a solar-powered UAV-assisted communication system for platooning vehicles. In Proceedings of the 2023 9th International Conference on Mechanical and Electronics Engineering (ICMEE), Xi’an, China, 17–19 November 2023; pp. 49–54. [Google Scholar]
- Gupta, S.; Patel, N.; Kumar, A.; Jain, N.K.; Dass, P.; Hegde, R.; Rajaram, A. Intelligent resource optimization for scalable and energy-efficient heterogeneous IoT devices. Multimed. Tools Appl. 2024, 24, 1–25. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Ning, Z.; Song, Q.; Guo, L.; Guo, S.; Obaidat, M.S. Wireless powered mobile edge computing networks: A survey. ACM Comput. Surv. 2023, 55, 1–37. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Cai, Z.; Li, Y.; Gao, H. Computation scheduling for wireless powered mobile edge computing networks. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 596–605. [Google Scholar]
- Mustafa, E.; Shuja, J.; uz Zaman, S.K.; Jehangiri, A.I.; Din, S.; Rehman, F.; Mustafa, S.; Maqsood, T.; Khan, A.N. Joint wireless power transfer and task offloading in mobile edge computing: A survey. Clust. Comput. 2022, 25, 2429–2448. [Google Scholar] [CrossRef]
- Ji, L.; Guo, S. Energy-efficient cooperative resource allocation in wireless powered mobile edge computing. IEEE Internet Things J. 2018, 6, 4744–4754. [Google Scholar] [CrossRef]
- Barman, S.; Reza, A.W.; Kumar, N.; Karim, M.E.; Munir, A.B. Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. Renew. Sustain. Energy Rev. 2015, 51, 1525–1552. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Dai, L.; Wang, B.; Peng, M.; Chen, S. Hybrid precoding-based millimeter-wave massive MIMO-NOMA with simultaneous wireless information and power transfer. IEEE Trans. Commun. 2019, 37, 131–141. [Google Scholar] [CrossRef]
- Na, Z.; Zhang, M.; Jia, M.; Xiong, M.; Gao, Z. Joint uplink and downlink resource allocation for the Internet of Things. IEEE Access 2019, 7, 15758–15766. [Google Scholar] [CrossRef]
- Chen, X.; Ng, D.W.K.; Yu, W.; Larsson, E.G.; Al-dhahir, N.; Schober, R. Massive access for 5G and beyond. IEEE J. Sel. Areas Commun. 2021, 39, 615–637. [Google Scholar] [CrossRef]
- Prasad, K.N.R.S.V.; Hossain, E.; Bhargava, V.K. Energy efficiency in massive MIMO-based 5G networks: Opportunities and challenges. IEEE Wirel. Commun. 2017, 24, 86–94. [Google Scholar] [CrossRef]
- Zhong, C.; Suraweera, H.A.; Zheng, G.; Krikidis, I.; Zhang, Z. Improving the throughput of wireless powered dual-hop systems with full duplex relaying. IEEE Int. Conf. Commun. 2015, 2015, 4253–4258. [Google Scholar] [CrossRef]
- Ponnimbaduge Perera, T.D.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous wireless information and power transfer (SWIPT): Recent advances and future challenges. IEEE Commun. Surv. Tutor. 2018, 20, 264–302. [Google Scholar] [CrossRef]
- Shen, S.; Clerckx, B. Joint waveform and beamforming optimization for MIMO wireless power transfer. IEEE Trans. Commun. 2021, 69, 5441–5455. [Google Scholar] [CrossRef]
- Bi, S.; Zeng, Y.; Zhang, R. Wireless powered communication networks: An overview. IEEE Wirel. Commun. 2016, 23, 10–18. [Google Scholar] [CrossRef]
- Xu, B.; Chen, Y.; Carrión, J.R.; Zhang, T. Resource allocation in energy-cooperation enabled two-tier NOMA HetNets toward green 5G. IEEE J. Sel. Areas Commun. 2017, 35, 2758–2770. [Google Scholar] [CrossRef]
- Chang, Z.; Wang, Z.; Guo, X.; Yang, C.; Han, Z.; Ristaniemi, T. Distributed resource allocation for energy efficiency in OFDMA multicell networks with wireless power transfer. IEEE J. Sel. Areas Commun. 2019, 37, 345–356. [Google Scholar] [CrossRef]
- Lee, K.; Hong, J.P. Energy-efficient resource allocation for simultaneous information and energy transfer with imperfect channel estimation. IEEE Trans. Veh. Technol. 2016, 65, 2775–2780. [Google Scholar] [CrossRef]
- Wei, E.; Ozdaglar, A. Distributed alternating direction method of multipliers. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5445–5450. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Li, H.; Song, L.; Debbah, M. Energy efficiency of large-scale multiple antenna systems with transmit antenna selection. IEEE Trans. Commun. 2014, 62, 638–647. [Google Scholar] [CrossRef]
- Okafor, K.C.; Adebisi, B.; Akande, A.O.; Anoh, K. Agile gravitational search algorithm for cyber-physical path-loss modelling in 5G connected autonomous vehicular network. Veh. Commun. 2024, 45, 100685. [Google Scholar] [CrossRef]
- Okafor, K.C. Bamidele Adebisi, Kelvin Anoh Lightweight multi-hop routing protocol for resource optimisation in edge computing networks. Internet Things 2023, 22, 100758. [Google Scholar] [CrossRef]

| Aspect | EE-RAS Scheme | mEE-RAS Scheme |
|---|---|---|
| Optimization Problem | Resource allocation in NOMA MIMO with WPT | Resource allocation in NOMA MIMO with WPT and UE–BS connection model |
| Constraints | C1–C6 (max power, energy transfer time, power non-negativity, rate, antenna control, and subcarrier allocation) | C1–C7 (max power, energy transfer time, power non-negativity, rate, antenna control, subcarrier allocation, and UE–BS connection) |
| Iterative Algorithm | ADMM (Alternating Direction Method of Multipliers) | D-ADMM (Distributed Alternating Direction Method of Multipliers) |
| Number of Iterations (K) | Problem-specific | Problem-specific |
| Complexity of Solving Subproblems | Problem-specific, may involve matrix operations | Problem-specific, may involve matrix operations |
| Overall Computational Complexity | KComplexity of solving x-subproblem + Complexity of solving z-subproblem) | K(Complexity of solving x-subproblem + complexity of solving z-subproblem) |
| Size of Optimization Variables | ||
| UE–BS Connection Model Integration | Not applicable | Integrated for joint optimization of parameters |
| Joint Optimization of Parameters | Not applicable | Joint optimization of transmit power, time allocation, antenna selection, and subcarrier assignment |
| Co-channel interference Mitigation | Conventional WPT to mitigate co-channel interference during the wireless charging phase | UE–BS connection model used to assign each UE to a single BS for WPT to mitigate co-channel interference during the wireless charging phase |
| Energy-Efficient Resource Allocation | Not applicable | Energy-efficient resource allocation scheme integrated with the UE–BS connection approach |
| Comparative Analysis | Standard resource allocation model with ADMM | Enhanced model with UE–BS connection, joint optimization, interference mitigation, and energy efficiency |
| Advantages of Scenario 2 over Scenario 1 | Mitigates co-channel interference during the wireless charging phase, energy-efficient resource allocation, and joint optimization of multiple parameters | Offers additional benefits of UE–BS connection, interference mitigation, and energy efficiency in resource allocation. |
| Model equation for solving x-problem | ||
| Model equation for solving z-problem |
| S/N | Parameter (unit) | Value |
|---|---|---|
| 1 | Base stations, K | 6 |
| 2 | No of users, U | 15 |
| 3 | Cell radius (m) | 500 |
| 4 | Subcarrier, S | 20–40 |
| 5 | Pbs.max (dBm) | 46 |
| 6 | Puser.max (dBm) | 23 |
| 7 | Rmin (bit/s/Hz) | 0.1 |
| 8 | αk,u | 1/75 |
| 9 | Pmin (mW) | 20.3 |
| 10 | PLNA (mW) | 20 |
| 11 | η | 0.8 |
| 12 | e | 10−7 |
| 13 | B (Hz) | 1 |
| 14 | PDAC (mW) | 10 |
| 15 | PADC (mW) | 10 |
| 16 | Pfilr (mW) | 2.5 |
| 17 | Ptilt (mW) | 2.5 |
| 18 | Psyn (mW) | 50 |
| 19 | PIFA (mW) | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezekiel, A.E.; Okafor, K.C.; Tersoo, S.T.; Alabi, C.A.; Abdulsalam, J.; Imoize, A.L.; Jogunola, O.; Anoh, K. Enhanced Energy Transfer Efficiency for IoT-Enabled Cyber-Physical Systems in 6G Edge Networks with WPT-MIMO-NOMA. Technologies 2024, 12, 119. https://doi.org/10.3390/technologies12080119
Ezekiel AE, Okafor KC, Tersoo ST, Alabi CA, Abdulsalam J, Imoize AL, Jogunola O, Anoh K. Enhanced Energy Transfer Efficiency for IoT-Enabled Cyber-Physical Systems in 6G Edge Networks with WPT-MIMO-NOMA. Technologies. 2024; 12(8):119. https://doi.org/10.3390/technologies12080119
Chicago/Turabian StyleEzekiel, Agbon Ehime, Kennedy Chinedu Okafor, Sena Timothy Tersoo, Christopher Akinyemi Alabi, Jamiu Abdulsalam, Agbotiname Lucky Imoize, Olamide Jogunola, and Kelvin Anoh. 2024. "Enhanced Energy Transfer Efficiency for IoT-Enabled Cyber-Physical Systems in 6G Edge Networks with WPT-MIMO-NOMA" Technologies 12, no. 8: 119. https://doi.org/10.3390/technologies12080119
APA StyleEzekiel, A. E., Okafor, K. C., Tersoo, S. T., Alabi, C. A., Abdulsalam, J., Imoize, A. L., Jogunola, O., & Anoh, K. (2024). Enhanced Energy Transfer Efficiency for IoT-Enabled Cyber-Physical Systems in 6G Edge Networks with WPT-MIMO-NOMA. Technologies, 12(8), 119. https://doi.org/10.3390/technologies12080119











