Experimental Benchmarking of Existing Offline Parameter Estimation Methods for Induction Motor Vector Control
Abstract
1. Introduction
- This paper presents the practical determination of machine parameters of an induction motor (IM) using very good practical testing methods (meeting International Industry Practices like IEEE Standards). The motor used for Testing is a 90 kW (120 HP)/NEMA-B/IM.
- The values of the machine parameters obtained by the industry standard test method followed in the practical physical testing of the selected IM were found to be very near to those obtained in the other methods compared.
- Identification of best-performing method with the lowest error for vector control.
2. Materials and Methods
2.1. The Proposed Method
2.2. Steps of the Proposed Method
- Initial Parameter Estimation:
- The No-Load Test: Measure the stator winding resistance (R1) using a micro-ohm meter. Perform the no-load test by running the motor without any load and recording the voltage and current.
- The Short-Circuit Test: Conduct the short-circuit test by locking the rotor and applying a low voltage to measure the rotor resistance (R2) and leakage reactance (X2).
- Advanced Computational Techniques:
- Develop a spreadsheet program to automate calculations based on the collected test data.
- Simulate the motor using MATLAB to validate the experimental results and refine the parameter estimates.
- Field Validation:
- Compare the estimated parameters with those obtained from established benchmark methods, including IEEE Standard 112-2017.
- Validate the results through field tests on a 90 kW (120 HP) induction motor.
2.3. Description of Methodology
- (a)
- The no-rotor test: The no-rotor test is performed by disconnecting from load and dismantling the motor and measured the stator winding resistance (R1) with the help of a micro-ohm meter. This parameter will be useful in estimating the stator copper loss.
- (b)
- The no-load test: A no-load test is performed by running the motor without any load and measured the voltage and current of the motor. Readings are taken with varying voltage at rated frequency, as per the IEEE 112 guidelines. Auto-transformer of 100 kVA, 0–460 V, 50 Hz is used for this test. The data collected from this test are used to calculate the resistance (Rc) and leakage reactance of core (Xm) of the motor. These data are also used to separate the rotational and iron loss components from no-load loss.
- (c)
- The short-circuit test: A short-circuit or locked-rotor test is performed by locking the rotor. Three phase low voltage at rated frequency is applied to the motor so that the rated current is drawn by it. Later, the short circuit current is normalized to rated voltage with standard formulae. The data collected from this test are used to calculate the rotor resistance (R2) and leakage reactance (X2). After determining X2, the stator leakage reactance can be estimated as per NEMA standards.
- (d)
- The load test: A load test is performed by running the motor under load and measuring the voltage and current of the stator winding. The data collected from this are used to calculate rated current and power factor of the motor under full load conditions. Finally, the results are used to establish the technical specifications of motor as given on its name plate.
- (e)
- Comparison of results by validation: Induction motor parameters are estimated with the popular methods available in various textbooks and research papers. In this process, a spread sheet program is developed. Also, the circle diagram method is used for validation purposes. The proposed experiment work has been simulated using MATLAB (2022a).
2.4. Other Models
2.4.1. The d-q Model
2.4.2. The abc Model
2.5. Novelty of This Study
3. Experimental Setup for Case Study
4. Results and Discussion
4.1. Test Results
4.1.1. DC Resistance of Stator Winding (R1)
4.1.2. The No-Load Test
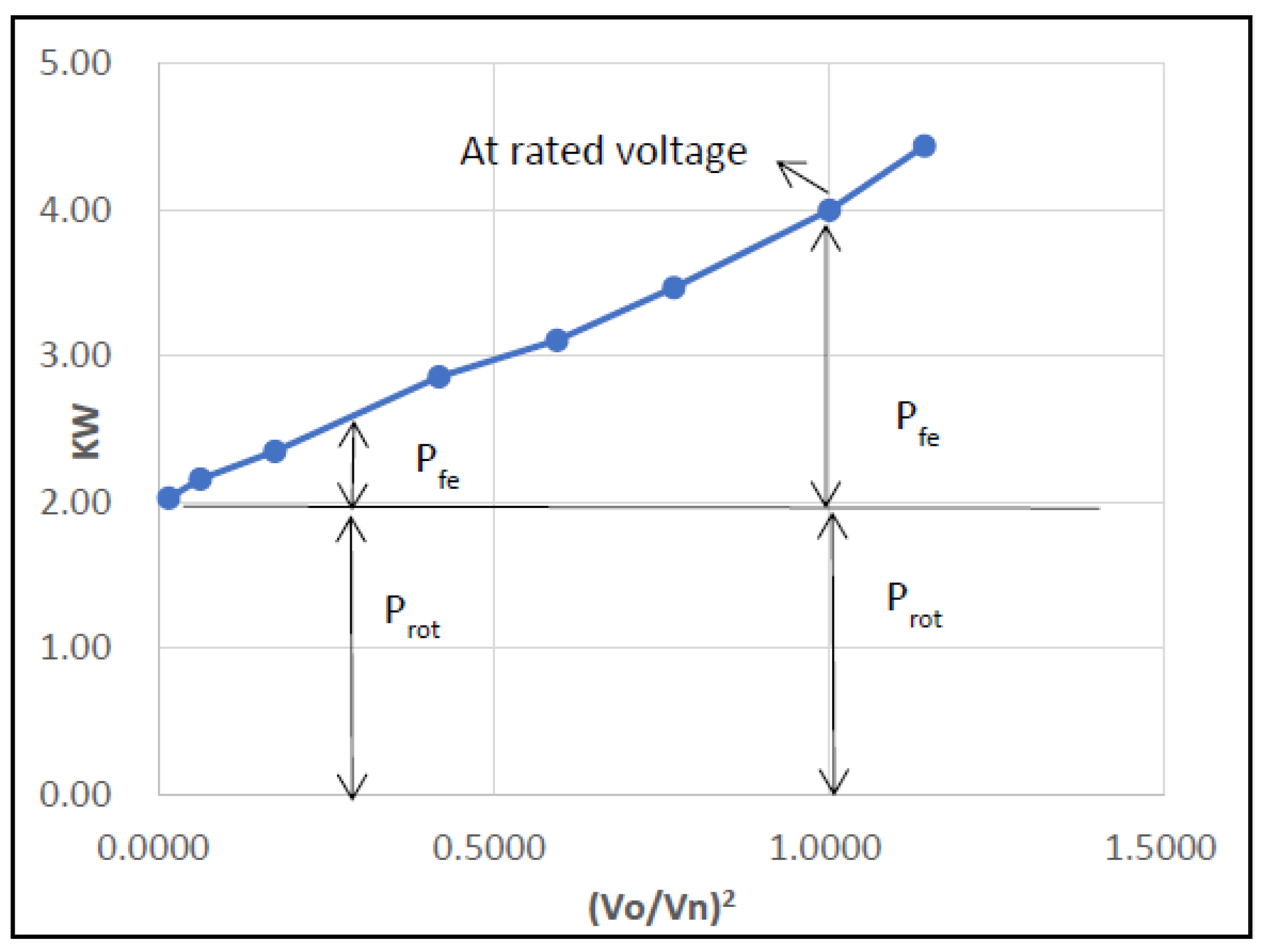
4.1.3. Separation of Core Losses
4.1.4. The Short-Circuit Test
4.1.5. The Load Test
4.2. Comparison with Standard Literature Methods
- In [26] the iron loss component is ignored, and estimates are made for exact equivalent circuit.
- In [1] the iron loss component is ignored, and estimates are made for exact equivalent circuit.
- In [27], the author has made calculation for both the approximate and exact equivalent circuits. However, he has ignored R2 in the L-method.
- In [29], the author has developed, a MATLAB program for parameter estimation. The steps used in code are given here:
- Collection of motor name plate data.
- Estimation of stator current at 50% and 100% loads.
- Estimation of rotor resistance with the help of above information.
- Estimation of core resistance by assuming 50% of No-load loss is iron loss.
- Estimation of rated slip and torque.
- Estimation of total reactance with the help of starting torque and rated torque.
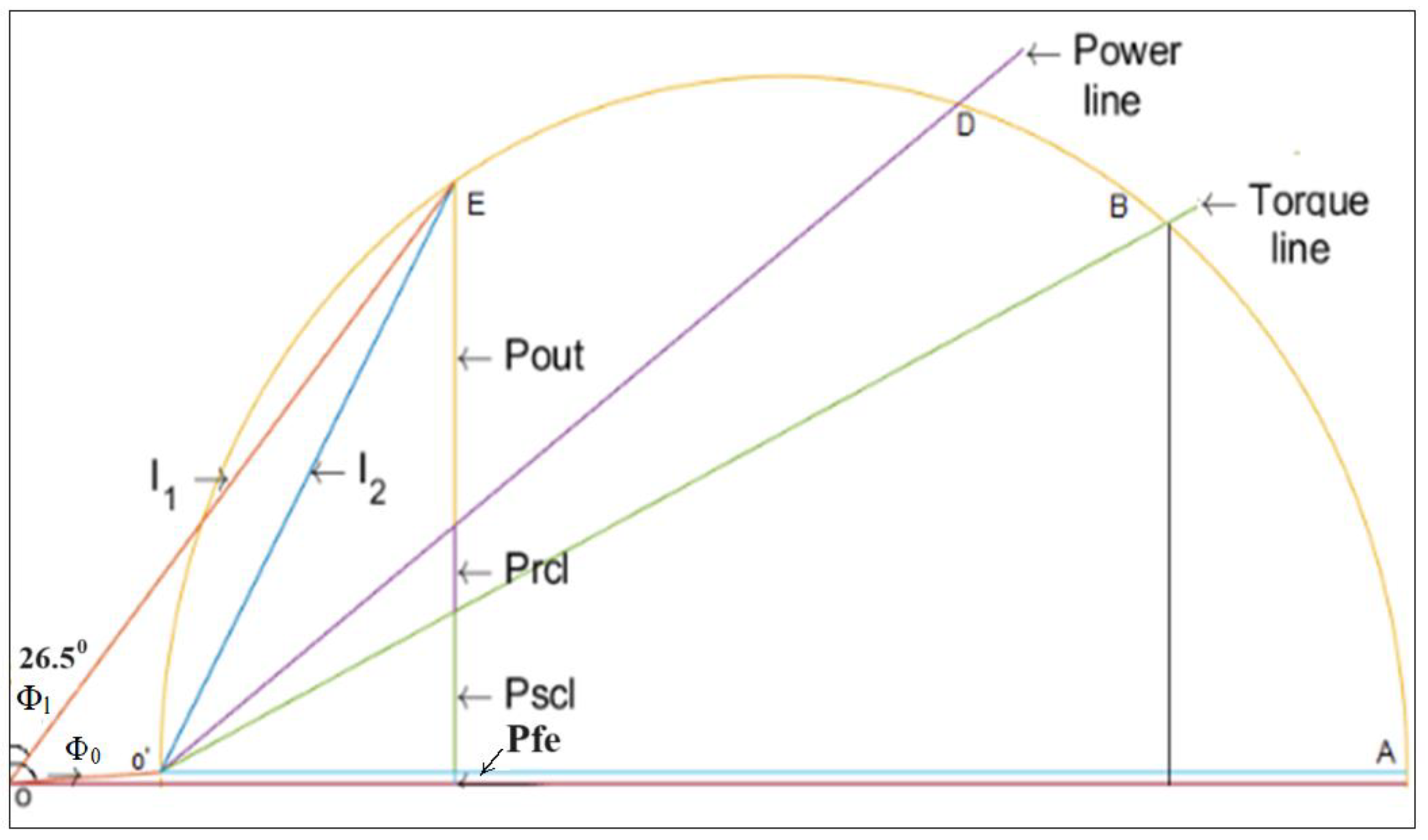
4.3. Comparison with the Circle Diagram Method
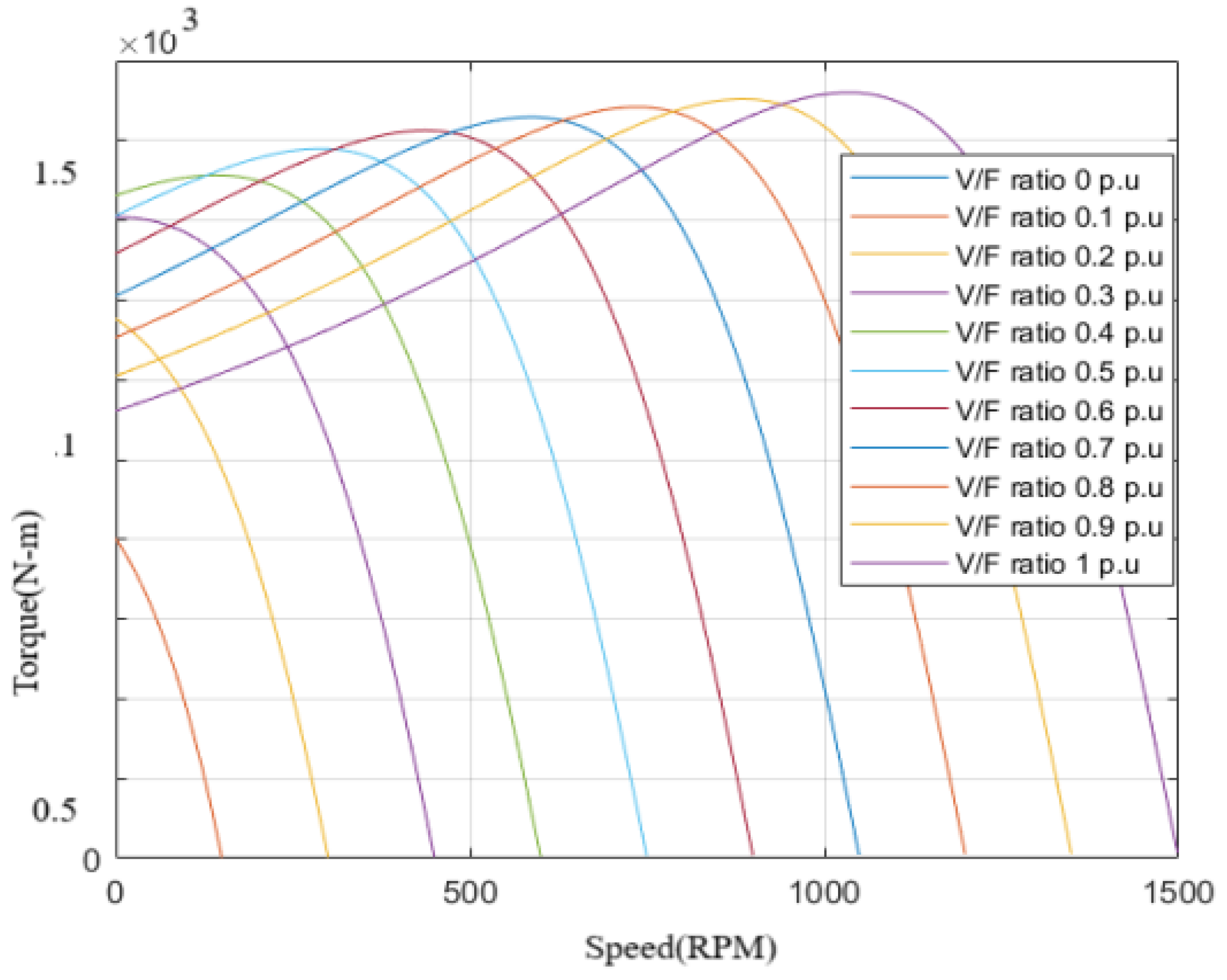
4.4. Vector Control of Motor with This Work
4.5. Benefits to Industry and Environment
4.6. Harmonic Effects in Inverter-Supplied Induction Motors
5. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fitzgerald, A.E.; Kingsley, C.; Umans, S.D. Electrical Machinery, 6th ed.; McGraw-Hill: New York, NY, USA, 2017. [Google Scholar]
- Harakuni, B.; Divatar, B.; Gurram, N.; Sheth, S.; Khaded, R.; Pattar, N. Parameter Estimation and Vector Control of Induction Motor Using Sciamble Workbench. In Proceedings of the IEEE 7th International Conference for Convergence in Technology (I2CT), Pune, India, 7–9 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Dash, S.; Chakravarty, S.; Giri, N.C.; Ghugar, U.; Fotis, G. Performance Assessment of Different Sustainable Energy Systems Using Multiple-Criteria Decision-Making Model and Self-Organizing Maps. Technologies 2024, 12, 42. [Google Scholar] [CrossRef]
- Chunyang, S.; Qinghui, W.; Tao, S.; Haixia, W. Induction Motor Torque Closed-Loop Vector Control System Based on Flux Observation and Harmonic Current Suppression. Control Eng. Pract. 2024, 142, 105755. [Google Scholar] [CrossRef]
- Shahin, A.; Elbuluk, M.E.; Toliyat, H.A. Hybrid Neural Network and Grey Wolf Optimization for Online Induction motor parameter estimation. IEEE Trans. Energy Convers. 2021, 36, 1031–1041. [Google Scholar]
- Chen, W.; He, J.; Chen, J.; Sun, Y. Adaptive Observer-Based Induction Motor Parameter Estimation Under Time-Varying Disturbances. IEEE Trans. Ind. Electron. 2021, 68, 76–85. [Google Scholar]
- Li, L.; Li, C.; Li, Y.; Wang, L. A Novel Online Parameter Identification Algorithm for Induction Motors Based on the Improved Differential Evolution and Multiple Adaptive Kalman Filter. IEEE Access 2020, 8, 21286–21297. [Google Scholar]
- Rajput, S.; Bender, E.; Averbukh, M. Simplified Algorithm for Assessment Equivalent Circuit Parameters of Induction Motors. IET Electr. Power Appl. 2020, 14, 426–432. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; Sehiemy, R.A.; Hamida, M.A. Hybrid Optimization Algorithm for Parameter Estimation of Poly-phase Induction Motors with Experimental Verification. Energy AI 2021, 5, 100083. [Google Scholar] [CrossRef]
- Ouambo, S.A.T.; Boum, A.T.; Imano, A.M. States and Parameters Estimation for Induction Motors Based on a New Adaptive Moving Horizon Estimation. J. Electr. Comput. Eng. 2022, 2022, 8687025. [Google Scholar] [CrossRef]
- Amaral, F.V.; Baccarini, J.M.R.; Coelho, F.C.R.; Baccarini, L.M.R. A High Precision Method for Induction Machine Parameters Estimation from Manufacturer Data. IEEE Trans. Energy Convers. 2020, 36, 1226–1233. [Google Scholar] [CrossRef]
- Mahesh, P.; Sabha, R.A.; Rajeev, K.A. An Improved Sliding Mode Observer for Parameter Estimation in Induction Motor Drive with Optimised Gains. Aust. J. Electr. Electron. Eng. 2023, 20, 235–250. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.; Sul, S.; Baloch, N.A. Stator Resistance Estimation Using DC Injection with Reduced Torque Ripple in Induction Motor Sensorless Drives. IEEE Trans. Ind. Appl. 2020, 56, 3744–3754. [Google Scholar] [CrossRef]
- Vukasinovic, J.; Štatkic, S.; Milovanovic, M.; Arsic, N.; Perovic, B. Combined method for the cage induction motor parameters estimation using two-stage PSO algorithm. Electr. Eng. 2023, 105, 2703–2714. [Google Scholar] [CrossRef]
- Danin, Z.; Sharma, A.; Averbukh, M.; Meher, A. Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor. Energies 2022, 15, 8834. [Google Scholar] [CrossRef]
- Rodriguez-Abreo, O.; Rodriguez-Resendiz, J.; Alvarez-Alvarado, J.M.; Garcia-Cerezo, A. Metaheuristic Parameter Identification of Motors Using Dynamic Response Relations. Sensors 2022, 22, 4050. [Google Scholar] [CrossRef] [PubMed]
- Stinga, F.; Selisteanu, D. Robust Estimation-Based Control Strategies for Induction Motors. Complexity 2020, 2020, 9235701. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Elsawy, M.A.; Denis, K.A.; Alkhalaf, S.; Ali, Z.M. Artificial Neural Based Speed and Flux Estimators for Induction Machine Drives with Matlab/Simulink. Mathematics 2022, 10, 1348. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Abdelwanis, M.I.; El-Sehiemy, R.A.; Abd-Elrazek, A.S. An Interior Search Algorithm Based on Chaotic and Crossover Strategies for Parameter Extraction of Polyphase Induction Machines. Neural Comput. Appl. 2022, 35, 6647–6664. [Google Scholar] [CrossRef]
- Sengamalai, U.; Anbazhagan, G.; Thentral, T.M.T.; Vishnuram, P.; Khurshaid, T.; Kamel, S. Three Phase Induction Motor Drive: A Systematic Review on Dynamic Modeling, Parameter Estimation, and Control Schemes. Energies 2022, 15, 8260. [Google Scholar] [CrossRef]
- Giri, N.C.; Mohanty, R.C. Turmeric crop farming potential under Agrivoltaic system over open field practice in Odisha, India. Environ. Dev. Sustain. 2024, 1–9. [Google Scholar] [CrossRef]
- Choudhary, A.; Mian, T.; Fatima, S.; Panigrahi, B.K. Nature-Inspired Artificial Bee Colony-Based Hyperparameter Optimization of CNN for Anomaly Detection in Induction Motor. Expert Syst. 2024, 41, e13407. [Google Scholar] [CrossRef]
- Jain, P.; Singh, B. Parameter Estimation of Induction Motor for Vector Control: A Review. IEEE Trans. Energy Convers. 2018, 33, 268–278. [Google Scholar]
- Aziz, A.G.M.A.; Abdelaziz, A.Y.; Ali, Z.M.; Diab, A.A.Z. A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques. Energies 2023, 16, 2854. [Google Scholar] [CrossRef]
- IEEE Standard 112-2017; IEEE Standard Test Procedure for Polyphase Induction Motors and Generators. IEEE: New York, NY, USA, 2017.
- Chapman, S.J. Electrical Machinery and Power System Fundamentals, 5th ed.; McGraw-Hill: New York, NY USA, 2012. [Google Scholar]
- Mashar, A. Determination of Three-Phase Induction Motor Equivalent Circuit Parameters Experimentally. IEEE Trans. Ind. Appl. 2013, 49, 2531–2539. [Google Scholar]
- Natarajan, R.; Misra, V. Parameter Estimation of Induction Motors Using a Spreadsheet Program on a Personal Computer. Electr. Power Syst. Res. 1989, 16, 157–164. [Google Scholar] [CrossRef]
- Haque, M. Determination of NEMA Design Induction Motor Parameters from Manufacturer Data. IEEE Trans. Energy Convers. 2008, 23, 997–1004. [Google Scholar] [CrossRef]
- Al-Jufout, S.A.; Al-Rousan, W.H.; Wang, C. Optimization of Induction Motor Equivalent Circuit Parameter Estimation Based on Manufacturer’s Data. Energies 2018, 11, 1792. [Google Scholar] [CrossRef]
- Salomon, C.; Sant’Ana, W.; Lambert-Torres, G.; Borges da Silva, L.; Bonaldi, E.; de Oliveira, L. Comparison Among Methods for Induction Motor Low-Intrusive Efficiency Evaluation Including a New AGT Approach with a Modified Stator Resistance. Energies 2018, 11, 691. [Google Scholar] [CrossRef]
- Ghosh, S. MATLAB Simulation of Circle Diagram in Three Phase Induction Motor. IETE J. Educ. 2022, 63, 63–77. [Google Scholar] [CrossRef]
- Agrawal, K.C. Electrical Power Engineering Reference & Applications Handbook, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Hu, J.; Jia, M.; Xiao, F.; Fu, C.; Zheng, L. Motor Vector Control Based on Speed-Torque-Current Map. Appl. Sci. 2020, 10, 78. [Google Scholar] [CrossRef]







| S. No. | Parameter | Value |
|---|---|---|
| 1 | Power output | 90 KW (120 HP) |
| 2 | Number of phases and connection | 3 & Delta |
| 3 | Rated voltage | 415 Volts |
| 4 | Type of induction motor | Squirrel-cage |
| 5 | Rated current | 160 Amps |
| 6 | Efficiency at full load | 91.56% |
| 7 | Power factor at full load | 0.87 |
| 8 | Normal speed | 1485 RPM |
| 9 | NEMA code | B |
| 10 | Rated torque (Tr) | 594 N-m |
| 11 | Starting torque (Tm) | 1070 N-m |
| Type of Test | Voltage (Volts) | Frequency (Hz) | Current (Amperes) | Speed (RPM) | Total Power (kW) |
|---|---|---|---|---|---|
| No-load | 415 | 50 | 45 | 1495 | 4 |
| Short-circuit (tested) | 75 | 50 | 160 | 0.00 | 7.2 |
| Short-circuit (calculated) | 415 | 50 | 889.2 | 0.00 | 105.4 |
| Full load | 415 | 50 | 160 | 1483 | 100.8 |
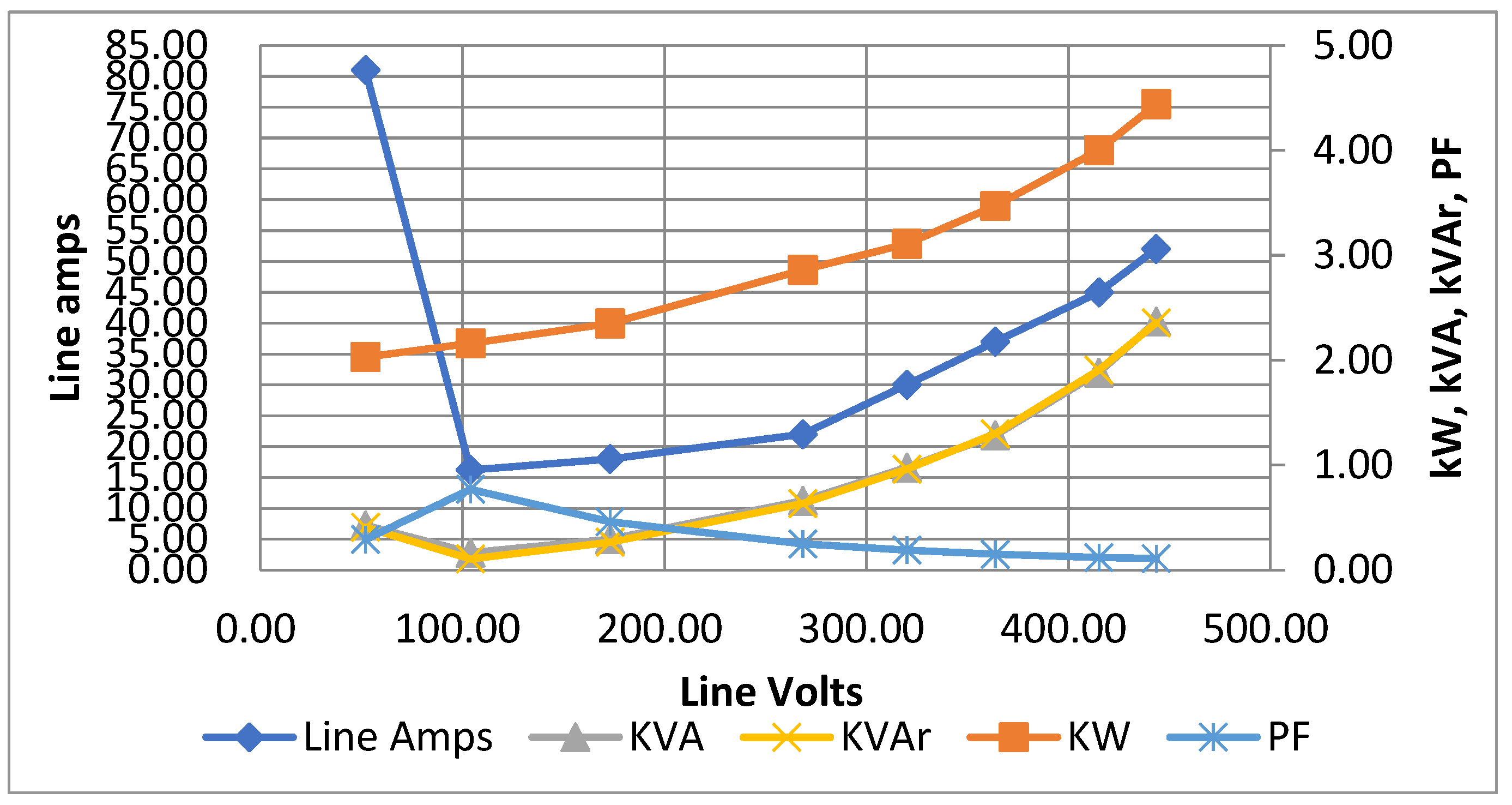
| Voltage (Volts) | Frequency (Hz) | Current (A) | Active Power, P(kW) | Apparent Power, S (kVA) | Reactive Power, Q (kVAr) | Power Factor (Cos Ø-lag) |
|---|---|---|---|---|---|---|
| 52.00 | 50.00 | 81.00 | 2.03 | 7.24 | 6.94 | 0.29 |
| 104.00 | 50.00 | 16.20 | 2.16 | 2.81 | 1.79 | 0.77 |
| 173.00 | 50.00 | 18.00 | 2.35 | 5.01 | 4.50 | 0.46 |
| 268.47 | 50.00 | 22.00 | 2.86 | 11.20 | 10.80 | 0.25 |
| 320.00 | 50.00 | 30.00 | 3.11 | 16.61 | 16.36 | 0.19 |
| 363.73 | 50.00 | 37.00 | 3.47 | 21.84 | 22.11 | 0.15 |
| 415.00 | 50.00 | 45.00 | 4.00 | 32.00 | 32.40 | 0.12 |
| 443.41 | 50.00 | 52.00 | 4.44 | 40.25 | 40.05 | 0.11 |
| Voltage (Vo) (Volts) | (Vo/Vn)2 | No-Load Power P0 (kW) | Prot (kW) | Pfe (kW) |
|---|---|---|---|---|
| 52.00 | 0.02 | 2.03 | 2.00 | 0.03 |
| 104.00 | 0.06 | 2.16 | 2.00 | 0.16 |
| 173.00 | 0.17 | 2.35 | 2.00 | 0.35 |
| 268.47 | 0.42 | 2.86 | 2.00 | 0.86 |
| 320.00 | 0.59 | 3.11 | 2.00 | 1.11 |
| 363.73 | 0.77 | 3.47 | 2.00 | 1.47 |
| 415.00 | 1.00 | 4.00 | 2.00 | 2.00 |
| 443.41 | 1.14 | 4.44 | 2.00 | 2.44 |
| Reference | Method | Findings | Limitations |
|---|---|---|---|
| [26] | Approximate circuit calculation | R1, R2, X1, X2 and Xm | Iron loss component is ignored. |
| [1] | Approximate circuit calculation | R1, R2, X1, X2 and Xm | Iron loss component is ignored. |
| [27] | L-Model | R2 is ignored | Approx. equiv. circuit is used. |
| [27] | T-Model | R1, R2, X1, X2 and Xm | Exact equivalent circuit is used. |
| [28] | Spread sheet | Assumed that the Iron loss and rotational losses are equal | Nil. |
| [29] | MATLAB code | Nil. |
| Name Plate Data | Estimates | ||||||
|---|---|---|---|---|---|---|---|
| S. No. | Description | Symbol (Unit) | Value | S. No | Description | Symbol (Unit) | Estimated Value |
| 1 | Shaft Output power | HP | 120 | 1 | Input phase voltage | Vph (Volts) | 415. |
| 2 | Input Line Voltage | VL (volts) | 415 | 2 | Synchronous speed | Ns (RPM) | 1500 |
| 3 | Supply Frequency | F(Hz) | 50 | 3 | Rated slip | Sr | 0.0100 |
| 4 | Rated Current at Full load | Ir (Amps) | 160 | 4 | Total resistance (stator + rotor) | Rt (Ohms) | 0.0445 |
| 5 | Number of Poles | P | 4 | 5 | Constant loss (core + stray + fri. and windage) | PK (Watts) | 4138.1881 |
| 6 | NEMA Motor class | A, B, C or D | B | 6 | Magnetizing resistance (core loss is 50% of const. loss) | Rm (Ohms) | 249.7107 |
| 7 | Rated efficiency | Effr | 0.9156 | 7 | No-load active current | Ior (Amps) | 1.6619 |
| 8 | Efficiency at 75% load | Eff 0.75 | 0.9068 | 8 | Rated Pf angle | Or (Radians) | 0.5156 |
| 9 | Current at 75% load | I 0.75 (Amps) | 126.00 | 9 | Pf angle at 75% load | O 0.75 (Radians) | 0.5355 |
| 10 | Rated Power factor at full load | Pfr | 0.87 | 10 | Ir SinΦ | ʎ (Amps) | 58.3649 |
| 11 | Power factor at 75% load | Pf 0.75 | 0.86 | 11 | Magnetizing current | Im (Amps) | 20.5234 |
| 12 | Rated speed at full load | N (RPM) | 1485 | 12 | Magnetizing reactance per phase | Xm (Ohms) | 20.2209 |
| 13 | Starting torque to FL torque ratio | Ts (=%Tr) | 180 | 13 | Work component | ᴪ (Amps) | 137.7541 |
| 14 | Maximum torque to FL torque ratio | Tm (=%Tr) | 250 | 14 | Rotor current per phase ref. to stator | I2′ (Amps) | 149.6084 |
| 15 | Connection | Delta or Star | Delta | 15 | Rotor power factor | Pf2 | 0.9208 |
| NEMA Design Motors empirical relation for leakage reactance | 16 | Rotor resistance per phase ref. to stator | R2′ (Ohm) | 0.0135 | |||
| Class | X1 | X2 | X1/X2 | 17 | Stator resistance per ph. | R1 (Ohm) | 0.0310 |
| A | 0.5 | 0.5 | 1 | 18 | Start. to Max torque ratio | A (Amp) | 0.7200 |
| B | 0.4 | 0.6 | 0.667 | 19 | Work component 1 (for estimation purpose) | Β (Amps) | 0.6940 |
| C | 0.3 | 0.7 | 0.429 | 20 | Work component 2 (for estimation purpose) | ꭇ (Amps) | 0.4250 |
| D | 0.5 | 0.5 | 1 | 21 | Rotor leakage reac. per phase referred to stator | X2′ (Ohms) | 0.0317 |
| 22 | Stator leakage reac. per ph. | X1 (Ohm) | 0.0211 | ||||
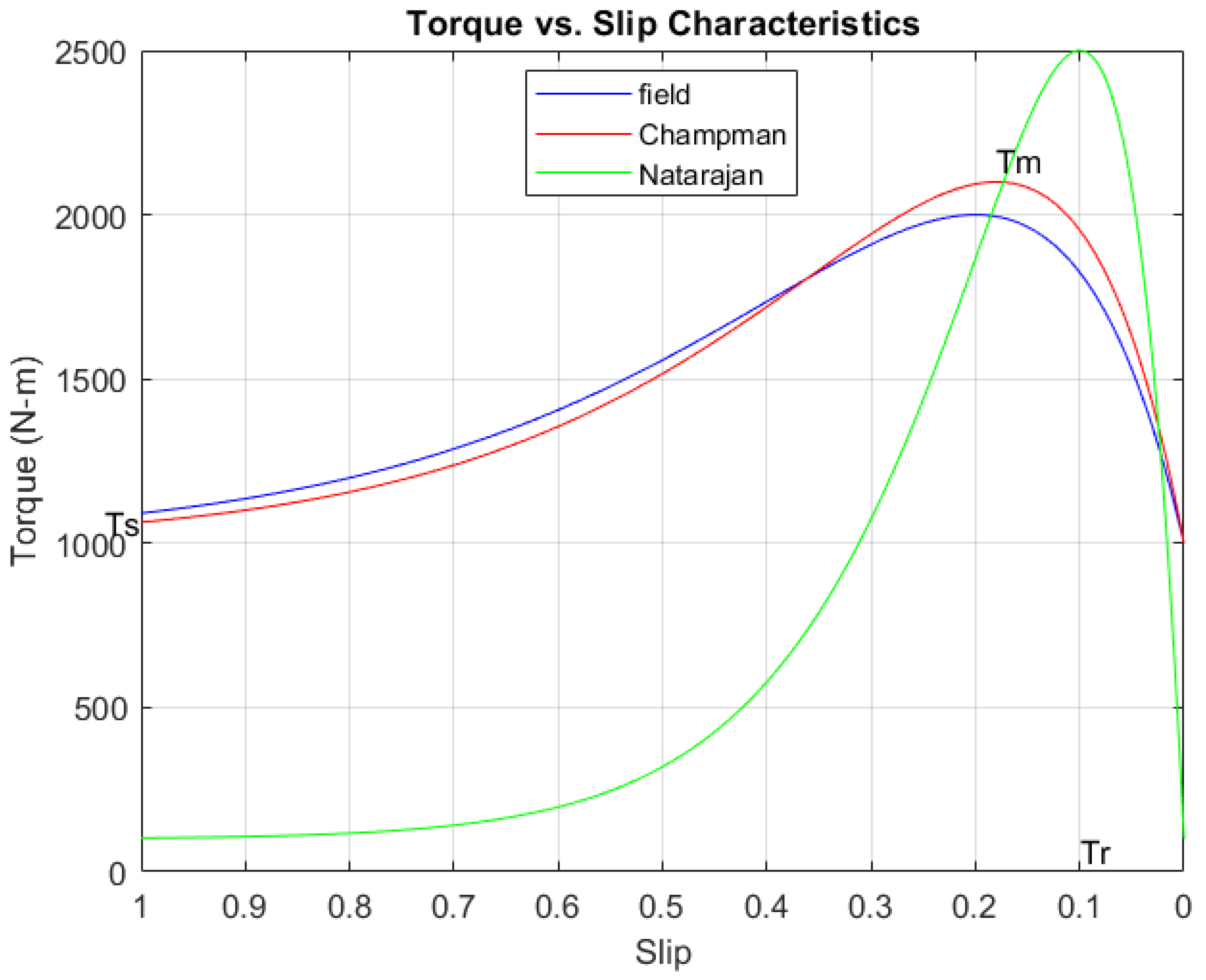
| Parameter (Ω) | Method 1 Field Experiments | Method 2 [27] | Method 3 [1] | Method 4 (L-Model) [28] | Method 5 (T-Model) [28] | Method 6 [29] | Method 7 [30] | The Best Method w.r.t. Field Test (Number) |
|---|---|---|---|---|---|---|---|---|
| R1 | 0.05963 | 0.05963 | 0.05963 | 0.05963 | 0.05963 | 0.05963 | 0.0963 | All methods except 7 |
| R2 | 0.2351 | 0.2813 | 0.2351 | Ignored | 0.283 | 0.0135 | 0.0135 | 3 |
| Rc | 274.97 | Ignored | Ignored | 274.83 | 260.5 | 225.18 | 175.31 | 4 |
| X1 | 0.3047 | 0.285 | 0.285 | 0.2874 | 0.274 | 0.0211 | 0.216 | 2, 3 |
| X2 | 0.4569 | 0.4763 | 0.475 | 0.4791 | 0.4562 | 0.0317 | 0.323 | 3 |
| Xm | 15.66 | 15.684 | 15.565 | 9.23 | 9.22 | 17.02 | 17.40 | 2, 3 |
| Parameter (Ω) | Field Experiments | E. Fitzgerald & Co (Textbook) [1] | Error [%] |
|---|---|---|---|
| R1 | 0.05963 | 0.05963 | 0 |
| R2 | 0.2351 | 0.2351 | 0 |
| Rc | 274.97 | Ignored | - |
| X1 | 0.3047 | 0.285 | 6.50 |
| X2 | 0.4569 | 0.4750 | 3.96 |
| Method | Efficiency at 50% Load | Efficiency at Full Load | Notes |
|---|---|---|---|
| Baseline Method (Traditional) | 87.5% | 89.3% | Based on empirical equations |
| Proposed Method (This Study) | 89.0% | 91.3% | Utilizes advanced computational techniques for parameters estimation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reddy, B.K.; Ayyagari, K.S.; Kumar, Y.P.; Giri, N.C.; Rajgopal, P.V.; Fotis, G.; Mladenov, V. Experimental Benchmarking of Existing Offline Parameter Estimation Methods for Induction Motor Vector Control. Technologies 2024, 12, 123. https://doi.org/10.3390/technologies12080123
Reddy BK, Ayyagari KS, Kumar YP, Giri NC, Rajgopal PV, Fotis G, Mladenov V. Experimental Benchmarking of Existing Offline Parameter Estimation Methods for Induction Motor Vector Control. Technologies. 2024; 12(8):123. https://doi.org/10.3390/technologies12080123
Chicago/Turabian StyleReddy, Butukuri Koti, Krishna Sandeep Ayyagari, Yemula Pradeep Kumar, Nimay Chandra Giri, Panganamamula Venkata Rajgopal, Georgios Fotis, and Valeri Mladenov. 2024. "Experimental Benchmarking of Existing Offline Parameter Estimation Methods for Induction Motor Vector Control" Technologies 12, no. 8: 123. https://doi.org/10.3390/technologies12080123
APA StyleReddy, B. K., Ayyagari, K. S., Kumar, Y. P., Giri, N. C., Rajgopal, P. V., Fotis, G., & Mladenov, V. (2024). Experimental Benchmarking of Existing Offline Parameter Estimation Methods for Induction Motor Vector Control. Technologies, 12(8), 123. https://doi.org/10.3390/technologies12080123








