Fuzzy Guiding of Roulette Selection in Evolutionary Algorithms
Abstract
:1. Introduction
- −
- define estimators used as input values that best characterize the course of evolution;
- −
- determine the number and shape of membership functions for each estimator;
- −
- design the fuzzy controller, such as deciding the number of input estimators, building a fuzzy rule base, and selecting a defuzzification method;
- −
- choose which parameters of the evolutionary algorithm should be adapted and determine how they will be modified.
- The paper introduces a novel method for controlling evolution in evolutionary algorithms by modifying the selection probability. A fuzzy logic controller to analyze the fitness of individuals in the current generation and the evolutionary history in previous generations is presented.
- The paper introduces and discusses new estimators that play a crucial role in fine-tuning selection probability, based on individuals’ fitness and average fitness in history.
- Linguistic variables, as well as their membership functions for the FLC’s inputs and output, are defined.
- The rule base is obtained using human experience, the EA experts’ knowledge, and an automatic learning technique.
- Experiments on a wide set of benchmark functions show that the proposed algorithm achieves better quality solutions and very good performance compared to standard evolutionary algorithms. The effectiveness and performance of the newly developed algorithm are tested, and the results of optimization are compared to other implementations of EAs and methods presented in previous works. These results demonstrate some advantages of the new algorithm over earlier methods.
- A novel algorithm called FLC-EA is introduced.
- A thorough investigation and discussion of new estimators, which play a crucial role in fine-tuning the selection probability, is presented.
- An FLC that controls the selection probability in EAs was developed.
- Experiments on a wide set of benchmark functions and a real-world problem were conducted.
2. Materials and Methods
2.1. The Proposed Method for Tuning Selection Probability in Evolutionary Algorithms
2.1.1. Estimators for FLC
- −
- Individual’s quality—calculated as the difference between the fitness function of the individual and the average current population’s fitness.where:—quality of individual i;—fitness of individual i;—population size.
- −
- The ratio of successful reproductions—calculated as the relation of the number of reproductions where the offspring is better than the parents to the total number of reproductions.where:—the ratio of successful reproductions;—the number of successful reproductions;—the total number of reproductions.
- −
- The growth ratio in history—calculated as the relation of average fitness in the current generation to average fitness in history.where:—the ratio of growth in history;—fitness of individual i;—history size;—population size.
- −
- Relative distance—calculated as distance between average fitness in the population and fitness of the best individual found until now.where:—relative distance of average fitness in the population to fitness of the best individual found until now;—fitness of individual i;—the best individual found until now;—population size.
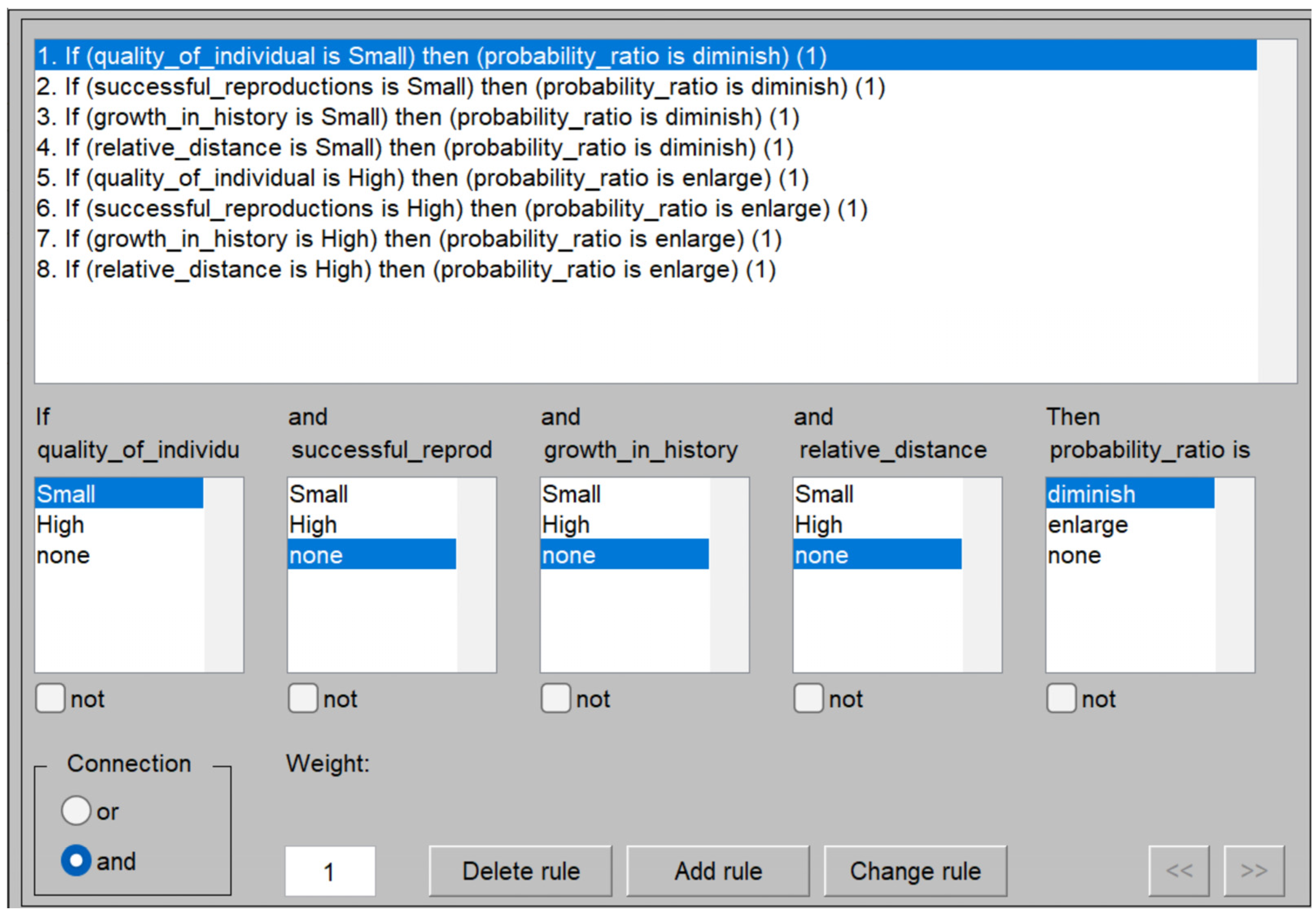
2.1.2. The Rules Base for FLC
- Enlarge selection probability for high-quality individuals:
- Individuals with fitness values above the generation’s average will have their selection probability increased.
- This prioritization allows such individuals to contribute more offspring, enhancing the algorithm’s ability to exploit existing good solutions.
- Enlarge selection probability for populations with many positive reproductions:
- Individuals that produce offspring with better fitness than their own will gain higher selection probabilities.
- This encourages the exploitation of successful reproduction patterns.
- Enlarge selection probability for populations with a high historical growth ratio:
- If the average fitness value in the current population exceeds the historical average fitness, it suggests evolutionary progress.
- Increasing selection probability under these conditions enhances exploitation and accelerates convergence.
- Enlarge selection probability when the relative distance to the best solution is small:
- As the algorithm progresses, the gap between the population’s average fitness and the best found fitness decreases.
- Increasing selection probability in this final phase focuses the algorithm on refining the best solutions, improving exploitation and convergence.
- Diminish selection probability for low-quality individuals:
- Individuals with fitness values below the generation’s average will have their selection probability reduced.
- This limits their contribution to the parent pool, promoting exploitation of better solutions.
- Diminish selection probability for populations with few positive reproductions:
- Individuals that produce offspring with lower fitness than their own will have their selection probability diminished.
- This encourages exploration by reducing focus on unsuccessful reproduction patterns.
- Diminish selection probability for populations with a low historical growth ratio:
- If the population’s average fitness is below the historical average, it indicates a lack of evolutionary progress.
- Reducing selection probability in such cases focuses resources on better exploitation strategies.
- Diminish selection probability when the relative distance to the best solution is large:
- In the initial stages, the average fitness of the population is often far from the best found fitness.
- Reducing selection probability during this phase promotes genetic diversity, enhancing the algorithm’s exploratory capabilities.
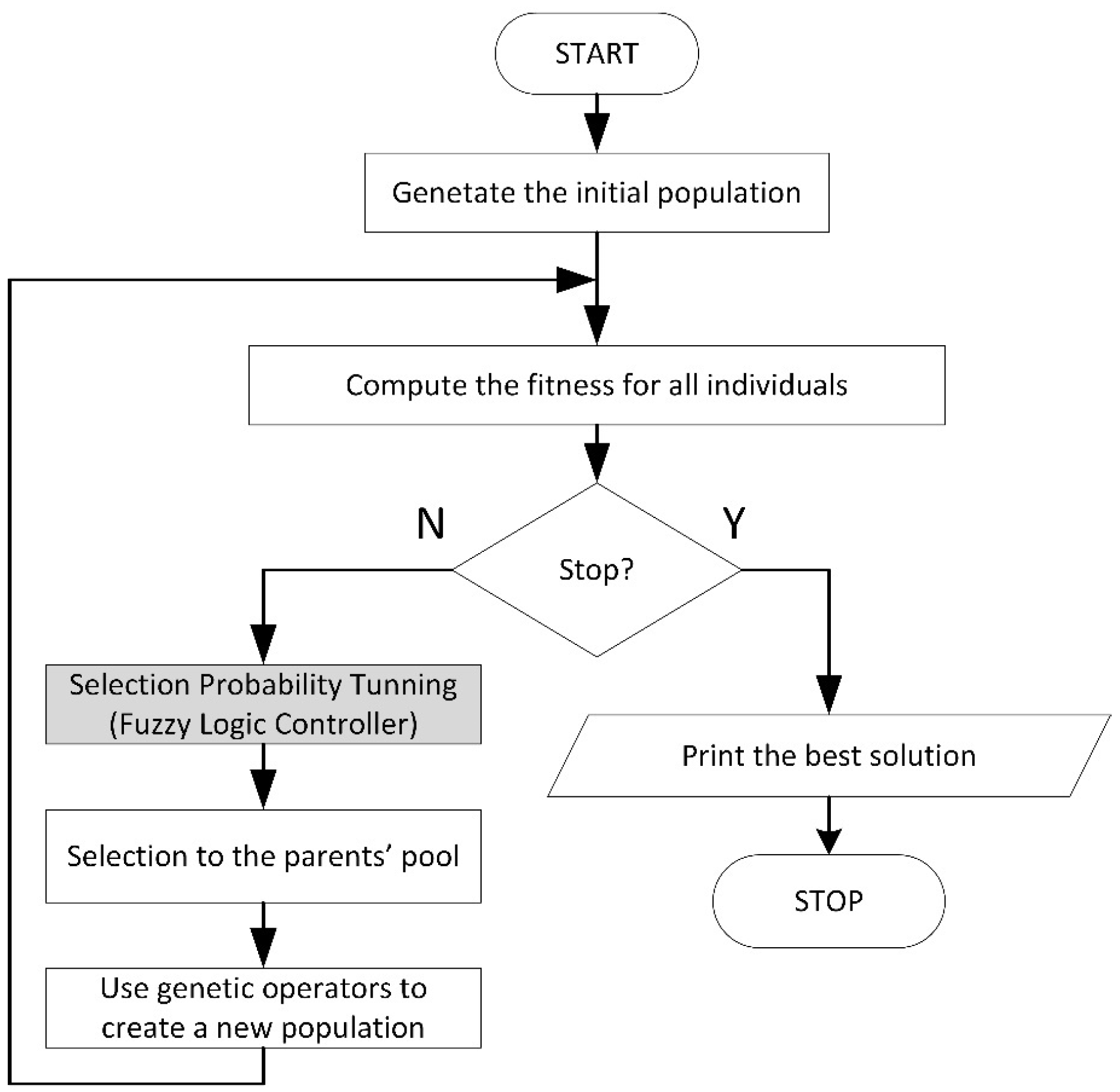
2.1.3. The Modified Evolutionary Algorithm
| Algorithm 1 Adaptive Parameter Evolutionary Algorithm | |
| 1 | int generation ← 0 |
| 2 | initialize first population |
| 3 | evaluate first population |
| 4 | keep best in population |
| //Main evolutionary loop | |
| 5 | while (!termination condition) do |
| 6 | generation++ |
| //Adjust parameters if enough history is available | |
| 7 | if (generation > history_size) then |
| 8 | evaluate estimators for FLC |
| 9 | alter selection probability by FLC |
| 10 | end if |
| //Perform genetic algorithm operations | |
| 11 | select individuals to parent pool |
| 12 | perform crossover and mutation |
| 13 | evaluate population |
| 14 | apply elitism |
| 15 | end while |
| 16 | end |
2.1.4. The Parameters of Modified Evolutionary Algorithm
- −
- Human-like decision making: FL-based systems model human decision making, making the control model easier to understand.
- −
- Simplified modeling of complex problems: FL allows for modeling complex systems without requiring precise mathematical formulations.
- −
- Robustness to uncertainty: FL-based systems are resistant to small changes in input data or noise, ensuring stable operation under uncertain conditions.
- −
- Scalability and flexibility: These systems can be easily expanded by adding new rules without requiring a complete redesign, making them adaptable to the problem at hand.
- −
- Real-time efficiency: FL works well in real-time systems due to its low computational requirements.
- −
- population size: 25;
- −
- crossover probability: 0.8;
- −
- mutation probability was selected depending on the number of variables in the optimized function so that at least one of the individual’s genes was modified.
2.2. The Set of Test Functions
- −
- Selected CEC2015 test functions [26]. All of them are minimization problems, with the minimum shifted to 0 and the search range [−100, 100] for each dimension d. In the experiments, 50 and 100 dimensions were used for the functions CEC_f1, CEC_f2, CEC_f3:—high conditioned elliptic function. It is defined as:—cigar function. It is defined as:—discus function. It is defined as:
- −
- . The product of 5 to 20 sines has been used to test the algorithm’s ability to determine the exact solution. It is defined as:
- −
- Rastrigin function: It is defined on the domain , for d = 2, 5, 10 dimensions. The function minimum is at point . It is defined as:
- −
- Styblinski–Tang function: It is defined for , for all d = 2, 5, 10 dimensions. The minimum of the function is located at the point . It is defined as:
- −
- Rosenbrock function: It is defined for 2 dimensions in domain , for each dimension. The function minimum is at point . It is defined as:
- −
- Shubert function: It is defined for 2 dimensions in domain , for each dimension. The function minimum . It is defined as:
- −
- . A simple function of two variables in domain , for each dimension. The function maximum is at point . It is defined as:
- −
- . The very complex function used to test the algorithm’s ability to find a global optimum and avoid local optima. The function maximum is at point . It is defined as:where:;;
2.3. Real-World Test Problem
2.3.1. Connected Facility Location Problem
- −
- Network Nodes Location Problem: Network nodes must be placed within a given geographic area to minimize the total length of communication links between nodes and terminals. Placing network nodes closer to computer terminals reduces the total communication distance, leading to decreased latency and improved overall network performance. The placement must also consider real-world constraints such as physical barriers, existing infrastructure, and geographic boundaries.
- −
- Network Nodes Number Problem: The number of network nodes should be minimized to reduce infrastructure costs and simplify network management, while ensuring effective coverage and connectivity. A smaller number of nodes may lead to longer distances between terminals and nodes, potentially increasing communication delays and causing network congestion.
- −
- Terminal Assignment Problem: Each computer terminal must be assigned to its nearest network node to minimize the total link length between nodes and terminals. This assignment involves solving the nearest neighbor problem efficiently while ensuring proper load balancing to prevent overloading specific nodes.Formally, ConFLP within a given 2D geographic area can be stated as:where:—This function represents the total link length between network nodes and computer terminals. It could be expressed as the sum of the distances between each computer terminal and its assigned network node.—This function assigns each computer terminal to a specific network node. This could be based on criteria like the shortest distance, load balancing, or other optimization goals.—These are the coordinates of the network nodes, where A represents the 2D area in which these nodes are positioned.—n represents the current number of network nodes.
- −
- Node positions by geographical coordinates: This table contains the coordinates of each network node. The number of genes in an individual equals the number of network nodes (n). Each gene consists of two real numbers, representing the x and y coordinates of a node.
- −
- Terminal-node associations: This table assigns each terminal to a network node using integers. The number of genes in an individual equals the number of terminals. A value i at position k indicates that terminal k is connected to node i.
2.3.2. Clustering Problem
3. Results
3.1. Experiments on a Simple, Monotone Function
3.2. Experiments on High-Dimensional Benchmark Functions from CEC2015
3.3. Test on a Set of Complex, Non-Trivial, and Difficult-to-Optimize Functions
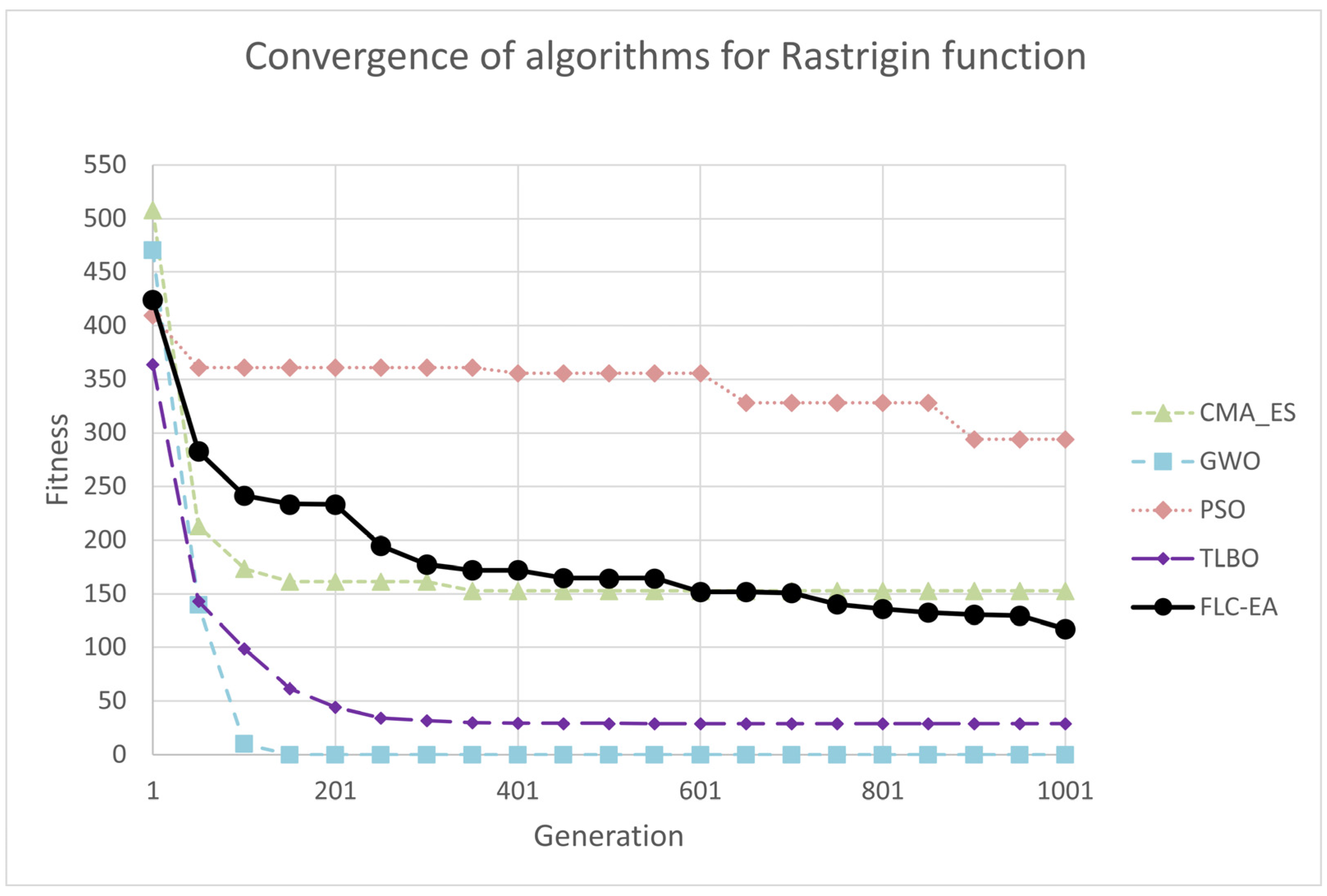
3.4. Test on Multi-Modal Functions
3.5. Comparition of Proposed Method to Reinforcement-Learning-Based Algorithm
- −
- Gaming: training artificial agents for games like chess, Go, and video games.
- −
- Robotics and autonomous vehicles: teaching robots or self-driving cars to navigate and perform tasks.
- −
- Healthcare: optimizing treatment plans and aiding in drug discovery.
- −
- Finance: portfolio optimization and automated trading strategies.
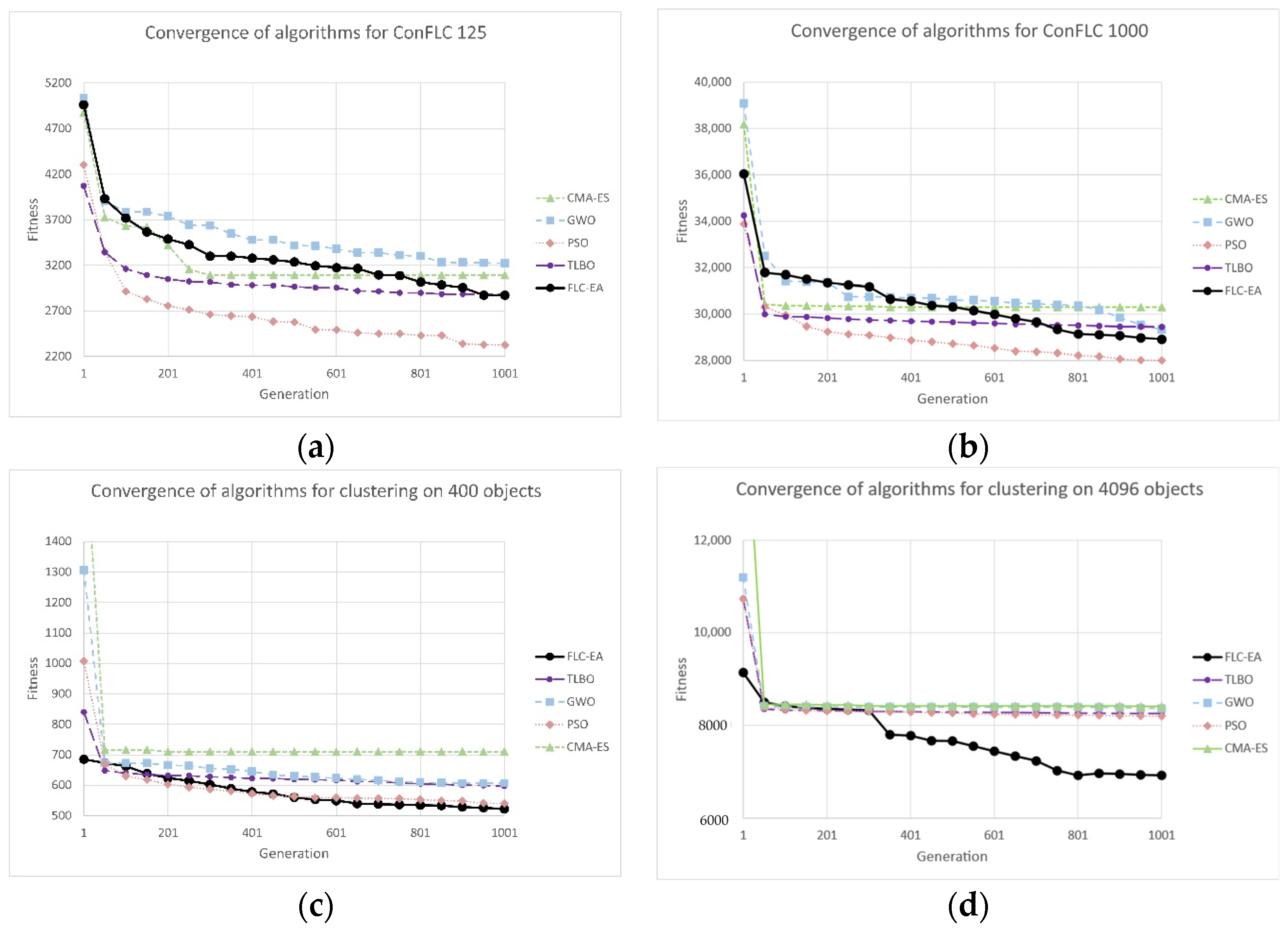
3.6. Test of Algorithm’s Performance on Real-World ConFLP Problem
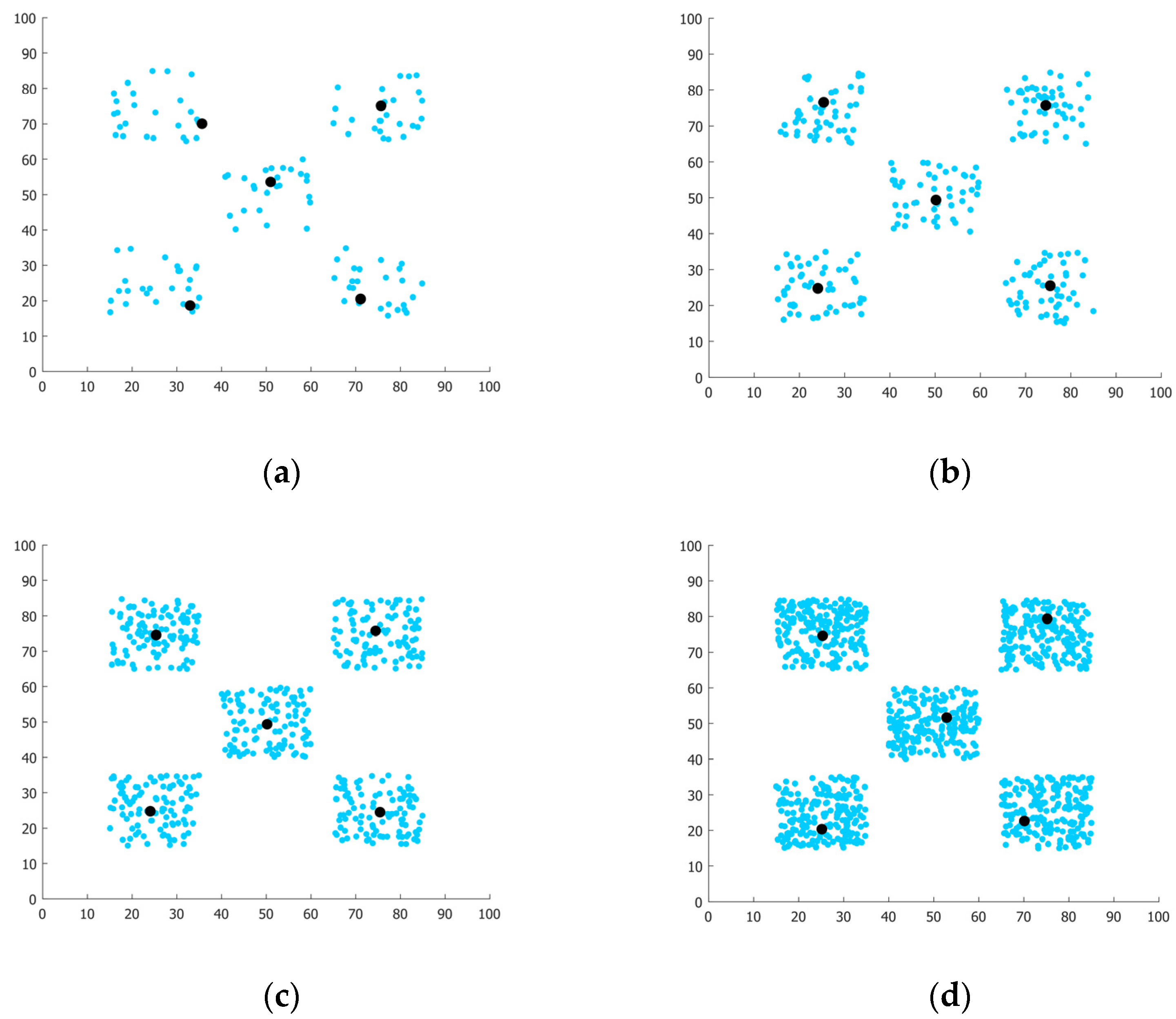
3.7. Test of Algorithm’s Performance on Clustering Problem
3.8. Evaluation Algorithm’s Convergence to Global Optima
4. Discussion
- −
- Transparency: Fuzzy logic introduces a transparent, easy-to-interpret method for modeling and expressing human knowledge and strategies within the evolutionary process. The use of simple IF-THEN rules enables both experts and non-experts to understand and engage in designing algorithms to solve optimization processes.
- −
- Incorporating human expertise: Fuzzy logic enables the integration of domain-specific knowledge directly into the optimization process. Experts can encode their knowledge into the fuzzy rule base and guide the EA to align with human goals and constraints. This enhances the relevance of the optimization results and their consistency with the user’s expectations.
- −
- Robustness and adaptability: The FLC-EA system is better equipped to handle a wide range of benchmarks and real-world problems. It can adapt the fuzzy rule base or membership functions to changing problem constraints or user requirements.
- −
- Human–machine collaboration: The transparency and interpretability of fuzzy logic foster effective collaboration between humans and the optimization system. Experts can actively participate in refining rules and strategies, leading to more effective outcomes in complex decision-making processes aligned with user goals.
- −
- Time-consuming process of development: Tuning FLC parameters, such as the rule database, the number, and the shape of membership functions, is a complex task. This complexity arises from the high dimensionality of the problem, the size of the dataset, and the intricate interactions between various parameters.
- −
- Computational expense: FLC parameter tuning often requires extensive experimentation, which can be both time consuming and resource intensive. Developers must evaluate numerous configurations and rely on trial-and-error methods, particularly when using manual tuning approaches. This can delay project timelines and significantly increase the costs of software development.
- −
- High resource requirements for automated tuning: While automated tuning techniques are generally more efficient than manual methods, they often demand substantial computational resources. This is especially true for complex problems, making such methods expensive and potentially inaccessible in resource-constrained environments.
- −
- Lack of reproducibility: The parameter tuning process can introduce variability in model performance, making it challenging to reproduce results consistently. This variability can hinder efforts to replicate models or develop similar projects.
- −
- Complexity of parameter interactions: Interactions between parameters are often complex and non-linear, making it difficult to predict how adjustments to one parameter will impact the overall model performance. This complexity can lead to suboptimal tuning decisions, as developers may lack a full understanding of the implications of their choices.
- −
- FLC parameter tuning is computationally expensive: A standard EA can often be more effective, particularly in problems where the fitness function calculation is computationally simple.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EAs | Evolutionary algorithms |
| EER | Exploration and exploitation relationship |
| FLC | Fuzzy logic controller |
| FOP | Function optimization problem |
| MFs | Membership functions |
| LVs | Linguistic variables |
| MOP | Multiple-objective optimization problem |
| ConFLP | Connected facility location problem |
| STP | Spanning Tree Protocol |
| FIS | Fuzzy inference system |
| RL | Reinforcement learning |
| TLBO | Teaching-learning-based optimization |
| CMA-ES | Covariance matrix adaptation evolution strategy |
| GWO | Grey Wolf Optimizer |
| PSO | Particle swarm optimization |
References
- Yan, R.; Gan, Y.; Wu, Y.; Liang, L.; Xing, J.; Cai, Y.; Huang, R. The Exploration-Exploitation Dilemma Revisited: An Entropy Perspective. arXiv 2024, arXiv:2408.09974. [Google Scholar]
- Pagliuca, P. Analysis of the Exploration-Exploitation Dilemma in Neutral Problems with Evolutionary Algorithms. J. Artif. Intell. Auton. Intell. 2024, 1, 8. [Google Scholar] [CrossRef]
- Rajabi, A.; Witt, C. Self-Adjusting Evolutionary Algorithms for Multimodal Optimization. Algorithmica 2022, 84, 1694–1723. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- de Brito, F.H.; Teixeira, A.N.; Teixeira, O.N.; de Oliveira, R.C.L. A Fuzzy Intelligent Controller for Genetic Algorithms’ Parameters. In International Conference on Natural Computation; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 633–642. [Google Scholar] [CrossRef]
- Tavakoli, S. Enhancement of Genetic Algorithm and Ant Colony Optimization Techniques using Fuzzy Systems. In Proceedings of the 2009 IEEE International Advance Computing Conference, Patiala, India, 6–7 March 2009. [Google Scholar]
- Pytel, K. The Fuzzy Genetic Strategy for Multiobjective Optimization. In Proceedings of the Federated Conference on Computer Science and Information Systems, Szczecin, Poland, 18–21 September 2011. [Google Scholar]
- Pytel, K.; Nawarycz, T. A Fuzzy-Genetic System for ConFLP Problem. In Advances in Decision Sciences and Future Studies; Progress & Business Publishers: Krakow, Poland, 2013; Volume 2. [Google Scholar]
- Herrera, F.; Lozano, M. Adaptation of Genetic Algorithm Parameters Based on Fuzzy Logic Controllers. 2007. Available online: https://api.semanticscholar.org/CorpusID:18275513 (accessed on 10 November 2023).
- Lin, L.; Gen, M. Auto-tuning strategy for evolutionary algorithms: Balancing between exploration and exploitation. Soft Comput. 2009, 13, 157–168. [Google Scholar] [CrossRef]
- Varnamkhasti, M.J.; Lee, L.S.; Bakar, M.R.; Leong, W.J. A genetic algorithm with fuzzy crossover operator and probability. Adv. Oper. Res. 2012, 2012, 956498. [Google Scholar] [CrossRef]
- Syzonov, O.; Tomasiello, S.; Capuano, N. New Insights into Fuzzy Genetic Algorithms for Optimization Problems. Algorithms 2024, 17, 549. [Google Scholar] [CrossRef]
- Samsuria, E.; Mahmud, M.S.A.; Wahab, N.A.; Romdlony, M.Z.; Abidin, M.S.Z.; Buyamin, S. Adaptive Fuzzy-Genetic Algorithm Operators for Solving Mobile Robot Scheduling Problem in Job-Shop FMS Environment. Robot. Auton. Syst. 2024, 176, 104683. [Google Scholar] [CrossRef]
- Santiago, A.; Dorronsoro, B.; Fraire, H.J.; Ruiz, P. Micro-Genetic algorithm with fuzzy selection of operators for multi-Objective optimization: μFAME. Swarm Evol. Comput. 2021, 61, 100818. [Google Scholar] [CrossRef]
- Im, S.; Lee, J. Adaptive crossover, mutation and selection using fuzzy system for genetic algorithms. Artif. Life Robot. 2008, 13, 129–133. [Google Scholar] [CrossRef]
- Gao, X.; Xie, W.; Wang, Z.; Zhang, T.; Chen, B.; Wang, P. Predicting human body composition using a modified adaptive genetic algorithm with a novel selection operator. PLoS ONE 2020, 15, e0235735. [Google Scholar] [CrossRef]
- Pytel, K. Hybrid Multievolutionary System to Solve Function Optimization Problems. In Proceedings of the Federated Conference on Computer Science and Information Systems, Prague, Czech Republic, 3–6 September 2017. [Google Scholar]
- Pytel, K. Hybrid Multi-Evolutionary Algorithm to Solve Optimization Problems. Appl. Artif. Intell. 2020, 34, 550–563. [Google Scholar] [CrossRef]
- Pytel, K.; Nawarycz, T. The Fuzzy-Genetic System for Multiobjective Optimization. In Proceedings of the International Symposium on Swarm and Evolutionary Computation/Symposium on Swarm Intelligence and Differential Evolution, Zakopane, Poland, 29 April–3 May 2012; pp. 325–332. [Google Scholar] [CrossRef]
- Pytel, K.; Nawarycz, T. Analysis of the Distribution of Individuals in Modified Genetic Algorithms. In Proceedings of the 10th International Conference on Artificial Intelligence and Soft Computing (ICAISC 2010), Zakopane, Poland, 13–17 June 2010; pp. 197–204. [Google Scholar] [CrossRef]
- Pytel, K. Fuzzy logic applied to tunning mutation size in evolutionary algorithms. Sci. Rep. 2025, 15, 1937. [Google Scholar] [CrossRef] [PubMed]
- Jensi, R.; Wiselin, G. An improved krill herd algorithm with global exploration capability for solving numerical function optimization problems and its application to data clustering. Appl. Soft Comput. 2016, 46, 230–245. [Google Scholar] [CrossRef]
- Potter, M.; De Jong, K. A cooperative coevolutionary approach to function optimization. In Parallel Problem Solving from Nature; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1994; Volume 866. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Liang, J.; Qu, B.; Suganthan, P.; Chen, Q. Problem definitions and evaluation criteria for the CEC 2015 competition on learning-based real-parameter single objective optimization. In Technical Report201411A, Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report; Nanyang Technological University: Singapore, 2014; Volume 29, pp. 625–640. [Google Scholar]
- Karger, D.; Minkoff, M. Building Steiner trees with incomplete global knowledge. In Proceedings of the Proceedings 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 613–623. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Lu, S.; Han, S.; Zhou, W.; Zhang, J. Recruitment-imitation mechanism for evolutionary reinforcement learning. Inf. Sci. 2021, 553, 172–188. [Google Scholar] [CrossRef]
- Wang, H.; Yu, X.; Lu, Y. A reinforcement learning-based ranking teaching-learning-based optimization algorithm for parameters estimation of photovoltaic models. Swarm Evol. Comput. 2025, 93, 101844. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Heris, M.K. Teaching-Learning-Based Optimization in MATLAB. Yarpiz. 2015. Available online: https://yarpiz.com/83/ypea111-teaching-learning-based-optimization (accessed on 16 June 2022).
- The Fundamental Clustering Problems Suite. Available online: https://www.uni-marburg.de/fb12/datenbionik/data/ (accessed on 15 September 2023).
- Yarpiz/Mostapha Heris. CMA-ES in Matlab. 2022. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52898-cma-es-in-matlab (accessed on 16 June 2022).
- Mirjalili, S. Grey Wolf Optimizer (GWO). Available online: https://www.mathworks.com/matlabcentral/fileexchange/44974-grey-wolf-optimizer-gwo (accessed on 13 June 2022).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kóczy, L.T. Computational complexity of various fuzzy inference algorithms. Ann. Univ. Sci. Bp. Sect. Comp. 1991, 12, 151–158. [Google Scholar]

| Algorithm | Dimension Size | The Number of Generations | The Running Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | Min Value | Average Value | Max Value | σ | ||
| EA | 5 | 4693 | 10,898.5 | 24,386 | 5708.4 | 0.26 | 0.540 | 1.22 | 0.278 |
| 10 | 21,481 | 46,591.7 | 72,196 | 14,013.2 | 1.80 | 3.666 | 5.44 | 1.072 | |
| 20 | 207,270 | 250,109 | 345,307 | 42,042.2 | 29.05 | 35.716 | 49.38 | 6.392 | |
| FLC-EA | 5 | 2114 | 6188.1 | 14,732 | 3840.1 | 0.13 | 0.334 | 0.61 | 0.151 |
| 10 | 6790 | 13,363.1 | 21,539 | 5001.2 | 0.68 | 1.026 | 1.49 | 0.299 | |
| 20 | 37,795 | 45,190.7 | 58,356 | 7074.3 | 4.74 | 6.134 | 8.33 | 1.264 | |
| Algorithm | Function | Dimension Size | The Number of Generations | The Running Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | Min Value | Average Value | Max Value | σ | |||
| EA | CEC_f1 | 50 | 31,510 | 33,922.7 | 35,905 | 1358.5 | 6.5 | 6.96 | 7.4 | 0.30 |
| 100 | 37,877 | 40,511.2 | 43,039 | 1891.2 | 18.0 | 19.18 | 20.7 | 0.77 | ||
| CEC_f2 | 50 | 863,016 | 1,046,476.0 | 1,210,955 | 97,090.6 | 144.0 | 175.10 | 201.0 | 16.34 | |
| 100 | 858,736 | 904,124.2 | 1,056,167 | 56,535.3 | 259.0 | 273.10 | 318.0 | 16.79 | ||
| CEC_f3 | 50 | 31,464 | 33,340.3 | 36,243 | 1816.4 | 5.4 | 6.04 | 7.3 | 0.61 | |
| 100 | 60,587 | 66,627.7 | 77,322 | 4766.8 | 18.7 | 20.73 | 23.6 | 1.81 | ||
| FLC-EA | CEC_f1 | 50 | 15,537 | 17,815.7 | 18,904 | 1134.8 | 3.1 | 3.83 | 4.8 | 0.48 |
| 100 | 22,079 | 25,037.3 | 27,040 | 1344.6 | 9.3 | 11.03 | 11.9 | 0.75 | ||
| CEC_f2 | 50 | 159,626 | 203,278.7 | 259,870 | 30,706.9 | 26.5 | 33.67 | 45.0 | 5.13 | |
| 100 | 157,404 | 167,989.9 | 188,238 | 10,955.1 | 46.6 | 51.27 | 55.6 | 3.25 | ||
| CEC_f3 | 50 | 15,859 | 18,180.4 | 20,146 | 1370.4 | 2.5 | 3.13 | 3.51 | 0.25 | |
| 100 | 25,334 | 28,594.4 | 30,701 | 1646.9 | 7.3 | 9.42 | 10.85 | 1.01 | ||
| Algorithm | Function | Dim. Size | The Number of Generations | The Running Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | Min Value | Average Value | Max Value | σ | |||
| EA | Rastrigin | 2 | 4683 | 8841.4 | 20,323 | 4544.5 | 0.16 | 0.288 | 0.54 | 0.121 |
| 5 | 19,775 | 50,067.1 | 84,228 | 21,334.4 | 0.91 | 2.365 | 3.98 | 0.981 | ||
| 10 | 62,918 | 134,660.6 | 329,182 | 80,650.2 | 5.03 | 10.612 | 25.64 | 6.230 | ||
| Styblinski–Tang | 2 | 977 | 2094.5 | 3711 | 1048.5 | 0.05 | 0.085 | 0.12 | 0.022 | |
| 5 | 3321 | 10,465.7 | 13,956 | 3941.4 | 0.20 | 0.560 | 0.73 | 0.196 | ||
| 10 | 20,455 | 39,374.8 | 67,366 | 17,382.1 | 1.48 | 2.841 | 4.79 | 1.236 | ||
| Rosenbrock | 2 | 2626 | 5091.1 | 7652 | 1885.0 | 0.08 | 0.138 | 0.19 | 0.037 | |
| Shubert | 2 | 4212 | 9056.4 | 16,943 | 4164.9 | 0.23 | 0.449 | 0.89 | 0.206 | |
| FLC-EA | Rastrigin | 2 | 419 | 3040.4 | 9632 | 2785.2 | 0.07 | 0.144 | 0.33 | 0.075 |
| 5 | 6597 | 19,526.4 | 53,574 | 15,501.5 | 0.35 | 0.914 | 2.82 | 0.773 | ||
| 10 | 4696 | 31,862.5 | 56,953 | 16,612.2 | 0.43 | 2.266 | 3.92 | 1.092 | ||
| Styblinski–Tang | 2 | 472 | 1215.1 | 2599 | 647.6 | 0.05 | 0.198 | 0.54 | 0.141 | |
| 5 | 324 | 2238.7 | 4036 | 1238.3 | 0.08 | 0.178 | 0.24 | 0.057 | ||
| 10 | 4924 | 10,863.9 | 19,091 | 4289.8 | 0.39 | 0.758 | 1.54 | 0.331 | ||
| Rosenbrock | 2 | 322 | 2333.5 | 4973 | 1406.6 | 0.07 | 0.127 | 0.18 | 0.034 | |
| Shubert | 2 | 1343 | 3924.2 | 7654 | 2115.6 | 0.13 | 0.368 | 1.24 | 0.342 | |
| Algorithm | Function | The Number of Generations | The Running Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | Min Value | Average Value | Max Value | σ | ||
| EA | f2 | 1124 | 3983.4 | 8690 | 2569.03 | 0.07 | 0.178 | 0.33 | 0.1004 |
| f3 | 8360 | 36,091.7 | 75,261 | 23,355.20 | 0.38 | 1.537 | 3.23 | 0.9683 | |
| FLC-EA | f2 | 248 | 1482.8 | 3466 | 1022.07 | 0.08 | 0.122 | 0.21 | 0.0426 |
| f3 | 594 | 13,942.1 | 32,880 | 9477.15 | 0.13 | 0.759 | 1.62 | 0.4385 | |
| Algorithm | Function | Size | The Number of Generations | |||
|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | |||
| FLC-EA | f1 | 2 | 2114 | 6188.1 | 14,732 | 3840.1 |
| 5 | 6790 | 13,363.1 | 21,539 | 5001.2 | ||
| 10 | 37,795 | 45,190.7 | 58,356 | 7074.3 | ||
| CEC_f1 | 50 | 15,537 | 17,815.7 | 18,904 | 1134.8 | |
| 100 | 22,079 | 25,037.3 | 27,040 | 1344.6 | ||
| CEC_f2 | 50 | 159,626 | 203,278.7 | 259,870 | 30,706.9 | |
| 100 | 157,404 | 167,989.9 | 188,238 | 10,955.1 | ||
| CEC_f3 | 50 | 15,859 | 18,180.4 | 20,146 | 1370.4 | |
| 100 | 25,334 | 28,594.4 | 30,701 | 1646.9 | ||
| Rastrigin | 2 | 419 | 3040.4 | 9632 | 2785.2 | |
| 5 | 6597 | 19,526.4 | 53,574 | 15,501.5 | ||
| 10 | 4696 | 31,862.5 | 56,953 | 16,612.2 | ||
| Styblinski–Tang | 2 | 472 | 1215.1 | 2599 | 647.6 | |
| 5 | 324 | 2238.7 | 4036 | 1238.3 | ||
| 10 | 4924 | 10,863.9 | 19,091 | 4289.8 | ||
| Rosenbrock | 2 | 322 | 2333.5 | 4973 | 1406.6 | |
| Shubert | 2 | 1343 | 3924.2 | 7654 | 2115.6 | |
| f2 | 2 | 248 | 1482.8 | 3466 | 1022.0 | |
| f3 | 2 | 594 | 13,942.1 | 32,880 | 9477.1 | |
| TLBO | f1 | 2 | 19 | 24.9 | 31 | 2.4 |
| 5 | 52 | 70.6 | 90 | 12.0 | ||
| 10 | 201 | 248.3 | 339 | 37.8 | ||
| CEC_f1 | 50 | 48 | 50.7 | 53 | 1.4 | |
| 100 | 54 | 54.9 | 56 | 0.8 | ||
| CEC_f2 | 50 | 30 | 31.4 | 33 | 1.1 | |
| 100 | 33 | 34.4 | 36 | 1.2 | ||
| CEC_f3 | 50 | 33 | 35.8 | 38 | 1.4 | |
| 100 | 36 | 38.2 | 40 | 1.5 | ||
| Rastrigin | 2 | 4 | 15.4 | 74 | 3.6 | |
| 5 | 145 | 784.2 | 4646 | 1310.3 | ||
| 10 * | 220 | 1659.7 | 4715 | 1443.8 | ||
| Styblinski–Tang | 2 | 10 | 15.4 | 21 | 3.6 | |
| 5 * | 21 | 40.4 | 81 | 18.4 | ||
| 10 ** | - | - | - | - | ||
| Rosenbrock | 2 | 36 | 64.9 | 97 | 19.9 | |
| Shubert | 2 | 32 | 40.8 | 48 | 5.1 | |
| f2 | 2 | 26 | 42.2 | 75 | 13.1 | |
| f3 | 2 | 10 | 17.6 | 31 | 6.5 | |
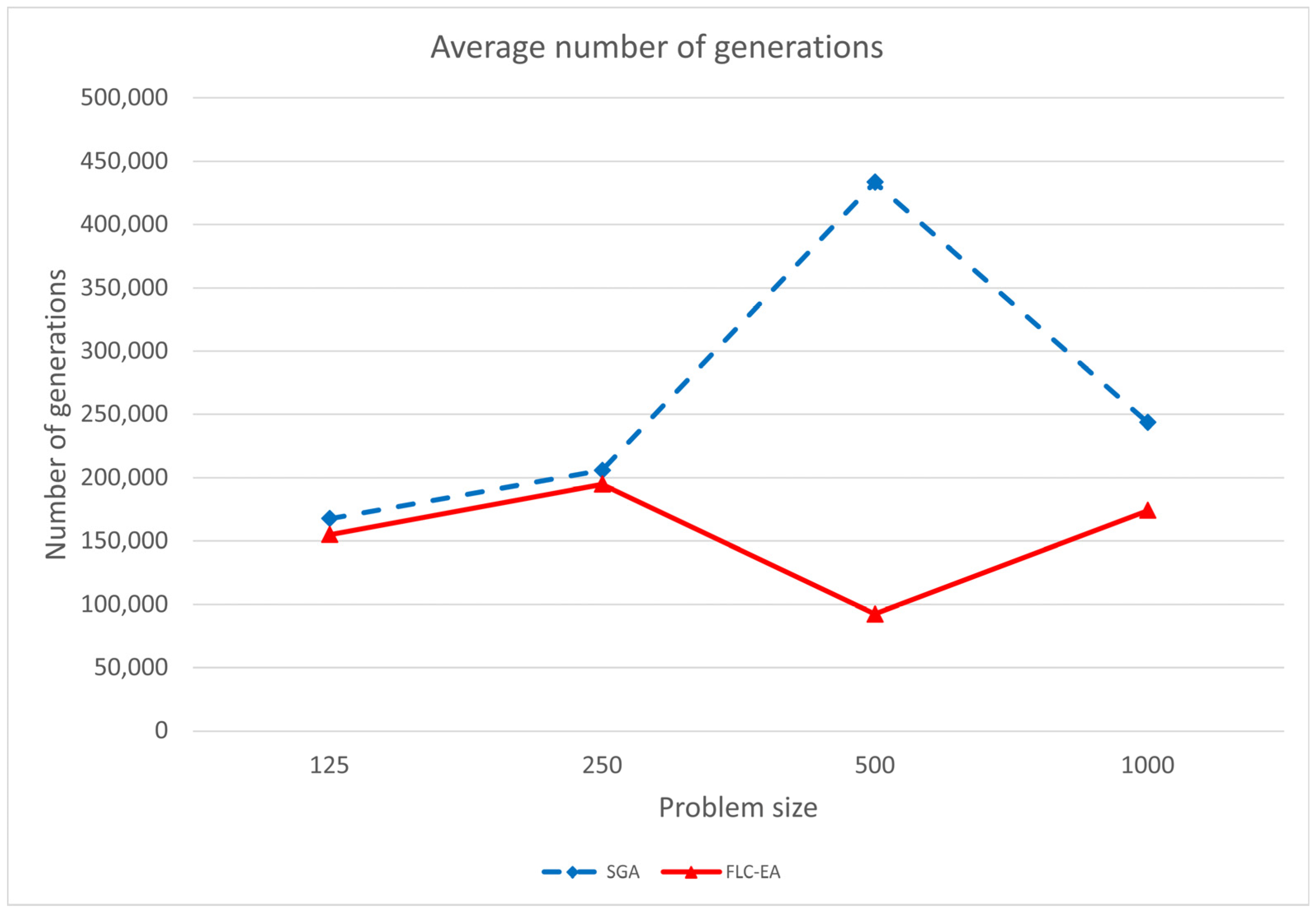
| Algorithm | Problem Size | Constant C | Stop Criterion | The Number of Generations | |||
|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | ||||
| SGA | 125 | 7500 | 6300 | 48,010 | 167,594.6 | 285,740 | 0.53 × 1011 |
| 250 | 15,000 | 13,150 | 92,350 | 205,769.3 | 483,001 | 1.74 × 1011 | |
| 500 | 30,000 | 25,000 | 213,906 | 433,440.2 | 1,092,699 | 6.51 × 1011 | |
| 1000 | 120,000 | 47,000 | 152,301 | 25,6785.5 | 641,331 | 1.79 × 1011 | |
| FLC-EA | 125 | 7500 | 6300 | 41,761 | 96,255.4 | 141,282 | 0.12 × 1011 |
| 250 | 15,000 | 13,150 | 49,010 | 121,622.1 | 176,979 | 0.16 × 1011 | |
| 500 | 30,000 | 25,000 | 28,733 | 87,851.2 | 207,987 | 0.21 × 1011 | |
| 1000 | 120,000 | 47,000 | 131,543 | 170,097.9 | 214,802 | 0.49 × 1011 | |
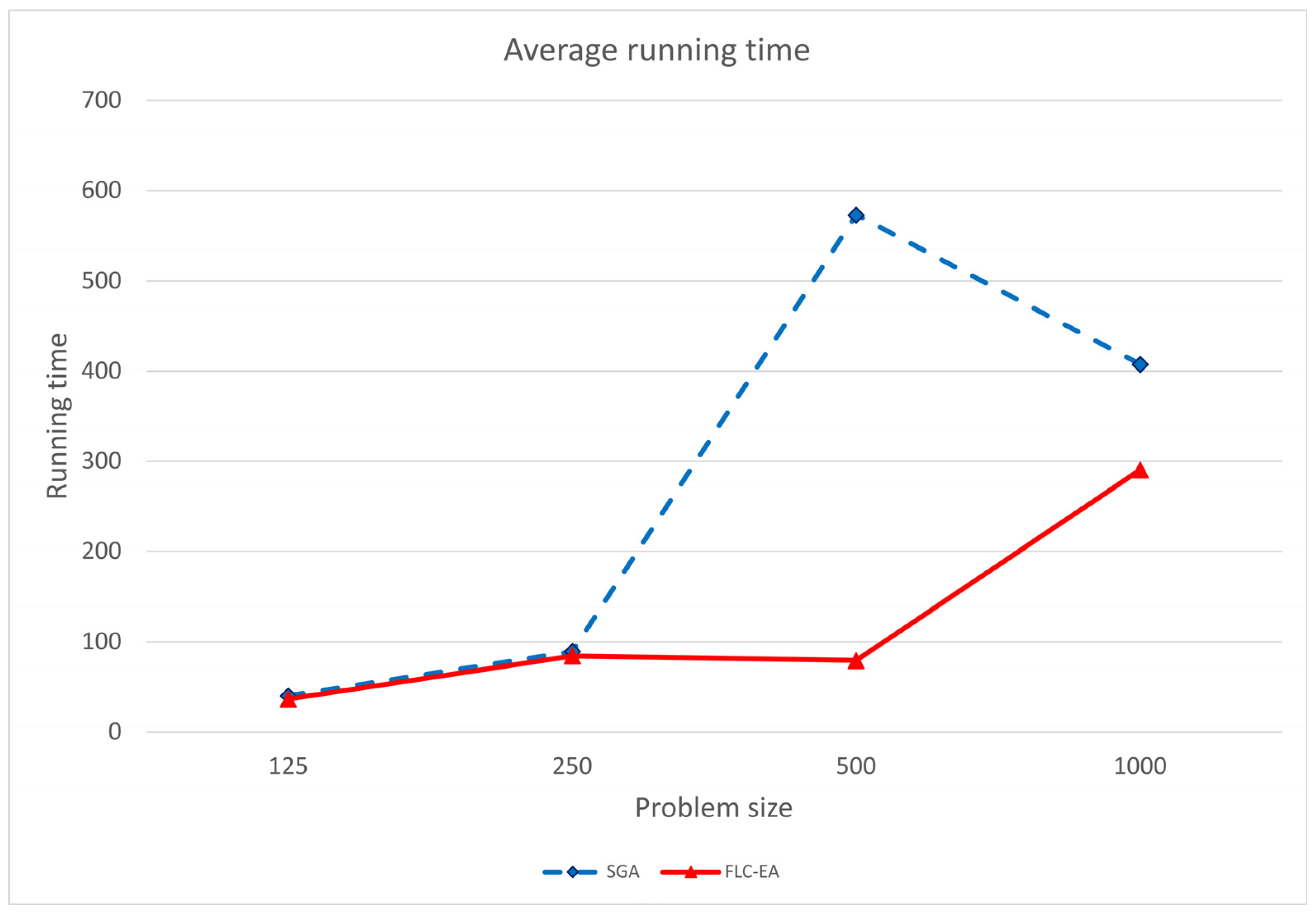
| Algorithm | Problem Size | Constant C | Stop Criterion | The Running Time (s) | |||
|---|---|---|---|---|---|---|---|
| Min Value | Average Value | Max Value | σ | ||||
| SGA | 125 | 7500 | 6300 | 11.5 | 40.26 | 69.2 | 2941.27 |
| 250 | 15,000 | 13,150 | 40.0 | 89.16 | 207.0 | 33,041.66 | |
| 500 | 30,000 | 25,000 | 224.0 | 573.13 | 2069.2 | 2,981,111.76 | |
| 1000 | 120,000 | 47,000 | 253.0 | 426.85 | 1066.0 | 496,622.85 | |
| FLC-EA | 125 | 7500 | 6300 | 14.9 | 34.76 | 53.0 | 1506.59 |
| 250 | 15,000 | 13,150 | 39.7 | 81.55 | 110.2 | 5455.62 | |
| 500 | 30,000 | 25,000 | 44.1 | 125.59 | 285.9 | 38,356.11 | |
| 1000 | 120,000 | 47,000 | 310.2 | 404.61 | 509.9 | 29,700.81 | |
| Problem name | Algorithm | Lsun | TwoDiamonds | WingNut | EngyTime |
|---|---|---|---|---|---|
| Number of objects | 400 | 800 | 1070 | 4096 | |
| Number of clusters | 3 | 2 | 2 | 2 | |
| Number of dimensions | 2 | 2 | 2 | 2 | |
| Stop criterion | 600 | 820 | 1300 | 8395 | |
| Number of generations to stop criterion | EA | 22,849 | 3851 | 11,642 | 19,621 |
| FLC-EA | 6056 | 2916 | 2350 | 1350 | |
| Running time to stop criterion [s] | EA | 18.8 | 6.5 | 23.7 | 158.6 |
| FLC-EA | 6.5 | 4.1 | 8.2 | 22.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pytel, K. Fuzzy Guiding of Roulette Selection in Evolutionary Algorithms. Technologies 2025, 13, 78. https://doi.org/10.3390/technologies13020078
Pytel K. Fuzzy Guiding of Roulette Selection in Evolutionary Algorithms. Technologies. 2025; 13(2):78. https://doi.org/10.3390/technologies13020078
Chicago/Turabian StylePytel, Krzysztof. 2025. "Fuzzy Guiding of Roulette Selection in Evolutionary Algorithms" Technologies 13, no. 2: 78. https://doi.org/10.3390/technologies13020078
APA StylePytel, K. (2025). Fuzzy Guiding of Roulette Selection in Evolutionary Algorithms. Technologies, 13(2), 78. https://doi.org/10.3390/technologies13020078






