Abstract
Ground segmentation in LiDAR point clouds is a foundational capability for autonomous systems, enabling safe navigation in applications ranging from urban self-driving vehicles to planetary exploration rovers. Reliably distinguishing traversable surfaces in geometrically irregular or sensor-sparse environments remains a critical challenge. This paper introduces a hybrid framework that synergizes multi-resolution polar discretization with sparse convolutional neural networks (SCNNs) to address these challenges. The method hierarchically partitions point clouds into adaptive sectors, leveraging PCA-derived geometric features and dynamic variance thresholds for robust terrain modeling, while a SCNN resolves ambiguities in data-sparse regions. Evaluated in structured (SemanticKITTI) and unstructured (Rellis-3D) environments, two different versions of the proposed method are studied, including a purely geometric method and a hybrid approach that exploits deep learning techniques. A comparison of the proposed method with its purely geometric version is made for the purpose of highlighting the strengths of each approach. The hybrid approach achieves state-of-the-art performance, attaining an F1-score of 95.4% in urban environments, surpassing the purely geometric (91.4%) and learning-based baselines. Conversely, in unstructured terrains, the geometric variant demonstrates superior metric balance (80.8% F1) compared to the hybrid method (75.8% F1), highlighting context-dependent trade-offs between precision and recall. The framework’s generalization is further validated on custom datasets (UMH-Gardens, Coimbra-Liv), showcasing robustness to sensor variations and environmental complexity. The code and datasets are openly available to facilitate reproducibility.
1. Introduction
In an increasingly complex technological landscape, marked by substantial advances in the field of artificial intelligence (AI) algorithms, the attainment of fully autonomous navigation has emerged as a key challenge. This capability is regarded as a critical enabling technology across a range of domains, including robotics and environmental monitoring. In these domains, the interpretation of terrain through point cloud analysis serves as the foundational element for the development of safe and adaptive navigation systems [1].
Historically, the analysis of ground planes was approached through terrain analysis algorithms based on heuristic methods. These pioneering techniques relied on geometric computations to model ground conditions [2,3,4]. However, such early frameworks exhibited critical limitations, including limited adaptability to dynamic environments, insufficient robustness under contextual variations, and an over-reliance on predefined rule-based thresholds.
The exponential progress in computational power, sensor technology and AI algorithms has revolutionized ground detection techniques. In this technological transition, LiDAR-based sensing systems have become a fundamental component, offering distinct advantages, including precise measurements, long-range detection capabilities, and resistance to ambient light variations and electromagnetic interference. These developments have given rise to a variety of methodologies for ground plane detection through spatial environmental representations, including two-dimensional occupancy maps [5], digital elevation models (DEMs) [6], and voxel-based 3D occupancy frameworks [7,8,9]. Ground segmentation in point clouds, however, transcends these conventional approaches, serving as a critical enabler for advanced applications such as road boundary extraction [10,11], target tracking [12], and object detection [13,14].
The complexity of ground segmentation, a task requiring the precise separation of traversable terrain from obstacles in dense and heterogeneous point clouds, coupled with the significant challenges of generating and annotating large-scale datasets for robust algorithm evaluation, forms the core motivation for this research. Current methods struggle to adapt to dynamic environments where sensor noise and geometric irregularities degrade performance, particularly in unstructured terrains. Furthermore, the manual annotation of LiDAR data is still very time-consuming.
The present study proposes a novel LiDAR point cloud ground segmentation method that combines the following two complementary approaches: an advanced geometric analysis and AI techniques. The core innovation lies in a multi-resolution cylindrical space discretization framework, explicitly designed to mitigate the usual sparsity of LiDAR point clouds. This spatial partitioning strategy enables robust terrain characterization, effectively addressing the limitations of conventional segmentation methods that struggle with heterogeneous point distributions. As a complementary methodological component, we introduce a sparse neural network based on TE-NeXt (Traversability Estimation ConvNeXt) [15] that operates in regions where low point density hinders reliable geometric segmentation. This hybrid architecture leverages geometric features for structural coherence while employing learned feature representations to resolve ambiguities in data-sparse zones, thereby achieving comprehensive traversable-terrain separation across diverse environmental conditions.
The integration of geometric analysis and AI techniques introduces a novel paradigm to address the inherent challenges of 3D point cloud traversable terrain segmentation, achieving superior performance in both structured and unstructured environments. In summary, the main contributions of this paper are as follows:
- A novel pipeline that maximizes geometric feature extraction while compensating for information-scarce regions through TE-NeXt [15], enabling robust terrain modeling in sparse point clouds.
- Rigorous benchmarking on structured (SemanticKITTI) and unstructured (Rellis-3D) environments, preserving raw point cloud integrity by evaluating all scene elements without algorithmic modifications or data preprocessing.
- Introduction of novel LiDAR domain adaptation datasets to validate model generalization across sensor configurations and environmental conditions, addressing critical gaps in cross-sensor generalization for ground segmentation.
The remaining sections of the paper are structured as follows: Section 2 outlines the prevailing methodologies employed for addressing ground segmentation. Section 3 presents the proposed method in detail. Then, Section 4 presents the databases on which the performance of the method has been evaluated. The subsequent section (Section 5) provides a comparison of the results of the proposed method with the state of the art. In addition, a qualitative evaluation is provided with data collected by the authors in two very different contexts to validate the adaptation and applicability in real-world environments. Finally, Section 6 presents the conclusions drawn from the study.
2. Related Work
This section introduces the most representative techniques in the context of ground segmentation and traversability analysis. The state of the art has been divided into different parts as follows: Section 2.1 describes probabilistic models for ground segmentation, Section 2.2 provides a detailed exposition of methods based on geometric heuristics, Section 2.3 offers a comprehensive introduction to methods employing visual data, and ultimately, Section 2.4 offers a state-of-the-art overview of methods based on AI techniques.
2.1. Probabilistic Ground Segmentation Models
Probabilistic methods represent a sophisticated approach to terrain analysis, providing a robust framework for dealing with uncertainty in spatial measurements captured by sensors. Thus, Markov Random Fields (MRFs) [16] are considered as one of the main probabilistic methods for the task of ground segmentation. Zhang et al. [17] developed a multi-label MRF in polar coordinates, incorporating local smoothness constraints and slope thresholds to filter obstacles. On the other hand, Huang et al. [18] employed an MRF that operates on local features such as height and gradients between adjacent points.
Among the predominant probabilistic approaches for ground segmentation, Gaussian Process Regression (GPR) [19] is distinguished by its unique approach to deriving probabilistic estimations through continuous surface modeling, compared to discrete grid-based methods. Chen et al. [20] introduced sparse covariance functions to GPR-based pipelines, improving computational efficiency while preserving discriminative power for the identification of ground points in sparse and noisy point clouds.
Following the probabilistic methodology, Del Pino et al. [21] used a probabilistic graph-based model to represent and analyze the ground geometry. It applies stochastic estimation techniques to iteratively update the ground plane parameters (height and slope).
2.2. Geometric-Based Ground Segmentation Methods
In the context of ground segmentation for LiDAR point clouds, geometric approaches have emerged as the predominant strategy, primarily due to their real-time processing capabilities. These methods excel in transforming complex 3D spatial data into computationally efficient 2.5D representations, thereby facilitating precise terrain surface identification in dynamic and unstructured environments. However, a critical limitation of this approach is the frequent occurrence of under-segmentation artifacts, where points from distinct objects are erroneously merged into a single segment. Recent studies have sought to address these challenges through various innovative techniques. Proposals such as [22] developed an elevation map employing euclidean clustering principles and an adaptive multi-plane extraction method based on Random Sample Consensus (RANSAC) [23]. Similarly, Steinke et al. [24] proposed a 2D elevation map representation coupled with a point height variance analysis approach to classify cells as terrain. Expanding on the concept of data representation, Oh et al. [25] introduced a graph-based approach known as Tri-Grid Field (TGF) to model terrain geometry, facilitating the analysis of local convexity and concavity to determine environmental traversability.
Another prevalent form of representation of the three-dimensional environment is the Digital Terrain Model (DTM). Studies such as Refs. [26,27] aim to create such models by applying morphological filters to airborne LiDAR data for ground segmentation. Morphological operations are employed to filter objects based on their size and height relative to the terrain, thereby preserving steep features. The DTMs represent the bare-earth surface by excluding non-ground features such as buildings and vegetation while preserving key terrain characteristics like slopes, ridges, and cliffs. Morphological filters, while effective in simple terrain, face challenges in complex environments (urban, mountainous, and forested) due to their parameter sensitivity, computational limitations, and difficulty in preserving topographic detail.
However, the challenges of processing raw and unorganized point clouds have driven the development of methods that directly operate on 3D spatial data without prior structuring. Himmelsbach et al. [28], LineFit, pioneered a uniform angular sector discretization framework to mitigate radial sparsity in LiDAR point clouds, particularly at increasing sensor distances. This approach implements an adaptive linear adjustment to estimate straight-line equations per radial bin, with ground points determined through a multi-criteria filter. Conversely, Zermas et al. [29] proposed the technique named Ground Plane Fitting (GPF), dividing point clouds into three parts along the x-axis, implementing a deterministic plane estimation algorithm that utilizes adaptive seed selection with low spatial variance for ground plane estimation based on Principal Component Analysis (PCA). This approach avoids stochastic methods such as RANSAC [23], bypassing the time-consuming computation of iterations and introducing robustness to point density.
Recent advances in the field have addressed the sensitivity to point density variations through the implementation of non-uniform polar discretization strategies. Lim et al. [30], Patchwork, introduced the Concentric Zone Model (CZM), partitioning the spatial domain into annular subregions. In line with the methodology of Zermas et al. [29], the authors of this work implemented a Regional Ground Plane Fitting (R-GPF) that estimates partial planes in each bin by principal component analysis, with adaptive selection of initial seeds to avoid local minima. Building on this work, Lee et al. [31], Patchwork++, incorporated Temporal Terrain Reversal (TGR) to mitigate partial under-segmentation issues by leveraging information from previous frames.
Further advancements in the area include the work of Deng et al. [32] and Dong et al. [33], who proposed voxel neighborhood continuity analysis. These approaches utilize contextual relationships between adjacent voxels to enhance segmentation robustness in complex terrains with abrupt elevation changes. Deng et al. [32], RT-GS, determined ground continuity between adjacent grids by comparing the normal vectors and average heights of ground planes, while Dong et al. [33] employed spatial relationships between sectors to address areas with insufficient information for confident plane extraction.
2.3. Visual-Based Ground Segmentation Methods
Visual ground segmentation methods have emerged as a computationally efficient paradigm for terrain identification in complex urban environments. These approaches exploit the structured nature of LiDAR data by projecting 3D point clouds onto 2D representations, enabling the application of image processing techniques while preserving spatial relationships. Early work by Moosmann et al. [34] introduced a local convexity criterion operating directly on spherical range images, enabling ground–object separation in non-flat environments without compromising 3D geometric representation.
This foundational work inspired subsequent advances in range-image processing, such as Bogoslavskyi et al. [35]. The authors developed a slope-based segmentation method which transformed raw LiDAR scans into slope images through pairwise row-pixel analysis, followed by Savitsky–Golay smoothing and ground labeling.
Contemporary techniques such as the Jumping Convolution Process (JCP) [36] or DipG-Seg [37] demonstrate this progression through hierarchical refinement frameworks. These approaches combine non-linear filtering with majority-vote kernel convolutions based on convolution to improve segmentation accuracy. Despite these advancements, fundamental limitations persist in purely image-based segmentation. The widespread reliance on independent slope features, calculated from isolated vertical pixel pairs, proves to be inadequate for complex terrains. This constraint arises from the limited receptive field of slope operators, which cannot capture contextual relationships across adjacent regions.
2.4. Learning-Based Ground Segmentation Methods
Machine learning has emerged as a principal paradigm for addressing ground segmentation challenges. Recent techniques, such as PSVM [38] and PSVM-2 [39], take advantage of Support Vector Machine (SVM) classifiers to analyze geometric descriptors derived from raw LiDAR point clouds. These include surface normals, local curvature metrics, and contextual terrain features. A key innovation in these approaches is their multi-resolution pyramidal framework, which hierarchically fuses spatial information across varying scales to enhance segmentation robustness in heterogeneous environments.
However, these methods rapidly transitioned toward visual data as the primary input, largely driven by the remarkable performance of convolutional neural networks (CNNs) in image classification tasks. This shift was the key factor that led to the development of specialized network architectures such as GA-Nav [40], DeconvNet [41], or the bilateral architecture proposed in [42]. All of these frameworks exclusively utilize visual inputs for pixel-wise terrain classification, aiming to identify traversable paths by distinguishing navigable ground surfaces from obstacles in complex environments.
From a two-dimensional perspective to a three-dimensional domain, CNNs become impractical when handling sparse 3D point clouds, where data sparsity stems from the irregular spatial distribution of non-zero measurements. The direct application of conventional 2D convolution kernels to these irregular 3D structures results in computational demands that scale cubically with data density. Thus, two possible approaches emerge.
The first alternative integrates geometric priors with learned representations to balance adaptability and computational efficiency. GndNet [43] exemplifies this approach by employing an encoder–decoder architecture that relies on PointNet and a Pillar Feature Encoding network to estimate terrain elevation in grids. SectorGS-Net [44] focuses on sector-wise feature encoding, enabling more adaptive and context-aware ground segmentation in complex outdoor environments. Recent hybrid frameworks, such as those proposed by Atas et al. [45], combine geometric features with robot dynamics (orientation and movement) through a fully connected neural network.
The second approach is based on the notion of sparse convolution, a concept derived from signal processing. Conventional 2D convolution systematically scans all grid positions; in contrast, sparse convolution dynamically focuses computational resources on occupied voxels via hash-based memory management. By eliminating redundant computations in empty spaces, SCNNs achieve significant gains in both computational efficiency and memory utilization, enabling real-time performance in autonomous systems that rely on LiDAR-based terrain analysis. Studies such as [46,47] use SCNNs to predict per-voxel traversability from geometric features (height, density, and structural context).
In light of the significant advancements witnessed in recent years, an alternative approach involves the utilization of Large Language Models (LLMs) to facilitate 3D segmentation through textual instructions. Researchers have proposed approaches based on contrastive learning, which aims to align a textual description with geometric points belonging to a specific class. This alignment can be achieved through the fusion of 3D embeddings [48] or by directly processing point clouds [49,50].
3. Methodology
The method proposed in this article primarily falls within the geometric approaches category, with a secondary emphasis on machine learning paradigms through the use of a sparse neural network to overcome the sensitivity of geometric approaches to sparse data as point clouds. Specifically, our approach lies at the intersection of non-uniform polar discretization methods (such as those proposed by Lim et al. [30] and Lee et al. [31]) and approaches that utilize neighborhood analysis to enhance robustness in complex terrains (Deng et al. [32] and Dong et al. [33]). The main limitations this method aims to overcome are as follows: (i) robustness to the incremental dispersion of data inherent to LiDAR technology and (ii) independence from parameter selection or decision thresholds that determine the performance of geometric methods, limiting their adaptability to diverse environment. By addressing these aspects, the proposed method offers a more versatile and robust solution for ground segmentation in diverse environments, bridging the gap between purely geometric and learning-based approaches.
3.1. Problem Statement
Given a LiDAR point cloud , where , we define the ground segmentation task as a binary segmentation problem, wherein each point of the cloud is assigned a label {0,1} obstacle and traversable ground, respectively. Therefore, the datasets under consideration have been reduced to two labels. Points within the traversability category are defined as follows: road, parking, sidewalk, other ground, and lane marking in structured environments (SemantincKITTI) and terrain, grass, dirt, and mud in unstructured environments (Rellis-3D). Conversely, the obstacle category includes all other classes represented in the datasets under review, such as building, bicycle, car, person, and so forth.
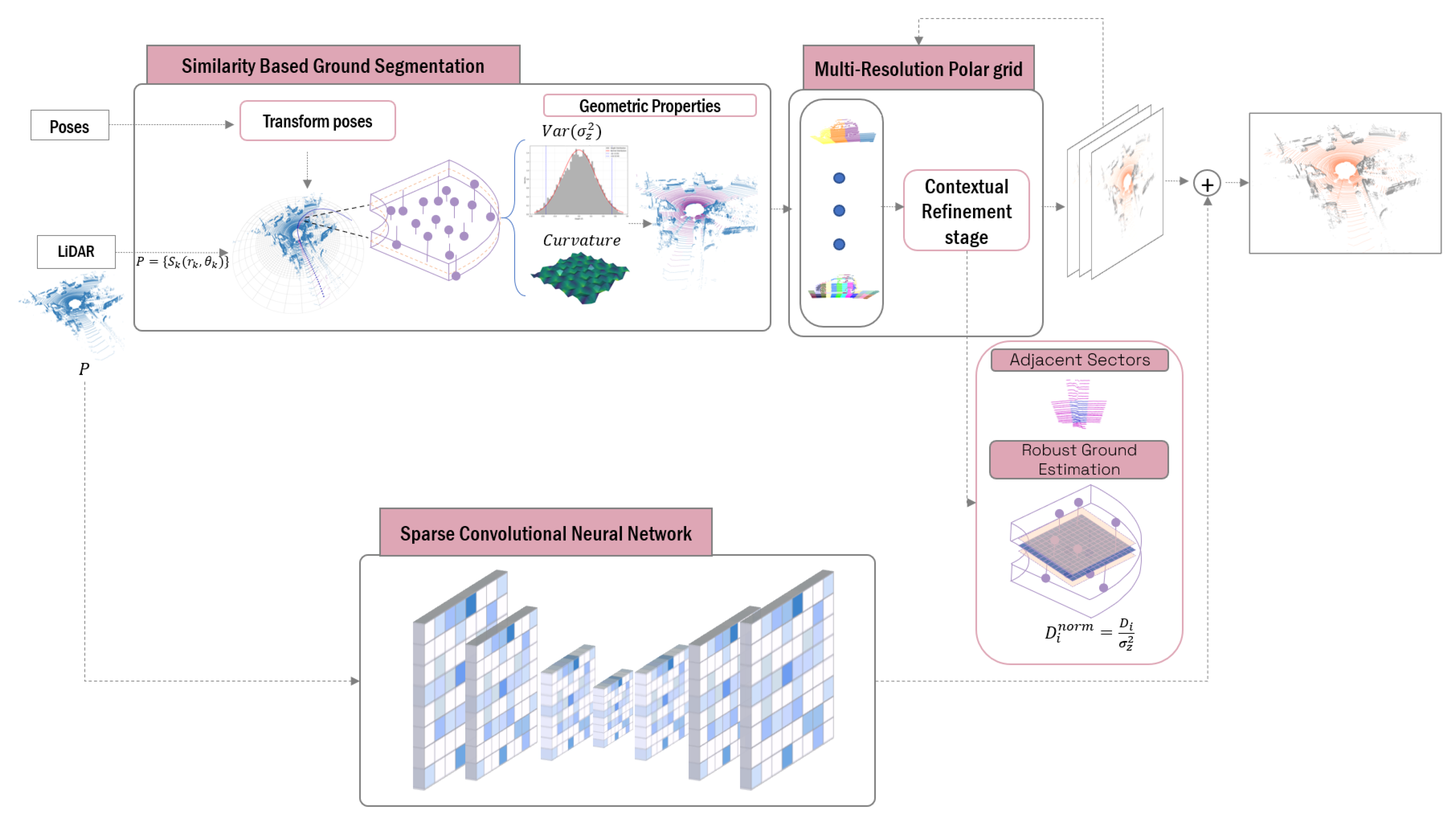
This section introduces a novel methodology for traversable ground segmentation in 3D point cloud data, combining an iterative multi-resolution polar mapping framework with TE-NeXt [15] to address the challenges of terrain feature extraction across diverse environmental conditions, as illustrated in Figure 1. The method begins by discretizing the spatial domain into coarse-resolution polar sectors by means of CZM. This initial discretization establishes the core representation of the environment, allowing the efficient extrapolation of geometric knowledge from historically traversed regions across the entire discretized space.
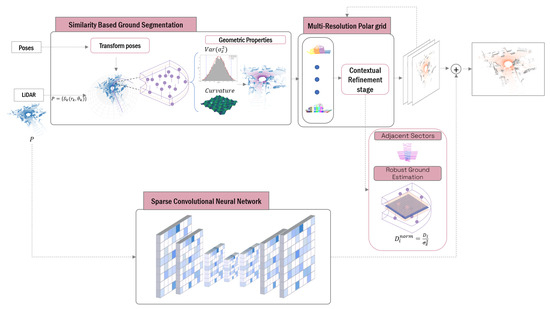
Figure 1.
Multi-stage traversable ground segmentation framework overview. This figure illustrates the processes involved in the segmentation of traversable ground. Given an input point cloud, prior knowledge is employed to identify analogous sectors. Thereafter, the discretization and calculation of ground detection planes are performed iteratively through various resolutions.
Following this initialization, sector classification is iteratively refined using geometric criteria designed to minimize the dependence on point density. Thus, at each level of resolution, for each sector and its adjacencies, the plane coefficients are estimated after a selection of seeds suitable for carrying out Principal Component Analysis (PCA), mitigating the density-dependent limitations in traditional methods like RANSAC. In order to address the limitations of the geometric approach, as will be discussed in Section 5, TE-NeXt [15] is introduced. This network is based on an encoder–decoder architecture adapted to the three-dimensional domain and follows the development philosophy presented in ConvNeXt [51].
3.2. Similarity-Based Ground Segmentation
The representation of continuous domains through finite elements constitutes the main strategy in 3D data processing. In the context of point cloud-based ground segmentation, single-plane surface detection reveals limitations when applied to complex terrains. Therefore, the procedure of dividing the three-dimensional space into zones of variable geometry allows for the extraction of local features, the modeling of surface variability, and the mitigation of point-cloud scattering effects. Thus, the proposed approach implements the polar discretization designed in [30], partitioning the 3D space, , into sectors with adaptive radial resolution.
Existing methodologies in the literature, as discussed in Section 2, rely on the aforementioned discretization and human-defined thresholds to classify individual points as traversable ground or obstacles. These approaches aim to achieve optimal segmentation by manually tuning geometric or statistical criteria, such as slope limits or elevation variances. In contrast, modern machine learning (ML) paradigms, particularly self-supervised methods, exploit learnt patterns from historical data to automate decision-making. The proposed method extends this concept by incorporating spatio-temporal context, ensuring that the initial ground plane estimation is based on both historical and future positional experiences. This strategy is tested in widely used datasets in the field, which provide spatio-temporal pose associations for each point cloud. The decision to utilize positional data is grounded in the fact that the proposed method is specifically tailored for intelligent mobile systems. Positional information allows the incorporation of terrain features from previously traversed areas, which serve as key discriminative factors for identifying traversable ground. In the absence of such positional data, the method can still be implemented; however, it would lack of the similarity-based component for detecting traversable ground.
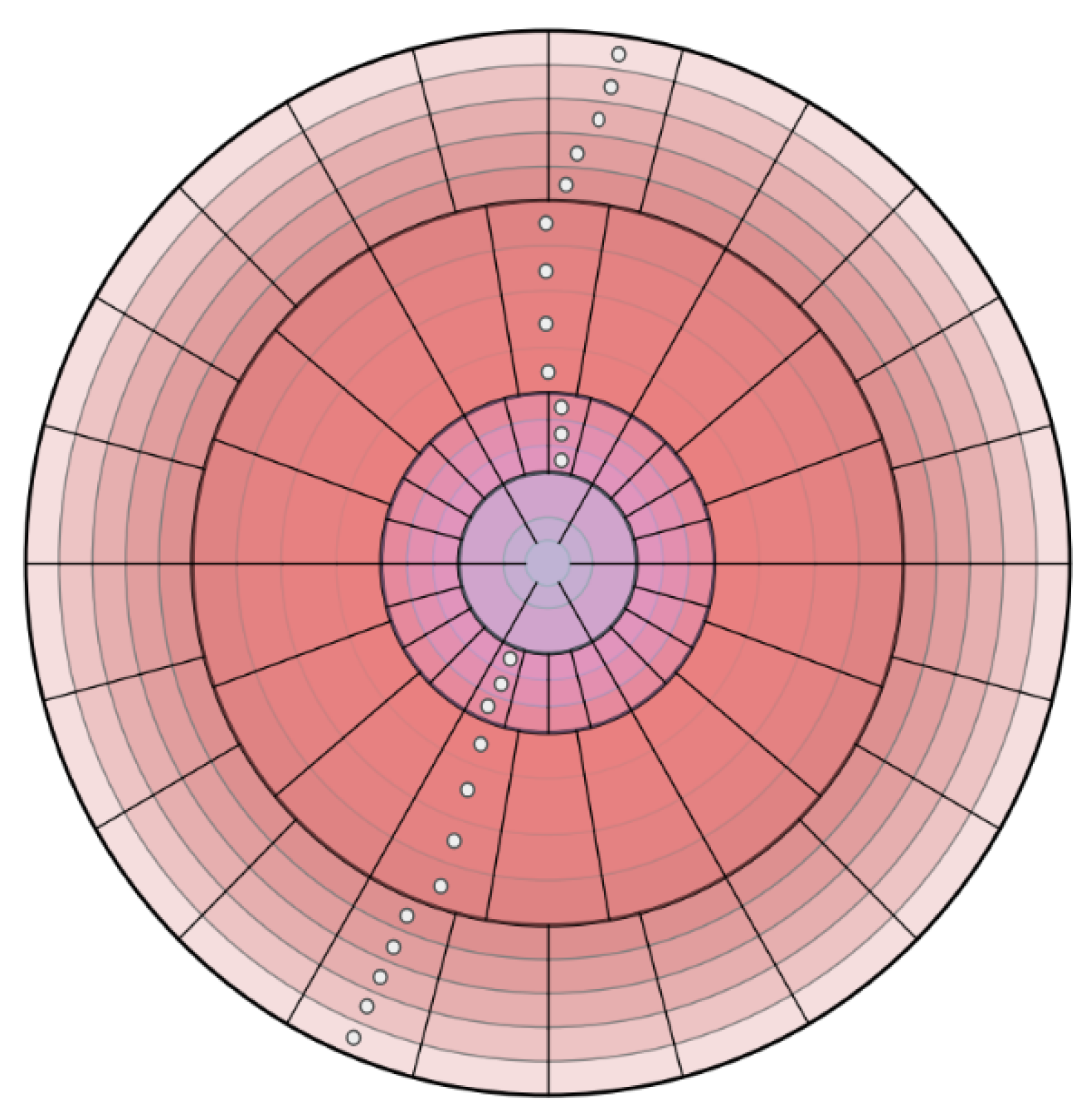
Figure 2 illustrates a concentric zone model applied to 3D point clouds. The space is divided into polar segments with varying resolutions based on the radial distance from the sensor. Specifically, the model partitions the space into distinct zones, which are further subdivided into X concentric rings. Each ring corresponds to an annular region defined by two radii, and . Additionally, each ring is segmented into angular sectors determined by azimuthal and polar angles in spherical coordinates. Furthermore, the coordinates which define the prior geometric knowledge from regions previously traversed by the robotic platform are represented as white points in Figure 2. This knowledge contributes to the identification of traversable terrain properties by means of historical navigation data. Coordinate transformations are facilitated by the global reference frames associated with each point cloud, which are obtained through classical algorithms such as the Iterative Closest Point (ICP) or visual odometry. Specifically, positions, , are projected into the current sensor frame, L, via Equation (1). This equation represents the homogeneous transformations applied to positional data measured in a global reference system, G, to a local system, L. The matrix is the homogeneous transformation matrix that allows the transformation of coordinates from the global system to the local system. The coordinates of the positions, j, expressed in the global system G are denoted as .
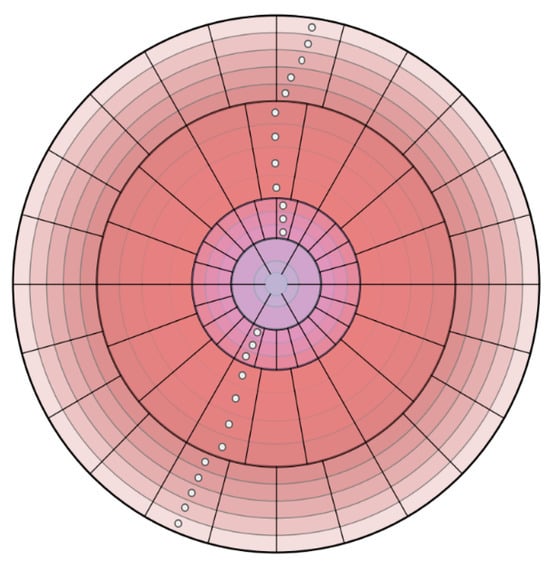
Figure 2.
Projection of Cartesian coordinates at the coarsest polar resolution level (Level 0).
Once the Cartesian coordinates are projected into the local polar grid, an adaptive threshold is computed based on two sector-wise geometric properties derived from PCA. First, the height variance, represented as in Equation (2), quantifies elevation consistency within each K sector, where represents the mean height of the N points in the sector. Second, the surface curvature, , is derived from the eigenvalues, Equation (3), where lower curvature values indicate planar regions characteristic of ground surfaces.
To establish dynamic thresholds, the method aggregates these metrics across K sectors, computing the global mean and standard deviation of both geometric properties extracted. Thus, a sector is classified as traversable if it satisfies the dual thresholding criterion shown in Equation (4), where and are tunable parameters controlling the classification confidence. Algorithm 1 delineates the implementation of the aforementioned methodology.
| Algorithm 1 Ground Segmentation via similarity search |
|
3.3. Multi-Resolution Polar Grid
Following the initial classification of sectors based on the geometric criteria outlined previously, the method addresses residual cases where traversable ground points remain misclassified due to the following two primary challenges:
- 1.
- 2.
- Sparse data ambiguities are present in sectors with minimal point density (e.g., distant regions). There is an absence of sufficient data for reliable PCA-based feature extraction (Equation (3)).
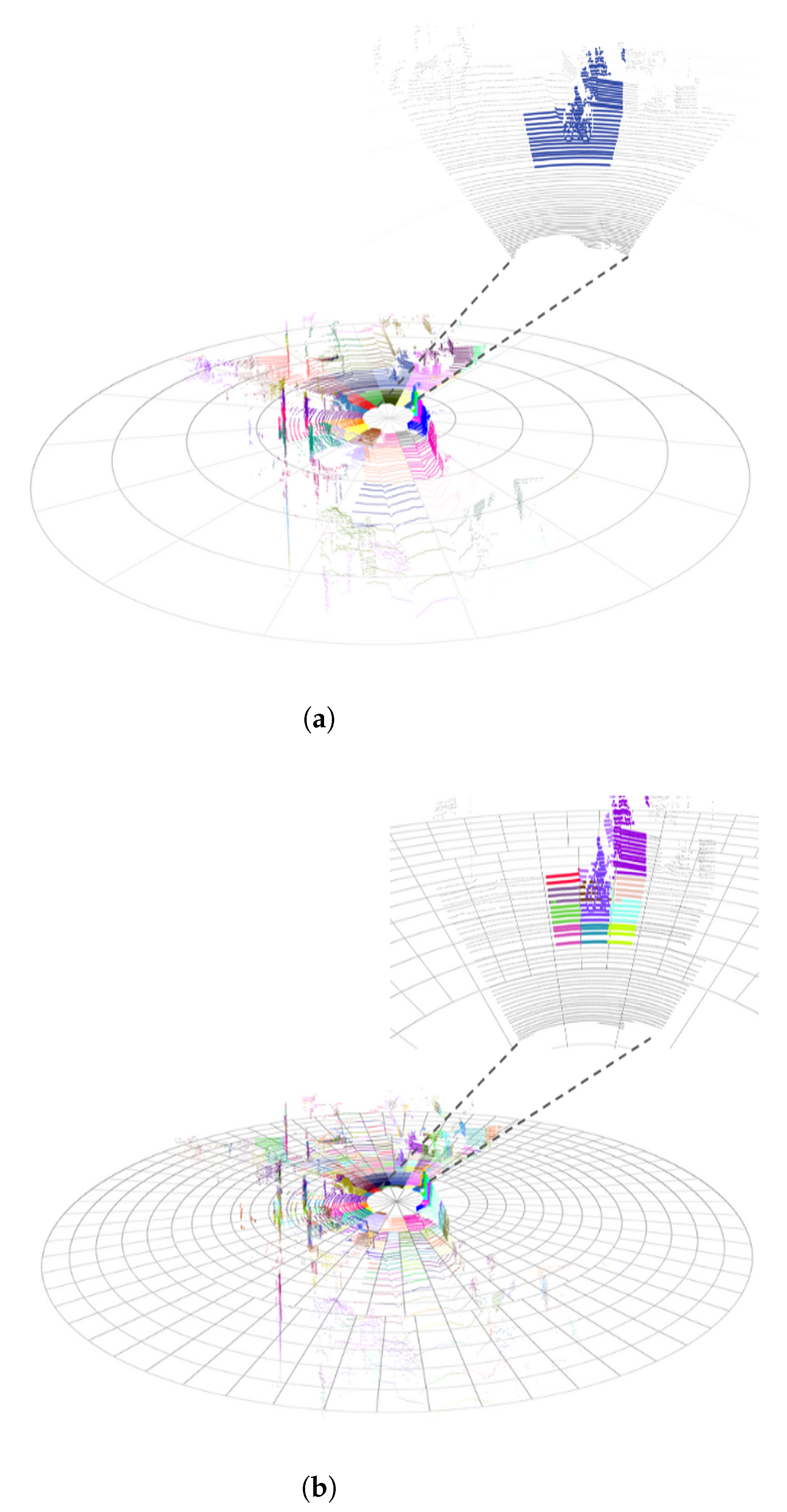
To address these challenges, we propose a hierarchical multi-resolution polar discretization framework comprising N distinct resolution levels. To illustrate the disparities among various resolutions, refer to Figure 3. The level of discretization, as illustrated in Figure 3a, demonstrates a uniform resolution, signifying a coarser discretization, with individual cells encompassing larger spatial domains equidistant from the sensor origin. Conversely, the finest granularity is achieved at Level , as demonstrated in Figure 3b, where high-resolution cells enable the precise localization of terrain features. The framework’s adaptive granularity allows the progressive refinement of geometric feature isolation, critical for robust ground plane detection.
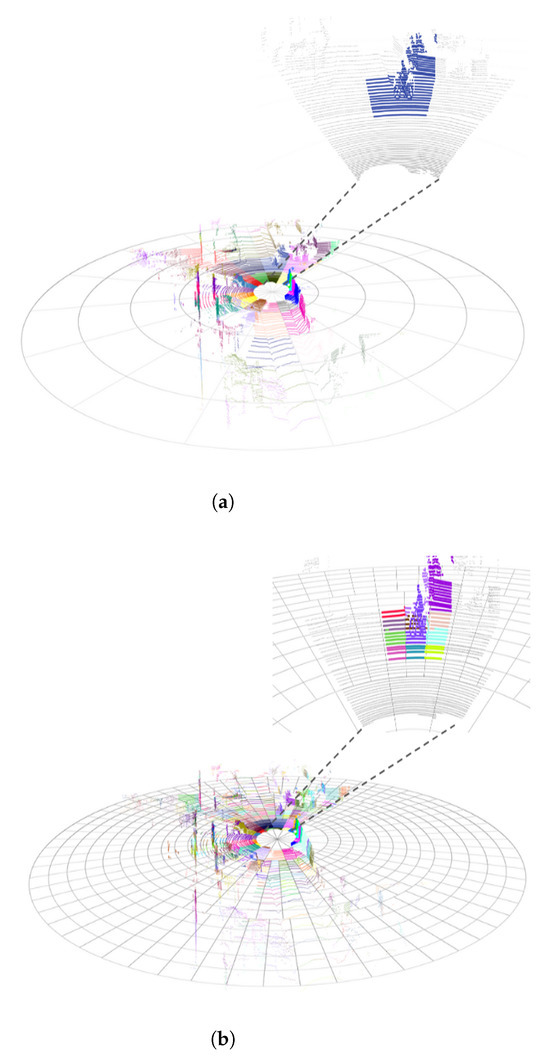
Figure 3.
Multi-resolution polar grid overview. (a) Uniform resolution grid. (b) Variable resolution grid.
Contextual Refinement Stage
For each resolution level, sectors classified as obstacles by the similarity-based module undergo a neighborhood-centric geometric analysis. This analysis selectively incorporates neighboring sectors that share the same spatial discretization, ensuring alignment within the same area. Consequently, the algorithm aggregates geometric data from the R-adjacent sectors for every unclassified circular sector. Given the possibility of encountering geometries that distort the geometrical study, this work follows the philosophy of [31]. The pipeline implements a three-stage filtering process as follows:
- Height-based point prioritization: It addresses geometric distortions caused by vertical structures (e.g., vegetation and walls) by selectively retaining low-elevation points as candidates for traversable ground plane estimation.
- Robust plane estimation: The retained points serve as seeds for traversable ground plane estimation via PCA. The optimal plane , where n is the normal vector and d the planar offset.
- Geometric consistency validation: Given that the point-plane distance, , is a relative quantity contingent on the plane’s orientation and offset (normal vector n and d, respectively) and the dynamic threshold, derived from seed point elevations, , is an absolute measure, where is the mean elevation, is the standard deviation of elevation seeds and k is a statistical confidence parameter; the direct comparison of and is dimensionally inconsistent, as they encode distinct physical and statistical phenomena. To establish a valid decision framework, we normalize the distance by the standard deviation . This normalization converts geometric deviations into unitless multiples of the standard deviation, where k determines how many standard deviations away from the mean, , the threshold should be set. This allows for controlling the sensitivity of the threshold to outliers or deviations, Equation (5). By expressing deviations in terms of statistical significance, this approach bridges geometric and empirical criteria, ensuring cross-domain compatibility and interpretable validation.
The process is described in detail in Algorithm 2.
| Algorithm 2 Ground segmentation via multi-resolution polar discretization |
|
3.4. Sparse Convolutional Neural Network
As previously stated in Section 2.4, sparse convolutional neural networks are becoming the most predominant approach to process point clouds in recent years. Thus, given any point cloud, B, a sparse vector S is defined according to Equation (6), as a set of coordinates, , describing the cloud after applying a part-integer function and a scaling factor, v, that determines the degree of discretization of the space. Furthermore, the sparse vectors enable the storage of feature vectors, , associated with all the discretized spaces represented. The calculation of these values is derived from the weighting of the feature vectors, , of each point that is encompassed in a discretized space, . The processing of the input data is carried out using the Minkowski Engine library (https://github.com/NVIDIA/MinkowskiEngine, accessed on 3 April 2025) [52].
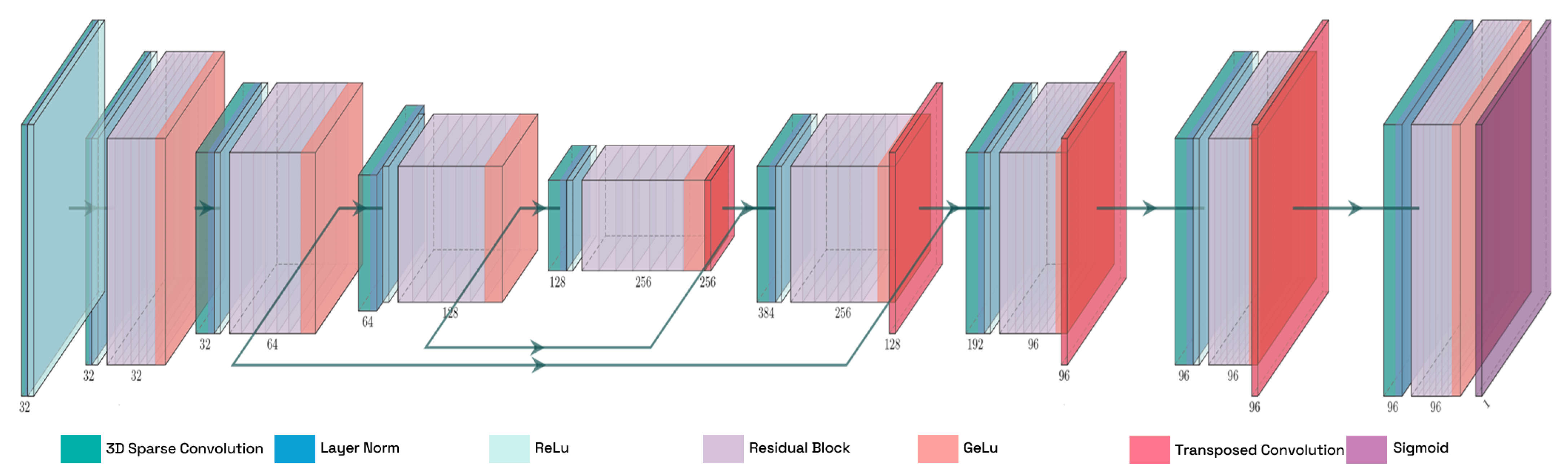
Figure 4 illustrates TE-NeXt architecture [15], which is the sparse network employed through the proposed method. TE-NeXt is a dedicated convolutional neural network, specifically designed for the 3D semantic segmentation of point clouds, with a particular emphasis on the estimation of traversability. TE-NeXt builds upon the U-Net style architecture [53], replacing the standard residual blocks, introduced by classical ResNet networks [54], with a proprietary block inspired by ConvNeXt [51] design principles. This block demonstrates greater abstraction than classical ResNet blocks since it allows the employment of large 3D kernel sizes to model long-range dependencies combined with linear convolutions that reduce computational cost, allow cross-channel mixing and adjust dimensions for skip connections.
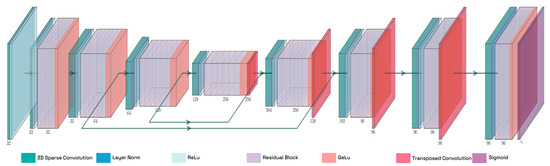
Figure 4.
Detailed illustration of the TE-NeXt architecture. A LiDAR point cloud is subjected to the extraction of descriptors at varying resolutions on the left-hand side of the image. Once the information has been encoded, the initial dimensions are recovered in order to obtain a label for each given point.
4. Datasets and Experimental Setup
In order to perform a quantitative evaluation of the performance of the proposed method, a comparison is made against two publicly available and widely recognized datasets in autonomous navigation research, as follows:
- SemanticKITTI [55]: It represents a comprehensive large-scale dataset for LiDAR-based semantic scene understanding, extending the KITTI Vision Odometry Benchmark [56]. This benchmark offers dense per-point semantic annotations across the full 360° field of view captured by the Velodyne HDL-64E LiDAR sensor, with over 43,000 LiDAR scans from 22 sequences. The sequences cover a variety of highly structured environments including city streets, residential areas, highways, and countryside roads.
- Rellis-3D [57]: It is a multimodal dataset explicitly designed for off-road robotic perception and autonomous navigation, serving as a critical counterpart to urban-centric autonomous driving benchmarks. The dataset comprises 13,556 annotated LiDAR scans organized into five sequences, acquired using an Ouster OS1-64 sensor. Each sequence captures unstructured natural terrains—including vegetated slopes, gravel paths, and muddy surfaces—under varying illumination and weather conditions.
The evaluation framework is presented in Table 1, in which the previously mentioned datasets can be observed. In addition to these datasets, an alternative method of validation has been developed. Two datasets have been captured in real and very different contexts in order to validate the generalization of the algorithm. The experiments are based on structured and unstructured environments, in the cities of Elche (Spain) and Coimbra (Portugal), respectively. More specifically, the datasets have been collected as follows:

Table 1.
Summary of the datasets employed in the evaluation.
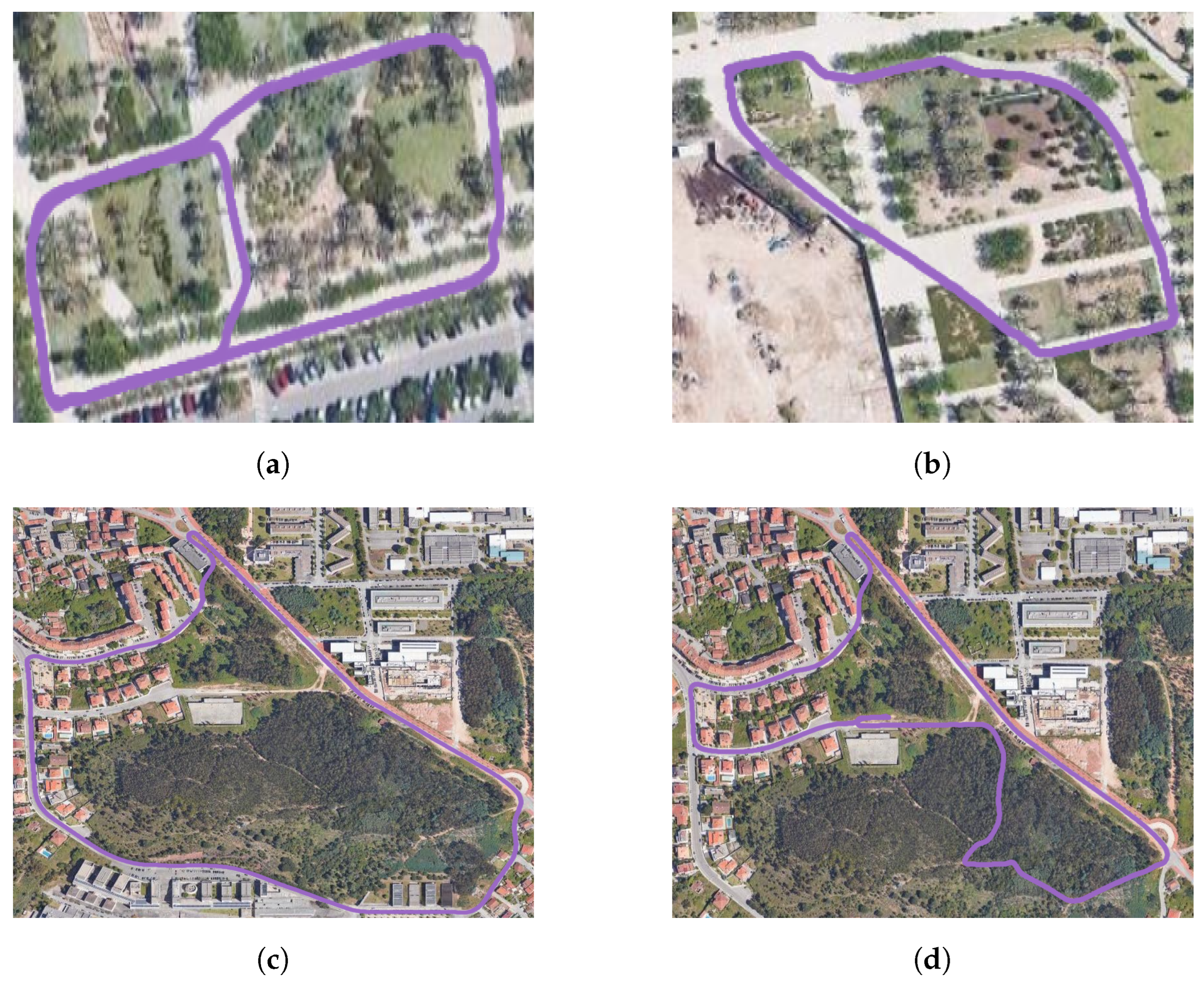
- UMH-Gardens: The study focuses on two sequences situated within the university campus of the Miguel Hernández University of Elche, utilizing the HUSKY A-200 robotic platform. This platform is equipped with an Ouster OS1-128 LiDAR and a georeferenced system with real-time kinematic (RTK) technology, ensuring centimetric precision in measurement. The trajectories followed to capture these sequences are shown in Figure 5a,b.
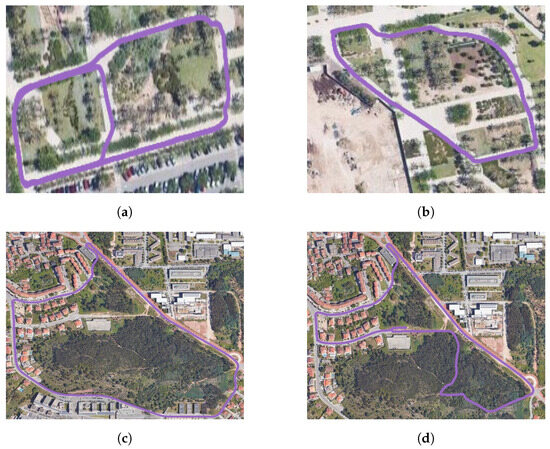 Figure 5. Representation of the data collected. (a,b) Traversed environments within the University of Elche campus. (c,d) Environments captured within the city of Coimbra. The trajectories followed are colored in purple
Figure 5. Representation of the data collected. (a,b) Traversed environments within the University of Elche campus. (c,d) Environments captured within the city of Coimbra. The trajectories followed are colored in purple .
.
- Coimbra-Liv: This dataset has been captured using a combustion vehicle with the aim of covering a large area of forest in the surroundings of the city of Coimbra. The vehicle was equipped with a LiDAR Livox HAP sensor, which stands out because of its high angular resolution, though at the expense of a reduced horizontal field of view. Furthermore, the vehicle was also equipped with an enclosed multi-dual-frequency RTK GNSS receiver, which has been designed for use in outdoor environments and is capable of providing centimeter-accurate positioning. The trajectories followed in these experiments are illustrated in Figure 5c,d.
5. Results and Discussion
The evaluation is conducted across two distinct environmental contexts to rigorously assess generalization. First, structured urban environments are analyzed, ensuring equitable comparison with state-of-the-art methods. These settings are characterized by geometric regularity (e.g., flat roads and vertical curbs), which facilitates direct performance comparison with existing geometric and learning-based approaches. Secondly, unstructured natural terrains are evaluated in order to quantify robustness in geometrically inconsistent scenarios.
As a complement to the quantitative benchmarks, this article presents qualitative results for the custom-captured UMH-Gardens and Coimbra-Liv datasets introduced in Figure 5. These proprietary datasets, acquired in mixed urban–natural environments, provide a realistic case study for validating the efficacy of the proposed method under real-world conditions.
5.1. Evaluation Metrics
The proposed method and other competitive state-of-the-art methods are evaluated on the following three widely used metrics: precision, recall, and the F1-score. In this context, precision measures the proportion of correctly classified ground points (true positives, TP) relative to all points predicted as ground, . It evaluates the model’s ability to avoid false positives (FP), which is particularly critical in safety-critical applications like autonomous navigation, where misclassifying obstacles as ground can lead to dangerous outcomes. Recall measures the proportion of correctly classified ground points relative to all actual ground points in the dataset, . It reflects the model’s ability to identify all ground points, minimizing the false negatives (FN) and ensuring that critical terrain features are not missed. The F1-score is the harmonic mean of precision and recall, , providing a single metric that balances these two aspects. It is particularly useful when there is an imbalance between FP and FN, as it penalizes extreme values in either metric.
5.2. Quantitative Evaluation
5.2.1. Results in Structured Environments
Structured environments are defined as urban areas that are generally created under human supervision and therefore stand out for their regular geometries. Table 2 presents the results of the traversable ground segmentation methods evaluated on the SemanticKITTI dataset [55]. The proposed method is implemented in the following two distinct versions:

Table 2.
Traversable ground estimation performance of methods in urban environments (SemanticKITTI).
- Pure geometric version: Relies exclusively on geometric heuristics derived from multi-resolution polar discretization and adaptive thresholding.
- Hybrid geometric-SCNN version: Combines geometric heuristics with TE-NexT [15] to address regions where geometric distortions prevent reliable heuristic-based classification.
The pure geometric version achieves the highest precision (95.1%) among all methods, demonstrating its ability to minimize false positives by strictly adhering to geometric rules. However, this is achieved at the cost of a low recall (88.0%), which leads to false negatives in complex regions, such as sloped surfaces or areas with sparse point distributions. In contrast, the hybrid version successfully mitigates this trade-off by exploiting the SCNN to refine ambiguous regions where heuristic-based methods obtain low precision. This approach significantly improves recall (96.3%) while maintaining high precision (94.5%), resulting in an F1-score of 95.4%. While Patchwork++ achieves the highest recall (99.3%), its lower precision (73.23%) leads to a reduced F1-score compared to the proposed hybrid method.
To address the demands of real-world applications, Table 3 presents a detailed comparison of the performance of both variants of the method (pure geometric and hybrid geometric-SCNN), together with the best performing state-of-the-art method, P-SVM2, on all SemanticKITTI sequences. We conduct a comprehensive scene migration experiment designed to evaluate the method’s robustness across diverse structured environments with limited training data. The hybrid variant is exclusively trained on the SemanticKITTI sequence 08. Following our previous analysis, the experimental results reveal distinct performance characteristics between the pure geometric and hybrid variants. The geometric method achieves superior precision scores, demonstrating its effectiveness in minimizing false positives through strict geometric constraints. However, this conservative classification strategy has been shown to have a significant impact on the system’s recall performance, as it frequently misclassifies legitimate traversable ground points in complex or ambiguous regions as obstacles. The hybrid geometric-SCNN approach, conversely, exhibits more balanced performance metrics. While its precision does not exceed that of the pure geometric variant, it achieves substantially higher recall rates, since it learns from features to decide ambiguous cases. This balanced trade-off is reflected on its superior F1-score, indicating greater overall segmentation reliability.

Table 3.
Generalization comparison of the proposed method on the SemanticKITTI database (structured environments).
5.2.2. Results in Unstructured Environments
Following the same methodology described in the previous section, Table 4 presents the performance of the proposed method in unstructured environments, such as natural terrains. To the best of our knowledge, there exist no results previously published on the traversable ground segmentation on unstructured datasets such as the Rellis-3D or any other similar dataset. Consequently, given the scarcity of robust approaches specifically designed for these challenging scenarios, the comparison is more limited. The table includes results from the two variants of the proposed method (previously explained), as well as those from a sparse convolutional neural network (TE-NeXt) and classical approaches such as RANSAC.

Table 4.
Traversable ground estimation performance of methods in natural environments (Rellis-3D).
As observed in structured environments, the purely geometric variant of the proposed method demonstrates the highest precision, achieving a value of 78.6%. This result is expected due to the restrictive nature of geometric constrains when classifying traversable ground points. On the contrary, both versions that incorporate neural networks report significantly lower precision values, indicating that their predictions generate a considerable number of false positives. In unstructured environments, this limitation can be particularly critical for safety-demanding applications, where false positives may lead to the misclassification of obstacles as traversable terrain.
Similarly to the findings observed in structured environments (Section 5.2.1), the recall metrics of learning-based methods demonstrate a higher efficacy, with values approaching 91%, which signifies the inference of fewer false negatives. In terms of metric stability, the geometric approach demonstrates the most balanced performance, achieving an F1-score of 80.77%, reflecting its robustness and reliability across diverse sequences. The hybrid method closely follows, with an F1-score of 75.8%, while TE-NeXt achieves a score of 76.8%. These results highlight the importance of balancing precision and recall in safety-demanding applications like autonomous navigation in unstructured terrains.
Table 5 presents the performance of the proposed methods across individual test sequences in the Rellis-3D dataset, excluding sequence 04, which was used for training the neural network in the comparison. The results provide a detailed breakdown of precision, recall, and F1-score for each sequence, offering insights into the behavior of both geometric and learning-based approaches under varying terrain conditions.

Table 5.
Generalization comparison of the proposed method on the Rellis-3D database (unstructured environment).
The geometric approach consistently achieves the highest precision across all test sequences, with values ranging from 72.0% to 93.6%, and an overall precision of 78.6%. This result highlights its restrictive nature when classifying traversable points, as it minimizes false positives by confidently rejecting obstacles points. However, this conservative characteristic comes at the cost of recall, where the geometric method lags behind other approaches. The trade-off between precision and recall is evident in learning-based methods, which tend to classify more points as traversable, including false positives. This bias reduces false negatives but increases false positives, leading to lower precision scores (e.g., TE-NeXt achieves 66.2% overall precision). Unlike in structured environments, the hybrid approach does not generate the best overall results (F1-score), mainly due to the absence of well-defined geometries that allow the neural networks to establish discriminative patterns between the inferred classes.
5.3. Qualitative Evaluation
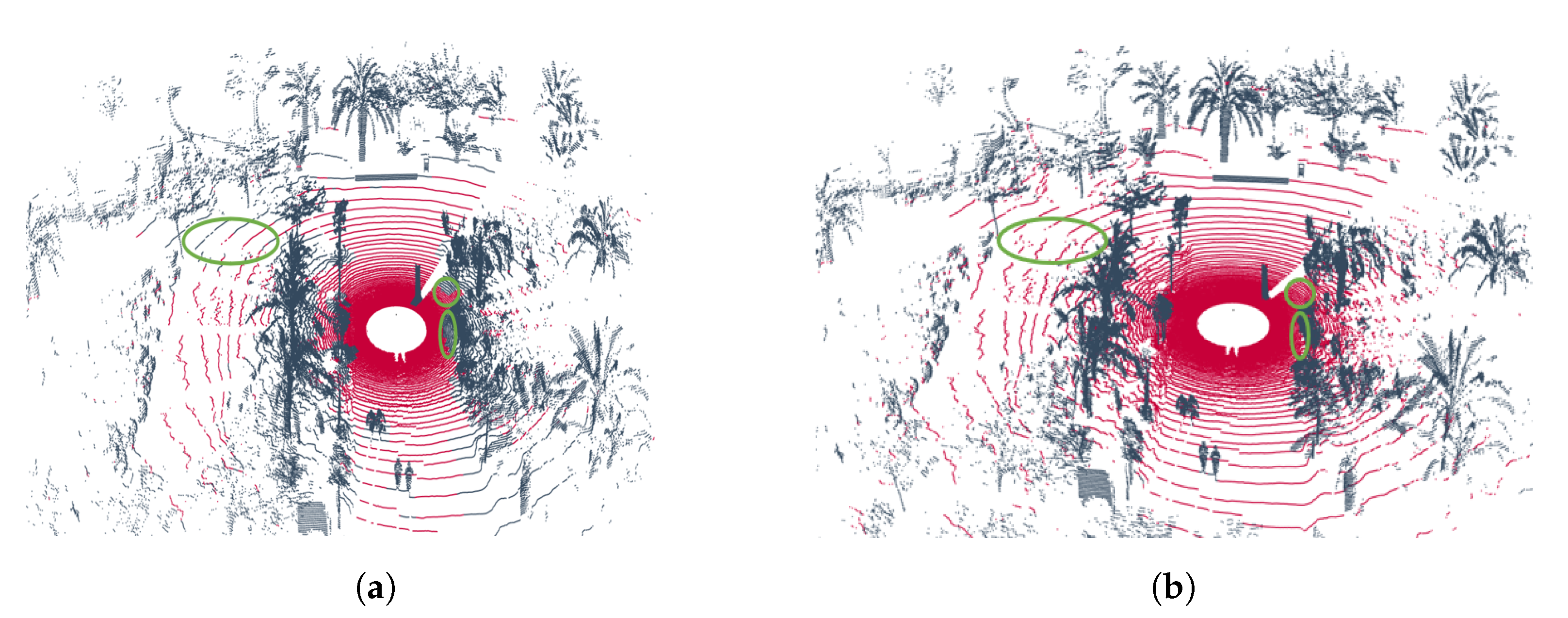
As illustrated in Figure 6, the output point clouds generated by the two variants introduced in the previous section, the geometric version and the hybrid version, are based on samples collected from the two trajectories that define the UMH-Gardens experiment. Specifically, Figure 6a,c corresponds to the results of the purely geometric approach, while Figure 6b,d shows the output of the hybrid method described in Figure 1.
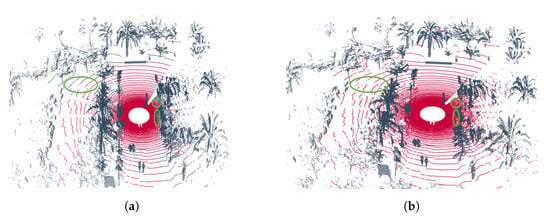
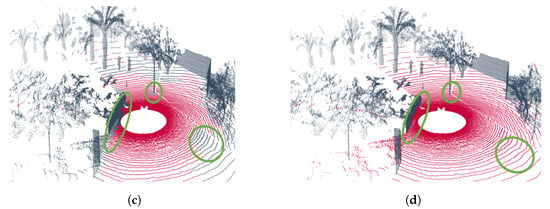
Figure 6.
Results of the UMH-Gardens experiment. (a) Point cloud labeled using the pure geometric method from the UMH-Gardens dataset on the trajectory shown in Figure 5a. (b) Point cloud labeled using the hybrid method from the UMH-Gardens dataset on the trajectory shown in Figure 5a. (c) Point cloud labeled using the pure geometric method from the Coimbra-Liv dataset on the trajectory shown in Figure 5b. (d) Point cloud labeled using the hybrid method from the Coimbra-Liv dataset on the trajectory shown in Figure 5b. The points classified as ground are represented in  , and the points classified as non-ground are represented in
, and the points classified as non-ground are represented in  .
.
 , and the points classified as non-ground are represented in
, and the points classified as non-ground are represented in  .
.
In these figures, one can observe the previously mentioned facts from Section 5.2.1, in which the results were discussed. In structured environments, the geometric version generates numerous false negatives, highlighted in green circles throughout Figure 6a,c, due to the lack of flexibility of the geometric heuristics. Conversely, the hybrid version employs a neural network in these areas that has been geometrically discarded as ground and re-evaluates them, Figure 6b,d. Additionally, it is observed that despite employing polar discretization that offers advantages over dispersion, in distant areas, minor distortions result in the misclassification of ground points.
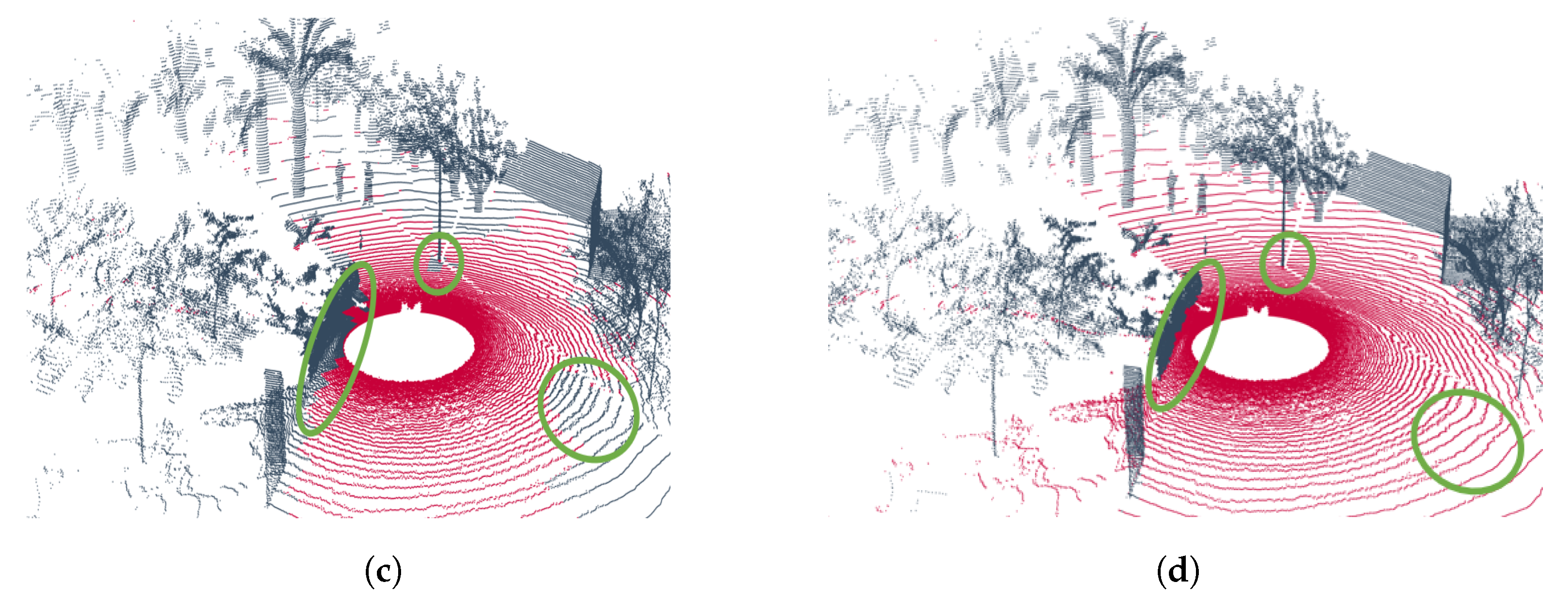
Figure 7 illustrates the results obtained from the Coimbra-Liv experiment, which was designed to evaluate performance in semi-structured and unstructured environments. Figure 7a,b emphasizes the errors previously discussed in Section 5.2.2. Specifically, the geometric variant exhibits a tendency to generate false negatives (low recall) in regions that should be classified as traversable ground, highlighting its restrictive nature.


Figure 7.
Results of the Coimbra-Liv experiments. (a) Point cloud segmented using the geometric method on the trajectory shown in Figure 5c. (b) Point cloud segmented using the hybrid method on the trajectory shown in Figure 5c. (c) Point cloud segmented using the geometric method on the trajectory shown in Figure 5d. (d) Point cloud segmented using the hybrid method on the trajectory shown in Figure 5d. The points classified as ground are represented in  , and the points classified as non-ground are represented in
, and the points classified as non-ground are represented in  .
.
 , and the points classified as non-ground are represented in
, and the points classified as non-ground are represented in  .
.
Conversely, the hybrid variant addresses this issue by introducing a bias toward traversable ground classification (reducing false negatives but increasing false positives). This effect is evident at the boundaries of the car geometry in Figure 7b, where the points are incorrectly classified as traversable ground. Consequently, the learning-based approach achieves lower precision due to an increase in false positives.
The same behavior is observed in Figure 7c,d, where the highlighted regions indicate areas where the hybrid method generates false positives. These results highlight the trade-off between precision and recall in hybrid approaches, especially in complex environments.
6. Conclusions
This paper has presented a hybrid traversable ground segmentation method for point clouds, combining geometric heuristics with deep learning techniques. Inspired by self-supervised learning methodologies, the proposed approach incorporates a similarity search module based on prior knowledge to perform an initial classification. Subsequently, multi-resolution polar discretizations are employed to apply geometric heuristics to refine the segmentation process. Finally, the incorporation of a sparse convolutional neural network technique is intended to enhance the flexibility of the final outcome, particularly with regard to points classified as ground. This approach is motivated by the observation that the geometric study imposes significant restrictions on the segmentation process.
The experiments focus on two versions of the proposed method as follows: the purely geometric variant and the hybrid variant. The findings highlight that both approaches exhibit distinct advantages and limitations depending on the environment in which they operate. In structured environments, the hybrid version achieves an F1-score of 95.4%, outperforming the geometric variant, which achieves 91.2%. This improvement is attributed to the restrictive nature of geometric heuristics when applied to point cloud data, where measurements are often distorted due to light reflection or sensor noise, leading to a high number of false negatives.
Conversely, in natural environments where geometries are diffused and clearly separating traversable ground points is a non-trivial task, the geometric variant demonstrates better metric balance, achieving an F1-score of 80.8% compared to 75.8% for the hybrid method. The flexibility that benefits the hybrid approach in structured settings becomes a disadvantage in natural terrains, as its less restrictive classification criteria lead to reduced performance under such conditions. Nonetheless, the hybrid approach confers higher reliability in terms of recall, which benefits non-critical approaches that require a higher spatial resolution at the cost of precision.
Future work will include the addition of visual information through a LiDAR-camera system, which will allow visual features to be introduced into the sparse tensors. Possibly with the aim of mitigating the main problem of supervised learning—the annotation process—we will investigate the usage of a hybrid method that allows the continuous estimation of traversability.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, A.S. and E.H.; validation, A.S., D.V., and A.G.; formal analysis, A.S.; investigation, A.S.; resources, A.S.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, D.V, A.G., and C.V.; visualization, A.S.; supervision, D.V. and A.G.; project administration, D.V. and A.G.; funding acquisition, D.V., A.G., and C.V. All authors have read and agreed to the published version of the manuscript.
Funding
MICIU/AEI/10.130-39/501100011033: TED2021-130901B-I00; European Union NextGenerationEU/PRTR: TED2021-130901B-I00; MICIU/AEI/10.13039/501100011033: PID2023-149575OB-I00; FEDER, UE: PID2023-149575OB-I00; Fundação para a Ciência e a Tecnologia: UIDB/50022/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available: https://github.com/ARVCUMH/hybrid_geometric_neural_traversability.git (accessed on 3 April 2025).
Acknowledgments
This research work is part of the project TED2021-130901B-I00, funded by MICIU/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR. It is also part of the project PID2023-149575OB-I00, funded by MICIU/AEI/10.13039/501100011033 and by FEDER, UE. Finally, national funds sponsored this research through FCT—Fundação para a Ciência e a Tecnologia—under project base funding (reference: UIDB/50022/2020), DOI: 54499/UIDB/50022/2020.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kabir, M.M.; Jim, J.R.; Istenes, Z. Terrain detection and segmentation for autonomous vehicle navigation: A state-of-the-art systematic review. Inf. Fusion 2025, 113, 102644. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man. Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Almeida, C.M.D.; Monteiro, A.M.V.; Câmara, G.; Soares-Filho, B.S.; Cerqueira, G.C.; Pennachin, C.L.; Batty, M. GIS and remote sensing as tools for the simulation of urban land-use change. Int. J. Remote Sens. 2005, 26, 759–774. [Google Scholar] [CrossRef]
- Moravec, H.; Elfes, A. High resolution maps from wide angle sonar. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 116–121. [Google Scholar]
- Langer, D.; Rosenblatt, J.; Hebert, M. A behavior-based system for off-road navigation. IEEE Trans. Robot. Autom. 1994, 10, 776–783. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3D euclidean signed distance fields for on-board mav planning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1366–1373. [Google Scholar]
- Han, L.; Gao, F.; Zhou, B.; Shen, S. Fiesta: Fast incremental euclidean distance fields for online motion planning of aerial robots. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 4423–4430. [Google Scholar]
- Sun, P.; Zhao, X.; Xu, Z.; Wang, R.; Min, H. A 3D LiDAR data-based dedicated road boundary detection algorithm for autonomous vehicles. IEEE Access 2019, 7, 29623–29638. [Google Scholar] [CrossRef]
- Wang, G.; Wu, J.; He, R.; Yang, S. A point cloud-based robust road curb detection and tracking method. IEEE Access 2019, 7, 24611–24625. [Google Scholar] [CrossRef]
- Adnan, M.; Slavic, G.; Martin Gomez, D.; Marcenaro, L.; Regazzoni, C. Systematic and comprehensive review of clustering and multi-target tracking techniques for LiDAR point clouds in autonomous driving applications. Sensors 2023, 23, 6119. [Google Scholar] [CrossRef]
- Fan, L.; Xiong, X.; Wang, F.; Wang, N.; Zhang, Z. Rangedet: In defense of range view for LiDAR-based 3D object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2918–2927. [Google Scholar]
- Wu, J.; Xu, H.; Tian, Y.; Pi, R.; Yue, R. Vehicle detection under adverse weather from roadside LiDAR data. Sensors 2020, 20, 3433. [Google Scholar] [CrossRef]
- Santo, A.; Cabrera, J.J.; Valiente, D.; Viegas, C.; Gil, A. TE-NeXt: A LiDAR-Based 3D Sparse Convolutional Network for Traversability Estimation. arXiv 2024, arXiv:2406.01395. [Google Scholar]
- Cross, G.R.; Jain, A.K. Markov random field texture models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 1, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Morris, D.D.; Fu, R. Ground segmentation based on loopy belief propagation for sparse 3D point clouds. In Proceedings of the 2015 International Conference on 3D Vision, Lyon, France, 19–22 October 2015; pp. 615–622. [Google Scholar]
- Huang, W.; Liang, H.; Lin, L.; Wang, Z.; Wang, S.; Yu, B.; Niu, R. A fast point cloud ground segmentation approach based on coarse-to-fine Markov random field. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7841–7854. [Google Scholar] [CrossRef]
- Vasudevan, S.; Ramos, F.; Nettleton, E.; Durrant-Whyte, H. Gaussian process modeling of large-scale terrain. J. Field Robot. 2009, 26, 812–840. [Google Scholar] [CrossRef]
- Chen, T.; Dai, B.; Liu, D.; Song, J. Sparse Gaussian process regression based ground segmentation for autonomous land vehicles. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 3993–3998. [Google Scholar]
- del Pino, I.; Santamaria-Navarro, A.; Zulueta, A.G.; Torres, F.; Andrade-Cetto, J. Probabilistic graph-based real-time ground segmentation for urban robotics. IEEE Trans. Intell. Veh. 2024, 9, 4989–5002. [Google Scholar] [CrossRef]
- Liu, H.; Song, R.; Zhang, X.; Liu, H. Point cloud segmentation based on Euclidean clustering and multi-plane extraction in rugged field. Meas. Sci. Technol. 2021, 32, 095106. [Google Scholar] [CrossRef]
- Fischler Furthermore, M. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Steinke, N.; Goehring, D.; Rojas, R. Groundgrid: LiDAR point cloud ground segmentation and terrain estimation. IEEE Robot. Autom. Lett. 2023, 9, 420–426. [Google Scholar] [CrossRef]
- Oh, M.; Jung, E.; Lim, H.; Song, W.; Hu, S.; Lee, E.M.; Park, J.; Kim, J.; Lee, J.; Myung, H. TRAVEL: Traversable ground and above-ground object segmentation using graph representation of 3D LiDAR scans. IEEE Robot. Autom. Lett. 2022, 7, 7255–7262. [Google Scholar] [CrossRef]
- Hui, Z.; Jin, S.; Xia, Y.; Nie, Y.; Xie, X.; Li, N. A mean shift segmentation morphological filter for airborne LiDAR DTM extraction under forest canopy. Opt. Laser Technol. 2021, 136, 106728. [Google Scholar] [CrossRef]
- Song, H.; Jung, J. An object-based ground filtering of airborne LiDAR data for large-area dtm generation. Remote Sens. 2023, 15, 4105. [Google Scholar] [CrossRef]
- Himmelsbach, M.; Hundelshausen, F.V.; Wuensche, H.J. Fast segmentation of 3D point clouds for ground vehicles. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 560–565. [Google Scholar]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast segmentation of 3D point clouds: A paradigm on LiDAR data for autonomous vehicle applications. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5067–5073. [Google Scholar]
- Lim, H.; Oh, M.; Myung, H. Patchwork: Concentric zone-based region-wise ground segmentation with ground likelihood estimation using a 3D LiDAR sensor. IEEE Robot. Autom. Lett. 2021, 6, 6458–6465. [Google Scholar] [CrossRef]
- Lee, S.; Lim, H.; Myung, H. Patchwork++: Fast and robust ground segmentation solving partial under-segmentation using 3D point cloud. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 13276–13283. [Google Scholar]
- Deng, W.; Chen, X.; Jiang, J. A Staged Real-Time Ground Segmentation Algorithm of 3D LiDAR Point Cloud. Electronics 2024, 13, 841. [Google Scholar] [CrossRef]
- Dong, L.; Liu, D.; Dong, Y.; Park, B.; Wan, Z. An efficient ground segmentation approach for LiDAR point cloud utilizing adjacent grids. Mach. Vis. Appl. 2024, 35, 108. [Google Scholar] [CrossRef]
- Moosmann, F.; Pink, O.; Stiller, C. Segmentation of 3D LiDAR data in non-flat urban environments using a local convexity criterion. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 215–220. [Google Scholar]
- Bogoslavskyi, I.; Stachniss, C. Fast range image-based segmentation of sparse 3D laser scans for online operation. In Proceedings of the RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 163–169. [Google Scholar]
- Shen, Z.; Liang, H.; Lin, L.; Wang, Z.; Huang, W.; Yu, J. Fast ground segmentation for 3D LiDAR point cloud based on jump-convolution-process. Remote Sens. 2021, 13, 3239. [Google Scholar] [CrossRef]
- Wen, H.; Liu, S.; Liu, Y.; Liu, C. Dipg-seg: Fast and accurate double image-based pixel-wise ground segmentation. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5189–5200. [Google Scholar] [CrossRef]
- Fusaro, D.; Olivastri, E.; Donadi, I.; Evangelista, D.; Menegatti, E.; Pretto, A. Pyramidal 3D feature fusion on polar grids for fast and robust traversability analysis on CPU. Robot. Auton. Syst. 2023, 170, 104524. [Google Scholar] [CrossRef]
- Li, W.; Fusaro, D.; Olivastri, E.; Mosco, S.; Bellotto, N.; Pretto, A. P-SVM2: Enhancing LiDAR-based Traversability Analysis with Augmented Point Cloud Descriptor for Autonomous Mobile Systems. In Proceedings of the 2024 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE International Conference on Robotics, Automation and Mechatronics (RAM), Hangzhou, China, 8–11 August 2024; pp. 352–359. [Google Scholar]
- Guan, T.; Kothandaraman, D.; Chandra, R.; Sathyamoorthy, A.J.; Weerakoon, K.; Manocha, D. Ga-nav: Efficient terrain segmentation for robot navigation in unstructured outdoor environments. IEEE Robot. Autom. Lett. 2022, 7, 8138–8145. [Google Scholar] [CrossRef]
- Sharma, S.; Ball, J.E.; Tang, B.; Carruth, D.W.; Doude, M.; Islam, M.A. Semantic segmentation with transfer learning for off-road autonomous driving. Sensors 2019, 19, 2577. [Google Scholar] [CrossRef]
- Urrea, C.; Vélez, M. Enhancing Autonomous Visual Perception in Challenging Environments: Bilateral Models with Vision Transformer and Multilayer Perceptron for Traversable Area Detection. Technologies 2024, 12, 201. [Google Scholar] [CrossRef]
- Paigwar, A.; Erkent, Ö.; Sierra-Gonzalez, D.; Laugier, C. GndNet: Fast ground plane estimation and point cloud segmentation for autonomous vehicles. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 2150–2156. [Google Scholar]
- He, D.; Abid, F.; Kim, Y.M.; Kim, J.H. SectorGSnet: Sector learning for efficient ground segmentation of outdoor LiDAR point clouds. IEEE Access 2022, 10, 11938–11946. [Google Scholar] [CrossRef]
- Atas, F.; Cielniak, G.; Grimstad, L. From Simulation to Field: Learning Terrain Traversability for Real-World Deployment. arXiv 2025, arXiv:2501.06904. [Google Scholar]
- Frey, J.; Hoeller, D.; Khattak, S.; Hutter, M. Locomotion policy guided traversability learning using volumetric representations of complex environments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 5722–5729. [Google Scholar]
- Ruetz, F.A.; Lawrance, N.; Hernández, E.; Borges, P.V.; Peynot, T. ForestTrav: 3D LiDAR-only forest traversability estimation for autonomous ground vehicles. IEEE Access 2024, 12, 37192–37206. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, T.; Zhang, W.; Pang, J.; Liu, X. Llava-3D: A simple yet effective pathway to empowering lmms with 3D-awareness. arXiv 2024, arXiv:2409.18125. [Google Scholar]
- He, S.; Ding, H.; Jiang, X.; Wen, B. Segpoint: Segment any point cloud via large language model. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September—4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 349–367. [Google Scholar]
- Huang, K.C.; Li, X.; Qi, L.; Yan, S.; Yang, M.H. Reason3D: Searching and reasoning 3D segmentation via large language model. In Proceedings of the International Conference on 3D Vision 2025, Singapore, 25–28 March 2025. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Choy, C.; Gwak, J.; Savarese, S. 4d spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3075–3084. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; proceedings, part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. Semantickitti: A dataset for semantic scene understanding of LiDAR sequences. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9297–9307. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Jiang, P.; Osteen, P.; Wigness, M.; Saripalli, S. Rellis-3D dataset: Data, benchmarks and analysis. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1110–1116. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).